Descriptores específicos de los niveles de Van Hiele en el aprendizaje de la semejanza de polígonos-Specific descriptors Van Hiele levels in learning the similarity of polygons

Descriptores específicos de los niveles de Van Hiele en el aprendizaje de la semejanza de polígonos¹

Specific descriptors Van Hiele levels in learning the similarity of polygons

Níveis de descritores específicos Van Hiele em aprender a semelhança de polígonos

Élgar Gualdrón²

¹Artículo de investigación

²Universidad de Pamplona, Pamplona (Colombia). Contacto: elgargualdron@yahoo.es

Fecha de recepción: enero 2014, Fecha de aceptación: julio de 2014

Resumen

En este artículo se presentan los resultados preliminares de una investigación que estudia las formas y la evolución del razonamiento que tienen los estudiantes al abordar tareas relacionadas con la semejanza. En una primera etapa se elabora una caracterización a priori de los descriptores de nivel de Van Hiele basados en estudios previos de Gualdrón y Gutiérrez (2007), los cuales se confirman y amplían mediante una intervención, usando una unidad de enseñanza diseñada siguiendo las líneas de Lemonidis (1991) y el modelo de razonamiento de Van Hiele siguiendo las líneas de Gutiérrez y Jaime (1998). La muestra del estudio es un grupo de estudiantes de noveno grado (14-15 años) de un colegio de Pamplona, Norte de Santander (Colombia). Los análisis preliminares del conjunto de datos muestran interesantes formas de resolución de ciertas tareas en las cuales los participantes utilizan un lenguaje rico y muestran variadas formas de razonamiento.

Palabras clave: niveles de Van Hiele, matemáticas escolares, geometría, semejanza, homotecia, Teorema de Thales.

Abstract

Preliminary results of an investigation in which are being studied, among other things, the forms and the evolution of reasoning that students have to deal with tasks related to the similarity presented in this work. In a first moment we developed a-priori characterization descriptors Van Hiele level based on previous studies Gualdrón & Gutierrez (2007), which confirmed and extended by an intervention using a teaching unit designed along the lines of Lemonidis (1991) and the model of Van Hiele thinking along the lines of Gutierrez & Jaime (1998). The study sample is a group of ninth graders (14-15 years old) from a college of Pamplona, Norte de Santander (Colombia). Preliminary analyzes show interesting ways of solving certain tasks in which participants use a rich language and show various forms of reasoning.

keywords: Van Hiele levels, School mathematics, Geometry, Similarity, Dilation, Thales theorem.

Resumo

Os resultados preliminares de uma pesquisa em que estão sendo estudados, entre outras coisas, as formas e a evolução do raciocínio que os alunos têm de lidar com tarefas relacionadas com a similaridade. Em primeira instância foi desenvolvida uma caracterização a-priori dos descritores do nível de Van Hiele baseados em estudos prévios Gualdrón e Gutierrez (2007), que foram confirmados e estendidos através de uma intervenção usando uma unidade de ensino seguindo o modelo de Lemonidis (1991) e o modelo de Van Hiele entre os linhamentos de Gutierrez e Jaime (1998). A amostra do estudo é um grupo de alunos do nono ano (14-15 anos) de uma escola de Pamplona, Norte de Santander (Colômbia). Análises preliminares dos dados demostraram formas interessantes de resolver determinadas tarefas em que os participantes usaram uma linguagem rica e mostraram diversas formas de raciocínio.

Palavras-chave: Níveis de Van Hiele, Matemática escolar, Geometria, Similaridade, Homotetia, Teorema de Thales.

Introducción

El proceso de enseñanza-aprendizaje de temas geométricos demanda más investigación dirigida a conocer las formas que tienen los estudiantes de adquirir de manera adecuada y significativa los conocimientos geométricos, particularmente el de semejanza de polígonos (Gualdrón, 2006).

A pesar de que la semejanza es una noción fundamental para muchos argumentos matemáticos y aplicaciones en matemáticas, que debería ser estudiada en detalle (Hansen, 1998; NCTM, 2000), son pocos los estudios que se pueden encontrar. La mayoría de hallazgos sobre el concepto de semejanza están incluidos en estudios sobre razonamiento proporcional, el cual ha sido estudiado extensamente (Hart, 1984; Hart y otros, 1981, 1989; Lamon, 1993; Fernández, 2001; Margarit, Gómez y Figueras, 2001). Se encuentran algunos trabajos que utilizan la semejanza como contexto para estudiar la relación entre el conocimiento profesional del educador de matemáticas de secundaria y su práctica (Escudero y Sánchez, 1999), o se encuentran trabajos que estudian la comprensión de los profesores de primaria en formación del concepto de semejanza (Swoboda y Tocki, 2002; Gerretson, 2004).

Teniendo en cuenta lo expuesto y con la pretensión de que los estudiantes, a partir de situaciones matemáticas concretas, desarrollen su proceso de razonamiento, adquieran y comprendan conceptos y relaciones matemáticas que favorezcan el aprendizaje de la semejanza; además, pretendemos que las situaciones planteadas favorezcan el tránsito de los estudiantes de un nivel de razonamiento a otro superior. Ante este panorama hemos formulado la siguiente pregunta de investigación: ¿cuáles son las características que describen los niveles de razonamiento de Van Hiele para la semejanza?

Marco conceptual

Para realizar el diseño y posterior análisis de las actuaciones de los estudiantes, después de realizar una intervención usando la unidad de enseñanza de la semejanza, se tuvieron en cuenta los estudios de Lemonidis (1991) y el modelo de razonamiento de Van Hiele (Gutiérrez y Jaime, 1998; Gualdrón y Gutiérrez, 2007).

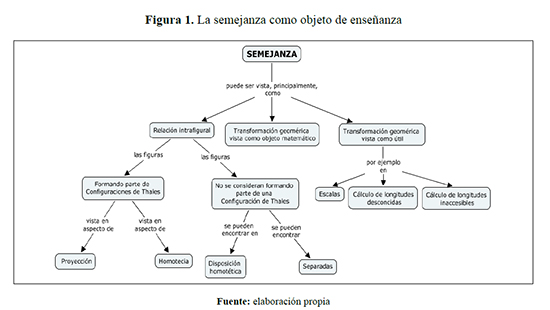
La semejanza como objeto de enseñanza.

Desde el punto de vista de la enseñanza de la semejanza se analizaron los estudios de Lemonidis (1991) y una ampliación al esquema presentado por este autor (Gualdrón, 2008). El esquema caracteriza tres aproximaciones que se consideran importantes al abordar la semejanza como objeto de enseñanza:

a) Relación intrafigural: donde se destaca la correspondencia entre elementos de una figura y los correspondientes de su semejante, estando ausente la idea de transformar una figura en otra. Dentro de esta aproximación distinguen las siguientes situaciones:

• Cuando las figuras forman parte de una configuración de Thales, en la que se consideran los aspectos de proyección y homotecia, con sus correspondientes razones.

• Cuando las figuras no se consideran formando una configuración de Thales, en la que se considera a las figuras separadas y en disposición homotética.

b) Transformación geométrica vista como útil: La transformación geométrica se percibe como una aplicación del conjunto de los puntos del plano en él mismo. Se utiliza la semejanza como útil en la resolución de problemas escalas, cálculo de longitudes desconocidas y cálculo de longitudes inaccesibles.

c) Transformación geométrica vista como objeto matemático: Se caracteriza porque hay un tratamiento en el que se busca la transformación resultante de dos o más transformaciones.

En este sentido, Vasco (1998) plantea que “El currículo colombiano [en geometría] no se apoya en la geometría transformacional”. Además, plantea que el enfoque de enseñanza de la semejanza por transformaciones se dirige más a la matemática vista como ciencia y no está guiada por los aspectos psicológicos del aprendizaje de las matemáticas. En consecuencia, y dadas las edades de los estudiantes en las que se desarrollará el estudio (14-15 años), se decide contemplar únicamente la relación intrafigural y la transformación geométrica vista como útil. El siguiente esquema muestra un resumen de la forma como la semejanza puede ser abordada cuando se la trata como objeto de enseñanza.

El modelo de razonamiento de Van Hiele.

El modelo de Van Hiele (Van Hiele, 1957; Usiskin, 1982; Burger y Shaughnessy, 1986; Gutiérrez y Jaime, 1996) es un excelente referente teórico para la organización y evaluación de la enseñanza y el aprendizaje de la geometría. Un buen ejemplo de ello es NCTM (2000). Este modelo, desde su aparición, ha sido ampliamente estudiado, no solamente en su aplicación (Jaime, 1993; Guillén 1997; Ding y Jones, 2006) sino también en su ampliación y mejoramiento (Gutiérrez, Jaime y Fortuny, 1991; Gutiérrez y Jaime, 1998). No obstante, la semejanza es un tema de geometría en el que la investigación sobre la aplicación del modelo de Van Hiele es muy limitada (Gualdrón, 2006). En esta investigación se han utilizado los descriptores de nivel que resultaron de tener en cuenta estudios previos de Gualdrón (2006) y una ampliación de estos. El modelo intenta explicar cómo progresan los estudiantes en su habilidad de razonamiento geométrico e incluye dos aspectos importantes:

Primer aspecto, el Descriptivo, en cuanto que intenta explicar cómo razonan los estudiantes. Esto se hace a través de la definición de cuatro “niveles de razonamiento”(por ejemplo, Jaime y Gutiérrez, 1990, Burger y Shaughnessy, 1986).

• Primer nivel: la consideración de los conceptos es global. No se tienen en cuenta elementos ni propiedades.

• Segundo nivel: la característica fundamental es que los conceptos se entienden y manejan a través de sus elementos.

• Tercer nivel: la característica básica de este nivel consiste en el establecimiento de relaciones entre propiedades.

• Cuarto nivel: está caracterizado por la comprensión y el empleo del razonamiento formal, aspiración de todo profesor para sus estudiantes de enseñanza secundaria.

Segundo aspecto, el Prescriptivo, porque da unas pautas a seguir en la organización de la enseñanza para lograr que los estudiantes progresen en su forma de razonar. Esto se lleva a cabo mediante la consideración de cinco “fases de aprendizaje”(por ejemplo, Jaime y Gutiérrez, 1990, Burger y Shaughnessy, 1986).

• Fase primera (Información): su finalidad es la obtención de información recíproca profesor alumno.

• Fase segunda (Orientación dirigida): el profesor dirige a los alumnos para que éstos vayan descubriendo, lo cual constituye la esencia de ese nivel.

• Fase tercera (Explicitación): su objetivo es que los estudiantes sean conscientes de las características y propiedades aprendidas anteriormente y consoliden el vocabulario propio del nivel.

• Fase cuarta (Orientación libre): dirigida a consolidar los aspectos básicos del nivel.

• Fase quinta (Integración): tiene como objetivo establecer y completar la red de relaciones objeto de ese nivel para el concepto que se trabaja.

Unidad de enseñanza de la semejanza

La unidad de enseñanza se diseñó con el objetivo de fortalecer la adquisición de los niveles 1, 2 y 3 de Van Hiele, y caracterizar los niveles de razonamiento en el tema de polígonos a partir de la intervención.

En el diseño de las actividades3 se tuvo en cuenta dos aspectos: primero, el tipo de papel sobre el cual se presentaron cada una de las 43 actividades, y segundo, el tipo de figura sobre la que los estudiantes debían trabajar. De esta forma, las tareas fueron escogidas/diseñadas para que los estudiantes trabajaran sobre hojas de papel blanco o cuadriculado y manipularan diversas superficies poligonales,4 tanto cóncavas como convexas. Las tareas contenían problemas de cálculo, problemas de identificación de relaciones, problemas de construcción, y problemas de demostración. Cada actividad fue diseñada para ser presentada en hojas individuales, y sobre las cuales los estudiantes debían justificar cada uno de los procesos que los conducía a la respuesta numérica, gráfica o verbal. Para el desarrollo de cada una de las actividades, los estudiantes podían utilizar reglas, escuadras, cinta métrica, compás, transportador de medidas angulares, tijeras y calculadora. La unidad tenía como característica esencial la enseñanza basada en el descubrimiento guiado basado en las orientaciones del profesor que guía al estudiante sin influir directamente en los razonamientos de los mismos.

Metodología

La investigación propuesta, de tipo cualitativo, se llevó a cabo con 27 estudiantes de noveno grado (14–15 años), del colegio del Rosario de Pamplona. La implementación de la unidad de enseñanza se realizó durante el horario normal de clases en el aula habitual aula de matemáticas del grado noveno; en el desarrollo de cada actividad, primero se trabajó de manera individual y después en grupos de tres estudiantes. La recolección de la información se hizo a través de video grabación en el momento del trabajo individual y en el grupal y de las producciones de los estudiantes las hojas que debían entregar al finalizar cada actividad. El investigador, cuando lo consideraba necesario, realizó algunas entrevistas después de clase a algunos estudiantes con el fin de pedir una ampliación aclaración/justificación a respuestas dadas en las hojas de trabajo. A partir del análisis de las producciones de los estudiantes y los registros fílmicos, se obtuvieron datos cualitativos que permitieron construir la caracterización de los descriptores de los niveles de razonamiento. El profesor titular del curso orientó el desarrollo de las diferentes actividades y el investigador participó como observador participativo.

Análisis y discusión

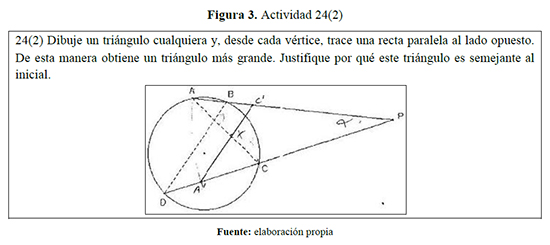
A continuación se presentan algunos de los aspectos relevantes del análisis de los datos recogidos. Se muestran algunos ejemplos representativos de formas de razonamiento y se harán algunos comentarios sobre ellos. En la actividad número 24, como se muestra a continuación, se pedía la justificación de la semejanza de los triángulos formados en las partes 1 y 2; Carlos utiliza la homotecia para justificar la semejanza. Es decir, justifica primero por qué se presenta la homotecia y luego la utiliza para justificar la semejanza

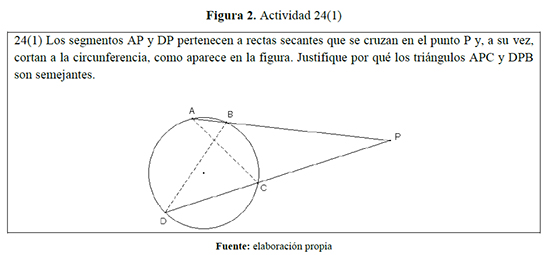
En la actividad 21, como se muestra a continuación, Carlos utiliza el teorema de Thales para justificar la semejanza de los triángulos dispuestos en la figura y luego utiliza una propiedad matemática que han “descubierto”con su profesor “Los triángulos en posición de Thales son semejantes”.

En la actividad 37, como se muestra a continuación, Francisco utiliza el teorema de Thales para justificar la semejanza de los triángulos dispuestos en la figura. Luego, utiliza una correspondencia adecuada, entre figuras semejantes, para justificar que los segmentos BC y AC son iguales.

En los ejemplos presentados, el razonamiento exhibido por los estudiantes se ha clasificado como de nivel 3 de Van Hiele, donde logran demostrar, informalmente, algunas propiedades relacionadas con la semejanza de figuras planas.

Para cada nivel de razonamiento se enunciará a continuación aquellos descriptores iniciales que han sido validados por las respuestas de los estudiantes y los descriptores emergentes obtenidos en la experimentación. Los descriptores marcados con un asterisco son los descriptores emergentes.

Nivel 1. Reconocimiento

Los estudiantes perciben la semejanza de figuras de manera global, por lo que:

1.1. Reconocen figuras semejantes basándose en la apariencia de ellas, es decir, utilizando únicamente estrategias de tipo visual. Pueden presentarse casos en que no reconozcan la semejanza entre dos figuras porque alguna esté girada.

1.2. Ven las figuras como un todo y describen las diferencias y similitudes entre ellas usando términos como “más grandes”, “más pequeños”, “estirados”, “ampliados”. Por ejemplo, cuando un estudiante esté decidiendo sobre la semejanza de dos rectángulos, podría decir “este rectángulo no es tan largo como éste”. También pueden incluir atributos irrelevantes en las descripciones que hacen.

1.3. Empiezan a percibir algunas características matemáticas de la semejanza, pero aún lo hacen de manera aislada. Por ejemplo, algunos pueden tomar medidas de los ángulos y darse cuenta que en las figuras semejantes éstas son iguales, sólo que no lo ven como una condición necesaria para la semejanza.

1.4. Pueden identificar, utilizando argumentos de tipo visual, la semejanza entre figuras cuando pertenecen a una configuración de Thales aspecto de proyección o aspecto de homotecia o están en disposición homotética. 1.5. Pueden identificar y explicar, utilizando argumentos de tipo visual, la semejanza de figuras en mosaicos.

Nivel 2. Análisis

La consideración de la semejanza de figuras a través de sus elementos y propiedades permite a los estudiantes:

2.1. Construir o dibujar figuras semejantes a una figura dada teniendo en cuenta explícitamente aspectos matemáticos como la medida de los ángulos o las longitudes de los lados.

2.2. Determinar aspectos matemáticos específicos de las figuras semejantes, como la proporcionalidad de longitudes de los segmentos y la igualdad de las medidas de los ángulos, así que pueden inducir las condiciones necesarias para que las figuras sean semejantes.

2.3. Descubrir que la posición de las figuras semejantes es irrelevante, es decir, que no es necesario que las figuras semejantes tengan la misma posición.

2.4. Entender que la congruencia de figuras planas es un caso particular de la semejanza de figuras planas.

2.5. Inducir algunas propiedades relacionadas con la semejanza en triángulos rectángulos.

2.6. Comprender que la figura resultante, al aplicar una homotecia, es semejante a la figura dada.

2.7. Relacionar la semejanza de triángulos con el teorema de Thales, comprendiendo que los triángulos en posición de Thales son semejantes.

2.8. Utilizar configuraciones de triángulos en posición de Thales o en disposición homotética con centro de homotecia en un vértice para demostrar relaciones de semejanza entre ellos.

2.9. Realizar construcciones o dibujos de figuras semejantes al darles el factor de semejanza y además predecir si la figura resultante será una ampliación, una reducción o una figura idéntica a la dada. También pueden realizar construcciones o dibujos de figuras semejantes usando homotecias y teorema de Thales.

2.10. Relacionar la razón de semejanza con las escalas. Es decir, comprender que la escala es la razón de semejanza entre una reproducción foto, mapa, plano, entre otros y la realidad que representa dicha reproducción.

2.11. Identificar relaciones de semejanza en figuras planas complejas dos o más figuras planas entrecruzadas.

2.12. Demostrar propiedades relacionadas con la semejanza de figuras verificando que se cumplen en algunos casos.

2.13. Utilizar la definición de semejanza para la solución de situaciones matemáticas, por ejemplo determinar longitudes accesibles o inaccesibles.

2.14. Identificar la semejanza de figuras relacionándolas con la transformación, ampliación y reducción de una figura respecto de otra.

2.15 Comprender que los rectángulos coincidentes en un vértice y que comparten una diagonal son semejantes.

Nivel 3. Abstracción

Al establecer relaciones entre las propiedades y comprender planteamientos generales, los estudiantes consiguen:

3.1. Determinar empíricamente y justificar de manera deductiva informal las condiciones suficientes para la semejanza de rectángulos y triángulos incluyendo criterios AA, LLL, LAL.

3.2. Distinguir entre condiciones suficientes y necesarias para la semejanza de figuras. Por ejemplo, ellos reconocen que, en los triángulos, es suficiente que dos ángulos correspondientes sean iguales para que sean semejantes, mientras que en los demás polígonos no es suficiente dicha condición, pero sí es necesaria.

3.3. Demostrar informalmente algunas propiedades relacionadas con la semejanza de figuras planas.

3.4. Demostrar informalmente situaciones matemáticas relacionadas con la semejanza.

3.5. Plantear más de una demostración informal de propiedades o situaciones matemáticas relacionadas con la semejanza.

Conclusiones

Se han analizado las argumentaciones que los estudiantes propusieron para justificar la semejanza y se ha encontrado que los estudiantes poseen más y mejores herramientas de razonamiento si se hace una comparación con los resultados de estudios previos (Gualdrón, 2006), en donde no se estableció ningún vínculo entre la semejanza y el teorema de Thales y la homotecia. Estos hallazgos sugieren que en la enseñanza del tema se debería establecer un vínculo directo entre la semejanza y la homotecia y el teorema de Thales.

Se ha logrado que la mayoría de los estudiantes alcancen razonamientos hasta de tercer nivel de Van Hiele en la semejanza, lo cual es altamente positivo dado que generalmente, a nivel escolar, estos alcanzan segundo nivel de razonamiento de Van Hiele (Gualdrón, 2006).

Los resultados de este estudio aportan a la literatura sobre formas efectivas de mejoramiento del razonamiento, específicamente, en tareas relacionadas con la semejanza. El análisis cualitativo de los datos permitió confirmar y afinar el listado a priori de descriptores de nivel planteados y, en otros casos, permitió obtener descriptores emergentes.

Referencias

Burger, W. F., and Shaughnessy, J. M. (1986). Characterizing the Van Hiele levels of development in geometry. Journal for Research in Mathematics Education, 17(1), 31-48.

Ding, L., and Jones, K. (2006). Students geometrical thinking development at grade 8 in Shangai. In J. Novotná, H. Moraová, M. Krátká and N. Stehlíková (Eds.), Proceeding of the 30 Conference of the International Group for the Psychology of Mathematics Education, 1, 382.

Escudero, I. and Sánchez, V. (1999). The relationship between professional knowledge and teaching practice: The case of similarity. In O. Zaslavsky (Ed.), Proceedings of the 23rd PME Conference, 2, 305-312.

Fernández, A. (2001). Precursores del razonamiento proporcional: Un estudio con alumnos de primaria. Tesis doctoral. España: Universidad de Valencia.

Gerretson, H. (2004). Pre-service elementary teachers understanding of geometric similarity: The effect of dynamic geometry software. Focus on Learning Problems in Mathematics, 26 (3), 12-23.

Gualdrón, E. (2006). Los procesos de aprendizaje de la semejanza por estudiantes de 9� grado. Memoria de investigación, Departamento de Didáctica de las Matemáticas. España: Universidad de Valencia.

Gualdrón, E. y Gutiérrez, Á. (2007). Una aproximación a los descriptores de nivel de razonamiento de Van Hiele para la semejanza. En M. Camacho, P. Flórez y P. Bolea (Eds.). Memorias del XI Simposio de la Sociedad Española de Investigación en Educación Matemática, 11(1), 369-380.

Gualdrón, E. (2008). Improving the ways of reasoning in similarity in 14 and 15 years old students. In O. Figueras, J.L. Cortina, S. Alatorre, T. Rojano and A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of de PME 20th and PME-NA 32nd Conference, 1, 266.

Guillén, G. (1997). El Modelo de Van Hiele aplicado a la geometría de los sólidos. Observación de procesos de aprendizaje. Tesis doctoral. España: Universidad de Valencia.

Gutiérrez, A., y Jaime, A. (1996). Uso de definiciones e imágenes de conceptos geométricos por los estudiantes de Magisterio. En J. Giménez, S. Llinares y M. V. Sánchez (Eds.), El proceso de llegar a ser un profesor de primaria. Cuestiones desde la educación matemática. Granada: Comares.

Gutiérrez, A., and Jaime, A. (1998). On the assessment of the Van Hiele levels of reasoning. Focus on Learning Problems in Mathematics, 20, 2 y 3, 27-46.

Gutiérrez, A., Jaime, A. and Fortuny, J. M. (1991). An alternative paradigm to evaluate the acquisition of the Van Hiele levels. Journal for Research in Mathematics Education, 22 (3), 237-251.

Hansen, V. L. (1998). Everlasting geometry. In C. Mammana and V. Villani (Eds.), Perspectives on the teaching of geometry for the 21st century. An ICMI study. Dordrecht, Holanda: Kluwer Academic Publishers.

Hart, K. M. and others. (1981). Children‘s understanding of mathematics: 11-16. London: John Murray Ltd.

Hart, K. M. (1984). Ratio: Children‘s strategies and errors. A report of the strategies and errors in secondary mathematics projects. London: NFER-Nelson.

Hart, K. M. and others. (1989). Childrens mathematical frameworks 8-13: A study of classroom teaching. Windsor, G.B.: NFER-Nelson.

Jaime, A. (1993). Aportaciones a la interpretación y aplicación del modelo de Van Hiele: La enseñanza de las isometrías del plano. La evaluación del nivel de razonamiento. Tesis doctoral. España: Universidad de Valencia.

Jaime, A., Chapa, F. y Gutiérrez, �. (1992). Definiciones de triángulos y cuadriláteros: Errores e inconsistencias en libros de texto de E.G.B. Epsilon, 23, 49-62.

Jaime, A. y Gutiérrez, A. (1990). Una propuesta de fundamentación para la enseñanza de la geometría: El modelo de Van Hiele. En S. Llinares y M.V. Sánchez (Eds.), Teoría y Práctica en Educación Matemática. Sevilla: Alfar.

Lamon, S. J. (1993). Ratio and proportion: Connecting content and children‘s thinking. Journal for research in mathematics education, 24, 41-61.

Lemonidis, C. (1991). Analyse et réalisation dune expérience denseignement de lhomothétie. Recherches en Didactique des Mathématiques 11(23), 295-324.

Margarit, J., Gómez, B. and Figueras, O. (2001). Ratio comparison: Performance on ratio in similarity task. Proceedings of the 25th PME Conference, 1, 340.

N.C.T.M. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.

Swoboda, E. and J. Tocki (2002). How to prepare prospective teachers to teach mathematics: Some remarks. Second International Conference on the Teaching of Mathematics (at the undergraduate level), 2, 1-10.

Usiskin, Z. (1982). Van Hiele levels and achievement in secondary school geometry. ERIC: Columbus, USA.

Van Hiele, P. M. (1957). El problema de la comprensión (en conexión con la comprensión de los escolares en el aprendizaje de la geometría). Utrecht, Holanda (Traducción al español para el proyecto de investigación Gutiérrez y otros, 1991). Holanda: Universidad de Utrecht.

Vasco, C. E. (1998). Dynamic geometry in the colombian school curriculum. Perspectives on the teaching of geometry for the 21st century. An ICMI study. C. Mammana and V. Villani. Dordrecht, Holanda, Kluwer Academic Publishers.