DOI:
https://doi.org/10.14483/23448350.7687Published:
10/21/2014Issue:
Vol. 20 No. 3 (2014): September-December 2014Section:
Research ArticlesLa argumentación como estrategia de enseñanza y de aprendizaje de las matemáticas-The argumentation like strategy of education and of learning of the mathematics
Keywords:
argumentación, enseñanza, aprendizaje, comprensión, trabajo colaborativo. (es).Downloads
References
Chevallard. (1998). La transposición didáctica del saber sabio al saber ensenado. (Vol. 5, II). Argentina: Aique Grupo editor.
Dorio, I., Massot, I. y Sabariego, M. (2009). Características Generales de la Metodología Cualitativa. En R. Bisquerra (Coord.), Metodología de la Investigación Educativa (2ª ed.). Madrid: La Muralla. S.A.
Lakatos, I. (1976). Proofs and refutations – the logic of mathematical discovery. Cambridge, MA: The University Press.
Maldonado, L. F., Drachman, R., De-Groot, R., Gutiérrez, J., Muñoz, O., Bernal, R., Lizcano, A., Macías, D., Serrano, E., Vargas, E. C., Rodríguez, G. E., Rodríguez, M. S., y Jaime, R. V. (2012). Argumentación para el aprendizaje colaborativo de la matemática. Bogotá: Ediciones Fundación Universidad Central
Schwarz, B. B., Hershkowitz, R. and Prusak, N. (2010). Argumentation and mathematics. In Howe, C. and Littleton, K. (Eds.), Educational dialogues: understanding and promoting productive interaction. Estados Unidos y Canadá: Routledge.
Toulmin, S.E. (1958). The uses of argument. Cambridge: Cambridge University Press.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
La argumentación como estrategia de enseñanza y de aprendizaje de las matemáticas1
The argumentation like strategy of education and of learning of the mathematics
A argumentação como estratégia de educação e de aprendizagem da matemática
Eliécer Aldana Bermúdez2
1Artículo de investigación
2Universidad del Quindío (profesor). Contacto: eliecerab@uniquindio.edu.co
Fecha de recepción: enero 2014, Fecha de aceptación: julio de 2014
Resumen
El presente artículo hace referencia a la importancia de la argumentación como estrategia de enseñanza y de aprendizaje de las matemáticas, es decir, cómo la argumentación puesta al servicio de la enseñanza puede generar un mayor aprendizaje de los estudiantes en la clase. Para ello se ha puesto de manifiesto un enfoque teórico de comprensión matemática, y una metodología de tipo cualitativo con un estudiante universitario, a quien se le plantearon algunas tareas con el propósito de analizar los argumentos que utiliza y la relación que establece entre ellos. A partir ejemplos, se muestra la comprensión que hace el estudiante de algunos conceptos matemáticos de acuerdo con los argumentos que utiliza en la resolución de las tareas matemáticas planteadas.
Palabras clave: argumentación, enseñanza, aprendizaje, comprensión, trabajo colaborativo.
Abstract
The text that here one presents refers to the importance of the argumentation as strategy of education and of learning of the mathematics, that is to say, how the argumentation put to the service of the education can generate a major learning of the students in the class. For it there has been revealed a theoretical approach of mathematical comprehension, and a methodology of qualitative type with a university student, to whom some tasks appeared him, with the intention of analyzing the arguments that it uses and the relation that it establishes between them. To dividing examples, there appears the comprehension that there does the student of some mathematical concepts of agreement with the arguments that it uses in the resolution of the mathematical raised tasks.
keywords: Argumentation, education, learning, comprehension, collaborative work.
Resumo
O texto aqui apresentado refere-se à importância do argumento como uma estratégia para o ensino e aprendizagem da matemática, ou seja, como o raciocínio a serviço da educação pode gerar maior aprendizagem dos alunos em sala de aula. Este revelou uma abordagem teórica para o entendimento matemático e uma metodologia qualitativa com um estudante universitário, a quem eles levantaram algumas tarefas, a fim de analisar os argumentos utilizados ea relação estabelecida entre eles. Como exemplos, estudante compreensão fazendo alguns conceitos matemáticos de acordo com os argumentos usados na resolução de tarefas matemáticas das questões apresentadas.
Palavras-chave:Argumentação, a educação, a aprendizagem, a compreensão, o trabalho colaborativo.
PRESENTACIÓN DEL PROBLEMA
La experiencia vivida por el autor del presente artículo, como estudiante y profesor investigador ha permitido registrar cómo los jóvenes, en su gran mayoría, no presentan una competencia comunicativa para argumentar sus posturas académicas, son poco expresivos en la forma como justifican la resolución de las tareas matemáticas, se quedan en los procesos, en las respuestas, muestran unas concepciones poco firmes, en algunos casos lo hace producto de la memoria, sin saber el porqué proceden de una forma determinada y no están acostumbrados a realizar tareas diferentes a las habituales en el aula de clase.
La argumentación cumple un rol fundamental en el proceso de enseñanza y guía la acción educativa, porque genera un proceso de comunicación entre pares, entre el educador y el educando, propicia el diálogo y permite un trabajo colaborativo en el aula de clase que facilita la tarea del profesor en cuanto a la mediación e interacción en el proceso docente educativo. No obstante durante el proceso de la clase en matemáticas, dadas las características del área, los saberes se adquieren generalmente bajo un paradigma de tipo reproduccionista, donde poco se privilegia la interacción en la clase en forma de un proceso heurístico que ponga en acción, en diálogo, las tres dimensiones del triángulo didáctico, el educando, el educador y el saber.
Diagnosticar los saberes previos del educando facilita el punto de partida del educador a la hora de generar procesos de enseñanza aprendizaje, pues esto le permite establecer un contrato didáctico que, en términos de Chevallard (1982), hace referencia a los compromisos y los resultados que espera el profesor del alumno y viceversa. Deben existir reglas o acuerdos que se apliquen en la situación didáctica, en este sentido la argumentación es un estilo de enseñanza práctica que garantiza el pensamiento racional, consciente y duradero del estudiante, porque todo lo que construye lo hace desde la acción, el proceso, hasta llegar a la construcción misma del objeto matemático en abstracto, lo que implica mejorar las condiciones académicas de los estudiantes y ayuda a disminuir la deserción escolar.
Se trata de responder a la pregunta ¿cómo la argumentación contribuye para que los conceptos matemáticos sean comprendidos y utilizados? Desde este punto de vista, la argumentación al servicio del aprendizaje y de la enseñanza debe avivar el desarrollo de las competencias disciplinares, comunicativas, actitudinales, argumentativas, procedimentales y conceptuales propias del rigor de las ciencias matemáticas, en el sentido que se busca el paso de un pensamiento matemático elemental a un pensamiento de naturaleza avanzado.
MARCO CONCEPTUAL
En este apartado se hace referencia, en primer lugar, al desarrollo de competencias como lo plantea Maldonado (2012), en el cual pone de manifiesto el esfuerzo por optimizar el desarrollo de competencias conceptuales como las relacionadas con aspectos teóricos propios del saber matemático con los conceptos fundantes de esta disciplina en particular. Asimismo, las competencias modelativas como proceso que permite al sujeto modelar situaciones problema de su realidad o entorno inmediato a partir de la resolución de un problema en contexto. Las operativas como aquellas que se relacionan con la comparación y ejercitación de procedimientos o manejo de algoritmos. Las competencias explicativas demuestran la capacidad que tienen los sujetos para argumentar, confrontar y justificar los procesos relacionados con una actividad que implica el desarrollo lógico del pensamiento matemático. Las competencias comunicativas se refieren a la capacidad del estudiante para expresar y encadenar juicios de razonamientos y deducciones durante el aprendizaje colaborativo; en este sentido, el desarrollo de competencias debe generar la creación de redes sociales de aprendizaje matemático, y de esta manera contribuir a mejorar las condiciones académicas de los estudiantes y por ende a motivarlos en el aprendizaje y con ello contrarrestar la deserción escolar universitaria asociada al bajo rendimiento académico.
La argumentación es un proceso que hace referencia al porqué de lo que hace el estudiante mediante la exposición de razonamientos para justificar un procedimiento matemático, para ello parte de la identificación de una situación, para llegar a juicios de razonamientos y análisis desde el saber matemático. El proceso argumentativo lo realiza el estudiante desde dos habilidades propias del lenguaje: la oralidad y la escritura, en este sentido los argumentos que utiliza un aprendiz durante el proceso de aprendizaje de un concepto matemático se evidencia por la capacidad que tenga para mostrar un conjunto de proposiciones que establezcan una relación de coherencia entre lo que el sujeto piensa, dice y demuestra durante la resolución de una tarea en particular. Por ejemplo, el paso del lenguaje hablado al escrito, del lenguaje verbal al lenguaje algebraico, de una representación tabular a la interpretación de una gráfica.
Por su parte, la matemática es un sistema lógico formal, es un proceso constructivo mediante el cual se definen símbolos, reglas de transformación y reglas de inferencia, en este sentido es necesario diferenciar entre demostración y argumentación. La demostración es entendida como un proceso de derivación de conclusiones válidas a partir de expresiones iníciales bien formuladas como un sistema lógico formal que está dado por la asignación de valores de verdad a las proposiciones, con la aceptación de la verdad de las proposiciones iníciales.
De otro lado, la argumentación tiene origen en la discusión de una tesis enfrentada a tesis alternativas de solución a un problema. Su origen retórico tiene como finalidad convencer a posibles opositores. Para la mayoría de los matemáticos formalistas, la discusión no tiene cabida y tampoco la argumentación. Por ejemplo, si se va a demostrar que la suma de dos números impares es un número par, hay una prueba formal que no admite discusión; aunque no desconocen que para esta prueba se necesita imaginación, que se requiere de conocimientos previos y posibilidades de transformación integrando conocimientos o haciendo descubrimiento de fórmulas no conocidas.
Desde la argumentación no se niega el diálogo como medio de creación, lo cual hace de la demostración un proceso sinérgico; pues en cada paso de la solución del problema habrían alternativas de equivalencia para realizar la transformación sin violar el principio de igualdad. Todo este proceso es un escenario fecundo para el diálogo y la construcción colectiva que podemos llamar “argumentación matemática”, Lakatos (1974 citado por Maldonado, 2012).
Entonces, desde el punto de vista de la demostración, el centro de atención es la prueba formal de la demostración, y desde la argumentación interesa el conocimiento ontológico de los elementos constitutivos del concepto de número, por ejemplo, par, impar, cardinal, ordinal, seriación, comparación y clasificación entre otros. Podría entonces pensarse que para algunos la argumentación no tiene validez, por los posibles juicios de razonamientos subjetivos que se puedan realizar y que sólo tiene validez la demostración como sucede por ejemplo para algunos investigadores entre lo que es la investigación cualitativa versus investigación cuantitativa, pues no se trata de decir quién tiene la verdad o qué es mejor, simplemente son dos procesos diferentes pero que en esencia se complementan, pues no existe encadenamiento de juicios de razonamiento sin la argumentación.
En el ámbito de la Educación Matemática la argumentación como estrategia de aprendizaje colaborativo en la solución de problemas tiene sentido para construir significado de las estructuras conceptuales y para relacionar estos significados con escenarios donde potencialmente se puede utilizar la estructura matemática para leer la estructura de la matemática escolar. Los procesos argumentativos son importantes en relación con los procesos educativos y de formación, al respecto, desde el enfoque de Toulmin (1954), la argumentación aporta diferentes formas de una definición formal, ejemplos, relaciones de un concepto con otros conceptos, contra-ejemplos y refutaciones.
Desde este punto de vista, los autores coinciden en plantear que la argumentación es una forma de estudio de clase que permite la interacción, el razonamiento, los juicios de valor, es una forma de justificar los procedimientos que realizan los estudiantes para dar cuenta de la forma como comprenden un concepto matemático y para el profesor de conocer y comprender cómo aprende su alumno.
METODOLOGÍA
Este es un estudio de tipo cualitativo “orientada a la comprensión, cuyo objetivo es describir e interpretar la realidad educativa desde dentro” (Dorio, I., Massot, I. y Sabariego, M., 2009, p. 281); tiene que ver con la forma como los estudiantes comprenden un concepto y es reflexiva porque plantea cómo los profesores pueden utilizar la argumentación al servicio de la enseñanza y del aprendizaje de los estudiantes. Por tanto, lo que se presenta tiene que ver con un estudio de caso en el cual se analizan los argumentos que plantea un estudiante universitario cuando se le presenta una tarea en la cual, más que los procedimientos, se espera que justifique sus razonamientos. Para ello, se han utilizado algunos cuestionarios que ponen en evidencia lo que el estudiante sabe hacer con lo que conoce, una entrevista para complementar la información obtenida a partir del cuestionario mediante la argumentación que hace el estudiante de la forma como ha resuelto la tarea, y un mapa conceptual que muestra la imagen del concepto que tiene el estudiante del concepto de integral definida.
ANÁLISIS DE DATOS
Para ejemplificar lo que es la argumentación al servicio de la enseñanza y del aprendizaje de las matemáticas se tomó como objeto de investigación la comprensión matemática y como objeto matemático de investigación el concepto de integral definida desde algunos de los elementos matemáticos que lo configuran.
Por ejemplo:
El alumno hace inicialmente una representación gráfica de la función.
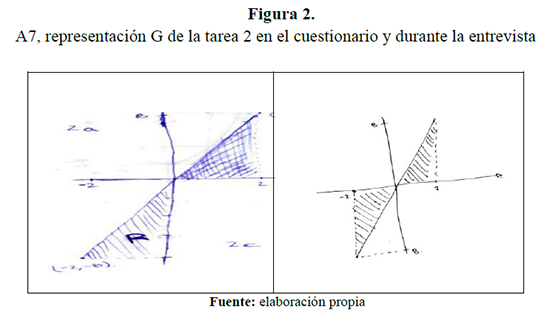
En el cuestionario dibuja la gráfica de la función, sombrea el área que se le pide calcular, y a partir de la representación gráfica (G), calcula el área de forma algebraica (A).
A pesar de que el resultado es correcto, en la sucesión de igualdades se olvidó multiplicar por dos al pasar del primer a segundo término, aunque luego lo corrigió en la siguiente igualdad. En la entrevista, él mismo describe lo que hizo de la siguiente forma:
- A7: Aquí vemos 2 triángulos (traza el gráfico).
- I: ¿Cómo calculó el área geométricamente?
- A7: Geométricamente, es la suma de 2 triángulos de base 2 y de altura 8, que en su defecto podría calcularse el área de un rectángulo.
- I: ¿Por qué?
- A7: El intervalo es de -2 a 2.
- I: ¿Qué valor obtuvo al graficar el área?
- A7: 16 unidades cuadradas.
Para calcular el área gráficamente, forma dos triángulos que, como él dice, conformarían un rectángulo, y durante la entrevista, igual que en el cuestionario, a partir del gráfico calcula el área total y obtiene 16 unidades cuadradas. Aplica el elemento matemático área como aproximación (ACA) de forma A, porque utiliza la fórmula del área del triángulo y como los triángulos son iguales entonces la duplica para obtener el área total. En cuanto al cálculo de la integral, en el cuestionario da la siguiente solución de forma A:
Además, el estudiante muestra la relación que establece entre el área y la integral:
- I: ¿Qué valor obtuvo al calcular la integral?
- A7: 0 unidades cuadradas.
- I: ¿Cuál es la diferencia entre calcular el área gráficamente y calcular esa integral?
- A7: Pienso que si me dicen calcule esta integral y me da cero puede tener sentido, si me dicen calcule la integral que corresponde a este gráfico me parece que así como se plantea aquí, es una integral sin contexto.
- I: ¿Qué quiere decir sin contexto?
- A7: Que no me está representando un área.
- I: ¿Cómo son los 2 resultados?
- A7: Los dos resultados son diferentes.
- I: ¿Por qué son diferentes?
- A7: Porque uno es un ejercicio de calcular una integral y el otro de calcular un área.
- I: ¿Cuándo le piden calcular el área a qué debe llegar?
- A7: Debo obtener un número real positivo.
- I: ¿Cuándo le piden calcular una integral, cuál puede ser ese valor?
- A7: Si la integral es definida puede ser un número real positivo, negativo o cero.
Distingue el elemento matemático la integral definida (LID) de su aplicación como área de regiones planas porque argumenta que cuando se aplica la Integral Definida como área, ésta representa un valor positivo, mientras que el cálculo de la Integral Definida es un valor real positivo, negativo o cero.
En esta otra tarea:
Este alumno analiza los valores que toma según sea positiva o negativa la función 2x ?1, aunque en el planteamiento se confunde entre las abscisas y las ordenadas y considera los casos en que x sea positivo o negativo.
Esto mismo lo expresa durante la entrevista. Está trasfiriendo directamente lo que recuerda del valor absoluto de x, al valor absoluto de 2x -1.
- A7: El valor absoluto de esa función,
habría que redefinirla, como la función
va a valer 2X-1 , si X es mayor que 0
vale -(2X-1) , si X es menor o igual a
0. (A7E4).
A pesar de ello, para poder representar gráficamente la función, tiene que dar valores a x para obtener valores de y.
- I: ¿Podría decirme cómo ha esbozado
el gráfico de la función?
- A7: Teniendo la función, tabulé le di a
x tres valores.
(A7E4).
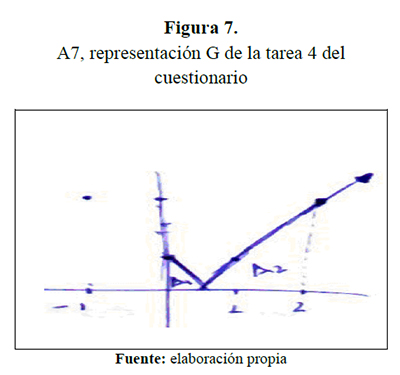
Finalmente representa la gráfica correctamente.
Una vez representada gráficamente la función, el estudiante calcula el área limitada por la gráfica relacionando varios elementos matemáticos de forma A.
En la columna de la derecha se puede ver cómo aplica el elemento matemático el ACA. A partir del gráfico calcula el área de los triángulos que conforman el área total, las suma y obtiene el área que se le pide. Para ello ha necesitado coordinar los registros gráfico y algebraico. En la columna de la izquierda utiliza los elementos matemáticos: la integral definida (LID), propiedades de la integral definida (PID) y el teorema fundamental del cálculo (TFV), porque calcula el área a partir del planteamiento de una integral, aplica la propiedad de la unión de intervalos correctamente y utiliza la regla de Barrow para hallar las primitivas y evaluarlas en los límites respectivos. Cuando se le preguntó por la solución mediante el cálculo de las áreas de los triángulos lo justifica de la siguiente forma:
El estudiante describe los procedimientos utilizados en el desarrollo de la tarea, y compara los valores obtenidos a partir del uso del elemento ACA y del elemento LID:
- I: ¿Cómo son los valores obtenidos?
- A7: Son exactamente iguales(A7E4).
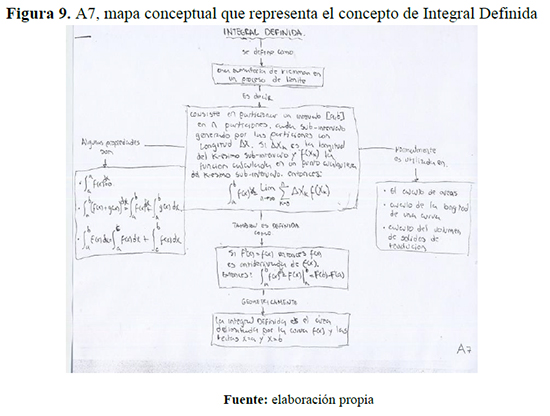
En este mismo sentido, y con el objeto de confrontar la información descrita anteriormente, en el mapa conceptual que se presenta a continuación se ponen de manifiesto los elementos matemáticos gráficos, algebraicos y analíticos que este alumno recuerda. Los mismos elementos que plantea en esta representación son los que utilizó a largo del cuestionario y durante la entrevista para la resolución y argumentación de las tareas.
CONCLUSIONES
El conocimiento humano es una construcción social donde cada construcción nueva se apoya en construcciones previas. La argumentación es una forma de comunicación y diálogo para evaluar, definir y estimular producciones. No todos los temas de estudio son ideales para un estudio argumentativo; en consecuencia, la elección requiere un análisis didáctico y fundamentación previa. La argumentación surge si se explican las actividades en clase, y los criterios del ejercicio argumentativo consistente con las metas pedagógicas.
REFERENCIAS
Chevallard. (1998). La transposición didáctica del saber sabio al saber ensenado. (Vol. 5, II). Argentina: Aique Grupo editor.
Dorio, I., Massot, I. y Sabariego, M. (2009). Características Generales de la Metodología Cualitativa. En R. Bisquerra (Coord.), Metodología de la Investigación Educativa (2� ed.). Madrid: La Muralla. S.A.
Lakatos, I. (1976). Proofs and refutations – the logic of mathematical discovery. Cambridge, MA: The University Press.
Maldonado, L. F., Drachman, R., De-Groot, R., Gutiérrez, J., Muñoz, O., Bernal, R., Lizcano, A., Macías, D., Serrano, E., Vargas, E. C., Rodríguez, G. E., Rodríguez, M. S., y Jaime, R. V. (2012). Argumentación para el aprendizaje colaborativo de la matemática. Bogotá: Ediciones Fundación Universidad Central
Schwarz, B. B., Hershkowitz, R. and Prusak, N. (2010). Argumentation and mathematics. In Howe, C. and Littleton, K. (Eds.), Educational dialogues: understanding and promoting productive interaction. Estados Unidos y Canadá: Routledge.
Toulmin, S.E. (1958). The uses of argument. Cambridge: Cambridge University Press.
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.