DOI:
https://doi.org/10.14483/23448350.7688Published:
10/21/2014Issue:
Vol. 20 No. 3 (2014): September-December 2014Section:
Research ArticlesLa perspectiva sociocultural en el análisis de la práctica de los docentes universitarios de precálculo: la enseñanza de la función exponencial-The sociocultural perspective on the analysis of the practice of university teachers of pre calculation: the teaching of the exponential function
Keywords:
precálulo, universitarios, función exponencial, enseñanza, práctica, docentes. (es).Downloads
References
Camacho, M. (2011). Investigación en didáctica de las matemáticas en el bachillerato y primeros cursos de universidad. En M. Marín, G. Fernández, L. J. Blanco y M. Palarea (Eds.), Investigación en Educación Matemática XV. Ciudad Real, España: Sociedad Española de Investigación en Educación Matemática & Servicio de publicaciones de la Universidad de Castilla-La Mancha.
Dubinsky, E. (1991). Reflective abstraction in advanced mathematical thinking. In D. Tall (Ed.), Advanced Mathematical Thinking. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Dubinsky, E. (1996). Aplicación de la perspectiva piagetiana a la educación matemática universitaria. Educación Matemática, 8(3), 24-41.
Dubinsky, E. (2000). De la investigación en matemática teórica a la investigación en matemática educativa: un viaje personal. Revista Latinoamericana de Investigación en Educación Matemática, 3(1), 47-70.
Dubinsky, E. and Lewin, P. (1992). Reflexive abstraction in mathematics education: The genetic decomposition of induction and compactness. Journal of Mathematical Behavior, 5, 55-92.
Dubinsky, E. and Mcdonald, M. (2001). APOS: A constructivist theory of learning in undergrad mathematics education research. In D. Holton (Ed.), The teaching and learning of mathematics at university level: An ICMI Study. New York: Kluwer Academic Publishers.
Gavilán, J. M. (2005). El papel del profesor en la enseñanza de la derivada. Análisis desde una perspectiva cognitiva. Tesis doctoral. Departamento de Didáctica de las Matemáticas. Universidad de Sevilla. Edición Digital @tres, S.L.L. (2010).
Gavilán, J. M., García, M. y Llinares, S. (2007a). La modelación de la descomposición genética de una noción matemática. Explicando la práctica del profesor desde el punto de vista del aprendizaje potencial de los estudiantes. Educación matemática, 19(2), 5-39.
Gavilán, J. M., García, M. y Llinares, S. (2007b). Una perspectiva para el análisis de la práctica del profesor de matemáticas. Implicaciones metodológicas. Enseñanza de las Ciencias, 25(2), 157-170.
García, M., Gavilán, J. M. y Llinares, S. (2012). Perspectiva de la práctica del profesor de matemáticas de secundaria sobre la enseñanza de la derivada. Relaciones entre la práctica y la perspectiva del profesor. Enseñanza de las Ciencias, 30(3), 219 – 235.
Llinares, S. (2000). Comprendiendo la práctica del profesor de matemáticas. En J. P. da Ponte y L. Sarrazina (Eds.), Educaçao Matemática em Portugal, Espanha e Italia Lisboa. Actas da Escola de Verao-1999. Lisboa, Portugal: SEM-SPCE.
Moreno, M. M. (2011). Introducción al Seminario II sobre investigación en didáctica de las matemáticas por niveles educativos. En M. Marín, G. Fernández, L. Blanco y M. Palarea (Eds.), Investigación en Educación Matemática XV (pp. 119-123). Ciudad Real, España: Sociedad Española de Investigación en Educación Matemática & Servicio de publicaciones de la Universidad de Castilla-La Mancha.
Sánchez, M. (2010). How to stimulate rich interactions and reflections in online mathematics teacher education? Roskilde, Dinamarca: Roskilde Universitet.
Sánchez, M. (2011). A review of research trends in mathematics teacher education. PNA, 5(4): 129-145.
Schön, D. A. (1983). The reflective practitioner: How professionals think in action. New York, United States of America: Basic Books.
Vargas, J. (2011). Atlas.ti y una descomposición genética como herramientas de análisis de la práctica docente: la función exponencial. En Espacios de reflexión e intercambio de saberes. Colombia: Escuela de matemática, Universidad Pedagógica y Tecnológica de Duitama.
Vargas, J. (2013). Análisis de la práctica del docente universitario de precálculo. Estudio de casos en la enseñanza de las funciones exponenciales. Tesis doctoral (inédita). Universidad de Salamanca.
Vargas, J., González, M. T. y Llinares, S. (2011a). Atlas.ti como herramienta de análisis de la práctica docente: el caso de la función exponencial. En M. M. Moreno y N. Climent (Eds.), Investigación en Educación Matemática. Comunicaciones de los grupos de investigación de la SEIEM. XIV Simposio de la SEIEM. Lleida, España: Edicions de la Universitat de Lleida. Acceso: 4/10/12. Recuperado de: http://www.seiem.es/publicaciones/archivospublicaciones/comunicacionesgrupos/GruposXIVSimposio.pdf
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
La perspectiva sociocultural en el análisis de la práctica de los docentes universitarios de precálculo: la enseñanza de la función exponencial1
The sociocultural perspective on the analysis of the practice of university teachers of pre calculation: the teaching of the exponential function
A perspectiva sociocultural na análise da prática de professores universitários de cálculo: o ensino da função exponencial
Jeannette Vargas Hernández2
1Artículo de investigación
2Docente Investigadora. Universidad Colegio Mayor de Cundinamarca. Doctora en Educación Matemática. Universidad de Salamanca. Contacto: jvargash@unicolmayor.edu.co
Fecha de recepción: febrero 2014, Fecha de aceptación: julio de 2014
Resumen
En este artículo se presentarán algunos resultados de una investigación de corte cualitativo que se enfoca en un estudio de caso; el caso de Ernesto. En ella se dio respuesta a las preguntas: ¿cómo modelan los profesores de precálculo en su práctica docente los mecanismos de construcción del concepto de función exponencial? y ¿cuáles son las características que subyacen a las prácticas analizadas?
Palabras clave: precálulo, universitarios, función exponencial, enseñanza, práctica, docentes.
Abstract
Some results from a qualitative-style research will be presented. The research is focused on the study of Ernesto�s case. It was given answer to the questions: in which way precalculus teachers give form to the means of construction of the exponential function concept and which are the characteristics that are underneath the analyzed practices?
keywords: precalculus, college, exponential function, teaching, practice teaching.
Resumo
Alguns resultados de uma pesquisa qualitativa de estilo será apresentado. A pesquisa está centrada no estudo de caso de Ernesto. Foi dada resposta às perguntas: de que forma os professores precalculus dar forma aos meios de construção do conceito de função exponencial e quais são as características que estão debaixo das práticas analisadas?
Palavras-chave:precalculus, universitários, função exponencial, de ensino, de ensino prática.
Introducción
La literatura de investigación en educación muestra que, hace aproximadamente cuatro décadas, la enseñanza se consideraba un arte y, en consecuencia, era difícil de analizar, intervenir y someter a ciertas reglas. La manera de concebir al profesor y la enseñanza, desde la teoría y la investigación educativa, ha sufrido una evolución que se puede ver en términos del objeto específico de estudio o de la complejidad considerada.
En la década de los años ochenta, y a partir de autores como Donald Schön (1983, 1987), se asume que los profesores generan conocimiento sobre la enseñanza a partir del trabajo práctico que realizan en aulas particulares, y que ese conocimiento merece ser investigado. Al mismo tiempo, surge con fuerza el interés en las creencias, desde diversas disciplinas como psicología, ciencias políticas, antropología y educación.
Entre los educadores, el interés en el estudio de las creencias y concepciones de los profesores lo alimentó el cambio de paradigma, el pasar de concebir al profesor como un técnico a concebirlo como un ser pensante, reflexivo.
Así, a finales de la década de los años noventa surge el interés por comprender la gestión del docente y comienza a considerarse la importancia de analizar la actividad de los docentes en el aula. De igual manera, las creencias y las concepciones adquieren un papel prominente como base para estudiar a los profesores de matemáticas y su enseñanza.
Según Sánchez (2010, 2011), en la actualidad, en el campo de la educación matemática se percibe un aumento de los estudios que investigan las creencias del profesor al igual que aspectos particulares de las prácticas de los docentes en el aula decisiones fuera del aula de clase, los recursos usados por los profesores para definir el contenido de las lecciones, aspectos concretos de las prácticas de los docentes en el aula; por ejemplo, los tipos de preguntas formuladas durante las clases. Sin embargo, es necesario ampliar la investigación en el campo a nuevas temáticas (Camacho, 2011) de manera que los problemas de investigación también se sitúen en el nivel universitario (Moreno, 2011). Esta investigación aborda el análisis de la práctica de docentes en el nivel universitario y se enfoca en la enseñanza de funciones exponenciales, pretendiendo contribuir a llenar los espacios vacíos mencionados por Camacho y Moreno.
Referentes teóricos
En esta investigación se acude a que la visibilidad del discurso y la naturaleza de las acciones del profesor provienen de una perspectiva sociocultural y se reconoce que la práctica docente es una actividad mediada por el uso de ciertos “instrumentos” (Llinares, 2000) y por lo tanto permiten caracterizarla. Desde esta perspectiva, en segundo lugar, se asume “que los instrumentos utilizados y su forma de utilización influyen en el tipo de comprensión matemática” (Llinares, 2000, p.115) y el objetivo del profesor es favorecer dicha comprensión de los estudiantes.
En este artículo se presentan aspectos analizados concernientes al discurso en la práctica profesional de docentes universitarios, al enseñar la función exponencial en cursos de precálculo. Aspectos del discurso que forman parte de una investigación más amplia en la cual se analizan las fases de planificación y de gestión en el aula, tomando como referencia, por una parte, los mecanismos de construcción de un concepto matemático: interiorización, encapsulación y tematización, propuestos por Ed Dubinsky (1991 y 1996) y su grupo (Dubinsky, E. y Lewin, P., 1992; Dubinsky, E. y Mcdonald, M., 2001) en su teoría Action Process Object Schema (APOS); y por otra parte, la modelación de la descomposición genética de un concepto, constructo expuesto desde un marco sociocultural por Gavilán (2005).
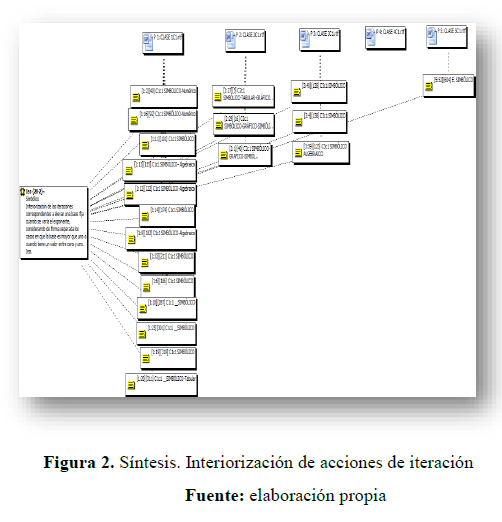
En esta investigación el mecanismo de interiorización conlleva la construcción mental de una forma de conocer proceso a partir de una serie de acciones sobre objetos cognitivos, es decir, las formas de conocer como acciones se interiorizan en procesos (Vargas, J, 2013). Así, para el concepto funciones exponenciales, se identifican tanto en el registro de representación simbólico como en el gráfico los siguientes descriptores del mecanismo:
Simbólico
- Interiorización de las iteraciones correspondientes a elevar una base fija cuando se varía el exponente, considerando de forma separada los casos en que la base es mayor que uno o cuando tiene un valor entre cero y uno.
- Interiorización de las acciones de comparación de diferencias y cocientes de dos valores de la variable dependiente e independiente respectivamente, para buscar las relaciones entre ellas Y2/Y1 = aX2-x1
- Interiorización de las acciones de aplicar valores muy “grandes” a x y la aproximación de los valores de y a cero en el caso de la función decreciente y para valores de x muy “pequeños” en el caso de la función creciente.
Gráfico
- Interiorización de las acciones de ubicar diferentes puntos en la curva función exponencial en el proceso de construcción de la gráfica de la función sin recurrir a realizar las acciones de remplazar en la fórmula diversos valores.
- Representación del triángulo característico para diferentes puntos de la gráfica de una función.
Aspectos metodológicos
En el desarrollo de la investigación se distinguen claramente tres momentos. En el primero, tras la apropiación de un marco teórico, se construye una propuesta de descomposición genética del concepto función exponencial (Vargas, 2013). En el segundo, se recoge información directa de las sesiones de aula de los docentes de precálculo mientras enseñan la función exponencial y, a través de entrevistas semiestructuradas, se recoge nuevamente información directa sobre las intenciones de las acciones del profesor en cada una de las clases. En el tercero, se examina y analiza la práctica del docente, a través del constructo modelación de la descomposición genética para, posteriormente, determinar las características subyacentes a esa práctica, que determinarán lo que se denomina la perspectiva de la práctica (García; Gavilán,y Llinares, 2012).
Respecto al segundo momento, se realiza la grabación de las sesiones de clase en las que se trabaja el concepto de función exponencial y de entrevistas video-grabadas, anteriores y posteriores a cada una de las sesiones para obtener información sobre su planificación. Para la clasificación, depuración y análisis de los datos se usa el programa Atlas.ti (Vargas, 2011, Vargas, Gonzáles y Llinares, 2011) y se realizan tres niveles de análisis: uno descriptivo y dos de inferencias para establecer los resultados de la investigación.
Se recurre a la viñeta como herramienta para organizar y presentar los resultados de los análisis de la práctica del docente (Gavilán y otros 2007a, 2007b). En ella se muestra una descripción detallada de los segmentos de la lección, considerados en términos de las tareas propuestas, los mecanismos de construcción potenciados por el profesor, el uso de los sistemas de representación y las relaciones entre los elementos del concepto. Los análisis relativos a la forma en que el profesor propicia la construcción de conocimiento y usa los instrumentos.
Lo anteriormente enunciado se ejemplifica, a través del caso de Ernesto, en la siguiente sección del presente artículo que es parte de la viñeta del mecanismo de interiorización; conformada tanto por segmentos de las clases del docente, segmentos de entrevistas e inferencias de los investigadores. Se analizan las relaciones entre los elementos matemáticos del concepto, el discurso del docente y el uso y justificación de la representación simbólica en situaciones de iteración.
Iteración de acciones de cálculo correspondientes a elevar la base fija a diferentes exponentes
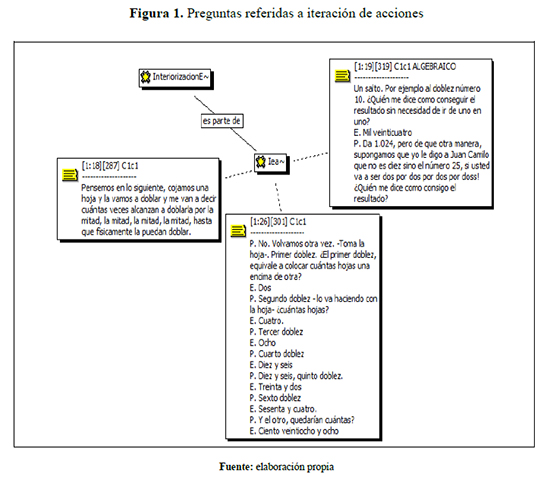
En la clase 1, Ernesto propone una situación de doblez de papel para que el estudiante reflexione sobre la iteración y su representación por medio de un exponente. Para ello pide a los estudiantes tomar una hoja, doblarla por la mitad y luego nuevamente doblarla y así sucesivamente hasta que la situación física lo permita.
La tarea de dobleces del papel ([301], [319]) propicia ciertas preguntas que conducen a reflexionar sobre las acciones correspondientes a repetir una serie de pasos un cierto número de veces. En este caso se trata de la multiplicación de dos por dos, luego otro dos y así sucesivamente. Esta multiplicación de factores iguales se puede expresar mediante el uso de exponentes naturales para representar dicho fenómeno. Ernesto organiza los datos en el tablero utilizando una representación tabular de la relación entre los dobleces y el grosor, mediante el siguiente diálogo:
[1][313:321]
P: Sexto doblez
E: Sesenta y cuatro.
P: Y el otro, ¿quedarían cuántas?
E: Ciento veintiocho y ocho
P: O sea, esta que ya no puedo doblar, sería 128.
Hagamos una tablita donde se muestre eso -en el tablero dibuja y va hablando- a ver doblez número, equivale a que grosor dos el segundo cuatro, ¿el tercero cuánto fue?
E: Ocho
P: Cuarto diez y seis, quinto treinta y dos - escribe puntos sucesivos y dice - yo voy a pegar aquí un brinco, un salto.
Haciendo uso de esta representación tabular [1][324:327], Ernesto expone a los estudiantes las potencias de dos que se han obtenido y los lleva a conjeturar sobre exponentes y potencias de pasos posteriores que no se pueden obtener en la actividad física de dobleces del papel. Estas reflexiones, suscitadas alrededor de la acciones de iteración y uso de los exponentes, forman parte de la interiorización de una función exponencial con base mayor que uno identificada en la descomposición de la función exponencial.
[1][324:327] SIMBÓLICO-Tabular P: Esto que está acá viene siendo las potencias de dos, esto es dos a la cero, esto es dos a la uno, doblez tres dos a la tres, doblez cuatro dos a la cuatro, y así. El profesor completa la tabla en el tablero.
De manera que en el doblez 10 ¿sería dos a la? La secuencia en el uso de la iteración que el profesor utiliza en la clase 1, es nuevamente usada en la clase 4 donde Ernesto presenta una tarea como parte de una evaluación corta escrita. En ella, los estudiantes deben imaginar que son participantes de un “reality”, que han ganado una prueba, y que se les da a elegir entre dos premios. El ganador puede decidir, de forma justificada, si prefiere que le entreguen un premio que consiste en recibir un millón de pesos anual desde el momento actual hasta su muerte – bajo el supuesto que vivirá hasta los 80 años – o un premio que consiste en que en el primer año le dan 100 pesos, el siguiente año el doble, 200, el siguiente el doble del anterior 400, etcétera.
Cada estudiante realiza su elección por escrito que entrega al profesor y, posteriormente, en la clase 5, se trata de trabajar a través de la iteración. A continuación se presenta el diálogo correspondiente a la segunda opción de premio:
Voy a colocar algunas para que ustedes me digan con cuál función podría ser. A ver Año cero, o sea el año en que uno recibe el premio, supongamos que en el año cero recibe los cien pesos. Año uno, ¿cuánto es?
E: Doscientos P: Doscientos, pero voy a escribir el doscientos de esta forma: como cien por dos. Ahorita vamos a ver por qué es conveniente escribirlo así. Año dos, ¿cuánto recibiría la persona?
- E: Cuatrocientos
- P: Cuatrocientos, el doble del año anterior. ¿Pero eso equivale a decir cien por cuanto?
- E: Por cuatro
- P: Por cuatro, o sea ¿cien por dos a la qué?
- E: A la dos.
- P: A la dos, ¿sí? Aquí yo voy colocando los exponentes y voy a colocar aquí también ¿por dos a la qué?
- P: Bien, año tres, de una vez acá, quién me dice aquí cuánto es sin necesidad de
En relación al registro gráfico, en la clase 2, Ernesto retoma los datos numéricos y el registro tabular de la actividad de dobleces del papel y continúa con la modelación del mecanismo de interiorización proponiendo a los estudiantes la tarea de realizar la gráfica de la función x y 2 x . Dicha tarea parte de una representación tabular mediante la repetición de acciones de cálculo correspondientes a elevar la base fija, en este caso dos, e ir variando el exponente remplazándolo primero por sucesivos números enteros positivos para hallar el valor correspondiente.
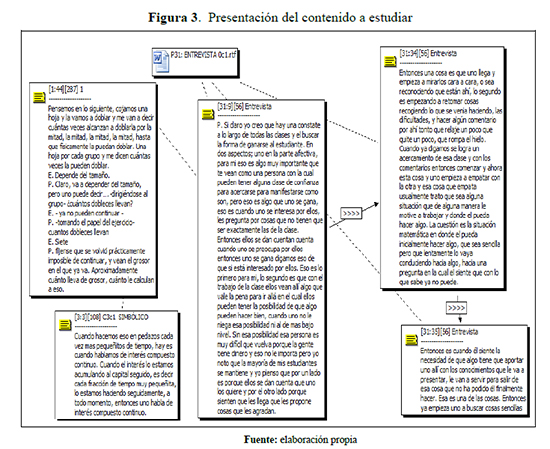
Ernesto se interesa tanto por la adquisición de conceptos, como en el desarrollo de procedimientos y el fomento de actitudes positivas hacia la propia materia y el trabajo académico en general. Ya en la primera entrevista manifiesta estas ideas [31][33:36] que luego se muestran en su práctica docente.
- [31][33:36]
- I: ¿O sea que la experiencia de
dictar precálculo es agradable?
- P: Para mí, si. Y eso depende
de uno, uno puede hacer que el
estudiante no se sienta bien
presentando una cosa toda fea,
pero si uno logra de alguna
manera estimular al estudiante con
las cosas que le presenta para que
él tenga alguna satisfacción, o sea,
hay ahí una cuestión muy humana
y es que tú ves a una persona
contenta haciendo algo, que te
manifiesta con tranquilidad las
dudas, hay una relación muy
buena, que no solamente se limita
al contenido sino que la parte de
los afectos, de las emociones uno
las tiene en cuenta. Si uno no
tuviera en cuenta eso, para mí eso
sería una cosa terrible, porque uno
cada semestre hace lo mismo.
Pero entonces claro las
generaciones van cambiando y
uno tiene que ir ajustando cosas, la
tecnología le hace también a uno
modificar cosas, entonces uno se
va moviendo.
La organización de sus clases tiene en cuenta este aspecto afectivo. Ernesto considera relevante comenzar por elementos del contenido que le permitan al estudiante tener algún éxito y luego le plantea tareas guiadas para que pueda ahondar en otras construcciones.
Conclusiones
Los aspectos anteriores muestran un modelo de la enseñanza de las matemáticas centrada en el estudiante. Es una visión constructivista del aprendizaje de las matemáticas. Se centra en el estudiante, a quien se le involucra activamente en la práctica de hacer matemáticas.
El profesor es visto como facilitador y estimulador del aprendizaje del estudiante, planteando interesantes preguntas y situaciones de investigación, desafíos que le permitan al estudiante pensar y le ayuden a descubrir sus propios argumentos.
En este caso, la modelación del mecanismo de interiorización de la función exponencial privilegia la idea de iteración de las acciones como el medio usado por el profesor para que sus estudiantes construyan los procesos correspondientes a una función exponencial particular, bien en el registro numérico, bien en el algebraico o a través de una actividad manual concreta, que lleva a conjeturar sobre exponentes y potencias mediante una representación tabular, simbólica y gráfica.
Referencias
Camacho, M. (2011). Investigación en didáctica de las matemáticas en el bachillerato y primeros cursos de universidad. En M. Marín, G. Fernández, L. J. Blanco y M. Palarea (Eds.), Investigación en Educación Matemática XV. Ciudad Real, España: Sociedad Española de Investigación en Educación Matemática & Servicio de publicaciones de la Universidad de Castilla-La Mancha.
Dubinsky, E. (1991). Reflective abstraction in advanced mathematical thinking. In D. Tall (Ed.), Advanced Mathematical Thinking. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Dubinsky, E. (1996). Aplicación de la perspectiva piagetiana a la educación matemática universitaria. Educación Matemática, 8(3), 24-41.
Dubinsky, E. (2000). De la investigación en matemática teórica a la investigación en matemática educativa: un viaje personal. Revista Latinoamericana de Investigación en Educación Matemática, 3(1), 47-70.
Dubinsky, E. and Lewin, P. (1992). Reflexive abstraction in mathematics education: The genetic decomposition of induction and compactness. Journal of Mathematical Behavior, 5, 55-92.
Dubinsky, E. and Mcdonald, M. (2001). APOS: A constructivist theory of learning in undergrad mathematics education research. In D. Holton (Ed.), The teaching and learning of mathematics at university level: An ICMI Study. New York: Kluwer Academic Publishers.
Gavilán, J. M. (2005). El papel del profesor en la enseñanza de la derivada. Análisis desde una perspectiva cognitiva. Tesis doctoral. Departamento de Didáctica de las Matemáticas. Universidad de Sevilla. Edición Digital @tres, S.L.L. (2010).
Gavilán, J. M., García, M. y Llinares, S. (2007a). La modelación de la descomposición genética de una noción matemática. Explicando la práctica del profesor desde el punto de vista del aprendizaje potencial de los estudiantes. Educación matemática, 19(2), 5-39.
Gavilán, J. M., García, M. y Llinares, S. (2007b). Una perspectiva para el análisis de la práctica del profesor de matemáticas. Implicaciones metodológicas. Enseñanza de las Ciencias, 25(2), 157-170.
García, M., Gavilán, J. M. y Llinares, S. (2012). Perspectiva de la práctica del profesor de matemáticas de secundaria sobre la enseñanza de la derivada. Relaciones entre la práctica y la perspectiva del profesor. Enseñanza de las Ciencias, 30(3), 219 – 235.
Llinares, S. (2000). Comprendiendo la práctica del profesor de matemáticas. En J. P. da Ponte y L. Sarrazina (Eds.), Educaçao Matemática em Portugal, Espanha e Italia Lisboa. Actas da Escola de Verao-1999. Lisboa, Portugal: SEM-SPCE.
Moreno, M. M. (2011). Introducción al Seminario II sobre investigación en didáctica de las matemáticas por niveles educativos. En M. Marín, G. Fernández, L. Blanco y M. Palarea (Eds.), Investigación en Educación Matemática XV (pp. 119-123). Ciudad Real, España: Sociedad Española de Investigación en Educación Matemática & Servicio de publicaciones de la Universidad de Castilla-La Mancha.
Sánchez, M. (2010). How to stimulate rich interactions and reflections in online mathematics teacher education? Roskilde, Dinamarca: Roskilde Universitet.
Sánchez, M. (2011). A review of research trends in mathematics teacher education. PNA, 5(4): 129-145.
Schön, D. A. (1983). The reflective practitioner: How professionals think in action. New York, United States of America: Basic Books.
Vargas, J. (2011). Atlas.ti y una descomposición genética como herramientas de análisis de la práctica docente: la función exponencial. En Espacios de reflexión e intercambio de saberes. Colombia: Escuela de matemática, Universidad Pedagógica y Tecnológica de Duitama.
Vargas, J. (2013). Análisis de la práctica del docente universitario de precálculo. Estudio de casos en la enseñanza de las funciones exponenciales. Tesis doctoral (inédita). Universidad de Salamanca.
Vargas, J., González, M. T. y Llinares, S. (2011a). Atlas.ti como herramienta de análisis de la práctica docente: el caso de la función exponencial. En M. M. Moreno y N. Climent (Eds.), Investigación en Educación Matemática. Comunicaciones de los grupos de investigación de la SEIEM. XIV Simposio de la SEIEM. Lleida, España: Edicions de la Universitat de Lleida. Acceso: 4/10/12. Recuperado de: http://www.seiem.es/publicaciones/archivospublicaciones/comunicacionesgrupos/GruposXIVSimposio.pdf
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.