DOI:
https://doi.org/10.14483/23448350.7690Published:
10/21/2014Issue:
Vol. 20 No. 3 (2014): September-December 2014Section:
Research ArticlesFilosofía, Matemáticas y Educación: una perspectiva histórico-cultural en Educación Matemática-Philosophy, Mathematics and Education: A Cultural-Historical Perspective on Mathematics Education
Keywords:
Sistemas de práctica matemática, Teorías en Educación Matemática, Teoría de la actividad, configuración epistémica. (es).Downloads
References
Arboleda, L. C. (2011). Objetividad matemática, historia y educación matemática. En L. C. Recalde y G. I. Arbeláez (Eds.), Los números reales como objeto matemático: una perspectiva histórico epistemológica. Cali: Universidad del Valle.
Bajtin, M. (1990). El problema de los géneros discursivos (T. Bubnova, Trans.). En M. Bajtin. (Ed.), La estética de la creación verbal. (10 ed.). México: Siglo XXI Editores.
Bajtín, M. (1993). ¿Qué es el lenguaje? (A. Bignani, Trans.). En A. Silvestri y G. Blanck (Eds.), Bajtin y Vigotski: la organización semiótica de la conciencia.. Barcelona,: Anthropos.
Bourdieu, P. (1977). Outline of a theory of practice (R. Nice, Trans.). Cambridge: University Press.
Bourdieu, P. (2007). El sentido práctico (A. Dilon, Trans.). Buenos Aires: Siglo XXI Editores.
Bourdieu, P. and Johnson, R. (1998). Practical Reason: On the Theory of Action. California: Stanford University Press.
Calderón, D. (2003). Género discursivo, discursividad y argumentación. Enunciación (8).
Clements, M. A., Bishop, A., Keitel-Kreidt, C., Kilpatrick, J., and Leung, F. K.-S. (Eds.). (2013). Third International Handbook of Mathematics Education. New York: Springer.
Cobb, P. (2006). Supporting a discourse about incommensurable theoretical perspectives in mathematics education. Philosophy of Mathematics Education Journal, (19).Available: http://www.people.ex.ac.uk/PErnest/pome19/index.htm
Cole, M. (1999a). Cultural psychology: some general principles and a concrete example. In Y. Engestrom, R. Miettinen and R.-L. Punamaki (Eds.), Perspectives on activity theory. New York: Cambridge University Press.
Cole, M. (1999b). Psicología cultural: una disciplina de pasado y del futuro (T. d. Amo, Trans.). Madrid: Ediciones Morata.
Cole, M., and Wertsch, J. (1996). Beyond the individual-social antinomy in discussions of Piaget and Vygotsky. Human Development, 39(5), 250-256. Doi: 10.1159/000278474
D'Amore, B. (2005). Bases filosóficas, pedagógicas, epistemológicas y conceptuales de la didáctica de la matemática (M. I. F. Pinilla, Trans.). Mexico: Editorial Reverte.
D'Amore, B. y Godino, J. (2007). El enfoque ontosemiótico como un desarrollo de la teoría antropológica en didáctica de las matemáticas. Revista Latinoamericana de Investigación en Matemática Educativa., 10, 191-218.
Daniels, H. (2003). Vygostky y la pedagogía (G. Sánchez Barberan, Trans.). Barcelona: Ediciones Paidos.
Daniels, H. (2008). Reflections on points of departure in the development of sociocultural and activity theory. In B. v. Oers, W. Wardekker, E. Elbers and R. v. d. Veer (Eds.), The transformation of learning: advances in cultural-historical activity theory. New York: Cambridge University Press.
Davidov, V. (1988). La enseñanza escolar y el desarrollo psíquico, Investigación psicológica teórica y experimental. (M. Shuare, Trans.). Moscú: Editorial Porgreso.
Detlefsen, M. (2005). Formalism. In S. Shapiro (Ed.), The Oxford handbook of philosophy of mathematic and logic. New York: Oxford University Press.
Dewey, J. (1960). Experiencia y Educación (7ma ed.). Buenos Aires: Editorial Losada.
Engeström, R., and Kuutti, K. (2006). Activity theory. In K. Brown (Ed.), Encyclopedia of language and linguistics (2 ed.). Amsterdam: Elsevier Ltd.
Engeström, Y. (1999). Activity theory and individual and social transformation. In Y. Engestrom, R. Miettinen and R.-L. Punamaki (Eds.), Perspectives on activity theory. New York: Cambridge University Press.
Engeström, Y. (2009). The future of activity aheory: A rough draft. In A. Sannino, H. Daniels and K. D. Gutiérrez (Eds.), Learning and expanding with activity theory. New York: Cambridge University Press.
Engeström, Y., and Sanino, A. (2010). Studies of expansive learning: Foundations, findings and future challenges. Educational Research Review, 5, 1-24. Doi: 10.1016/j.edurev.2009.12.002
Epple, M. (2004). Knot Invariants in Vienna and Princeton during the 1920s: Epistemic configurations of mathematical research. Science in Context, 17, 131-164.
Ferreirós, J. (2010). Mathematical Knowledge and the Interplay of PracticesEPSA Philosophical Issues in the Sciences. In M. Suárez, M. Dorato and M. Rédei (Eds.), EPSA Philosophical Issues in the Sciences. Dordrecht: Springer Netherlands.
Frege, G. (1996a). Consideracionse sobre Sentido y Referencia (U. Moulines, Trans.). En J. Mosterín (Ed.), Escritos Filosóficos (1 ed.). Barcelona: CRITICA.
Frege, G. (1996b). Función y Concepto (U. Moulines, Trans.). En J. Mosterín (Ed.), Escritos Filosóficos (1 ed.). Barcelona: CRITICA.
Giaquinto, M. (2005). Mathematical activity. In P. Mancuso, K. F. Jørgensen and S. A. Pedersen (Eds.), Visualization, explanation and reasoning styles in mathematics (Vol. 327). Netherlands: Springer. Available: http://link.springer.com/chapter/10.1007%2F1-4020-3335-4_5. Doi: 10.1007/1-4020-3335-4_5
Giusti, E. (2000). La naissance des objets mathématiques (G. Barthélemy, Trans.). Turin Ellipses.
Gueudet, G., and Trouche, L. (2012). Teachers’ work with resources: documentational geneses and professional geneses. In G. Gueudet, L. Trouche and B. Pepin (Eds.), From text to ‘Lived’ resources: mathematics curriculum materials and teacher development. Dordrecht: Springer.
Godino, J., Batanero, C. y Font, V. (2008). Un enfoque ontosemiótico del conocimiento matemático y la instrucción matemática. Paper presentado en el Seminario del Doctorado Interinstitucional de Educación, Universidad del Valle.
Godino, J., and Font, V. (2007). La noción de configuración epistémica como herramienta de análisis de textos matemáticos: su uso en la formación de profesores. En C. Crespo (Ed.), Acta Latinoamericana de Matemática Educativa Vol.20 (1 ed.). Mexico: Comité Latinoamericano de Matemática Educativa.
Hegedus, S. and Moreno-Armella, L. (2010). Accommodating the instrumental genesis framework within dynamic technological environments. For the Learning of Mathematics, 30(1), 26-31.
Hegedus, S. and Moreno-Armella, L. (2011). The emergence of mathematical structures. Educational Studies in Mathematics. Doi: 10.1007/s10649-010-9297-7
Kaptelinin, V. (2005). The object of activity: making sense of the sense-maker. Mind, Culture, and Activity, 12(1), 4-18. Doi: 10.1207/s15327884mca1201_2
Kitcher, P. (1984). The nature of mathematical knowledge (1 ed.). New York: Oxford University Press.
Kozulin, A. (2000). Instrumentos psicológicos. La educación desde una perspectiva sociocultural (G. S. Barberán, Trans.). Barcelona: Ediciones Paidos.
Kozulin, A. (2003). The concept of activity in Soviet psychology: Vygotsky, his disciples and critics. In H. Daniels (Ed.), An Introduction to Vygotsky. London, New York.: Routledge. Taylor and Francis Group eLibrary.
Leave, J. (1991). La cognicion en la practica. Barcelona: Paidos.
Leontiev, A. N. (1978). Activity, consciousness, and personality. New Jersey: Prentice-Hall.
Martínez, M. C. (2005). La argumentación en la dinámica enunciativa del discurso. Cali: Universidad del Valle.
Moreno-Armella, L. and Hegedus, S. (2009). Co-action with digital technologies. ZDM Mathematics Education, 41(4), 505-519. Doi: 10.1007/s11858-009-0200-x
Rabardel, P. et Bourmaud, G. (2005). Instruments et systèmes d'instruments. In P. Rabardel et P. Pastré (Eds.), Modèles du sujet pour la conception: Dialectiques activités développement (1 ed.). Toulouse, France: OCTARÈS Éditions.
Rabardel, P. (2005). Instrument subjectif et développement du pouvoir d'agir. Dans P. Rabardel et P. Pastré (Eds.), Modèles du sujet pour la conception: Dialectiques activités développement (1 ed.). Toulouse, France: OCTARÈS Éditions.
Rabardel, P. (2003). From artefact to instrument. Interacting with Computers, 15, 641-645. Doi: 10.1016/j.intcom.2003.09.004
Radford, L. (2006). Elementos de una teoría cultural de objetivación. Revista Latinoamericana de Investigación en Matemática Educativa., Numero especial, 103-120.
Radford, L. (2008). The etics of being an knowing: Towards a cultural theory of learning. In L. Radford, G. Schubring and F. Seeger (Eds.), Semiotics in Mathemathics Education: Epistemology, History, Classroom, and Culture. Rotherdam: Sense Publishers.
Radford, L. (2009). Why do gestures matter? Sensuous cognition and the palpability of mathematical meanings. Educational Studies in Mathematics, 70(2), 111-126. Doi: 10.1007/s10649-008-9127-3
Radford, L. (2010). Algebraic thinking
from a cultural semiotic perspective. Research in Mathematics Education, 12(1), 1-19. Doi: 10.1080/14794800903569741
Radford, L. (2013). Three Key Concepts of the Theory of Objectification: Knowledge, Knowing, and Learning. Journal ofResearch in Mathematics Education, 2(1), 7-44. Doi: 1 0.4471/redimat.201 3.1 9
Restivo, S., and Collins, R. (2010). Mathematics and civilization. Philosophy of Mathematics Education Journal, (25). Available : http://people.exeter.ac.uk/PErnest/pome25/index.html website:
Ricoeur, P. (2001). Del texto a la acción. Ensayos de hermenéutica II (P. Corona, Trans. 1 ed.). Angentina: Fondo de Cultura Económica.
Roth, W.-M., and Radford, L. (2011). A Cultural-Historical perspective on mathematics teaching and learning. The Netherlands: Sense Publishers.
Silvestri, A. and Blanck, G. (1993). Bajtín y Vigotski: la organización semiótica de la conciencia (1 ed.). Barcelona: Anthropos.
Sriraman, B. and English, L. (Eds.). (2010). Theories of Mathematics Education. Seeking New Frontiers. New York: Springer Berlin Heidelberg.
Stetsenko, A. (2005). Activity as object-related: resolving the dichotomy of individual and collective planes of activity. Mind, Culture, and Activity, 12(1), 70-88. Doi: 10.1207/s15327884mca1201_6
Trouche, L. (2002). Geneses instrumentales, aspects individuels et colletives. In D. Guin et L. Trouche (Eds.), Calculatrices Symboliques. Transformer un outil en un instrument du travail mathématique: un probleme didactique (1 ed.). Grenoble.: La Pense Savage éditions
Vasco, C. (1994). La Educación Matemática: una disciplina en formación. Matemáticas: Enseñanza Universitaria, 3(2), 59-75.
Vygotsky, L. (1993). Pensamiento y lenguaje (J. M. Bravo, Trans.) Obras escogidas II (Vol. 2). Madrid: Visor.
Vygotsky, L. (1994). The development of thinking and concept formation in adolescence (T. Prout and R. v. d. Veer, Trans.). In R. van der Veer and J. Valsiner (Eds.), The Vygotsky reader. Cambridge , Massachusetts: Blackwell Publishers.
Vygotsky, L. (1995). Problemas del desarrollo de la psique (L. Kuper, Trans.) Obras escogidas III (Vol. 3,). Madrid: Visor.
Wertsch, J. V. (1988). Vygostki y la formación social de la mente (J. Zanón y M. Cortés, Trans. 1 ed.). Barcelona: Paidos.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Filosofía, Matemáticas y Educación: una perspectiva histórico-cultural en Educación Matemática1
Philosophy, Mathematics and Education: A Cultural-Historical Perspective on Mathematics Education
Filosofia, Matemática e Educação: Uma Perspectiva Histórico-Cultural em Educação Matemática
Gilberto Obando Z2
Luis Carlos Arboleda A3
Carlos Eduardo Vasco U4
1Artículo de investigación
2Universidad de Antioquia. Facultad de Educación, Medellín, Colombia. Contacto: gobando1715@gmail.com
3Universidad del Valle, Instituto de Educación y Pedagogía, Cali, Colombia. Contacto: luis.carlos.arboleda@gmail.com
4Universidad Distrital Francisco José de Caldas, Doctorado Interinstitucional en Educación, Bogotá, Colombia. Contacto:carlosevasco@gmail.com
Fecha de recepción: enero de 2014, Fecha de aceptación: julio de 2014
Resumen
Sobre la base de planteamientos epistemológicos derivados de la teoría de la actividad, en este artículo se argumenta en favor de una postura sobre el conocimiento matemático que posiciona los procesos individuales y sociales de su constitución como polos de una dualidad dialéctica mediada por los sistemas de prácticas socialmente compartidos. Con base en estos planteamientos, y tomando en consideración la noción de configuración epistémica, en la segunda parte se presenta una caracterización de los sistemas de práctica matemática. Como resultado de lo anterior, se presentan elementos teóricos y metodológicos que se han mostrado potentes en algunos estudios de las prácticas matemáticas de los individuos en condiciones institucionales específicas.
Palabras clave: Sistemas de práctica matemática; Teorías en Educación Matemática; Teoría de la actividad; configuración epistémica.
Abstract
In this article, based on epistemological approaches derived from activity theory, the authors argue in favor of a conception on the mathematical knowledge that positions the individual and social processes of its formation as poles of a dialectic duality mediated by socially shared practice system. Based on these approaches, and taking into consideration the notion of epistemic configuration, a characterization of mathematical practice systems is proposed in the second part. As a result of these considerations, a few theoretical and methodological elements for the study of individuals’ mathematical practices in specific institutional conditions are presented.
keywords: Mathematical practice systems; Theories in Mathematics Education, Activity Theory; Epistemic configuration.
Resumo
Neste artigo, com base em abordagens epistemológicas derivadas da teoria da atividade, argumenta-se em favor de uma posição sobre o conhecimento matemático que posiciona os processos individuais e sociais de sua formação como polos de uma dualidade dialética mediada por sistemas práticos socialmente compartilhados. Com base nestas aproximações, e tendo em conta a noção de configuração epistêmica, a segunda parte apresenta uma caracterização dos sistemas de práticas matemáticas. Como consequência do acima apresenta elementos teóricos e metodológicos importantes para o estudo das práticas matemáticas de indivíduos em condições institucionais específicas.
Palavras-chave: Sistemas de prática matemática, Teorias em Educação Matemática, Teoria da Atividade, Configuração epistêmica.
Introducción
La educación matemática, en su proceso de consolidación, ha transitado por diferentes caminos teóricos, algunos complementarios, otros excluyentes, pero en todo caso, fundamentados en procesos interdisciplinares que muestran su complejidad (Vasco, 1994), al punto que se considera, en el presente, un campo de investigación y de prácticas en construcción, un cruce de caminos de diferentes enfoques teóricos y metodológicos (Clements, Bishop, Keitel-Kreidt, Kilpatrick y Leung, 2013; D'Amore, 2005; Sriraman y English, 2010). Aún con el riesgo de simplificar la complejidad de la discusión, puede decirse que estos enfoques se despliegan entre el individualismo monismo epistémico y cognitivo, y las posturas de corte dialógico en donde lo cognitivo y epistemológico se explican como procesos eminentemente culturales.
Siendo conscientes de las tensiones generadas en este debate acerca de si lo individual o lo social es lo determinante en los procesos de constitución del conocimiento, en este artículo, sobre la base de planteamientos que provienen de la teoría de la actividad y de una filosofía de la práctica, se busca argumentar en favor de cuestiones relativas tanto al conocimiento matemático, como a su aprendizaje. Se muestra que lo individual y lo social lo institucional son polos de una tensión dialéctica movilizada a partir de los sistemas de prácticas históricamente constituidos. Como lo manifestó John Dewey, se trata de reconocer que la construcción de la experiencia humana no es sólo el producto de la acción mental del individuo, sino también el resultado de los procesos sociales subyacentes a las relaciones humanas:
[…] vivimos, del nacimiento hasta la muerte, en un mundo de personas y cosas, que en gran medida son lo que son por lo que se ha hecho y transmitido desde las actividades humanas previas. Cuando se pasa por alto este hecho, la experiencia se trata como si fuera alguna cosa exclusivamente dentro del cuerpo y la mente de un individuo. No debería ser necesario decir que la experiencia no se produce en un vacío. Hay fuentes fuera de un individuo que dan lugar a la experiencia. (Dewey, 1960, p. 43)
Estas fuentes externas provienen de la cultura en forma de sistemas de prácticas institucionalizadas que reglan las formas de acción de los individuos acción orientada a una finalidad, acción con otros, y que a su vez posicionan al individuo frente a esa acción conjunta habitus, en el sentido de Bourdieu.
Los individual y lo social del conocimiento
Una práctica o mejor, un sistema de prácticases un conjunto de estructuras dinámicas objetivas y de condiciones objetivadas socialmente que orientan y limitan las formas de hacer y de pensar de los individuos adscritos a una institucionalidad específica, pero a la vez, en tanto la adscripción institucional de la acción del individuo no es una imitación ciega ni una repetición mecánica, es también el conjunto de posiciones subjetivas que condicionan la manera como el individuo actualiza su acción en un aquí y un ahora (Bourdieu, 1977, 2007; Bourdieu y Johnson, 1998). Estas estructuras dinámicas objetivas permiten el mínimo de acuerdos posibles para la movilización de la actividad de los individuos y generan, por tanto, una disposición de los sujetos, unas formas de sensibilidad para la orientación subjetiva y objetiva de su acción. Por su parte, el posicionamiento subjetivo es el que permite al sujeto, en el marco de las disposiciones objetivas de su campo, “ver” la ocasión para la acción, imprimir un enfoque o forma específica a su actividad, hacer de su práctica un objeto de reflexión. En el marco de esta tensión continua entre el conjunto de restricciones que un sistema de prácticas impone al individuo, y el posicionamiento subjetivo en la práctica actuada, es donde el sujeto toma distancia en un acto de creación libertad creativa en el marco de las condiciones del campo de prácticas que le permite reflexionar sobre su práctica, transformar su acción y construir conocimiento.
De otro lado, lo institucional denota ese espacio simbólico con límites más o menos definidos de prácticas compartidas por un colectivo de individuos, los practicantes de esa comunidad, espacio donde se comparte, se negocia, se actúa con los otros donde también se excluye, en donde resuenan las voces presentes de muchos otros y las voces pasadas que han constituido la memoria cultural de la comunidad. El término institucional hace notar que cuando se despliega una práctica en, o con, las matemáticas, ésta se hace bajo unas condiciones específicas que le dan las marcas propias de un momento, época y lugar maneras de hacer, de pensar, de relacionarse con y a través de las matemáticas, fines, medios, utilidad, entre otros, que imprimen a la acción del individuo unas condiciones que él comparte con otros individuos. Lo institucional dispone al individuo en un conjunto de formas de acción socialmente constituidas, que le permiten ser en y desde la cultura a través de su acción.
Lo individual es la inscripción del ser en ese capital simbólico construido por la comunidad: el individuo es, en tanto es reconocido por otros, en oposición a otros lo comunal se constituye sobre la base de las subjetividades de los individuos. El individuo se hace en la medida que se inscribe en ese conjunto de prácticas compartidas, y esa inscripción es aprendizaje. A la acción de aprender, siguiendo a Radford (2008, 2010), se le puede llamar la subjetivación del saber, es decir, apropiarse del legado cultural institucionalizado en la comunidad, hacer objeto aquellas estructuras idealizadas en la cultura, constituirse como individuo en el seno de una comunidad a través de la acción reflexiva con y sobre las prácticas socialmente compartidas. Por otro lado, aprender es también un proceso semiótico cultural de objetivación de ciertos saberes, un proceso reflexivo de transformación de las prácticas matemáticas que lo lleva a hacerse críticamente consciente de una forma codificada de pensar y de hacer (Radford, 2013). A través del aprendizaje, el individuo a partir de sus prácticas se posiciona en relación a los otros, a la cultura.
Objetos y conceptos matemáticos: síntesis de la acción humana
Sobre los objetos matemáticos
Restivo y Collins (2010) afirman que “los objetos con los que tratan las matemáticas modernas…son reales en el siguiente sentido. Ellos no son cosas,…, ellos son, por el contrario, las operaciones, las actividades que los matemáticos pueden realizar.” (p. 11, cursivas en el original).
Los objetos matemáticos provienen, no de la abstracción de objetos reales mediante la descripción de sus características principales, sino de un proceso de objetivación de procedimientos. Ellos no provienen de una realidad exterior, independiente del hombre, representando la esencia desprovista de impurezas materiales, sino que ellos formalizan la acción humana (Giusti, 2000, pp. 25-26, cursivas en el orginal).
Los objetos matemáticos antes que ser abstracciones sobre otros objetos son abstracciones sobre la acción instrumentalmente mediada, con y sobre tales objetos si se quiere de nivel previo. El objeto sintetiza un campo complejo de experiencias, es la percepción de un conjunto complejo de operaciones y relaciones que se tematizan5 a partir de la experiencia vivida para la constitución de nuevos objetos. Para el caso de las matemáticas, los objetos sintetizan no solo las formas de relación de las personas con los otros objetos de conocimiento matemático heredados de la cultura, sino también las formas de relación con el resto del mundo.6 Ese es el eterno ciclo creativo, en donde nuevos objetos emergen como formas idealizadas de patrones de actividad sobre los objetos culturalmente ya constituidos. Estas formas idealizadas, estos patrones de actividad se fijan en el signo que, a partir de ese momento, es la forma objetivada del objeto de conocimiento constituido.
Esta constitución de objetos es lo que Radford (2009, 2013) denomina objetivación, entendida ésta como un proceso social activo y creativo de construcción de sentidos y significados para los objetos de conocimiento en relación con las formas culturales de hacer y de pensar conocimiento matemático. Estos sentidos y significados descansan no sólo en el cuerpo de conocimientos estructurados formalmente conceptos, objetos, axiomas, teoremas, entre otros, sino también, en las acciones gestos, técnicas, modos de hacer, en los medios para dichas acciones signos, instrumentos, y otros en las formas de razonamiento y de enunciación géneros discursivos, en términos bajtinianos aceptadas como válidas y, en general, en el conjunto de ideologías7 que permiten ciertas formas de significación en relación con los objetos de conocimiento. Esta superestructura simbólica, como dice Radford (2008, 2009), conforma el espacio simbólico de los medios semióticos de objetivación, que la cultura pone a disposición de los individuos para su posicionamiento ante el mundo, para la constitución de su experiencia matemática.
Sobre los conceptos matemáticos
En palabras de Frege (1996a, 1996b), un concepto es toda predicación que se realice sobre los objetos. Así por ejemplo, al afirmar que un cuadrado es una figura geométrica con sus cuatro lados iguales y sus cuatro ángulos iguales, la idea de igualdad en ángulos, y de igualdad en lados, expresan dos propiedades atribuibles a todo aquello que sea cuadrado, o a la inversa, toda figura geométrica que haga verdaderas estas esta proposición cumplir al tiempo las dos propiedades, los dos conceptos es el objeto cuadrado. Así pues, los conceptos se expresan, toman forma, se constituyen a través de la palabra.
De otra parte, y siguiendo los planteamientos de Vygotsky (1993, 1994), detrás del concepto no sólo está la conexión del objeto con su significado, sino que, en ese proceso de elaboración del significado, la palabra que designa el objeto sintetiza el conjunto de operaciones mentales que permiten la abstracción de los atributos del objeto que son resaltados en un determinado concepto. Dicho de otra manera, el proceso de formación de un concepto implica un proceso de generalización de atributos, pero sobre todo, la síntesis de dichos atributos en una nueva unidad, el concepto formado. Finalmente, los conceptos matemáticos, en tanto conceptos científicos, deben ser considerados como pertenecientes a una red sistémica, esto es, que cada nuevo concepto debe posicionarse en el marco de una red compleja de relaciones con otros conceptos relativos al mismo y a otros objetos , lo cual permite relacionar diferentes objetos entre sí.
Actividad orientada: objetivación-subjetivación del ser
En una primera aproximación se puede entender la actividad como una categoría filosófica que “refleja la relación del sujeto humano como ser social hacia la realidad externa, relación mediatizada por el proceso de transformación y cambio de esta realidad” (Davidov, 1988, p. 11). Esta categoría se erige como “…la abstracción teórica de toda práctica humana universal, que tiene un carácter histórico-social…” (Davidov, 1988, p. 27). Se puede entonces entender la actividad como el conjunto de acciones desarrolladas por los seres humanos, en contextos particulares de práctica, socialmente orientada a un fin (intencional) (Leontiev, 1978; Ricoeur, 2001). Esta orientación intencional es regulada por la adscripción a un sistema de prácticas en un campo de experiencias determinado. La práctica objetiviza la acción del individuo, la orienta hacia objetos específicos de su campo de experiencias.
La actividad es un proceso colectivo en el cual la inter-acción es la base para la construcción de sentidos y significados, es decir, la construcción de una conciencia individual que no es una conciencia solipsista en el marco de los procesos sociales subyacentes, en tanto la acción del individuo en el proceso de objetivación está determinada por los agentes, instituciones o instrumentos del campo ser con otros. Esto muestra el carácter intersubjetivo de la actividad, en función del carácter re-flexivo de las acciones humanas. La re-flexión, siguiendo a Radford (2006, 2008), es la dialéctica entre una realidad constituida histórica y culturalmente y un sujeto que a través de sus acciones refracta y modifica dicha realidad, pero que además, se vuelve sobre sí mismo para construir un cambio de estructura en su existencia. La reflexión es la forma por medio de la cual el individuo refracta sobre sí mismo, a través de su acción, el conjunto de instrumentos que la cultura pone a su disposición. Esto significa que la acción del individuo no es pasiva frente a los instrumentos sino que, en su acción reflexiva, los transforma, los re-significa. Esta autonomía del sujeto en el campo, en términos de conciencia o capacidad reflexiva sobre su propia práctica, es lo que puede llamarse la subjetividad: “La subjetividad aparece como forma de participación y contribución a la práctica social, de cambio de avance, y así, como la forma en que las realizaciones prácticas de los humanos son conducidas hacia sí mismos, hacia otras personas, hacia su mundo” (Stetsenko, 2005, p. 82). Pertenecen al dominio de la subjetividad los ideales, conductas y valores a los que apela el sujeto para darle sentido a su práctica (ver por ejemplo, Detlefsen, 2005, sobre los ideales en las matemáticas en el siglo XIX). La subjetivación es entonces el acto por medio del cual el individuo se constituye como ser, es la manera como en función de su acción reflexiva se posiciona frente al mundo. Es la manera como el individuo regula su participación en los entornos de la actividad práctica social, y por ende, la forma como habita las instituciones, las hace vivir en la revisión y transformación continua de dichos sistemas de prácticas (Bourdieu, 2007).
Lo Histórico–Cultural: 9 fundamentos semiótico-cognitivos
De acuerdo con lo antes expuesto, el desarrollo del individuo en función de la experiencia humana debe comprenderse como un proceso mediado culturalmente, institucionalmente situado en contextos específicos de práctica las acciones de los individuos y el contexto para la acción forman una unidad inseparable, y cognitivamente distribuido en los otros, los instrumentos, los entornos sociales y naturales (Cole y Wertsch, 1996).
Medición y cultura: construcción semiótica de la conciencia
Vygotsky introduce elementos de orden cultural en los mecanismos explicativos de los procesos del desarrollo humano. Estos procesos son ser estudiados en dos grupos de fenómenos, totalmente interconectados, aunque perfectamente diferenciados. De un lado, en relación con el dominio de los medios externos de desarrollo cultural: el lenguaje, la escritura, el cálculo, el dibujo, entre otros. De otro lado, el de las funciones psíquicas superiores, tales como la percepción, la atención voluntaria, la memoria lógica, la formación de conceptos, el lenguaje oral, el lenguaje escrito, y demás. El estudio de estos dos grupos de fenómenos pone de manifiesto la tesis central de la teoría vygotskiana, a saber, la conciencia, la experiencia humana, como expresión de su conducta, tiene naturaleza doble: se desarrolla en el plano de la cultura, de sucesos históricamente constituidos, y en el plano interno de la construcción de los esquemas cognitivos. Es en esto que se basa el principio de internalización: la reconstrucción interna, por parte del individuo, de los planos sociales en las funciones psicológicas superiores.
El signo es el medio a través del cual se realiza este proceso en tanto que, de un lado, todo signo es una construcción cultural, y de otro, la acción humana a través del signo le permite al individuo apropiarse de ese legado cultural presente en él formas de hacer, operaciones, y de pensar cristalizadas en el signo, y al hacer esto, el individuo constituye su conciencia, su capacidad crítica frente a esa realidad exterior, posicionándolo frente a su hacer y su saber. Así, los signos, a través de 10 Internalización no es una simple copia de la realidad exterior en la mente de las personas, es un proceso reconstructivo en el que la constitución de esa realidad exterior en los planos cognitivos, modifica la cognición misma del individuo la actividad de los individuos, permiten reconstruir para sí lo que la humanidad ha construido en la cultura. Es en este sentido que Vygotsky refiere la función instrumental de signo, esto es, en relación con algún tipo de operación psicológica memorizar, recordar, informar, elegir, calcular, entre otras, los signos son los instrumentos de la actividad humana es este caso, actividad psicológica, los medios para la ejecución de las acciones cognitivas necesarias en los procesos de constitución de la conciencia como fenómeno cultural.
Actividad y mediación: acción instrumentada, acción con el otro.
Así pues, el concepto de actividad emerge, en la teoría vygotskiana, como un principio explicativo que permite comprender cómo la cultura permea el proceso de constitución de la conciencia humana. Para Vygotsky, es la “actividad humana concreta histórica la que constituye el generador detrás de los fenómenos de la conciencia” (Kozulin, 2003, p. 102). El desarrollo se debe considerar como resultado de las acciones culturalmente significativas y no sólo como un fenómeno biológico.
...la cultura origina formas especiales de conducta, modifica la actividad de las funciones psíquicas, edifica nuevos niveles en el sistema de comportamiento humano del desarrollo... En el proceso de desarrollo histórico, el hombre social modifica los modos y procedimientos de su conducta, transforma sus inclinaciones naturales y funciones, elabora y crea nuevas formas de comportamiento específicamente culturales (Vygotsky, 1995, p. 34).
Cultura y desarrollo se co-determinan. Cuando el individuo actúa sobre su entorno para transformarlo en busca de bienestar, ese medio transformado genera nuevas condiciones para el desarrollo del individuo (Hegedus y Moreno-Armella, 2011).
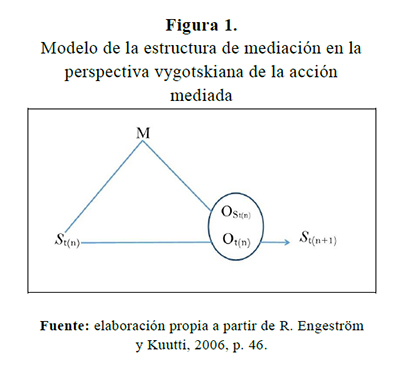
Dialéctica sujeto-objeto: acción medida instrumentalmenteLa idea de mediación instrumental de Vygotsky, o como lo han llamado los teóricos actuales, la acción mediada, es base fundamental para dar cuenta del carácter eminentemente situado histórica y culturalmente de la acción del individuo
En este modelo, S representa un sujeto, M los instrumentos artefactos, signos, símbolos, textos, fórmulas, medios gráfico-simbólicos, explicaciones de otros, y demás y O el objeto/motivo de la actividad.12 La línea St(n)O representa formas de relación natural entre el sujeto y el objeto/motivo sin mediación, mientras que la línea St(n)MO, las interacciones entre el sujeto y el objeto/motivo mediadas instrumentalmente. El subíndice “t(n)” bajo la letra “S” indica un estado específico en un tiempo t dado, de modo que St(n) será el estado del conocimiento del sujeto S en un tiempo t(n) dado, y OSt(n) es el objeto/motivo representado por el sujeto, en el tiempo t(n), vía los medios de mediación, mientras que Ot(n) es el objeto/motivo en sí mismo en dicho tiempo t(n) por lo general, el objeto, como construcción social, no coincide con la representación que el sujeto se hace de dicho objeto, la cual depende de las formas de mediación en el sujeto. Finalmente, St(n+1) es el estado de conocimiento del sujeto en un tiempo posterior a su acción sobre el objeto/motivo O.
A esta perspectiva vygotskiana se le han criticado aspectos como: a) su idea de mediación semiótica, que separa dos procesos de mediación interna y externa a través de dos tipos de instrumentos signos y artefactos y pone el peso de la mediación cognitiva sobre los signos, lo cual deja por fuera toda una serie de acciones e instrumentos para la acción que también inciden en la formación misma de la conciencia en tanto construcciones culturales, b) no mostrar de manera explícita otras formas de mediación entre en el sujeto y el objeto, no presente en los signos o artefactos como instrumentos de mediación, como son las formas de acción social. Parafraseando a Engeström (1999), el modelo triangular da la impresión de que el sujeto actúa en solitario en relación con el objeto/motivo de su actividad, y no muestra las interacciones de los otros con ese mismo objeto/motivo, con el sujeto mismo. Dicho de otra forma, no muestra que la acción del sujeto está inmersa en un complejo sistema de actividades, en el cual las re-presentaciones del sujeto sobre su objeto/motivo de la actividad hacen parte de un sistema estructurado de percepciones y cogniciones pertinentes en el marco de las condiciones institucionales que delimitan las prácticas de los individuos.
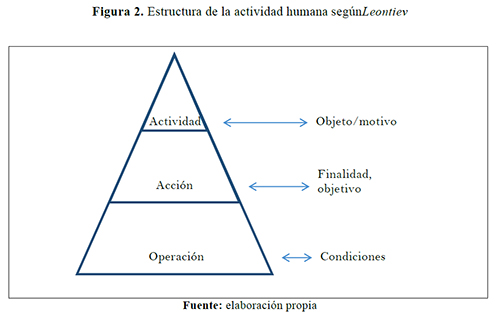
Dialéctica sujeto-objeto: acción medida socialmenteComo se expresó, la actividad se define en relación al conjunto de acciones socialmente dirigidas (orientadas) con el objetivo de alcanzar un fin. Debido a esta orientación hacia una finalidad, la actividad es de naturaleza social, y es la vía por la que el humano ejerce control sobre sí mismo, y sobre los demás. La actividad es entonces un complejo de relaciones entre las personas en el curso de su acción objetiva y en el marco de sistemas de prácticas relativas a un mismo campo. La actividad tiene como principales elementos constitutivos el objeto/motivo, las acciones y las operaciones.
El objeto/motivo de la actividad, aquello hacia lo que se orientan objetivamente las acciones humanas, tiene una doble finalidad: externamente, orienta y dirige el curso mismo de la actividad; e internamente, es representación mental en el sujeto, lo cual permite al ser humano reflexionar sobre la actividad misma y transformarla (Kaptelinin, 2005; Leontiev, 1978). De esta manera, la orientación de la actividad por el objeto/motivo permite la transformación mutua del uno sobre el otro sujeto y objeto, en una doble dimensión que proyecta el objeto sobre la mente de los sujetos, pero que a la vez proyecta la mente de los individuos sobre los objetos de la realidad objetiva (Kaptelinin, 2005). Es decir, la actividad, en la dialéctica entre el acto físico y la representación mental, hace posible la anticipación de la acción por parte de los sujetos actuantes a partir de un proceso estructurado de planificación.
Las acciones son el conjunto de procesos por medio de los cuales los individuos planifican representan mentalmente dice Leontiev un objetivo, y cuyo fruto es alcanzar dicha finalidad objetiva. De esta manera, acciones y finalidades están estrechamente unidas. Las finalidades se dan arbitrariamente en el desarrollo de circunstancias objetivas. Su delimitación y toma de conciencia no es ni automática ni instantánea, sino un proceso de prueba a través de la acción.
Pero las acciones, además de la intención, comportan el cómo lograrlas, es decir, el conjunto de procesos a partir de los cuales se hace concreta la acción. Leontiev llamó a estos procesos las operaciones de la actividad. Las operaciones no están determinadas por la acción en sí misma sino por las condiciones (objetivo-objeto) para ser realizada.
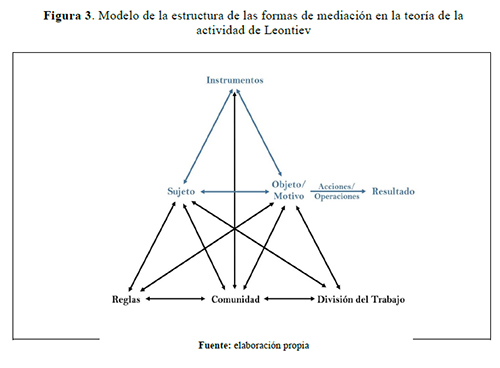
Autores contemporáneos (Cole, 1999a; R. Engeström y Kuutti, 2006; Y. Engeström, 1999, 2009) encuentran en los planteamientos de Leontiev tres elementos nuevos en la noción de mediación: la división social del trabajo, las relaciones con la comunidad, y las reglas o convenciones para la acción. Se amplía el horizonte de la idea de mediación más allá de mediación instrumental, al incluir elementos que permiten comprender la acción del sujeto en el marco de formas sociales más complejas (figura 3).
En este modelo, la división social del trabajo implica que en el curso de la actividad, por lo general, lo que hace un individuo sea sólamente parte de un conjunto de acciones con otros, y por lo tanto, la distribución de las tareas delimita las relaciones de poder y los posicionamientos de unos frente a otros. La comunidad permite comprender los procesos de colaboración entre los diferentes individuos involucrados en la actividad sistemas de prácticas que permiten las interacciones entre los individuos en un marco institucional determinado. Las reglas se refieren a ese conjunto de normas, explícitas e implícitas que regulan las acciones de los individuos en el seno de una comunidad códigos de comportamiento, normas que orientan la acción, entre otros.
Este nuevo modelo expande el triángulo inicial para abarcar las dimensiones sociales y colaborativas de la actividad reglas, comunidad, al igual que incluir las relaciones de poder que se dan en las mismas división social del trabajo. Las flechas entrantes y salientes de cada uno de los puntos, indican que se trata de un modelo sistémico aunque algunas de las interacciones sean difíciles de identificar lo que indica que cada nodo media entre los demás, y todos conjuntamente en la relación sujeto–objeto/motivo de la actividad. Igualmente, el sujeto tiene que ser visto como un individuo en comunidad y, por tanto, la acción que conecta el objeto/motivo de la actividad con el resultado es en realidad un cúmulo de acciones que marchan en paralelo para poder llegar a la meta.
Acción instrumentada: cognición distribuida
Como se puede concluir de las secciones anteriores, la actividad práctica orientada a un fin es objeto de diferentes formas de mediación, una de las cuales se da a través de los instrumentos con los cuales se configura la acción. Los instrumentos, a la vez que síntesis sociales de los procesos de inter-acción, son mediadores en la forma como los individuos se apropian de dichas construcciones sociales entre ellas, el conocimiento. La acción del humano a través de instrumentos la actividad comporta, para ese individuo, apropiarse de la experiencia de la práctica social, la cual, hecha conciencia, se constituye en conocimiento (Leontiev, 1978).
Para Leontiev, el instrumento es a la vez el objeto con el que se realiza la acción laboral, pero también, el objeto social que sintetiza unos modos de acción socialmente elaborados. El instrumento es el conjunto complejo de métodos y operaciones socialmente elaboradas y cristalizadas en él.Es una construcción social material y simbólica, y por tanto una abstracción, una generalización de las acciones culturales cristalizadas en su estructura (Leontiev, 1978).
Alex Kozulin retoma la noción de instrumento psicológico de Vygotsky, y lo redefine alrededor de conceptos más amplios: signos, símbolos, textos, fórmulas, medios gráfico-simbólicos. En sus palabras, “Los instrumentos psicológicos son los recursos simbólicos que ayudan a los individuos a dominar sus propias funciones psicológicas ‘naturales’...” (Kozulin, 2000, p. 15). En ese sentido, los instrumentos no son sólo prótesis que amplifican las capacidades humanas para hacer cosas. Son verdaderas extensiones de su cuerpo, de su mente, que llevan la cognición humana más allá del cuerpo, distribuyéndola en los instrumentos para la acción, en los otros con los que se actúa. Decía Dewey que cuando el niño aprende a hablar, no solo tiene nuevas necesidades y deseos, también se le abren nuevas posibilidades para un saber subsiguiente (Dewey, 1960)
De esta manera, la construcción del instrumento que realiza el ser humano se hace indisociable del el desarrollo mismo de las acciones prácticas humanas, en tanto toda acción es mediada por el uso de un instrumento (físico o simbólico). El individuo, en el curso de su actividad, co-actúa con el instrumento, y en el desarrollo de esta co-acción, se modifican mutuamente (Hegedus y Moreno-Armella, 2010; Moreno-Armella & Hegedus, 2009). Este proceso de co-acción determina lo que se ha denominado la génesis instrumental, entendida en un doble movimiento: el primero, en relación al proceso mediante el cual los instrumentos son incorporados al sistema de actividades de los individuos dando forma a su acción, y donde la apropiación del instrumento es contextualmente situada dentro de, y con respecto a, un determinado sistema de prácticas (instrumentación), y el segundo, en función de la manera como la evolución y desarrollo de las formas de acción instrumentada de los individuos, y las condiciones de entorno dentro de las cuales se desarrollan tales acciones, afectan al instrumento mismo (instrumentalización).
Sistemas de práctica matemática
Configuración epistémica
Como se expresó en las secciones anteriores, toda práctica, desde el punto de vista institucional, descansa sobre un conjunto de valores y visiones que demarcan las fronteras dentro de las cuales se desarrollan los episodios particulares de la investigación matemática en épocas y lugares específicos. Estos valores y visiones toman forma en relación a las técnicas disponibles, a los tópicos de investigación y problemas en consideración, a las orientaciones heurísticas, entre otras; propias o características de una comunidad en el momento particular en el que desarrolla su actividad matemática. Este conjunto de recursos institucionales físicos e intelecutales constituyen lo que Moritz Eppe (2004) denominó una configuración epistémica, esto es, la episteme que hace posible la existencia de prácticas matemáticas determinadas: que reconocen su campo de problemas de una determinada manera, reconocen ciertas técnicas o formas de heurísticas y no otras, y reconocen formas de razonar o enunciar específicas, entre otras.
Godino y colaboradores (Godino y Font, 2007) introducen la noción de configuración epistémica de manera similar, con la ventaja de aplicar sus análisis no al ámbito de la investigación matemática, sino a los fenómenos de constitución de conocimiento matemático en contextos escolares. En su perspectiva, una configuración epistémica refiere a la estructura de objetos y sus respectivos sistemas de significados, al conjunto de elementos inmediatos al entorno del aula de clase, sus formas de organización, sus formas de significación. De esta forma, la atención se fija en el proceso vivido por el saber escolar su tiempo y espacio, en sus sentidos y significados, y para los fines de un análisis micro-didáctico detallado, el estudio de las configuraciones epistémicas centra la mirada en el cómo se constituyen los sistemas de práctica matemática en el aula de clase, en la forma como se estructuran los sentidos y significados de los elementos que la constituyen y que se construyen a partir de la práctica misma, y por ende, de los sentidos y significados para los objetos de conocimiento matemático desde el punto de vista del saber institucionalizado, para diferenciarlo del conocimiento como fue apropiado por el alumno.
Práctica matemática
Las prácticas son siempre realizadas por personas, y por tanto, al decir “práctica matemática” se están refiriendo cierta forma de acción de los individuos, en sus relaciones entre sí, y con el medio, a través de los procesos de objetivación tanto de la cantidad y la forma por ejemplo, medir, contar, comprar, vender, intercambiar, construir, fabricar, estimar, describir, localizar, como de la variación de una u otra movimiento, cambio, comparación, transformación, y otras.
Los medios para la acción, ese legado cultural a partir del cual se despliega cualquier práctica matemática, se pueden caracterizar a partir de los siguientes elementos: los objetos de conocimientos con y sobre los cuales se actúa los conceptos que se enuncian sobre los mismos, los instrumentos para la acción, las técnicas que permiten tales instrumentos, los problemas, en tanto metas que orientan la acción, las formas de discursividad que permiten poner el hacer en el lenguaje formas de decir, de escribir, de comunicar, y finalmente el conjunto de visiones metamatemáticas que permiten la toma de decisiones sobre el hacer cosmovisiones, valoraciones sobre las matemáticas, fines de las matemáticas, posturas filosófica y ontológicas.
Los elementos antes enunciados no sólo constituyen la práctica sino que, en el curso de la actividad matemática, son emergentes de la práctica misma en la medida que se forman, se transforman, se sustituyen (Kitcher, 1984). En este sentido, dichos elementos no son estáticos sino que cambian en el tiempo, y este cambio determina la constitución de nuevo conocimiento matemático. El cambio de las prácticas se ve en la medida que, o nuevas técnicas sustituyen parcial o totalmente las anteriores, o bien nuevos objetos emergen para brindar una mejor comprensión de las técnicas utilizadas, y por ende, una mejor justificación de las mismas. Pero a la vez, este proceso permite la emergencia de nuevos instrumentos para la acción, y el ciclo continua.
Los problemas por resolver
Los problemas por resolver son esos campos válidos de indagación, y de cuyo tratamiento emerge el conocimiento matemático objeto de estudio. El análisis de los problemas en términos de las prácticas matemáticas es importante en tanto permite comprender cómo en las situaciones17 que éstos propician se articulan los objetos de conocimiento que problematizan, las técnicas e instrumentos disponibles para su tratamiento y, en general, los conceptos que se movilizan en los discursos que se constituyen en relación a la solución de tales problemas.
Para dar cuenta de lo anterior, y apoyándose en Rabardel y Bourmaud (2005), el análisis de los problemas al interior de una práctica se puede hacer desde dos perspectivas: 1) tipos de situaciones, referidas al conjunto de problemas agrupados en función de características lo suficientemente cercanas para que la actividad de los sujetos se desarrolle con cierto nivel de estabilidad; y 2) familias de actividad, para referir a la a la finalidad de la acción común, es decir, en función de las prácticas matemáticas que despliegan los individuos al enfrentar los problemas. De esta manera se pueden diferenciar los aspectos propiamente estructurales del problema por resolver, de los relacionados con las formas de actuación del individuo al enfrentarse con el mismo. Los problemas se pueden mirar en función de dos principios que responden a su estructura, y a la forma de la actividad de los individuos.
La estructura apunta a identificar en los problemas la naturaleza de las cantidades o las formas involucradas continuas o discretas, las representaciones y las cuantificaciones de las mismas procesos de medici&oacut;en, simbolización, graficación, entre otras, las acciones sobre estas agregar-desagregar, agrandar-achicar, transformar, y otras, las relaciones entre ellas comparación por cociente o por diferencia, covariación, y su status lógico lo dado o lo desconocido. Por su parte las familias de actividad apuntan a identificar la estructura de la acción que el sujeto configura en función de los instrumentos disponibles. Por ejemplo, calcular, explicar, justificar, formular, representar, modelar, aplicar (Giaquinto, 2005).
Formas de discursividad
Desde una perspectiva bajtiniana, las prácticas se hacen signo a través del lenguaje. Pero a la inversa, es el lenguaje un mecanismo fundamental para la constitución de tales prácticas. En este sentido, el lenguaje cumple una doble función, es el instrumento fundamental en la construcción de la conciencia humana, y a la vez, determina el desarrollo social del ser humano, “Con la ayuda del lenguaje se crean y se forman los sistemas ideológicos, la ciencia, el arte, la moral, el derecho, y al mismo tiempo crea y forma la conciencia de cada hombre” (Bajtín, 1993, p. 242). Todo sistema de prácticas está en estrecha conexión con el uso social de la lengua.
A cada forma de práctica se corresponden formas específicas de uso, o mejor, esferas distintas del uso de la lengua. Estas esferas de uso de la lengua, estas prácticas sociales del uso, toman forma a través del enunciado. La unidad básica, el enunciado que fusiona contenido temático, estilo y construcción composicional está indisolublemente unido a una esfera de comunicación: “todo enunciado tomado aisladamente es, por supuesto, individual, pero cada esfera dada del uso de la lengua elabora sus tipos relativamente estables de enunciados, a los que denominaremos géneros discursivos” (Bajtin, 1990, p. 248). Así, “los géneros discursivos son especies de esquemas […] que orientan la construcción de formas típicas de enunciados donde se dibujan, se muestran simulacros del mundo relacionados con los grandes dominios de la actividad” (Martínez, 2005, p. 14, cursivas del original). El género discursivo es una especie de “práctica social discursiva, mediada por un contrato de comunicación e intercambio verbal� (Calderón, 2003) entre dos interlocutores ligados por una situación de comunicación específica.
Finalmente, los actos enunciativos propios de las prácticas sociales y humanas tienen sentido en el marco del desarrollo de procesos discursivos:
La discursividad puede entenderse como la característica particular que define la comunicación social como actividad verbal. [lo cual significa que] 1) Se trata de una actividad humana de tipo semiótico y de naturaleza verbal… 2) Esta actividad permite la configuración de sujetos discursivos; … 3) La actividad discursiva es realizada en la cotidianidad por sujetos de habla o enunciadores, quienes desarrollan e interiorizan su experiencia discursiva en los procesos de constante interacción con los enunciados individuales ajenos. (Calderón, 2003).
De esta forma, el sujeto asume un papel dialógico ante los demás, es la suma de la multitud de voces pasadas y presentes, y su voz es la réplica a otras voces.
La elaboración de formas discursivas es fundamental en el desarrollo de las matemáticas. A través de éstas el lenguaje se extiende más allá de los límites de la acción física, como se puede ver, por ejemplo, en la teoría de los números reales. El objeto número real, como objeto abstracto, no estaba en los griegos; se desarrolló a través de un lenguaje que hizo posible la extensión de las operaciones a aquellos ámbitos que superaban los límites de lo físico los números complejos, los irracionales, entre otros. Se puede hablar entonces de una doble funcionalidad del lenguaje en la actividad matemática: es el vehículo para realizar las operaciones matemáticas pero también el medio para expresarlas (Kitcher, 1984).
Instrumentos y procedimientos
Como se dijo, los instrumentos son ese conjunto de recursos simbólicos signos, símbolos, textos, fórmulas, medios gráfico-simbólicos, artefactos, software, gestos que constituyen los medios para la acción matemática. Además, los instrumentos que median las prácticas matemáticas en el aula de clase, dado que cristalizan en su estructura ciertas formas de relación que pueden ser puestas en analogía con formas de relación entre conceptos y objetos matemáticos, en lo que se ha llamado el campo simbólico del artefacto, son portadores de conocimiento y por ende, tienen capacidad de generar procesos de aprendizaje cuando son usados en el curso de la actividad de las personas. Igualmente, este potencial del instrumento para incorporar conocimiento es lo que le da la posibilidad de estar en permanente desarrollo incorporando las modificaciones que le hacen los individuos a través de su uso, generando lo que Moreno y Hegedus (2010; 2009) han denominado la zona de desarrollo próximo del instrumento, refiriéndose a ese potencial de uso del instrumento, que lo pone, en la relación mediadora entre el individuo y su actividad, más allá de los fines para los que ha sido utilizado.
Objetos y conceptos
Como se mostró ampliamente en las secciones anteriores, objetos y conceptos tienen una base firme en la acciones de individuo y por tanto, en su constitución, un punto crucial lo determinan, de un lado, el tipo de problemas al que se enfrentan las personas, a los cuales se orienta su práctica; y de otro, los instrumentos disponibles para la acción. En particular, el uso funcional de los signos juega un papel central en la formación de objetos y conceptos, a través de ellos se dispone de los medios para dirigir objetivamente la acción, analizar y destacar atributos, abstraer y sintetizar.
A manera de síntesis
En suma, al proponer la dialéctica entre lo individual y lo social dialéctica mediada por las prácticas sociales en palabras de Cobb (2006), se trata es de investigar la persona-individual-en-la-práctica-cultural. Se plantea entonces no una separación entre los aspectos individuales o sociales en la construcción de conocimiento, sino que, por el contrario, se muestra que lo social y lo individual son como las dos caras de una misma moneda, lo individual y lo social se constituyen uno al otro dialécticamente.
La teoría de la actividad entrega entonces una serie de instrumentos para la comprensión de esa dialéctica. La noción de mediación instrumental, o mejor aún, de acción mediada instrumentalmente, entendiendo el instrumento en el sentido amplio de los medios culturales de objetivación, es un lente potente para comprender la manera en que la cultura media en los procesos de constitución del conocimiento y de la conciencia humana. De manera similar, la acción del sujeto en el marco de la actividad colectiva, la orientación social de la acción sobre un objetivo, la planeación de la acción y la ejecución de la misma, y el uso de los instrumentos para la acción, permiten comprender cómo los procesos sociales se constituyen en procesos mentales. De otro lado, la subjetivación del ser, presente en los mecanismos de regulación de la participación en las prácticas sociales por parte del sujeto, en su reflexión sobre la acción, en su orientación hacia el objeto de la actividad produciendo nuevos objetos/motivos para la acción, creando o transformando los instrumentos, produciendo nuevos sentidos y significados para el sistema de prácticas, muestran el retorno del sujeto sobre el mundo social y cultural, “la subjetividad humana, al retornar sobre el mundo a través de la actividad, inevitablemente cambia al mundo, posiciona al sujeto en sí mismo frente a la realidad material de las prácticas humanas en sus formas objetivas reificadas [en los instrumentos y los objetos de la actividad]” (Stetsenko, 2005, p. 83).
Al aplicar estas ideas sobre la actividad es necesario preguntarse, para una práctica determinada, cuáles son sus instrumentos y cuáles las operaciones propias de dicha actividad. Se puede proponer, al menos para las prácticas matemáticas, que la actividad consiste en acciones orientadas a la solución de problemas. Los instrumentos son fundamentalmente de orden semiótico: el lenguaje natural, las notaciones algebraicas, las gráficas cartesianas, las figuras geométricas, entre otras. Por su parte, las operaciones se constituyen a partir de todos los procesos, formas de hacer matemáticas, construidos históricamente por la humanidad, que se han cristalizado en los diferentes sistemas de representación que se usan en las matemáticas los registros algebraicos, las representaciones cartesianas, las figuras geométricas, y otros. Los procesos de instrumentación e instrumentalización el movimiento continuo entre lo individual y lo social, muestran la manera como avanza el conocimiento matemático es el caso, por ejemplo, de la emergencia de los procesos algebraicos sobre los aritméticos, lo cual implica una profunda transformación en la actividad matemática de las personas.
Tal noción de práctica matemática no es estática, sino que es institucionalmente situada, semióticamente mediada, históricamente constituida, a la vez que dinámicamente transformada en el tiempo. El carácter institucional de la práctica se evidencia en los tipos de restricciones sobre el lenguaje, sobre las técnicas, que el campo impone a los individuos en el seno de la comunidad es el caso de los intuicionistas frente a los formalistas en los albores del siglo XX. El carácter individual se evidencia en el posicionamiento del individuo frente al sistema de prácticas en la acción reflexiva sobre su práctica y por ende en los procesos creativos del individuo libertad creativa en el marco de las reglas definidas por el campo. En ese movimiento individual-social, las prácticas se transforman, emergen nuevas técnicas, nuevos objetos, nuevos conceptos, nuevos discurso, en fin, nuevas condiciones para acción práctica.
En este marco, el aprendizaje debe ser entendido como un proceso de transformación constante del individuo transformación de las prácticas, en el contexto de un ordenamiento disposición delimitado por los sistemas de prácticas socialmente objetivados que orientan la actividad de los sujetos, y de un posicionamiento frente a dichos sistemas de actividad determinado por la subjetividad del ser.
Agradecimientos
Este artículo es derivado de la tesis doctoral del primer autor titulada Sistemas de prácticas asociados a las razones, las proporciones y la proporcionalidad: el caso de las configuraciones epistémicas en algunos grados de la educación básica, tesis elaborada en el marco del énfasis en Educación Matemática del Doctorado Interinstitucional en Educación de la Universidad del Valle.
Referencias
Arboleda, L. C. (2011). Objetividad matemática, historia y educación matemática. En L. C. Recalde y G. I. Arbeláez (Eds.), Los números reales como objeto matemático: una perspectiva histórico epistemológica. Cali: Universidad del Valle.
Bajtin, M. (1990). El problema de los géneros discursivos (T. Bubnova, Trans.). En M. Bajtin. (Ed.), La estética de la creación verbal. (10 ed.). México: Siglo XXI Editores.
Bajtín, M. (1993). ¿Qué es el lenguaje? (A. Bignani, Trans.). En A. Silvestri y G. Blanck (Eds.), Bajtin y Vigotski: la organización semiótica de la conciencia. Barcelona,: Anthropos.
Bourdieu, P. (1977). Outline of a theory of practice (R. Nice, Trans.). Cambridge: University Press.
Bourdieu, P. (2007). El sentido práctico (A. Dilon, Trans.). Buenos Aires: Siglo XXI Editores.
Bourdieu, P. and Johnson, R. (1998). Practical Reason: On the Theory of Action. California: Stanford University Press. Calderón, D. (2003). Género discursivo, discursividad y argumentación. Enunciación (8).
Clements, M. A., Bishop, A., Keitel-Kreidt, C., Kilpatrick, J., and Leung, F. K.-S. (Eds.). (2013). Third International Handbook of Mathematics Education. New York: Springer.
Cobb, P. (2006). Supporting a discourse about incommensurable theoretical perspectives in mathematics education. Philosophy of Mathematics Education Journal, (19).Available: http://www.people.ex.ac.uk/PErnest/pome19/index.htm
Cole, M. (1999a). Cultural psychology: some general principles and a concrete example. In Y. Engestrom, R. Miettinen and R.-L. Punamaki (Eds.), Perspectives on activity theory. New York: Cambridge University Press.
Cole, M. (1999b). Psicología cultural: una disciplina de pasado y del futuro (T. d. Amo, Trans.). Madrid: Ediciones Morata.
Cole, M., and Wertsch, J. (1996). Beyond the individual-social antinomy in discussions of Piaget and Vygotsky. Human Development, 39(5), 250-256. Doi: 10.1159/000278474
D'Amore, B. (2005). Bases filosóficas, pedagógicas, epistemológicas y conceptuales de la didáctica de la matemática (M. I. F. Pinilla, Trans.). Mexico: Editorial Reverte.
D'Amore, B. y Godino, J. (2007). El enfoque ontosemiótico como un desarrollo de la teoría antropológica en didáctica de las matemáticas. Revista Latinoamericana de Investigación en Matemática Educativa., 10, 191-218.
Daniels, H. (2003). Vygostky y la pedagogía (G. Sánchez Barberan, Trans.). Barcelona: Ediciones Paidos.
Daniels, H. (2008). Reflections on points of departure in the development of sociocultural and activity theory. In B. v. Oers, W. Wardekker, E. Elbers and R. v. d. Veer (Eds.), The transformation of learning: advances in cultural-historical activity theory. New York: Cambridge University Press.
Davidov, V. (1988). La enseñanza escolar y el desarrollo psíquico, Investigación psicológica teórica y experimental. (M. Shuare, Trans.). Moscú: Editorial Porgreso.
Detlefsen, M. (2005). Formalism. In S. Shapiro (Ed.), The Oxford handbook of philosophy of mathematic and logic. New York: Oxford University Press.
Dewey, J. (1960). Experiencia y Educación (7ma ed.). Buenos Aires: Editorial Losada.
Engeström, R., and Kuutti, K. (2006). Activity theory. In K. Brown (Ed.), Encyclopedia of language and linguistics (2 ed.). Amsterdam: Elsevier Ltd.
Engeström, Y. (1999). Activity theory and individual and social transformation. In Y. Engestrom, R. Miettinen and R.-L. Punamaki (Eds.), Perspectives on activity theory. New York: Cambridge University Press.
Engeström, Y. (2009). The future of activity aheory: A rough draft. In A. Sannino, H. Daniels and K. D. Gutiérrez (Eds.), Learning and expanding with activity theory. New York: Cambridge University Press.
Engeström, Y., and Sanino, A. (2010). Studies of expansive learning: Foundations, findings and future challenges. Educational Research Review, 5, 1-24. Doi: 10.1016/j.edurev.2009.12.002
Epple, M. (2004). Knot Invariants in Vienna and Princeton during the 1920s: Epistemic configurations of mathematical research. Science in Context, 17, 131-164.
Ferreirós, J. (2010). Mathematical Knowledge and the Interplay of PracticesEPSA Philosophical Issues in the Sciences. In M. Suárez, M. Dorato and M. Rédei (Eds.), EPSA Philosophical Issues in the Sciences. Dordrecht: Springer Netherlands.
Frege, G. (1996a). Consideracionse sobre Sentido y Referencia (U. Moulines, Trans.). En J. Mosterín (Ed.), Escritos Filosóficos (1 ed.). Barcelona: CRITICA.
Frege, G. (1996b). Función y Concepto (U. Moulines, Trans.). En J. Mosterín (Ed.), Escritos Filosóficos (1 ed.). Barcelona: CRITICA.
Giaquinto, M. (2005). Mathematical activity. In P. Mancuso, K. F. Jørgensen and S. A. Pedersen (Eds.), Visualization, explanation and reasoning styles in mathematics (Vol. 327). Netherlands: Springer. Available: http://link.springer.com/chapter/10.1007%2F1-4020-3335-4_5. Doi: 10.1007/1-4020-3335-4_5
Giusti, E. (2000). La naissance des objets mathématiques (G. Barthélemy, Trans.). Turin Ellipses.
Gueudet, G., and Trouche, L. (2012). Teachers’ work with resources: documentational geneses and professional geneses. In G.
Gueudet, L. Trouche and B. Pepin (Eds.), From text to ‘Lived’ resources: mathematics curriculum materials and teacher development. Dordrecht: Springer.
Godino, J., Batanero, C. y Font, V. (2008). Un enfoque ontosemiótico del conocimiento matemático y la instrucción matemática. Paper presentado en el Seminario del Doctorado Interinstitucional de Educación, Universidad del Valle.
Godino, J., and Font, V. (2007). La noción de configuración epistémica como herramienta de análisis de textos matemáticos: su uso en la formación de profesores. En C. Crespo (Ed.), Acta Latinoamericana de Matemática Educativa Vol.20 (1 ed.). Mexico: Comité Latinoamericano de Matemática Educativa.
Hegedus, S. and Moreno-Armella, L. (2010). Accommodating the instrumental genesis framework within dynamic technological environments. For the Learning of Mathematics, 30(1), 26-31.
Hegedus, S. and Moreno-Armella, L. (2011). The emergence of mathematical structures. Educational Studies in Mathematics. Doi: 10.1007/s10649-010-9297-7
Kaptelinin, V. (2005). The object of activity: making sense of the sense-maker. Mind, Culture, and Activity, 12(1), 4-18. Doi: 10.1207/s15327884mca1201_2
Kitcher, P. (1984). The nature of mathematical knowledge (1 ed.). New York: Oxford University Press.
Kozulin, A. (2000). Instrumentos psicológicos. La educación desde una perspectiva sociocultural (G. S. Barberán, Trans.). Barcelona: Ediciones Paidos.
Kozulin, A. (2003). The concept of activity in Soviet psychology: Vygotsky, his disciples and critics. In H. Daniels (Ed.), An Introduction to Vygotsky. London, New York.: Routledge. Taylor and Francis Group eLibrary.
Leave, J. (1991). La cognicion en la practica. Barcelona: Paidos.
Leontiev, A. N. (1978). Activity, consciousness, and personality. New Jersey: Prentice-Hall.
Martínez, M. C. (2005). La argumentación en la dinámica enunciativa del discurso. Cali: Universidad del Valle.
Moreno-Armella, L. and Hegedus, S. (2009). Co-action with digital technologies. ZDM Mathematics Education, 41(4), 505-519. Doi: 10.1007/s11858-009-0200-x
Rabardel, P. et Bourmaud, G. (2005). Instruments et systèmes d'instruments. In P. Rabardel et P. Pastré (Eds.), Modèles du sujet pour la conception: Dialectiques activités développement (1 ed.). Toulouse, France: OCTARÈS Éditions.
Rabardel, P. (2005). Instrument subjectif et développement du pouvoir d'agir. Dans P. Rabardel et P. Pastré (Eds.), Modèles du sujet pour la conception: Dialectiques activités développement (1 ed.). Toulouse, France: OCTARÈS Éditions.
Rabardel, P. (2003). From artefact to instrument. Interacting with Computers, 15, 641-645. Doi: 10.1016/j.intcom.2003.09.004
Radford, L. (2006). Elementos de una teoría cultural de objetivación. Revista Latinoamericana de Investigación en Matemática Educativa., Numero especial, 103-120.
Radford, L. (2008). The etics of being an knowing: Towards a cultural theory of learning. In L. Radford, G. Schubring and F. Seeger (Eds.), Semiotics in Mathemathics Education: Epistemology, History, Classroom, and Culture. Rotherdam: Sense Publishers.
Radford, L. (2009). Why do gestures matter? Sensuous cognition and the palpability of mathematical meanings. Educational Studies in Mathematics, 70(2), 111-126. Doi: 10.1007/s10649-008-9127-3
Radford, L. (2010). Algebraic thinking from a cultural semiotic perspective. Research in Mathematics Education, 12(1), 1-19. Doi: 10.1080/14794800903569741
Radford, L. (2013). Three Key Concepts of the Theory of Objectification: Knowledge, Knowing, and Learning. Journal ofResearch in Mathematics Education, 2(1), 7-44. Doi: 1 0.4471/redimat.201 3.1 9
Restivo, S., and Collins, R. (2010). Mathematics and civilization. Philosophy of Mathematics Education Journal, (25). Available : http://people.exeter.ac.uk/PErnest/pome25/index.html
Ricoeur, P. (2001). Del texto a la acción. Ensayos de hermenéutica II (P. Corona, Trans. 1 ed.). Angentina: Fondo de Cultura Económica.
Roth, W.-M., and Radford, L. (2011). A Cultural-Historical perspective on mathematics teaching and learning. The Netherlands: Sense Publishers.
Silvestri, A. and Blanck, G. (1993). Bajtín y Vigotski: la organización semiótica de la conciencia (1 ed.). Barcelona: Anthropos.
Sriraman, B. and English, L. (Eds.). (2010). Theories of Mathematics Education. Seeking New Frontiers. New York: Springer Berlin Heidelberg.
Stetsenko, A. (2005). Activity as object-related: resolving the dichotomy of individual and collective planes of activity. Mind, Culture, and Activity, 12(1), 70-88. Doi: 10.1207/s15327884mca1201_6
Trouche, L. (2002). Geneses instrumentales, aspects individuels et colletives. In D. Guin et L. Trouche (Eds.), Calculatrices Symboliques. Transformer un outil en un instrument du travail mathématique: un probleme didactique (1 ed.). Grenoble.: La Pense Savage éditions
Vasco, C. (1994). La Educación Matemática: una disciplina en formación. Matemáticas: Enseñanza Universitaria, 3(2), 59-75.
Vygotsky, L. (1993). Pensamiento y lenguaje (J. M. Bravo, Trans.) Obras escogidas II (Vol. 2). Madrid: Visor.
Vygotsky, L. (1994). The development of thinking and concept formation in adolescence (T. Prout and R. v. d. Veer, Trans.). In R. van der Veer and J. Valsiner (Eds.), The Vygotsky reader. Cambridge, Massachusetts: Blackwell Publishers.
Vygotsky, L. (1995). Problemas del desarrollo de la psique (L. Kuper, Trans.) Obras escogidas III (Vol. 3,). Madrid: Visor.
Wertsch, J. V. (1988). Vygostki y la formación social de la mente (J. Zanón y M. Cortés, Trans. 1 ed.). Barcelona: Paidos.
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.