DOI:
https://doi.org/10.14483/23448350.7691Published:
10/21/2014Issue:
Vol. 20 No. 3 (2014): September-December 2014Section:
Research ArticlesDiseños didácticos con incorporaciones tecnológicas para el aprendizaje de las formas geométricas, en primeros grados de escolaridad de estudiantes sordos-Instructional technology designs for learning geometric shapes additions in early grades of schooling of deaf students
Keywords:
diversidad, didáctica de la geometría, trayectorias hipotéticas de aprendizaje, población sorda, ALTER-NATIVA, tecnologías de la información y la comunicación, diseños didácticos. (es).Downloads
References
Clemens, D., and Samara, J. (2009). Early childhood mathematics education research. New York: Routledge.
Cobb, P., Confrey, J., Disessa, A., Lehrer, R. and Schauble, L. (2003). Desing experiment in Educational Research. Educational Researcher, 32(1), 9-13.
Cobb, P. and Gravemeijer, K. (2008). Experimenting to support and understand learning processes. In Kelly, A.E., Lesh, R.A. and Baek, J.Y. (Eds.), Handbook of design research methods in education. Innovations in Science, Technology, Engineering and Mathematics Learning and Teaching. Mahwah, NJ: Lawrence Erlbaum Associates.
Collins, A., Joseph, D. and Bielaczyc, K. (2004). Design research: theoretical and methodological issues. Journal of the Learning Sciences, 13(1), 15-42.
Confrey, J. (2006). The evolution of design studies as methodology. In Sawyer, R.K. (Ed.). The Cambridge Hand-book of the Learning Sciences. Nueva York: Cambridge University Press.
Laborde, C. (1989). Hardiesse et raison des recherches francaises en didactique des mathématiques. Dans G. Vergnaud, J. Rogalski et M. Artigue (Eds.), Actes de la 13eme Conference internationale de Psychology of Mathematics Education, 1, 46-61. Paris, France.
León, O., Bonilla, M., Romero, J., Gil, D., Correal, M., Avila, C., Bacca, J., Cavanzo, A., Guevara, C., Saiz, M., García, R., Saiz, E., Rojas, N., Peralta, M., Flores y W., Márquez, A. (2013a). Referentes curriculares con incorporación de tecnologías para la formación de profesorado de matemáticas. México: Universidad pedagógica Nacional.
León, O., Bonilla, M., Romero, J., Gil, D., Correal, M., Avila, C., Bacca, J., Cavanzo, A., Guevara, C., Saiz, M., García, R., Saiz, E., Rojas, N., Peralta, M., Flores y W., Márquez, A. (2013b). Orientaciones para la integración de las TIC en la enseñanza de las matemáticas. Acceso: noviembre 18 de 2013. Recuperado de:
http://boppo.udg.edu:8000/ATutor/bounce.php?course=30
Martín-Barbero, J. (2009). Cuando la tecnología deja de ser una ayuda didáctica para convertirse en mediación cultural. Revista Electrónica teoría de la Educación y Cultura en la Sociedad de la Información, 101, 19-31.
Menchinskaya, N. (1969). The psychology of mathematics concepts: fundamentals problems and methods of research. In: Kilpatrick y Wirszup (Eds.), Soviets studies in the psychology of learning and teaching mathematics (Vol. I). Stanford, California: School Mathematics Study Group, (NCTM).
Molina, M., Castro, E., Molina, L. y Castro, E. (2011). Un acercamiento a la investigación de diseño a través de los experimentos de enseñanza. Enseñanza de las Ciencias, 29(1), 075–088.
Moreno, L., y Kaput, J. (2005). Aspectos semióticos de la evolución histórica de la aritmética y el álgebra. En M. Alvarado, y B. Brizuela (Eds.), Haciendo Números. México: Paidós.
Sarama, J., Clements D. H., and Vukelic, E.B. (1996) The role of a computer
manipulative in fostering specific psychological/mathematical processes. In E. Jakubowski, D. Watkins, and H. Biske (Eds), Proceedings of the Eighteenth Anual meeting of the North American chapter of the International Group for the Psychology of Mathematics Education. Columbus, Ohio: Eric Clearinghouse for Science.
Shavelson, R. J., Phillips, D.C., Towne, L. and Feuer, M.J. (2003). On the science of education design studies. Educational Researcher, 32(1), 25-28.
Simon, M. (1995). Reconstructing Mathematics Pedagogy from a Constructivist Perspective. Journal for Research in Mathematics Education, 26(2), 114- 145. Access: October 2010. Available: http://www.jstor.org/stable/749205.
Steffe, L. and Thompson, P.W. (2000). Teaching experiment methodology: underlying principles and essential elements. In Kelly, A.E. and Lesh, R.A. (Eds.), Handbook of research design in mathematics and science education. Mahwah: NJ: LAE.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Diseños didácticos con incorporaciones tecnológicas para el aprendizaje de las formas geométricas, en primeros grados de escolaridad de estudiantes sordos1
Instructional technology designs for learning geometric shapes additions in early grades of schooling of deaf students
Projetos de tecnologia de instrução para aprender adições formas geométricas em séries iniciais de escolarização de alunos surdos
Olga Lucía León2
Faberth Díaz Celis3
Marcela Guilombo4
1Artículo de investigación que presenta los resultados del proyecto ALTER-NATIVA financiado por la Unión Europea ALFA III y el proyecto: “La mediación instrumental en el aprendizaje de la geometría en población sorda”, financiado por COLCIENCIAS y la Universidad Distrital
2Docente de planta de la Universidad Distrital Francisco José de Caldas. Bogotá. Colombia. Contacto:olleon@udistrital.edu.co, olgleon@yahoo.co
3Estudiante de la Maestría en Educación de la Universidad Distrital Francisco José de Caldas. Bogotá. Colombia. Contacto: faberththd@yahoo.com
4Estudiante de la Maestría en Educación de la Universidad Distrital Francisco José de Caldas y Joven investigadora de Colciencias. Bogotá. Colombia. Contacto: marcelaguilombo@gmail.com
Fecha de recepción: febrero de 2014, Fecha de aceptación: julio de 2014
Resumen
Este artículo presenta resultados de investigaciones sobre diseños didácticos con incorporaciones tecnológicas para el aprendizaje de la geometría en estudiantes sordos, de los primeros grados de escolaridad. Los resultados profundizan en la relación trayectorias de aprendizaje y diseños didácticos para la enseñanza inicial de la geometría y presentan una experiencia focal con estudiantes sordos. Se destacan las mediaciones semióticas y tecnológicas en los procesos de significación de las formas geométricas. La metodología recupera los fundamentos de los “experimentos de enseñanza”, en particular la estructura denominada “el ciclo de enseñanza”.
Palabras clave:diversidad, didáctica de la geometría, trayectorias hipotéticas de aprendizaje, población sorda, ALTERNATIVA, tecnologías de la información y la comunicación, diseños didácticos.
Abstract
This article presents research results on didactic design using technology to teach geometry to deaf students in elementary school. The results look in depth at the relations between learning trajectories and didactic designs to teach geometry. The article emphasizes in semiotic and technological mediation, in order that the students build the meanings of geometrical shapes. The methodology that we use is based on “teaching experiments”, and particularly the “teaching cycle”.
keywords:Diversity, Geometry Didactics, Hypothetic Learning Trajectories, Deaf Population, ALTER-NATIVA, Information and Communication Technologies, Didactic Designs.
Resumo
Este artigo apresenta resultados de pesquisa sobre projeto didático usar a tecnologia para ensinar geometria para surdos no ensino fundamental. Os resultados em profundidade olhar para as relações entre as trajetórias de aprendizagem e projetos didáticos para ensinar geometria. O artigo enfatiza a mediação semiótica e tecnológica, a fim de que os alunos constroem os significados das formas geométricas. A metodologia que usamos é baseado Que em "experiências de ensino" e, particularmente, o "ciclo de ensino".
Palavras-chave:Diversidade, Geometria Didática, hipotéticos Aprendizagem Trajetórias, Deaf População, alternativo, Tecnologias de Informação e Comunicação, projetos didáticos.
La relación necesaria entre “diseño para todos” y “diseño con todos” en una didáctica para la didáctica de la matemática
La relación entre “diseño para todos” y “diseño con todos” es un punto de partida necesario para una reflexión didáctica sobre la didáctica de las matemáticas, en la formación de un estudiante para profesor, que produce diseños para todos y promueve la interacción entre poblaciones diversas.
En lo que concierne a poblaciones en situación de diversidad, las reflexiones didácticas de los formadores de profesores sobre la didáctica de la matemática, han considerado por muchos años que todos los estudiantes a los que se dirigen los diseños didácticos tienen procesos de percepción visual similares, sin embargo, algunos de los estudiantes no visualizaran por efecto de una percepción visual, o no organizan el mundo como efecto del uso de lenguas no naturales para ellos.
La reflexión sobre cómo desarrollar procesos didácticos que promuevan los aprendizajes didácticos en un estudiante para profesor y que acojan la diversidad de poblaciones, plantea al formador de profesores tres tipos de exigencias:
- De orden epistemológico, que hace referencia a quiénes son “todos”, cuando se consideran diseños curriculares y didácticos en matemáticas. ¿Son sujetos epistemológicos con potencial de aprendizaje o sujetos con existencia real en la sociedad y con necesidades de aprendizajes específicas
- De orden social, referido a las formas de concentración de las poblaciones y a los escenarios que promueven la educación “con todos”. El problema de una educación “con todos”, consiste en una educación que se realiza en el momento de vida apropiado, en el lugar necesario, con los recursos adecuados y sin marginaciones de población. Los escenarios que permiten a las tecnologías y a la educación desarrollar una educación sin marginaciones, en un ambiente de revolución digital en América Latina y el Caribe, son: 1) el escenario que proporcionan las redes digitales; 2) el escenario de las redes de inmigrantes; 3) el escenario de la escuela pública; 4) el escenario de los derechos humanos (Martín Barbero, 2009); y 5) el escenario de la formación de profesores en ambientes interdisciplinarios.
- De orden curricular, relacionado con la formación didáctica y la vinculación de campos como la cantidad, la forma y la magnitud que estructuran la matemática escolar y procesos como diseñar, gestionar y evaluar unidades didácticas, que estructuran la formación en una didáctica de la matemática escolar.
Las tres exigencias se vinculan a la necesidad de desarrollar en el estudiante para profesor una experiencia con un cierto tipo de conocimiento característico de su profesión: el conocimiento profesional del profesor de matemáticas. Dos prácticas consolidan ese tipo de conocimiento, la práctica matemática, es decir, formular, probar, construir modelos, lenguajes, conceptos, teorías, intercambiar construcciones y reconocer construcciones útiles a prácticas matemáticas en cada cultura, y la práctica didáctica entendida como acciones orientadas a atender requerimientos y resolver problemas relacionados con las tareas profesionales y articuladoras del enseñar y aprender matemáticas (León y otros, 2013a).
Los diseños didácticos “para todos” y “con todos” en la formación de profesores manifiestan la presencia de:
- La accesibilidad al manejo de la información de la situación, bien sea por registro escrito, registro visual, registro auditivo o registro viso-gestual.
- La accesibilidad a la situación por audición, visión, aspectos táctiles o por aspectos perceptuales de otros órdenes
- Accesibilidad a las formas de representar y operar las relaciones y los objetos matemáticos emergentes de la información.
- Accesibilidad a las formas de comunicar y cooperar en el estudio de la información que propone la situación.
En este tipo de reflexión didáctica, el aprender a enseñar matemáticas es un proceso paulatino de incorporación en una comunidad de práctica, comporta un reto de aprendizaje que comienza por reconocer los alcances de las ideas, costumbres, teorías y modos de trabajo y enseñanza adquiridos, proceso a cargo de quien quiere saber y usar las matemáticas en sus culturas.
Incorporaciones tecnológicas en los diseños didácticos
En los diseños didácticos “para todos” y “con todos” los usuarios de los escenarios naturales participan y tienen efecto en sus procesos de aprendizaje, profesores y estudiantes en espacios escolares, que acogen la diversidad e identifican factores asociados a la implementación de los diseños. Se trata de lograr comunidades competentes para interactuar con poblaciones diversas generando procesos de identificación y de negociabilidad de significados. Se trata de sentir y comprender qué se pierde cuando se está imposibilitado de realizar, de participar, de interactuar en diversidad. ¿Hablar de experiencias matemáticas con estudiantes sordos?, ¿visualizar procesos matemáticos con estudiantes ciegos?, ¿objetivar en matemáticas o razonar acerca de algo en diferentes lenguas?, ¿cuál es el papel de las interacciones entre las viejas y las nuevas tecnologías en la configuración de respuestas a estas preguntas? Hay pocos estudios acerca de las interacciones comprometidas en las preguntas antes formuladas, pues interrogan un sistema de relaciones casi inédito (León y otros, 2013a).
Los referentes curriculares para la formación de profesores en contextos de diversidad (León y otros, 2013a), proponen al formador de profesores:
- Propiciar estructuras curriculares que fomentan una educación matemática para que las sociedades coexistan, reconozcan y promuevan la humanidad en sus diversas manifestaciones.
- Considerar a América Latina como una fuente de recursos para la formación matemática de sus estudiantes para profesor
- Considerar la educación matemática y la didáctica de la matemática como procesos, resultados y campos de producción de conocimiento en educación, desarrollados por comunidades de profesores, estudiantes, familias y sociedades, y por los sistemas educativos.
- Considerar las TIC en la educación matemática como una nueva narrativa para las matemáticas (Moreno y Kaput, 2005), su enseñanza y aprendizaje.
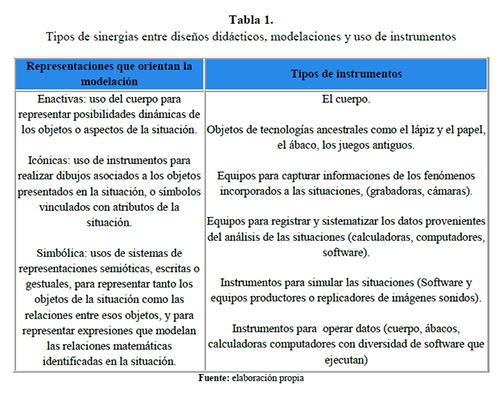
Puede decirse que toda mediación instrumental es una mediación semiótica debido a que produce negociación de significados (León y otros, 2013b). En los diseños didácticos que vinculan situaciones como enunciados escritos, sistema de gráficos, videos o juegos, emergen tipos de representaciones que orientan la modelación matemática necesaria para el desarrollo del diseño. La tabla 1 presenta las relaciones necesarias entre instrumentos y modelaciones.
Las instituciones educativas disponen, a través de los currículos, estructuras para organizar la formación de sus estudiantes, así como la intención de dicha formación. Ubica trayectos a ser recorridos por sus estudiantes, y ciertas maneras de transitar y de no transitar por estos trayectos. Para las instituciones que forman profesores, el currículo tiene una función instrumental, que, entre otras, media la formación didáctica.
La investigación de diseño y la metodología de experimentos de enseñanza
La investigación de diseño o investigación basada en diseño, según Cobb y Gravemeijer (2008), es una forma de estudiar los diseños didácticos, entendidos como proyectos de acción para sistematizar la manera en la que el sujeto se apropia del objeto de conocimiento. Esta forma de investigación, cualitativa, involucra el proceso de configuración de acciones para la enseñanza y el estudio sistemático de secuencias particulares de aprendizaje en contexto.
La investigación basada en diseño reconoce la dependencia existente entre el diseño del docente-investigador y el análisis del observador-investigador, que se genera en el contexto de los ambientes de aprendizaje (Cobb y Gravemeijer, 2008). A partir de las relaciones entre la teoría educativa, la práctica y los instrumentos, se estudia el proceso de aprendizaje y se analizan los modos con los cuales éste se sustenta y se organiza mediante recursos didácticos o herramientas conceptuales (Cobb, Confrey, DiSessa, Lehrer y Schauble, 2003; Cobb y Gravemeijer, 2008).
Este tipo de investigación aplica las teorías del aprendizaje y enseñanza a situaciones diversas y permite fundamentar empíricamente el conocimiento. Así mismo, aporta información sobre el diseño instruccional relativo a un dominio de aprendizaje específico, que puede servir para la generación de nuevos modelos teóricos (Cobb y otros, 2003; Shavelson, Phillips, Towne y Feuer, 2003).
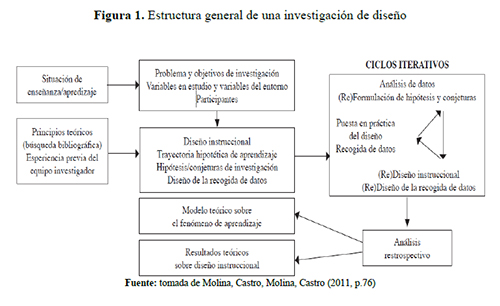
La figura 1 muestra la estructura general de una investigación de diseño, en la que se inicia con una situación de enseñanza-aprendizaje contextualizada, de la cual no se pueden determinar a priori todos sus parámetros.
A partir de la formulación de un problema y sus correspondientes objetivos de investigación, se caracteriza el contexto y se propone un diseño instruccional en forma de hipótesis o conjetura. Esta forma de diseño experimental no pretende la confirmación de los constructos teóricos previos, sino que busca la acomodación del modelo teórico a la realidad observada, según esta siga siendo viable a la vista de los datos obtenidos (Confrey, 2006; Steffe y Thompson, 2000). La investigación se produce a través de ciclos continuos de puesta en práctica, análisis de datos y rediseño (Collins, Joseph y Bielaczyc, 2004), los cuales van acompañados de ciclos de actividades y recolección de datos, reformulación de conjeturas y rediseño instruccional.
Además de fortalecer modelos teóricos de aprendizajes en un contexto, el análisis de la investigación puede servir de modelo para otros diseños. Entre los estudios de diseño que se aplican con mayor frecuencia se destacan los experimentos de enseñanza (Cobb y Gravemeijer, 2008). Un experimento de enseñanza consiste en una secuencia de episodios de enseñanza en los que los participantes son normalmente un investigador-docente, uno o más alumnos y uno o más investigadores-observadores (Steffe y Thompson, 2000), con una duración variable —una sesión de aprendizaje, una conjunto de sesiones o un curso completo— y una “atmósfera” a observar que puede ser un espacio-laboratorio para entrevistas o un aula de clase completa.
Los experimentos de enseñanza reconocen, siguiendo a Menchinskaya (1969) que “ni los conceptos científicos, ni los cotidianos brotan espontáneamente, ambos se forman bajo la influencia de la enseñanza de adultos” (p. 79) y proponen que los niños forman conceptos científicos como resultado de recibir instrucción en la escuela de temas específicos. Los adultos pueden ayudar a los niños en su intento de aprender matemáticas, sin embargo, no son las intervenciones de los adultos en sí las que determinan las construcciones de los niños, son las experiencias de los niños, en estas intervenciones, las que son interpretadas por ellos en términos de sus propias estructuras conceptuales.
El ciclo de enseñanza y las trayectorias hipotéticas de aprendizaje
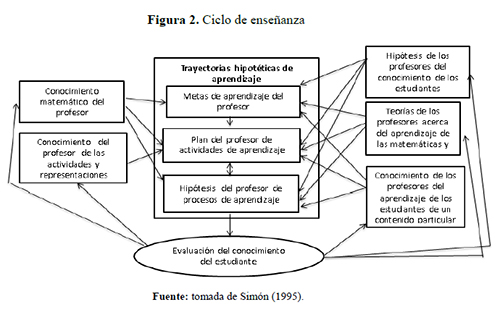
Los experimentos de enseñanza han llevado al desarrollo del Ciclo de Enseñanza de Matemáticas (ver figura 2), como un modelo esquemático en el que se genera una trayectoria hipotética de aprendizaje, el profesor-investigador diseña una secuencia para la situación didáctica en el aula.
La figura del Ciclo de Enseñanza describe la relación entre los diversos ámbitos de conocimiento de los profesores, la trayectoria hipotética de aprendizaje y las interacciones con los estudiantes. La evaluación del conocimiento de los estudiantes es un proceso que conduce a un ajuste permanente de la trayectoria hipotética de aprendizaje.
Los conocimientos matemáticos del profesor sobre la geometría euclidiana, la topología y la geometría proyectiva, junto con sus hipótesis acerca del estado de conocimiento geométrico de sus estudiantes y de las teorías sobre aprendizaje de la noción de forma, le permiten establecer las metas de aprendizaje del curso.
El profesor puede establecer de manera paralela o secuencial, los niveles por los cuales él considera que sus estudiantes pueden avanzar en la ruta de aprendizaje para desarrollar una experiencia geométrica con la forma o diseñar una secuencia de actividades que puede ayudar a los niños a avanzar de un nivel a otro. Para la toma de decisiones sobre los niveles y las actividades, el profesor requiere conocer —haber consultado, analizado o experimentado— alguna secuencia de actividades que muestren éxito para propiciar el avance de los estudiantes.
Poner en práctica el diseño de las actividades sobre la noción de forma por parte del profesor, va acompañado de un proceso de evaluación en el que se establecen las características de la Trayectoria Real de Aprendizaje (TRA) de la noción forma que cada estudiante recorre. La recolección de datos y el análisis de los mismos, permiten hacer un rediseño de las hipótesis y conjeturas del modelo y de una reformulación de las actividades propuestas.
Aunque el profesor propone un objetivo inicial y un plan para la instrucción, por lo general, éste debe ser modificado muchas veces —tal vez continuamente— durante el estudio de un área conceptual. Cuando los estudiantes comienzan a participar en las actividades previstas, el profesor observa y se comunica con ellos, generando una nueva comprensión sobre las concepciones de los estudiantes. El ambiente de aprendizaje se desarrolla como resultado de la interacción entre el profesor y los estudiantes que se dedican al aprendizaje. Los elementos necesarios para dinamizar las decisiones que toma el profesor en un Ciclo de Enseñanza son:
- El pensamiento y la comprensión de los estudiantes tienen un lugar central en el diseño y la ejecución de la instrucción —proceso continuo de recopilación de datos y generación de hipótesis—.
- El conocimiento de matemáticas del profesor avanza al mismo tiempo que crece su conocimiento de cómo aprenden sus estudiantes.
- La planificación para la instrucción incluye la generación de trayectorias hipotéticas de aprendizaje, en las que se toman decisiones sobre los propósitos para la instrucción y sobre las hipótesis de los procesos de aprendizaje de los alumnos.
- El cambio continúo del conocimiento del profesor, cambia de forma continua las trayectorias hipotéticas de aprendizaje.
Entender el aprendizaje como un proceso de construcción individual y social, proporciona a los maestros un marco conceptual sobre el aprendizaje de sus estudiantes y las decisiones, en cuanto a la naturaleza y secuencia de las matemáticas que han de ser enseñadas, proceden de hipótesis sobre la epistemología y el aprendizaje de las matemáticas Laborde (1989).
La expresión “Trayectorias Hipotéticas de Aprendizaje” (THA) se usa para referirse a las predicciones del profesor sobre el camino por el que el aprendizaje puede continuar. Son hipotéticas debido a que las trayectorias reales de aprendizaje dependen de la condición de existencia de cada individuo y a que el aprendizaje de los individuos tiene ciertas regularidades. Las THA proporcionan al profesor un criterio racional para decidir el diseño que él considera la mejor conjetura de cómo puede avanzar el aprendizaje.
Las THA analizadas por Sarama, Clements y Vukelic (1996), “ayudan a los maestros a entender la variedad de niveles de conocimiento y de pensamiento de sus clases y de los individuos dentro de ellas, como fundamentales para satisfacer las necesidades de todos los niños” (p.16). Los autores expresan que la propuesta de las THA contribuye en dar respuesta a preguntas como: ¿qué metas o propósitos se deben establecer en el aprendizaje de las matemáticas en niños y niñas?, ¿por dónde empezar el aprendizaje de las matemáticas en cada momento de desarrollo de los niños y niñas?, ¿cómo sabemos a dónde ir con el aprendizaje de las matemáticas de los niños y niñas?, ¿cómo podemos favorecer el aprendizaje para que los niños y niñas vayan alcanzando las metas o propósitos?.
Las THA tienen tres partes: 1) una meta o propósito matemático, entendido como el conjunto de los conceptos y habilidades que son matemáticamente centrales, coherentes, y consistentes con el pensamiento de los niños y generadoras de futuros aprendizajes; 2) una ruta de desarrollo a lo largo de la cual los niños progresan, constituída por los niveles de pensamiento cada uno más sofisticado que el anterior y que conducen a la meta matemática; 3) un conjunto de actividades instruccionales, o tareas relacionadas para cada uno de los niveles de pensamiento, que fomentan el paso de un nivel a otro.
Entonces, “las trayectorias de aprendizaje describen las metas, el pensamiento, y los procesos de aprendizaje de los niños en los distintos niveles y las actividades de aprendizaje en las cuales ellos podrían participar” (Clements y Sarama, 2009, p.17) y están “basadas en el desarrollo mental progresivo” (Clements y Sarama, 2009, p.252).
Los niveles propuestos en las trayectorias pueden describir la ruta de aprendizaje que ocupa el periodo de vida correspondiente al tiempo de escolarización o pueden abarcar la ruta de aprendizaje que siguen las personas durante toda su vida. En el segundo caso, Clements y Sarama (2009), aumentan la cantidad de niveles y proponen el aprendizaje como una condición del ser humano que trascurre de manera permanente desde el nacimiento.
El proceso de escolarización organiza intencionalmente las actividades que ayudan al estudiante a avanzar en su aprendizaje, pero no constituye el único dispositivo cultural que lo promueve. Otras interrelaciones, como las experiencias familiares, las interacciones con el ambiente, las necesidades de adaptación al medio socio cultural y los estímulos de los medios de comunicación, favorecen el desarrollo de los niveles de las trayectorias de aprendizaje.
Las trayectorias hipotéticas de aprendizaje de la noción forma para estudiantes sordos y oyentes
El aprendizaje de la geometría, considerado como un gran campo del saber didáctico, presenta trayectorias hipotéticas de aprendizaje para objetos matemáticos específicos, que se enmarcan en el espacio, la forma y la magnitud. Autores como Clements y Sarama (2009) centran su atención en la forma y la enuncian como el gran descriptor, estableciendo que las abstracciones geométricas de las formas son las figuras geométricas.
En los primeros años de vida de una persona sorda u oyente, se desarrolla la capacidad de distinguir o reconocer las formas, este proceso es de gran importancia porque permite la discriminación de los objetos según sus lados y esquinas, a partir de una comparación en la que se privilegian las percepciones visuales y táctiles, Clements y Sarama (2009) proponen para el desarrollo de avances conceptuales tres THA de la noción forma, y consideran que las THA se fundamentan en que el aprendizaje de la persona se da a partir del desarrollo progresivo y sucede según la complejidad de las tareas que se proponen. Este desarrollo refleja una jerarquización progresiva, que le permite organizar estructuras previas y elaborar un plan mental para construcciones más complejas.
Las tres THA propuestas por Clements y Sarama (2009) para la noción forma están fuertemente relacionadas con el reconocimiento de la geometría como una importante fuente de modelación que permite interpretar, entender y apreciar un mundo que se torna particularmente geométrico.
Cada una de las tres THA asociadas a la noción de forma geométrica hace explícitos macro procesos como se presenta en la tabla 2.
Trayectoria real de aprendizaje en un grupo focal de niños sordos
Las trayectorias de aprendizaje están vinculadas a la vida del aprendiz, es decir, no sólo suceden en la institucionalidad, inician con la vida. Por ejemplo, son los padres quienes, en la mayoría de casos, inician el desarrollo de las trayectorias de manera implícita, procurando que sus hijos aprendan algunas nociones antes de llegar a la escuela. Cuando un niño llega al aula regular hace uso de un lenguaje y de los diferentes elementos aprendidos en el hogar, los cuales le ayudan a avanzar hábilmente en su aprendizaje. En consecuencia, el desarrollo del aprendizaje está mediado por el ambiente en el cual se encuentra el niño.
La gran mayoría de niños sordos tienen padres oyentes que no saben cómo comunicarse con sus hijos sordos, situación que genera un dialogo limitado entre padres e hijo. En algunos casos, los niños llegan al aula e inician su escolaridad con bajos desarrollos en su lengua y las experiencias necesarias para su aprendizaje no han podido desarrollarse debido a las limitaciones comunicativas que tiene en su ambiente.
La THA de las formas geométricas, se propuso a un grupo de niños sordos de un aula multigradual especializada para la población, en una institución escolar de Bogotá (Colombia) cuya población mayoritaria es oyente. La docente que enseña a los niños sordos es oyente y tiene manejo de Lengua de señas Colombiana (LSC).
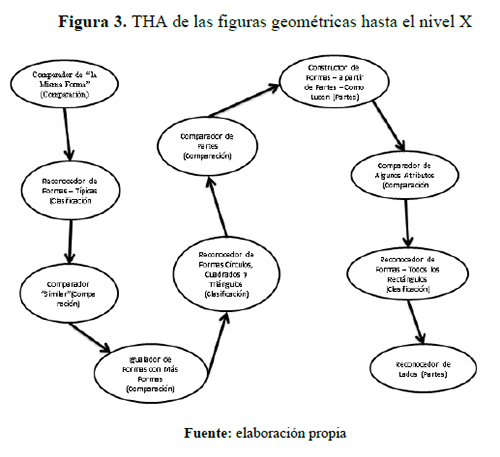
La THA de las formas geométricas considera indicadores de avances de niveles acompañados de un sistema de actividades. El diseño de investigación consideró los diez primeros niveles de la THA de las figuras (figura 3).
La Trayectoria Real de Aprendizaje (TRA) que se presenta en adelante, evidencia las formas y modos en que el aprendiz pasó o no por los niveles. Para el seguimiento de la TRA se establecieron rejillas que permitieron identificar el cumplimiento de indicadores del nivel de la THA, para cada estudiante y para cada nivel. A continuación se presentan las rejillas de registro de datos del estudiante sordo ζ. La rejilla que presenta la figura 4 relaciona los indicadores del nivel con los artefactos producidos por el estudiante que dan razón de la presencia del indicador.
El estudiante sordo ζ en el primer nivel de la trayectoria denominado “comparador de la misma forma”, orienta figuras que le son familiares como se ilustra en la figura 5.
Luego, en el nivel IV, el niño ζ además de orientar las formas puede igualar una mayor variedad de figuras de diferentes tamaños y con diferentes orientaciones.
En este nivel, la TRA también evidencia un avance en la expresión de LSC del niño sordo, al proponer a través de su lengua una manera de nombrar las formas, en las figuras 6 y 7 se evidencia el desarrollo de la expresión “lo mismo que” o “igual a”, considerando solo el atributo forma cuadrada, como el invariante identificado y nominado por su lengua.
Para el desarrollo del lenguaje se observa que, a medida que los niños van realizando las actividades de la THA, sus expresiones lingüísticas evidencian su avance en los niveles de desarrollo de una trayectoria real. Los niños reflejan de esta manera una jerarquización progresiva que
les permite establecer relaciones, organizar estructuras y construir planes mentales para actividades más complejas.
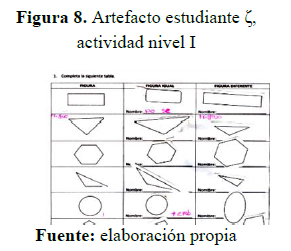
En la actividad donde se debe seleccionar un grupo de láminas con figuras que consideren igual a la de la primera columna y otro grup que consideren diferente. El estudiante ζ, como se muestra en la figura 8, logra identificar las figuras iguales en forma y no en tamaño, pero no logra escribir el nombre de las mismas en español.
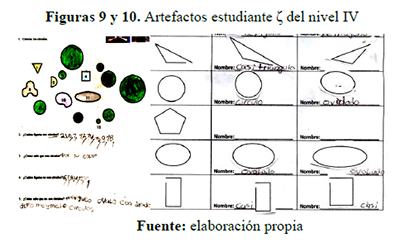
En las figuras 9 y 10, se muestran artefactos que fueron producidos en un nivel superior, y que evidencian un desarrollo en el español escrito de los estudiantes sordos al asignar nombres a las formas que no consideran círculos. Del mismo modo, se evidencian un desarrollo en los procesos de clasificación, al asignar la palabra “deforme” a las formas que no están en las clasificaciones geométricas desarrolladas hasta el momento (figura 9). El uso de la palabra “casi” (figura 10) es otra evidencia de su desarrollo lingüístico
A medida que los niños van desarrollando las actividades de la trayectoria hipotética sus expresiones lingüísticas se vuelven indicadores de avance en los niveles de desarrollo de una trayectoria real. Este desarrollo refleja una jerarquización progresiva, permitiéndole establecer relaciones, organizar estructuras y construir planes mentales para actividades más complejas.
Conclusiones
Los “diseños para todos” y los “diseños con todos” transforman la acción didáctica de un formador de profesores en lo que se refiere a promover la enseñanza y aprendizaje de la didáctica de las matemáticas en los estudiantes para profesor. Se configura el campo que se denomina de “Didáctica de la didáctica de las matemáticas”, un campo que considera la didáctica de las matemáticas como un objeto enseñable y aprendible.
Las relaciones entre práctica, mediación instrumental y significado abogan por un currículo de formación de profesores generado a partir de los siguientes cinco principios: diversidad, flexibilidad, integrabilidad, accesibilidad e interdisciplinariedad, considerando los cinco escenarios que otorgan dimensión a las sinergias entre tecnologías y educación para todos.
Los ciclos de enseñanza aportan una metodología de investigación sobre diseños didácticos, que relaciona las teorías, saberes y prácticas, e hipótesis de aprendizaje, con el propósito de aportar a la acción cotidiana del profesor de matemáticas en la toma de decisiones. En este tipo de metodología la presencia de Trayectorias Hipotéticas de Aprendizaje y Trayectorias Reales de Aprendizaje es un indicador del aprendizaje.
La noción de forma se puede desarrollar desde varias trayectorias de aprendizaje y esto es algo que no pueden ignorar las trayectorias hipotéticas de aprendizaje que se proponen desde las instituciones escolares. Considerar diferentes trayectorias hipotéticas de aprendizaje es valorar en los diseños didácticos diversidad de condiciones para que poblaciones diversas puedan negociar sus significados.
Para el caso de las poblaciones sordas las trayectorias hipotéticas de aprendizaje de la forma se vinculan a trayectorias reales de aprendizaje que evidencian una relación muy fuerte entre lengua y aprendizaje de las matemáticas.
Referencias
Clemens, D., and Samara, J. (2009). Early childhood mathematics education research. New York: Routledge.
Cobb, P., Confrey, J., Disessa, A., Lehrer, R. and Schauble, L. (2003). Desing experiment in Educational Research. Educational Researcher, 32(1), 9-13.
Cobb, P. and Gravemeijer, K. (2008). Experimenting to support and understand learning processes. In Kelly, A.E., Lesh, R.A. and Baek, J.Y. (Eds.), Handbook of design research methods in education. Innovations in Science, Technology, Engineering and Mathematics Learning and Teaching. Mahwah, NJ: Lawrence Erlbaum Associates.
Collins, A., Joseph, D. and Bielaczyc, K. (2004). Design research: theoretical and methodological issues. Journal of the Learning Sciences, 13(1), 15-42.
Confrey, J. (2006). The evolution of design studies as methodology. In Sawyer, R.K. (Ed.). The Cambridge Hand-book of the Learning Sciences. Nueva York: Cambridge University Press.
Laborde, C. (1989). Hardiesse et raison des recherches francaises en didactique des mathématiques. Dans G. Vergnaud, J. Rogalski et M. Artigue (Eds.), Actes de la 13eme Conference internationale de Psychology of Mathematics Education, 1, 46-61. Paris, France.
León, O., Bonilla, M., Romero, J., Gil, D., Correal, M., Avila, C., Bacca, J., Cavanzo, A., Guevara, C., Saiz, M., García, R., Saiz, E., Rojas, N., Peralta, M., Flores y W., Márquez, A. (2013a). Referentes curriculares con incorporación de tecnologías para la formación de profesorado de matemáticas. México: Universidad pedagógica Nacional.
León, O., Bonilla, M., Romero, J., Gil, D., Correal, M., Avila, C., Bacca, J., Cavanzo, A., Guevara, C., Saiz, M., García, R., Saiz, E., Rojas, N., Peralta, M., Flores y W., Márquez, A. (2013b). Orientaciones para la integración de las TIC en la enseñanza de las matemáticas. Acceso: noviembre 18 de 2013. Recuperado de: http://boppo.udg.edu:8000/ATutor/bounce.php?course=30
Martín-Barbero, J. (2009). Cuando la tecnología deja de ser una ayuda didáctica para convertirse en mediación cultural. Revista Electrónica teoría de la Educación y Cultura en la Sociedad de la Información, 101, 19-31.
Menchinskaya, N. (1969). The psychology of mathematics concepts: fundamentals problems and methods of research. In: Kilpatrick y Wirszup (Eds.), Soviets studies in the psychology of learning and teaching mathematics (Vol. I). Stanford, California: School Mathematics Study Group, (NCTM).
Molina, M., Castro, E., Molina, L. y Castro, E. (2011). Un acercamiento a la investigación de diseño a través de los experimentos de enseñanza. Enseñanza de las Ciencias, 29(1), 075–088.
Moreno, L., y Kaput, J. (2005). Aspectos semióticos de la evolución histórica de la aritmética y el álgebra. En M. Alvarado, y B. Brizuela (Eds.), Haciendo Números. México: Paidós.
Sarama, J., Clements D. H., and Vukelic, E.B. (1996) The role of a computer manipulative in fostering specific psychological/mathematical processes. In E. Jakubowski, D. Watkins, and H. Biske (Eds), Proceedings of the Eighteenth Anual meeting of the North American chapter of the International Group for the Psychology of Mathematics Education. Columbus, Ohio: Eric Clearinghouse for Science.
Shavelson, R. J., Phillips, D.C., Towne, L. and Feuer, M.J. (2003). On the science of education design studies. Educational Researcher, 32(1), 25-28.
Simon, M. (1995). Reconstructing Mathematics Pedagogy from a Constructivist Perspective. Journal for Research in Mathematics Education, 26(2), 114- 145. Access: October 2010. Available: http://www.jstor.org/stable/749205.
Steffe, L. and Thompson, P.W. (2000). Teaching experiment methodology: underlying principles and essential elements. In Kelly, A.E. and Lesh, R.A. (Eds.), Handbook of research design in mathematics and science education. Mahwah: NJ: LAE.
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.