Algunas consideraciones sobre los numerales mayas-Some considerations about Mayan numerals

Algunas consideraciones sobre los numerales mayas¹

Some considerations about Mayan numerals

Algumas considerações sobre os numerais maias

Oscar Fernández Sánchez²

Harold Duque Sánchez3³

¹Artículo de investigación

²Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: oscarf@utp.edu.co

³Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: harold1@utp.edu.co

Fecha de recepción: febrero 2014, Fecha de aceptación: julio de 2014

Resumen

Para los mayas, a diferencia de Occidente, la matemática tiene un significado que sobrepasa los numerales y las operaciones entre ellos. Según su cosmovisión, la Deidad, la creadora del universo, es soberana en cuanto al cálculo matemático (Cabrera, 1992). La matemática maya ofrece la posibilidad de realizar las operaciones aritméticas de suma, resta, multiplicación, división y cálculo de raíces de forma sencilla, dado que la cultura maya logró sintetizar la cantidad mediante tres símbolos y logró sintetizar el valor con el sistema posicional en base veinte (Calderón, 1966). Se pretende en este artículo hacer un reconocimiento de los numerales mayas, su concepción metafórica y algunas operaciones aritméticas.

Palabras clave: numeral maya, metáfora, suma, multiplicación.

Abstract

For the Maya, unlike the West, mathematics goes beyond numerals and operations between them. According to their Cosmovision, the Godhead, who created the universe, is sovereign in terms of mathematical calculation (Cabrera, 1992). The Mayan mathematics provides the possibility to perform arithmetic operations of addition, subtraction, multiplication, division and calculation of simple roots, as the Mayan culture was able to synthesize the amount by three symbols and they synthesize the value by based twenty systems (Calderon, 1966). This article pretends do recognition the Mayan numerals, their metaphorical conception and some of their arithmetic operations.

keywords:Mayan Numeral, metaphor addition, multiplication

Resumo

Para os maias, ao contrário do Ocidente, a matemática vai além dos números e as operações entre eles. De acordo com sua visão de mundo, a Divindade, o criador do universo, é soberano em termos de cálculo matemático (Cabrera, 1992). A matemática maia fornece a capacidade de realizar operações aritméticas de adição, subtração, multiplicação, divisão e cálculo de raízes simples, como a cultura maia foi capaz de sintetizar a quantidade de três símbolos e conseguiu sintetizar sistema baseado em valor posicional vinte (Calderon, 1966). Em este artigo se procura fazer um reconhecimento dos numerais maias, sua concepção metafórica e algumas operações aritméticas.

Palavras-chave:Numeral maia, metáfora, adição, multiplicação.

Introducción

En este artículo se muestran algunos aspectos de la aritmética del pueblo maya, con el ánimo de contribuir a la difusión de este conocimiento ancestral. Los Mayas, usando granos de maíz de dos colores, piedras y varas de madera para representar los numerales del 1 al 5, y colocando estos objetos en una cuadrícula dibujada en el suelo —en la tierra o en la arena— podían llevar a cabo, en corto tiempo, complejas operaciones matemáticas utilizando los algoritmos fundamentales de la aritmética (Calderón, 1966).

La importancia de los granos de maíz para hacer las cuentas puede constatarse en el Popol Vuh, donde Ixpiyacoc e Ixmucané —la pareja de sabios abuelos—, antes de la formación del humano, hacen una adivinación por medio de unos extraños cálculos utilizando granos de maíz y de tzité “echen la suerte con granos de maíz y de tzité” (Anónimo, 1997, p. 21).

La difusión de esta temática en nuestros contextos se justifica como una contribución a la recuperación de los símbolos ancestrales de los pueblos americanos. Dado que “el uso de los símbolos como expresión del poder de una cultura que conquista, sobre otra que es conquistada y sometida. La cultura subyugada se ve obligada a adoptar y usar toda la simbología que trae la cultura conquistadora” (Fernández y Angulo, 2010, p. 208), y los libros de texto que se usan para dar clases de matemáticas en las escuelas de la mayoría de países de América Latina, enseñan aritmética con símbolos traídos de la cultura Indoeuropea.

La temática tratada aquí se enmarca teóricamente desde la perspectiva del programa Etnomatemática del Dr. Ubiratan D’Ambrosio (1987), quien a partir de la década de los años setenta, muestra gran preocupación por aspectos inherentes al conocimiento matemático, como es, su dimensión política, el devenir histórico de dicho conocimiento y sus implicaciones pedagógicas, para lo cual promueve el hacer investigaciones sobre los conocimientos que se producen en el seno de las relaciones que se dan dentro de las comunidades diferenciadas cultural y socialmente, así como las formas en que esos conocimientos producidos se difunden entre los miembros jóvenes de dicha comunidad. El conocimiento matemático de los pueblos latinoamericanos, y en particular el de los mayas, ha sufrido de un desplazamiento para dar lugar al conocimiento matemático que traían los europeos y que fue impuesto a nuestros pueblos de manera forzada.

Para los mayas, la matemática va mucho más allá de las superficiales simbolizaciones mediante puntos y barras y las operaciones con dichas representaciones. Según su cosmovisión, la Deidad, la creadora del universo, es soberana en cuanto al cálculo matemático y como lo cuestiona Cabrera “¿Cómo si no poder establecer las medidas y equilibrios tan a la perfección, de tal manera que permitan la existencia de los astros, sus movimientos tan exactamente calculados, los balances químicos y físicos del universo?” (1992, p. 263).

Contenido

Los numerales mayas

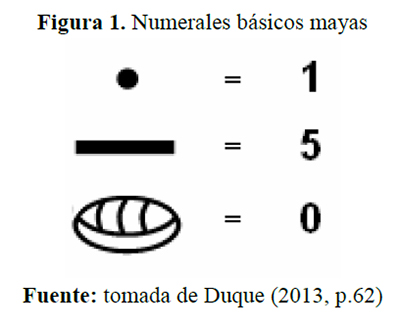
Los mayas para representar sus numerales utilizan únicamente tres símbolos (ver figura 1). Un punto, para describir cantidades de una a cuatro unidades; una raya para representar cinco unidades y una forma ovalada para el cero, “el magnífico descubrimiento en este campo del intelecto maya para la humanidad” (Cabrera, 1995, p.205).

Respecto a poseer un sistema de numeración, la cultura maya ha sido “la civilización que universalmente ha logrado el más alto grado de abstracción” (Cabrera, 1995, p.205).

Los símbolos que aparecen en la figura 1, son los más sencillos; los escribas mayas, usaban estos símbolos junto con los glifos para nombrar los kines (días) y los winiles (meses de 20 kines) (Grube, 2006) para registrar fechas en los llamados códices (ver figura 2).

La característica más sobresaliente de estos símbolos es que tienen un valor intrínseco, según Calderón (1966, p.15) “en sí mismos contienen la multiplicidad que describen”, es decir, con el numeral es fácil identificar el número, pues si un punto es el numeral de la unidad, dos puntos serán el numeral del número dos, o una raya con un punto encima describen como numeral el número seis, una raya con dos puntos encima, el número siete, y así sucesivamente.

Calderón (1966, p.25), comenta que “el maya sólo precisaba recoger un puño de gravillas, cortar una vara, trazar con ella una cuadrícula en el suelo y después romperla en trozos convenientes”. Los mayas utilizaron, además de puntos y rayas, una forma más estética de representar los números, mediante glifos en forma de cabeza o cefalomorfos, también glifos en forma de cuerpo entero (ver figura 3).

Para el maya cada número es sagrado, cada glifo cefalomorfo tiene su significado expresando alguna relación con la naturaleza. Es importante resaltar el cambio notorio en la escritura de los números cefalomorfos a partir del diez —representación del mundo de abajo— cuya característica principal es que todos llevan claramente la mandíbula sin carne.

Cabrera (1995, pp. 206-209 citado en Duque, 2013, p. 67), da una descripción de los elementos característicos en los números cefalomorfos de la siguiente manera:

Concepción metafórica de los numerales mayas

La inclusión de la palabra metáfora en un tema matemático no deja de causar extrañeza, pero Lizcano brinda una justificación cuando dice que “por ser las matemáticas uno de los ámbitos donde la imaginación menos se somete a las restricciones de la llamada realidad, ofrece una de las vías más francas para acceder al fondo imaginario de los pueblos y las culturas” (Lizcano, 2006, p. 41), y agrega que es en la metáfora donde el imaginario se refleja más fielmente, es decir, la metáfora es aquello en que la letra, la palabra o la imagen se soportan, pues es a través de estos elementos comunicativos que el imaginario se hace evidente (Lizcano, E. 2006, citado en Fernández, 2010, p. 177).

Sobre la metáfora

Sobre la metáfora, dice Perelman (1997) que ésta “es una analogía condensada, gracias a la fusión del tema y del foro. Tomando como base la analogía: A es a B como C es a D, surgen las metáforas: “A de D”, “C de B”; “A es C”. Por ejemplo, de la analogía “la vejez es a la vida lo que la noche es al día”, se derivan las metáforas: “la vejez del día”, “la noche de la vida” o “la vejez es una noche”” (Perelman, 1997, citado en Fernández, 2010, p. 179).

Para Serna, la metáfora “en su concepción original, como trasteo de atributos de un campo semántico a otro, las metáforas inducen una ontología rizomática, cuando saltan de lo concreto a lo abstracto, del animal al hombre, de la naturaleza a la cultura, de los elementos a los sentimientos, para citar algunos casos; cuando desordenan las parcelaciones del horizonte del sentido laboriosamente construidas por la academia” (Serna, 2007, citado en Fernández, 2010, p. 179).

Lakoff y Johnson en (1995) explican el origen de las metáforas llamadas orientacionales y ontológicas. Ellos afirman que las primeras surgen de las experiencias básicas de la orientación espacial humana, y que “nuestras experiencias con objetos físicos (especialmente nuestros propios cuerpos) proporcionan la base para una variedad extraordinariamente amplia de metáforas ontológicas, es decir formas de considerar acontecimientos, actividades, emociones, ideas, etc., como entidades y sustancias” (p. 64).

Concepción metafórica de los numerales mayas

La representación del cero usada inicialmente en forma de flor incompleta y luego completa, para hacer las inscripciones en las estelas, expresa en sus cuatro pétalos el cosmos con sus cuatro puntos cardinales. Cuando Huracán o Corazón del Cielo, inicia la construcción del Universo, lo que hace inicialmente es medir y construir las cuatro direcciones, con sus respectivos ángulos (Cabrera, 2007, citado en Fernández, 2010, p. 184).

La figura de media flor de cuatro pétalos representa lo incompleto de la creación, cuando sólo se había creado la categoría espiritual, y faltaba la material, como lo da a entender el autor del Popol Vuh (Anónimo, 1997), cuando expresa que el equilibrio entre estas dos categorías acabadas de crear, es determinado con la creación del ser humano del maíz, aquel que le dará el equilibrio necesario para la buena marcha del Universo.

Al representar el cero y asumirlo como concha de molusco, o caracol, se expresa que se ha completado la unidad matemática, el ciclo de 20 unidades se ha completado, por lo tanto, es necesario pasar a una categoría superior. Con esto debe ser claro que el numeral para el cero indica la existencia de una categoría llena —a diferencia del vacío denotado por el numeral en Occidente— y sobre esta categoría como base se construye una nueva entidad, pero sin destruir lo anterior (Cabrera, 1997).

El numeral para la unidad como un punto representa una semilla de maíz o de fríjol, y a su vez como semilla representa el mundo subterráneo. Los mayas observaron que la semilla de maíz cuando se siembra, se tarda, en promedio, cinco días para germinar y que empiece a brotar una nueva planta, es por este hecho que este cinco es representado por el perfil de la tierra con una barra horizontal, así el cinco representa el mundo de en medio, donde habitan los Mayas y el cero representa el nivel espiritual, está asociado con el mundo de arriba. Tres símbolos matemáticos para los tres niveles ceremoniales: el mundo de abajo o Xibalba como también lo llaman, la Tierra, como mundo de en medio y el Cielo, como mundo de arriba (Cabrera, 1997).

El sistema de numeración maya es en base veinte, esto ve expresado en el vocablo Hun Uinic, en lengua Maya-K’iché, para referirse a veinte unidades, que en maya-yucateco, se escribe Hun Winic, y en las dos lenguas se usa para referirse a “un ser humano” (Cabrera, E. 1997, citado en Fernández, 2010, 186).

De esto se sigue que para ellos ser humano y veinte unidades es igual, es decir, 20 unidades entonces son 20 dedos, los posibles unos que puede representar un ser humano con sus dedos. Las direcciones básicas del cosmos son cuatro, al igual que el número de extremidades del ser humano; el centro más las cuatro direcciones da el cinco, y cinco son los dedos en la mano del ser humano, por cuatro extremidades, resulta el veinte, como el número cabalístico que constituye una unidad humana. La pareja, mujer y hombre se unen en un veinte entrelazado y amoroso del cual surge un nuevo ser humano, que representa un nuevo veinte, una nueva categoría matemática, llena de esperanza que le aportará bien a la humanidad y para la gloria de las energías cósmicas (Cabrera, 1997, citado en Fernández, 2010, p. 186).

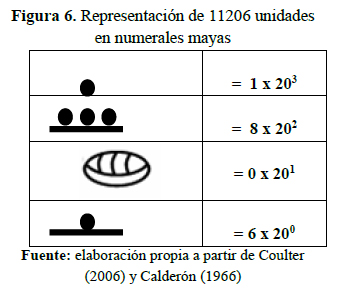
Según Cabrera en (1997), para la representación en forma vertical y el valor ascendente de los numerales, los mayas tuvieron en cuenta que el Sol respecto a la humanidad se mueve de abajo hacia arriba, alcanzando su mayor esplendor en el cenit, por ejemplo para representar el número 11206, se escribe como en la figura 6, y se lee de abajo hacia arriba, aumentando el valor a medida que se asciende en los niveles de representación.

Algunas operaciones aritméticas con numerales mayas

En esta sección se ilustrará la forma como, según Calderón (1966), los mayas efectuaban sumas y multiplicaciones, usando semillas de maíz o frijol, pedacitos de varitas de madera que tomaban del bosque y trazaban una cuadrícula en el suelo.

La suma

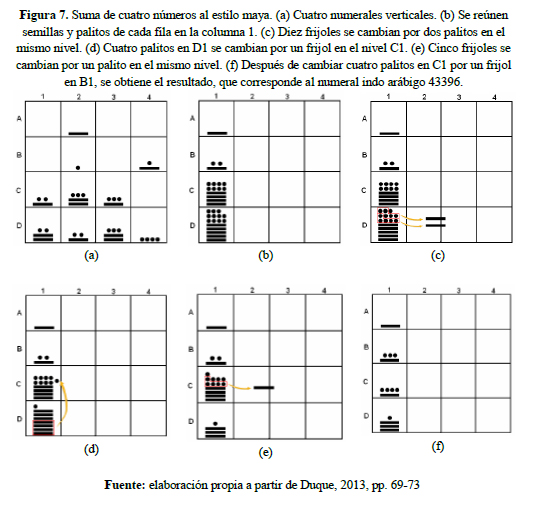
La operación de la suma se explicará con el siguiente ejemplo: se desea sumar las cuatro cantidades que aparecen en las cuatro columnas de la cuadricula en la figura 7(a). Para esto se reúnen en la primera columna conservando la fila en la que se encuentran, todos los frijoles y palitos. Queda como en la ilustración 7(b). Enseguida se aplican dos reglas para los numerales que se derivan de la notación posicional en sistema vigesimal.

Esta reglas son: cada que se reúnan cinco frijoles, se cambian por un palito y por cada cuatro palitos en una casilla, se cambian por un frijol la casilla en el nivel superior (ver figura 7 d). Los numerales que se suman en el ejemplo corresponden a los numerales indoarábigos 152, 40667, 173 y 2404.

La multiplicación

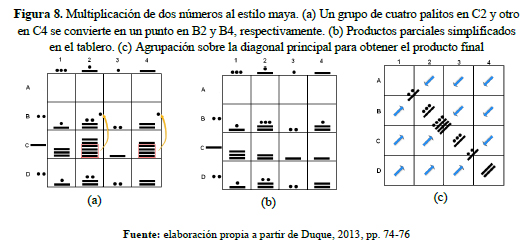
Aquí se muestra con un ejemplo la forma como, según Calderón (1966), los mayas efectuaban la multiplicación. Entre los números que se ilustran abajo y cuyo equivalente en números arábigos es 902 y 26425 respectivamente, a lo largo del margen izquierdo y del margen superior del tablero se colocan los marcadores correspondientes a los dos factores, de tal forma que las posiciones de mayor rango queden más cerca de la esquina superior izquierda. En caso de que alguno de los números tenga más cifras, se deja un espacio vacío (cero) por cada cifra faltante en el número con menos cifras, luego se llena cada casilla con el producto parcial de los guarismos correspondientes a cada fila y su respectiva columna, y enseguida se simplifica este resultado, cambiando cada grupo de cinco frijoles por un palito y cada grupo de cuatro palitos por un frijol en la posición inmediatamente superior. Este proceso comienza en la posición más baja de cada columna (ver figura 8 ) y b). Por último, se procede a juntar los frijoles y palitos sobre la diagonal principal del tablero, siguiendo igualmente la regla de cambiar cada grupo de cinco frijoles por un palito y cada grupo de cuatro palitos por un frijol en la posición inmediatamente superior. Este valor en notación arábiga es 23835350, que es el resultado de la multiplicación (ver figura 8 c).

Conclusiones

En este artículo se mostró una manera alternativa de trabajar las operaciones aritméticas. Así mismo, se ilustra cómo la cultura ancestral de los Mayas logró, con tan sólo tres símbolos, representar números de grandes magnitudes en una forma con la cual se pueden efectuar operaciones como la suma, y sobre todo, la multiplicación entre números grandes, sin necesidad de las tradicionales tablas de multiplicar, con las cuales muchas generaciones fueron formadas. Lo cual muestra que la simbología constituida por los numerales de la cultura indoeuropea y usados en las clases de matemática, en las escuelas latinoamericanas, no son únicos, sino que también existen desde antes del
desigual encuentro de dicha cultura con los pueblos latinoamericanos, y que por cuestiones de poder, fueron impuestos a los pueblos dominado. En muchos aspectos, numerales como los del pueblo maya, son más funcionales didácticamente, pues como lo anota Calderón (1966), la característica más sobresaliente de los numerales mayas es que tienen un valor intrínseco, según él (p. 15) “en sí mismos contienen la multiplicidad que describen”, es decir, con el numeral es fácil identificar el número, pues si un punto es el numeral de la unidad, dos puntos serán el numeral del número dos, y así sucesivamente.

A diferencia de los numerales indoarábigos de Occidente, los numerales del pueblo Maya, tienen un significado estrechamente relacionado con sus creencias, su concepción del universo y la forma como se relacionan con el medio natural y social, lo que hace que la aritmética tenga sentido para los niños mayas. Un sentido del que carecen los numerales indoarábigos que se enseñan a los niños en las escuelas latinoamericanas.

Las investigaciones de Calderón (1966), muestran que cualquier individuo del pueblo maya, en cualquier lugar que estuviese, tenía a su disposición su propia “calculadora”, bastaba con desgranar una mazorca o recoger del suelo un puñado de piedritas y partir una esterilla en varios pedacitos para sumar, restar, multiplicar o dividir, cualquier cifra, no importa lo grande que fuese.

Referencias

Anónimo. (1997). Popol Vuh, Antiguas Historias del Quiché de Guatemala. Bogotá: Panamericana.

Cabrera, E. (1992). Cosmogonía Maya. En La Cosmovisión Maya (Vol.1 y 2). Guatemala: Liga Maya.

Cabrera, E. (1995). Calendario Maya. En La Cosmovisión Maya (Vol.2). Guatemala: Liga Maya.

Calderón, H. (1966). La Ciencia Matemática de los Mayas. México, D. F.: Orión.

Coulter, L. (2006). Secretos en Piedra, Todo Sobre los Jeroglíficos Mayas. Ciudad de Guatemala: Piedra Santa.

Fahsen, F y Matul, D. (2007). Los Códices de Dresde, París y Grolier. Guatemala: Liga Maya de Guatemala. Amanuense.

Fernández, O. (2010). Pensamiento Matemático de los Mayas, una creación metafórica. Entre Ciencia e Ingeniería, (8), 174-188.

Fernández, O. y Angulo, M. (2010). El símbolo matemático como expresión de poder. Scientia et Technica, (44), 207-210.

D’Ambrosio, U. (1987). Etnomatemáticas: ¿Qué podrán ser? Una recapitulación y reconsideración. En Boletín del Grupo Internacional de Estudios sobre Etnomatemática (ISGEm). 3 (1). Acceso: febrero de 2011. Recuperado de: http://vello.sites.uol.com.br/ubi.htm

Duque, H. (2013). El sentido del número en la cultura Maya. Tesis de maestría. Pereira: Universidad Tecnológica de Pereira.

Grube, N. (2006). Mayas, una Civilización Milenaria. Barcelona: Könemann.

Lakoff, G. y Johnson, M. (1995). Metáforas de la vida cotidiana. (Trad. de Carmen González Marín). Madrid: Cátedra.

Lizcano, E. (2006). Metáforas que nos Piensan. Sobre Ciencia, Democracia y otras Poderosas Ficciones. Ediciones Bajo Cero, licencia de Creative Commons.

Perelman, Ch. (1997). El Imperio Retórico, Retórica y Argumentación. (Trad. de Adolfo León Gómez). Bogotá: Norma.

Pitss, M. (2008). Libro 1: Escribir con grifos Mayas. (The Aid and Education Proyect). Acceso: Noviembre de 2012. Recuperado de: http://www.famsi.org/spanish/research/pitts/GlifosMayasLibro1.pdf

Pitss, M. (2008). Libro 2: Los números Mayas y el calendario Maya. (The Aid and Education Proyect). Acceso: Noviembre de 2012. Recuperado de: http://www.famsi.org/spanish/research/pitts/GlifosMayasLibro2.pdf

Serna, J. (2007). Ontologías Alternativas. Aperturas de Mundo desde el Giro Lingüístico. Rubí, Barcelona: Anthropos y Pereira: Universidad Tecnológica de Pereira.