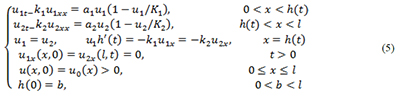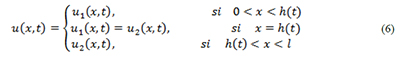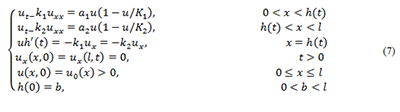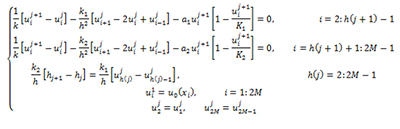DOI:
https://doi.org/10.14483/23448350.7695Published:
10/21/2014Issue:
Vol. 20 No. 3 (2014): September-December 2014Section:
Research ArticlesModelo matemático y simulaciones numéricas para un problema de frontera libre ecológico-Mathematical model and numerical simulations for a free boundary problem of ecological
Keywords:
Dinámica poblacional, modelo matemático, frontera libre, método de diferencias finitas, algoritmo, simulaciones numéricas. (es).Downloads
References
Apostol T. M. (1976). Análisis Matemático. Segunda Edición. Editorail Reverté.
Burden, R. L y Faires, J. D. (2003). Análisis Numérico. Séptima edición. Thomson.
Kim, K. and Lin Z. (2009). A free boundary problem for a parabolic system describing an ecological model. Linear Analysis: Real World Applications. Vol.10.
Lamé G. et Clapeyron B. P. (1831). Memoire sur la Solidification par Refroidissement d'un Globe Liquide. Ann. Chimie Physique, Vol. 47.
Mathews J. H. y Fink K. D. (2008). Métodos Numéricos con Matlab. Tercera edición. Pearson Prentice Hall.
Murray J. D. (2002). Mathematical Biology I: An Introduction. Third Edition. Springer.
Murray J. D. (2003). Mathematical Biology II: Spatial Models and Biomedical Application. Third Edition. Springer.
Okubo A. and Levin S. A. (2002). Diffusion and Ecological Problems: Modern Prespectives. Second Edition. Springer.
Stefan J. (1889). Ueber dir Theorie der Eisbildung, Insbesonder ueber die Eisbildung im Polarmeer. Zit. Akad. Wiss. Wien, Math. Cl., Vol. 98.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Modelo matemático y simulaciones numéricas para un problema de frontera libre ecológico1
Mathematical model and numerical simulations for a free boundary problem of ecological
Modelagem matemática e simulaÇao numérica de um problema de frontera libre em ecología
Deccy Y. Trejos Angel2
Oscar A. Ramírez Céspedes3
1Artículo de Investigación.
2Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: dytrejosa@udistrital.edu.coo
2Universidad Federal de Goiás, Goiânia, Brasil. Contacto: oscarexud@hotmail.com
Fecha de recepción: febrero 2014, Fecha de aceptación: julio de 2014
Resumen
En este artículo se estudia una aproximación numérica del Problema de Frontera Libre (PFL) de un sistema de ecuaciones diferenciales de tipo parabólico unidimensional, asociado con la evolución de la interface, que describe la partición regional de dos grupos de individuos de una misma especie que interactúan en un límite espacial para obtener sus propios hábitats y que es a priori totalmente desconocido. Considerando la dinámica local del sistema, el esquema implícito de diferencias finitas es utilizado, obteniendo así un sistema algebraico no lineal de ecuaciones en cada paso de tiempo. Finalmente, algunas simulaciones de la distribución de densidad poblacional y de la evolución de la frontera libre conforme al tiempo son exhibidas en diferentes escenarios, en base a un algoritmo propuesto e implementado en MATLAB, esto permite validar el modelo matemático PFL.
Palabras clave: Dinámica poblacional, modelo matemático, frontera libre, método de diferencias finitas, algoritmo, simulaciones numéricas.
Abstract
In this paper, we study a numerical approximation Free Boundary Problem (FBP) of a system of differential equations of nonlinear one-dimensional parabolic type, associated with the evolution of the interface, which describes the regional partition of two groups of individuals in a same species interacting in a spatial limit to obtain their own habitat and that is a priori completely unknown. Taking into account the local dynamic of the system, the implicit finite difference scheme is used, obtaining a nonlinear algebraic system of equations in each time step. Finally, some simulations of the distribution of population density and the evolution of the free boundary are displayed according to the time in different scenarios, based on an algorithm proposed and implemented in MATLAB, this validates the mathematical model FBP.
keywords: Population dynamics, mathematical model, free boundary, finite difference method, algorithm, numerical simulations
Resumo
Neste trabalho, estuda-se uma aproximação numérica do Problema de Fronteira Livre (PFL) de um sistema de equações diferencias do tipo parabólico unidimensional, associado com a evolução da intefase, que descreve a partição regional de dois grupos de indivíduos de uma espécie que interatuam em um limite espacial para obter seus próprios habitats e que a priori é totalmente desconhecido. Tendo em conta a dinâmica local do sistema, o esquema de diferencias finito é utilizado, obtendo assim um sistema algébrico não linear de equações em cada passo do tempo. Finalmente algumas simulações numéricas da distribuição espacial e da evolução da fronteira livre conformo ao tempo são exibidas em diferentes cenários, em base a um algoritmo proposto e implementado em MATLAB, isso valida o modelo matemático PFL.
Palavras-chave:Dinâmica populacional, modelo matemático, fronteira livre, método de diferenças finitas, algoritmo, simulações numéricas.
Introducción
En matemática, el primer estudio sobre lo que, en el presente, se denomina frontera libre, se le atribuye a Lamé y a Clapeyron en el año 1831, quienes buscaron las soluciones explícitas para el proceso de solidificación de un globo líquido (Lamé y Clapeyron, 1831). Stefan estudió nuevamente este tipo de problemas en sus trabajos sobre el crecimiento del espesor del hielo en el agua a bajas temperaturas (Stefan, 1889). Ese problema es conocido en matemática como el problema de Stefan y frecuentemente se utiliza para explicar el concepto de frontera libre.
Un fenómeno interesante en la dinámica de poblaciones es la partición regional de las especies como el caso de dos grupos de animales que interactúan en un punto —interfase o frontera intermedia— para obtener sus propios hábitats.
Para modelar el caso unidimensional de esta situación, se asume que los grupos son de la misma especie con funciones de densidad poblacional y , y estos se encuentran sometidos a la dispersión — y coeficientes de dispersión, es la velocidad con la cual se expande cada grupo y está dado en unidad de longitud2/unidad de tiempo— y a un crecimiento logístico. Además, están ubicados en y respectivamente, donde el punto que separa ambas regiones es la frontera libre del problema, las densidades en ese punto son iguales y es totalmente desconocida.
ara modelar matemáticamente la dinámica en torno de la frontera libre, se asume que, desde hasta habrá fluido a través de una cierta cantidad de densidad poblacional; luego, por la Ley de conservación de la masa (Murray, 2002) se tiene:
Realizando un razonamiento análogo para U2 , entonces queda formulado el Problema de Frontera Libre (PFL) que describe la interface entre dos grupos de individuos de una misma especie, asumiendo que no existe entrada ni salida de flujo por las fronteras fijas (X = 0 y X = l),
Donde, u0C2(0,b)nC2(b,l), ku10 E C1(0,l) y (cerca de la interfase los flujos y las densidades de las poblaciones son continuos).
Los términos, Ut y Uxx denotan la primera derivada parcial respecto a la variable temporal t y la segunda derivada parcial con respecto a la variable espacial x, respectivamente de u(x,t). La primera y segunda ecuación de (5) del lado izquierdo de la igualdad, es conocida como ecuación de dispersión-reacción (Murray, 2003) y establece que la población se expande, sin acumularse en ningún lugar en particular, es decir, los individuos se dispersan en la región y se espera que cuando t=00 sea uniforme, esto es, que las densidades de las poblaciones tienden a las fronteras fijas respectivamente, las ecuaciones del lado derecho de la igualdad representa el crecimiento logístico (Murray, 2002) de ambos grupos, mientras que la tercera ecuación de (5) establece que una proporción de individuos del grupo uno pasa al grupo dos y viceversa, pero la cantidad total de individuos se conserva.
Kwang Ik Kim y Zhigi Lin mostraron en el artículo “A free boundary problem for a parabolic system describing an ecological model” que este modelo está bien planteado y demostrando existencia y unicidad de la solución (Kim y Lin, 2009).
Problema de Frontera Libre Discreto.
Sin pérdida de generalidad, se define:
Luego, el sistema parabólico (5) con frontera libre se puede reescribir como,
Para hallar la solución del sistema (7) se usa el método numérico implícito de diferencias progresivas (Burden y Faires, 2003), primero se inicia discretizando el dominio espacial (0,l) por medio de una partición uniforme 2M con subintervalos disjuntos, cuya distancia está dada por h= i/2M2, entonces la partición está definida por 0=X1 < X2 < Xi < Xi+1 < X2M = l .
De forma análoga se discretiza el tiempo ![]() tomando en consideración un tiempo final
tomando en consideración un tiempo final ![]() por una partición uniforme con distancia
por una partición uniforme con distancia ![]() donde
donde ![]() .
.
Sea R la malla que consta de 2XNM nodos de la forma< (xi,xj), es decir: R = {(xi,xj), i = 1:2M,j = 1:N}, Donde M y N son enteros positivos.
Para resolver numéricamente (7), se calculan las aproximaciones a los valores exactos u(x,t) en los puntos de la malla:, obteniendo el siguiente sistema:
Simulaciones numéricas
Para resolver numéricamente el sistema de ecuaciones no lineales escrito en la sección 2, se emplea el método de Newton-Raphson (Mathews y Fink, 2008) y para visualizar la simulación, se usó el paquete matemático MATLAB 7.1.
Se han tomado los siguientes parámetros hipotéticos de la literatura (Murray, 2003), (Okubo y Levin, 2002) y se colocó una población inicial uniformemente distribuidos en ![]() dado por
dado por ![]() ya que satisface las condición del artículo (Kim y Lin, 2009), la tasa de crecimiento para
ya que satisface las condición del artículo (Kim y Lin, 2009), la tasa de crecimiento para ![]() y
y ![]() dados por
dados por ![]() año y
año y ![]() año, respectivamente. Se simulará la distribución de la densidad poblacional para los dos grupos en tres escenarios, variando los valores de la capacidad de carga con el mismo coeficiente de dispersión
año, respectivamente. Se simulará la distribución de la densidad poblacional para los dos grupos en tres escenarios, variando los valores de la capacidad de carga con el mismo coeficiente de dispersión ![]() año y cuando se varía la posición de la frontera libre en el instante
año y cuando se varía la posición de la frontera libre en el instante ![]() , esto es:
, esto es:
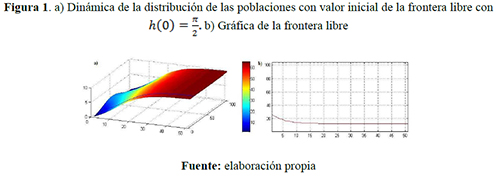
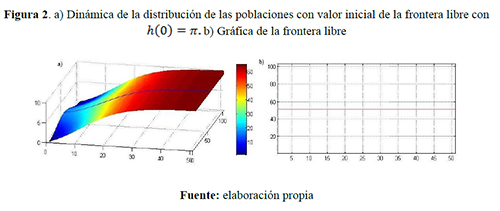
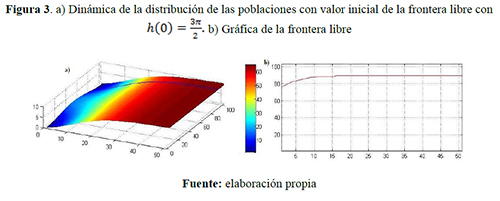
Escenario 1. Capacidades de carga iguales ![]() individuos/año: figura 1. 2 y 3.
individuos/año: figura 1. 2 y 3.
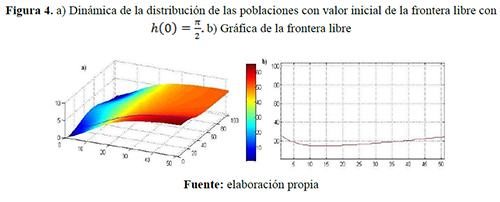
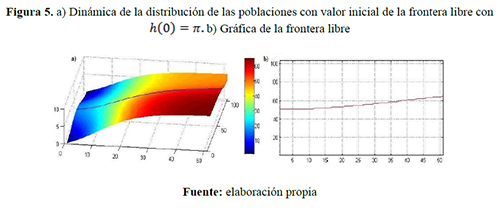
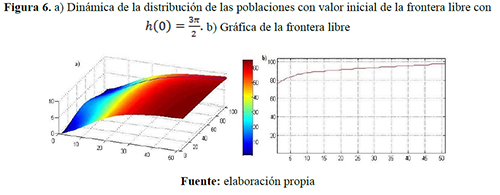
Escenario 2. Capacidades de carga diferentes ![]() individuos/año: figuras 4, 5 y 6.
individuos/año: figuras 4, 5 y 6.
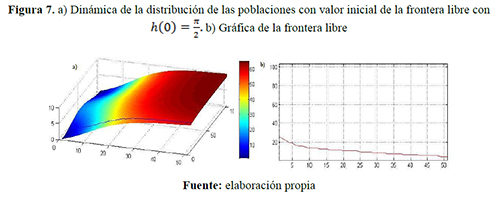
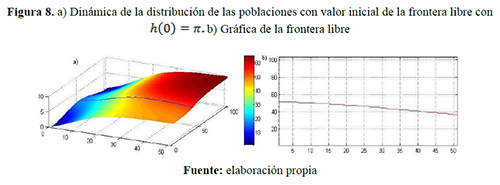
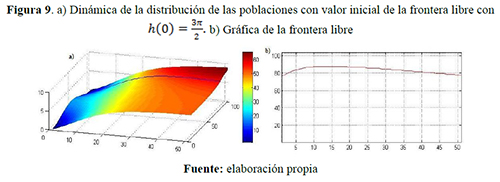
Escenario 3. Capacidades de carga diferentes ![]() individuos/año: figuras 7, 8 y 9.
individuos/año: figuras 7, 8 y 9.
Las siguientes simulaciones corresponden a valores diferentes de los coeficientes de dispersión y con capacidades de carga iguales:
Escenario 4 y 5. Coeficiente de dispersión diferente ![]() año y
año y ![]() año, respectivamente y capacidades de carga iguales
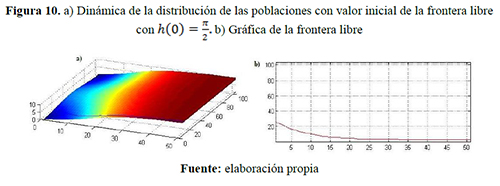
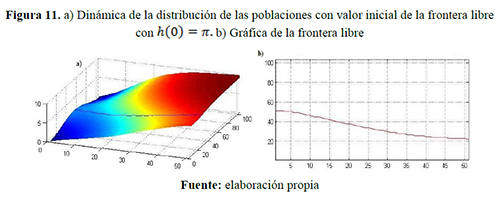
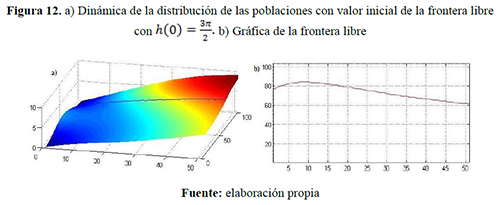
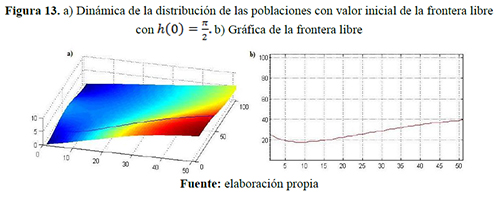
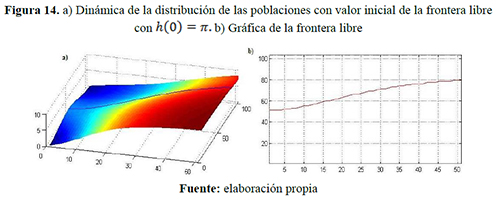
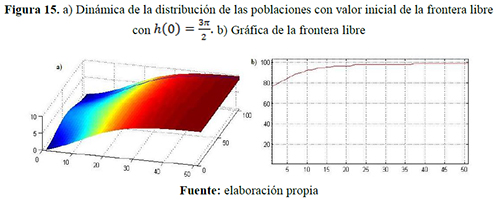
año, respectivamente y capacidades de carga iguales ![]() individuos/año: figuras 10, 11 y 12 para el escenario 4 y figuras 13, 14 y 15 para el escenario 5.
individuos/año: figuras 10, 11 y 12 para el escenario 4 y figuras 13, 14 y 15 para el escenario 5.
Los colores cálidos —amarillo, naranja y rojo— y los colores fríos —verde, azul y morado— que se visualizan en las siguientes figuras indican respectivamente densidad poblacional progresivamente mayores y menores.
Discusión y resultados
Comparando los resultados presentados en los tres primeros escenarios considerados y variando la posición inicial de la frontera libre, se visualiza que, a través de este punto de frontera libre, se está presentando una relevante transferencia de densidad poblacional y un aumento de la región ocupada por uno de los grupos. Sin embargo, el movimiento de dicha frontera disminuye debido a la tendencia de las distribuciones espaciales hacia las capacidades de carga correspondientes; por ejemplo: en el escenario 1, donde las capacidades de carga son iguales, la frontera libre se estabiliza conforme al tiempo transformándose en una nueva frontera fija, esto ocurre porque las poblaciones disminuyen su dispersión debido a que las distribuciones son cada vez más uniformes y tienden al mismo limite, es decir que bajo esta consideraciones la región de una de los grupos disminuirá pero luego ésta se fijará evitando la extinción de alguno de los grupos. Lo contrario ocurre en el escenario 2, en el que una capacidad de carga del grupo uno es mayor que la del grupo dos, lo que genera, a partir de un instante de tiempo, la densidad poblacional del grupo uno sea superior que la del otro grupo y por tanto la frontera libre tienda a una de las fronteras fijas establecidas, es decir, tal grupo ocupará toda la región, lo contrario ocurre en el escenario 3 el grupo dos ocupa toda la región.
Cuando la dispersión de uno de los grupos es mayor que el otro (escenarios 4 y 5) la frontera libre se mueve más rápidamente hacia las fronteras fijas, esto es, el grupo con mayor dispersión tiende a invadir el espacio del grupo de menor dispersión. En la figura 14 se muestra el comportamiento de la población cuando la frontera libre se encuentra en los bordes, esto es
y
respectivamente, la frontera no se mueve debido a que la dirección de los grupos no es hacia afuera si no hacia el interior de la región y por las condiciones de contornos.
Conclusiones
Esta investigación se centró únicamente en hacer una aproximación numérica para el PFL de dos grupos de animales que compiten por espacio en una región determinada, empleando el esquema implícito, este método es incondicionalmente estable y por consiguiente convergente. Obteniendo así, la estructura de un algoritmo para las simulaciones numéricas y que sirve para analizar el comportamiento del modelo matemático.
Con respecto a las simulaciones numéricas que se realizaron, se pudo observar que el movimiento de la Frontera Libre y su correlación con la distribución de las densidades poblaciones de los grupos en el espacio es lógico bajo las hipótesis y suposiciones ecológicas consideradas, con un estudio más detallado y con datos reales es posible emplear los resultados obtenidos en control y extinción de grupos ecológicos en regiones fijas.
Referencias
Apostol T. M. (1976). Análisis Matemático. Segunda Edición. Editorail Reverté.
Burden, R. L y Faires, J. D. (2003). Análisis Numérico. Séptima edición. Thomson.
Kim, K. and Lin Z. (2009). A free boundary problem for a parabolic system describing an ecological model. Linear Analysis: Real World Applications. Vol.10.
Lamé G. et Clapeyron B. P. (1831). Memoire sur la Solidification par Refroidissement d'un Globe Liquide. Ann. Chimie Physique, Vol. 47.
Mathews J. H. y Fink K. D. (2008). Métodos Numéricos con Matlab. Tercera edición. Pearson Prentice Hall.
Murray J. D. (2002). Mathematical Biology I: An Introduction. Third Edition. Springer.
Murray J. D. (2003). Mathematical Biology II: Spatial Models and Biomedical Application. Third Edition. Springer.
Okubo A. and Levin S. A. (2002). Diffusion and Ecological Problems: Modern Prespectives. Second Edition. Springer.
Stefan J. (1889). Ueber dir Theorie der Eisbildung, Insbesonder ueber die Eisbildung im Polarmeer. Zit. Akad. Wiss. Wien, Math. Cl., Vol. 98.
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.