DOI:
https://doi.org/10.14483/23448393.20094Published:
2023-05-31Issue:
Vol. 28 No. 2 (2023): May-AugustSection:
Electrical, Electronic and Telecommunications EngineeringDefending State-Feedback Based Controllers Against Sensor Attacks
Defensa de Controladores Basados en Realimentación de Estados Contra Ataques en Sensores
Keywords:
Cyber-physical systems, unknown input observer, sensor attack, false data injection. (en).Keywords:
Sistemas Ciber-Físicos, Observador de Entrada Desconocida, Ataques en sensores, Inyección de Datos Falsos. (es).Downloads
References
K. E. Hemsley and D. R. E. Fisher, "History of industrial control system cyber incidents," Tech. Rep., Idaho National Lab. (INL), Idaho Falls, ID, USA, Dec. 2018. [Online]. Available: https://doi.org/10.2172/1505628 DOI: https://doi.org/10.2172/1505628
R. M. Lee, M. J. Assante, and T. Conway, "Malicious control system cyber security attack case study - Maroochy water services, Australia," McLean, VA: The MITRE Corporation, 2008.
R. Langner, "Stuxnet: Dissecting a cyberwarfare weapon," IEEE Secur Priv, vol. 9, no. 3, pp. 49-51, May-Jun. 2011. [Online]. Available: https://doi.org/10.1109/MSP.2011.67 DOI: https://doi.org/10.1109/MSP.2011.67
A. Nourian and S. Madnick, "A systems theoretic approach to the security threats in cyber physical systems applied to Stuxnet," IEEE Trans. Dependable Secure Comput., vol. 15, no. 1, pp. 2-13, Jan.-Feb. 2018. [Online]. Available: https://doi.org/10.1109/TDSC.2015.2509994 DOI: https://doi.org/10.1109/TDSC.2015.2509994
M. Abrams and J. Weiss, "Analysis of the cyber attack on the Ukrainian power grid," SANS ICS Report, Mar. 2016.
Y. Z. Lun, A. D'Innocenzo, F. Smarra, I. Malavolta, and M. D. D. Benedetto, "State of the art of cyber-physical systems security: An automatic control perspective," J. Syst. Softw., vol. 149, pp. 174-216, Jul. 2019. [Online]. Available: https://doi.org/10.1016/j.jss.2018.12.006 DOI: https://doi.org/10.1016/j.jss.2018.12.006
H. S. Sánchez, D. Rotondo, T. Escobet, V. Puig, and J. Quevedo, "Bibliographical review on cyber attacks from a control oriented perspective," Annu. Rev. Control, vol. 48, pp. 103-128, Dec. 2019. [Online]. Available: https://doi.org/10.1016/j.arcontrol.2019.08.002 DOI: https://doi.org/10.1016/j.arcontrol.2019.08.002
L. Cao, X. Jiang, Y. Zhao, S. Wang, D. You, and X. Xu, "A survey of network attacks on cyber-physical systems," IEEE Access, vol. 8, pp. 44219-44227, Mar. 2020. [Online]. Available: https://doi.org/10.1109/ACCESS.2020.2977423 DOI: https://doi.org/10.1109/ACCESS.2020.2977423
M. Kordestani and M. Saif, "Observer-based attack detection and mitigation for cyber-physical systems: A review," IEEE Syst. Man Cybern. Syst., vol. 7, no. 2, pp. 35-60, Mar. 2021. [Online]. Available: https://doi.org/10.1109/MSMC.2020.3049092 DOI: https://doi.org/10.1109/MSMC.2020.3049092
W. Duo, M. Zhou, and A. Abusorrah, "A survey of cyber attacks on cyber physical systems: Recent advances and challenges," IEEE/CAA J. Autom. Sin., vol. 9, DOI: https://doi.org/10.1109/JAS.2022.105548
H. Fawzi, P. Tabuada, and S. Diggavi, "Secure estimation and control for cyber-physical systems under adversarial attacks," IEEE Trans. Automat. Control, vol. 59, no. 6, pp. 1454-1467, Jun. 2014. [Online]. Available: https://doi.org/10.1109/TAC.2014.2303233 DOI: https://doi.org/10.1109/TAC.2014.2303233
Y. H. Chang, Q. Hu, and C. J. Tomlin, "Secure estimation based Kalman filter for cyber-physical systems against sensor attacks," Automatica, vol. 95, pp. 399-412, Nov. 2018. [Online]. Available: https://doi.org/10.1016/j.automatica.2018.06.010 DOI: https://doi.org/10.1016/j.automatica.2018.06.010
R. Deng, G. Xiao, and R. Lu, "Defending against false data injection attacks on power system state estimation," IEEE Trans. Industr. Inform., vol. 13, no. 1, pp. 198-207, Feb. 2017. [Online]. Available: https://doi.org/10.1109/TII.2015.2470218 DOI: https://doi.org/10.1109/TII.2015.2470218
L. F. Cómbita, N. Quijano, and A. A. Cárdenas, "On the stability of cyber-physical control systems with sensor multiplicative attacks," IEEE Access, vol. 10, pp. 39716-39728, 2022. [Online]. Available: https://doi.org/10.1109/ACCESS.2022.3164424 DOI: https://doi.org/10.1109/ACCESS.2022.3164424
L. An and G.-H. Yang, "Fast state estimation under sensor attacks: A sensor categorization approach," Automatica, vol. 142, p. 110395, Apr. 2022. [Online]. Available: https://doi.org/10.1016/j.automatica.2022.110395 DOI: https://doi.org/10.1016/j.automatica.2022.110395
P. Weng, B. Chen, S. Liu, and L. Yu, "Secure nonlinear fusion estimation for cyber-physical systems under FDI attacks," Automatica, vol. 148, p. 110759, Feb. 2023. [Online]. Available: https://doi.org/10.1016/j.automatica.2022.110759 DOI: https://doi.org/10.1016/j.automatica.2022.110759
C. Wang, J. Huang, D. Wang, and F. Li, "A secure strategy for a cyber physical system with multi-sensor under linear deception attack," J. Franklin Inst., vol. 358, no. 13, pp. 6666-6683, Sep. 2021. [Online]. Available: https://doi.org/10.1016/j.jfranklin.2021.06.029 DOI: https://doi.org/10.1016/j.jfranklin.2021.06.029
X. Wang and P. Zhao, "An adaptive control scheme against state-dependent sensor attacks and input-dependent actuator attacks in cyber-physical systems," IET Control Theory Appl., vol. 17, no. 8, pp.1061-1075, Mar. 2023. [Online]. Available: https://doi.org/10.1049/cth2.12443 DOI: https://doi.org/10.1049/cth2.12443
K. H. Johansson, "The quadruple-tank process: a multivariable laboratory process with an adjustable zero," IEEE Trans. Control Syst. Technol., vol. 8, no. 3, pp. 456-465, May 2000. [Online]. Available: https://doi.org/10.1109/87.845876 DOI: https://doi.org/10.1109/87.845876
G. F. Franklin, M. L. Workman, and D. Powell, "Digital Control of Dynamic Systems," 3rd ed., Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc., 1997.
K. Ogata, "Discrete-Time Control Systems," 2nd ed., USA: Prentice-Hall, Inc., 1995.
C. L. Phillips and H. T. Nagle, "Digital Control System Analysis and Design," 3rd ed., USA: Prentice-Hall, Inc., 1995.
X. He, Z. Wang, and D. Zhou, "Robust fault detection for networked systems with communication delay and data missing," Automatica, vol. 45, no. 11, pp. 2634-2639, Nov. 2009. [Online]. Available: https://doi.org/10.1016/j.automatica.2009.07.020 DOI: https://doi.org/10.1016/j.automatica.2009.07.020
J. Chen and R. J. Patton, "Robust Model-based Fault Diagnosis for Dynamic Systems," Norwell, MA, USA: Kluwer Academic Publishers, 1999. [Online]. Available: https://doi.org/10.1007/978-1-4615-5149-2 DOI: https://doi.org/10.1007/978-1-4615-5149-2
C. T. Chen, "Linear System Theory and Design," New York: Oxford University Press, Inc., 1984.
L. F. Cómbita, A. Cárdenas, and N. Quijano, "Mitigating sensor attacks against industrial control systems," IEEE Access, vol. 7, pp. 92444-92455, 2019. [Online]. Available: https://doi.org/10.1109/ACCESS.2019.2927484 DOI: https://doi.org/10.1109/ACCESS.2019.2927484
K. Liu, A. Selivanov, and E. Fridman, "Survey on time-delay approach to networked control," Annu Rev. Control, vol. 48, pp. 57-79, 2019. [Online]. Available: https://doi.org/10.1016/j.arcontrol.2019.06.005 DOI: https://doi.org/10.1016/j.arcontrol.2019.06.005
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 15 de noviembre de 2022; Revisión recibida: 26 de abril de 2023; Aceptado: 5 de mayo de 2023
Abstract
Context:
This paper is motivated by the need to improve the resilience of industrial control systems. Many control systems currently operating in the industry were designed and implemented before the boom in communications (wired and wireless networks) within industrial control systems. However, nowadays, they operate connected to the communications network. This increase in connectivity has made these systems susceptible to cyber-attacks that seek to deteriorate the proper operation of the control loop, even when affecting only one sensor.
Method:
Concepts from fault tolerant control and classic control theory are used to show that it is possible to reconstruct the system state without (any) one of the system outputs. This is employed in the control action signal recalculation through an algorithm of attack detection and isolation, in order to prevent an attack being from fed back to the system, mitigating its effect. This work shows the effectiveness of our proposal with simulations on a four tanks testbed using Matlab and Simulink.
Results:
This work demonstrates that a bank of unknown input observers can be designed to recover true information from attacked sensors, i.e., the information without the effect of the attack. Therefore, the estimate obtained from said observers can be utilized for computing a control action that mitigates the effect of the attack.
Conclusions:
This mitigation prevents a single sensor attack from significantly impairing the action of low-level controllers, improving the resilience of the system by only modifying the digital controller architecture. This development is limited to cyber-attacks on system sensors happening one at a time, which can still seriously compromise the system behavior. Future work will address the extension of the results to situations with simultaneous attacks on more than one sensor and/or consider attacks on the control system actuators.
Keywords:
cyber-physical systems, unknown input observer, sensor attack, false data injection..Resumen
Contexto:
La motivación de este artículo es la necesidad de mejorar la resiliencia en sistemas de control industriales. Muchos de los sistemas de control que operan actualmente en la industria fueron diseñados e implementados antes de que se diera el boom de las comunicaciones (cableadas a inalámbricas) dentro de los sistemas de control industrial. Sin embargo, estos sistemas funcionan conectados en red. Dicho incremento en la conectividad ha hecho que estos sistemas sean susceptibles a ataques cibernéticos que buscan degradar la operación adecuada del lazo de control con tan solo afectar un sensor.
Método:
Se utilizan conceptos de control tolerante a fallos y teoría de control clásica para demostrar que es posible estimar el estado del sistema sin una de las salidas del sistema (cualquiera). Esto se emplea para recalcular la acción de control a partir de un algoritmo que detecta y aisla el ataque, evitando que este sea realimentado al sistema y, por ende, mitigando su efecto. Este trabajo muestra la efectividad de nuestra propuesta con simulaciones desarrolladas sobre Matlab y Simulink para un sistema de cuatro tanques.
Resultados:
Este trabajo demuestra que se puede diseñar un banco de observadores de entrada desconocida para recuperar la información real de sensores atacados, i.e., la información del sensor sin el efecto del ataque. Por lo tanto, el estimado obtenido de dicho banco de observadores puede utilizarse para para recalcular la acción de control que mitigue el efecto del ataque.
Conclusiones:
Esta mitigación previene que ataques en algún sensor puedan comprometer significativamente el desempeño del sistema, mejorando su resiliencia a partir únicamente de la modificación de la arquitectura del controlador digital. Este desarrollo está limitado a ataques que ocurren uno a la vez en cualquier sensor, pero que aún así pueden afectar fuertemente el desempeño del sistema. Los trabajos futuros abordarán la extensión de los resultados a situaciones donde ocurran ataques simultáneos en más de un sensor y/o considerarán ataques en los actuadores del sistema.
Palabras clave:
sistemas ciberfísicos, observador de entrada desconocida, ataques en sensores, inyección de datos falsos..Introduction
The growing incorporation of sensors, actuators, and controllers with digital communication capabilities in process control systems has enabled data collection and analysis from the operational physical world, which allows optimizing manufacturing processes to increase efficiency and reduce costs. Consequently, the inclusion of these digital capabilities opens an opportunity for intruders to gain knowledge of process data and use it fraudulently. However, most of these episodes are not publicly reported, unlike the enterprise cyber-threats and incidents that are widely documented 1
In the scientific literature, there is evidence of the concern about the security of control systems of critical infrastructures for at least the two last decades. However, it is just about twelve years since some reports of successful cyber-attacks led public policies and funds to increase the security of cyber-physical systems. Some of the vulnerabilities of the process control systems show the need to find tools to build more secure control systems. Public reports of computer attacks on control process systems demonstrate the relevance of these malicious actions since 2000. As a starting point for a discussion on security issues in process control systems, a brief description of the first three known attacks is shown below.
In March 2000, the wastewater system of the Maroochy Shire Council (Queensland) reported issues with its pumping stations. Radiofrequency communications between pumping stations and the control center failed. Hence, the pumps had an improper operation, and the alarms did not signal the faults to the system operator 2).
Stuxnet has been widely considered as the first computer virus to attack a process control system. This computer worm was first detected in June 2010. The purpose was to attack an uranium enrichment process control based on a Supervisory Control And Data Acquisition (SCADA) system. The virus penetrated through a USB memory to infect the whole corporate network and went undetected. At the same time, as the virus identified the machines where designated people automated the manufacturing process based on Siemens Program Logic Controllers (PLCs), the worm uploaded the last updated file running on the controller to the Internet. The virus exploited a “zero-day” vulnerability before the security experts identified it. After achieving the domination of the target, the intruders could spy, in detail, on the operation of the control systems and generate actions that could degrade their performance in the worst way. In this regard, rotor speed and over-pressure strategies were simultaneously used on the centrifuges to attack the uranium enrichment process. Modifying the rotor speed can cause a severe decrease in the useful life of the centrifuge. A chronic over-pressure condition inside the centrifuge can hinder uranium enrichment and erroneously indicate the end of the centrifuge’s useful life, which implies the need to replace the centrifuging equipment. Tamper control actions did not generate any alarm activation because the data obtained from the correct operation of the process supplanted the genuine values of the measurements of abnormal situations 3, (4
In 2015, the first known successful cyber-attack on a power grid was reported. In this attack, 30 substations of the Ukrainian power distribution network were successively attacked, which caused several outages 5. As a result of this incident, about 230.000 people were left without electricity for up to six hours. Similar to the aforementioned cases, there are more incidents across several industries.
The security of cyber-physical systems (CPSs) is an issue that has currently sparked great attention in researchers. Among the different topics developed by the control systems community over the years, there are definitions of cyber-attacks, the design of effective attacks, various techniques for attack detection and isolation, and the design of resilient controllers, as well as some works related to attack mitigation, all of them with variations for linear and nonlinear systems, with or without noise, and for either continuous or discrete-time systems. Recent surveys and works in CPS security (6-10) agree on the fact that cyber-attack response has received considerably less attention than attack detection and isolation, which is the gap to which this work contributes.
A relatively new topic related to the one discussed in this paper is secure estimation, which consists of the capability to reconstruct the system state even when the CPS of interest is under attack. The authors of 11 establish the maximum number of allowed corrupted sensors in order to be able to recover the information from all sensors in the system. This work requires the corrupted sensors not to change over time. In 12, a more flexible condition for the structure of the corrupted sensors is considered, as well as the practical incidence of noise. However, these works assume that there are low-level control loops that cannot be accessed by attackers, but, in cyber-security, it is well known that this feature is usually related to the available budget of the attacker 13. Besides, an attack on one sensor of a low-level controller is enough to cause changes in the stability of the overall system, which can have catastrophic consequences, as demonstrated in 14.
In the context of multi-sensor schemes, where redundant information helps to improve the security and accuracy of state estimation, some works can be mentioned: 15-17. A particular approach to achieving a fast-secure estimation is presented in 15, where the authors leverage the advantage of sensor redundancy in some systems. Therein, a quantification of the measurements’ degree of similarity is defined, which allows for a convenient categorization of the sensors and increases the computational efficiency of the state estimation. For nonlinear systems, in 16, methods of nonlinear fusion estimation in a distributed framework are utilized in order to obtain a secure estimation, in cases where sensor measurements are corrupted with false data injection attacks. In this approach, no prior information about the attack is necessary. In 17, the encryption of the information transmitted and received through a wireless channel of a control system is shown to be effective against linear deception attacks. This work provides valid results even if the attacker has information about the watermark used to encrypt the innovation sequence.
However, the aforementioned redundancy is not a typical property of industrial control systems. The authors of 18 develop an adaptive controller for time-invariant and time-varying deception attacks. The adaptive controller is also effective when both a sensor attack and an actuator attack coexist. They also provide an in-depth analysis of the stability of the control system under attack. In contrast with our work, this strategy requires the total design of a new controller and cannot be used to improve the security of legacy control systems.
Bearing this in mind, this study developed a strategy for low-level controllers in industrial control systems or critical infrastructure. Our goal is to use analytical redundancy to prevent attacks in these low-level controllers from harming the operation of the whole system.
Our main contributions focus on a low-budget defense strategy design and the efficient implementation of this mitigation strategy, which can be summarized as follows:
1. This work shows that a system state without the effect of the attack can be recovered with the design of a bank of unknown input observers (UIOs), as well as providing the necessary conditions for the existence of a solution for each UIO.
2. The mitigation algorithm and the bank of UIOs can be developed in the same PLC where the local controller is implemented.
3. This UIO design shows how to choose the decoupling matrix, which allows the state estimation to be achieved without the effect of the attack.
4. The way in which disturbances affect a system is usually assumed to be known. Hence, it can be used in the design of the UIOs. This is not a valid assumption in the case of the disturbances produced by attacks on sensors. Therefore, this work makes some remarks on how to decouple the disturbance from the original system to be able to estimate the system state using a bank of UIOs
The remainder of the paper is organized as follows. Section 2 presents the general setup of an existing, working control system. Section 3 shows how to reconstruct the original system state without the effect of the attack. Afterwards, Section 4 depicts the general scheme to detect and isolate attacks, in order to be able to reconstruct the system state. Later, in Section 5, system state reconstruction is applied to the four tanks system benchmark 19, with the aim to show how a system can recover its controlled operation even in the presence of attacks. Finally, some conclusions are drawn, and future works are proposed.
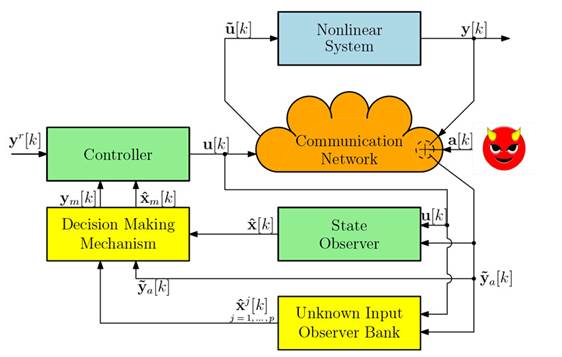
Existing System Setup
This study considers a physical system that works with a digital controller in a closed loop through a network, i.e., an existing cyber-physical control system, as depicted in Fig. 1, without considering the attack and the mitigation mechanism (yellow blocks). The controller allows the system to maintain a specific behavior, where the system would normally be able to follow a reference input and maintain specific characteristics in the transient response. Since the real system is considered to be generally nonlinear, its behavior is modeled as
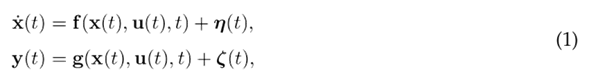
where x(t) ∈ R n, u(t) ∈ Rm, and y(t) ∈ Rp are the system state, input, and output, respectively. The vectors η and ζ represent noise, disturbances, or variations in the model parameters, related to the system state in the first equation and to the system output in the second equation. Since the closed-loop system works with a digital controller, this study assumes that the controller is designed with the more straightforward approximation, i.e., a noiseless discrete-time linear approximation of the system, which can be expressed as

where x[k] ∈ Rn,
 ∈ Rm, and y[k] ∈ Rp are the discrete-time system state, input, and output, respectively. The signal d[k] ∈ R corresponds to disturbances such as noise, nonlinearities, model inaccuracies, or uncertainties; and the matrix E ∈ Rn×1 represents how the disturbances affect the system. Note that the system input is not u[k] but
∈ Rm, and y[k] ∈ Rp are the discrete-time system state, input, and output, respectively. The signal d[k] ∈ R corresponds to disturbances such as noise, nonlinearities, model inaccuracies, or uncertainties; and the matrix E ∈ Rn×1 represents how the disturbances affect the system. Note that the system input is not u[k] but
 , which represents u[k] after passing through the network. A ∈ Rn×n, B ∈ Rn×m and C ∈ Rp×n are the dynamic, input, and output matrices of the system, respectively. This kind of system model defined by 2 can be obtained from either: (i) modeling the system, linearizing it, and discretizing it; or (ii) learning the discrete-time model from input-output data, using an adequate sampling time according to the closed-loop system’s dynamical behavior 20.
, which represents u[k] after passing through the network. A ∈ Rn×n, B ∈ Rn×m and C ∈ Rp×n are the dynamic, input, and output matrices of the system, respectively. This kind of system model defined by 2 can be obtained from either: (i) modeling the system, linearizing it, and discretizing it; or (ii) learning the discrete-time model from input-output data, using an adequate sampling time according to the closed-loop system’s dynamical behavior 20.
The controller that works with the system is considered to be a tracking control with state feedback, i.e., a servo system 21, represented as

where yr [k] ∈ Rp is the system reference input (the one to be followed by the system),
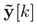 represents y[k] after passing through the network, and
represents y[k] after passing through the network, and
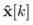 is the estimated state. Note that the first equation in (3) expresses the integrator state (which, in this case, is considered as an interior variable of the controller in Fig. 1), where v[k] ∈ Rp is a discrete-time approximation of the error integral, with the error defined as e[k] = yr [k] − y[k]. The control signal u[k] is obtained as a linear combination of the states, through the state feedback gain KS ∈ Rm×n, and a linear combination of the error integral, through the integral gain KI ∈ Rm×p
is the estimated state. Note that the first equation in (3) expresses the integrator state (which, in this case, is considered as an interior variable of the controller in Fig. 1), where v[k] ∈ Rp is a discrete-time approximation of the error integral, with the error defined as e[k] = yr [k] − y[k]. The control signal u[k] is obtained as a linear combination of the states, through the state feedback gain KS ∈ Rm×n, and a linear combination of the error integral, through the integral gain KI ∈ Rm×p
Figure 1: Control systems with mitigation of sensor attacks mechanism included
As usual, it is assumed that not all the system states are available for implementing the part of the controller related to state feedback. In order to estimate the system states, a full-order current observer is used 20, 22, with the following dynamics:

where
 is the predicted estimate, which is based on a model prediction from the previous time estimate, corrected by the measurement of the output, becoming
is the predicted estimate, which is based on a model prediction from the previous time estimate, corrected by the measurement of the output, becoming
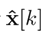 . L ∈ Rn×p is the observer gain that guarantees that the matrix A − L C A is Hurwitz, when the pair (A, C A) is observable. It is assumed that the controller and the observer have been properly designed
. L ∈ Rn×p is the observer gain that guarantees that the matrix A − L C A is Hurwitz, when the pair (A, C A) is observable. It is assumed that the controller and the observer have been properly designed
Since the system and the controller are coupled by a network, the control signal received by the system is not u[k] but
 , and the output signal received by the controller is not y[k] but
, and the output signal received by the controller is not y[k] but
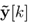 , where
, where

And

The Kronecker delta function δ[τ k − i] is used to represent the random communication delays and the missing stochastic data. The time delay τ k is a random variable considered to be an integer multiple of the sampling time T s , introduced to describe the possibility of data missing, as well as the size of the delay at time instant k23.
Unknown Input Observers for the Recovery of the State Without the Effect of the Attack
Consider the closed-loop control system of the previous section with a model such as that in 2, a controller as in 3, and an observer as in 4. The system is disturbed with a sensor attack (after passing through the network),with

where a[k] is a vector of p functions that represents the attack signals, and Fa ∈ Rp×p represents the outputs affected by the attack a[k], i.e., only one output at a time.
In this particular case, for the system in 2, the disturbances d[k] are considered to represent the state variables’ alteration due to the change in the control signal produced by a sensor attack. Subsequently, under the assumption that only one attack is occurring concurrently, it is considered that these modifications can be encapsulated by a single signal. Therefore, the matrix Fa represents the unattacked outputs acting on the system state
This work takes interest in estimating the output signals without the effect of the attack, in order to compensate the control action signal and prevent the attack from feeding back the system and causing it to collapse. A bank of p UIOs was used, one for each sensor that could be attacked, where each UIO does not take consider the jth output. That is to say
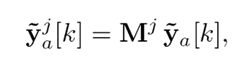
where Mj ∈ R(p−1)×p is a transformation matrix equal to an identity one without the jth row, with j = 1, 2, . . . , p. The hypothesis behind using UIOs without one of the outputs is that, since there is no more than one attack at the same time, if the attacked output is not involved, then an unbiased estimation of all the state variables of the system can be achieved - and, therefore, the outputs.
The jth UIO is described using the following state-space representation, which is inspired by 24

where
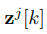 ∈ Rn is the dynamic (first) approximation of the estimated state vector, and xj [k] ∈ Rn is the estimated state vector, which corresponds to the UIO that does not use the information of the j th output for the estimation process, i.e.,
∈ Rn is the dynamic (first) approximation of the estimated state vector, and xj [k] ∈ Rn is the estimated state vector, which corresponds to the UIO that does not use the information of the j th output for the estimation process, i.e.,
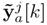 is the output vector
is the output vector
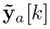 whose jth component is eliminated. Fj ∈ Rn×n, Tj ∈ Rn×n, Kj ∈ Rn×(p−1), and Hj ∈ Rn×(p−1) are design matrices such that the estimated state of the UIO,
whose jth component is eliminated. Fj ∈ Rn×n, Tj ∈ Rn×n, Kj ∈ Rn×(p−1), and Hj ∈ Rn×(p−1) are design matrices such that the estimated state of the UIO,
 , converges to x[k] when there is no attack, i.e., Fa = 0. When the jth UIO 8) is applied to the system 3, decomposing Kj = K j 1 + K j 2 , the estimation error
, converges to x[k] when there is no attack, i.e., Fa = 0. When the jth UIO 8) is applied to the system 3, decomposing Kj = K j 1 + K j 2 , the estimation error
 is governed by the following equation
is governed by the following equation

Note that Ej is used instead of E and dj [k] instead of d[k], indicating that each UIO considers its own perturbations. That is because, for each UIO, a way to approximate the control action modification is to assign more weight to the state variables related with the outputs used directly by the jth UIO.
Consider the UIOs’ behavior, neglecting the effect of the attack on the output sensors (Fa = 0), in order to see how the UIOs estimate the system state. For this case,
 and 9 yield
and 9 yield

It is known that a proper state estimation is achieved when the estimation error for the jth UIO takes the following form:

In addition, the eigenvalues of Fj must be stable in order for the estimation error to converge to zero. This implies that, for the UIO to estimate the state, all the terms on the right side of 10 but the first must be equal to zero. That is, it must be ensured that




When considering the effect of the attack on the outputs (Fa ̸= 0) while holding 12- 15, the estimation error of the jth UIO is governed by

which, depending on the form of HjFj a and Kj 1Fj a, will eventually converge proportionally to a[k] or zero. That is to say, if there is an attack on the jth output, and since the jth UIO does not consider that output, then ej [k] → 0, i.e., xj[k] → x[k], which produces the estimation of the outputs without the effect of the attack. On the other hand, if there is an attack on the i th output, and since the jth UIO considers that output, ej [k] ∝ a[k], and the estimated state will not aid in recovering the outputs without the effect of the attack.
In order to design the UIOs, Eqs. (12)-(15) need to be solved. Note that it is only necessary to solve 12 for Hj , which allows solving the rest of the equations if it can be ensured that (Aj 1 , C) is detectable, with Aj 1 = (I − HjCj )A. A Lemma addressing the existence of a solution to 12 is introduced below:
Lemma 3.1. Eq. (12) is solvable if and only if

is Ej full column rank, then a special solution to 12 is
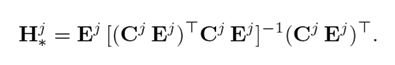
Proof. When 12 has a solution Hj , then Hj Cj Ej = Ej or

i.e., Ej⊤ belongs to the range space of the matrix (Cj Ej ) ⊤, and this leads to

i.e.,

However,

and, since (Ej) is full column rank
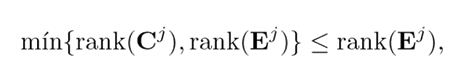
then

Therefore, the only way to satisfy 18 and 19 is that rank(Cj Ej ) = rank(Ej ). Thus, the necessary condition is proven.
When rank(Cj Ej ) = rank(Ej) holds true, Cj Ej is a full column rank matrix, and there is a left inverse of Cj Ej:

Clearly, Hj = Ej (Cj Ej ) + is a solution to 12.
Now, a lemma is introduced to show the equivalence of the detectability of an augmented system and the one of the original system.
Now, a lemma is introduced to show the equivalence of the detectability of an augmented system and the one of the original system.
Lemma 3.2. Let Cj 1 = [ Cj Cj A]⊤ . Then, the detectability of the pair (C j 1 , A) is equivalent to that of the pair (Cj , A).
Proof. The observability of a system can also be verified if

for any s ∈ C (see Theorem 5-13 in 25). Therefore, if s1 ∈ C is an unobservable mode of the pair (Cj 1 , A), then

This means that a vector α ∈ Cn will exist, such that

which implies that

This is to say that s1 is also an unobservable mode of the pair (Cj , A). Now, if s2 ∈ C is an unobservable mode of the pair (Cj , A), then
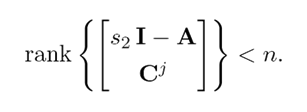
This means that a vector β ∈ Cn can always be found, such that
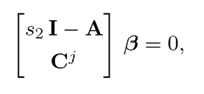
which can be rewritten as

Multiplying by Cj on the left of the first equation in (22),
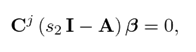
which is equivalent to
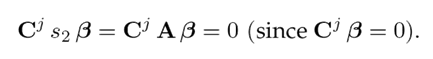
Hence,

i.e., s 2 is also an unobservable mode of the pair (Cj1 , A). As the pairs (Cj 1 , A) and (Cj 1 , A) have the same unobservable modes, their detectability is formally equivalent.
At this point, it is important to include the necessary and sufficient conditions for the UIOs.
Theorem 3.1. The conditions for 8 to be an UIO for the system defined by (3) are:



Proof. According to Lemma 3.1, 12 is solvable when condition 1 holds true. A special solution for Hj is

In this case, the system dynamics matrix is

which can be stabilized by selecting the gain matrix Kj 1 due to condition 2. Finally, the remaining UIO matrices described in 8 can be calculated using 14 - 15. Thus, the observer 8 is a UIO for the system defined in the two first rows of 3
Since 8 is a UIO for 3, 12 is solvable. This leads to the fact that condition 1 holds true according to Lemma 3.1. The general solution of the matrix Hj for 12 can be calculated as

where Hj 0 ∈ Rn×(p−1) is an arbitrary matrix and (Cj Ej )+ is the left inverse of Cj Ej , as defined in 20. Substituting the solution for Hj into 13, the system dynamics matrix Fj is

where
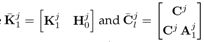 Since the matrix Fj is stable, the pair
Since the matrix Fj is stable, the pair
 is detectable, as well as the pair (Cj , Aj
1 ), according to Lemma 3.2
is detectable, as well as the pair (Cj , Aj
1 ), according to Lemma 3.2
Once the necessary conditions to design the bank of UIOs have been verified, it is necessary to prove that it is possible to recover the state estimation of the output without the effect of the attack from the jth UIO.
Theorem 3.2. Suppose that 8 is the jth UIO for the system defined by 3. If there is an attack in the jth output, then an estimation of the output without the effect of the attack can be obtained from the jth UIO.
Proof. Considering that there is an attack on the system 3, i.e., Fa ¹ 0. In fact, since one simultaneous attack Fa is considered, this can be written as a set of unitary column vectors with all but one element different from zero. Consider a simpler case, where a[k] is a scalar function and Fa is a unitary vector. Assuming that the attack affects the j th output, the form of Fa is
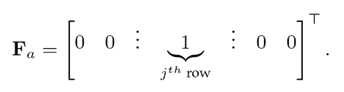
Then, Fj
a = 0(p−1)×1 (Fj
a equals Fa without the jth row. In this assumption, the only element different from zero, and clearly 16, will become 11. The above implies that
 . Therefore,
. Therefore,
 can be found, which represents the estimation of the outputs without the effect of the attack.
can be found, which represents the estimation of the outputs without the effect of the attack.
Now, considering the general case where a[k] is a vector of p functions and Fa ∈ Rp×p , the previous procedure holds, albeit only for the time intervals where each attack is happening, under the assumption that no more than one attack will occur concurrently.
Detection, Isolation and Mitigation
Note that Theorem 3.2 provides the opportunity to recalculate the control signal to prevent the attack from being fed back to the system. However, this is possible only if we know when and where the attack takes place, which we do not know a priori. In order to answer these questions, this study proposes the use of the already working full order current observer described by 4 to know when an attack occurs within a process known as detection, and, since UIOs are used to recalculate the control signal, they could also be used to determine where the attack takes place, in a process known as isolation. The complete scheme for mitigating the effect of the attack in a closed-loop control system is shown in Fig. 1, where the decision-making mechanism includes attack detection and isolation and mitigation, which includes recovering the state and, therefore, the sensor output, both without the effect of the attack.
To find out when an attack takes place, full order current observer-associated residues are defined as

where ||x||2 stands for the 2-norm of a vector x ∈ Rn. An attack is detected when

where τD is a threshold associated with the maximum estimation error that the system could supposedly tolerate. In order to find τD a number of simulations have to be carried out in different conditions, with the aim to minimize false alarms. Then, a binary variable b[k] is used to denote whether or not an attack is active at time k in any sensor of the system, as

The isolation process is carried out using the UIOs bank, each of them with dynamics given by (8). The j th UIO’s associated residue is defined as

An attack is isolated in output j when an attack has been detected at time k, i.e.,

where τj I is a threshold associated with the maximum estimation error that the system could supposedly tolerate in the jth UIO. In the same way as before, it is necessary to carry out several simulations in order to adjust the value of τ j I , aiming to not generate many false alarms while also not neglecting many attacks. The isolation of an attack in the sensor of the jth output at k is denoted using the variable lj [k]:

Because lj [k] produces false alerts regarding the isolation of an attack, a mechanism based on (26) is used to prevent them. Thus, the new variable L[k] is built, which represents the isolation of an attack on the j th sensor at time k with a reduced number of or no false alerts. Using the variables b[k] and L[k], the variable mj [k] is defined, which indicates that an attack is detected in the j th sensor at time k and must hence be mitigated. The signal mj [k] is given by

where & is the logical operator “AND". In 29, mj[k] = 1 when there is an attack on the jth sensor.
Finally, with the definition of mj [k], the mitigated state estimation can be mitigated as
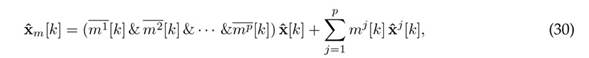
where mj [k] represents thelogical operator "NOT.acting on the binary variable mj [k]. In 30, the first term on the right side shows that, if there is no attack in any output, the full order current observer estimation is used. The second term shows that, if there is an attack in sensor j, the estimation of the jth UIO is used. Therefore, the controller that mitigates attacks on the system can be written as
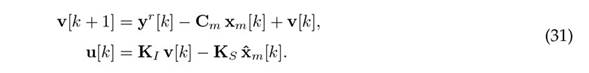
Note that the aforementioned mitigation mechanism is different from the one in 26, which constitutes an improvement, as the use of the mitigated state in the control calculation reduces the effect of the attack on the system even more.
Numerical Results
This section considers the four tanks benchmark initially proposed in 19. A tracking controller with state feedback is used, working with a full order current observer. The objective of this section is to show (i) the system working in closed-loop before any attack is considered, (ii) the effect of an attack on one output, and (iii) the effect on the system of using the proposed mitigation mechanism.
System model
The four tanks benchmark system is described in detail in 19. It has two inputs related to the pumps, u1 and u2, which allow liquid to be fed into the tanks. The heights of the four tanks, hi i = 1, 2, 3, 4, are the state variables of the system, and the height of tanks 1 and 2 are the system outputs. The four tanks system model can be written as

where Ai is the area of the i-th tank, ai is the outflow section of the i-th tank (at the bottom of the tank), g is the acceleration of gravity, γ j ∈ [0, 1] for j = 1, 2 is a proportional constant that divides a pump flow uj in two parts (γj and its complement to feed two different tanks), and kj are the pump gains. The parameters of the system are the same as in 19, as shown in Table I
Table I: Four tanks system parameters
The controller used with the system has form as that in 3, with
And
The full order current observer for the system is as described in 4, with

Closed-Loop system behavior
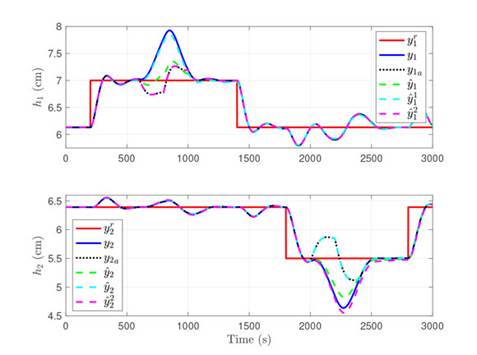
The closed-loop system behavior with the controller and the observer is shown in Fig. 2, considering no delays in the communication network (for information about the effects of the delays induced by the network on control systems, see 27). The figure shows the behavior of the outputs when a change in the reference input is introduced. The coupling between the system variables is evident, given that variations in one reference input affects the related output and the opposite one.
Fig. 2 also shows the output variables estimated by the full order current observer,  , where the estimates of the outputs are similar to their ideal values. However, since the variables and their estimate have differences, such offset can be used to determine the detection threshold. The full order current estimator-associated threshold was selected after performing multiple simulations, considering the system behavior in light of various inputs. This, in order to select a value that does not generate false alarms when there is no attack. In that sense, for the four tanks system, τD = 0, 033. full order current estimator-associated threshold was selected after performing multiple simulations, considering the system behavior in light of various inputs. This, in order to select a value that does not generate false alarms when there is no attack. In that sense, for the four tanks system, τD = 0, 033.
, where the estimates of the outputs are similar to their ideal values. However, since the variables and their estimate have differences, such offset can be used to determine the detection threshold. The full order current estimator-associated threshold was selected after performing multiple simulations, considering the system behavior in light of various inputs. This, in order to select a value that does not generate false alarms when there is no attack. In that sense, for the four tanks system, τD = 0, 033. full order current estimator-associated threshold was selected after performing multiple simulations, considering the system behavior in light of various inputs. This, in order to select a value that does not generate false alarms when there is no attack. In that sense, for the four tanks system, τD = 0, 033.
Figure 2: System response to variations in the reference inputs. The top figure shows the behavior of level 1, and the bottom one the behavior of level 2. The reference is shown in red, the measured output in blue, the attacked output as a dotted black line, the estimation of the full order current observer in dashed green, and the estimations of UIOs 1 and 2 in dashed cyan and magenta, respectively
UIOs bank design
Even though the system sensors have not been attacked yet, this subsection deals with the design process of the UIOs, as well as their behavior, in order to show their associated residuals and how to set their thresholds. In order to design the UIO bank, linear discrete-time representation of the syste
 m is needed. Such representation is obtained by linearization through the Jacobian, around an equilibrium point defined by and
m is needed. Such representation is obtained by linearization through the Jacobian, around an equilibrium point defined by and
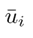 (Table I). The linearized model is discretized using the zero-order hold technique 20, with T = 1 s, obtaining a model such as the one in 2, with
(Table I). The linearized model is discretized using the zero-order hold technique 20, with T = 1 s, obtaining a model such as the one in 2, with

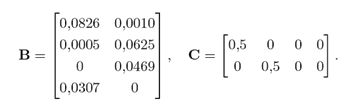
With the linear discrete-time model, the design process for the UIO bank may begin. Let us start with UIO 1. First, it is necessary to select the value of the E1 matrix, which defines the way in which the perturbation d[k] acts on the system. For this case, the following was selected

which implies that we consider that the greatest effect of the attack takes place in state 2, which is related to the only output that UIO 1 works with (output 2)
After obtaining E1 , 12- 15 must be satisfied. From 12, H1 can be calculated. With H1 , T1 can be obtained from 14. In order to find F 1 using 13, observability must first be verified, or, at least, the detectability of the pair (A1 1 , C1 ). The rank of the observability matrix of the pair (A1 1 , C1) is 1 instead of n = 4, which means that the system is not completely observable. Moreover, there is only one observable mode. Then, the pair (A1 1 , C1) must be transformed into its observability canonical form, in order to (i) verify whether the nonobservable modes of the system are stable and, if that is true, (ii) to define the closed-loop desired mode for UIO 1. Effectively, in this case, the three nonobservable modes are stable and, therefore, a good location for the only observable mode could be z = 10−3 , in order to guarantee that the convergence of the estimation error is faster than the closed-loop system dynamics. Given the above, the following is found

With F1 , from 15, K1 2 can be calculated. Finally, K1 = K1 1 + K1 2 is obtained, which completes UIO 1 design process.
A similar process is followed to design UIO 2, where
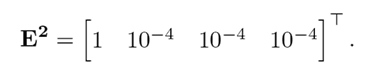
For this case,

and the design can be completed as before.
State estimation via the bank of UIOs is very similar to the one obtained with the full order current observers, and, even though the residues have different shapes, the definition of the thresholds is carried out in the same way, with τ 1 I = 0,0315 and τ 2 I = 0,0420.
Figure 3: System response with attacks on both sensors. The top figure shows the behavior of level 1, and the bottom figure the behavior of level 2. The reference is shown in red, the measured output in blue, the attacked output in a dotted black line, the estimation of the full order current observer in dashed green, and the estimations of UIOs 1 and 2 in dashed cyan and magenta, respectively.
Impact of the attack on the system
Attacks in both output sensors at different times are considered. In this case, the attack signal is defined by
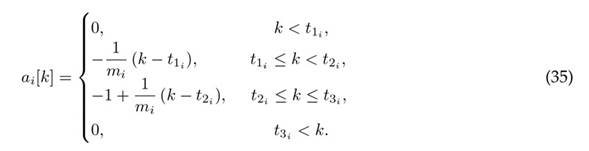
For a1[k], m1 = 200, t11 = 600s, t21 = 800s, t31 = 1000s, and for a2[k], m2 = −200, t12 = 2000s, t22 = 2200s, t32 = 2400s.
Therefore
 The closed-loop response system with the attack is shown in Fig. 3. Here, it can be observed that the attack mainly affects one output, i.e.,
The closed-loop response system with the attack is shown in Fig. 3. Here, it can be observed that the attack mainly affects one output, i.e.,
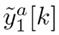 is affected directly by a1[k]. However, due to the coupling in the system variables, the effect of the attack is also visible in the other output.
is affected directly by a1[k]. However, due to the coupling in the system variables, the effect of the attack is also visible in the other output.
In addition, Fig. 3 shows the output variables for the attacked system, as estimated by the full order current observer, UIO 1, and UIO 2, in dashed green, cyan and magenta lines, respectively. The estimate of the full-order observer is not good during either of the attack times. Note that UIO 1’s estimate for output 1 matches the real measurement (blue line), while output 2 tends to the sensor value. Something similar happens with UIO 2, where the estimation of output 1 coincides with the sensor value, while the estimations of output 2 tend to the real measurement. As shown in Fig. 3, this is exactly what was expected from the UIOs. It is important to mention that the attacks affect the energy used by the controllers to keep the tank levels at the desired values, given that they have to make a different effort (when compared to normal operation) to increase - or decrease - the tank levels depending on the shape of the attacks
Attack mitigation
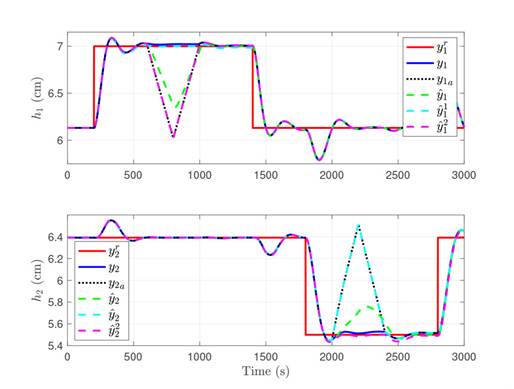
This subsection shows the results of using UIO estimations to recalculate the control action and mitigate the attacks. Fig. 4 shows the outputs with the reconfiguration mechanism activated. Notice the difference with Fig. 3, where the deviation for the outputs with attacks is higher due to the input change. Meanwhile, in Fig. 4, the deviation is even smaller than the overshoot. Therefore, it can be seen that the proposed mitigation scheme indeed helps to achieve a behavior closer to the system without attack. Note that the same observations holds for each estimation mentioned in the previous subsection. UIO i very closely estimates the output i, and the full order observer lies in the middle, but helps to avoid corrections for longer times.
Figure 4: System response with mitigation of attacks on both sensors. The top figure shows the behavior of level 1, and the bottom figure the behavior of level 2. The reference is shown in red, the measured output in blue, the attacked output in dotted black lines, the estimation of the full order current observer in dashed green, and the estimations of UIO 1 and 2 in dashed cyan and magenta, respectively.
Conclusions
This paper we have studied the problem of defending low-level controllers based on state-feedback against sensor attacks. It shows that, for an attacked system with only one attack at a time, using a bank of unknown input observers, it is possible to recover the complete state of the system without the effect of the attack and, therefore, the output. It also shows how the control action can be re-computed with the uncorrupted information once the attack has been detected and isolated. This work improves the results shown in 26, obtaining less oscillations in the steady state for the mitigated response - in that work, only the output was recovered. The proposed mechanism was tested on an existing control system with the four tank system testbed, with no simultaneous attacks on the sensors of the outputs of the system, showing satisfying results. The results of this work show a way to improve the resilience of low-level controllers in order to make them suitable for more sophisticated mechanisms such as secure estimation, where it is assumed that the low-level controller is secure
Acknowledgements
Acknowledgment
This work was partially supported by the Studies Commission No. 015 of 2014 of Universidad Distrital Francisco José de Caldas. We thank the anonymous reviewers for their careful reading of our manuscript and their insightful comments and suggestions.
References
License
Copyright (c) 2023 Luis Francisco C´ombita, Nicanor Quijano, Alvaro C´ardenas

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










