DOI:
https://doi.org/10.14483/23448393.22002Publicado:
2025-08-01Número:
Vol. 30 Núm. 2 (2025): Mayo-agostoSección:
Ingeniería Eléctrica, Electrónica y TelecomunicacionesImplementation of a Generalized Predictive Controller with Fuzzy Suppression and Weighting Parameters for a Level Plant with Interconnected Concentric Tanks
Implementación de un controlador predictivo generalizado con parámetros difusos de supresión y ponderación para una planta de nivel con tanques concéntricos interconectados
Palabras clave:
Weighting factors, Fuzzy logic, Generalized predictive control (en).Palabras clave:
ponderación , control predictivo generalizado, lógica difusa (es).Descargas
Referencias
S. Ávila-Becerril, G. Espinosa-Pérez, O. D. Montoya, and A. Garcés, "Passivity-based control of islanded microgrids with unknown power loads,"IMA J. Math. Control Info., vol. 37, no. 4, pp. 1548–1573, Oct. 2020. https://doi.org/10.1093/imamci/dnaa025
C.-A. Bojan-Dragos, R.-E. Precup, E. M. Petriu, R.-C. Roman, E.-L. Hedrea, and A.-I. Szedlak-Stinean, "GWO-based optimal tuning of controllers for shape memory alloy wire actuators,"IFAC-PapersOnLine, vol. 55, no. 15, pp. 39–44, 2022. https://doi.org/10.1016/j.ifacol.2022.07.605
R. E. Precup, R. C. David, R. C. Roman, A. I. Szedlak-Stinean, and E. M. Petriu, .Optimal tuning of interval type-2 fuzzy controllers for nonlinear servo systems using slime mould algorithm,"Int. J. Syst. Sci., vol. 54, no. 15, pp. 2941–2956, 2021. https://doi.org/10.1080/00207721.2021.1927236
R. E. Precup, A. T. Nguyen, and S. Blažiˇc, .A survey on fuzzy control for mechatronics applications,"Int. J. Syst. Sci., vol. 55, no. 4, pp. 771–813, 2023. https://doi.org/10.1080/00207721.2023.2293486
J. Liu and Z. Chen, .Application of intelligent optimization algorithm in the remote flow generalized predictive control of metering pump,ïn 2021 5th Asian Conf. Art. Intell. Tech. (ACAIT), 20021, pp.
- 320, 2021. http://doi.org/10.1109/ACAIT53529.2021.9731264
L. Ai, D. Zhang, K. L. Teo, and L. Deng, "Generalized predictive temperature control in tubular chemical reactors by means of proper orthogonal decomposition and least squares support vector machine,ïn 2020 39th Chinese Control Conf. (CCC), 2020, pp. 2407-2412. http://doi.org/10.23919/CCC50068.2020.9189120
J. Cai, S. Li, and J. Gui, "DOB-based generalized predictive cross-coupling position control for biaxial system,ïn 2019 IEEE Int. Symp. Pred. Control Electrical Drives Power Electronics (PRECEDE), 2019, pp. 1-6. http://doi.org/10.1109/PRECEDE.2019.8753296
J. X. Wu, K. Wang, T. Wang. and J. Li, Ïnterleaved generalized predictive control for dual three-phase PMSM with low computation burden,ïn 2022 25th Int. Conf. Electrical Mach. Syst.(ICEMS), 2022, pp. 1-5. http://doi.org/10.1109/ICEMS56177.2022.9983096
G. Flores, N. Aldana, and M. Rakotondrabe, "Model predictive control based on the generalized Bouc-Wen model for piezoelectric actuators in robotic hand with only position measurements,"IEEE Control Syst. Lett., vol. 6, pp. 2186-2191, 2022. http://doi.org/10.1109/LCSYS.2021.3136456
Y. Jingya, Y. Yi, H. Qingqing, G. Haiqin, R. Xiaolin, and G. Long, "Design and research of temperature control system based on generalized predictive control,ïn 2021 40th Chinese Control Conf. (CCC), 2021, pp. 2663-2668. http://doi.org/10.23919/CCC52363.2021.9549812
J. Smoczek and J. Szpytko, Çonstrained generalized predictive control with particle swarm optimizer for an overhead crane,ïn 2017 22nd Int. Conf. Meth. Mod. Autom. Robot. (MMAR), 2017, pp. 756-761. http://doi.org/10.1109/MMAR.2017.8046923
A. Mouhou, A. Badri, A. Ballouk, and Y. Sayouti, "Genetic algorithms optimization of tuning parameters of generalized predictive control,ïn 2017 Int. Conf. Electrical Info. Tech. (ICEIT), 2017, pp. 1-5. http://doi.org/10.1109/EITech.2017.8255281
M. R. Arahal, F. Barrerro, and del M. Castilla, “Optimización de funciones de coste para control predictivo de máquinas de inducción multifásicas,” Rev. Iberoamer. Autom. Infor. Ind., vol. 16, no. 1, pp. 48–48, 2018. https://doi.org/10.4995/riai.2018.9771
R. E. Pérez-Guzmán, M. Rivera, and P. W. Wheeler, "Weighting factor design in model predictive control for power converters,"2019 IEEE Chilean Conf. Electrical Electronics Eng. Info. Comm. Tech.(CHILECON), 2019, pp. 1-6. https://doi.org/10.1109/CHILECON47746.2019.8988109
A. Thamallah, A. Sakly, and F. M’Sahli, “A new constrained PSO for fuzzy predictive control of quadruple-tank process,” Measurement, vol. 136, pp. 93–104, 2019. https://doi.org/10.1016/j.measurement.2018.12.050
C. Cheng, C. Peng, and T. Zhang, "Fuzzy K-means cluster based generalized predictive control of ultra supercritical power plant,"IEEE Trans. Ind. Infor., vol. 17, no. 7, pp. 4575-4583, 2021. https://doi.org/10.1109/TII.2020.3020259
N. He, G. Xu, and M. Zhang, .Automated GPC tuning based on fuzzy logic and event triggered mechanism,"2021 4th IEEE Int. Conf. Ind. Cyber-Phys. Syst. (ICPS), 2021, pp. 725-730. https://doi.org/10.1109/ICPS49255.2021.9468236
Z. Chen, J. Cui, Z. Lei, J. Shen, and R. Xiao, "Design of an improved implicit generalized predictive controller for temperature control systems,"IEEE Access, vol. 8, pp. 13924-13936, 2020. https://doi.org/10.1109/ACCESS.2020.2965021
R. Cordero, T. Estrabis, M. A. Brito, and G. Gentil, "Development of a resonant generalized predictive controller for sinusoidal reference tracking,"IEEE Tran. Circ. Syst, II Express Briefs, vol. 69, no. 3, pp. 1218-1222, 2022. https://doi.org/10.1109/TCSII.2021.3102535
D. S. Bhandare, V. S. Jape, H. H. Kulkarni, S. M. Mahajan, P. Sable, and Y. Pawar, .Automatic liquid level control of two tank system using PLC,ïn 2024 Int. Conf. Intell. Syst. Adv. App. (ICISAA), 2024, pp. 1–6. https://doi.org/10.1109/ICISAA62385.2024.10828622
M. Huo, H. Luo, X. Wang, Z. Yang, and O. Kaynak, Real-time implementation of plug-and-play process monitoring and control on an experimental three-tank system,"IEEE Trans. Ind. Infor., vol. 17, no. 9, pp. 6448–6456, 2021. https://doi.org/10.1109/TII.2020.3030812
C. Pu, J. Ren, and J. Su, "The sliding mode control of the drum water level based on extended state observer,"IEEE Access, vol. 7, pp. 135942–135948, 2019. https://doi.org/10.1109/ACCESS.2019.2940056
A. C. da Silva Júnior, R. Munoz, M. D. L. Á. Quezada, A. V. L. Neto, M. M. Hassan, and V. H. C. de Albuquerque, Ïnternet of water things: A remote raw water monitoring and control system,"IEEE Access, vol. 9, pp. 35790–35800, 2021. https://doi.org/10.1109/ACCESS.2021.3062094
B. A. Londoño Narcizo and I. D. Urán Ospina, "Diseño e implementación de planta didáctica de nivel con tanques concéntricos interconectados para la implementación de técnicas de control convencional y avanzado", Master’s thesis, Politécnico Colombiano Jaime Isaza Cadavid, Colombia, 2016. [Online]. Available: https://polijic.primo.exlibrisgroup.com
J. Gonzales, W. Luque, A. Sullca, and M. Tomairo, .Analysis of fuzzy PID controllers with modified smith predictor and generalized predictive controller for a time delay plant,ïn 2021 IEEE XXVIII Int. Conf. Electronics Electrical Eng. Comp. (INTERCON), 2021, pp. 1-4. https://doi.org/10.1109/INTERCON52678.2021.9532632
D. Naunay, P. Ayala, J. Andino, W. Martínez, J. Llanos, and D. Arcos-Avilés, "Generalized predictive control strategy applied to a single-phase T-type voltage source inverter in stand-alone operation mode,ïn 2021 IEEE 22nd Work. Control and Model. Power Electronics (COMPEL), 2021, pp. 1-7. https://doi.org/10.1109/COMPEL52922.2021.9646005
P. V. S. Reddy, "Generalized fuzzy logic with twofold fuzzy set: Learning through neural net and application to business intelligence,ïn 2021 Int. Conf. Fuzzy Theory App. (iFUZZY), 2021, pp. 1-5. https://doi.org/10.1109/iFUZZY53132.2021.9605090
M. I. Gómez Borges, A. V. Acosta Corzo, and Y. Fundora Curbelo, "Programación de un controlador lógico difuso en un PLC M241: Aplicación práctica a un túnel de lavado industrial de textil,"Rev. Cubana Cien. Infor., vol. 14, no. 3, pp. 105–123, 2020.
G. Senthilkumar and R. Ramakrishnan, “A comparative study of predicting burn off length in continuous drive solid state friction welding for ASTM A516 steel by regression analysis, fuzzy logic analysis and finite element analysis,” J. App. Sci. Eng., vol. 24, no. 3, pp. 359–366, 2021. https://doi.org/10.6180/jase.202106_24(3).0011
R. Medina et al., .Evaluación del índice de riesgo de transformadores de distribución mediante técnicas de lógica difusa,ïn 2022 IEEE Biennial Cong. Argentina (ARGENCON), 2022, pp. 1-8. https://doi.org/10.1109/ARGENCON55245.2022.9939752
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 23 de marzo de 2024; Aceptado: 26 de mayo de 2025
Abstract
Context:
This paper employs fuzzy logic in the unconventional adjustment of suppression and weighting factors within a generalized predictive controller (GPC).
Method:
The control strategy is applied to a level plant featuring interconnected concentric tanks. For the tuning process, a fuzzy proportional-integral-derivative PID controller is compared against the proposed GPC equipped with fuzzy suppression and weighting parameters. Evaluation metrics related with response time and integration criteria are employed in this comparison.
Results:
The results demonstrate the superiority of the GPC combined with fuzzy logic over the fuzzy PID controller. Dynamic weighting factors contribute to enhanced control performance, as evidenced by the evaluation metrics.
Conclusions:
The proposed approach proved to be effective in improving control performance in the tested system. This approach offers a promising alternative to traditional methods, especially in systems where dynamic adjustments are beneficial.
Keywords:
weighting factors, generalized predictive control, fuzzy logic.Resumen
Contexto:
Este documento emplea lógica difusa en el ajuste no convencional de factores de supresión y ponderación dentro de un controlador predictivo generalizado (GPC).
Métodos:
La estrategia de control se aplica en una planta a nivel que cuenta con tanques concéntricos interconectados. Para el, se compara un controlador PID difuso con el GPC propuesto, equipado con parámetros de supresión y ponderación difusos. Se emplean métricas de evaluación relacionadas con el tiempo de respuesta y criterios de integración para la comparación.
Resultados:
Los resultados demuestran la superioridad del GPC combinado con lógica difusa sobre el controlador PID difuso. Los factores de ponderación dinámica contribuyen a mejorar el rendimiento del control, como lo evidencian las métricas de evaluación.
Conclusiones:
El enfoque propuesto resultó ser efectivo para mejorar el rendimiento de control en el sistema probado. Este enfoque ofrece una alternativa prometedora a los métodos tradicionales, especialmente en sistemas que se benefician de ajustes dinámicos.
Palabras clave:
ponderación, control predictivo generalizado, lógica difusa.Introduction
Optimal control plays a crucial role in modern engineering since it allows systems to operate efficiently, reliably, and with minimal resource usage. It provides a mathematical foundation for making real-time decisions that balance performance with constraints, making it essential in complex and dynamic environments. One key application is microgrids, where optimal control can be used to manage energy distribution effectively, especially when power loads are uncertain and the grid operates in islanded (i.e., isolated) mode 1. Additionally, optimal control techniques are valuable for the optimal tuning of controllers, which is particularly beneficial in systems involving shape memory alloy (SMA) wire actuators, allowing for a precise and adaptive response 2. Furthermore, fuzzy controllers, which are often guided by optimal control principles, have shown strong potential in managing nonlinear servo systems, offering a robust performance despite system uncertainties and nonlinearities 3. A survey that focuses on the fundamental aspects of fuzzy control for mechatronics applications can be consulted in 4.
Generalized predictive control (GPC) is a strategy belonging to the family of model predictive control (MPC), which seeks to minimize a cost function by predicting the controlled output of a system. GPC requires several tuning parameters, including weighting factors acting on the control effort and on the discrepancy between the output and the desired reference trajectory 5. The success of GPC has been reported in several processes and in different productive sectors, such as the chemical, aeronautics, energy efficiency, robotics, and mechanical industries, proving to be a solid strategy for controlling processes in different areas 6(9.
The weighting factors of GPC in conventional tuning are set to constant values, without considering that varying them can improve controller performance 10. Defining the point values for the weighting factors of a GPC is also a design problem. Sometimes, engineers regard the tuning of the weighting parameters as an optimization problem, proposing solutions that combine metaheuristic strategies with the controller. In 11, for instance, a particle swarm optimizer (PSO) was employed to tune a GPC with constraints on the control signal and on the transient behavior of a bridge crane. The results demonstrated the robustness of the controller to variations in operating conditions. The effects of incorporating a genetic algorithm (GA) to tune the parameters of a GPC are shown in 12. Here, an improvement in controller performance, including disturbance rejection, was achieved.
In general, there are no analytical, numerical, or theoretical methods to determine the values of the GPC weighting factors. Therefore, it is necessary to establish strategies for particular systems since the dynamics of the processes unquestionably exhibit variations reflected in the models that describe their behavior. Some research works have focused on varying GPC weighting parameters, achieving considerable improvements in controller performance.
In 13, an optimized weighting strategy was presented, varying the weighting factors for each operating point while implementing bilinear interpolation to cover the entire workspace. The results show that the proposed technique allows obtaining smaller deviations in the working region.
A case involving the variation of the weighting parameters of a tuned predictive controller for a power converter is reported in 14. Here, three types of cost functions with weighting factor variations were identified, selecting the ideal function for the objectives stated in the design of the model-based predictive controller. Simulation results demonstrated the effectiveness of the strategy for multi-objective control in power converters. The hybridization of a model-based predictive controller is shown in 15, which was carried out by implementing fuzzy logic to obtain the predictive model of the system and as a mechanism for establishing the conditions that ensured the closed-loop stability of a plant.
The combination of a GPC and fuzzy logic to switch controllers in the global model of a power plant is presented in 16. By means of fuzzy pattern clustering, the plant model was divided into local models, and the controllers were tuned based on each of them. Subsequently, controller planning was performed to jointly regulate the entire operating region of the plant. In discussing the results, the authors concluded that, by means of simulated schemes, this strategy exhibits a better performance than conventional proportional-integral-derivative (PID) and GPC controllers. Apart from modeling, fuzzy logic has been combined with GPC to tune controller parameters. 17 reported a strategy that enables the online tuning of GPC parameters through event triggering and fuzzy logic, demonstrating that it is an efficient combination that allows reducing the energy consumption of the system.
The proposed approach, which combines a GPC with fuzzy logic, offers several advantages over both general optimal and non-optimal control strategies. Compared to traditional optimal control approaches, due to its predictive nature, GPC provides enhanced adaptability to system dynamics and disturbances, allowing for a better handling of model uncertainties and external perturbations. The integration of fuzzy logic further improves the controller’s robustness by incorporating expert knowledge and linguistic rules, enabling effective decision-making even in the presence of nonlinearities and modeling inaccuracies 18.
In contrast to non-optimal methods such as PID or conventional rule-based controllers, the GPC-fuzzy combination offers improved performance in terms of setpoint tracking, disturbance rejection, and stability. While classical controllers typically require extensive tuning and may struggle with varying operating conditions, the predictive capability of GPC ensures proactive adjustments, and the fuzzy logic component enhances flexibility in dynamic environments 19.
This paper is structured as follows. It begins a description of a plant with interconnected concentric tanks, outlining the mathematical model that represents the system dynamics. The GPC is then tuned with static suppression and weighting parameters. Subsequently, fuzzy logic is implemented, generating a table of linguistic variables to tune the suppression and weighting parameters for the GPC. This is done to establish the block diagram and implement the controller. Afterwards, the performance of the proposed approach is compared against that of a fuzzy PID controller, both implemented on the aforementioned plant. Finally, the conclusions drawn from this work are presented.
Methodology
Water level control is a common challenge in industrial settings, and it has been extensively analyzed in numerous research works. For instance, in 20, the authors focus on developing and implementing a water level control system based on a programmable logic controller (PLC), and 21 present the real-time implementation of a plug-and-play process monitoring and control system for an experimental three-tank setup. Furthermore, the control of interconnected concentric tanks, such as the one presented herein, is crucial in various industrial applications, including chemical processing, wastewater treatment, and pharmaceutical manufacturing. Practical implementations for controlling water levels have also been reported 22,23.
Level plant with interconnected concentric tanks
Fig. 1 shows the studied level plant, which consists of two interconnected concentric tanks, a data acquisition card, two centrifugal pumps, an electrical circuit based on solid state relays, and an electronic circuit that allows for signal coupling. Together, the aforementionedelementsenabletheimplementation of control strategies for the level variable. As described in 24, the plant was designed to implement controllers and process monitoring and supervision schemes.
Figure 1: Level plant with interconnected concentric tanks
The transfer function representing the dynamics of the plant is obtained from the open-loop excitation of the system, from which first-order with delay (FOD) and second-order with delay (SOD) models are derived. To select the model that best fits the real plant dynamics, two indicators are calculated: the mean squared error (MSE) and the correlation coefficient (r), as expressed in Eqs. (1)) and (2), respectively.
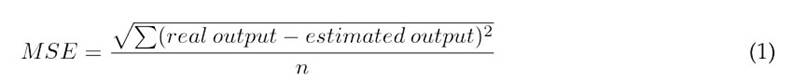

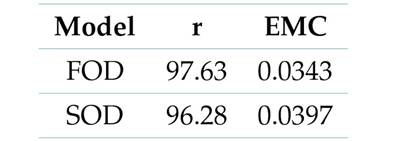
Table I shows the results of the two indicators calculated for each model, showing that the FOD model is the closest to the real dynamics of the interconnected concentric tank plant —see Eq. (3).
Table I: Indicators used for plant model selection

Then, the continuous-time FOD model is discretized, selecting the sampling period (T) via the system bandwidth criterion, obtaining T = 21 s. The discrete time model HGp(z) of the interconnected
concentric tank plant, which will be used for tuning the GPC with fuzzy weighting factors, is shown in Eq. (4).
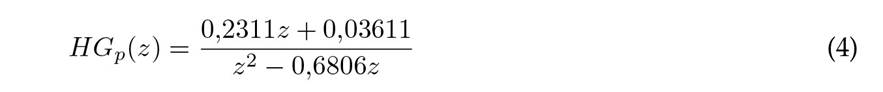
Generalized predictive control
TheGPCstrategycalculates a series of predictions for the control action while seeking to minimize a cost function. The index to be minimized corresponds to a quadratic function that calculates the control effort by measuring the difference between the predicted process output and the reference trajectory up to the maximum prediction horizon 25,26.
The disturbance model used by our GPC is the CARIMA (i.e., the controller auto-regressive moving-average) model to predict the system output, as indicated in 5.
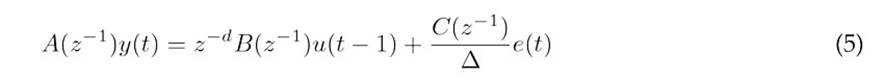
where:

The GPC strategy consists of applying a sequence of control signals that minimizes the cost function indicated in Eq. (6)
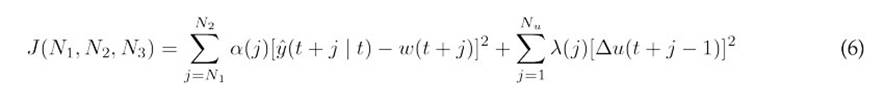
where:


The factors α(j) and λ(j) denote series weighting and suppressing the error and control effort, respectively. The controller output is given by Eq. (7).

where k is the first row of the matrix given by Eq. (8).

Fuzzy logic
Fuzzy logic constitutes a flexible alternative that allows incorporating structures supported by linguistic rules into the solution of problems. This facilitates the handling of incomplete information and uncertainty. Since fuzzy logic seeks to simulate the human intellect, the experience of engineers and expert operators can be introduced into the design 27)- (929.
The implementation of fuzzy logic involves three steps: 1) fuzzification, where a degree of membership is assigned to the inputs via membership functions in order to obtain the fuzzy set of variables; 2) linguistic rules, where the expert, by means of propositions, expresses their acquired knowledge of the process; and 3) defuzzification, where a quantifiable value is assigned to the process outputs. This value comes from the fuzzy inference performed to obtain the linguistic rules. The fuzzy inference system then obtains a conclusion based on input information in fuzzy terms 30. In control systems, fuzzy logic is implemented in the following sequence:
-
Determine the inputs and outputs of the fuzzy syste
-
Elaborate the input and output variable characterization template
-
Define the linguistic variables
-
Define the universe of discourse for each input and output variable
-
Define the fuzzy sets for each input and output variable
-
Define the semantic rules for each linguistic variable
-
Establish the rules according to an analysis of the behavior of the system’s input and output variables
Subsequently, the transfer function of the plant is rewritten in negative powers (z−1), as indicated in Eq. (9), and the discrete delay (d) is determined.
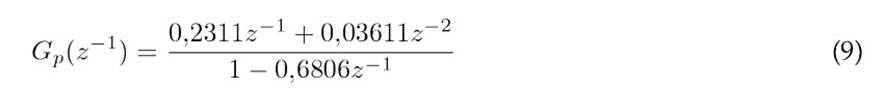
The studied system has a delay d = 1 and amaximumcoefficient m = 2.Fortheinitial tuning of the GPC, a control horizon (Hc = 5), a maximum prediction horizon (Hmaxc = 5), a minimum prediction horizon (N1 = 1), and T = 21 s are defined.
A, B, and ˆA are defined by the following polynomials:


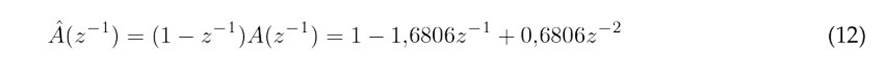
The expressions used to obtain the prediction are given in Eqs. (13)-(15).



The polynomials Ej+1, Fj, and Gj, corresponding to each prediction, are obtained as indicated in Eqs. 16-30.


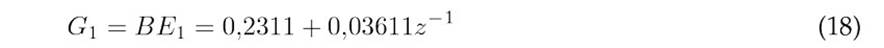
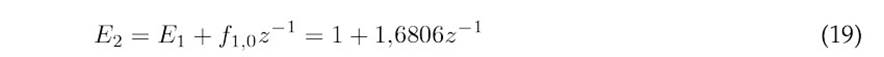


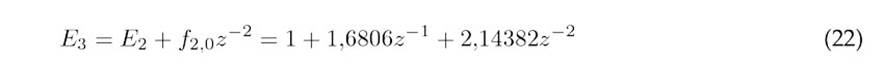

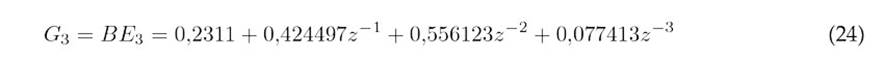

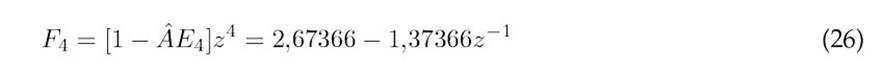


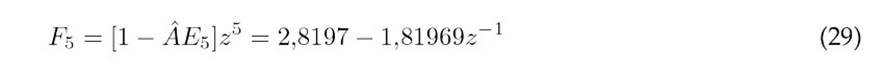
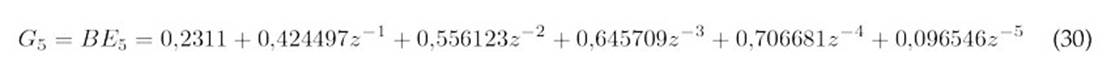
The prediction equation is given by(31).

Where:


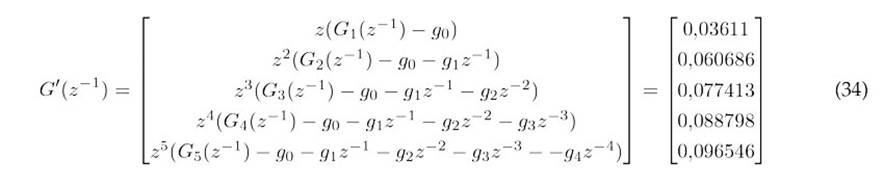

Eq. (31) can be expressed as indicated below:

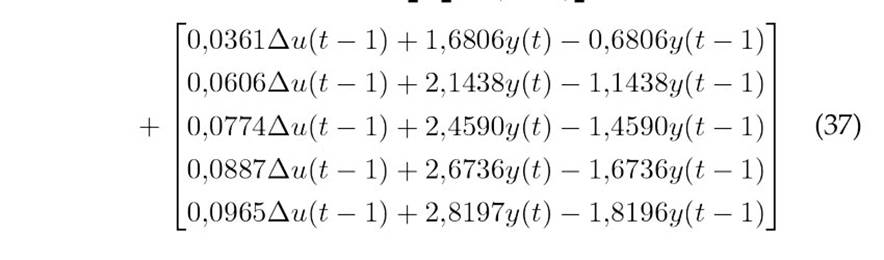
Fuzzy suppression and weighting parameters for the GPC
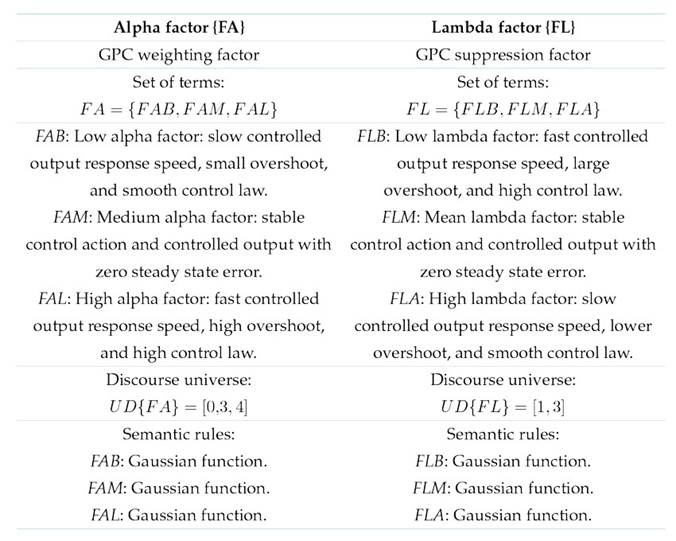
To design the system that enables the fuzzy variation of the GPC weighting factors, a linguistic characterization template is constructed for both the inputs and outputs of the system. This is shown in Tables II and III, along with the corresponding definitions, the universe of discourse, the set of terms for each variable, the definition of each term, and the semantic rules or membership functions for each term in each set. The inference and if-then rules are defined based on an analysis of the controlled output, the control error signal, and the control law. A total of 27 semantic rules are defined.
Table II: Template for characterizing the input variable

Table III: Template for characterizing the output variables
Results and discussion.
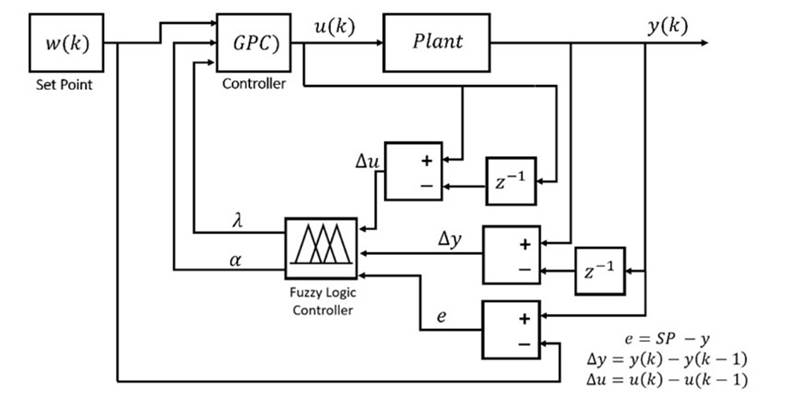
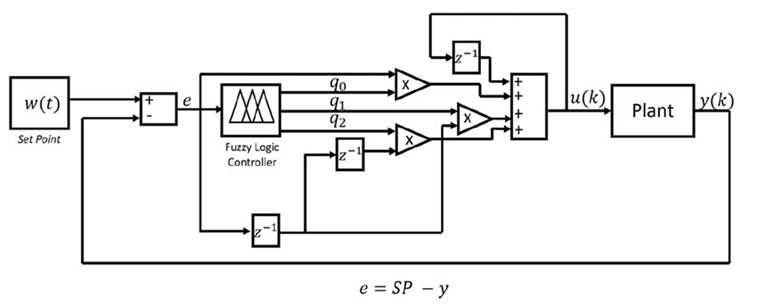
To implement the GPC with mobile fuzzy suppression and weighting factors, the block diagram shown in Fig. 2 was followed. The inputs and outputs of the system were configured according to the linguistic characterization templates. The parameters delivered by the fuzzy system correspond to the suppression and weighting factors, which were in turn configured as inputs to the GPC. The controller is in charge of generating the control law at each instant during the execution of the algorithm, while the plant delivers the controlled output to provide system feedback. The block diagram was programmed and implemented in the LabVIEW software.
Figure 2: Block diagram of the GPC with fuzzy weighting factors
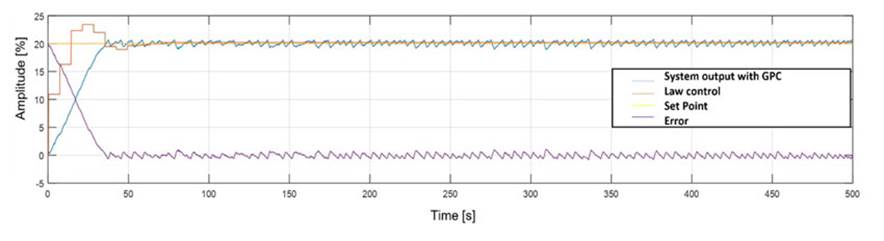
Fig. 3 illustrates the responses of the final implementation of the GPC with fuzzymoving suppression and weighting factors in the studied level plant with interconnected concentric tanks. The responses were obtained for a set point value equal to 20%, determining the behavior of the control error, the set point, the controlled output, and the control law over time. The results show that the output follows the desired reference with an average error equal to ±0.0630%,. Moreover, the control law does not exhibit saturation and shows an under-damped behavior with a maximum output of 24%. After 50 s, it stabilizes without abrupt changes.
Figure 3: Response of the GPC with fuzzy moving suppression and weighting factors in the studied level plant with interconnected concentric tanks
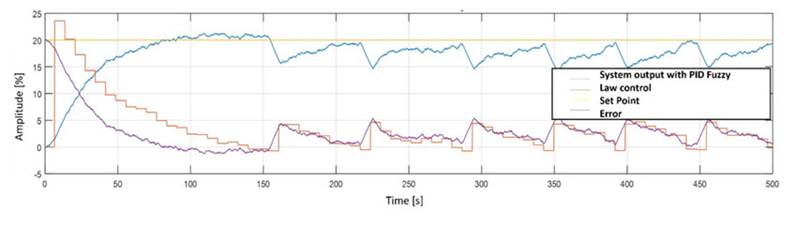
As previously mentioned, a fuzzy PID controller was used for comparison, following the block diagram shown in Fig. 4. The responses of this controller are shown in Fig. 5, indicating a sustained oscillation in the output, caused by behavior of the control law. There is an evident steady-state error, as well as an overshoot of 21.2%.
Figure 4: Block diagram of the fuzzy PID controller
Figure 5: Response of the fuzzy PID controller in the studied level plant with interconnected concentric tanks
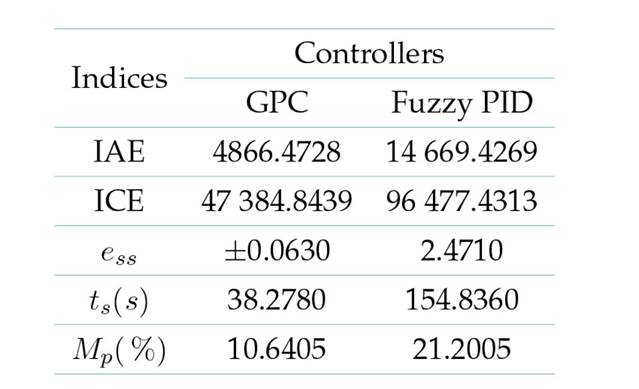
Toevaluate the controllers, we used metrics related to response time (Mp, ts(s), and ess), and metrics related to error integration criteria (IAE and ICE). The results are shown in Table IV. Note that the GPC with fuzzy weighting factors performs better than the fuzzy PID controller in all performance metrics.
Table IV: Performance comparison between the implemented controllers
Conclusions
In this work, aGPCstrategywascombinedwithfuzzylogicinordertotunethemovingsuppression and weighting factors of the controller, unlike conventional methods that use constant values. This strategy yielded satisfactory results, as confirmed through the graphical and numerical responses obtained and a comparison against a fuzzy PID controller. Both strategies were tuned for a level plant with interconnected concentric tanks. We started by selecting the plant model from two statistical metrics, wherein the FOD model was deemed to be the best fit for real plant dynamics. Then, the GPC was tuned until the cost function was obtained. Subsequently, fuzzy logic was used to establish the variable and fuzzy weighting factors until there was a control action for each instant during the execution of the algorithm. It was possible to demonstrate that varying the weighting factors in combination with fuzzy logic yields a solid control strategy. The behavior over time of the control law also stood out, characterized by a sustained performance without abrupt oscillations; there was constant current consumption in the plant under a stable regime, without current peaks in the recirculation pumps.
References
Licencia
Derechos de autor 2025 Sara Correa Tamayo, Juan David Ospina Correa, Jhon Alexander Ramírez Urrego, Jesus Maria Lopez Lezama, Nicolas Muñoz Galeano

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)