DOI:
https://doi.org/10.14483/23448393.2277Published:
2001-11-30Issue:
Vol. 7 No. 1 (2002): January - JuneSection:
Science, research and developmentSoftware para Determinar el Patrón de Radiación de Bocinas Cónicas Lisas
Keywords:
Bocinas cónicas, Patrón de radiació (es).Downloads
References
Lo, Y. T. & Lee. S. W. "Antenna Handbook". Vol. II: Antenna Theory. Edited by Van Nostrand Reinhold. New York. U.S.A. 1993. pp. 8-46 8-49.
Balanis, Constantine A. " Antenna Theory Analysis and Design". Second Edition. Edited by John Wiley & Sons, Inc. USA. 1997. pp. 695-697.
Aizemberg, G. Z.; Iampolski, B. G. y Teriochin, O. N. "Antenas de UHF. Vol.1. Editado por Comunicaciones. Moscú. 1977. pp. 269-274.
Matlab. "Reference Guide". Edited by MathWorks, Inc. U.S.A. 2000.
Jasik, henry. "Antenna Engineering Handbook". Edited by Jasik Laboratories, Inc. New York. U.S.A. 1961. pp. 10-11 10-13.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:1 pág:88-90
Software para determinar el patrón de radiación de Bocinas Cónicas Lisas
Rafael Pérez Alfonso y Roberto Jiménez Hernández
Resumen
El presente trabajo reporta los resultados obteni- dos con un software de modelación de bocinas cónicas lisas. Primero se muestra el análisis teórico necesario para la determinación del patrón de radiación para el modo TE11, considerando en el interior de la bocina un frente de onda esférico con centro en el vértice del cono. Luego se muestran los resultados obtenidos del programa de computación que implementa este método comparando con los resultados medidos reportados internacionalmente para bocinas de varios errores de fase en la abertura.
Palabras clave:
Bocinas cónicas, Patrón de radiación.
Abstract
A theoretical analysis to determine the radiation pattern for smooth-walled conical horns with inner spherical-wave fronts is presented here. The results obtained with the proposed software are compared to the internationally reported measured values for horns of varied aperture phase errors.
Key words:
Conical Horns, Radiation patterns.
I. INTRODUCCIÓN
Las antenas de bocina cónica son muy utilizadas en las bandas de frecuencias de microondas en la excitación de antenas reflectoras y para mediciones de parámetros eléctricos porque proporcionan ganancia media, baja razón de onda estacionaria, ancho de banda relativamente grande y son fáciles de construir en la práctica.
Las bocinas cónicas lisas han sido ampliamente tratadas en toda la bibliografía referente al tema [1] [2]. Pero los algoritmos para la determinación del patrón de radiación se han evitado aludiendo siempre la complejidad matemática del método; mostrando sólo algunos patrones medidos, pero casi nunca el procedimiento teórico necesario para obtener las características de radiación. Este trabajo muestra un método para la obtención del campo radiado por una bocina cónica lisa (Modo TE11) en el haz principal y primeros lóbulos secundarios (&Oacuxte;ptica Geométrica).
II. ANÁLISIS TEÓRICO.
La ley aproximada de distribución de fase en la abertura de una bocina cónica lisa puede ser obtenida suponiendo que el frente de onda de la bocina tiene forma esférica con centro en el vértice del cono. Entonces la distribución de fase en la abertura se determina aproximadamente por:
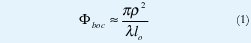
donde ρ es la distancia desde el punto en el plano de abertura hasta el centro de la abertura de la bocina,
λ es la longitud de onda de trabajo, y
lo es la longitud axial de la bocina. (Ver Figura 1)
Determinando así el retraso en fase del campo en un punto arbitrario de la abertura de la bocina.
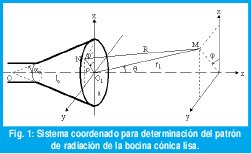
La fase de la intensidad de campo radiada por la bocina (ΦM) en un punto alejado sería la fase del campo en la abertura (Φboc) mas la constante de fase determinada por la diferencia de trayectoria (Φr). (Ver Figura 1)
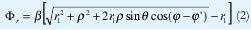
donde 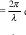 β= es la constante de desplazamiento de fase.
β= es la constante de desplazamiento de fase.
Y como 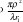 sin2 θ<< 1 al realizar el desarrollo binomial se tiene que:
sin2 θ<< 1 al realizar el desarrollo binomial se tiene que:
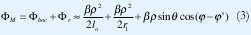
El campo en la zona de Fresnel puede ser expresado como:
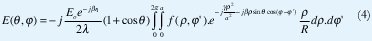
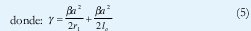
f (ρ, φ') es la distribución de amplitud en el plano de abertura, y a es el radio de la bocina. (Ver Figura 1).
Realizando un cambio de variable de integración, tal que ρ=v.a y como Rr1, se obtiene el campo radiado como [3]:
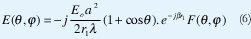
donde
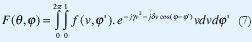
δ= βasin θ y
f (v, φ') es la ley de variación de la amplitud del campo en el plano de abertura de la bocina, que para una distribución de amplitud no simétrica respecto al eje, con excitación TE11 desde la guía de onda se puede representar como [3]:
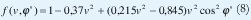
III. RESULTADOS LOGRADOS
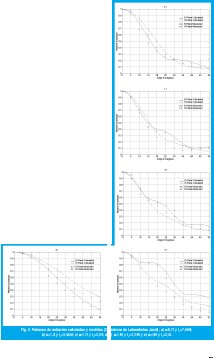
El método anterior ha sido desarrollado en un software sobre Matlab v. 6.0 para Windows [4]. Al ejecutar este programa y entrar como datos la frecuencia de trabajo, el diámetro, el semi-ángulo de vuelo de la bocina y la distancia al punto lejano para evaluar el patrón de radiación; se obtendrá el patrón de radiación en el haz principal y primeros lóbulos secundarios para ambos planos principales.
Para verificar los resultados se compararon estos patrones teóricos con patrones medidos reportados por los Laboratorios Jasik. Seguidamente se muestran cinco ejemplos para varios errores de fase en la abertura, donde sobre cada ventana, resultado del software, se han superpuesto los valores medidos por Jasik [5].
IV. CONCLUSIONES
Con este trabajo se obtuvo un instrumento útil y rápido para la obtención del patrón de radiación de bocinas cónicas lisas (Modo TE11). Este campo radiado en el haz principal y primeros lóbulos secundarios es muy útil para modelar antenas reflectoras excitadas con bocinas de este tipo, así como para determinar el campo que incide en el borde de un subreflector en un sistema doble espejo.
Los resultados se han comparado con patrones medidos reportados en la literatura, observándose una excelente coincidencia para bocinas de diferentes errores de fase. La exactitud del software es mayor para bocinas cuyo error de fase máximo en la abertura es cercano al óptimo ¼λ ó 135° El método mostrado aquí es fácilmente aplicable para el cálculo de patrones radiados con otras distribuciones de campo en la abertura de la bocina.
V. AGRADECIMIENTOS
Los autores quisieran agradecerle al Grupo de Estudios sobre Medios y Sistemas Radioeléctricos, de la Universidad Central de Las Villas por el gran apoyo en este trabajo. También, muy especialmente, al Dr. Ing. Francisco Lee Tenorio por la revisión de este trabajo.
REFERENCIAS
[1] Lo, Y. T. & Lee. S. W. "Antenna Handbook". Vol. II: Antenna Theory. Edited by Van Nostrand Reinhold. New York. U.S.A. 1993. pp. 8-46 - 8-49.
[2] Balanis, Constantine A. " Antenna Theory - Analysis and Design". Second Edition. Edited by John Wiley & Sons, Inc. USA. 1997. pp. 695-697.
[3] Aizemberg, G. Z.; Iampolski, B. G. y Teriochin, O. N. "Antenas de UHF". Vol.1. Editado por Comunicaciones. Moscú. 1977. pp. 269-274.
[4] Matlab. "Reference Guide". Edited by MathWorks, Inc. U.S.A. 2000.
[5] Jasik, henry. "Antenna Engineering Handbook". Edited by Jasik Laboratories, Inc. New York. U.S.A. 1961. pp. 10-11 - 10-13.
Rafael Pérez Alfonso
Msc. Ingeniería en Telecomunicaciones, Universidad Central de las Villas, Cuba.
Roberto Jiménez Hernández
Ingeniero en Telecomunicaciones, Universidad Central de las Villas, Cuba. Doctor en Ciencias Técnicas, Instituto Electrónico de Telecomunicaciones de Moscú. Profesor titular Facultad de Ingeniería Eléctrica, Universidad Central de las Villas, Cuba.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










