DOI:
https://doi.org/10.14483/23448393.3497Published:
1999-11-30Issue:
Vol. 5 No. 1 (2000): January - JuneSection:
Science, research and developmentDiseño e implementación de un sistema de visión artificial basado en redes neuronales.
Keywords:
Separación fondo de figura, interacciones cortico-geniculares, Teoría de Resonancia Adaptativa, redes neuronales, visión artificial. (es).Downloads
References
. Johnson JB., The Schottky effect in low frequency circuits, Phys. Rev. 26, 71-85, (1925).
Schottky W., Phys. Rev.28, 74-103, (1926).
. Motchenbacher C.D,Fifchen EC, Low noise Elaytronic Design John Wiley 7, (1973).
Bell D.A.,Electrical Noise,Van Nostrand, London, chap. 10, (1960).
. Bell D.A., A survey of 1 /fnoise in electrical conductors, J. Phys. Soc., 72, 27-32, (1980).
. Van der Ziel A., Flicker noise in electronic devices, Advances in Elect. andPhys., 49, 225-297, (1979). Weissman M.B., Survey of recent noise theories.
Proc. 6th Int. Conf on noise in Physical Systems held at the National Bureau of Standards, Gaithersburg,MD, USA, pp. 133-142, (1981).
. Hooge EIV., 1 /fnoise, Physica, 83 B, 14-23, (1976).
Machlup S., Earthquakes, thunderstorms and other noises, Proc. 6th Int. Conf on noise in physical systems held at the National Bureau of Standards, Gaithersburg, Md, USA, pp. 157- 160, (1981).
Gadner M,White and brown music,fractal curves and one-over-f fluctuations,Scientific American, 238 (4),16-32 ,(1978).
MushaT, 1/ffluctuations in biological systems, Proc. 6 th Int. Conf on noise in physical systems held at the National Bureau of Standards, Gaithersburg, Md, USA,pp 143-146, (1978).
Voss R.F. and Clarke J., Flicker Ilf noise;equilibrium temperature and resistance fluctuations,Phys. Rev. B, 13, pp. 556-573,(1976).
Hooge EN, 1/f noise is no surface effect.,Phys.Lett.A, 29, pp. 139-140, (1969).
. Van Kampen IV.G., Some theoretical aspects of noise, Ninth Int. Conf on Noise in Physical Systems, World Scientific Publishing Co. Pte Ltd., Montreal,pp.3 1 11, (1987).
. Kiss L.B, Heszler P and Hrásko I?, Non-validity of the quatum 1/f noise model, Ninth Int. Conf on Noise in Physical Systems,World Scientific Publishing Co. Pte Ltd., Montreal, pp.3-11, (1987).
. Stoisiek M and Wolf D., Recent investigations on the stationarity of 1 /fnoise Phys., 47, 362-364, (1976).
. Van der Ziel A., On the noise spectra of semiconductor noise and offlicker effict, Physica, 16,359-372, (1950).
. Brophy J.J. ,Phys. Rev. 166, 827-831, (1968).
. Hooge EN and Hoppenbrouvwers AM, Amplitude distribution of 1 /fnoise, Physica,45 386-392, (1969).
. Dutta I?, Eberhard W and Horn PM, 1/f noise in metals film;the role of the substrate,Solid State Communications,27, 1389-1391,(1978).
. Eberhard W and Horn PM,Temperature dependence of noise in silver and cooper,Phys. Rev. Lett.39,643- 646, (1977).
. Hooge EN and Gaal L.M,Fluctuations with a 1/fipectrum in the conductance of ionic solutions and in the voltage of concentration cells, Phillips Res. Rev.,26,77-90,(1971).
. Kleinpenning G.M, uy noise in thermo e.mf of intrinsic and extrinsic semiconductors,Physica. 77,7890,(1974).
. Iones B.K, Excess of conductance noise in silicon resistors,Proc. 6th Int. Conf. Noise in Physical Systems held at the National Bureau Of Standards, Gaithersburg, MD, USA, pp 206-209, (1981).
. Kleinpenning G.M, 1 /fnoise in hall effect;fluctuations in mobilityjAppl. Phys., 51, 3438, (1980).
. Bernamount J.,Fluctuations de potentiel aux bornes d'un conducteur metallique de faible volume parcouru par un courant,A. de Phys.,7,7 1- 140,(1937).
. Prudenziati M an al., Temperature dependence of Ilf noise in thich film resistors, Proc. 6 th Int. Conf on noise in physical systems held at the National Bureau of Standards, Gaithersburg, Md, USA,pp 202-205,(1978).
. Melsac R. and Wall PD., Science 105,97 1978,(1965).
. Takakura K, and al _uf controlled transcutaneous electrical stimulation for pain reliefNinth Int. Conf on Noise in phsysical systems, Montreal,279-282, (1987).
. Rogers C. T., Noise in very small electronic devices; understanding the origin of the 1/f spectrum, Ninth Int. Confon Noise in phsysical systems, Montreal,293-302,(1987).
. Van der Ziel A., Limiting Flicker noise in Mosfets, Solid State Elect.18, 301, 1031 (1975).
. Smith D.,Low frequency noise in biased solidtantalum capacitors,Ninth Int. Conf on Noise in phsysical systems Montrea1,311-314,(1987).
. Handel PH., 1/f noise - an 'Infiared' Phenomenon, Phys. Rev Lett., 34,1492-1495,(1975).
. Alzate Marco A., Generation of simulated fractal and multifractal traffic; IX Congreso nacional de estudiantes de sistemas, U Distrital, Santafé de Bogotá, 27-33, (2000P).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación y Desarrollo
Ingeniería, 2000-00-00 vol:5 nro:1 pág:37-46
Diseño e implementación de un sistema de visión artificial basado en redes neuronales.
Santiago Olivera Botello
Estudiante de último semestre de ingeniería electrónica. Realizó su proyecto de grado sobre visión artificial basada en Redes neuronales. E-mail: santiago@ieee.org
Resumen
En este trabajo se implementó un sistema de procesamiento visual basado en modelos biológicos. Se logró la fusión satisfactoria de tres módulos independientes: separación de fondo de figura (FGS), filtro de invarianza (filtro W&W) y sistema de categorización (Fuzzy ART), los cuales, actuando en conjunto, permiten el reconocimiento automático e invariante a posición, ángulo y escala de las figuras presentes en la escena en cuestión.
Palabras Clave.- Separación fondo de figura, interacciones cortico-geniculares, Teoría de Resonancia Adaptativa, redes neuronales, visión artificial.
Abstract
It 's been implemented a visual processing system based on biological models. Three independent different stages have been succesfully put together: figure-ground separation (FGS), invariant filter (What & Where filter) and a categorization system (Fuzzy ART), which working as a whole, allow the position, orientation and scale invariant automatic recognition of figures in a given scene.
Key Words.- Figure-ground separation, corticogeniculate interactions, Adaptive Resonance Theory, neural networks, artificial vision.
I. INTRODUCCIÓN
En este artículo se muestra la implementación de un sistema de visión artificial utilizando redes neuronales artificiales. Dado que las arquitecturas neuronales utilizadas son basadas en la naturaleza, muchos de los modelos empleados están basados en teorías fisiológicas. Son dos los campos teóricos fundamentales sobre los cuales está desarrollado el sistema: por un lado, la fisiología de la visión humana, en especial las interacciones entre los núcleos laterales geniculados (LGN) del hipotálamo y la región cortical del cerebro y, por el otro, la teoría de resonancia adaptativa (ART) que, de hecho, es una arquitectura neuronal artificial basada en esas interacciones cortico-geniculares mencionadas anteriormente.
La arquitectura empleada describe un modelo de red neuronal de tipo auto-organizativo que realiza reconocimiento automático de patrones presentes en una escena. El sistema se puede dividir en tres módulos funcionales básicos: la primera etapa realiza separación entre fondo y figura (FGS) para cada una de las imágenes en la escena (aísla cada imagen de su fondo y de las demás figuras de la escena); la siguiente etapa es de invarianza y se encarga de hacer que cada una de las imágenes, anteriormente separadas sean invariantes a traslaciones, rotaciones y cambios de escala; y por último, la etapa de categorización se encarga de identificar y aprender los patrones que representan las imágenes aisladas e invariantes.
II. MODELOS DE VISIÓN ARTIFICIAL
La arquitectura que se utilizó en este proyecto está basada en un modelo de red neuronal autoorganizada para reconocimiento invariante de patrones propuesta por primera vez por Gail Carpenter y Stephen Grossberg de la Universidad de Boston en 1988 [1]. Las etapas funcionales primarias del sistema son:
- Descuento de las condiciones variables de iluminación.
- Detección, regularización y completado de fronteras en la figura. Supresión de ruido por dentro y fuera de la imagen.
- Separación figura-fondo.
- Filtrado para obtener invarianza bajo traslación, rotación y cambios de escala.
- Categorización y aprendizaje de los patrones procesados.
Se puede considerar entonces, que la primera etapa en el desarrollo del proyecto fue el sistema de separación figura-fondo (FGS). Este sistema comprende las tres primeras capas de procesamiento de la imagen. Mediante este proceso, una figura u objeto en la escena es separado de otras figuras y de su fondo. Aunque el conocimiento de los objetos puede llegar a facilitar el proceso de separación, este no es indispensable ya que el sistema debe tener la capacidad de reconocer imágenes nuevas con las que jamás haya sido enfrentado.
Esta etapa es un paso esencial en cualquier sistema de reconocimiento de patrones, ya que los objetos a reconocer pueden variar su posición, orientación y escala dentro de la escena. Dado que la etapa final de categorización y aprendizaje de los objetos en la imagen requiere que estos sean representados invariantes a cambios en posición, orientación y escala, y esta invarianza no se puede lograr si los objetos se encuentran unidos al resto de la escena, es indispensable la aplicación de este procedimiento.
A. FGS EN LA TEORÍA FACADE
Basado en modelos biológicos, FACADE se compone de dos sistemas de procesamiento fundamentales: el Sistema de Contorno de Frontera (BCS: Boundary Contour System) y el Sistema de Contorno de Características (FCS: Feature Contour System) [2]. El sistema realiza un procesamiento jerárquico y en paralelo, en donde interaccionan BCS y FCS para crear una representación de la escena apta para su procesamiento; en esta representación, los componentes o figuras que codifican diferentes características en cuanto a color, profundidad y tamaño, son separados unos de otros en diferentes niveles de la red, los cuales se usan posteriormente para reconocimiento visual de objetos.
1) Iluminación Variable y Relleno
El hecho de que la intensidad y la frecuencia de las señales que llegan al elemento sensor sean variables crea incertidumbre que puede llegar a causar errores en el sistema de categorización y aprendizaje. La arquitectura de esta primera etapa utiliza una red en paralelo de neuronas on-center/off-surround (excitatorias en el centro e inhibitorias en el exterior) que amplifica las regiones de alto contraste y atenúa las de bajo contraste; sin embargo, este proceso crea otro tipo de incertidumbre (se pierde información de color, texturas e intensidad lejos de la frontera) que deberá ser solucionado en etapas posteriores del sistema.
Esta primera etapa también activa topográficamente la red de relleno (figura 1), la cual utiliza un proceso de difusión no lineal para completar la representación de brillo en las regiones previamente amplificadas o atenuadas.
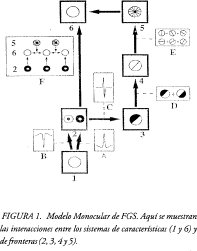
El modelo monocular tiene básicamente tres tipos de procesos. El primero está a cargo del primer módulo FCS (2) y consiste básicamente en eliminar la variación de iluminación y algo del ruido; las siguientes etapas (3,4,5) son bancos de filtros orientados que corresponden al BCS y su función principal es extraer las fronteras de las figuras conectadas en la escena y, por último, la etapa (6) es otro módulo FCS que realiza el proceso de difusión que crea el relleno dentro de las fronteras previamente obtenidas por BCS.
A esta secuencia de procesamiento se le conoce como F-B-F (Feature-Boundary-Feature) debido al orden en que interactúan los subsistemas. Los cuadros representados por letras muestran el tipo de filtro utilizado en cada etapa. En especial, F muestra que el proceso de relleno utiliza la información de fronteras de 5 y la info'rmación topográfica de la imagen original en 2.
B. FGS UTILIZANDO UNA RED MONOCROMÁTICA FBF
Los modelos anteriormente vistos llevaron a crear una teoría general para procesamiento visual utilizando redes FBF. En este modelo, una hipótesis básica es que el proceso de relleno es activado por fuentes de entrada activadas internamente. De hecho, la red "colorea" cada una de las figuras conectadas de la imagen utilizando una "tinta" generada internamente. Ahora se describe paso a paso el proceso que se sigue para lograr la separación.
1 Paso 1. Descontar Iluminación Variable
Al igual que en la teoría FACADE, se utilizan células ON-center/OFF-surround (ON-C) para lograr realzar la diferencia de contrastes dentro de la imagen. Se usan además las células opuestas OFF-C en paralelo con las ON-C; de esta manera se obtiene una imagen que es el negativo de los contrastes obtenidos anteriormente, la cual facilitará el procesamiento más adelante.
Las células ON-C responden mejor a un disco de alta iluminación rodeado por un anillo de baja iluminación, las OFF-C hacen exactamente lo contrario. Una célula OFF-C con su centro sobre una línea negra en un fondo blanco, será excitada en el centro por la línea negra y por las partes ON que llegan al fondo blanco, y será inhibida por la región ON que está sobre la línea negra; de esta manera, la mayor excitación (menor inhibición) de la célula será en el borde interior de la línea. De forma análoga se infiere que una célula ON-C tendrá su mayor activación en el borde exterior de la célula.
2 Paso 2. Filtro CORT-X 2
Las señales provenientes de la primera etapa son sometidas ahora a una serie de filtros conocidos como CORT-X 2 [3] cuya función es crear una representación de fronteras de las figuras en la escena. CORT-X 2 detecta, regulariza y completa fronteras provenientes de contrastes en bordes, texturas o sombras, mientras suprime ruido. La primera etapa, capa de células simples, está formada por detectores de contraste orientados, sensibles a orientación, cantidad, dirección y escala del contraste de la imagen en una posición dada. La sensibilidad a la orientación es resultado de su forma elíptica. Cada punto de la imagen cuenta con varios de estos detectores con diferentes orientaciones (doce en este caso). La sensibilidad a la cantidad y dirección de contraste se produce gracias a que, al dividir la elipse por su eje más largo, media célula es excitatoria y la otra célula inhibitoria. Las salidas de estas redes de células simples en paralelo se combinan en cada posición para formar la segunda etapa de procesamiento del filtro, denominada capa de células complejas; estas células, al igual que las simples son sensibles a cantidad, orientación y escala de contraste de la imagen, pero no a dirección de contraste. Estas propiedades se logran sumando en todas las posiciones cada uno de los pares de células con la misma orientación, sin tener en cuenta la dirección de contraste.
La siguiente etapa de filtrado se diseña para controlar el ruido cerca de las fronteras, las células complejas se convierten en células hipercomplejas. En esta etapa, las células de una orientación determinada compiten espacialmente; así, cada célula compleja excita la hipercompleja correspondiente a su orientación y posición mientras inhibe a las hipercomplejas con igual orientación pero diferente posición. Esta etapa se conoce como primera etapa competitiva. En la siguiente etapa, segunda etapa competitiva, la competencia es entre orientaciones entre células de la misma posición; es así como la orientación ganadora será aquella que recibió la mayor cantidad de activación de su célula hipercompleja.
Las operaciones finales en este paso incluyen varias etapas competitivas y cooperativas dentro de las que se destaca la cooperación de largo rango cuyo objetivo es completar las fronteras faltantes resultado en la mayoría de los casos del ruido presente en la imagen. Las células cooperativas juegan el papel de las células bipolares en el BCS [4].
3) Paso 3. Relleno
La salida del filtro CORT X-2 se envía a M redes de relleno. Cada una de estas redes recibe una señal de relleno generada algunas veces por la misma imagen original de la escena y otras por las mismas características internas del sistema. Esta señal que recibe comienza a expandirse debido a un proceso de difusión hasta que es inteirtimpida por alguna frontera o se termina por su propia naturaleza. De esta manera, cada una de las figuras de la imagen inicial va a quedar totalmente rellena, por lo menos en alguna de las redes de relleno.
4) Paso 4. FGS por Doble Oposición
Para terminar el proceso de FGS, cada una de las redes de relleno que contiene las figuras de la escena, es sometida nuevamente a una etapa de células ONC y OFF-C; en caso de que en este punto hubiera persistido aún algún hueco en la frontera de las figuras, el hecho de restar las OFF-C de las ON-C regulariza y corrige cualquier fuga (no muy grande, aunque es muy poco probable que haya una fuga grande) que haya podido ocurrir en el proceso de relleno. Ese proceso de doble inhibición, la de las células ON/OFF y la de la resta entre ellas, es análogo al que en neurofisiología realizan las células de doble oposición.
En resumen, una red FBF logra separa las figuras del fondo de una escena mediante el uso de arreglos de redes que regularizan la iluminación y generan segmentación de fronteras y señales del vecino más cercano para el relleno, lo cual ofrece como resultado una representación de la escena óptima para ser categorizada y aprendida.
III. MODELO DE PERCEPCIÓN
La figura 2 muestra el diagrama de bloques del modelo de procesamiento visual utilizado en este trabajo (los rectángulos muestran etapas FCS mientras que los ligeramente curvos a los lados corresponden a módulos BCS). Este modelo incluye células ON/OFF retinales y de los LGN, células corticales simples, complejas e hipercomplejas, células hipercomplejas de alto orden, células bipolares y células ON/OFF de doble oposición para el relleno. A continuación se explicará la dinámica del modelo. Algunas etapas ya han sido tratadas previamente, de manera que no se enfatizará en ellas.
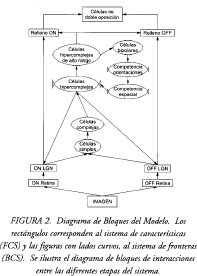
Las salidas de las células LGN activan la primera etapa de procesamiento cortical BCS, células simples, cuyos campos receptivos orientados son sensibles a orientación y dirección de contraste. Parejas de células simples con la misma orientación se suman para formar las células complejas; este proceso hace que de aquí en adelante el sistema sea sensible a la orientación del contraste, pero no a su dirección.
Las células complejas activan la capa de células hipercomplejas a través de una red ON/OFF (competencia espacial) creando señales de contraste más fuertes hacia los bordes de las figuras. De esta manera, las células complejas excitan a células hipercomplejas de igual orientación y posición y a la vez inhiben a las hipercomplejas de igual orientación y diferente posición. Esta competencia entre células hipercomplejas cumple dos funciones principales: por un lado, fortalece y agudiza la respuesta del sistema a bordes de brillo orientados (formados por fronteras reales o contrastes de color, texturas, sombras, etc.) y por el otro, inician el proceso de incremento de contraste al final de las líneas, lo que permitirá, en etapas sucesivas, implementar el sistema de reconocimiento de imágenes ilusorias como el disco de Ehrenstein.
Las células hipercomplejas entran a una capa de competición entre orientaciones en la misma posición, conocida como de células hipercomplejas de alto orden. Esta competencia tiende a clarificar cuál es la orientación dominante en cada punto de la imagen. La salida de las células hipercomplejas de alto rango se alimenta a las células bipolares en donde se inicia un proceso mediante el cual se agrupan y completan fronteras de largo alcance. Estas células se activan sólo si sus dos campos receptivos están suficientemente activados por las células hipercomplejas de la orientación adecuada.
La salida de las células bipolares se realimenta a las células hipercomplejas después de pasar por varias etapas de procesamiento competitivo (en otros trabajos, las señales de las células bipolares son realimentadas directamente a las hipercomplejas aunque, por supuesto, con algunos cambios en el preprocesamiento [6]). Primero, las salidas de las células bipolares entran a una etapa competitiva en orientación para determinar qué orientación está recibiendo la mayor cantidad de apoyo cooperativo. La siguiente etapa competitiva tiene lugar sobre las posiciones vecinas y su objetivo es determinar la mejor ubicación para la frontera emergente. Estas etapas competitivas-cooperativas son necesarias para determinar el mejor agrupamiento de fronteras, ya que las posibilidades son variadas. Las células hipercomplejas que reciben el mayor apoyo cooperativo, iniciado por las células bipolares, se fortalecerán y en el siguiente ciclo excitarán a las mismas células bipolares correspondientes. Este proceso de interacciones entre las células hipercomplejas y las bipolares tiende a estabilizarse rápidamente (generalmente en tres ciclos), creando un estado de resonancia que completa las fronteras con las células más favorecidas y suprime a las menos favorecidas, encontrando así la mejor combinación de activaciones para completar la frontera.
Cada segmentación de frontera creada en BCS genera señales topográficas hacia los campos de relleno (FIDO's: Filling-In Domains). Los FIDO's también reciben señales provenientes de los LGN ON y OFF respectivamente. Las entradas provenientes de los LGN's activan sus células objetivo y activan el proceso de relleno. Este proceso de relleno está restringido a los compartimentos creados por el BCS. Las actividades de relleno de las células OFF son restadas de las de las células ON en la etapa de células de doble oposición, cuyas actividades representan los patrones de brillo de cada una de las figuras percibidas.
IV FILTRO DE INVARIANZA
Como ya se ha mencionado en varias ocasiones, este modelo, al igual que muchos sistemas de procesamiento de imágenes, requiere de otra etapa de preprocesamiento, que haga las señales obtenidas en la etapa previa invariantes a desplazamiento, rotación y escala. Una forma estándar de lograr esta invarianza es utilizar la transformada de Fourier para lograr invarianza a desplazamiento y una transformación polar logarítmica para la invarianza a escala [7]. Esta aproximación, sin embargo, hace que la representación invariante ya no esté en el plano cartesiano y se pierde información no invariante debido a que no se tiene en cuenta la fase de la señal.
Una estrategia para lograr invarianza, que no presenta los problemas del caso anterior, está inspirada en el procesamiento cerebral de las señales corticales que llevan la información de dónde se encuentra un objeto y qué es el objeto [8] [9].
El filtro está formado por un canal dónde (where channel) y una canal qué (what channel). El canal dónde computa la posición, orientación y tamaño de la imagen inicial. El canal qué, códifica las señales de la imagen de acuerdo a los resultados obtenidos por el canal dónde. El reconocimiento de la imagen, que es la etapa siguiente a la de invarianza, se realiza con base en la salida del canal qué.
A. FILTROS ORIENTADOS
Los filtros que se usan para determinar la orientación y tamaño de las figuras son elípticos. Cada filtro tiene una elipse central de valores positivos (excitatorios), rodeada por un anillo de valores muy negativos (gran inhibición) y terminan en una región de valores ligeramente positivos. La mayor respuesta de un filtro de este tipo (frente a una figura obtenida previamente) se obtiene cuando su escala y orientación corresponden perfectamente a las de la figura.
Cada filtro está determinado por un ángulo de orientación, un factor de escala (tamaño), una posición y un factor de elongación (longitud de su eje principal). Cuando una figura encaja perfectamente dentro del área de mayor excitación del filtro, la respuesta de este es muy fuerte; sin embargo, si la figura se enfrenta a un filtro de mayor tamaño, la respuesta continuará siendo fuerte ya que toda el área de la imagen se encuentra dentro del área positiva del filtro.
Se puede utilizar un mecanismo de competición entre orientación para cada escala [10], con el fin de determinar la orientación óptima. Se observa que, para esa figura que maximiza la excitación del filtro, se obtiene una gran inhibición al cambiar su orientación a una perpendicular a la que tenía, ya que gran parte de la figura va a caer dentro del área altamente inhibitoria del filtro; sin embargo, si se toma el caso del filtro más grande, la inhibición causada al rotar la figura no es tan fuerte; por esta razón, se puede emplear una realimentación competitiva entre orientaciones en la misma escala, que sirva para enfatizar esas diferencias [11].
Las diferencias pequeñas de actividades entre orientaciones perpendiculares de la figura son inhibidas, mientras que las diferencias grandes son magnificadas; de esta manera se logra determinar la mejor orientación y escala del filtro.
V. SISTEMA DE CATEGORIZACIÓN
La última etapa del sistema es la de categorización y aprendizaje. Para esta etapa se escogió una red de categorización no supervisada del tipo ART (Adaptive Resonance Theory) [12] dado que presenta características que la hacen mejor que cualquier otra red empleada para categorización. El modelo usado específicamente es una versión difusa de ART conocida como Fuzzy ART [13]. A continuación se esbozan las características principales de Fuzzy ART y al final, en los apéndices, se mostrará la inspiración y teoría fundamentales que hacen tan deseables a los sistemas ART para funciones de categorización. Cabe anotar que todos estos modelos están inspirados en modelos biológicos, específicamente del cerebro humano.
La teoría de Fuzzy ART es básicamente igual a la del primer modelo de la teoría (ART 1) sólo que introduce algunos operadores de la teoría de conjuntos difusos. Por ejemplo, el operador intersección de ART 1 se cambia por el operador MIN de la teoría de conjuntos difusos. De hecho, Fuzzy ART se reduce a ART 1 en respuesta a vectores de entrada binarios, pero también puede establecer categorías estables en respuesta a vectores de entrada análogos.
El aprendizaje es estable porque todos los pesos adaptativos pueden solamente decrecer en el tiempo. Un proceso extra, denominado codificación de complemento, utiliza las respuestas de células ON/OFF para prevenir la proliferación de categorías. Esta codificación de complemento normaliza los vectores de entrada mientras preserva las amplitudes de activación individuales.
A. ALGORITMO DE FUZZYART
El vector de entrada es un vector M-dimensional en el cual cada componente se encuentra en el intervalo (0,1). En general, las figuras de la escena, aisladas de su fondo, rellenas e invariantes tienden a ser totalmente binarias, mas en algunas ocasiones el patrón no es del todo binario, razón por la cual se requiere un modelo de categorización de señales análogas.
El patrón que define cada una de las categorías de aprendizaje es un vector de pesos (M pesos para cada categoría). El número N de categorías codificadas puede ser arbitrariamente grande. Inicialmente todos los pesos de todas las categorías tienen el valor de 1 y se dice que la categoría no está comprometida. Cada elemento de los vectores de peso es monótonamente decreciente, con lo cual se asegura su convergencia. Fuzzy ART tiene un único vector de pesos que reúne las funciones de los vectores de subida y de bajada presentes en ART 1.
Los parámetros que determinan la dinámica del sistema Fuzzy ART son: el parámetro de escogencia (*), que participa en el proceso de escogencia de la categoría óptima para determinado patrón de entrada; un parámetro de aprendizaje (*), que determina la velocidad del aprendizaje y un parámetro de vigilancia (*), que define el tamaño de las categorías. La escogencia de la probable mejor categoría para un patrón de entrada dado se realiza con base en la función de escogencia T (Las ecuaciones para Fuzzy ART aparecen al final en el apéndice de ecuaciones). Esta función utiliza el factor alfa para medir la similitud entre un vector de entrada y los vectores de pesos de cada una de las categorías disponibles. La función T, ordena de arriba hacia abajo todas las categorías, determinando así el orden de búsqueda de la categoría adecuada para cada vector de entrada. En el caso de que más de una categoría presente un factor de escogencia máximo, el factor alfa ayuda a definir cuál de las categorías debe ir primero.
B. RESONANCIA O RESET
La resonancia ocurre en el sistema cuando se cumple el criterio de vigilancia, es decir, la categoría escogida como probable candidato a almacenar los datos de la señal de entrada cumple con los requisitos mínimos requeridos, determinados por el parámetro de vigilancia. Por el contrario, si la categoría escogida no logra cumplir con el criterio de vigilancia, ocurre el reset; en este caso, el valor de la función de escogencia para la categoría que causó el reset se vuelve -1 por el tiempo que el patrón que se está trabajando permanezca en la entrada del sistema.
C. APRENDIZAJE
En caso de que se haya presentado resonancia, el vector de pesos correspondiente a la categoría que la originó es adaptado a la nueva señal de entrada. Para una codificación eficiente y eliminación de ruido en los patrones de entrada, se usa aprendizaje rápido en el caso de que se trate de una categoría aún no comprometida (básicamente, el vector de entrada se convierte en el vector de pesos de la categoría), es decir, un patrón de entrada que no se asemeja a ninguna de las posible categorías existentes en la red; de lo contrario, para nodos previamente comprometidos se utiliza aprendizaje lento, con lo cual se asegura la estabilidad del sistema.
D. NORMALIZACIÓN DE LA ENTRADA
En los sistemas ART se presenta el problema de proliferación de categorías en el caso de que los vectores de entrada no estén normalizados [14]. Por esta razón, en Fuzzy ART, todos los patrones de entrada tienen norma igual a una constante. La manera típica de lograrlo es dividiendo cada vector sobre su norma, pero su desventaja es que varía la escala real de las señales de entrada; un método alternativo es la codificación complemento en la cual se duplica el tamaño del vector. El nuevo vector está compuesto ahora por el vector antiguo y el vector complementario al antiguo, de esta manera la norma de cualquier vector de entrada será igual al número de elementos dentro del vector codificado.
VI. RESULTADOS
En este capítulo se muestran los logros alcanzados con el modelo de visión previamente descrito. Estos resultados han sido divididos en dos partes: la primera, muestra gráficamente algunas de las respuestas de las diferentes etapas del proceso, lo cual facilita la comprensión del mismo, y la segunda, muestra y analiza las medidas del desempeño del sistema.
A. RESPUESTAS DEL SISTEMA

La figura 3 muestra una de las imágenes con las que se probó al modelo. Prueba sus capacidades manejando diferentes intensidades, puntas agudas e imágenes ilusorias. Los canales ON/OFF de la retina crean una representación con gran contraste que permite descontar las diferencias de luminancia y, como se verá en un ejemplo más adelante, ayudan a manejar el ruido. Cada una de las imágenes es el negativo de la otra.
IMAGEN NO DISPONIBLELos canales ON/OFF de LGN han recibido realimentación de la primera etapa de células hipercomplejas. Se inicia entonces el proceso de intensificar la actividad de las células correspondientes a los finales de línea.
IMAGEN NO DISPONIBLEYa se empiezan a ver los resultados de la realimentación. En los bordes de las barras se intensifica la actividad y también se ve favorecida la actividad de las células en las esquinas, por ejemplo en las puntas del triángulo.
Una vez que las señales pasan el ciclo competitivocooperativo (CC), las figuras son separadas de su fondo y de otras figuras. La siguiente etapa, las hace invariantes para luego pasar a la etapa de categorización. Es importante notar que el sistema sobrellevó el problema de luminancia (círculo) y de esquinas (triángulo).
IMAGEN NO DISPONIBLELa figura 6 muestra ocho de las matrices de relleno. Aquí, cada figura ha sido totalmente separada de su fondo y de las demás figuras.
IMAGEN NO DISPONIBLEEn la figura 7 se muestran algunos ejemplos de las imágenes centradas. A estas figuras se les ha hallado el centro de masa y se ha logrado una posición invariante para ellas.
IMAGEN NO DISPONIBLEEn la figura 8 se muestra la representación invariante a posición, ángulo y escala, de cada una de las figuras en la imagen. También se hicieron algunas pruebas añadiendo ruido aleatorio a la señal. La figura 9 muestra el caso de un ruido del 20%. Como se puede ver, el resultado en las células hipercomplejas es bastante bueno a pesar de que no se ha llevado a cabo el ciclo CC.
IMAGEN NO DISPONIBLEB. DESEMPEÑO DEL SISTEMA
La primera respuesta del sistema en la que se puede medir su desempeño es el resultado de la etapa de relleno; el proceso de separación de figuras y fondo es indispensable para el desempeño del resto del sistema. La siguiente evaluación del desempeño se realiza en el filtro de invarianza; el desempeño de esta etapa, no sólo muestra si dicho filtro es capaz de hacer la imagen invariante, sino también muestra la calidad del sistema FGS. Como se puede ver en las figuras 3, 4 y 5 de la sección anterior, esta separación fondo-figura es muy buena, el único defecto que se podría encontrar es que la forma de la figura resultado no es exactamente igual (pero es muy parecida) a la de la imagen de entrada, pero no es realmente un defecto ya que no influye en la categorización de las figuras.
En la tabla I se muestran los resultados de 10 pruebas del sistema de invarianza cuando la imagen de entrada no tiene ruido. Aquí se utilizaron dos métodos diferentes para hallar COM: el algoritmo genético y una búsqueda exhaustiva basada en la función de evaluación del algoritmo genético. La tabla muestra el número de veces que se logró hallar el centro de masa.
TABLA I. Invarianza sin ruido. Como se puede ver, el desempeño del sistema es excelente. El algoritmo genético genera pequeños errores eventualmente, a cambio de una mejora considerable en la velocidad.
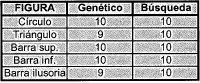
La tabla II muestra el resultado de otras 10 pruebas realizadas al sistema, pero ahora con una imagen de entrada que incluye un patrón de ruido del 10%.
TABLA II. Invarianza con ruido=10%. El error al hallar el centro de masa no implica un desacierto total, simplemente que el punto exacto del centro de masa no ha sido hallado correctamente, pero en la mayoría de los casos se halla un punto muy cercano.
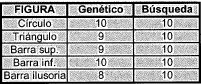
Una tercera tabla (tabla III) muestra los resultados de 10 pruebas con una imagen con patrón de ruido del 20%.
TABLA III. Invarianza con ruido=20%. Inclusive con un patrón de error del 20%, el desempeño del sistema no varia mucho, aún es igualmente eficiente.
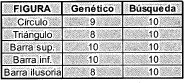
Se puede decir que el desempeño del sistema es excelente. El algoritmo genético no es tan bueno como la búsqueda exhaustiva, pero compensa su desempeño con el hecho de ser mucho más rápido. La naturaleza del proceso es en general aleatoria, ya que el ruido es aleatorio.
Los problemas en el triángulo son causados por las esquinas y en las barras debido a que son tres barras diferentes (las dos en la imagen y una tercera que se forma debido a las fronteras ilusorias en el medio de las barras).
El sistema de categorización implementado consta de 10 categorías en su capa F2. La tabla IV muestra las categorías asociadas por el sistema a cada una de las figuras.
TABLA IV. Desempeño del Sistema de Categorización. Esta tabla indica la cantidad y el porcentaje de veces que el sistema categorizó correctamente cada una de las figuras.
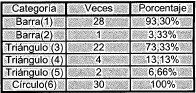
Aunque la idea es que el sistema asocie una categoría por figura del sistema, no hay ningún problema que asocie varias categorías a una misma figura (como por ejemplo en triángulo), igual si el resultado es la categoría tres, la cuatro o la cinco, se reconoce la figura como un triángulo.
La medición de desempeño está hecha sobre las 30 pruebas anteriormente realizadas. Se puede ver que en las figuras asociadas a más de una categoría, existe una categoría predominante que reconoce el patrón generalizado y las otras reconocen pequeñas variaciones de ese patrón.
El número de figuras que no entran en ninguna de estas categorías, consideradas ruido, es mínimo. Los errores son causados principalmente por el sistema de invarianza.
VII. CONCLUSIONES Y RECOMENDACIONES
- Se ha comprobado la versatilidad de la integración . de los diferentes módulos que conforman el sistema en el proceso de tratamiento de imágenes basado en modelos biológicos.
- Los resultados obtenidos muestran la calidad del proceso de separación fondo de figura realizado por el modelo propuesto en la teoría FACADE y FBF.
- El algoritmo genético propuesto para hallar el centro de masa, mejora el desempeño del sistema principalmente en cuanto al tiempo. Sin embargo, aún se puede continuar mejorándolo (principalmente en la función de evaluación), con el fin de incrementar su eficiencia.
- Vale la pena incluir en el trabajo algunas técnicas algorítmicas y matemáticas que mejorarían su velocidad. Por ejemplo, es posible encontrar para cada núcleo gausiano sus dos vectores base y convolucionar la imagen con cada uno de estos dos vectores en lugar de con el núcleo completo, lo cual aceleraría notoriamente el sistema.
- Se puede reducir el tiempo de procesamiento del sistema haciéndolo menos preciso y luego corrigiendo los errores ocasionados por esa imprecisión manipulando el parámetro de vigilancia del sistema de categorización.
- Las debilidades en cuanto a tiempo de procesamiento que presenta el sistema, son debidas casi en su totalidad al carácter secuencial del sistema en el que se simula.
- El sistema implementado es una gran herramienta académica y de investigación en el área de neuroingeniería.
VIII. REFERENCIAS
[1] Carpenter, G., y Grossberg, S. The ART of adaptive pattern recognition by a self-organizing neural network. Computer. 21. 1988.
[2] Grossberg, S. Neural Networks and Natural Intelligence. Cambridge, MA: MIT Press. 1988.
[3] Bradski, G y Grossberg, S. East LearningVIEWNET architectures for recognizing 3-D objects from multiple 2-D views. Technical Report CAS/CNSTR-93-053. Boston University. 1995.
[4] Grossberg, S. y Mingolla, E. Neural dynamics of perceptual grouping; textures, boundaries and emergent segmentations. Perception and Psychophysics. 38. 1985.
[5] Kelly, E, y Grossberg, S. Neural dynamics of 3-D perception: figure-ground separation and lightness perception. Technical Report CAS/CNS TR-98-026. Boston University. 2000.
[6] Cavanagh, P. Image transforms in the visual system. En Fi gural Synthesis. Hillsdale, NJ. 1984.
[7] Carpenter, G. A., et al. A what-and-where neural network for invariant image pre processing. Proceedings of the International Joint Conference on Neural Netwoks. 1992.
[8] Carpenter, G. A., et al. The What-and-Where filter a spatial mapping neural network for object recognition and image understanding. Technical Report CAS/CNS-93-043. Boston University. Junio 1993.
[9] Grossberg, S. Studies of mind and brain. Boston. 1982.
[10] Seibert, M, y Waxman, A. M Spreading activation layers, visual saccades, and invariant representations ofneural pattern recognition systems. 1989.
[11] Carpenter, G. A., y Grossberg, S. A massively parallel architecture for self-organizing neural pattern recognition machine. Computer Vision, Graphics an Image Processing. 37. 1987.
[12] Carpenter, G. A., et al. Fuuzy ART an adapti ve resonance algorithm for rapid, stable classification of analog patterns. Proceedings of the International Joint Conference on Neural Networks. 1991.
[13] Moore, B. ART 1 and pattern clustering. Proceedings of the 1988 Conneccionist Models Summe<r School. San Mateo, CA. 1989.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










