DOI:
https://doi.org/10.14483/udistrital.jour.reving.2017.2.a04Published:
2017-05-05Issue:
Vol. 22 No. 2 (2017): May - AugustSection:
Computational IntelligenceCaracterización de Señales EEG mediante Wavelet Packet y Entropía Difusa para Tareas de Imaginación Motora
Characterization of EEG Signals Using Wavelet Packet and Fuzzy Entropy in Motor Imagination Tasks
Keywords:
BCI, EEG, Wavelet Packet. (en).Keywords:
BCI, EEG, WaveletPacket (es).Downloads
References
T. M. Vaughan, “Guest editorial brain-computer interface technology: a review of the second international meeting”. IEEE Transactions on Neural Systems and Rehabilitation Engineering, Volumen 11, Número 2, 2003, pp. 94– 109.
J. Wang, G. Xu, L. Wang, and H. Zhang, “Feature extraction of brain- computer interface based on improved multivariate adaptive autoregressive models”. 2010 3rd International Conference on Biomedical Engineering and Informatics, 2010, 895–898.
D. Croz-Baron, J. M. Ramírez, M. Baker, V. Alarcon-Aquino and O. Carrera, “A BCI motor imagery experiment based on parametricfeature extraction and Fisher Criterion”. CONIELECOMP 2012, 22nd International Confe-rence on Electrical Communications and Computers, 2012, 257–261.
C. Chen, W. Song, J. Zhang, Z. Hu and H. Xu, “An Adaptive Feature Extraction Method for Motor-Imagery BCI Systems”. 2010 International Conference on Computational Intelligence and Security, 2010, 275–279.
D. Hu, W. Li, and X. Chen, “Feature extraction of motor imagery EEG signals based on Wavelet Packet decom-position”. The2011IEEE/ICMEInternationalConferenceonComplexMedicalEngineering, 2011, 694–697.
L. Zou, X. Wang, G. Shi, and Z. Ma, “EEG feature extraction and pattern classification based on motor imagery in brain-computer interface”. 9th IEEE International Conference on Cognitive Informatics (ICCI0010), 2010, 536–541.
J. Kevric and A. Subasi, “Comparison of signal decomposition methods in classification of EEG signals for motor-imagery BCI system”. Elsevier, Biomedical Signal Processing and Control, volumen 31, 2017, 398-406.
Pfurstcheller G. et. al. BCI competition 2008, Graz Data Set 2b. [En línea]. Disponible en: http://www.bbci.de/competition/iv/
S. Mallat, “A theory for multiresolution signal decomposition: The wavelet representation”. IEEE Trans. Pattern Anal. Machine Intell, vol. 11, pp. 674693, 1989.
I. Daubechies, “Orthonormal bases of compactly supported wavelets”. Commun. Pure Appl. Math., vol. XLI, pp. 909-996, 1988.
R. R. Coifman, Y. Meyer, S. R. Quake, and M. V. Wickerhauser, “Signal Processing and Compression with Wave-let Packets”. Prog. Wavelet Anal. Appl., pp. 77–93, 1993.
M. Akay, “Wavelet applications in medicine”. IEEE Spectrum, vol. 34, no. 5, pp. 50–56, May 1997.
Y.U. Khan, J. Gotman, “Wavelet based automatic seizure detection in intracerebral electroencephalogram, Clin”. Neurophysiol, Volumen 114, número 5, 2003, 898–908.
D. Deng, “Fatigue Detection of Drivers Based on Electroencephalograph”. International Conference on Indus-trial Informatics, IEEE. 2016.
G. Garg, V. Singh, J. R. P. Gupta, and A. P. Mittal, “Wrapper based wavelet feature optimization for EEG sig-nals”. Biomed. Eng. Lett., vol. 2, no. 1, pp. 24–37, 2012.
L. Shaw and A. Routray, "Statistical features extraction for multivariate pattern analysis in meditation EEG using PCA”. 2016 IEEE EMBS International Student Conference (ISC), Ottawa, 2016.
L. Sun and Z. R. Feng, "Classification of imagery motor EEG data with wavelet denoising and features selec-tion”. 2016 International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Jeju, 2016, pp. 184-188.
A. De Luca and S. Termini, “A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory”. Inf. Control, volumen 20, número 4, 1972, 301–312.
RN.Khushaba, A. Al-Jumaily,A.Al-Ani”.Novel feature extraction method based on fuzzy entropy and Wavelet Packet transform for myoelectric Control”. 2007 Int Symp Commun Inf Technol, 2007, 352–357.
R. Leeb, F. Lee, C. Keinrath, R. Scherer, H. Bischof, G. Pfurtscheller. “Brain-computer communication: motiva-tion, aim, and impact of exploring a virtual apartment”. IEEE Transactions on Neural Systems and Rehabilitation Engineering, volumen 15, 2007, 473–482.
J. Rafiee, M.A. Rafiee, N. Prause, M.P. Schoen, “Wavelet basis functions in biomedical signal processing”. Ex-pert Systems with Applications, Volumen 38, 2011, 6190–6201.
H. Zhang, C. Guan, K.K. Ang, C. Wang, “BCI competition IV—data set I: learning discriminative patterns for self-paced eeg-based motor imagery detection”. Front. Neurosci. Volumen 6, 2012.
R. Leeb, F. Lee, C. Keinrath, R. Scherer, H. Bischof, G. Pfurtscheller, “Brain– computer communication: moti-vation, aim, and impact of exploring a virtual apartment”. IEEE Trans. Neural Syst. Rehab. Eng. Volumen 15, número 4, 2007, 473–482.
G. Pfurtscheller, C. Brunner, A. Schlögl, F.L. da Silvab, “Mu rhythm (de) synchronization and EEG single-trial classification of different motor imagery tasks”. Neuroimage, Volumen 31, número 11, 2006, 153–159.
B. Medina & L. Duque, “Fuzzy entropy relevance analysis in DWT and EMD for BCI motor imagery applica-tions”. Revista de Ingeniería, Volumen 20, número 15, 2015, 9-19.
Maouia Bentlemsan, et al., “Random Forest and Filter Bank Common Spatial Patterns for EEG-Based Motor Imagery Classification”. 2014 Fifth International Conference on Intelligent Systems, Modelling and Simulation. 2014, 235-238.
Xiaojing Guo, et. al. “Envelope detection based on online ICA algorithm and its application to motor imagery classification”. 6th Annual International IEEE EMBS Conference on Neural Engineering, 2013, 1058-1061.
Seung-Hyeon Oh, Yu-Ri Lee, and Hyoung-Nam Kim. “A Novel EEG Feature Extraction Method Using Hjorth Parameter”. International Journal of Electronics and Electrical Engineering, Volumen 2, número 2, 2014, 106-110.
J. Delgado Saa, M. Çetin. “A latent discriminative model-based approach for classification of imaginary motor tasks from eeg data”, J. Neural Eng. Volumen 9, Número 2, 2012.
K. K. Ang, Z. Y. Chin, Ch. Wang, C. Guan and H. Zhang. “Filter bank common spatial pattern algorithm on BCI competition IV Datasets 2a and 2b”. Frontiers in Neuroscience, Volumen 6, 2012.
JR. Landis and GG. Koch. “The measurement of observer agreement for categorical data”. Biometrics 33:159-174, 1977.
D. Coppieters’t Wallant, V. Muto, G. Gaggioni, M. Jaspar, S.L. Chellappa, C. Meyer & C. Phillips. “Automatic artifacts and arousals detection in whole-night sleep EEG recordings”. Journal of neuroscience methods, 258, 124-133, 2016.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Caracterización de Señales EEG Mediante Wavelet Packet y Entropía Difusa para Tareas de Imaginación Motora
Characterization of EEG Signals Using Wavelet Packet and Fuzzy Entropy in Motor Imagination Tasks
Boris Medina Salgado
Universidad De Sucre. Sincelejo - Colombia,
boris.medina@unisucre.edu.co
Ramón Alvarez López
Universidad De Sucre. Sincelejo - Colombia,
ramon.alvarez@unisucre.edu.co
Recibido: 17/11/2016. Modificado: 04/02/2017. Aceptado: 18/02/2017.
Abstract
Background:Clinical rhythm analysis on advanced signal processing methods is very important in medical areas such as brain disorder diagnostic, epilepsy, sleep analysis, anesthesia analysis, and more recently in braincomputer interfaces (BCI).
Method:Wavelet transform package is used on this work to extract brain rhythms of electroencephalographic signals (EEG) related to motor imagination tasks. We used the Competition BCI 2008 database for this characterization. Using statistical functions we obtained features that characterizes brain rhythms, which are discriminated using different classifiers; they were evaluated using a 10fold cross validation criteria.
Results:The classification accuracy achieved 81.11 % on average, with a degree of agreement of 61 %, indicating a "suitablec¸oncordance, as it has been reported in the literature. An analysis of relevance showed the concentration of characteristics provided in the nodes as a result of Wavelet decomposition, as well as the characteristics that more information content contribute to improve the separability decision region for the classification task.
Conclusions:The proposed method can be used as a reference to support future studies focusing on characterizing EEG signals oriented to the imagination of left and right hand movement, considering that our results proved to compared favourably to those reported in the literature.
Keywords:BCI, EEG, Wavelet Packet.
Language: Spanish
Resumen
Contexto:El análisis de ritmos clínicos en los métodos de procesamiento de señales avanzadas es de mucho interés en áreas médicas, tales como el diagnosticó de los trastornos cerebrales, la epilepsia, el análisis del sueño o la anestesia y, más recientemente, en las interfaces cerebro computador (BCI).
Método:En este trabajo se aplica la Transformada Wavelet Packet a fin de extraer los ritmos cerebrales de señales electroencefalografías (EEG) relacionadas a tareas de imaginación motora, contenidas en la base de datos de la competencia BCI 2008. Usando funciones estadísticas ampliamente aplicadas en la literatura, se obtiene la matriz de datos que caracteriza los ritmos cerebrales, que son discriminadas mediante diferentes clasificadores y evaluados usando criterio de validación cruzada de diez pliegues.
Resultados:La exactitud de clasificación se acerca al 81.11 % en promedio, con un grado de acuerdo de 61 %, lo que indica una concordancia adecuada, como ha sido previamente reportada en la literatura. Un análisis de relevancia mostró la concentración de características aportadas en los nodos producto de la descomposición Wavelet, así como las características que mayor contenido de información contribuyen a mejorar la región de decisión de separabilidad para la tarea de clasificación.
Conclusiones:El método propuesto puede ser utilizado como referencia para apoyar futuros estudios en la tarea de caracterización de señales EEG orientadas a la imaginación de movimiento de la mano derecha e izquierda, teniendo en cuenta que nuestros resultados demostraron ser favorables en comparación con los propuestos en la literatura.
Palabras clave:BCI, EEG, Wavelet Packet.
Idioma: Español
1. Introducción
La imaginación de movimiento de la mano izquierda y derecha puede modificar la actividad cerebral en las principales áreas sensoriomotoras, usando, por ejemplo, un estímulo externo a través de visualización de imágenes en una pantalla, que permitan imaginar una acción voluntaria relacionada, capturadas mediante registros electroencefalógrafos (EEG), dando lugar a cambios en los ritmos clínicos mu (?) y beta (?) definidos en el rango espectral de este tipo de señales.
Los sistemas basados en interfaz cerebro-computador (BCI) requieren un método eficaz de procesamiento en línea para clasificar las señales de EEG, con el fin de construir un sistema que permita la comunicación con su entorno a los pacientes con discapacidad física [1].
Se han empleado diversas técnicas de extracción de características para tal fin, principalmente, los modelos autorregresivos [2] y [3], patrones espaciales comunes [4], y la Transformada Wavelet [5] y [6]. En este trabajo se presenta un método efectivo para la caracterización de las señales de electroencefalografía en tareas de imaginación motora, usando la Transformada Wavelet Packets, que ha demostrado ser promisorio en el tratamiento de señales EEG [7]. Dicho método se emplea para descomponer la señal EEG en subbandas frecuenciales y de acuerdo a la información espectral de interés con base en los ritmos clínicos detectados en las EEG, se extraen las características que posteriormente serán usadas como patrones en los clasificadores k-vecinos cercanos (KNN), máquinas de vectores de soporte (SVM) y análisis discriminante lineal (LDA). Hemos usado el criterio de la entropía difusa como método para la discriminación de características de interés; con ello se logra reducir el espacio de dimensionalidad del conjunto de datos y extraer las características de mayor relevancia; una reducción de la dimensionalidad supone un mejoramiento en la precisión y una reducción del costo computacional. La aplicación de este método se utilizó para analizar el conjunto de datos aportados por Competition Graz BCI 2008, dataset 2b [8].
2. Métodos
2.1. Descomposición Wavelet Packets (WP)
La Transformada Wavelet ha mostrado resultados prometedores en el tratamiento de señales EEG, debido a las características no estacionarias de la señal, además de reflejar sus coeficientes en el dominio del tiempo-frecuencia y su capacidad de descomposición multiresolución.
La Transformada Wavelet Packet (WP), introducida por Coifman et al [9] es una generalización de la descomposición Wavelet y ofrece una gama más detallada de posibilidades para el análisis de la señal [10] y [11]. WP proporciona una transformación nivel por nivel de la señal desde el dominio del tiempo al dominio de frecuencia. Se calcula utilizando un conjunto de filtros que conducen a la disminución de la resolución de tiempo y aumento de la resolución de frecuencia. Los componentes de frecuencia, a diferencia de la Transformada Wavelet, son de igual tamaño, ya que WP divide no solo la subbanda de baja frecuencia, sino también la subbanda de alta frecuencia [12]. En el análisis Wavelet, una señal se divide en coeficientes de aproximación y coeficientes de detalle. Los coeficientes de aproximación se subdividen entonces en un segundo nivel que contiene, a su vez, coeficientes de aproximación y coeficientes de detalle y así sucesivamente.
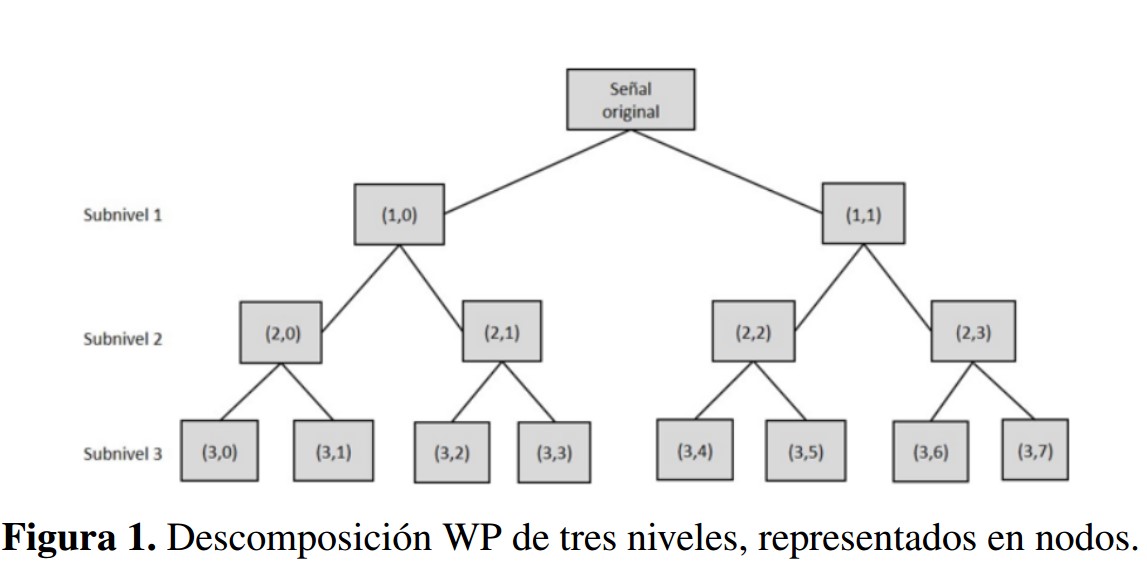
En el análisis WP, los coeficientes de detalle, así como los de aproximación se pueden dividir. Esto produce más 22n 1 caminos diferentes para codificar la señal. WP puede iterar no solo la salida del filtro de paso bajo a través de un filtrado adicional, sino también el filtro de paso alto. Esta capacidad de iterar las salidas a través de filtros de paso alto significa que el WP permite más funciones de descomposición (paquetes) a una escala dada. El nivel superior del árbol WP es la representación temporal de la señal. Cada subnivel de descomposición produce un aumento en la compensación en la resolución tiempo frecuencia; así, el nivel inferior en la descomposición WP es la representación en frecuencia de la señal. El análisis WP puede proporcionar una resolución de frecuencia más precisa que el análisis Wavelet. La Figura 1 muestra una descomposición WP en tres niveles de la señal, cada subnivel lo conforman nodos que contienen los coeficientes de la descomposición, así, el nodo (3; 0) representa el primer nodo de la descomposición en el tercer subnivel.
Una WP es obtenida mediante (1) y (2) dados en [9], donde es denominada Wavelet madre, i es el parámetro de modulación, j es el parámetro de dilación, k es el parámetro de traslación, y los filtros discretos h(k) y g(k) también llamados filtros ortogonales conjugados, están asociados con la función de escala y Wavelet madre.
Los coeficientes Wavelet correspondiente a la señal x(t) pueden ser obtenido mediante (3) y los componentes WP a un nodo particular puede ser obtenido mediante (4).
Los coeficientes derivados de la descomposición Wavelet son demasiado largos para ser usados como características para su clasificación; en el presente trabajo se emplearon funciones estadísticas para caracterizar los coeficientes Wavelet en cada uno de los subniveles de descomposición de nuestro interés.
2.2. Extracción de características
Un conjunto de funciones estadísticas que se han empleado en la literatura para el análisis de señales EEG en sistemas BCI, han sido seleccionadas para extraer la matriz característica X[n] sobre la cual se entrenará el clasificador. Estas medidas estadísticas se consideran para extraer la matriz de espacio de características X[n] que servirá de entrada a los algoritmos de clasificación SVM, KNN y LDA.
2.2.1. Coeficiente de variación
La media (μ), la desviación estándar (σ) y el coeficiente de variación (CV) son frecuentemente usadas como características cuando la amplitud de una señal EEG es empleada en su análisis [13] y [14]. El coeficiente de variación para una señal está definido como en (5):
donde,
CV permite comparar el nivel de dispersión de la variación de la amplitud de la señal [13]. En nuestro estudio se calcularán valores de CV de los nodos (5; 2), (5; 3) y (5; 4) al quinto nivel de descomposición Wavelet.
2.2.2. Energía relativa
Con el algoritmo de descomposición WT se obtiene un conjunto de coeficientes para cada nodo, dentro del n-esimó nivel de descomposición. A partir de estos coeficientes es posible calcular la energía relativa para cada nivel (1,..., n). La energía relativa para j-esimó nivel de descomposición se define como (7), y es utilizado para extraer información útil de la señal sobre el proceso en estudio [15] y [16].
Ej está dada como en (8).
2.2.2. Varianza
La varianza (VAR) de los coeficientes WP es calculada como el promedio del cuadrado de la desviación estándar de la señal y está definida como en (9).
2.2.2. Potencia espectral (PSD)
La potencia espectral ha sido ampliamente usada para el análisis de señales EEG, como en [17] y representa la potencia de una señal distribuida en frecuencia, y se obtiene como la Transformada de Fourier de la función de autorrelación de la señal x(t), dada mediante (10), donde fs es la frecuencia de muestreo de la señal, n el número de muestras y DFFT es la Transformada discreta de Fourier de la señal.
2.3. Reducción de características mediante entropía difusa
En el enfoque probabilístico, la entropía de Shannon es una medida bien conocida de la incertidumbre y se cubre ampliamente en la literatura [19]. Una extensión de la entropía de Shannon es el concepto de entropía difusa, en la que los conjuntos difusos se utilizan para ayudar a la estimación de la entropía. La entropía difusa se diferencia de la entropía de Shannon clásica en cuanto la entropía difusa contiene incertidumbres difusas (posibilista), mientras que la entropía de Shannon contiene incertidumbres con aleatoriedad (probabilística).
La entropía difusa, al igual que la entropía de Shannon satisface los cuatro axiomas de De LucaTermini [18]. La entropía de Shannon se define a partir de una variable aleatoria discreta (x) con función de probabilidad p(xi), dada por (11).
A partir de la entropía de Shannon, Khushaba, et al. [19] define la entropía difusa conjunta de los elementos de la clase i, denotada como H(f, ci), dada por (12), donde P (f, ci) puede ser interpretada como el grado en que la muestra predefinida para pertenecer a la clase i, realmente contribuye a esa clase específica.
La entropía difusa completa a lo largo de las c-clases está dada por (13):
El equivalente difuso para la probabilidad conjunta de los patrones de entrenamiento que pertenecen a la clase i, está dado por (14).
donde Ai es el conjunto de índices de los patrones de entrenamiento que pertenecen a la clase i, N P es el numeró total de patrones, y ik es el k-esimó valor de membresía difusa perteneciente a la clase i.
3. Marco experimental
En este trabajo hemos utilizado los datos recogidos durante experimentos de BCI en línea, y se han analizados como se describe en esta sección.
3.1. Base de datos
El conjunto de datos que se utilizó para la caracterización de patrones usando el método propuesto fue BCI Competition 2008 - Graz dataset 2b, proporcionado por el Departamento de Informática Médica, Instituto de Ingeniería Biomédica de la Universidad de Tecnología de Graz [8].
Esta base de datos consiste de información EEG de nueve sujetos estudiados en [20]. Los pacientes son diestros, poseen visión normal y se les pagó por participar en el experimento. Todos los voluntarios se sentaron en una silla mirando una pantalla ubicada aproximadamente a un metro de distancia al nivel de los ojos. Se proporcionaron cinco sesiones a cada paciente, las dos primeras contienen información de entrenamiento sin realimentación y las últimas tres sesiones fueron registradas con retroalimentación.
Se registró la información proveniente de tres canales (C3, Cz, and C4) con una frecuencia de muestreo de 250 Hz. Las grabaciones tuvieron un rango dinámico de 100 V para la proyección, y 50 V para la retroalimentación. Los registros fueron transportados por un filtro pasabanda entre 0.5 Hz y 100 Hz, con filtro de corte en 50Hz. La colocación de los electrodos bipolares (distancia larga o corta, mayor o menor posición anterior y posterior) fue ligeramente diferente para cada voluntario.
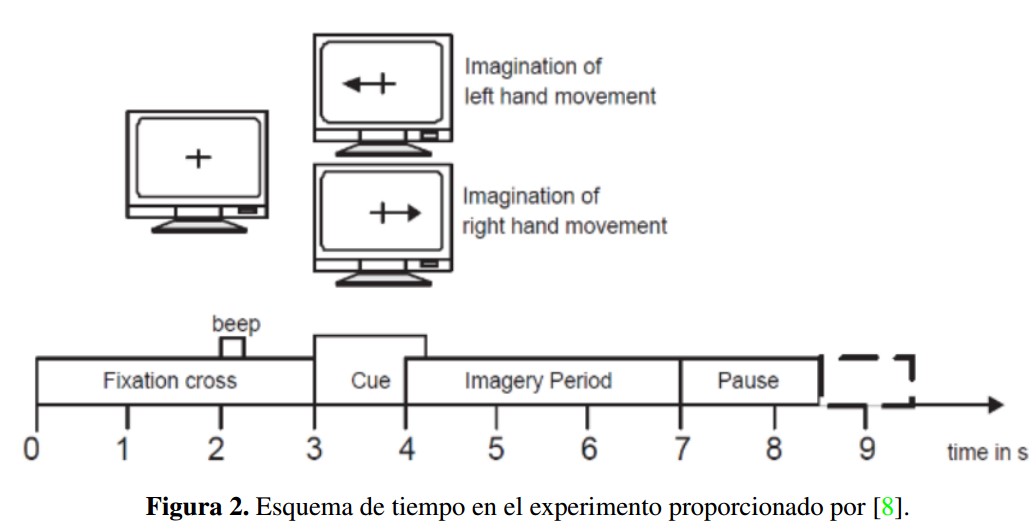
El experimento, representado mediante la Figura 2 consiste en dos clases denominadas imaginación motora (MI) de la mano izquierda (clase 1) y mano derecha (clase 2). Cada sujeto participó en dos sesiones de grabación sin realimentación registrada en dos días diferentes dentro de dos semanas. Cada sesión consistió en seis ejecuciones con diez ensayos cada uno y dos clases de imágenes. En total se hicieron 20 ensayos por ejecución y 120 ensayos por sesión. Los datos de 120 repeticiones de cada clase MI estaban disponibles para cada persona en total. Antes del entrenamiento de la primera imaginación de movimiento, el sujeto imaginó y ejecutó movimientos para cada parte del cuerpo y seleccionó la que podía imaginar mejor (por ejemplo, apretar una pelota o tirar de un freno).
Cada ensayo se inició con una señal fijada en pantalla en forma de cruz y un tono corto de advertencia acústica (1 kHz, 70 ms). Luego, una señal visual (una flecha que apunta hacia la izquierda o hacia la derecha, según la clase solicitada) se presentó durante 1,25 segundos. Después, a los pacientes les correspondía imaginar el movimiento de la mano correspondiente durante un periodo de cuatro segundos. Cada ensayo fue seguido de un breve descanso de al menos 1,5 segundos. Se añadió un tiempo aleatorio de hasta un segundo para evitar la ruptura de la adaptación.
Para las tres sesiones siguientes con retroalimentación se registraron cuatro ejecuciones, en las que cada serie constaba de veinte ensayos para cada tipo de imaginación de movimiento. Al comienzo de cada prueba (segundo 0) la retroalimentación en pantalla de un "smiley" gris (representación de una cara sonriente) se centró en la pantalla. En el segundo 2, se emitió un pitido corto de advertencia (1 kHz, 70 ms). La señal se presentó desde el segundo 3 al 7,5. Dependiendo de la señal, los sujetos estaban obligados a mover el "smiley" hacia el lado izquierdo o derecho imaginando movimientos de mano izquierda o derecha, respectivamente. Durante el periodo de retroalimentación el "smiley" cambió a verde cuando se movió en la dirección correcta, de lo contrario se convirtió en rojo.
3.2. Experimentos
Como primera instancia, seleccionamos los registros de las sesiones de entrenamiento aportados en [8]; Seleccionamos los datos registrados durante el periodo de imaginación motora, comprendido entre los tiempos de 4 a 7 segundos. Con base en ellos, aplicamos la Transformada Wavelet Packet (WP) para cada canal (C3, Cz y C4) en cada una de sesiones de ejecución para cada sujeto, usando cinco niveles de descomposición y Daubechies44 como Wavelet madre, que ha demostrado ser eficaz para muchos métodos de procesamiento de bioseñales basado en su semejanza [21].
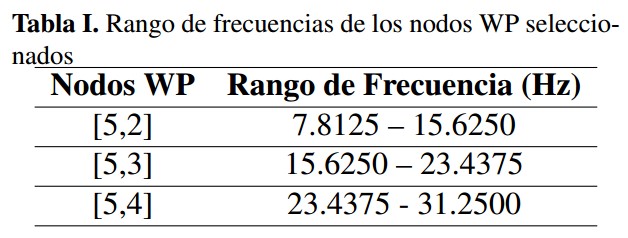
Una descomposición WP a cinco niveles permite obtener en ese nivel 32 nodos que corresponden a rangos de frecuencia comprendidos entre [07.8125], [7.812515.6250], ... , [242.1875250]. En nuestro estudio, seleccionamos los nodos WP mostradas en la Tabla I, teniendo en cuenta que las tareas de imaginación motora están asociadas con los ritmos de importancia clínica μ (8-13 Hz) y β (13-30 Hz) medidos sobre la corteza sensoriomotora [22]-[24].
A fin de caracterizar los ritmos cerebrales y representar la distribución de la frecuencia y la cantidad de cambios en ella, se calcularon funciones estadísticas ampliamente utilizadas en tareas de imaginación motora, sobre los coeficientes arrojados por la descomposición WP para cada nodo; estas son: Energía Relativa Wavelet (EneR), Varianza (Var), Desviación estándar (Std), Valor medio (Med), Coeficiente de variación (CV), Máximo pico PSD (MaxPSD) y Varianza de PSD (VarPSD).
En total se obtuvo un numeró de 63 características correspondientes a siete funciones evaluadas en los coeficientes WP asociados a los tres nodos de interés y tres canales C3, Cz y C4; Este conjunto de datos conforma el vector de características extraídas en cada ejecución X[n].
Usando la función fuzzy cmeans propuesta en [25], construimos los valores de membresía difusos ik para cada una de las características obtenidas en el conjunto de datos; cada una de estas refleja el grado de pertenencia de la muestra para cada una de las dos clases.
Combinando los valores de membresía ik obtenidos y las ecuaciones (4), (5) y (6), se calculó la entropía difusa sobre el espacio de características específicas. Un valor alto de entropía contribuye poco a la desviación entre las clases y los valores de entropía bajos presentan características más informativas. Así se logrará incrementar el resultado de precisión en la clasificación de los patrones de pensamiento injeridos en el presente trabajo.
El vector resultante de veintiún características fue entrenado y clasificado usando clasificadores KNN para cinco vecinos, máquinas de vector de soporte (SVM) con kernel lineal y Análisis discriminante lineal (LDA); asimismo, se evaluó el resultado mediante el criterio validación cruzada de diez pliegues (10cross validation), dividiendo aleatoriamente en diez las muestras, de tal manera que un subconjunto es usado como datos de prueba y los nueve subconjuntos restantes son usados como datos de entrenamiento, proceso que se realiza mediante diez iteraciones; finalmente se calcula el promedio de los resultados en cada iteración. La ejecución de los algoritmos se realizó sobre un PC de 64 bits con procesador Intel i5 de 2.8 GHz y 6 GB de RAM.
3.3. Resultados y discusiones
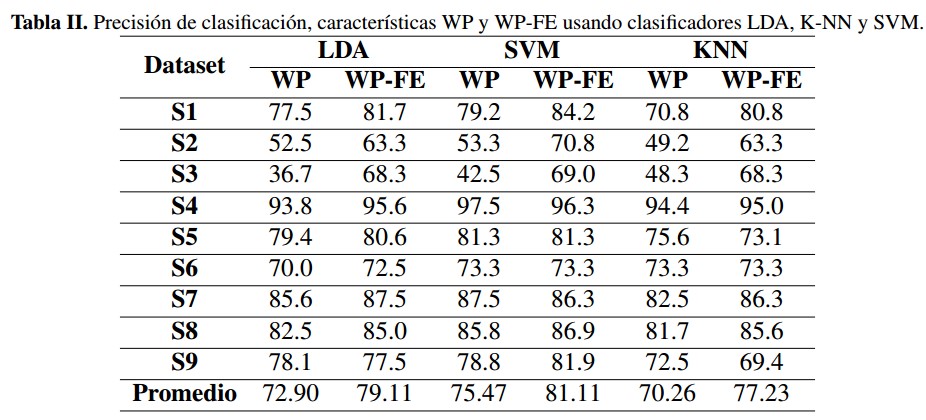
La Tabla II muestra los resultados de la mejor clasificación obtenida por sujeto, usando clasificadores LDA, KN N 5, y SV M. Estos resultados fueron evaluados sobre todas las 63 características del vector X[n], producto de la descomposición Wavelet Packet (WP), y sobre las veintiuna características más relevantes de acuerdo al algoritmo de entropía difusa ejecutado sobre el vector X[n] para reducir la dimensionalidad (WPFE). Se puede observar que la reducción de la dimensionalidad del vector característico produce un notorio incremento en la precisión de clasificación. El algoritmo de entropía difusa discrimina y selecciona las características con mayor contenido de información, logrando un conjunto de características relevantes que mejora la región de decisión de separabilidad para la tarea de clasificación. Asimismo, se observa que los clasificadores lineales SV M y LDA presentan mejores resultados de precisión respecto a KN N; se podría pensar que la frontera de decisión óptima es aproximadamente lineal.
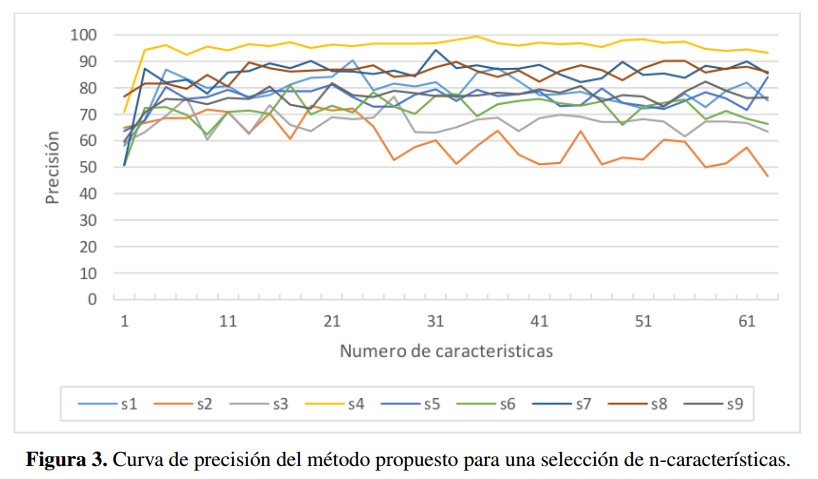
La Figura 3 muestra la precisión de clasificación del algoritmo WPFE en función del numeró de características elegidas en cada ejecución. Como se observa, la mejor precisión siempre fue observada en el sujeto 4, y haciendo un análisis cuantitativo de los promedios en cada ejecución, se encontró que el menor numeró de características que mejor entrega resultados de precisión es 21. Este valor fue el numeró de características más relevantes en nuestro algoritmo y nos permite reducir a la tercera parte el vector de características inicial, lo que puede traducirse en menor costo computacional durante la clasificación del conjunto de datos, pues al ejecutar los dos algoritmos encontramos que el tiempo de ejecución se reduce en un 14 %.
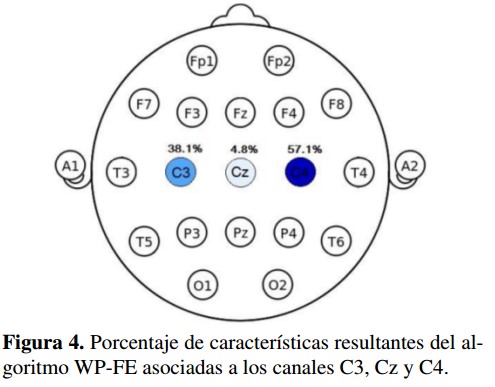
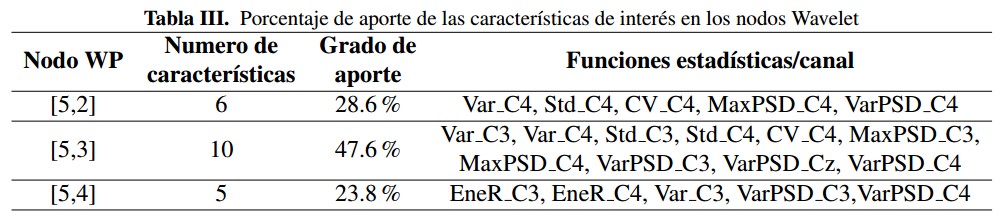
Un análisis de las características más relevantes seleccionadas a partir del algoritmo WPFE, detalla que los coeficientes Wavelet extraídos del nodo [5,3] presentan la mayor concentración de características, asociadas a los ritmos beta (β), como lo muestra la Tabla III. Es de verse también que las funciones aportadas por la potencia espectral y la varianza de los coeficientes entregan el mayor contenido de información en el vector característico final. Puede observarse en la figura 4 que esta discriminación de características proviene principalmente de los canales C3 y C4; el canal Cz aporta un mínimo contenido de información.
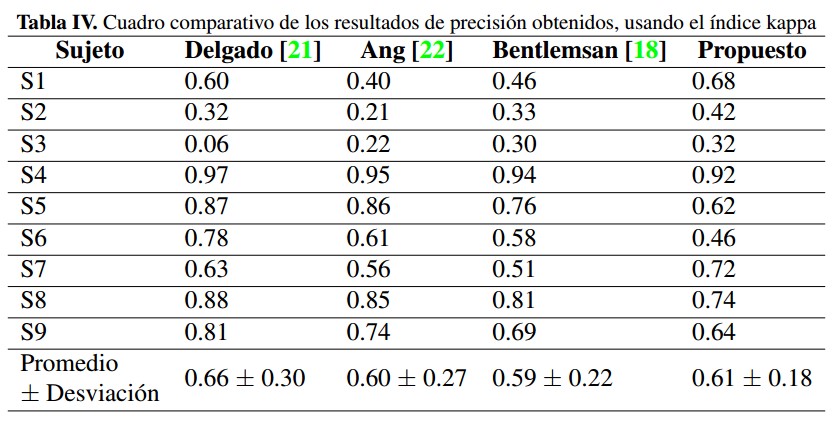
En este estudio, usamos el criterio kappa como medida para determinar el grado de concordancia de las observaciones y se compararon con resultados obtenidos por otros autores. Dichos resultados son mostrados en la Tabla IV.
Se puede observar que el valor medio del índice obtenido entre los sujetos en nuestro método se encuentra por encima de 0.6, valoración considerada de buena concordancia de acuerdo a [31] y [32], y aun así, presentan menor dispersión que los resultados obtenidos por los demás autores.
4. Conclusiones
En este trabajo se propuso un enfoque de caracterización de señales EEG para la imaginación de movimiento de la mano derecha e izquierda, basados en Wavelet Packet y entropía difusa. Esta técnica beneficia la extracción de información alrededor de los ritmos de importancia clínica y debido a su capacidad multiresolución y resolución espectral precisa.
El uso de funciones estadísticas específicas evaluadas en los coeficientes de cada nodo WP seleccionado permitió la extracción de características de interés asociadas a componentes en amplitud y frecuencia de los mismos. El algoritmo de entropía difusa ayudó a seleccionar características de relevancia y reducir el espacio de dimensionalidad, con lo que se pudo incrementar la precisión de clasificación respecto al numeró inicial de características y lograr una reducción del costo computacional.
Los resultados obtenidos muestran que las características basadas en PSD y varianza pueden proporcionar un valor de relevancia mayor que las otras características analizadas. Además, nuestro enfoque muestra que los canales C3 y C4 producen mayor actividad de imaginación de movimiento de la mano derecha e izquierda que el canal Cz.
Del trabajo realizado podemos inferir que la discriminación mediante clasificador SVM ha tenido estadísticamente resultados sustanciales para tenerlos en cuenta en futuros trabajos de caracterización de señales EEG en imaginación de movimiento de las manos derecha e izquierda, orientados al desarrollo de sistemas automatizados BCI. Como trabajo futuro se pretenden analizar otras metodologías de caracterización de patrones basado en combinaciones Wavelet y descomposición empírica, así como explorar otras funciones estadísticas que se identifiquen con las características no estacionarias de este tipo de señales,˜ buscando mejorar los resultados obtenidos y puedan ser aplicados en sistemas BCI orientados a personas con discapacidad motriz.
Referencias
[1] T. M. Vaughan, "Guest editorial braincomputer interface technology: a review of the second international meeting". IEEE Transactions on Neural Systems and Rehabilitation Engineering, Volumen 11, Numeró 2, 2003, pp. 94- 109."227
[2] J. Wang, G. Xu, L. Wang, and H. Zhang, "Feature extraction of brain computer interface based on improved multivariate adaptive autoregressive models". 2010 3rd International Conference on Biomedical Engineering and Informatics, 2010, 895-898. "227
[3] D. CrozBaron, J. M. Ramírez, M. Baker, V. AlarconAquino and O. Carrera, "A BCI motor imagery experiment based on parametricfeature extraction and Fisher Criterion". CONIELECOMP 2012, 22nd International Conference on Electrical Communications and Computers, 2012, 257-261. "227
[4] C. Chen, W. Song, J. Zhang, Z. Hu and H. Xu, "An Adaptive Feature Extraction Method for MotorImagery BCI Systems". 2010 International Conference on Computational Intelligence and Security, 2010, 275-279."227
[5] D. Hu, W. Li, and X. Chen, "Feature extraction of motor imagery EEG signals based on Wavelet Packet decomposition". The2011IEEE/ICMEInternationalConferenceonComplexMedicalEngineering, 2011, 694-697. "227
[6] L. Zou, X. Wang, G. Shi, and Z. Ma, "EEG feature extraction and pattern classification based on motor imagery in braincomputer interface". 9th IEEE International Conference on Cognitive Informatics (ICCI0010), 2010, 536- 541."227
[7] J. Kevric and A. Subasi, "Comparison of signal decomposition methods in classification of EEG signals for motorimagery BCI system". Elsevier, Biomedical Signal Processing and Control, volumen 31, 2017, 398406."227
[8] Pfurstcheller G. et. al. BCI competition 2008, Graz Data Set 2b. [En línea]. Disponible en: http://www.bbci.de/competition/iv/"228, 231, 232, 233
[9] S. Mallat, "A theory for multiresolution signal decomposition: The wavelet representation". IEEE Trans. Pattern Anal. Machine Intell, vol. 11, pp. 674693, 1989. "228, 229
[10] I. Daubechies, "Orthonormal bases of compactly supported wavelets". Commun. Pure Appl. Math., vol. XLI, pp. 909996, 1988."228
[11] R. R. Coifman, Y. Meyer, S. R. Quake, and M. V. Wickerhauser, "Signal Processing and Compression with Wavelet Packets". Prog. Wavelet Anal. Appl., pp. 77-93, 1993. "228
[12] M. Akay, "Wavelet applications in medicine". IEEE Spectrum, vol. 34, no. 5, pp. 50-56, May 1997. "228
[13] Y.U. Khan, J. Gotman, "Wavelet based automatic seizure detection in intracerebral electroencephalogram, Clin". Neurophysiol, Volumen 114, numeró 5, 2003, 898-908. "229, 230
[14] D. Deng, "Fatigue Detection of Drivers Based on Electroencephalograph". International Conference on Industrial Informatics, IEEE. 2016. "229
[15] G. Garg, V. Singh, J. R. P. Gupta, and A. P. Mittal, "Wrapper based wavelet feature optimization for EEG signals". Biomed. Eng. Lett., vol. 2, no. 1, pp. 24-37, 2012. "230
[16] L. Shaw and A. Routray, "Statistical features extraction for multivariate pattern analysis in meditation EEG using PCA". 2016 IEEE EMBS International Student Conference (ISC), Ottawa, 2016."230
[17] L. Sun and Z. R. Feng, C¸lassification of imagery motor EEG data with wavelet denoising and features selection". 2016 International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Jeju, 2016, pp. 184188. "230
[18] A. De Luca and S. Termini, "A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory". Inf. Control, volumen 20, numeró 4, 1972, 301-312."231, 236
[19] RN.Khushaba, A. AlJumaily,A.AlAni".Novel feature extraction method based on fuzzy entropy and Wavelet Packet transform for myoelectric Control". 2007 Int Symp Commun Inf Technol, 2007, 352-357."230, 231
[20] R. Leeb, F. Lee, C. Keinrath, R. Scherer, H. Bischof, G. Pfurtscheller. "Braincomputer communication: motivation, aim, and impact of exploring a virtual apartment". IEEE Transactions on Neural Systems and Rehabilitation Engineering, volumen 15, 2007, 473-482."231
[21] J. Rafiee, M.A. Rafiee, N. Prause, M.P. Schoen, "Wavelet basis functions in biomedical signal processing". Expert Systems with Applications, Volumen 38, 2011, 6190-6201. "233, 236
[22] H. Zhang, C. Guan, K.K. Ang, C. Wang, "BCI competition IVdata set I: learning discriminative patterns for selfpaced eegbased motor imagery detection". Front. Neurosci. Volumen 6, 2012. "233, 236
[23] R. Leeb, F. Lee, C. Keinrath, R. Scherer, H. Bischof, G. Pfurtscheller, "Brain computer communication: motivation, aim, and impact of exploring a virtual apartment". IEEE Trans. Neural Syst. Rehab. Eng. Volumen 15, numeró 4, 2007, 473482. "233
[24] G. Pfurtscheller, C. Brunner, A. Schlogl, F.L. da Silvab, "Mu rhythm (de) synchronization and EEG singletrial classification of different motor imagery tasks". Neuroimage, Volumen 31, numeró 11, 2006, 153-159. "233
[25] B. Medina & L. Duque, "Fuzzy entropy relevance analysis in DWT and EMD for BCI motor imagery applications". Revista de Ingeniería, Volumen 20, numeró 15, 2015, 919. "233
[26] Maouia Bentlemsan, et al., "Random Forest and Filter Bank Common Spatial Patterns for EEGBased Motor Imagery Classification". 2014 Fifth International Conference on Intelligent Systems, Modelling and Simulation. 2014, 235238.
[27] Xiaojing Guo, et. al. "Envelope detection based on online ICA algorithm and its application to motor imagery classification". 6th Annual International IEEE EMBS Conference on Neural Engineering, 2013, 10581061."
[28] SeungHyeon Oh, YuRi Lee, and HyoungNam Kim. "A Novel EEG Feature Extraction Method Using Hjorth Parameter". International Journal of Electronics and Electrical Engineering, Volumen 2, numeró 2, 2014, 106 110.
[29] J. Delgado Saa, M. C¸etin. "A latent discriminative modelbased approach for classification of imaginary motor tasks from eeg data", J. Neural Eng. Volumen 9, Numeró 2, 2012.
[30] K. K. Ang, Z. Y. Chin, Ch. Wang, C. Guan and H. Zhang. "Filter bank common spatial pattern algorithm on BCI competition IV Datasets 2a and 2b". Frontiers in Neuroscience, Volumen 6, 2012.
[31] JR. Landis and GG. Koch. "The measurement of observer agreement for categorical data". Biometrics 33:159174, 1977 . 235
[32] D. Coppieters't Wallant, V. Muto, G. Gaggioni, M. Jaspar, S.L. Chellappa, C. Meyer & C. Phillips. "Automatic artifacts and arousals detection in wholenight sleep EEG recordings". Journal of neuroscience methods, 258, 124133, 2016."236
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.


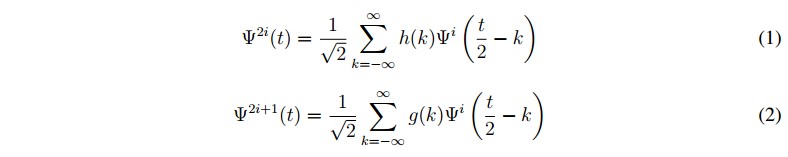
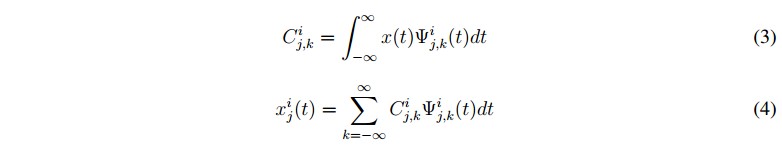
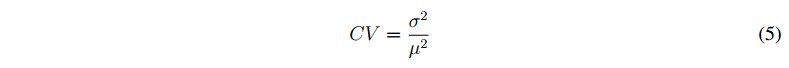
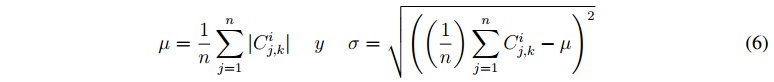
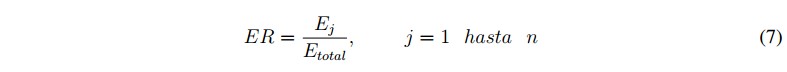
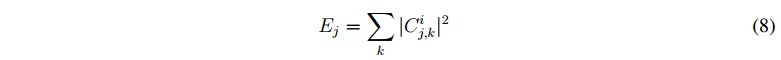
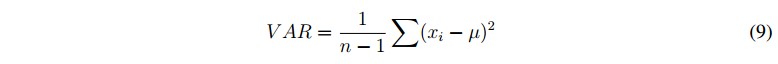
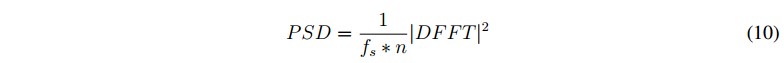
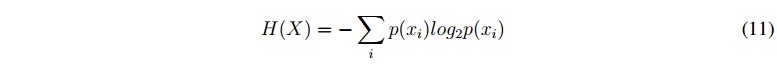
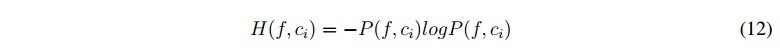
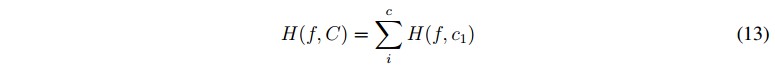
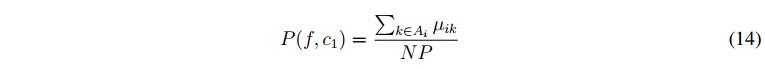


2.jpg)