DOI:
https://doi.org/10.14483/23448393.2708Published:
2000-11-30Issue:
Vol. 6 No. 2 (2001): July - DecemberSection:
Science, research, academia and developmentLas fuentes de voz en las redes de banda ancha ATM
Keywords:
ráfaga, grupo, multiplexor estadístico, fuentes de voz ON-OFF, ATM (es).Downloads
References
Recomendación G.721 de la UIT.
Recomendación G.729 de la UIT.
Yin N. and Hichyj Michael G., "Simple Model for Statisticlly Multiplexed Data Traffic in Cell Relay Networks" Motorola Codex, 1998 IEEE.
CCITT Rec I.362 B-ISDN ATM Adaptation Layer (AAL) functional description. Geneva 1991.
Falkner Matt. , Modeling ATM Networks with COMNET III, Version, 1.0, 1996.
Kuo Geng-Sheng and Ko Po-Chang, "Achieving Minimun Slice Loss for Real-Time MPEG-2-Based Video Networking in a FlowOriented Input-Queued ATM Switching Router System" IEEE Communications Magazine, 1999.
Schwartz, Mischa, Broadband Integrated Networks, Prentice Hall., PTR, 1996.
Stern, T.E., "A Queuering Analysis of Packets Voice", IEEE Globecom 83, San Diego ,CA., 1983: 2.5.1-2.5.6
Daigle, J.N. , J.D. Dangfort, "Models for Analysis of Packets Voice Communications Systems", IEEE JSAC, SAC-4, 6 (Sept. 1986): 847-855.
Maglaris, B. "Perfomance Models of Statistical Multiplexing in Packet Video Communications", IEEE Trans. on Commun., 36,7 (Julio del 88): 834-844
Poveda Zafra, José N. "Modelamiento de la red de núcleo ATM", memoria de Maestría en Teleinformática, Universidad Distrital, 2001.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2001-00-00 vol:6 nro:2 pág:88-93
Las fuentes de voz en las redes de banda ancha ATM
José Noé Poveda Zafra
Álvaro Betancourt Uscátegui
Resumen
El modelamiento de las fuentes de voz en las redes telemáticas utiliza procesos matemáticos cada día mas elaborados. Desde las ineficientes colas con tasa de servicio constante hasta los eficientes grupos de arribos de Poisson (ráfagas) que involucran múltiples celdas. El costo de la eficiencia se remite a la rigurosa formulación matemática en los modelos de los diferentes parámetros que presentan la red ATM, tales como la distribución de la longitud de las colas, la probabilidad de pérdida de celdas y la distribución de retardos tanto de celda como el de ráfaga. Además las fuentes de voz pueden ser agrupadas y multiplexadas bajo el esquema de habla y de silencio ( ON-OFF ) que involucran una conversación con parámetros como: la tasa pico, la tasa promedio y la tasa mínima de la fuente de voz. El artículo centra su atención en la utilización eficiente del ancho de banda en las redes de banda ancha basada en las fuentes multiplexadas y fuentes fluídas de voz.
Palabras clave: ráfaga, grupo, multiplexor estadístico, fuentes de voz ON-OFF, ATM.
Abstract
Modeling voice sources in telematic networks requires increasingly complex mathematical processes. The corresponding models range from simple constant bit rate models to more elaborated Poisson batch arrivals models. In search of efficient resource utilization, we need rigorous mathematical formulation of models that involve different ATM parameters such as length distribution, cell loss probability, cell delay distribution and burst delay distribution. Furthermore, grouping and multiplexing voice cells according to the ON-OFF pattern of a voice conversation require additional parameters such as peak, average and minimum cells rate. This paper focuses on efficient bandwith utilization on an ATM broadband network by multiplexing fluid flow voice sources.
Key words: burst, batch, statistically multiplexed, ON-OFF source voice, ATM.
I. INTRODUCCIÓN
En las redes telefónicas las señales de voz son análogas en su origen, luego requiere de procesos de digitalización, de codificación y de paquetización antes de realizar su transmisión. Existen esquemas eficientes basados en PCM sin degradar la calidad de la voz, como son el PCM diferencial, y el diferencial adaptativo ADPCM[1], voz a 8 Kbps especificado en la recomendación G.729 [2]. Una fuente de voz alterna entre periodos de habla y de silencio, basados en los modelos de fuentes ON-OFF [3]. La administración del tráfico RBC (Tasa de Bit Constante) reserva un ancho de banda constante independiente de si la fuente está en estado activo o en silencio, provocando un uso ineficiente de los recursos de la red. Para mejorar la eficiencia se utilizan detectores de actividad de voz de tal forma que las celdas son generadas únicamente durante los periodos de habla, a través de un esquema VBR (tasa de bit variable), utilizando codificación ADPCM logrando compresiones hasta de 4 a 1, sin degradación significativa de la voz.
Con la utilización de servicios VBR se requiere sincronización extremo-a-extremo entre la fuente y el destino. Este tipo de servicios es soportado por la capa de adaptación AAL2[4] de ATM. La tasa de bits pico es 64 Kbps, donde una celda ATM puede llevar de 5.5 a 5.875 ms de voz[5]. Los períodos de silencio corresponden a un 60-65% del tiempo de transmisión de las conexiones de voz en cada dirección. En promedio los periodos de habla y de silencio tienen una duración entre 352 y 650 ms respectivamente, donde la duración de los períodos de habla sigue aproximadamente una distribución exponencial, mientras que los períodos de silencio se aproximan menos a esta distribución.
Recientemente, mediante la combinación de diferentes clases de servicios se han propuesto nuevos servicios de mayor eficiencia en las redes ATM para fuentes de tiempo real.
El artículo se organiza de la siguiente manera: En la sección II se resume la evolución de los modelos de fuentes de voz. A continuación se centra en el modelo de voz en paquetes soportados matemáticamente. En la sección IV se describe el modelo de fuentes de voz multiplexadas para finalmente en la sección V referimos el modelo de fuentes fluidas de paquetes de voz.
II. MODELOS DE FUENTE DE VOZ
Cuando nacieron las redes telefónicas se desarrollaron modelos que en su tiempo fueron eficientes. La planeación del tráfico fue concebido para voz, aún hoy día es utilizado con el análisis tradicional de Erlang. El cambio continuo en tecnologías y plataformas de las redes evolucionan los modelos de tráfico. Los Erlangs pueden utilizarse en planeación de red de voz, así como en redes de conmutación de circuitos. La norma estadística estándar calcula una estimación de demanda basada en la llegada de la llamada la cual es aleatoria.
Nuevos servicios de voz y video como el RCBR, híbrido que aprovecha las principales ventajas de CBR y VBR se encuentran en estudio y se ha demostrado mayor eficiencia en el uso del ancho de banda respecto a los servicios intrínsicos de ATM[6].
III. MODELO DE FUENTES DE VOZ EN PAQUETES
La digitalización, codificación y paquetización de la voz, junto a los detectores del habla que evitan paquetizar los períodos de silencio, es una tecnología que genera modelos de tráfico diferentes a los modelos tradicionales de voz.
Los modelos de fuentes de voz de paquetes [7], tienen parámetros λ y α que representan la tasa de transición de silencio y habla respectivamente como se muestra en la figura 1. Los períodos de silencio se aproximan a una distribución exponencial para este tipo de tráfico.
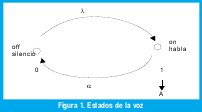
En los procesos de Poisson interrumpidos (PPI), se alternan entre períodos de silencio y de actividad, con distribuciones exponencialmente distribuídas y mutuamente independientes, así durante el tiempo de habla los tiempos entre arribos de paquetes conforman un proceso de Poisson, mientras que en los periodos de silencio no se generan paquetes.
Si α y λ son las tasas de transición de habla y de silencio respectivamente y 1/σA , y 1/σS las duraciones promedio de dichos periodos, tenemos que las funciones de distribución de los períodos de habla, silencio y el tiempo entre arribos de celdas son:
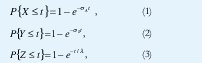
Adicionalmente πA y πS denotan los dos estados del proceso Markoviano on-off, y están representados por:

Al tomar a ø(s) como la transformada de Laplace del tiempo entre arribos de celdas y considerando el proceso 'on-off' justo antes del arribo de un paquete, el tiempo hasta el próximo evento es el mínimo entre X,Y. El evento es un arribo con probabilidad λ(λ + σA ) y corresponde al cambio de un estado de habla a un estado de silencio con probabilidad &sgma;A (λ + σA) , El mínimo está distribuido exponencialmente con tasa (λ + σA) y al final del periodo de silencio el proceso se repite,
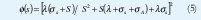
donde sus dos primeros momentos del tiempo entre arribos de paquetes son:
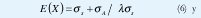
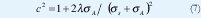
Un proceso PPI con parámetros (σs, &sugma;A, λ) es equivalente a una distribución hiperexponencial con parámetros ( p1 , µ1 , p2 , µ 2 ).
Otra forma de modelos de voz es la basada en el Proceso de Bernoulli Interrumpido (PIB), que es la versión discreta del (PPI), donde cada ranura de tiempo es igual al tiempo de celda en el medio y puede corresponder a un período de silencio o de habla. Una ranura en estado de habla (activo) contiene celdas con probabilidad α, y no contiene celdas con probabilidad ( 1 - α ), mientras que en estado de silencio no arriben celdas. Dada una ranura en estado de habla, la siguiente ranura permanece en estado de habla con una probabilidad p , y cambia a un estado de silencio con probabilidad (1-p). Análogamente permanece en un estado de silencio con probabilidad q, y cambia a un estado de habla con probabilidad (1-q). Por tal razón, ambos períodos están distribuidos geométricamente:
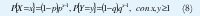
y la probabilidad de estado estable de estar en habla o en silencio está dada por:
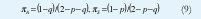
Tanto la media, la varianza como los momentos de tiempos entre arribos, pueden ser obtenidos a partir de la transformada Z del PIB así:
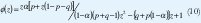
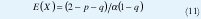
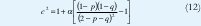
La probabilidad de que una ranura contenga una celda, definida como la utilización de la fuente es:
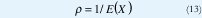
Si se asume que una ranura en estado de habla siempre contiene una celda, α = 1 , las ecuaciones se reducen a:
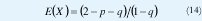
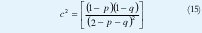
Los parámetros de (PIB) que satisfacen esas métricas no pueden ser obtenidos directamente de los momentos, siendo necesario utilizar algoritmos específicos para ser estimados[8]. El algoritmo busca la diferencia mínima entre el tercer momento de la distribución y el (PIB) con los parámetros estimados.
IV. MODELO DE FUENTES DE VOZ MULTIPLEXADAS
La composición del modelo para cada N fuentes de voz multiplexadas [9] puede ser hallado con sencillez, en el cual se presentan N fuentes en el "buffer" de acceso a la red. Cada fuente genera V cel/ seg en sus períodos de habla. Dadas las ventajas de la multiplexación estadística, la capacidad del enlace de salida en la red, puede ser menor que el máximo número de N*V cel/seg que pueden ser generadas. Lo anterior es suficiente para obtener la capacidad del enlace VC cel/seg, en donde C es un parámetro adimensional. En la multiplexación estadística C < N, pero cuanto menor?. Puede extenderse dado que la velocidad promedio de generación de celdas es VN / ( + ) . El parámetro C debe satisfacer el límite inferior de la desigualdad dada por:
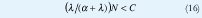
Para un 'buffer' infinito, esto representa la condición de estabilidad. Al dividir la anterior desigualdad por C, se define la utilización ρ así:
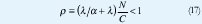
En los sistemas telefónicos analógicos para empaquetar múltiples llamadas de un pequeño número de circuitos telefónicos (trunks) se utiliza una técnica denominada sistema de interpolación del habla de tiempos asignados (TASI). Para los sistemas telefónicos digitales se utiliza la técnica llamada interpolación de voz digital (DSI).
Por ejemplo, si (λ/α + λ ) = 0.4 con un TASI en 2.5; C puede ser tan grande como 0.4N, por tanto ρ = 0.4 N / C . Para un ancho de banda de 1.272 Mbps caben 3000 cel/seg en un puerto de acceso ATM. Si cada fuente de voz en sus periodos de habla tiene una velocidad de generación de voz de V = 170 Cel/seg, entonces C = 3000/170 = 17,6. En este sistema se podrían acomodar entre 18 y (2.5*18) 45 usuarios.
Este modelo de paquetes de voz multiplexados, es interesante para hallar el desempeño y el diseño de los parámetros como la ocupación estadística de los 'buffers', la estadística de retardos (requeridos en para voz con QoS) y el tamaño de los "buffers" necesarios para asegurar una aceptable pérdida de celdas. En la figura 2 se muestran fuentes multiplexadas de dos estados. Estas fuentes están a la entrada del multiplexor con N-1 fuentes de la misma naturaleza. El modelo nacimiento-muerte del N+1 estado, representa el número de fuentes activas. Por ejemplo, en el estado i, las fuentes se activan y la tasa promedio de liberación de celdas al "buffer" es iV cel/seg. Para dos estados i, Ju representa el estado inicial de carga de la fuente K < N, y Jo es el estado final de carga de la fuente. Para el ejemplo anterior, con C = 17.6, los valores para C en el estado Ju = [C] = 17, y para Jo = [C] = 18 .
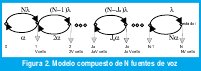
Cuando i>C el tráfico de la fuente causa que la cola esté llena y lo representa Ju, se dice que el sistema está en 'underload'. Cuando i<C la cola tiende a desocuparse, lo representa Jo y se dice que el sistema está en 'overload' y la tasa de carga de la cola en el estado i es V(C-i) cel/seg.
La probabilidad de que esté en estado permanente πi que la compone el estado i, es fácilmente descrita por la probabilidad de que i de N fuentes de dos estados estén activas (estado de habla), mientras que N-i estén inactivas (silencio). Entonces la probabilidad de que cada fuente esté activa es λ/(λ + α) , y se comporta como probabilidad binomial así:
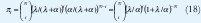
Otro análisis utilizando el esquema de nacimiento-muerte ('birth-death'), que utiliza el estado dependiente, es el proceso general nacimiento-muerte mostrado en la figura 3 que tiene los parámetros &lmabda;i que representan la tasa de transición sobre el estado i al estado i+1, y µi que representa la tasa de transición del estado i al estado i-1, la probabilidad de estado permanente iniciando en el estado i es:

donde π0 se halla de la sumatoria de todos los estados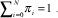 i = 1 .
i = 1 .
Otra representación del proceso nacimiento-muerte tomado de la figura 3 y construyendo una ecuación de balance en cada estado es como sigue:
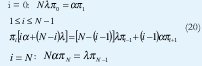
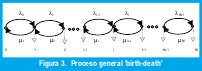
Dado el modelo de un multiplexor estadístico de fuentes de paquetes de voz, una representación analítica de las ecuaciones anteriores, se igualan a cero y se forma un vector π para (N+1) elementos, con valores πi :
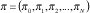
Para una matriz M de (N+1)*( N+1), tal que πM = 0 , la ecuación πM = 0 es un caso especial de la misma ecuación obtenida generalmente por cadena de Markow de tiempo continuo, del cual el proceso nacimiento-muerte, específicamente el modelo de N fuentes de voz multiplexadas es un caso especial. La matriz M representa el envío de tasas de transmisión entre estados con sumatorias de los elementos de fila igual a cero, y es llamada matriz generatriz infinitesimal de la cadena de Markov fundamental. De esta manera se puede calcular el desempeño y el diseño de parámetros tales como retardos, pérdidas estadísticas y tamaño del "buffer" requerido.
La matriz está dada por:
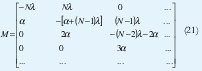
los autores [10] analizaron y compararon tres enfoques. El primero apunta a capturar el proceso de arribo periódico de tasa V de cada fuente y conduce a un modelo de procesos semi-Markov que es analizado basado en el trabajo realizado por Stern[9] en donde se aprecia que el modelo provee concordancia razonable con la simulación. En el segundo Modelo se hace el análisis aproximado de la generación de celdas por una fuente en estado de habla como un proceso de Poisson que produce paquetes exponencialmente distribuidos en longitud. Este es un ejemplo de Procesos de Poisson modulados por Markov (MMPP), que es un sistema fundamental para generar paquetes en tasas de Poisson a la tasa actual de cambio de estado a estado. La transmisión entre estados es gobernada por una cadena fundamental de Markov de tiempo continuo. El tercer modelo asume que cada fuente activa transmite uniformemente información con el enlace de transmisión; el servidor, también opera de la misma manera. Cada fuente es denominada modelo de flujo fluído y es aplicado a una variedad de problemas en comunicaciones de redes así como en otras aplicaciones[9].
V. MODELO DE FUENTES FLUIDAS DE PAQUETES DE VOZ
Con respecto a la figura 3 el período de habla se asume como una generación larga que pareciera un flujo continuo de fluido. Es aplicado así a un multiplexor estadístico. Aprovecha el número de fuentes N y la capacidad V*C es tan grande que no discretiza el 'buffer' debido al arribo y salida de celdas que pueden ser abandonadas[7,8,9]. La ocupación del 'buffer' es una variable aleatoria continua x, para hacer referencia al análisis del flujo fluído. Las unidades de x están definidas por el número arribos de celdas durante el periodo de habla (activo). Una fuente de voz genera celdas a una velocidad de V cel/s. En el período de habla de longitud promedio 1 /α segundos, el promedio incrementa x por V / celdas durante un periodo de habla. Esto es denominado 'unidades de información'. Un sistema con capacidad de CV cels/seg tendrá una capacidad equivalente de VC/(V/α) = αC unidades de información por segundo. El modelo de acceso al 'buffer' con N fuentes de voz multiplexadas, puede ser reemplazado por un modelo basado en fluídos. La ocupación del 'buffer' x es una variable aleatoria que se obtiene estadísticamente.
Se halla en primer lugar la distribución de probabilidad de x, que se obtiene mediante la distribución de ocupación del 'buffer' en unidades de celdas. A continuación se toma l como el estado del 'buffer' en unidades de celdas. Si x es incrementado por V/α celdas durante un período de habla, se obtiene l = xV /α como la conversión apropiada entre unidades de información y celdas. Entonces, la probabilidad P[l > i ] que la ocupación del 'buffer' l exceda algún número i está dada por:
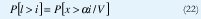
Y P[x > x0]es la probabilidad de que x exceda a x0. A manera de ejemplo, con una taza de celdas generadas de V = 170 cel/seg durante un período de habla. Si el promedio del período de habla tiene una longitud de 1/α = 1.25 seg., V/α = 212.5 cels. En este caso ésta es la unidad de información. Entonces:
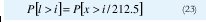
por ejemplo, para i = 1000 celdas
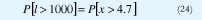
Dada la distribución de x, se toma como la parte inicial del problema el hallar la distribución de celdas del "buffer", asumiendo que el modelo fluído es exacto. Para hallar la distribución de x, el primer acercamiento plantea que si hay i fuentes activas, se están generando iα unidades de información por segundo en el "buffer". El "buffer" al mismo tiempo está vaciando celdas a una tasa de . El "buffer" se está llenando si i>C y se está desocupando si i<C. La diferencia es que ahora la ocupación del 'buffer' x es una variable aleatoria continua [8]. La probabilidad de que la ocupación del "buffer" sea menor o igual a x es:
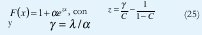
y la probabilidad de que la ocupación del "buffer" exceda a x es (1 - F(x)), siendo la función de distribución de probabilidad complementaria G(x):
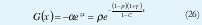
G(x) es llamada la función sobreviviente y es frecuentemente usada como una medida de la probabilidad de pérdida para x grande y el tamaño de la memoria requerida para una probabilidad de pérdida dada. G(x) decrece exponencialmente con x y por ende también el tamaño del buffer (en unidades de información). Luego la probabilidad de ocupación del 'buffer' que podría exceder i celdas puede ahora escribirse como:
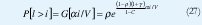
donde ρ es la utilización, dada por
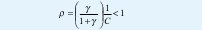
Esta ecuación muestra el tamaño de la tasa V de producir celdas por una capacidad C dada, o el grandor de la probabilidad de sobreflujo. El tamaño del "buffer" i debe incrementarse en proporción a V para mantener la pérdida fija. La probabilidad de sobreflujo se incrementa también con la longitud promedio de los periodos de habla 1/α.
Por ejemplo, al considerar γ= λ /α = 2 / 3 . el factor de actividad de la fuente 1 /α = 1.25 seg. Si se tiene que V = 170 cels/seg para un estándar de 64 Kbps para canales digitales de voz segmentados en celdas de 53 octetos, tendremos que V /α = 212.5 cels. Con una capacidad de transmisión es C = 0.5 dedicada para voz, se tiene que la entrada VC = 85 cels/seg. Entonces con = 0.5 tenemos:
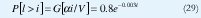
Si la probabilidad de ocupación del 'buffer' excede a i en 10-4 , entonces i = 3000 celdas, lo que sin duda muestra que se trata de un gran 'buffer' para una sola fuente de voz.
Si incrementamos la capacidad de transmisión C=0.8, manteniendo los demás parámetros fijos, con ρ = 0.5 tenemos:
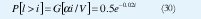
Manteniendo la probabilidad de ocupación del 'buffer' y el tamaño del buffer i, se reduce ahora a 450 celdas. Y muestra la sensibilidad de la probabilidad de sobreflujo para la capacidad de transmisión. El efecto para varias fuentes multiplexadas reduce los recursos y el tamaño requerido para el 'buffer' puede ser menor, dado que la capacidad de transmisión C es dimensionada de acuerdo al número de fuentes multiplexadas. La utilización ρ para varias fuentes, no es más que la extensión ρ para una sola fuente:
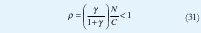
y la probabilidad de que la ocupación del 'buffer' exceda a x es aproximadamente:
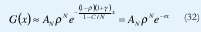
G(x) está deter minado por el parámetro exponencial así como por AN dado explícitamente y por ρN . El término exponencial e-rx de la probabilidad de sobreflujo del "buffer" es independiente del número de fuentes multiplexadas N. Si la capacidad es dimensionada correspondientemente, el pa rámetro r depende solamente de C/N. Obteniendo la probabilidad de G(x) que exceda la sobrecarga del 'buffer' el valor de x (en unidades de información), la probabilidad de que la sobrecarga del buffer no exceda i celdas es:
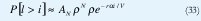
La primera aproximación es que el tamaño del 'buffer' i requerido para mantener la probabilidad de sobreflujo del "buffer" para una probabilidad deseada, es independiente del número de fuentes multiplexadas N, y provee así la capacidad C acordada. El número de buffer por fuente es i/N
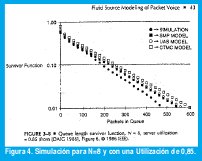
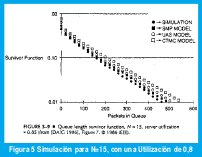
Dailgle y Langford [9] hicieron varios cálculos de flujos fluídos y los compararon con su simulación. Graficaron la probabilidad de sobreflujo del 'buffer' (pérdida) o función de supervivencia, versus el tamaño del buffer i (en celdas), tal como se muestra en las figuras 4 y 5 para N diferentes. El primer modelo denominado UAS (Uniform Arrival and Service). El segundo denominado SMP se basa en el modelo SemiMarkov, uno de los modelos que en la actualidad tiene mayor uso dada su caracterización se aprecia que el modelo provee concordancia razonable con la simulación. Por último, el modelo denominado CTMC correspondiente al Proceso Modulado por Markov. Los modelos estudiados muestran que el modelo de flujo fluído UAS se aproxima más a la simulación que el CTMC para fuentes multiplexadas de voz [12].
Las nuevas formas de modelos de fuentes de voz permiten disminuir los recursos de la red, los anchos de banda y los procesos en los nodos respectivos. Aún se trabaja en nuevos modelos híbridos y algoritmos de compresión para poder llevar las fuentes de voz en anchos de banda más pequeños. Los conceptos anteriores para tráfico de voz, se utilizan en el estudio del modelamiento de la red de núcleo ATM para un operador en particular [13].
VI. CONCLUSIONES
Los modelos de fuentes de voz transportadas en datos están en constante evolución con la tecnología. Las expresiones de grupos de celdas de voz multiplexadas tienen distribuciones acordes con las redes de banda ancha. Las altas velocidades troncales permiten ver al flujo de celdas de voz como un fluído, aspecto que optimiza el procesamiento, haciéndolo en grupos de celdas en lugar del proceso de celda a celda. De esta forma se hacen sencillos los modelos para el tamaño de los "buffers", la distribución de la longitud de la cola, la probabilidad de pérdida y los arribos de grupos de Poisson donde los grupos también tienen una distribución exponencial con respecto al número de celdas y sus estados bajo el esquema "ON-OFF".
Se han presentado los conceptos y formulaciones relacionados con el modelamiento del tráfico de voz para el análisis del desempeño en fuentes multiplexadas bajo esquemas ON-OFF. Se muestran las expresiones que orientan el comportamiento de los diferentes parámetros de dicho tráfico en redes de telecomunicaciones de banda ancha ATM, con el objeto de tener una utilización más eficiente del ancho de banda.
REFERENCIAS BIBLIOGRÁFICAS
[1] Recomendación G.721 de la UIT.
[2] Recomendación G.729 de la UIT.
[3] Yin N. and Hichyj Michael G., "Simple Model for Statisticlly Multiplexed Data Traffic in Cell Relay Networks" Motorola Codex, 1998 IEEE.
[4] CCITT Rec I.362 B-ISDN ATM Adaptation Layer (AAL) functional description. Geneva 1991.
[5] Falkner Matt. , Modeling ATM Networks with COMNET III, Version, 1.0, 1996.
[6] Kuo Geng-Sheng and Ko Po-Chang, "Achieving Minimun Slice Loss for Real-Time MPEG-2-Based Video Networking in a FlowOriented Input-Queued ATM Switching Router System" IEEE Communications Magazine, 1999.
[7] Schwartz, Mischa, Broadband Integrated Networks, Prentice Hall., PTR, 1996.
[8] Stern, T.E., "A Queuering Analysis of Packets Voice", IEEE Globecom 83, San Diego ,CA., 1983: 2.5.1-2.5.6
[9] Daigle, J.N. , J.D. Dangfort, "Models for Analysis of Packets Voice Communications Systems", IEEE JSAC, SAC-4, 6 (Sept. 1986): 847-855.
[10] Maglaris, B. "Perfomance Models of Statistical Multiplexing in Packet Video Communications", IEEE Trans. on Commun., 36,7 (Julio del 88): 834-844
[11] Poveda Zafra, José N. "Modelamiento de la red de núcleo ATM", memoria de Maestría en Teleinformática, Universidad Distrital, 2001.
José Noé Poveda Zafra
Ingeniero Electrónico Universidad Distrital, Magister en Teleinformática, Profesor Facultad de Ingeniería. jpoveda@atlas.udistrital .edu.co.
Alvaro Betancourt Uscátegui
Ingeniero Electrónico, Universidad Distrital ,Especialista en Telecomunicaciones Móviles, Universidad Distrital, Msc. Ciencias Financieras y de Sistemas, Universidad Central, Magister en Ingeniería, Informatique Appliquée, Ecole Polytechnique Université de Montreal, Canadá. Profesor Facultad de Ingeniería, Universidad Distrital, Coordinador de la Especialización en Telecomunicaciones Móviles abetancourt@ atlas.udistrital.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










