Herramienta de ingeniería para el estudiante: calculador de matrices

Herramienta de ingeniería para el estudiante: calculador de matrices

Engineering´s tool for students: matrix calculator

Recibido: 10-09-2015
Modificado: 02-11-2015
Aprobado: 02-11-2015

Lucio Nieto Bautista

Pasante de Ingeniero en Computación, Universidad Americana de Acapulco, Guerrero, México. Correo electrónico: noodle3030@gmail.com

René Edmundo Cuevas Valencia

Doctor en Enseñanza Superior por el Centro de Investigación y Docencia en Humanidades del Estado de Morelos (CIDHEM), México; magíster en Computación; Ingeniero en Computación, Universidad Autónoma de Guerrero (UAGro), México; docente Investigador por la UAGro y Miembro del Sistema Nacional de Investigadores del CONACYT, México. Correo electrónico: reneecuevas@uagro.mx

Angelino Feliciano Morales

Maestro en Enseñanza de la Matemática, UAGro; docente Investigador, UAGro, México. Correo electrónico: af_morales@hotmail.com

Resumen

En la actualidad, existen una gran variedad de aplicaciones que pueden ser implementadas con fines educativos, inclusive se puede hacer uso de libros digitales junto a dichas aplicaciones, esto ayudaría al estudiante a tener una percepción clara de los procedimientos matemáticos utilizados. Varias escuelas ya están haciendo uso de tabletas y aplicaciones móviles; por eso en este artículo se considera pertinente hablar de un software desarrollado en el entorno de Java para dar solución a la problemática de operaciones con matrices, el cual está basado en teoremas y métodos matemáticos bien conocidos. No debe ser difícil para el estudiante promedio el entender y adaptarse al programa, es muy fácil de usar y cuenta con las instrucciones detalladas en cada ventana.

Palabras clave

determinante, matriz escalar, traspuesta.

Abstract

In our days, we can use multiple apps for learning purposes. Even digital books can be implemented along this apps, this would help the student to have a more clear perception of mathematical procedures. Many schools are already making use of tablets and mobile apps, so in this article we will talk about a software developed in the Java environment to solve matrices of dimensions, which is based on theorems and well known mathematical methods. It shouldn’t be a problem for the average student to understand and adapt to this software, it’s easy to use and it has the instructions well explained on each window.

Keywords

determinant, scalar matrix, transpose

1. INTRODUCCIÓN

El software calculador de matrices es fácil de usar y ofrece diversas opciones para solucionar una matriz dada, por ejemplo: suma (suma de dos matrices cuadradas); resta (resta de dos matrices cuadradas); división (división por un numero escalar); determinante (obtiene el determinante para verificar si una matriz tiene solución); multiplicación (multiplicación por un escalar o producto punto); traspuesta (obtiene la traspuesta de la matriz dada); inversa (obtiene la inversa de la matriz dada).

Al realizar cualquiera de los procedimientos matriciales mencionados, el estudiante podrá corroborar sus resultados con los del software haciendo una comparación, en caso de tener resultados equivocados puede analizar los procedimientos usados para verificar y ubicar el error. Ya que el calculador de matrices se fundamenta en las reglas matemáticas, el usuario puede realizar las operaciones sin riesgo de omitir o dejar fuera estas reglas, el software se lo indicaría de inmediato, por ejemplo: dos matrices se pueden sumar solo si son cuadradas

2. ANTECEDENTES

El software educativo se ha implementado desde hace algunas décadas, hasta el momento existe una variedad de programas libres y propietarios que pueden dar solución a una matriz, inclusive algunos de ellos están disponibles en línea como es el caso del sitio web http://www.resolvermatrices.com/ o bien https://matrixcalc.org/es/, donde se ofrece al usuario la oportunidad de realizar las operaciones matriciales.

Entre los programas de escritorio pueden mencionarse los siguientes:

• Entre los programas de escritorio pueden mencionarse los siguientes:
• Sage: es un sistema algebraico computacional (CAS, por sus siglas en inglés) escrito en Python, luego una versión modificada de Pyrex (llamada inicialmente SageX y posteriormente Cython). Este programa unifica bajo un solo entorno lenguaje, jerarquía de objetos, toda una colección de software matemático y trata de cubrir los espacios de funcionalidad no atendidos por los anteriores [1].
• Matlab: el nombre está formado por la abreviatura de matrix laboratory (laboratorio de matrices) es una herramienta de software matemático que ofrece un entorno de desarrollo integrado (IDE, por sus siglas en inglés) con un lenguaje de programación propio (lenguaje M). Está disponible para las plataformas Unix, Windows, Mac OS X y GNU/Linux.

Entre sus prestaciones básicas están la manipulación de matrices, representación de datos y funciones, implementación de algoritmos, creación de interfaces de usuario (GUI) y la comunicación con programas en otros lenguajes y con dispositivos hardware [2].

• Derive: (pronunciado /dɪˈraɪv/) es un programa de cálculo matemático avanzado que comprende el manejo de variables, expresiones algebraicas, ecuaciones, funciones, vectores, matrices, trigonometría, etc.; también tiene capacidades de calculadora científica y puede representar funciones gráficas en dos y tres dimensiones en varios sistemas coordenados [3].

3. DESCRIPCIÓN DE LA FUNCIONALIDAD DEL SOFTWARE

En la ventana principal (Figura 1), despliega un menú con todas las opciones disponibles.

Diagrama de distribución de ventas según Micro Estrategias.

Fuente: elaboración propia.

3.1 Nueva matriz

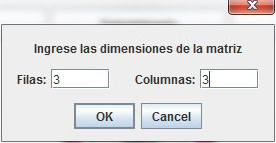
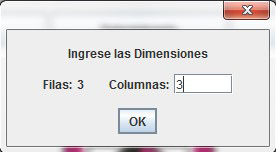
Como primera opción está ingresar los datos de una nueva matriz con la que se realizarán las operaciones. Una vez seleccionada la alternativa aparece otra ventana donde el software pregunta por el número de filas y columnas para poder introducir el orden de la matriz (Figura 2).

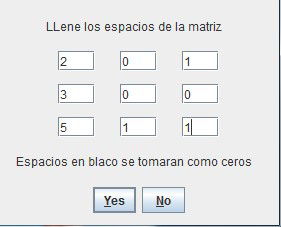
Después de especificar el orden de la matriz original, el software muestra una nueva ventana con espacios en blanco (Figura 3) que deben ser llenarlos, el número de plazas dependerá de la dimensión asignada a la matriz; cabe aclarar que al dejar espacios vacíos el software, por default, les asignará el valor cero a las posicióones (esto lo aclara el software con un pequeño mensaje).

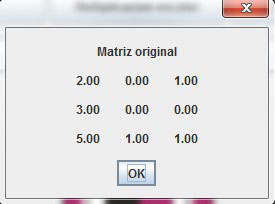
3.2 Mostrar matriz

Al estar llena la matriz se mostrarán los datos ordenados según la dimensión que se tenga, de lo contrario, si está vacía, el calculador de matrices muestra el mensaje: “matriz vacía, ingrese una nueva matriz” (Figura 4).

3.3 Suma

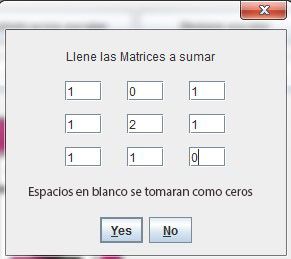
De igual manera, al elegir la opción matriz llena se abre otra ventana que pide los datos como en la primera opción. Para garantizar que se cumpla con la regla para suma de matrices, el calculador asigna una nueva matriz de la misma dimensión que la original con la cual se efectuará la operación (Figura 5).

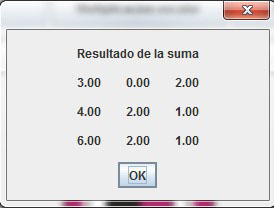
Después de haber ingresado los datos, al presionar la tecla enter, se mostrarán los resultados ordenados según la dimensión de la matriz (Figura 6).

3.4 Resta

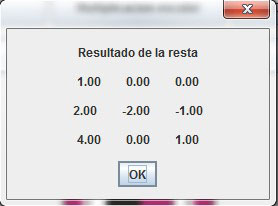
Esta opción es similar a la anterior, la diferencia es que ahora, en lugar de realizar la operación suma, efectúa la resta (Figura 7).

3.5 Producto punto

Siguiendo la misma condición, de estar llena la matriz efectúa la operación producto punto. Como se sabe, para poder llevar a cabo esta operación es necesario que el número de columnas de la matriz original coincida con el número de filas de la matriz a multiplicar. El calculador de matrices se asegura de aplicar las reglas matemáticas y por ello, al ingresar los datos de la segunda matriz, solo pregunta por la cantidad de columnas y pone por defecto como número de filas la cantidad de columnas de la matriz original (Figura 8).

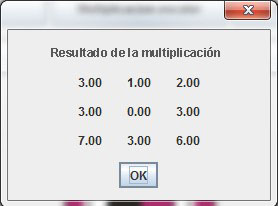
Al presionar enter mostrará el resultado en otra ventana con dimensiones del número de filas de la matriz original y el número de columnas de la matriz a multiplicar (Figura 9).

3.6 Multiplicación por un escalar

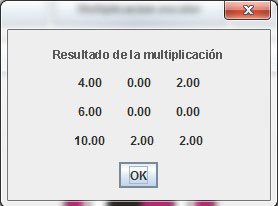
En esta opción, al estar llena la matriz, la operación será con la matriz original por un solo elemento, se realiza multiplicando al escalar por cada uno de los términos de la matriz, resultando una matriz con el mismo tamaño de la matriz original (Figura 10).

3.7 División escalar

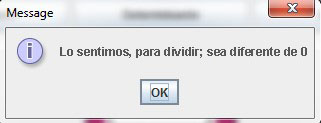
Para respetar las reglas matemáticas se pide que el escalar en esta ocasión sea diferente de cero, si el usuario llegase a introducir un cero como escalar, el calculador de matrices generará un mensaje donde aclara que la división por cero da una indeterminación. Esta opción es similar a la anterior, pero ahora en lugar de multiplicar, dividirá cada uno de los elementos de la matriz por el escalar, resultando una matriz del mismo orden que la matriz original (Figura 11).

3.8 Traspuesta

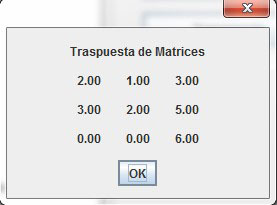
Si la matriz contiene elementos, esta opción le permite al usuario hacer un reacomodo de los mismos, intercambiando ordenadamente las columnas por las filas para que al final resulte una matriz traspuesta de diferente orden, en caso de no ser cuadrada (Figura 12).

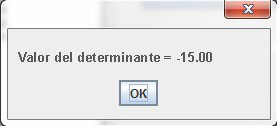
3.9 Determinante

De estar llena la matriz, de acuerdo con las reglas matemáticas, multiplica de manera cruzada sus elementos (el método se explica con más detalle en el tema multiplicación por un escalar), para arrojar como resultado un solo número que puede ser positivo o negativo; si el resultado es cero, entonces la matriz no tiene solución (Figura 13).

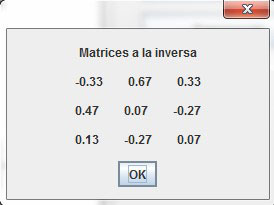
3.10 Inversa

En esta opción el proceso es mayor que los demás, ya que es necesario hacer uso de las opciones antes mencionadas. El calculador de matrices proporciona la solución a este problema por medio del método de determinantes si la matriz está llena; el primer paso consiste en calcular el determinante (diferente de cero, racional o entero), si el resultado es diferente de cero continuará con el procedimiento, de lo contrario el calculador de matrices enviará un mensaje aclarando que no tiene solución. Una vez terminada la operación, muestra el resultado; para comprobar que la matriz inversa es correcta, basta con multiplicarla por la matriz identidad (Figura 14).

4. MÉTODOS MATEMÁTICOS

4.1 Suma de matrices:

Si las matrices A=(a_ij) y B=(b_ij) tienen la misma dimensión, la matriz suma es: A+B=(a_ij+b_ij).

La matriz suma se obtiene sumando los elementos de las dos matrices que ocupan la misma posición, Dadas las siguientes matrices:

4.1.1 Propiedades de la suma de matrices

Interna: la suma de dos matrices de orden n es otra matriz cuya dimensión es nxn

Asociativa:

A + (B + C) = (A + B) + C

Elemento neutro:

A + 0 = A

Donde 0 es la matriz nula de la misma dimensión que la matriz A.

Elemento opuesto:

A+ (−A) = 0

La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

Conmutativa:

A + B = B + A [4].

4.2 Resta de matrices

Para poder sumar o restar matrices deben tener el mismo número de filas y columnas; es decir, se suman o restan los términos que ocupan el mismo lugar en las matrices [5], por ejemplo: Sean las matrices:

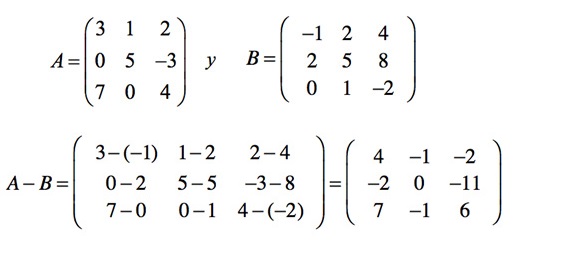
4. 3 Producto punto

Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B.

A_{m x n} x B_{n x p} = C_{m x p}

El elemento c_ij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos [6], por ejemplo:

Sean las matrices:

4.4 Producto escalar

Dada una matriz A=(a_ij) y un número real , k ∈ R se define la multiplicación de un número real por una matriz, en la que cada elemento está multiplicado por k [7].

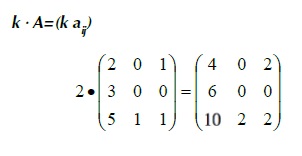
4.5 División de matrices por un escalar

La división de matrices se define como el producto del numerador multiplicado por la matriz inversa del denominador; es decir, sean las matrices A y B, tal que A/B = AB^-1: si una matriz está dividida por un escalar, todos los términos de la matriz quedarán divididos por dicho número [8], por ejemplo:

4.6 Matriz traspuesta

Dada una matriz A, se llama matriz traspuesta de A, a la matriz que se obtiene cambiando ordenadamente las filas por las columnas [9].

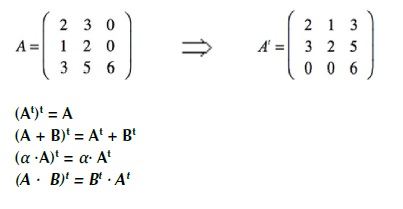
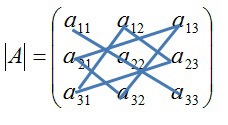
4.7 Cálculo de un determinante (método de Sarrus)

Pierre Sarrus (1798- 1861) fue un matemático francés que estableció una regla para calcular determinantes de orden tres

Los términos con signo + están formados por los elementos de la diagonal principal y los de las diagonales paralelas con su correspondiente vértice opuesto; también puede completarse con los dos primeros renglones o con las dos primeras columnas. Posteriormente, se multiplican los términos de la diagonal principal y sus paralelas, registrando el resultado con el signo que se haya obtenido [10].

Los términos con signo − están formados por los elementos de la diagonal secundaria y los de las diagonales paralelas con su correspondiente vértice opuesto; también puede completarse con los dos primeros renglones o con las dos primeras columnas. Posteriormente, se multiplican los términos de la diagonal secundaria y sus paralelas, luego se debe multiplicar el resultado por (-1) para cambiar el signo al producto obtenido.

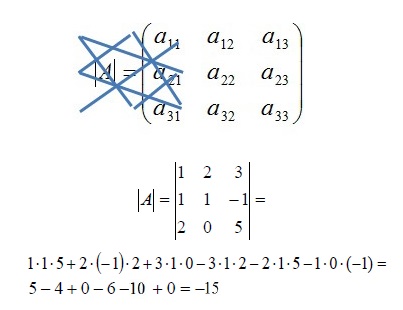
4.8 Cálculo de la matriz inversa:

4.8.1Calculando el determinante de la matriz, en el caso que el determinante sea nulo la matriz no tendrá inversa.

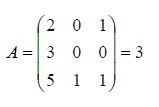
4.8.2Determinando la matriz adjunta, la cual se obtiene sustituyendo cada elemento por su adjunto.

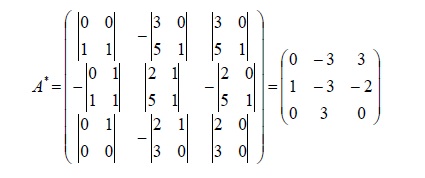
4.8.3Calculando la traspuesta de la matriz adjunta

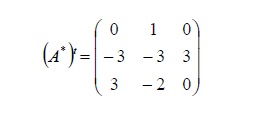
4.8.4La matriz inversa es igual al inverso del valor de su determinante por la matriz traspuesta de la adjunta [11].

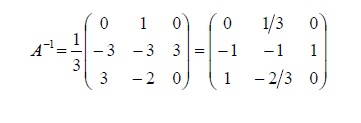
5. Aporte a la educación

Sin duda alguna, la utilización del software calculador de matrices por los estudiantes del nivel medio superior y superior resolvería la problemática que haya quedado pendiente con el trabajo en el aula como: la dificultad para comprender de las definiciones, la incomprensión de la operatividad con cada una de las operaciones con matrices.

Con el software es posible seguir el procedimiento de cada una de las operaciones realizadas, hay quienes en el aprendizaje son visuales y requieren de un ejemplo resuelto para poder entender los teoremas y procedimientos. El calculador de matrices brinda la oportunidad de visualizar las operaciones implementadas con un ejemplo. Ya que se trata de un software libre, está al alcance de todos.

6. Conclusión

Una vez realizado las pruebas con el software, se concluye que con este software se podrá verificar el resultado para tener la certeza de que está correcto y así evitar cometer errores con las matrices de mayor dimensión. El calculador de matrices no solo es útil en la escuela con los niveles medio superior, también en casa puede ser útil o en cualquier otro lugar, es la herramienta adecuada para un estudiante autodidacta; además, cabe resaltar que el propósito del calculador de matrices es brindarle al estudiante una herramienta de apoyo, para desarrollar sus habilidades matemáticas.

Agradecimientos

Agradezco a los profesores René Edmundo Cuevas Valencia y Angelino Feliciano Morales de la Universidad Autónoma de Guerrero y Gibrán Herrera García y Uziel Trujillo Colón de la Universidad Americana de Acapulco por su apoyo, enseñanzas y constante motivación a seguir creciendo no sólo como estudiante sino también como persona

Referencias

[1] SageMath, Noviembre, 2015. [En línea] Disponible en: https://es.wikipedia.org/wiki/Sage

[2] “MATLAB”, Noviembre, 2015. [En línea] Disponible en: https://es.wikipedia.org/wiki/MATLAB

[3] “Derive”. Noviembre 2015. [En línea] Disponible en: https://es.wikipedia.org/wiki/Derive

[4] Ditutor, “Suma de matrices”. Noviembre, 2015. [En línea] Disponible en: http://www.ditutor. com/matrices/suma_matrices.html

[5] Matsyr “Suma y resta de matrices”. Noviembre, 2015. [En línea] Disponible en: http://www. sectormatematica.cl/contenidos/matsyr.htm

[6] Vitutor, “Producto de matrices”. Noviembre, 2015. [En línea] Disponible en: http://www. vitutor.com/algebra/matrices/producto.html

[7] Ditutor. “Producto de matrices (escalar)”. Noviembre, 2015. [En línea] Disponible en: http://www. ditutor.com/matrices/multiplicacion_escalar.html

[8] Matdiv “División de matrices”. Noviembre, 2015. [En línea] Disponible en: http://www. sectormatematica.cl/contenidos/matdiv.htm

[9] Ditutor, “Matriz traspuesta”. Noviembre, 2015. [En línea] Disponible en: http://www.ditutor. com/matrices/matriz_traspuesta.html

[10] Vitutor, “Determinante”. Noviembre, 2015. [En línea] Disponible en: http://www.vitutor. com/algebra/determinantes/sarrus.html

[11] Vitutor, “Matriz inversa”. Noviembre, 2015. [En línea] Disponible en: http://www.vitutor. com/algebra/determinantes/inversa.html