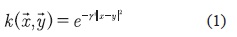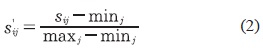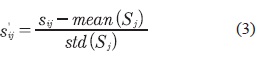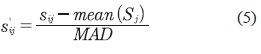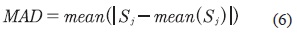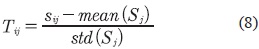Análisis del procesamiento de los datos de entrada para un localizador de fallas en sistemas de distribución

Análisis del procesamiento de los datos de entrada para un localizador de fallas en sistemas de distribución

Analysis of the input data processing for fault location in power distribution systems

Walter Julián Gil González¹, Juan José Mora Flórez², Sandra Milena Pérez Londoño³

¹Ingeniero electricista, candidato a magíster en Ingeniería Eléctrica. Investigador del Grupo de Investigación en Calidad de Energía Eléctrica y Estabilidad de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: wjgil@utp.edu.co
²Ingeniero electricista, doctor en Ingeniería Eléctrica. Docente titular de la Universidad Tecnológica de Pereira (UTP). Pereira, Colombia. Contacto: ijmora@utp.edu.co
³Ingeniera electricista, doctora en Ingeniería. Docente titular de la Universidad Tecnológica de Pereira (UTP). Pereira, Colombia. Contacto: saperez@utp.edu.co

Fecha de recepción: 15 de mayo de 2013-Fecha de aceptación: 23 de noviembre de 2013

Clasificación del artículo: investigación
Financiamiento: Colciencias, contrato 0977-2012

Resumen

En este artículo se presenta una comparación de cinco métodos de normalización de datos para un método de clasificación basado en la máquina de soporte vectorial (SVM), con el objetivo de determinar cuál es la influencia de éstos métodos en la precisión y el esfuerzo computacional del localizador de fallas en sistemas de distribución. La metodología propuesta se prueba en un sistema de distribución estándar de 34 nodos de la IEEE, el cual se subdivide en 11 zonas, de donde se obtiene una base de datos de 6442 registros de falla monofásica a diferentes condiciones de carga. La comparación de estos métodos de normalización muestra que el método Min-Max presentó un mejor rendimiento en tiempo computacional y precisión promedio del localizador de fallas, en los casos estudiados.

Palabras clave: atributos, máquinas de soporte vectorial, métodos de normalización, precisión y sistemas de distribución.

Abstract

Aimed to determine the effect of data normalization on the accuracy and the computational effort of a fault locator based on support vector machines (SVM), a comparison of five different data preprocessing strategies are analyzed in this paper. The proposed methodology is tested on an IEEE 34-bus test feeder, which is subdivided in eleven zones, by using a database of 6442 single-phase to ground faults obtained under different load conditions. Considering the testing scenarios, the comparison of the proposed preprocessing methods shows that Min-Max method has the best performance mainly considering computational effort and average accuracy on the fault locator.

Key words: Accuracy and power distribution systems, attribute, normalization methods, support vector machines.

Introducción

La calidad de la energía eléctrica en sistemas de distribución se ha convertido en un tema de amplia investigación, debido al interés que tienen los operadores de red en mejorar la continuidad del servicio, para cumplir con índices fijados por los entes regulatorios. Una de las causas que más afecta la continuidad del servicio, y por ende los índices de continuidad, son las fallas paralelas en el sistema. Debido a esto es necesario conocer de manera confiable y rápida dónde ocurrió la interrupción del servicio, para la restauración de este en el menor tiempo posible.

Para la solución del problema de localización de fallas en sistemas de distribución se han desarrollado diversas metodologías, como las presentadas en Mora, Carrillo y Meléndez (2008) y en Morales, Mora y Vargas (2009); estas se fundamentan en la estimación de la impedancia. Dichos métodos estiman la distancia en falla a partir de la tensión y corriente en estado de falla y prefalla, y de los parámetros que definen el modelo del sistema de potencia. Sin embargo, el resultado es una distancia que se puede cumplir para varios sitios, debido a la característica radial y ramificada de los sistemas de distribución, en lo que se denomina como la múltiple estimación de la falla (Morales, et al., 2009). Para la solución de este problema se proponen los métodos basados en el conocimiento (MBC) (Gutiérrez, Moray Pérez, 2010) (Thuka-ram, Khinchay Vijaynarasimha, 2005).

Los MBC se fundamentan en la extracción de conocimiento oculto en bases de datos. Generalmente, estas bases de datos requieren un procesamiento que comprende diferentes tareas tales como: manejo de ruido, manejo de datos faltan-tes, detección de datos anómalos, selección de atributos y normalización. La selección de atributos consiste en reconocer las características más significativas en una base de datos para los MBC, con el fin de mejorar el desempeño predictivo del clasificador para obtener el máximo rendimiento con el mínimo esfuerzo (Maldonado, 2007; Mal-donado y Weber, 2012). Por otra parte, la normalización de los datos consiste en transformar los valores dentro de la base de datos en un rango, generalmente entre cero y uno, lo cual puede mejorar la precisión, eficiencia y tiempos computa-cionales de los métodos MBC (Farrús, Anguita, Hernando y Cerd�, 2005; Al Shalabi y Shaaban, 2006; Sola y Sevilla, 1997).

En este artículo se propone realizar una comparación de la influencia de varios métodos de normalización aplicados en el procesamiento de los datos, ante diferentes atributos de entrada, para determinar cuál se adecua mejor al problema de localización de fallas en sistemas de distribución. El MBC que se utilizó es la máquina de soporte vectorial (SVM), el cual ha presentado alto desempeño en este problema, según se reporta en varios documentos (Gutiérrez et al., 2010; Thukaram etal., 2005).

Este artículo está dividido en cinco secciones. La siguiente sección presenta los aspectos teóricos básicos de las técnicas de normalización utilizadas y del método de clasificación. En la sección tres se muestra el desarrollo de la metodología propuesta. En la sección cuatro se discute la aplicación de la metodología, las pruebas y los resultados obtenidos. Finalmente, la sección cinco presenta las conclusiones más importantes de la investigación.

Aspectos Teóricos

Máquina de soporte vectorial (SVM)

La SVM es un MBC que se basa en los fundamentos de la teoría de aprendizaje estadístico desarrollada por Vapnik y Chervonenkis (Moguerza y Muñoz, 2006), la cual, a diferencia de otras teorías, tiene la ventaja de que no requieren ningún tipo de conjetura sobre la densidad de probabilidad de los datos. La arquitectura de la SVM solo depende de un parámetro de penalización denotado como C y la función kernel (incluyendo sus parámetros). En el caso de la función base radial (RBF) existe solo un parámetro γ, como se presenta en la ecuación (1) (Burges, 1998).

Donde, 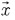y 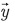son los atributos de entrada a los MBC.

Búsqueda tabú

La búsqueda tabú es una técnica metaheurística de optimización que se utiliza para resolver problemas de alta complejidad. Este tipo de técnicas proporcionan soluciones factibles con bajos costos computacionales y, aunque en algunos casos no alcanza el óptimo global del problema, siempre presenta soluciones de gran calidad. La idea básica de la búsqueda tabú es la utilización explícita de un historial de búsqueda (una memoria de corto plazo), tanto para escapar de los óptimos locales como para implementar una estrategia de exploración y evitar la búsqueda repetida en la misma región (Glover y Kochenberger, 2002). Esta memoria de corto plazo se implementa como una lista tabú, donde se mantienen las soluciones visitadas más recientemente para excluirlas de los próximos movimientos. En cada iteración se elige la mejor solución entre las permitidas y esta se añade a la lista tabú.

Métodos de normalización

La normalización de los datos es necesaria para adecuarlos a los problemas de clasificación, debido que estos no están definidos en las mismas escalas numéricas y en algunos casos siguen diferentes distribuciones. Las normalizaciones más utilizadas para los problemas de clasificación son: Min-Max, Z-score, Decimal-Scaling, Median and median absolutedeviationy Sigmoidfunction (Fa-rrúset al., 2005; Anil, Karthik y Arun, 2005;Sne-lick, Uludag, Mink, Indovina y Jain, 2005).

Min-Max (MM)

En este método el valor mínimo y máximo de la base de datos se desplaza a los valores 0 y 1, respectivamente, y todos los demás datos se transforman en el rango {0,1}, utilizando la ecuación (2) (Farrús etal., 2005).

Donde, S_ij es el dato i transformado del conjunto de datos j; S_ij es el dato i original del conjunto de datos /; min es el valor mínimo del conjunto de datos y; max_j es el valor máximo del conjunto de datos j.

Z-score (ZS)

Este método transforma los datos a una distribución con media 0 y desviación estándar 1. En la ecuación (3), los operadores mean() y std() denotan la media aritmética y la desviación estándar, respectivamente (Snelick etal., 2005).

Donde, S_j es el conjunto de datos j; mean(S_j) es la media aritmética del conjunto de datos j; std(S_j) es la desviación estándar del conjunto de datos j.

Decimal-scaling (DS)

Este método normaliza los datos en un valor entre -1 y 1, sin incluirlos. Los datos se normalizan según la ecuación (4) (Han y Kamber, 2006).

Donde, k es el menor número entero con el cual se cumple que el máximo (| S_ij |)<1.

Median and median absolutedeviation (MMAD)

Este método es insensible a valores atípicos y puntos en colas de la distribución. Por lo tanto, un esquema de normalización combinando la media y la desviación media absoluta de los datos sería un método más robusto. Los datos se normalizan según la ecuación (5) (Anil et al., 2005).

Donde MAD se calcula como se muestra en la ecuación (6).

Función sigmoial (SF)

Esta función también se conoce como una squashing function, porque transforma los datos en un rango de entrada entre 0 a 1. Esta función es no lineal y diferenciable, y permite que las técnicas de clasificación tengan un mejor manejo de los datos en problemas que no son linealmente separables. Los datos se normalizan según la ecuación (7) (Han y Kamber, 2006).

Donde T_iij y se calcula como se muestra en la ecuación (8).

Metodología

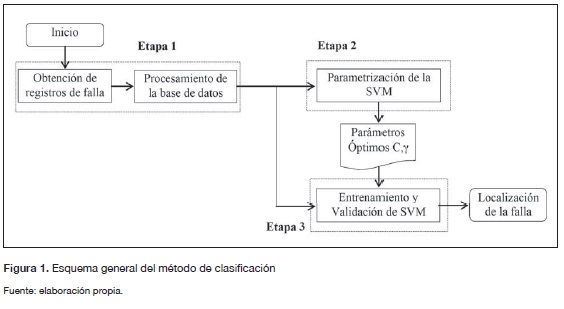
La metodología general utilizada para observar la influencia del procesamiento de datos de entrada en el problema de la localización de fallas en sistemas de distribución se presenta gráficamente en el esquema mostrado en la figura 1.

En la etapa 1 se obtienen los registros de falla del circuito bajo estudio y se realiza el preprocesa-miento de los datos. En este artículo se hace énfasis en dicha etapa, ya que es donde se muestra la estrategia de normalización para cada combinación de atributos en el procesamiento. En la etapa 2 se parametriza el SVM usando la técnica meta-heurística búsqueda tabú para el ajuste óptimo del localizador. Finalmente, en la etapa 3 se utilizan los parámetros encontrados (C,γ) en la etapa anterior y los datos procesados, para el entrenamiento y la validación del método y, así, localizar la falla.

Etapa 1

Esta etapa consiste en extraer y preparar la base de datos para el MBC y sigue varios pasos, los cuales se describen a continuación.

Adquisición de datos

Los datos utilizados para el entrenamiento se obtienen de la simulación del sistema de distribución analizado, a partir de un proceso conjunto de la herramienta de simulación Alternative Transients Program (ATP) y el software MATLAB. Esta herramienta permite la simulación automática de condiciones de falla monofásica, bifásica y trifásica, con diferentes valores de resistencia de falla (Pérez, Mora y Pérez, 2010).

Zonificación de la red de distribución

Los métodos de clasificación requieren que a cada uno de los datos de entrenamiento se le asigne una clase, con la cual se realizará la clasificación de un nuevo dato. Esta clase corresponde a una zona del sistema de distribución bajo análisis. Una zona no debe tener más de un lateral del circuito, para eliminar el problema de múltiple estimación (Gutiérrez et al., 2010). Además, es posible proponer una zonificación con zonas grandes, si así lo requiere el operador de red, aunque también es posible reducir su tamaño y así dar importancia a aquellas zonas donde la probabilidad de ocurrencia de fallos sea mayor, o donde sea necesario restaurar el servicio de forma más rápida.

Procesamiento de los datos de entrada

El procesamiento de datos es un paso muy importante para los problemas de clasificación, debido a que este proceso incluye extracción de características, depuración, normalización y selección de los datos, lo cual ayuda a mejorar la predicción de los MBC con menores esfuerzos computacio-nales. Si los datos no son procesados pueden ser inconsistentes, o contener información errónea e irrelevante para los MBC, lo cual puede producir menor precisión en los resultados (Kotsiantis, Kanellopoulosy Pintelas, 2006).

El primer paso del procesamiento de los datos de falla está asociado con la extracción de información significativa, denominada atributos. En este artículo, los atributos utilizados corresponden a la variación en magnitud de la tensión (dV) y de la corriente (di), y la variación angular de la tensión (dθ_v) y de la corriente de fase (d6_{). Para cada atributo se consideran medidas de fase y de línea.

Se analizan solo las combinaciones que contienen atributos de tensión y corriente (dV, dI, dθ_vdθ_I), debido a que estas combinaciones han presentado buenos resultados como se muestra en Gil (2011). Adicionalmente, a cada atributo se le asigna una etiqueta relacionada con la zona en la cual ocurrió la falla (Gutiérrez et al, 2010).

Finalmente, la base de datos se normaliza, debido a que puede existir gran diferencia entre los valores de un mismo atributo (Kotsiantis et al., 2006), o entre los valores de diferentes atributos. Con la normalización se evita que atributos con magnitudes más altas dominen en el cálculo de la zona. Adicionalmente, esta normalización puede disminuir el costo computacional, mejorar el desempeño y la precisión del método de clasificación (Al Shalabi y Shaaban, 2006; Sola y Sevilla, 1997; Snelick etal., 2005).

Otros problemas requieren el manejo de ruido, detección de datos anómalos y estrategias para manejar datos faltantes. Sin embargo, ninguna de dichas tareas se realiza en este caso debido a que las bases de datos obtenidas mediante simulación están completas.

Etapa 2

En esta etapa se determinan los parámetros óptimos para el clasificador (C,y) y se implementa la búsqueda tabú mediante la técnica de validación cruzada para 10 combinaciones de atributos que se utilizaron como entradas (Gutiérrez et al., 2010). El error de validación cruzada se utiliza como la función objetivo de la técnica de optimización, y así el algoritmo evoluciona hasta encontrar el menor error de validación.

La validación cruzada es un método que consiste en dividir la base de datos de entrenamiento en n partes iguales. A continuación, el localizador basado en SVM se entrena con los datos contenidos en las n-1 partes de la base de datos y la parte restante para hallar el error de validación, calculada como se muestra en la ecuación (9). Este proceso se repite n veces, lo que permite utilizar todas las muestras para hallar un error de validación con esta base de datos. Por último, se promedian los n valores de error encontrados y se obtiene un solo error de validación (Morales etal., 2009).

Esta etapa se realiza para cada método de normalización propuesto y para cada combinación de atributos de entrada.

Etapa 3

El desarrollo de esta etapa se hace con todos los datos de fallas registrados en la subestación. A partir de esos registros se entrena y se valida la SVM. La validación consiste en evaluar el rendimiento del localizador a partir del cálculo la precisión del método ante datos desconocidos (datos que no fueron considerados en la etapa de parametrización y entrenamiento). La precisión se calcula como se muestra en la ecuación (10).

Resultados de aplicación De la metodología propuesta En un sistema de distribución Prototipo

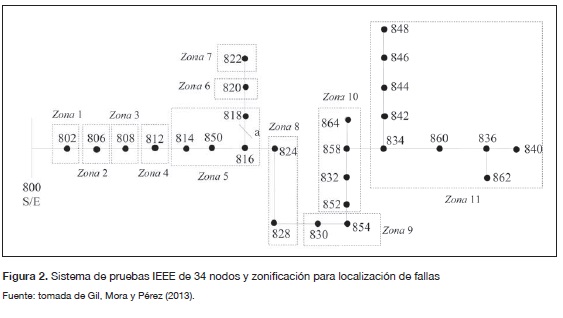
La metodología propuesta se prueba en el sistema IEEE de 34 nodos, presentado en IEEE, 2004, el cual es un circuito de distribución real ubicado en Arizona, operado a 26.7 kV. El sistema presenta cargas desbalanceadas, laterales monofásicos y múltiples calibres de conductor. El sistema de potencia de prueba se divide en 11 zonas, tal como se muestra en la figura 2.

Los escenarios considerados para probar la metodología contiene fallas monofásicas en todos los nodos, excepto en la subestación, utilizando diferentes resistencias de falla que varían entre 0,05Ω a 40 Ω, los cuales son valores comúnmente utilizados en este tipo de pruebas (Dagenhart, 2000). Adicionalmente, se simularon cuatro escenarios de carga, además de la nominal; los escenarios simulados fueron: variación de carga 30-60%, 60-85 %, 85-105 % y 30-105 %. Se obtuvieron en total 6642 datos para parametrización, entrenamiento y validación.

Prueba a condición nominal

Esta prueba se realizó con fallas simuladas a condición nominal del circuito en la parametrización, entrenamiento y validación. En la parametrización se utilizaron los valores de resistencia de 8, 16, 24,32 y 40 Ω, para un total de registros de fallas de 135 datos, para obtener los parámetros óptimos de la SVM (C,y). La base de datos para entrenamiento contiene 297 datos y está compuesta con valores de resistencia de fallas entre 0,05 Qa40Qen pasos de 4 Ω.

La base de datos de la validación está conformada por 810 casos simulados con resistencia de falla entre 1 a 39 Ω en pasos de 1 Ω (sin incluir los casos ya utilizados en la parametrización y entrenamiento).

Para cada método de normalización se trabajaron dos casos de normalización por atributo. El primer caso propuesto consiste en utilizar los atributos presentados en la sección "Procesamiento de los datos de entrada" como tres atributos individuales, uno por cada fase del sistema. Por ejemplo, los valores de la variación de la tensión de la fase a (dV_a se normalizan si se utilizan únicamente los valores de la tensión de la fase a. En el segundo caso se utilizó el conjunto de medidas de las tres fases como un solo atributo; es decir, la normalización del atributo dV_a tiene en cuenta los valores de las tres fase (dV_a, dV_b, y dV_c).

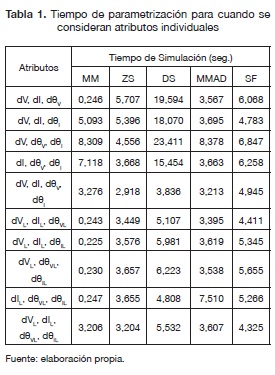
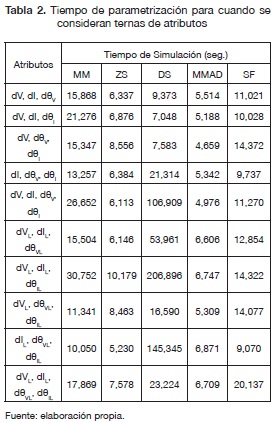
Las tablas 1 y 2 muestran los tiempos de parametrización para cada método de normalización y combinación de atributos. Solo se muestran estos tiempos debido a que el proceso de parametrizaciónes el que consume más tiempo de la metodología propuesta.

Como se puede observar en la tabla 1, el método de normalización escogido afecta el tiempo de parametrización del localizador. Se puede notar que el tiempo es menor cuando se utiliza el método de normalización MM, con un promedio de 2,8 segundos.

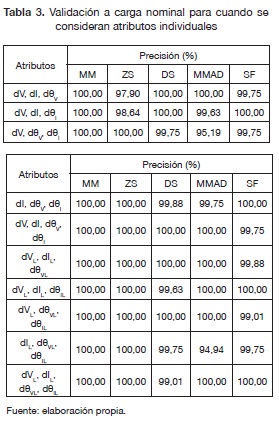
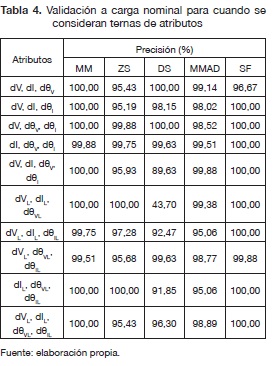
La tabla 2 muestra que para cuando se consideran ternas de atributos se consume un tiempo mayor sin importar el método de normalización. Además, en este caso el método de normalización MM no fue el más rápido. También, se observa que el método DS en promedio fue el más demorado sin importar cómo se manejen los atributos. Los resultados para la validación a condiciones nominales, para los cincos métodos de normalización y los dos casos se presentan en las tablas 3 y 4.

Prueba a diferentes condiciones de carga

En esta prueba se consideran todas las variaciones de carga propuestas en cuarto apartado. La base de datos para entrenamiento contiene 1485 datos y está compuesta con valores de resistencia de fallas entre 0,05 Qa40Qen pasos de 4 Ω. La base de datos de la validación está conformada por 4050 casos simulados con resistencia de falla entre 1 a 39 Ω en pasos de 1 Ω (sin incluir los casos ya utilizados en el entrenamiento).

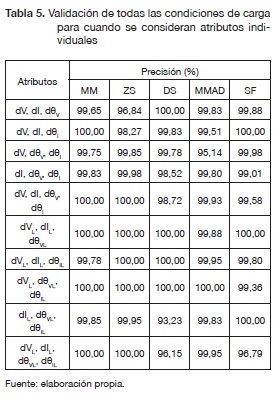
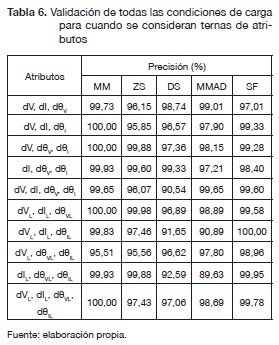
Los resultados para la validación de todas las condiciones de carga, los cinco métodos de normalización y para los dos casos propuestos en la sección "Prueba a condición nominal" se presentan en las tablas 5 y 6.

El tiempo requerido en la etapa de entrenamiento cuando se consideran atributos individuales es cerca de 1507 segundos usando un PC Core2Quad @2.66 GHz, 4GB RAM. En la tabla 5 se puede notar que el localizador tiene un buen desempeño con precisiones mayores a 93,23 % para todos los métodos de normalización. Adicionalmente, el método de normalización MM presentó un mejor desempeño en promedio que los otros de métodos de normalización.

En este caso los atributos de línea presentaron en promedio un mejor desempeño que los atributos de fase.

El tiempo requerido en la etapa de entrenamiento cuando se consideran ternas de atributos fue aproximadamente de 7157 segundos. Se observa en la tabla 6 que en promedio el rendimiento de los métodos de normalización bajaron y el tiempo de computacional subió respecto a cuando se consideran atributos individuales. Además, cuando se consideraron atributos individuales tuvo un mejor rendimiento de 1,85 % en promedio, respecto a cuando se consideran ternas de atributos.

Las combinaciones de atributos dV_L, dI_L, dθ_VL y dV_L, dI_L, dθ_VL, dθ_IL para ambos casos presentaron en promedio mejor desempeño, del 0,66 %, que las demás combinaciones analizadas.

Finalmente, se puede notar que el método DS en los dos casos propuestos fue inferior en precisión promedio y tiempo a los demás métodos utilizados en este artículo.

Conclusiones

El procesamiento de datos es muy importante para los métodos clasificación, debido a que este afecta directamente su rendimiento y su tiempo de ejecución. En el presente artículo se demuestra la influencia del procesamiento de los datos para un localizador de fallas y se consideran cinco métodos de normalización y diez combinaciones de atributos. En general, el localizador presentó un buen desempeño para todos los métodos de normalización utilizados; sin embargo, el método de normalización MM presentó el más alto desempeño, con una precisión promedio de 99,68 % para los dos casos analizados. Este hecho representa una ventaja, debido a que su formulación es más intuitivay su cálculo es simplificado.

También se observa que trabajar los atributos, cuando se consideran atributos individuales, tiene una gran ventaja en tiempo computacional y desempeño del clasificador, y es independiente del método de normalización utilizado. Además, cuando se consideran atributos individuales los tiempos de simulación de los atributos de línea son menores, en promedio de 3,82 segundos, que los atributos de fase.

Finalmente, utilizar combinaciones de atributos de línea tiene ventajas sobre los de fase en tiempo y desempeño para el problema de localización de fallas en sistemas de distribución.

Financiamiento

Este trabajo se realizó en el Grupo de Investigación en Calidad de Energía Eléctrica y Estabilidad (ICE²) de la Universidad Tecnológica de Pereira (UTP), por medio del proyecto de investigación "Desarrollo de localizadores robustos de fallas paralelas de baja impedancia para sistemas de distribución de energía eléctrica -LOFADIS2012-", contrato 0977-2012, financiado por Colciencias.

Referencias

Al Shalabi, L. y Shaaban, Z. (2006). Normalization as a Preprocessing Engine for Data Mining and the Approach of Preference Matrix. International Conference on Dependability of Computer Systems, 25-27 May.

Anil, J., Karthik, N. y Arun, R. (2005). Score Normalization in Multimodal Biometric Systems. Pattern Recognition, 38(12), 2270-2285.

Burges, C. (1998). A Tutorial on Support Vector Machines for Pattern Recognition. Data Mining and Knowledge Discovery, 2(2), 121-127.

Dagenhart, J. (2000). The 40-Ω Ground-Fault Phenomenon", IEEE Transactions on Industry Applications, 36(1), 30-32.

Farrús, M., Anguita, J., Hernando, J. y Cerd�, R. (2005). Fusión de sistemas de reconocimiento basados en características de alto y bajo nivel. Actas del III Congreso de la Sociedad Española de Acústica Forense, Santiago de Compostela, Spain, Oct.

Gil, W. (2011). Utilización de técnicas metaheu-risticas en la búsqueda de parámetros óptimos para la calibración de las máquinas de soporte vectorial (MSV), para la localización de fallas en sistemas de distribución. Tesis de Pregrado no publicada, Universidad Tecnológica de Pereira, Colombia.

Gil, W. Mora, J. y Pérez, S. (2013). Análisis comparativo de metaheurísticas para calibración de localizadores de fallas en sistemas de distribución. Ingeniería y Competitividad, 15(1), 103-115.

Glover, F. y Kochenberger, G. (2002). Handbook of Metaheuristics. EEUU: Kluwer Academic Publishers.

Gutiérrez, J., Mora, J. y Pérez, S. (2010). Strategy Based on Genetic Algorithms for an Optimal Adjust of a Support Vector Machine Used for Locating Faults in Power Distribution Systems. Revista de la Facultad de Ingeniería, 53, 174-187.

Han, J. y Kamber, M. (2006). Data Mining: Concepts and Techniques. New York: Morgan Kaufmann Publishers.

IEEE (2004). Guide for Determining Fault Location on AC Transmission and Distribution Lines. IEEE Std C37.114-2004, 1-36.

Kotsiantis, S., Kanellopoulos, D. y Píntelas, P. (2006). Data Preprocessing for Supervised Leaning. International Journal of Computer Science, 1(2), 111-117.

Maldonado, S. (2007). Utilización de support vector machines no lineal selección de atributos para credits coring. Tesis de Maestría no publicada, Universidad de Chile, Santiago de Chile, Chile.

Maldonado, S. y Weber, R. (2012). Modelos de Selección de Atributos para Support Vector Machines. Revista Ingeniería de Sistemas, 26, 49-70.

Moguerza, J. y Muñoz, A. (2006). Support Vector Machines with Applications. Statistical Science, 21 (4), 322-336.

Mora, J., Carrillo, G. y Meléndez, J. (2008). Comparison of Impedance Based Fault Location Methods for Power Distribution Systems. Electric Power Systems Research, 28(7), 657-666.

Morales, G., Mora, J. y Vargas, H. (2009). Fault Location Method Based on the Determination of the Minimum Fault Reactance for Uncertainty Loaded and Unbalanced Power Distribution Systems. Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), 2010 IEEE/PES, Sao Paulo, Brazil, 8-10 Nov.

Pérez, L., Mora, J. y Pérez, S. (2010). Diseño de una herramienta eficiente de simulación automática de fallas en sistemas eléctricos de potencia. Dyna, 77(164), 178-188.

Snelick, R., Uludag, U., Mink, U., Indovina, M. y Jain, A. (2005).Large-Scale Evaluation of Multimodal Biometric Authentication Using State-Of-The-Art Systems. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(3), 450-455.

Sola, J. y Sevilla, J. (1997). Importance of Input Data Normalization for the Application of Neural Networks to Complex Industrial Problems. IEEE Transactions on Nuclear Science, 44(3), 1464-1468.

Thukaram, D., Khincha, H. y Vijaynarasimha, H. (2005). Artificial Neural Network and Support Vector Machine Approach for Locating Faults in Radial Distribution Systems. IEEE Transactions on Power Delivery, 20(2), 710-721.