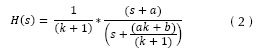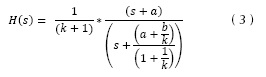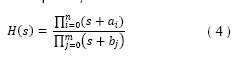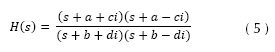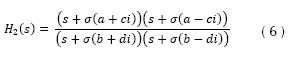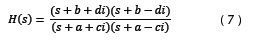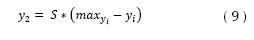DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.4.a04Publicado:
01-10-2015Número:
Vol. 19 Núm. 46 (2015): Octubre - DiciembreSección:
InvestigaciónMetodología para el uso de la técnica de localización de raíces en la planeación de rutas para robots móviles
Methodology for using root locus technique for mobile robots path planning
Palabras clave:
Root locus, path planning, mobile robots, image processing (en).Palabras clave:
Localización de raíces, planeación de rutas, robots móviles, procesamiento de imágenes (es).Descargas
Referencias
Akita, J., Watanabe, A., Tooyama, O., Miyami, M., & Yoshimoto, M. (10 de marzo de 2003). An image sensor with fast objects' position extraction function. IEEE Transactions on Electron Devices, 50(1), 184-190. doi:10.1109/TED.2002.806478
Ganguli, A., Cortés, J., & Bullo, F. (27 de Marzo de 2009). Multirobot Rendezvous With Visibility Sensors in Nonconvex Environments. IEEE Transactions on Robotics, 25(2), 340 - 352. doi:10.1109/TRO.2009.2013493
Hellerstein, J. L., Diao, Y., Parekh, S., & Tillbury, D. M. (2004). Proportional Control (1 ed.). Wiley-IEEE Press.
Landi, A., & Paoletti, F. (1995). Reciprocal root locus approach to path planning for multiple mobile robots. INRIA/IEEE Symposium on Emerging Technologies and Factory Automation. 2, págs. 345 - 352. Paris: IEEE. doi:10.1109/ETFA.1995.496675
Langer, R., Coelho, L., & Oliveira, G. (2007). K-Bug, A New Bug Approach for Mobile Robot's Path Planning. IEEE International Conference on Control Applications (págs. 403-408). Singapore: IEEE. doi:10.1109/CCA.2007.4389264
Maarouf, J. S., & Saliah-Hassane, H. (2011). An Improved Artificial Potential Field Approach to Real-Time Mobile Robot Path Planning in an Unknown Environment. IEEE International Symposium on Robotic and Sensors Environments (ROSE) (págs. 208 - 213). Montreal, QC: IEEE. doi:10.1109/ROSE.2011.6058518
Min-Ho, K., Jung-Hun, H., Yuanlong, W., & Min-Cheol, L. (2011). A path planning algorithm using artificial potential field based on probability map. 8th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI) (págs. 41 - 43). Incheon, Corea: IEEE. doi:10.1109/URAI.2011.6145929
Ogata, K. (2010). Ingeniería de Control Moderna (5 ed.). Pearson.
Ordoñez L., R. A., Martínez S., F., & García B., H. R. (Marzo de 2013). Proceso agroindustrial de la producción de panela. Tecnura, 17(35), 47-54. doi:http://dx.doi.org/10.14483/udistrital.jour.tecnura.2013.1.a04
Rairán A., J. D. (2007). Análisis de Sistemas Dinámicos y control PID (1 ed.). Bogotá, Colombia: Universidad Distrital Francisco José de Caldas.
Torres, J., Viáfara, R., & Martínez S., F. (Diciembre de 2014). Procesamiento de Imágenes para La Planeación de Rutas para Robots Móviles Basados en LEGO Mindstorms NXT. Redes de Ingeniería, 5(2), 16-27.
Vachhami, L., Mahindrakar, A. D., & Sridharan, K. (18 de Octubre de 2010). Mobile Robot Navigation Through a Hardware-Efficient Implementation for Control-Law-Based Construction of Generalized Voronoi Diagram. IEEE/ASME Transactions on Mechatronics, 16(6), 1083 - 1095. doi:10.1109/TMECH.2010.2076825
Xiaoqi, l., Jianshuai, W., Xiaoying, R., Zhang, B., & Li, Y. (Mayo de 2014). The study and application of the improved region growing algorithm for liver segmentation. Optik - International Journal for Light and Electron Optics, 125(9), 2142–2147.
Yi-Han, C., Ming-Chang, C., I-Hsum, L., Wei-Yen, W., & Shun-Feng, S. (2013). Image-based obstacle avoidance and path-planning system. International Conference on System Science and Engineering (ICSSE) (págs. 205 - 209). Budapest: IEEE. doi:10.1109/ICSSE.2013.6614660
Ziaei, Z., Oftadeh, R., & Matilla, J. (2014). Global Path Planning with Obstacle Avoidance for Omnidirectional Mobile Robot Using Overhead Camera. IEEE International Conference on Mechatronics and Automation (ICMA) (págs. 697-704). Tianjin, China: IEEE. doi:10.1109/ICMA.2014.6885782
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.4.a04
Investigación
Metodología para el uso de la técnica de localización de raíces en la planeación de rutas para robots móviles
Methodology for using root locus technique for mobile robots path planning
Mario Ricardo Arbulú Saavedra1
Fernando Martínez Santa2
Holman Montiel Ariza3
1 Ingeniero Mecánico Eléctrico, magister en Ingeniería Eléctrica, Electrónica y Automática, doctor en Ingeniería Eléctrica, Electrónica y Automática, posdoctorado en el National Institute Of Advanced Science And Technology Cnrs-Aist Jrl (Joint Robotics Laboratory). Director de investigación Escuela de Ingeniería, Corporación Unificada Nacional de educación superior CUN. Bogotá Colombia. Contacto: mario_arbulu@cun.edu.co
2 Ingeniero en Control Electrónico e Instrumentación, magister en Ingeniería Electrónica y de Computadores. Docente Investigador Ingeniería Electrónica, Corporación Unificada Nacional de educación superior CUN. Bogotá Colombia. Contacto: fernando_martinez@cun.edu.co
3 Ingeniero en Control Electrónico e Instrumentación, especialización en Telecomunicaciones, candidato a magister en Seguridad Informática. Docente Asistente Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: hmontiela@udistrital.edu.co
Como citar: Arbulú Saavedra, M. R., Martínez Santa, F., & Montiel Ariza, H. (2015). Metodología para el uso de la técnica de localización de raíces en la planeación de rutas para robots móviles. Revista Tecnura, 19(46), 49-64. doi:10.14483/udistrital.jour.tecnura.2015.4.a04
Fecha de recepción: 12 de noviembre de 2014 Fecha de aceptación: 24 de agosto de 2015
Resumen
Este artículo presenta el análisis y la metodología de implementación de la técnica de localización de raíces de sistemas dinámicos para la planeación de rutas libres de obstáculos para robots móviles. En primera instancia, se realiza un análisis e identificación del comportamiento morfológico de las trayectorias en dependencia de la ubicación de las raíces en el plano complejo, identificándose el tipo de trayectorias curvas y la característica de atracción y repulsión de estas en presencia de otras raíces, de forma similar al obtenido con la técnica de cargas de potencial artificial. Se plantea una metodología para implementación de esta técnica para la planeación de rutas de robots móviles, partiendo de tres métodos diferentes de ubicación de las raíces para los obstáculos presentes en el escenario. Dichas técnicas varían dependiendo de los puntos clave del obstáculo que son seleccionados para las raíces, tales como los bordes, los cruces con las trayectoria original, el centro y los vértices. Finalmente, se realiza un análisis de funcionamiento de la técnica en general y de la efectividad cada uno de los métodos evaluados, bajo 20 pruebas para cada uno, obteniendo un valor del 65% para el método seleccionado. También se proponen modificaciones o posibles mejoras a la metodología propuesta.
Palabras clave: Localización de raíces, planeación de rutas, robots móviles, procesamiento de imágenes.
Abstract
This paper shows the analysis and the implementation methodology of the technique of dynamic systems roots location used in free-obstacle path planning for mobile robots. First of all, the analysis and morphologic behavior identification of the paths depending on roots location in complex plane are performed, where paths type and their attraction and repulsion features in the presence of other roots similarly to the obtained with artificial potential fields are identified. An implementation methodology for this technique of mobile robots path planning is proposed, starting from three different methods of roots location for obstacles in the scene. Those techniques change depending on the obstacle key points selected for roots, such as borders, crossing points with original path, center and vertices. Finally, a behavior analysis of general technique and the effectiveness of each tried method is performed, doing 20 tests for each one, obtaining a value of 65% for the selected method. Modifications and possible improvements to this methodology are also proposed.
Keywords: Root locus, path planning, mobile robots, image processing.
Introducción
Uno de los problemas más evaluados en el área de la robótica es la planeación de rutas libres de obstáculos para robots móviles autónomos, los cuales se encuentran inmersos en ambientes con obstáculos conocidos. Las investigaciones han mostrado gran variedad de enfoques; esto, sumado a que en la actualidad se siguen haciendo nuevas propuestas al respecto, da a entender que no existe una solución absoluta al problema y que sigue siendo un nicho de investigación activo. Entre las diferentes técnicas exploradas para solucionar el problema de la planeación de rutas para robots móviles con sensores externos (Ziaei, Oftadeh, & Matilla, 2014) se encuentran: campos de potenciales artificiales (Maarouf & Saliah-Hassane, 2011; Min-Ho, Jung-Hun, Yuanlong, & Min-Cheol, 2011), diagramas de Voronoi (Vachhami, Mahindrakar, & Sridharan, 2010), grafos de visibilidad (Ganguli, Cortés, & Bullo, 2009), entre otros. La mayoría de estas técnicas están soportadas por medio de algoritmos o técnicas de procesamiento de imágenes, con el fin de hacer un procesamiento previo de las imágenes entregadas por la cámara y entregar una versión simplificada del entorno, incluyendo ubicación del robot, punto de llegada y obstáculos, al algoritmo principal de planeación (Yi-Han, Ming-Chang, I-Hsum, Wei-Yen, & Shun-Feng, 2013).
Por otra parte, la localización de raíces es una técnica utilizada para el cálculo y sintonización de compensadores o controladores en sistemas dinámicos (Hellerstein, Diao, Parekh, & Tillbury, 2004; Ogata, 2010; Ordoñez L., Martínez S., & García B., 2013). Partiendo de un sistema dinámico con raíces complejas, esta técnica genera una gráfica con las trayectorias recíprocas de dichas raíces en un plano complejo, ante la inclusión de un lazo de retroalimentación negativo (Rairán A., 2007). Las trayectorias generadas se pueden definir como funciones paramétricas de geometría conforme (Landi & Paoletti, 1995), por tanto la mayoría tiene una forma curva. A su vez, cada una de estas trayectorias se caracteriza por avanzar continuamente desde un polo hasta un cero del sistema.
Dadas las características de las trayectorias que se pueden generar por medio de la localización de raíces, el presente artículo propone utilizarlas como una posible solución al problema de la planeación de rutas libres de obstáculos para robots móviles con sensores externos. Para esto, el punto de partida y el de llegada del robot se ven plasmados como un polo y un cero respectivamente, ubicados en el plano complejo.
Conociendo el hecho de que ante la variación continua de una retroalimentación negativa los polos de un sistema dinámico tienden en una trayectoria paramétrica determinada hacia los ceros en el plano complejo, se procede a analizar el procedimiento para aplicar esta técnica para el cálculo de rutas libres de obstáculos para robots móviles con sensores externos. Se busca principalmente formular una metodología que permita la aplicación práctica de esta técnica en un entorno real. Dicho entorno es un robot en un ambiente rectangular con uno o varios obstáculos distribuidos en él; todo esto es capturado en imágenes por medio de una cámara ubicada en la parte superior, perpendicularmente al suelo.
Metodología
Localización de raíces
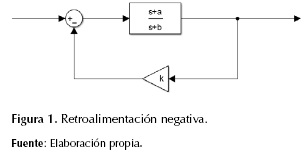
La localización de raíces es utilizada para el análisis de la respuesta en tiempo y cálculo de controladores en sistemas dinámicos. Esta consiste en partir de un sistema dinámico predeterminado, con un número y ubicación de raíces fijo y agregarle una retroalimentación negativa, por lo general una ganancia proporcional; de tal forma que la ubicación de cada uno de los polos o raíces del denominador sea en función de esta ganancia. Se parte de un sistema dinámico con una función de transferencia con un polo y un cero, ambos reales, como el mostrado en la ecuación (1), donde -a y -b son las posiciones del cero y el polo en el plano complejo respectivamente.
Se aplica una ganancia proporcional k en retroalimentación negativa como la mostrada en la figura 1. Del diagrama de bloques de la figura 1 y aplicando álgebra de bloques se obtiene la nueva función de transferencia de las ecuaciones (2) y (3), las cuales están en función de k.
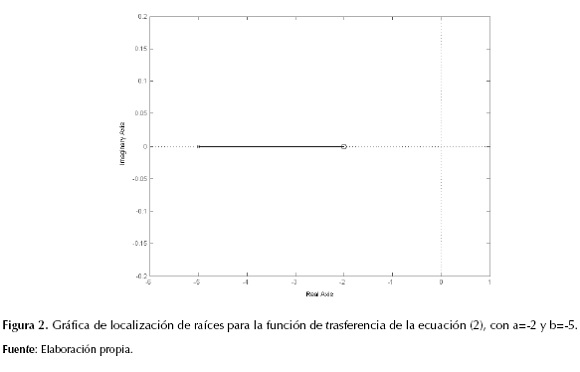
Aplicando la ganancia proporcional se modifica la ganancia total del sistema, así como la posición del polo, quedando intacto el cero. Tanto la ganancia como el polo quedan ahora en función de la ganancia k, por tanto se puede variar gradualmente el valor de k y graficar la trayectoria formada por todas las posibles posiciones del polo del sistema. Si la ganancia k es cero, de la ecuación (2) se obtiene que la posición del polo es -b, es decir que se ubica en su posición original. Cuando k tiende a infinito, la posición del polo es ahora la misma posición del cero del sistema, como se puede apreciar en la ecuación (3). De lo anterior se concluye que en un sistema dinámico con un polo y un cero, ambos reales, se puede graficar una trayectoria continua partiendo desde el polo hacia el cero si realizamos una retroalimentación negativa con una ganancia proporcional k, donde dicha trayectoria se define como una función paramétrica de k en un plano complejo. Para el ejemplo propuesto, la trayectoria es una línea recta horizontal desde el polo hacia el cero, debido a que se tratan de raíces reales. Esto se puede observar en la figura 2.
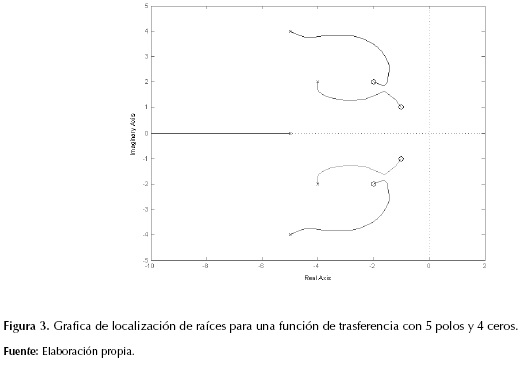
Se puede inferir que la trayectoria se genera debido a que la posición del polo del sistema se ve atraída hacia la ubicación del cero, cuando se aplica una ganancia en retroalimentación negativa. Así mismo cuando se tienen sistemas con múltiples polos y ceros, como el de la ecuación (4). Se tienen tantas trayectorias como el orden mayor de los polinomios de numerador y denominador de la función de trasferencia, es decir max(m, n), donde m es el número de polos y n el de ceros.
En la figura 3 se muestra la gráfica de localización de raíces de un sistema con cuatro polos complejos conjugados, cuatro ceros complejos conjugados y un polo real. En el caso de tener raíces complejas, es necesario que estas siempre sean conjugadas con respecto a la coordenada imaginaria, esto produce que las trayectorias sean recíprocas con respecto al eje real. En este caso cada polo tiende hacia un cero, generando cuatro trayectorias simétricas en pares con respecto al eje real del plano complejo; el polo restante tiende hacia el infinito, dado que no existe ningún otro cero hacia el cual avanzar. Nótese que existe una única trayectoria que une cada polo con un cero, pero esta se ve afectada por el resto ceros existentes.
Las trayectorias generadas con este método se pueden definir como funciones paramétricas de geometría conforme (Landi & Paoletti, 1995), es decir que las trayectorias generadas para sistemas de orden 2 coinciden con segmentos de circunferencia. Para sistemas de orden superior, la forma de dichas trayectorias puede variar dependiendo del orden mismo de los polinomios de numerador y denominador del sistema dinámico; estas pueden ser: rectas, parabólicas, circulares, elípticas y curvas complejas. A su vez, cada una de estas trayectorias se caracteriza por avanzar continuamente desde un polo hasta un cero del sistema, presentando repulsión entre raíces del mismo tipo y atracción entre tipos diferentes de raíces, de forma similar a como lo hacen las cargas que representan el robot, el punto de llegada y los obstáculos en la técnica de campos de potenciales artificiales (Maarouf & Saliah-Hassane, 2011).
Caracterización de la técnica de localización de raíces
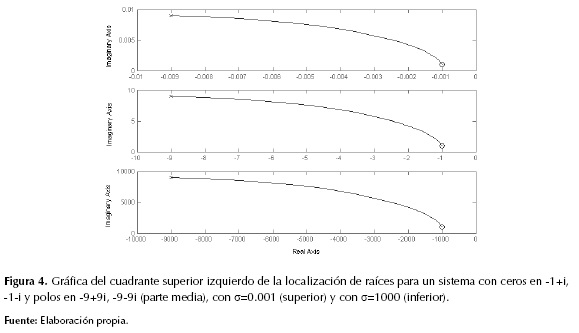
Adicional al comportamiento básico descrito de los polos en la técnica de localización de raíces, existen otras características importantes para tener en cuenta antes de realizar una implementación completa de planeación de rutas. La primera es que la escala de la posición de las raíces no cambia la forma de la trayectoria generada. Si partimos de un sistema dinámico con dos polos y dos ceros complejos conjugados como el mostrado en la ecuación (5), y si se aplica un factor de escala σ (ecuación (6)), la forma de la trayectoria resultante no se vea afectada, como se muestra en la figura 4.
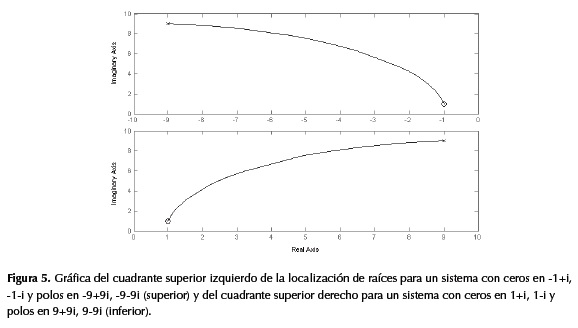
Por otro lado, así como las trayectorias generadas por cada par de polos complejos conjugados son recíprocas, es decir que son simétricas con respecto al eje real, si se tiene la misma disposición de polos y ceros en dos sistemas diferentes, pero se intercambia el semiplano derecho por el izquierdo, las trayectorias generadas para los dos sistemas presentan simetría con respecto al eje imaginario. Esto se puede observar en la figura 5).
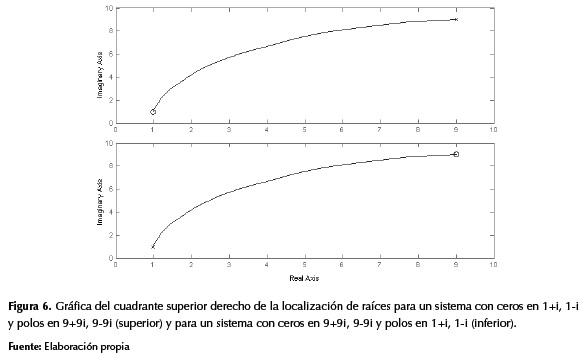
Sabiendo que cada polo de un sistema avanza por una trayectoria definida hasta alcanzar la posición de un polo, se puede decir también que se genera la misma trayectoria si se parte de un punto p(a,c) hacia un punto q(b,d) o viceversa. Es decir que las trayectorias de las raíces de los sistemas mostrados en las ecuaciones (5) y (7) son iguales, tal como se muestra en la figura 6.
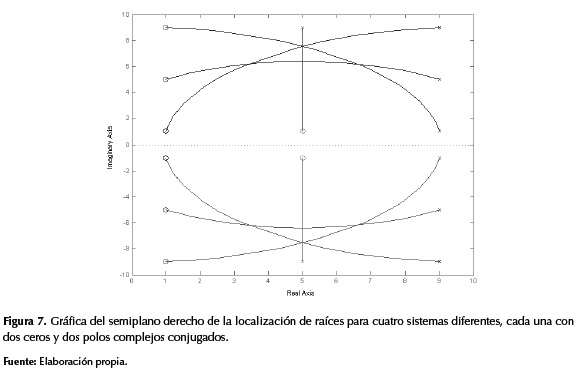
Las trayectorias generadas para sistemas con un par de polos y de ceros complejos tiende hacia arriba en el semiplano superior y hacia abajo en el semiplano inferior. En la figura 7 se muestran las gráficas de localización de cuatro sistemas dinámicos diferentes sobrepuestos uno al otro en los cuadrantes superior e inferior derecho. Se observa la tendencia que tienen las curvas generadas alejándose del eje real, así como también se ve una trayectoria totalmente recta, en el sistema cuyo polo y cero comparten la misma coordenada real.
La forma de las trayectorias de los polos se define por medio de funciones paramétricas en un plano complejo, la cual depende de la ubicación de todas las raíces del sistema dinámico representado, por tal razón hallar una función generalizada para un sistema de orden superior es una tarea demasiado ardua, de tal forma que se procede a utilizar el algoritmo de root locus en el software MATLAB®.
Utilización de la técnica de localización de raíces
Una vez conocidas las características morfológicas de las trayectorias generadas a partir de la técnica de localización de raíces en el plano complejo, se procede a plantear un procedimiento metodológico para su utilización como técnica de planeación de rutas libres de obstáculos para robots móviles. Dicho procedimiento metodológico consiste en tres pasos. Primero se identifican las coordenadas del robot y de los obstáculos utilizando algoritmos de procesamiento de imágenes; luego se genera la función de transferencia del sistema dinámico ubicando raíces en las coordenadas previamente obtenidas. Finalmente se obtiene la gráfica de root locus correspondiente a las rutas viables para la navegación del robot.
Captura y procesamiento de las imágenes del entorno
La captura y procesamiento de las imágenes del entorno es el paso previo a la aplicación del algoritmo de localización de raíces. Su objetivo es entregar la menor cantidad posible de información al algoritmo de planeación, es decir que de una imagen a color con el robot, los obstáculos y la marcación del punto de llegada se obtenga una imagen en blanco y negro con los obstáculos, las coordenadas de ubicación y la orientación del robot y las coordenadas del punto de llegada (Torres, Viáfara, & Martínez S., 2014). Esto se realiza utilizando diversos algoritmos de procesamiento de imágenes, tales como segmentación por colores y cálculo de centroides (Akita, Watanabe, Tooyama, Miyami, & Yoshimoto, 2003).
El algoritmo de segmentación por colores consiste en extraer de la imagen del escenario únicamente las partes de la imagen de determinado color, en este caso los marcadores ubicados sobre el robot, en el punto de llegada y el color de los obstáculos (Torres, Viáfara, & Martínez S., 2014).
Localización de las raíces en los puntos clave del escenario
Para utilizar la técnica de localización de raíces para la navegación de robots es necesario hacer coincidir el sistema coordenado de la imagen original del escenario con el del plano complejo. Teniendo en cuenta que el sistema coordenado de una imagen digital avanza de izquierda a derecha y de arriba hacia abajo, esta se hace coincidir con el cuadrante superior derecho del plano complejo para obtener solo distancias y posiciones positivas. Para lo cual es necesario una transformación entre el sistema coordenado de la imagen de entrada (x1, y1) y el sistema coordenado del plano complejo (x2, y2), como lo definen las ecuaciones (8) y (9), donde S es el factor de escala y maxyi es el máximo número de pixeles en la coordenada y, de la imagen de entrada.
La figura 8 muestra la transformación correspondiente a la imagen de entrada a coordenadas en el plano complejo. Se observa en la parte izquierda la imagen de entrada y sobre el fondo negro se identifica el punto de partida en azul, el punto de llegada en rojo y los obstáculos en blanco. En la parte derecha se observa el mapeo de los puntos de partida y llegada y el obstáculo. Aunque para esta aplicación solo se visualiza uno de los cuadrantes del plano complejo, cabe recordar que todas las raíces del sistema dinámico son complejas conjugadas, es decir que se tiene un comportamiento simétrico con respecto al eje real en el cuadrante inferior derecho. Para este ejemplo se tiene una imagen de entrada de 500*500 pixeles y el semiplano de salida va desde 0 a 10 en cada uno de los ejes coordenados, lo cual implica el uso de un factor de escala S de 0,02.
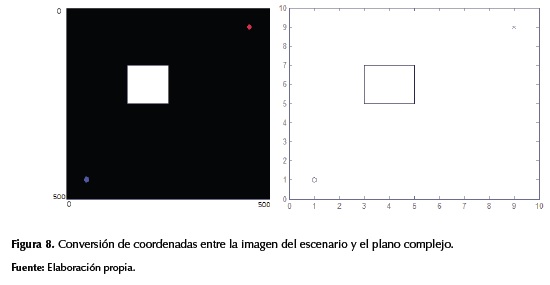
Después de conocer la ubicación exacta del robot y del punto de llegada se localizan sobre estos un polo y un cero respectivamente, de tal forma que al realizar la gráfica de root locus se obtiene una trayectoria semicircular entre el punto de llegada y el punto de salida como se muestra en la figura 9.
La trayectoria inicial generada depende únicamente del punto de partida y del de llegada, sin tener en cuenta el obstáculo. Por tal motivo esta trayectoria puede producir una colisión del robot con alguno de los obstáculos (figura 9).
Por lo tanto es necesario ubicar más raíces con el fin de desviar la trayectoria original de los obstáculos presentes, para esto se proponen tres métodos diferentes los cuales usan como referencia diferentes puntos clave de cada obstáculo. El primer método es la localización de las raíces usando el centro de los obstáculos, el segundo es usando los vértices de los obstáculos y el tercero, usando el borde de los obstáculos
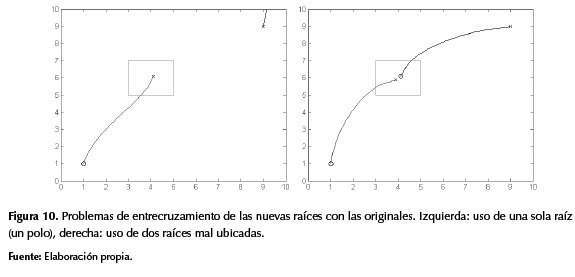
Para los tres métodos propuestos es necesario ubicar al menos dos raíces (un polo y un cero) por cada obstáculo, a una distancia relativamente corta entre ellas, con el fin de que se genere una trayectoria nueva entre este par de raíces y no se presente entrecruzamiento con el polo y el cero originales (figura 10), pero que a su vez afecten la trayectoria original.
Resultados
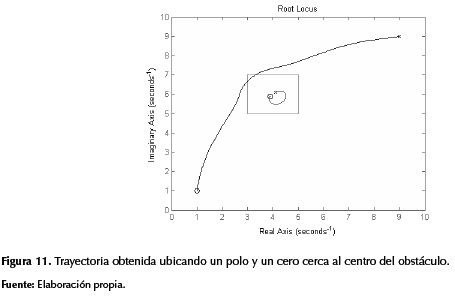
El primer método consiste en ubicar un polo y un cero muy cerca al centro del objeto, a una distancia muy pequeña entre estos; para este caso se define como distancia entre raíces del obstáculo la centésima parte del tamaño máximo del escenario, en coordenadas del plano complejo. Además, tanto el polo como el cero deben ser ubicados desde el centro del obstáculo en dirección hacia su igual de la trayectoria original con el fin de evitar entrecruzamiento (figura 10, derecha) de trayectorias (figura 11).
Adicionalmente, en la figura 11 se puede apreciar que a pesar de que la trayectoria original se ve afectada por el nuevo par de raíces, la desviación no es lo suficientemente grande como para evitar la colisión con el obstáculo. Esto se soluciona aumentando la distancia de separación entre las nuevas raíces.
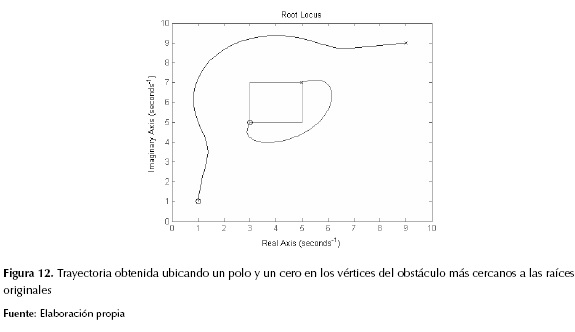
En el segundo método se ubican un polo y un cero en los vértices del obstáculo más cercanos a las raíces de la trayectoria original. Adicionalmente, tanto el polo como el cero deben ser ubicados en el vértice más cercano a su igual de la trayectoria original para evitar entrecruzamiento, como se aprecia en la figura 12.
Este método minimiza altamente el riesgo de colisión del robot con el obstáculo (en el caso de obstáculos con una alta simetría radial evita por completo la colisión), pero genera trayectorias bastante amplias que en dependencia de la ubicación de los obstáculos con respecto al escenario pueden sobrepasar los límites de este, lo que implica una colisión con las paredes del escenario en la aplicación real.
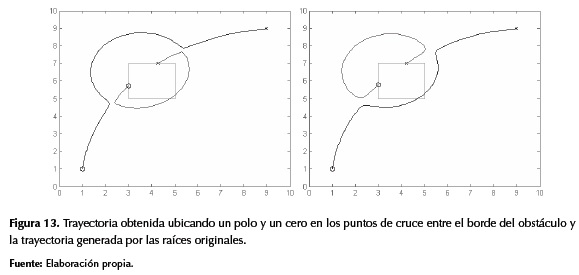
En el tercer método se procede a ubicar un polo y un cero sobre las intersecciones de los bordes del obstáculo y la trayectoria original. De la misma forma que los métodos anteriores, para evitar el entrecruzamiento de las raíces, el polo y el cero deben ser ubicados en el punto más cercano a su igual de la trayectoria original, en este caso el punto de cruce más cercano a cada una de las raíces del mismo tipo, como se ve en la figura 13.
Este método genera una trayectoria circular de desvío sobre la trayectoria principal, como se ve en la figura 13, donde se observa que la ruta generada evita la colisión (izquierda), pero si el obstáculo está levemente desplazado, se puede producir entrecruzamiento o la trayectoria obtenida produce colisión con el obstáculo (derecha).
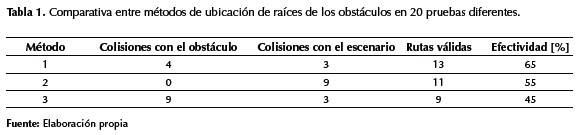
En los tres métodos empleados para la generación de rutas libres de obstáculos para robots móviles se limitaron a un solo obstáculo en el escenario. Se realizaron 20 pruebas para cada método ubicando arbitrariamente el obstáculo, después de lo cual se obtuvieron los resultados mostrados en la tabla 1.
La efectividad se calculó como la proporción entre las pruebas sin colisión y el total de estas. Lo anterior muestra que el método 1 evita en mayor medida las colisiones tanto con el obstáculo como con los bordes del escenario. El método 2 muestra que evita cualquier colisión con el obstáculo, pero genera una trayectoria tan amplia que muchas veces colisiona con el escenario. El método 3 genera muchas colisiones con el obstáculo, por eso su baja efectividad.
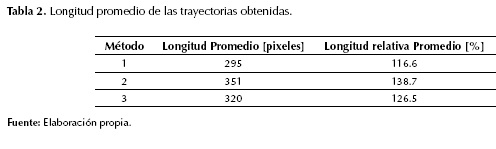
Las 20 pruebas se realizaron con imágenes con resolución de 450*450 pixeles, con las cuales se utiliza una modificación de la técnica de procesamiento de imágenes llamada crecimiento de regiones (Xiaoqi, Jianshuai, Xiaoying, Zhang, & Li, 2014), ampliamente empleada en segmentación de imágenes médicas, para realizar un conteo de la longitud por medio de pixeles de cada una de las trayectorias válidas. Teniendo en cuenta la longitud de una trayectoria ideal hallada con el algoritmo de planeación de rutas BUG (Langer, Coelho, & Oliveira, 2007) de 253 pixeles, se calcula la longitud relativa de cada trayectoria y la longitud relativa promedio sobre las 20 pruebas para cada método. Los resultados se resumen en la tabla 2.
La longitud relativa es calculada como la relación entre el número de pixeles de la trayectoria de referencia y el número de pixeles de las trayectorias obtenidas con cada una de los métodos. El resultado es que el método 1 obtiene trayectorias más cortas en promedio que los otros dos métodos probados.
Conclusiones
La caracterización realizada sobre las trayectorias generadas usando la técnica de localización de raíces en el plano complejo muestra que principalmente se pueden obtener curvas semicirculares para sistemas de orden bajo y curvas complejas para sistemas de orden superior, siendo solo posibles líneas rectas de forma vertical (solo son posibles líneas horizontales sobre el eje real). Este hecho imposibilita la obtención de líneas rectas diagonales, las cuales podrían ser la solución óptima en algunos de los posibles escenarios presentes.
La selección entre un polo o un cero para el punto de partida y por tanto su contraparte parar el punto de llegada es indiferente a la trayectoria inicial obtenida, solo teniéndose en cuenta a la hora de ubicar las raíces correspondientes a los obstáculos.
La escala del plano complejo tampoco tiene efecto sobre la forma de la trayectoria obtenida, por lo que es posible realizar una conversión del sistema coordenado de la imagen de entrada hacia el plano complejo omitiendo el factor de escala S.
Los métodos planteados presentan un mapeo fijo de la imagen del escenario a uno de los cuadrantes del plano complejo; si a esto se le suma que el comportamiento de las trayectorias generadas por root locus presenta convexidad con respecto al eje real, se obtiene un juego de trayectorias limitadas con una tendencia definida que no depende de los obstáculos presentes en el escenario.
Basta con localizar un par de raíces (un polo y un cero) en cada obstáculo para obtener un efecto de repulsión del robot hacia el obstáculo, teniendo en cuenta que estos deben estar ubicados basándose en puntos clave del obstáculo, pero siempre en dirección a su equivalente en la trayectoria original (punto de partida o llegada). En dado caso de que no se ubiquen correctamente las raíces, se puede dar el efecto de entrecruzamiento de raíces produciendo trayectorias con colisiones, lo cual hace que la metodología propuesta sea sensible a pequeños cambios en la posición de los obstáculos.
El método de ubicar las raíces en los vértices del obstáculo evita totalmente la colisión con un obstáculo radialmente simétrico, pero aumenta la probabilidad de colisión con las fronteras del escenario (tabla 1) y genera trayectorias mucho más largas (tabla 2).
El tercer método que consiste en ubicar las nuevas raíces en las intersecciones del borde del obstáculo y la trayectoria original presenta unas trayectorias relativamente cortas, pero con probabilidades altas de colisión con el obstáculo.
Después de las pruebas realizadas se concluye que la mejor opción es el primer método planteado (ubicar un polo y un cero cerca del centro del obstáculo), ya que aunque en algunas ocasiones presenta colisiones con el obstáculo, muestra un mejor promedio de efectividad con respecto a los otros dos métodos (tabla 1 y tabla 2).
Trabajo futuro
Para mejorar la eficiencia del método que ubica un polo y un cero en el centro del obstáculo, se puede aumentar la separación entre ellos; pero al ser esto un problema que depende también de la forma de los obstáculos, se puede hacer que dicha separación dependa del tamaño del objeto, lo cual se logra usando técnicas de procesamiento de imágenes.
Es posible plantear otro método usando el punto más cercano del borde del obstáculo en lugar de los vértices para ubicar las raíces.
Se puede utilizar un algoritmo de dilatación de imágenes sobre la imagen de entrada, con el fin de que cada obstáculo tenga en cuenta el radio mínimo del robot, ya que hasta el momento se trata al robot como un punto en el escenario. Así mismo, se puede pensar en calcular el esqueleto de la imagen de los obstáculos y usarla como referencia para obtener los puntos clave en la ubicación de raíces. Esto se plantea pensando en que el esqueleto es una representación simplificada del mismo obstáculo, el cual lo puede caracterizar de mejor forma. Dado que los métodos planteados funcionan únicamente para escenarios con un obstáculo, se pueden plantear otros para el problema de múltiples obstáculos.
Es posible realizar un algoritmo que ubique de forma adaptativa los polos y ceros de sistema partiendo de su ubicación base, con el fin reducir al mínimo la sensibilidad de la metodología planteada a los pequeños cambios de posición del obstáculo.
Referencias
Akita, J., Watanabe, A., Tooyama, O., Miyami, M., & Yoshimoto, M. (10 de marzo de 2003). An image sensor with fast objects' position extraction function. IEEE Transactions on Electron Devices, 50(1), 184-190. doi:10.1109/TED.2002.806478.
Ganguli, A., Cortés, J., & Bullo, F. (27 de Marzo de 2009). Multirobot Rendezvous With Visibility Sensors in Nonconvex Environments. IEEE Transactions on Robotics, 25(2), 340-352. doi:10.1109/TRO.2009.2013493.
Hellerstein, J. L., Diao, Y., Parekh, S., & Tillbury, D. M. (2004). Proportional Control (1 ed.). Wiley-IEEE Press.
Landi, A., & Paoletti, F. (1995). Reciprocal root locus approach to path planning for multiple mobile robots. INRIA/IEEE Symposium on Emerging Technologies and Factory Automation.2, págs. 345-352. Paris: IEEE. doi:10.1109/ETFA.1995.496675.
Langer, R., Coelho, L., & Oliveira, G. (2007). K-Bug, A New Bug Approach for Mobile Robot's Path Planning. IEEE International Conference on Control Applications (págs. 403-408). Singapore: IEEE. doi:10.1109/CCA.2007.4389264.
Maarouf, J. S., & Saliah-Hassane, H. (2011). An Improved Artificial Potential Field Approach to Real-Time Mobile Robot Path Planning in an Unknown Environment. IEEE International Symposium on Robotic and Sensors Environments (ROSE) (págs. 208-213). Montreal, QC: IEEE. doi:10.1109/ROSE.2011.6058518.
Min-Ho, K., Jung-Hun, H., Yuanlong, W., & Min-Cheol, L. (2011). A path planning algorithm using artificial potential field based on probability map. 8th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI) (págs. 41-43). Incheon, Corea: IEEE. doi:10.1109/URAI.2011.6145929.
Ogata, K. (2010). Ingeniería de Control Moderna (5 ed.). Pearson.
Ordoñez L., R. A., Martínez S., F., & García B., H. R. (Marzo de 2013). Proceso agroindustrial de la producción de panela. Tecnura, 17(35), 47-54. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2013.1.a04.
Rairán A., J. D. (2007). Análisis de Sistemas Dinámicos y control PID (1 ed.). Bogotá, Colombia: Universidad Distrital Francisco José de Caldas.
Torres, J., Viáfara, R., & Martínez S., F. (Diciembre de 2014). Procesamiento de Imágenes para La Planeación de Rutas para Robots Móviles Basados en LEGO Mindstorms NXT. Redes de Ingeniería, 5(2), 16-27.
Vachhami, L., Mahindrakar, A. D., & Sridharan, K. (18 de Octubre de 2010). Mobile Robot Navigation Through a Hardware-Efficient Implementation for Control-Law-Based Construction of Generalized Voronoi Diagram. IEEE/ASME Transactions on Mechatronics, 16(6), 1083-1095. doi:10.1109/TMECH.2010.2076825.
Xiaoqi, L., Jianshuai, W., Xiaoying, R., Zhang, B., & Li, Y. (Mayo de 2014). The study and application of the improved region growing algorithm for liver segmentation. Optik-International Journal for Light and Electron Optics, 125(9), 2142-2147.
Yi-Han, C., Ming-Chang, C., I-Hsum, L., Wei-Yen, W., & Shun-Feng, S. (2013). Image-based obstacle avoidance and path-planning system. International Conference on System Science and Engineering (ICSSE) (págs. 205-209). Budapest: IEEE. doi:10.1109/ICSSE.2013.6614660.
Ziaei, Z., Oftadeh, R., & Matilla, J. (2014). Global Path Planning with Obstacle Avoidance for Omnidirectional Mobile Robot Using Overhead Camera. IEEE International Conference on Mechatronics and Automation (ICMA) (págs. 697-704). Tianjin, China: IEEE. doi:10.1109/ICMA.2014.6885782.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.