DOI:
https://doi.org/10.14483//udistrital.jour.RC.2017.29.a10Published:
05/01/2017Issue:
Vol. 29 No. 2 (2017): May-August 2017Section:
Science EducationDiseño metodológico para la simulación del balance hídrico de una represa: caso Tunja, Colombia
Methodological design to simulate the water balance of a dam: Tunja, Colombia case
Keywords:
Simulación de Monte Carlo, Balance hídrico, Estocástico, Precipitación, Infiltración, Evapotranspiración, Caudal, Escorrentía (es).Keywords:
Monte Carlo simulation, water balance, stochastics, precipitation, infiltration, evapotranspiration, flow, runoff (en).Downloads
References
Abrishamchi, A., Ebrahimian, A., Tajrishi, M., & Mariño, M. A. (2005). Case Study: Application of Multicriteria Decision Making to Urban Water Supply. Journal of Water Resources Planning and Management.
Aguilera Navarro, M. A. (2007). Estimación de funciones de distribución de probabilidad, para caudales máximos, en la región del Maule. Chile: Universidad de Talca.
Allen, R. G., Pereira, L. S., Raes, D., & Smith, M. (2006). Evapotranspiración del cultivo Guías para la determinación de los requerimientos de agua de los cultivos. ONU.
Arriaga, I., Adeath, A., & Rivera, E. (2008). Population growth estimation for the coastal States of Mexico. Papeles de Población, 187-211.
Bedient, P., & Huber, W. (1992). Hydrology and Floodplain Analysis. United States: Addison-Wesley.
Bradley, D. (1992). Health enviroment and tropical development. Health and the environment.
Canavos, G. (1988). Probabilidad y Estadística: Aplicaciones y Métodos. Editorial McGraw-Hill .
Charalambous, J., Rahman, A., & Carroll, D. (2013). Application of Monte Carlo Simulation Technique to Design Flood Estimation: A Case Study for North Johnstone River in Queensland, Australia. Water Resources Management.
Chow, V., Maidment, D., & Mays. (1994). Hidrología Aplicada. Colombia: Editorial McGrawHill Interamericana S.A.
Domínguez Calle, E. A., Gonzalo Rivera, H., Vanegas Sarmiento, R., & Moreno, P. (2008). Relaciones demanda-oferta de agua y el índice de escasez de agua como herramientas de evaluación del recurso hídrico colombiano. Prospectiva.
Falkenmark, M. (1998). Forward to the future: a conceptual framwork for water dependence . AMBIO.
Fowea, T., Karambiria, H., Paturela, J.-E., Poussinc, J.-C., & Cecchic, P. (2015). Water balance of small reservoirs in the Volta basin: A case study of Boura reservoir in Burkina Faso. Elsevier.
Francosa, A., Elorzab, F., Bouraouia, F., Bidoglioa, G., & Galbiatia, L. (2003). Sensitivity analysis of distributed environmental simulation models: understanding the model behaviour in hydrological studies at the catchment scale. Reliability Engineering & System Safety, 205-218.
Gardener-Out, T., & Engleman, R. (1997). Water easing scarcity. Population Action International.
Garzón, A., & Rojas, A. (2014). Optimización del manejo del embalse Teatinos.
Heer, D. M., & Smith, D. O. (1968). Mortality level, desired family size, and population increase. Springer Link.
Horton, R. E. (1933). The Rôle of infiltration in the hydrologic cycle. Eos.
Hudson, N. (1997). Medición sobre el terreno de la erosión del suelo y de la escorrentía . Roma: Silsoe Associates.
IDEAM. (2010). Reporte del recurso hídrico. Ministerio de Ambiente.
IDEAM. (2015). Estudio nacional del agua. Ministerio del Medio Ambiente.
Jhon, Z. (Writer). (2005). Montecarlo Simulation [Motion Picture].
K4Health. (1998). Solutions for a Water-Short World. ohns Hopkins Bloomberg School of Public Health,Center for Communication Programs,The INFO Project.
Kurt, K. B., Lowell, K. E., & Hamilton, A. J. (2008). Parameter uncertainty, sensitivity analysis and prediction error in a water-balance hydrological model. Mathematical and Computer Modelling, 1134-1149.
Ordóñez, J., & Gálvez, J. (2012). Balance hidríco superficial, Contribuyendo al desarrollo de una Cultura del Agua y la Gestión Integral de Recurso Hídrico. Sociedad Geográfica de Lima.
Organización mundial de la salud (OMS). (2014). La OMS y el UNICEF destacan la necesidad de continuar mejorando el acceso a fuentes de agua potable y servicios de saneamiento mejorados. OMS.
Piedrahita Salazar, M. I. (2010). Modelo para el cálculo de la previsión de ajustes por cambio de precios en el tiempo en presupuestos de proyectos de infraestructura .
Population Reference Bureau. (1998). World population data sheet. Washington D.C.
Proactiva. (2014). Análisis y Formulación de la Ingeniería Básica de Alternativas para el Abastecimiento Futuro de Agua para la Ciudad de Tunja.
Pruppacher, H. R., Klett, J. D., & Wang, P. K. (1998). Microphysics of Clouds and Precipitation. Aerosol Science and Technology, 28(4), 381-382.
RAS. (2010). Reglamento Técnico para el sector de Agua Potable y Saneamiento Básico.
Rodriguez Puerto, R. (2012, 03 22). A Tunja no le falta agua por buen funcionamiento de pozos y represas. El Tiempo, p. 13.
Rose, D. (2014). El agua, un recurso escaso. Retrieved from Inspiraction: https://www.inspiraction.org/cambio-climatico/cc-al-detalle/escasez-de-agua
Sokolov, A. A., & Chapman, T. C. (1981). Methods for Water Balance Computation. Organizacion de las Naciones Unidas para la Educación, la Ciencia y la Cutura.
Tidwell, V. C., Passell, H. D., Conrad, S. H., & Thomas, R. P. (2004). System dynamics modeling for community-based water planning: Application to the Middle Rio Grande. Aquatic Sciences.
UNESCO. (2010). Water Balance. UNESCO.
UNESCO. (2014). La crísis mundial del agua. WEBWORLD.
Van Dam, J., & Feddes, R. (2000). Numerical simulation of infiltration, evaporation and shallow groundwater levels with the Richards equation. ELSEVIER.
Zapata, C. J., Piñeros, L. C., & Castaño, D. A. (2004). El método de simulación de Montecarlo en estudios de confiabilidad de sistemas de distribución de energía eléctrica. Scientia et Technica.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de febrero de 2017; Aceptado: de abril de 2017
Resumen
En este trabajo se aplica la técnica de simulación de Monte Carlo para modelar el balance hídrico de una represa que surte de agua potable a la ciudad de Tunja, en Colombia. Se analizan dos fuentes alternas de agua potable. Con el modelo se establece que la mejor fuente alternativa para el abastecimiento de agua para Tunja en los próximos 40 años es el embalse de La Copa. Se desarrolla un método para ajustar la precipitación, la infiltración, la escorrentía, la evapotranspiración y el caudal subterráneo y el de extracción a variables aleatorias. Las proyecciones generadas por medio de esta simulación son estimaciones realistas, ya que la simulación de Monte Carlo permite modelar los flujos de entrada y de salida pertenecientes al balance hídrico como variables estocásticas, de manera que se incluye la incertidumbre inherente a eventos naturales como las condiciones climáticas.
Palabras Clave:
simulación de Monte Carlo, balance hídrico, estocástico, precipitación, infiltración, evapotranspiración, caudal, escorrentía.Abstract
In this work, we use Monte Carlo simulation in order to model the water balance of a dam, which provides water for human consumption to Tunja in Colombia. This model predicts that the best alternative source of water for human consumption for next 40 years in Tunja is La Copa dam. The authors developed a method to adjust our results to precipitations, infiltration, runoff, evapotranspiration, and the subsurface flow and extraction flow; into random variables. Our projections are realistic since Monte Carlo simulation allows us to model input and output flows from water balance, as stochastic variables, so including uncertainty associated with possible states of the nature; for example, weather conditions.
Keywords:
Monte Carlo simulation, water balance, stochastics, precipitation, infiltration, evapotranspiration, flow, runoff.Resumo
Em este trabalho aplica-se a técnica de simulação de Monte Carlo para modelar o balanço hídrico de uma barragem que abastece de água potável à cidade de Tunja, na Colômbia. Duas fontes alternativas de água potável são analisadas. Com o modelo afirma-se que a melhor fonte alternativa de abastecimento de água para Tunja nos próximos quarenta anos é a barragem de La Copa. Um método foi desenvolvido para o ajuste as variáveis aleatórias da precipitação, a infiltração, o escoamento, a evapotranspiração e a água subterrânea e de extração. As projeções geradas por esta simulação são estimativas realistas, já que a simulação de Monte Carlo permite modelar o fluxo de entrada e de saída, como variáveis estocásticas pertencente ao balanço hídrico; de modo que incluem-se a incerteza inerente aos eventos naturais como as condições meteorológicas.
Palavras-chave:
Simulação de Monte Carlo, Balanço Hídrico, Estocásticos, Precipitação, Infiltração, Evapotranspiração, Caudal, Escoamento.Introducción
La escasez de agua es una situación inminente, por ello, desde antes de iniciar el siglo XXI se realizan estudios y campañas para proteger el recurso hídrico (K4Health, 1998). El acelerado crecimiento poblacional y la constante contaminación de los caudales de agua dulce genera niveles muy bajos de agua potable apta para el consumo humano (Bradley, 1992). La cantidad de recurso hídrico puede llegar a catalogarse escaso cuando el valor disponible per cápita por año es inferior a 1000 m3 (Falkenmark, 1998). Para el año de 1992, 31 países sufrían de escasez de agua, sobre todo en África y en el cercano oriente (Gardener-Out y Engleman, 1997).
Solo el 2.5 % del agua del planeta corresponde a agua dulce, de la cual el 30 % es subterránea y el 0.3 % es de caudales de lagos o ríos. Este recurso hídrico es utilizado en un 22 % para la industria, un 70 % para la agricultura y el 8 % para el consumo humano (Rose, 2014). El aumento en la población no solo afecta el consumo humano de agua, también la producción agrícola ya que la demanda de alimentos aumenta. En estudios recientes, se ha establecido que la superficie de la tierra de regadío duplicó su tamaño para el siglo XX (Unesco-WWAP, 2003). Además, el crecimiento en cantidad de uso del agua duplica la tasa de crecimiento poblacional (Rose, 2014).
Actualmente, alrededor de dos billones de personas en más de 40 países se encuentran afectados por la falta de agua potable (Organización mundial de la salud [OMS], 2014) y se estima que para el año 2025, 48 países sufrirán de escasez, lo que representaría un aproximado de 2.8 miles de millones de personas, equivalente al 35 % de la población mundial. Además, grandes países como Pakistán, India y China estarán en peligro de escasez (Population Reference Bureau, 1998). Para el año 2050 se proyecta que una de cada cuatro personas vivirá en una población con insuficiencia de agua (Gardener-Out y Engleman, 1997). La problemática tiene en alerta a todos los países del mundo, pues las proyecciones son preocupantes; sin embargo, los países en vía de desarrollo son los que presentan una mayor afectación (Unesco-WWAP, 2003).
En el caso de Colombia, uno de los países catalogados como Potencia hídrica, al igual que Brasil, Canadá y la Federación Rusa, enfrenta una situación diferente ya que presenta, al parecer, suficiente agua, pero con alta densidad poblacional en los polos de desarrollo (Domínguez Calle, Gonzalo Rivera, Vanegas Sarmiento y Moreno, 2008). En Colombia, para el año 1985, se tenía un aproximado de 60.000 m3 por habitante al año (Domínguez Calle et al., 2008), pero para el año 2000 esta cifra se redujo a 40.000 m3 por habitante al año. Aunque el valor registrado para el año 2000 continuaba siendo una cifra alta respecto a los estándares dados por Falkenmark, en las principales ciudades del país la cifra se reduce a 5.000 m3 para el año 2010 (Ideam, 2010). Esto es producto de la problemática comentada anteriormente. Por otro lado, se puede analizar que la tasa de reducción del recurso hídrico es considerable, lo que permite realizar estimaciones frente una posibilidad de llegar a valores inferiores a 1.000 m3 por habitante al año en un periodo de 30 años, esto si se continua con un comportamiento de uso y crecimiento igual.
La problemática de escasez de agua en Colombia debe evaluarse desde dos perspectivas: de un lado, el crecimiento poblacional y la inconciencia en el uso del recurso hídrico, y segundo, la migración de la población rural hacia los centros de desarrollo del país (Domínguez Calle et al., 2008). Según el estudio nacional de agua realizado por el Ideam, para el año 2015 el 43.8 % de la población se encuentra en un índice alto de escasez de agua, el 16.1 % en medio alto, y el 6.1 % en medio (Ideam, 2010 y 2015). Este comportamiento es causado por la alta demanda en zonas específicas del país y la poca infraestructura existente para prestar el servicio de agua potable a grandes cantidades de población (Ideam, 2015).
Teniendo en cuenta la evidente problemática global y la situación que presentan países como Colombia, en este documento se desarrolla una metodología que permite evaluar la cantidad de recurso hídrico disponible para una población en una ubicación urbana o rural específica así como alternativas para abastecimiento de agua potable. Por medio de un modelo probabilístico basado en la simulación de Monte Carlo para el balance hídrico de una represa, se pretende realizar un estudio de confiabilidad y de esta forma tener en cuenta la variabilidad y la incertidumbre de cada uno de las variables relevantes en el balance hídrico.
La simulación de Monte Carlo es un método que permite tener en cuenta la incertidumbre de los datos de entrada mediante la generación de escenarios. Este método puede ser aplicable para problemas con entradas estocásticas o determinísticas. En el caso de la situación problema que se trabaja en esta investigación, se utilizan variables estocásticas y valores determinísticos.
El documento se organiza, primero, con un acercamiento a las metodologías implementadas para el modelamiento de la disponibilidad del recurso hídrico, seguido de la explicación del método de Monte Carlo y de la metodología implementada para modelar las variables pertenecientes al balance hídrico y, finalmente, se desarrolla un caso de estudio y aplicación de la metodología propuesta.
Revisión de literatura
Tidwell, Passell, Conrad y Thomas proponen la utilización de la dinámica de sistemas para modelar el balance hídrico de una represa y el comportamiento de consumo por parte de la población por medio de un diagrama de ciclos causales (Tidwell et al., 2004). Para el modelamiento del balance hídrico establecen flujos que afectan negativa o positivamente el volumen de la represa. De esta forma, se establecen los mismos flujos pertenecientes al balance hídrico (precipitación, evaporación, infiltración, entre otros) que afectan en la oferta y demanda de agua para un condado, además modelan otros flujos que afectan a estas variables como, por ejemplo, el clima y la población. Este modelamiento surge con el fin de analizar el sistema y así planificar un abastecimiento de agua continuo para todas las partes que demandan. Lo interesante de este modelamiento es que reúne y toma diferentes variables tanto físicas (comprende del funcionamiento natural de la represa) como sociales que interactúan en el sistema. Además, modelan estas variables de forma evolutiva, lo que permite tener en cuenta los cambios en las variables físicas como, por ejemplo, el aumento en lluvias, fenómenos de sequía o lluvia abundantes; de igual forma permite contener el crecimiento de la población y los otros consumidores de las represas (Tidwell et al., 2004).
Por su parte, Abrishamchi, Ebrahimian, Tajrishi y Mariño proponen la aplicación de la metodología de toma de decisiones bajo un análisis multicriterio para el suministro continuo de agua a dos poblaciones en Irán (Abrishamchi et al., 2005). Esta metodología se basa en la búsqueda de información cuantitativa y cualitativa que permite desarrollar modelos para la toma de decisión por parte de un agente decisor. El método multicriterio permite evaluar las alternativas de forma integral ya que se contempla los diferentes criterios y/o variables que deben tenerse en cuenta para tomar la decisión. Estos criterios están definidos por expertos en el tema.
En este caso en particular hacen uso del método basado en la distancia, el cual es un modelo analítico de la metodología multicriterio. Esta es una metodología que encuentra la solución más cercana al ideal dado una distancia, para esto es necesario que se asigne un valor a los criterios por parte del agente (Abrishamchi et al., 2005).
En algunas ciudades de África se cuenta con varios reservorios que no son protegidos de forma adecuada por el desconocimiento que se tiene de su importancia en cuanto a la capacidad de suministro de agua. Fowea, Karambiria, Paturela, Poussinc y Cecchic (2015) realizan un estudio para evaluar y contabilizar los flujos de agua en los reservorios, dadas las estacionalidades. De esta forma, se identifican y estiman los flujos de demanda y oferta de agua con los errores asociados, esto con el fin de obtener el volumen del balance hídrico basado en pocos datos. El hecho de conocer la disponibilidad del recurso permite establecer una distribución de la represa y la forma de abastecimiento.
Van Dam y Feddes (2000) realizan un estudio que permite evaluar y cuantificar la infiltración, evaporación y el flujo de agua subterránea, teniendo en cuenta el volumen de agua y los sedimentos que cambian el comportamiento del flujo. Este caso de estudio es aplicado para reservorios que tienen un nivel bajo de agua. En este tipo de cuencas es de gran relevancia el estudio pues la composición del flujo está dada por agua y sedimentos. Este documento es un aporte para realizar el modelo de confiabilidad, ya que describe en profundidad el balance hídrico de una represa.
Charalambous, Rahman y Carroll (2013) desarrollan la necesidad de generar modelos que contemplen la variabilidad de los datos, en cuanto se pretende realizar proyecciones. En el caso de estudio de este artículo, se desea realizar proyecciones de la ocurrencia de inundaciones en Queensland, Australia. Aunque existen modelos de proyección de inundaciones para la zona, la probabilidad de falla supera el 40 % (Charalambous et al., 2013). La justificación presentada por estos autores es que ninguno de los modelos contempla el error que generan los datos históricos. En este trabajo se modela por medio del método de Monte Carlo el balance hídrico de una represa o cuenca, basado en datos históricos y generando comportamiento aleatorio. Las variables más representativas son las precipitaciones y el caudal subterráneo.
Metodología
Método de Monte Carlo
La simulación de Monte Carlo es una herramienta para la toma de decisiones que permite modelar el riesgo en los análisis cuantitativos. Este método arroja una serie de posibles resultados que contemplan la probabilidad de ocurrencia de los hechos bajo evaluación. Desde su aparición ha sido utilizada en diferentes campos como finanzas, energía, petróleo, transporte, medio ambiente, entre otros (Glasserman, 2013).
Este método permite tener en cuenta el riesgo mediante la creación de modelos probabilísticos que incorporan variables aleatorias de entrada, con una distribución de probabilidad. En el momento de ejecutar la simulación se calculan los resultados teniendo en cuenta la generación de números aleatorios con dichas funciones de probabilidad. La cantidad de iteraciones que la simulación realiza depende del número de variables aleatorias especificadas y puede ser necesario de miles a decenas de miles de cálculos. De esta forma, se asegura tener un error de la estimación que decrece dependiendo de la cantidad de iteraciones, como en el teorema del límite central (Piedrahita Salazar, 2010) (Zapata, Piñeros y Castaño, 2004).
Con la simulación de Monte Carlo se obtienen resultados probabilísticos, se pueden obtener las estadísticas básicas y sus percentiles y realizar análisis de sensibilidad (Glasserman, 2013).
Modelamiento
La metodología propuesta para esta investigación consiste en el modelamiento probabilístico del balance hídrico de una represa que sirve para una o varias poblaciones. De esta forma, se tendrá en cuenta un análisis continuo del volumen disponible a lo largo del tiempo (Zapata et al., 2004).
Balance hídrico
El balance hídrico se basa en la aplicación del principio de conservación de masa, el cual indica que la variación del volumen almacenado en la represa es la diferencia entre las entradas y las salidas de agua (Fowea et al., 2015). La técnica implica mediciones tanto de almacenamientos, como de flujos de agua, aunque algunas variables se eliminan en función del periodo de tiempo o del volumen. La ecuación general del balance es como en (1) (Sokolov y Chapman, 1981):
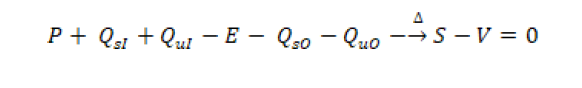
Donde,
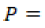 precipitación en forma de lluvia o nieve recibida en la superficie del suelo.
precipitación en forma de lluvia o nieve recibida en la superficie del suelo.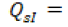 agua superficial recibida dentro de la cuenca desde fuera.
agua superficial recibida dentro de la cuenca desde fuera.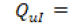 agua subterránea recibida dentro de la cuenca desde fuera.
agua subterránea recibida dentro de la cuenca desde fuera.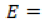 evaporación desde la superficie de la masa de agua.
evaporación desde la superficie de la masa de agua.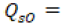 corrientes de agua superficial desde la cuenca.
corrientes de agua superficial desde la cuenca.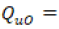 corrientes de agua subterránea desde la cuenca.
corrientes de agua subterránea desde la cuenca.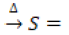 cambio considerado de la diferencia entre las entradas y las salidas.
cambio considerado de la diferencia entre las entradas y las salidas.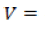 término residual o de diferencia.
término residual o de diferencia.
La ecuación (1) es una ecuación general dependiendo del tipo de superficie, periodo de tiempo que se desea calcular, datos disponibles, características hidrográficas e hidrológicas, entre otras. Esta podría simplificarse o ser más compleja. Por ejemplo, en los ríos las corrientes de aguas superficiales y subterráneas que salen son irrelevantes comparados con otros términos, por lo que estos dos se desechan de la ecuación (Sokolov y Chapman, 1981; Ordóñez y Gálvez, 2012).
El balance hídrico puede ser calculado para cualquier intervalo de tiempo. Para obtener los valores medios se debe realizar el cálculo para un año, para una estación o un mes. En el caso de esta investigación se realiza el cómputo del balance hídrico medio por mes, ya que en el trópico no hay estaciones. Sin embargo, algunas de las variables relevantes presentan estacionalidad en su comportamiento. Teniendo en cuenta el periodo de cálculo del balance hídrico, y que se desea desarrollar sobre una represa, la expresión del balance queda como en (2):
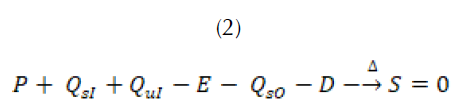
Para el caso de estudio se va a tener en cuenta la variable 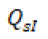 como la escorrentía,
como la escorrentía, 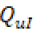 como la variable del caudal del río que desemboca en la represa y
como la variable del caudal del río que desemboca en la represa y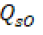 como la infiltración que se genera en el suelo de la misma. Dado que la represa no tiene un caudal de salida ya que no es continuación de un rio o una laguna, la variable
como la infiltración que se genera en el suelo de la misma. Dado que la represa no tiene un caudal de salida ya que no es continuación de un rio o una laguna, la variable 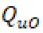 es remplazada por la variable
es remplazada por la variable 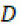 que representa la demanda de agua de la población y de los demás consumidores. En cuanto a la variable que representa el cambio en el volumen,
que representa la demanda de agua de la población y de los demás consumidores. En cuanto a la variable que representa el cambio en el volumen, 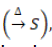 se implementa teniendo en cuenta el resultado del cálculo del balance hídrico del mes anterior. La variable, la
se implementa teniendo en cuenta el resultado del cálculo del balance hídrico del mes anterior. La variable, la 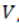 cual representa la incertidumbre de los datos es eliminada dado que las variables van a ser modeladas como aleatorias, teniendo en cuenta la distribución probabilística de las mismas.
cual representa la incertidumbre de los datos es eliminada dado que las variables van a ser modeladas como aleatorias, teniendo en cuenta la distribución probabilística de las mismas.
Modelamiento de la precipitación
La precipitación es considerada como el resultado de la condensación del vapor de agua en la atmosfera cuando el aire se encuentra saturado (Pruppacher, Klett y Wang, 1998).
Para el cálculo de la precipitación se debe tener el valor histórico de las precipitaciones mensuales para la zona a evaluar, como en (3), y al menos 15 datos reales históricos1, que es el valor mínimo para poder obtener una distribución de probabilidad de los datos (Canavos, 1988).
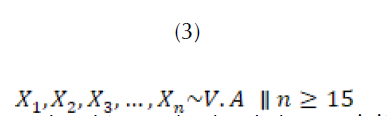
Para poder obtener el valor de las precipitaciones ocurridas en un mes en la zona acuífera específica se debe tener en cuenta el área superficial de la cuenca expresada en m2. De esta forma, se puede realizar el producto entre la cantidad de lluvia en mm (modelada con la función de probabilidad) y el área de la cuenca, como se muestra en (4) (Fowea et al., 2015).
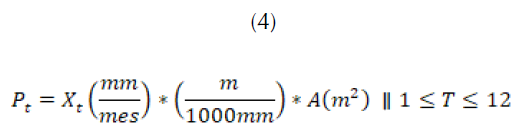
En la simulación realizada se genera una macro capaz de analizar hasta 50 datos históricos y hallar la distribución de probabilidad que más se ajusta. Las distribuciones de probabilidad obtenidas para los 12 meses deben repetirse por la cantidad de periodos que se desee modelar.
Modelamiento de la escorrentía
La escorrentía se entiende como el flujo de agua, en estado sólido o gaseoso, sobre la superficie de la tierra. Esta puede generarse por precipitaciones o por fundición de nieve en lugares muy fríos. Sin embargo, no todas las precipitaciones generan escorrentía porque el suelo puede absorber el agua (Hudson, 1997). Hay diferentes metodologías para contabilizar la escorrentía, estudios han llegado a la conclusión de que su valor está relacionado a otras variables como la precipitación, la inclinación, las horas de sol al mes, y la permeabilidad del terreno (Chow, Maidment y Mays, 1994).
Para el caso este modelo se tiene en cuenta como un porcentaje de la precipitación. Para hallar este porcentaje se deben realizar estudios previos que permitan evaluar la relación existente entre la cantidad de lluvia que cae directamente a la cuenca y aquella que permanece en los alrededores y que entra a la cuenca en forma de escorrentía. Para el cálculo del porcentaje se debe tener en cuenta tanto el perímetro de la represa que se desea evaluar como la inclinación del terreno donde está ubicada, como aparece en (5).
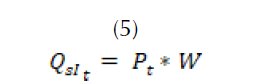
Donde,
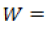 porcentaje de agua que entra como escorrentía.
porcentaje de agua que entra como escorrentía.
Modelamiento del caudal de entrada
El caudal es la cantidad de agua que lleva un río y varía según el mes en que se evalúe. En situaciones donde no se tiene acceso a datos históricos, no es posible realizar un cálculo confiable. En este estudio se plantea un método para obtener un valor del caudal promedio mensual, dadas las precipitaciones medias mensuales y el caudal promedio anual del río. Se toma como supuesto que el caudal va a seguir un comportamiento similar al de las lluvias promedio de la zona, puesto que las variaciones del caudal del río se deben al cambio en el volumen de precipitación. Lo anterior indica que en los meses que se presenta mayor precipitación, también habrá un mayor caudal del río (Bedient y Huber, 1992).
Con el valor promedio del caudal anual y la información histórica de las lluvias mensuales, se propone hallar el porcentaje (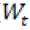 ) que representa el aporte de las precipitaciones promedio de cada mes en el valor total de las precipitaciones promedio anuales, como se muestra en (6) y (7).
) que representa el aporte de las precipitaciones promedio de cada mes en el valor total de las precipitaciones promedio anuales, como se muestra en (6) y (7).
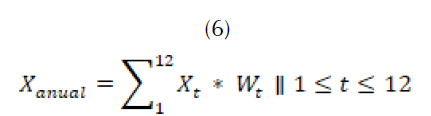
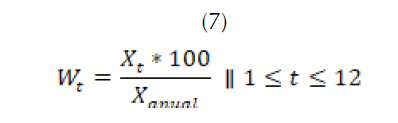
Donde,
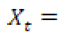 valor promedio de lluvias al mes en la zona.
valor promedio de lluvias al mes en la zona.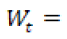 porcentaje de lluvia mensual del total de lluvias anuales.
porcentaje de lluvia mensual del total de lluvias anuales.
Con el porcentaje hallado de las variables mensuales sobre la variable anual, se puede calcular la media del caudal mensual, como en (8).
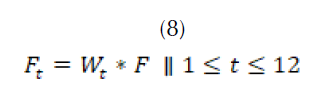
Donde,
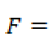 media anual del caudal del río.
media anual del caudal del río.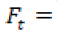 media mensual del caudal del río.
media mensual del caudal del río.
Este dato considera los valores promedios; sin embargo, para tener en cuenta la variabilidad de los datos se usa la desviación estándar (9).
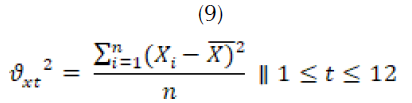
Donde,
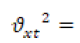 varianza de la precipitación para el mes t.
varianza de la precipitación para el mes t.
La desviación estándar sirve como base para calcular el porcentaje de la desviación respecto a las precipitaciones anuales esperadas (10).
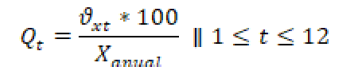
Donde,
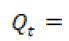 porcentaje de la desviación estándar con respecto al total precipitaciones esperado.
porcentaje de la desviación estándar con respecto al total precipitaciones esperado.
A partir este valor se calcula el valor de la desviación estándar del caudal mensual (11).
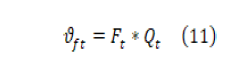
Donde,
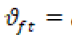 desviación del caudal para el mes t.
desviación del caudal para el mes t.
Con el promedio del caudal para cada mes y la desviación estándar se construye una variable aleatoria con distribución . Esta distribución proporciona el pronóstico del caudal mensual del río (12).
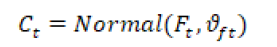
Para poder calcular la cantidad del flujo de entrada del caudal se debe conocer el porcentaje del río que desemboca en la cuenca. Con el valor aleatorio de la , y el porcentaje de descarga (), se puede obtener el valor del flujo de entrada mensual, como en (13), correspondiente al caudal del río (Aguilera Navarro, 2007).
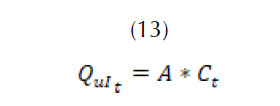
Donde,
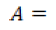 porcentaje del río que desemboca en la cuenca.
porcentaje del río que desemboca en la cuenca.
Modelamiento de la evapotranspiración
La evapotranspiración se conoce como la combinación entre la transpiración y la evaporación. La primera, contempla la pérdida de agua por la vaporización del agua líquida contenida en los tejidos de las plantas y, la segunda, corresponde a la perdida de agua a través de la superficie de suelo. Las dos ocurren al mismo tiempo y no hay forma de distinguirlas (Allen, Pereira, Raes y Smith, 2006).
Para cuantificar la evapotranspiración se conocen varios métodos, de los cuales tres han arrojado los cálculos más acertados: el método Thorntwaite, el método Turc y el método de Blanney-Criddle. Para el desarrollo de esta investigación se utiliza el método de Blanney-Criddle, considerado como el más apropiado para los intereses de la investigación (Allen et al., 2006). Este método propone una expresión donde la evapotranspiración está en función de la temperatura promedio mensual (en celsius), el porcentaje de horas de luz (en relación con el total de horas de luz anual) y el coeficiente de cultivo. Para el cálculo de la evapotranspiración, en (14) se incorporan pronósticos de la temperatura y del porcentaje de horas de luz, los cuales serán modelados de acuerdo a su comportamiento histórico.
Método de Blanney-Criddle
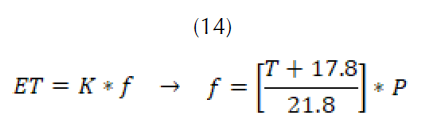
Donde,
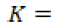 coeficiente de cultivo.
coeficiente de cultivo.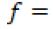 factor de temperatura y luminosidad.
factor de temperatura y luminosidad.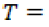 temperatura promedio mensual (°C).
temperatura promedio mensual (°C).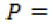 porcentaje de horas luz en el día en relación con el total anual (%).
porcentaje de horas luz en el día en relación con el total anual (%).
Para el modelamiento de se necesita conocer el valor promedio de las horas diarias de sol por mes y el total de horas promedio de sol al año. Es importante que estos promedios estén basados en información histórica relevante (más de 15 años). Con esto se puede calcular la media del porcentaje mensual de horas luz y la desviación, como se muestra en (15), (16) y (17).
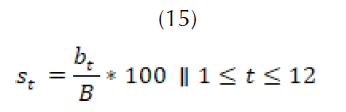
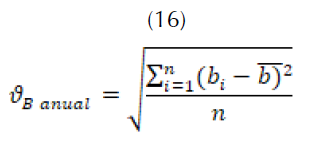
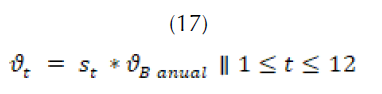
Donde,
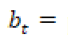 promedio de horas de sol al día en el mes t.
promedio de horas de sol al día en el mes t.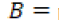 promedio de horas de sol al año.
promedio de horas de sol al año.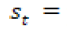 porcentaje promedio mensual de horas de luz al día en relación con el total anual.
porcentaje promedio mensual de horas de luz al día en relación con el total anual.
Con la información calculada se construye una distribución normal 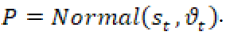 Para el modelamiento de la temperatura promedio mensual se requiere conocer datos históricos de la temperatura mínima, la media y máxima promedio. La mayoría de los datos globales referentes a la temperatura se encuentran catalogados en estas tres variables (Unesco-WWAP, 2015). Con esta información se construye una variable aleatoria con distribución triangular (18).
Para el modelamiento de la temperatura promedio mensual se requiere conocer datos históricos de la temperatura mínima, la media y máxima promedio. La mayoría de los datos globales referentes a la temperatura se encuentran catalogados en estas tres variables (Unesco-WWAP, 2015). Con esta información se construye una variable aleatoria con distribución triangular (18).
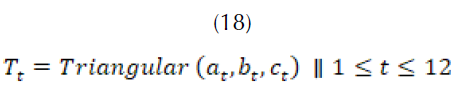
Donde,
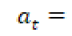 temperatura mínima promedio mensual para el mes t.
temperatura mínima promedio mensual para el mes t.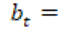 temperatura media promedio mensual para el mes t.
temperatura media promedio mensual para el mes t.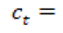 temperatura máxima promedio mensual para el mes t.
temperatura máxima promedio mensual para el mes t.
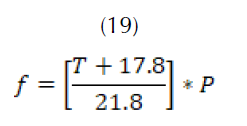
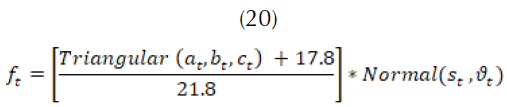
Para el cálculo de la evapotranspiración se requiere conocer el coeficiente de cultivo. Dicho coeficiente describe las variaciones de la cantidad de agua que las plantas extraen del suelo en todo su periodo de crecimiento; su cálculo depende de la ubicación del cultivo respecto a la longitud meridional y el tipo de suelo. Se tienen los coeficientes de cultivo para cada mes (Allen et al., 2006). Con esta información se calcula:
El resultado en (21) muestra la evapotranspiración para el sector. Para obtener el flujo de salida por evapotranspiración en la cuenca 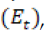 se debe multiplicar
se debe multiplicar 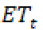 por el área de la represa en el momento t, como en (22).
por el área de la represa en el momento t, como en (22).
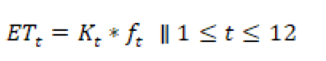
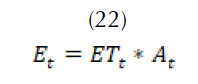
Esta área depende del volumen de agua contenido en la represa. El cálculo del área de la represa en función del volumen se halla con la ecuación (23).
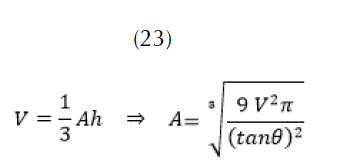
Se puede entonces calcular el área en función del volumen, que en este caso es el valor obtenido del balance hídrico, y de la inclinación de la represa. Al tomar la expresión (23), en la ecuación (22), se obtiene la función (25):
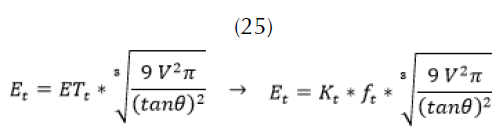
Modelamiento de la infiltración
La infiltración es el proceso por el cual el agua de la superficie entra al suelo. Se mide dada la capacidad del suelo de absorber el agua de la precipitación. La cantidad de infiltración en una represa es una de las variables más difíciles de medir y se debe realizar un estudio de suelo que permita conocer la permeabilidad del mismo (Fowea et al., 2015). Para su cálculo se utilizan valores establecidos que se derivan del tipo del suelo y del tiempo que lleva construida la represa. En este modelo se utilizan porcentajes a partir de datos históricos, los cuales arrojan la tasa de infiltración del terreno (Horton, 1933), como en (26).
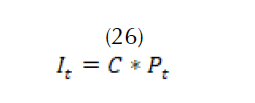
Donde,
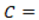 porcentaje de las precipitaciones que se convierte en infiltración.
porcentaje de las precipitaciones que se convierte en infiltración.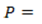 precipitaciones medias mensuales en la represa.
precipitaciones medias mensuales en la represa.
Según la Unesco, la infiltración se reduce a un porcentaje mínimo del volumen aportado por las precipitaciones siempre y cuando sea un terreno de poca permeabilidad (Unesco-WWAP, 2015).
Modelamiento de la demanda
Para el modelamiento de la demanda se debe tener claridad sobre los consumidores del agua almacenada en la represa o cuenca. Para este modelo se dividen en dos tipos: los consumidores pertenecientes a una ciudad, pueblo o municipios; y los otros consumidores, que podrían ser grandes empresas o distritos de riego. La demanda de la población requiere un análisis a mayor profundidad, ya que la población presenta una tasa de crecimiento. Para calcular su crecimiento se tienen en cuenta los últimos censos realizados (Arriaga, Adeath y Rivera, 2008), como se especifica en (27) y (28).
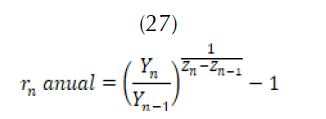
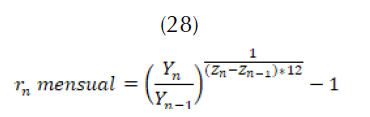
Donde los valores de los censos son, 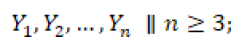 tomados en los años
tomados en los años 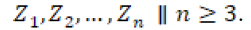 Se tiene en cuenta que .
Se tiene en cuenta que . 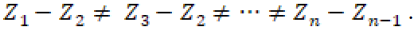
Con la información de las tasas se puede hallar el promedio ponderado, esto con el fin de traer el tamaño de la población a la fecha de realización del modelo desde el último censo (29) y (30).
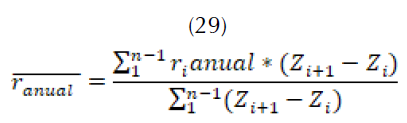
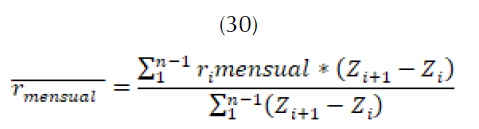
De esta forma se calcula la población en la actualidad y, para el caso de los pronósticos, se propone modelar la tasa de crecimiento como una distribución  (Heer y Smith, 1968) como en (32).
(Heer y Smith, 1968) como en (32).
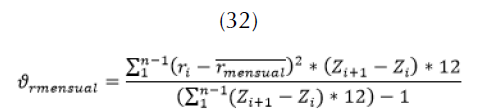
A partir de la distribución se halla el número de personas en el tiempo 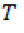 (33).
(33).
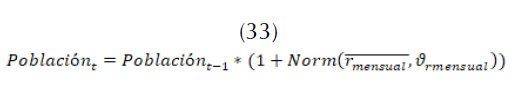
Los estándares mundiales estipulan que el cálculo de un balance hídrico debe contemplar el requerimiento mínimo de agua de una persona (Francosa, Elorzab, Bouraouia, Bidoglioa y Galbiatia, 2003; Kurt, Lowell y Hamilton, 2008). El recurso disponible por habitante debe oscilar entre 110 l/s y 150 l/s; este aspecto depende del tamaño de la población. Adicionalmente, se debe considerar una pérdida de agua (34).
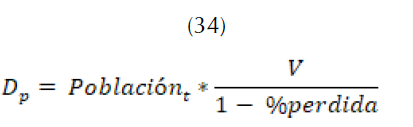
Donde,
valor constante que especifica el consumo por persona.
Para el cálculo de la demanda total se debe considerar que en ocasiones una cuenca o represa abastece a más de una población, por lo que debería realizarse el pronóstico para cada población por separado. En el caso de las otras demandas, suelen existir concesiones que indican el valor del caudal que se va a utilizar. Dada la información histórica se puede hallar un valor promedio de consumo y una desviación mensual. Esta variable puede ser limitada por el valor máximo de la concesión (35).
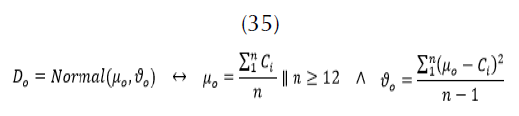
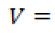 Con el valor de esta normal se calcula el caudal total de extracción por la demanda (36).
Con el valor de esta normal se calcula el caudal total de extracción por la demanda (36).
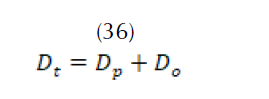
Caso de aplicación
El modelo propuesto se aplica en la ciudad de Tunja, capital del departamento de Boyacá, Colombia. Esta ciudad se encuentra a 130 km al noreste de Bogotá. Se toma como caso de aplicación dado que es una ciudad que puede presentar una problemática de suministro de agua en el corto plazo (Rodriguez Puerto, 2012).
En Tunja hace tan solo 17 años se estableció el suministro de agua continuo para la población, esto por la falta de infraestructura y sistemas de acueducto que permitieran la conexión a los hogares. Aunque en la actualidad el suministro de agua para Tunja es continuo, las proyecciones del crecimiento poblacional permiten evidenciar la problemática a mediano o corto plazo de escasez. Tunja se abastece por medio de la represa de Teatinos y de 12 pozos profundos; sin embargo, se estima que estos serán insuficientes en un periodo de tiempo inferior a 30 años (Proactiva, 2014).
Para evaluar la situación actual se desarrolla la simulación de Montecarlo sobre el pronóstico del balance hídrico de la represa de Teatinos, para los próximos 45 años, y también se modelan dos alternativas que corresponden a otras dos represas que podrían complementar el abastecimiento de agua a Tunja.
Represa de Teatinos
Modelamiento de la precipitación
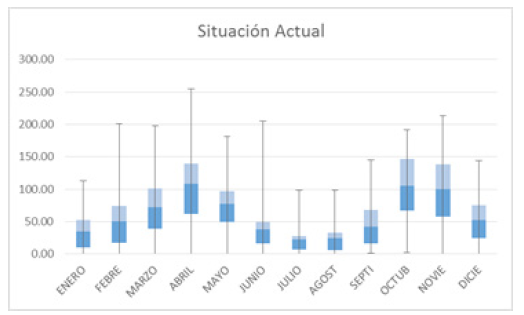
Para evaluar la represa de Teatinos se utilizó el histórico de lluvias en mm/mes de la estación de Samacá (lugar donde se encuentra la represa), desde 1960 hasta 2008 (información suministrada por el Ideam [2010]). En la figura 1 se puede observar el mínimo, máximo, media, quintil 25 y quintil 75 de las precipitaciones para cada uno de los meses.
Figura 1: . Precipitación mensual en Samacá, Boyacá.
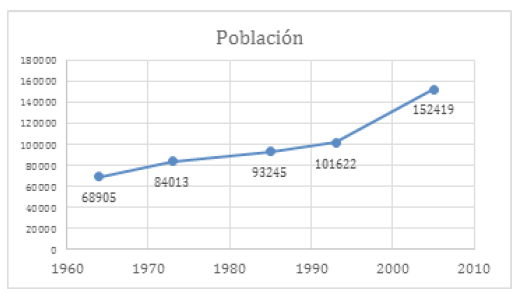
Figura 2: Grafico de crecimiento poblacion de Tunja.
Como se puede observar, el mes con mayor precipitación registrada es abril. Sin embargo, la media de precipitaciones de octubre y noviembre es similar y muy cercana a la reportada en este mes. Los meses de mayor sequía corresponden a julio y agosto. Dada la información de las precipitaciones se realizó un ajuste a una distribución de probabilidad (tabla 1).
Tabla 1: Distribuciones de probabilidad obtenidas mm/mes

En cuanto al área, se establece que la represa de Teatinos cuenta con 10’740.000 m2 (Proactiva, 2014). De esta forma, se puede aplicar la formulación sugerida para el cálculo del flujo de entrada por precipitaciones, en cada mes (37).
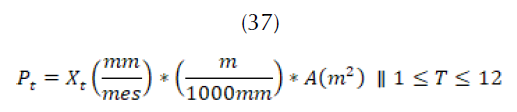
Modelamiento de la escorrentía
Para calcular la escorrentía total al mes en la represa de Teatinos se utiliza la información suministrada por la empresa de acueducto y alcantarillado de Tunja (Proactiva, 2014). Estudios realizados por la empresa encuentran que la relación de lluvias y escorrentía es 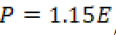 , donde
, donde 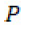 es la precipitación y
es la precipitación y 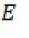 la escorrentía (Proactiva, 2014). De acuerdo con la ecuación (5), y según la relación obtenida de la empresa, obtenemos que
la escorrentía (Proactiva, 2014). De acuerdo con la ecuación (5), y según la relación obtenida de la empresa, obtenemos que 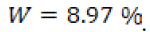 .
.
Para la precipitación se utilizan las mismas distribuciones de probabilidad encontradas anteriormente.
Modelamiento del caudal de entrada
Dado que el río Teatinos es el río que desemboca en la represa del mismo nombre, se tiene que el caudal medio anual es de 215 lt/s, y el porcentaje de desembocadura es del 88 % (Garzón y Rojas, 2005). De la información suministrada por el Ideam (2010), se puede hacer el cálculo de la media y de la deviación de las precipitaciones por mes y anuales: 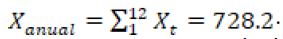 .
.
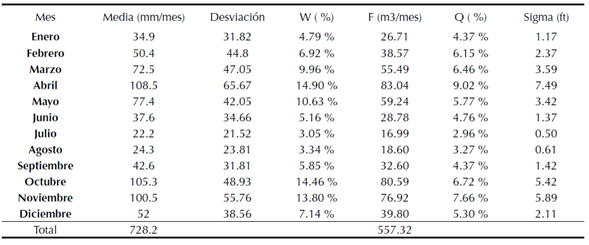
Con esta suma se calcula el porcentaje de cada mes según (7) y (8), para la media, y la desviación como en (11). Y también se calcula en términos del caudal como en (10). Los resultados se muestran en la tabla 2.
Tabla 2: Media, deviacion, porcentajes y calculo de caudal por mes.
Con los valores de 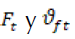 se construye una distribución
se construye una distribución 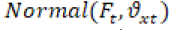 en cada uno de los meses para realizar el cálculo del caudal de entrada.
en cada uno de los meses para realizar el cálculo del caudal de entrada.
Modelamiento de la evapotranspiración
De la ecuación (14) se calcula , correspondiente al porcentaje de horas luz en el día en relación con el total anual. Para esto se utiliza el promedio de horas de sol al día por mes y el total de horas de sol por año. Con la información suministrada por el Ideam (2010) se calcula la media del porcentaje mensual de horas luz y la desviación (tabla 3).
Fuente: Ideam (2010).
Tabla 3: Informacion de horas de sol, porcentajes y desviacion de las horas de sol sobre el total anual por mes.
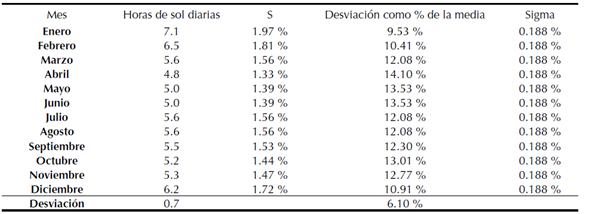
En cuanto a la temperatura promedio mensual, se utiliza la información histórica del municipio de Samacá y se construye una variable aleatoria que con distribución triangular (tabla 4).
Tabla 4: Temperatura minima, medio y maxima por
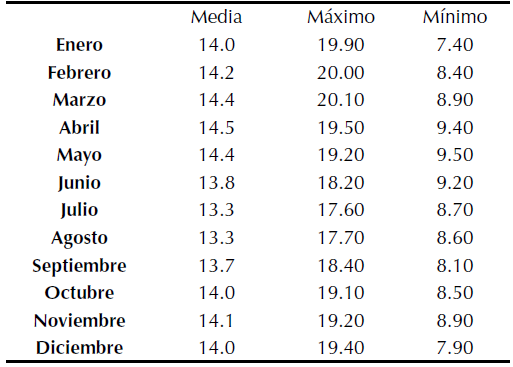
De igual forma, se requiere conocer el coeficiente de cultivo. Para este caso y dado la zona de ubicación, dicho coeficiente se muestra en la tabla 5.
Tabla 5: Coeficiente de cultivo por mes
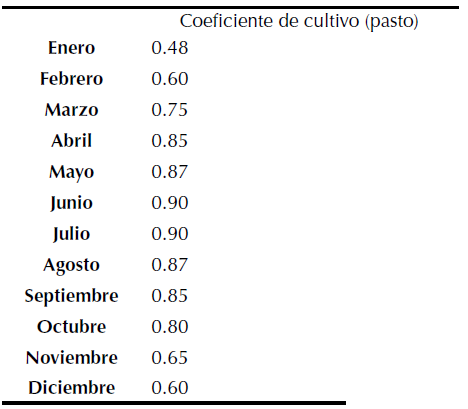
Modelamiento de la infiltración
Para el cálculo de la infiltración se tiene en cuenta un porcentaje del caudal de entrada dado por las precipitaciones, el cual depende del tipo de suelo y del tiempo que lleva construida la represa. Para la represa de Teatinos se tiene un porcentaje de 2.25 % (Garzón y Rojas, 2005). Las precipitaciones utilizadas son las mismas calculadas para su modelamiento.
Modelamiento de la demanda
Para las poblaciones en Colombia se cuenta con cinco censos, en el caso de Tunja tenemos los datos mostrados en la figura 4. Mediante la aplicación de la ecuación (28) se hallan las tasas de crecimiento (tabla 6).
Tabla 6: Tasas anuales y mensuales de crecimiento entre los anos de censo.

Como 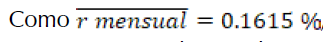 , se parte del último censo registrado para hacer el cálculo de la población al año 2015 (38).
, se parte del último censo registrado para hacer el cálculo de la población al año 2015 (38).
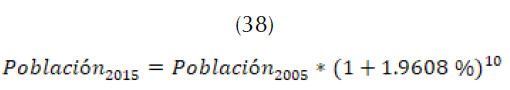
Con el fin de hacer las proyecciones se tendrá en cuenta una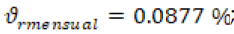 ; con lo cual se construye la distribución normal y se realiza el pronóstico del tamaño de la población para los próximos 30 años.
; con lo cual se construye la distribución normal y se realiza el pronóstico del tamaño de la población para los próximos 30 años.
El caudal de agua extraído por la población que se implementa para el cálculo es de 140 L/hab-día, que corresponde a la dotación mínima requerida para una ciudad como Tunja2. En cuanto al valor de agua no contabilizada este corresponde al 20 % (RAS, 2000). Por lo que el cálculo de la demanda en un periodo t en meses3, corresponde a (39):
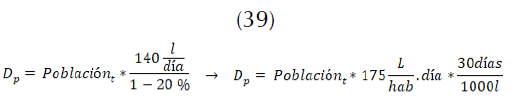
La demanda generada para la represa de Teatinos está establecida por la concesión que aprobó Corpoboyacá para la población de Tunja y la concesión con el distrito de riego Usochicamocha; de igual forma, se debe tener en cuenta un caudal ecológico. Para el cálculo del valor extraído por el distrito de riego se toma el caudal aprobado que corresponde a 350 l/s (Proactiva, 2014) y se tiene en cuenta el histórico para calcular la desviación. De esta forma se construye una variable con distribución . El caudal ecológico histórico permite hallar la media y desviación, con lo que se construye otra distribución Normal(129.4,12).
La suma de las demandas generadas por la población, el distrito de riego y el caudal ecológico es el total de extracción.
Resultados y alternativas
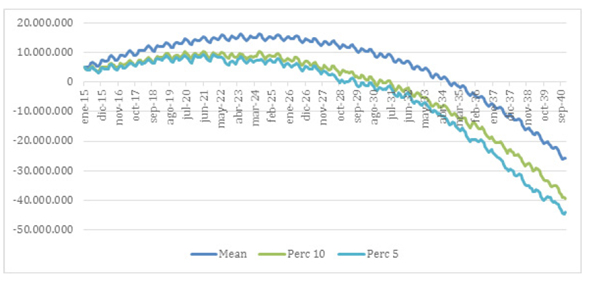
Al generar el modelo de Monte Carlo se realiza el pronóstico del balance hídrico de la represa de Teatinos para un periodo de 50 años, entre el 2015 y el 2065. El modelo trabajó 3685 variables aleatorias creadas, con 1000 realizaciones, y produce 432 pronósticos (figura 3).
Figura 3: Balance hidrico de la represa de Teatinos.
A partir del modelo se puede establecer que, con una probabilidad del 5 %, el balance hídrico de la represa alcanza su nivel de escasez para el periodo de octubre de 2030. En términos medios, para agosto del 2034 el agua almacenada en la represa de Teatinos será insuficiente para la demanda poblacional.
Con los resultados obtenidos se consideran dos alternativas de suministro de agua a mediano plazo que corresponden a dos represas cercanas a Tunja. La primera en consideración son las represas Gachaneca I y II, en el municipio de Samacá, muy cercanas a la represa de Teatinos. Y la otra es el embalse La Copa, que se encuentra al sur-oriente de Tunja. Cada una de estas represas cumple con los requerimientos mínimos en cuanto a la calidad del agua y la distancia máxima aceptada a la ciudad.
Para el cálculo del total del volumen de agua disponible para suplir la demanda de Tunja, se realiza el modelo del balance hídrico de la represa de Teatinos y el de la represa alterna. De esta forma se tiene el total disponible de ambas represas. Se debe tener en cuenta que las represas de Gachaneca y el embalse La Copa solo pueden otorgar un caudal máximo de extracción para la ciudad de Tunja.
En cuanto al modelo de las represas de Gachaneca I y II, que cumplen la función de una sola represa, se obtiene que el caudal ofertado es similar a el caudal demandado, por lo que el balance de la represa es casi constante y positivo. Es importante mencionar que en esta represa se cuenta con una demanda adicional que es el sistema de riego, hidromulos, lo que significa que no es una demanda creciente y que tiene un caudal de extracción concedido. El caudal que puede llegar a ser concedido a la ciudad de Tunja no superan los 80 l/s, en el mejor de los escenarios, además de no tener concesión para los meses de verano. Teniendo en cuenta el resultado del balance hídrico de las represas de Gachaneca y el valor máximo que puede llegar a ser concedido, se obtiene que con una probabilidad del 5 % el agua disponible sería suficiente para complementar el suministro de agua de la represa de Teatinos para la ciudad de Tunja hasta octubre del 2032. Con un 10 % de probabilidad hasta marzo del 2033 y en el valor medio hasta agosto del 2036 (figura 4).
Figura 4: Balance hidrico de las represas de Teatinos y Gachaneca I y II.
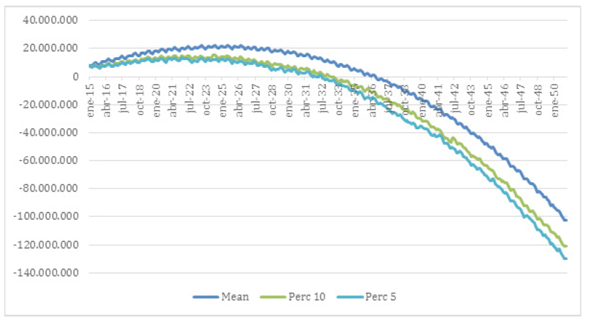
Para el modelo del embalse La Copa, el resultado indica que se puede otorgar una concesión de 240 l/s. Del cálculo del caudal disponible para abastecer a la ciudad de Tunja, dadas las represas de Teatinos y La Copa, se halla que con un 5 % de probabilidad el volumen de agua disponible logra suplir la demanda de Tunja por 27 años adicionales, con el 10 % de probabilidad alcanza para abastecer a la ciudad hasta febrero del 2043 y se obtiene una media para esta fecha de marzo del 2045 (figura 5).
Figura 5: Balance hidrico de las represas de Teatinos y La Copa.
De las dos alternativas disponibles se puede considerar que el embalse La Copa es la mejor opción pues permite un mayor caudal de extracción, un flujo constante para todos los meses del año y un mayor periodo de tiempo de suministro de agua continuo a la ciudad.
Conclusiones
En este trabajo se demuestra cómo aplicar la simulación de Monte Carlo para evaluar el balance hídrico de una represa. Por medio del análisis de los datos históricos de las variables del balance hídrico, precipitación, caudal subterráneo, escorrentía, caudal de extracción, infiltración y evapotranspiración; se incluye además el evento probabilístico de cada una de ellas. La ventaja de aplicar la simulación de Monte Carlo es su flexibilidad y tiene gran potencial para incluir la incertidumbre de los eventos naturales estocásticos como la precipitación, las horas de sol, entre otros.
Este modelo puede ser utilizado como método complementario al diseño de eventos, sobre todo cuando se pretende obtener un mayor grado de confiabilidad de las proyecciones de la oferta de un balance hídrico. La simulación de Monte Carlo tiene un alcance mayor al enfoque de diseño de eventos, debido a que proporciona estimaciones del volumen de agua almacenado en una represa más cercana a los datos reales y permite la evaluación de múltiples escenarios. Mediante esta herramienta, y con el alcance obtenido en este trabajo, se pueden pronosticar de forma cercana y de fácil aplicación las variables del balance hídrico de una gran represa o cuenca.
Referencias
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.


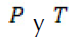 se calcula el factor de temperatura y luminosidad. Mediante (
se calcula el factor de temperatura y luminosidad. Mediante (