DOI:
https://doi.org/10.14483/23448350.13552Published:
01/01/2019Issue:
Vol. 34 No. 1 (2019): January-April 2019Section:
Science EducationUna propuesta para estudiar la complejidad de los programas de formación de profesores de matemáticas
A proposal to study the complexity of mathematics teacher training programs
Keywords:
field, curriculum, didactics of mathematics, training (en).Keywords:
Campo, Currículo, didáctica de las matemáticas, formación (es).Downloads
References
Anzola, O. (2016). El proceso de toma de decisiones: elemento central en la comprensión de las organizaciones. En: F. Ojeda, C. Núñez, M, Magallón y D. Álvarez (coords.), Perspectivas de la administración y la concepción organizacional contemporánea (pp. 113-123). México D.F.: Universidad Autónoma Metropolitana de México (UAM).
Bernstein, B. (1990). La construcción social del discurso pedagógico. Textos seleccionados. Bogotá: El Griot.
Bolívar, A. (2008). Didáctica y currículum: de la modernidad a la posmodernidad. Málaga, España: Aljibe.
Bourdieu, P. (2002). Campo de poder y campo intelectual. Itinerario de un concepto. Tucumán, Argentina: Montressor.
Brousseau, G. (1990). ¿Qué pueden aportar a los enseñantes los diferentes enfoques de la didáctica de las matemáticas? Enseñanza de las ciencias, 8(3), 259-267.
Calderón, D. (2012). El lenguaje en las matemáticas escolares. En D. Calderón (ed.), Perspectivas en la didáctica de las matemáticas (pp. 79-107). Bogotá: Universidad Distrital Francisco José de Caldas.
Da Silva, T. (1999). Documento de identidad. Una introducción a las teorías del currículo. Brasil: B. Horizonte.
Díaz, M. (1995). Aproximaciones al campo intelectual de la educación. En: J. Larrosa (ed.), Escuela, poder y subjetivación (pp. 333-359). Madrid: La Piqueta.
Dussel, I. (2001). La formación de docentes para la educación secundaria en América Latina. Perspectivas comparadas. En: C. Braslavsky, I. Dussel y P. Scaliter (eds.), Los formadores de jóvenes en América Latina. Desafíos, experiencias y propuestas (pp. 10-76). Uruguay: Unesco
Echeverri, J. y Zambrano, I. (2013). Un campo conceptual y narrativo de la pedagogía. En: Y. Pedraza y O. Pulido (ed.), Memorias del III Congreso Nacional y II Internacional de Investigación y Pedagogía. La educación del siglo XXI: ser, saber y producir en la incertidumbre y el caos (pp. 177-183). Tunja: UPTC. Recuperado de http://www.uptc.edu.co/eventos/2013/cf/cipni/memoria/memorias_preliminar_cip3.pdf.
Faquineto, J. (1887). Diccionario general etimológico de la lengua española. Madrid. Recuperado de https://archive.org/details/diccionariogener04echeuoft
Ferry, G. (1990). El trayecto de la formación. Los enseñantes entre la teoría y la práctica. México D. F.: Paidós.
Forero, F. (1993). Mejorar la docencia universitaria. Santafé de Bogotá: Universidad Pedagógica Nacional.
Garzón, D. (2017). Análisis de las decisiones del profesor de matemáticas en su gestión de aula. Revista Educación Matemática, 9(3). DOI: https://doi.org/10.24844/EM2903.05
Gil-Chaves, D. (2016). Una mirada sistémica de los programas de formación de profesores de matemáticas. Revista Horizontes Pedagógicos, 18(1), 110-125.
Gil-Chaves, D. (2016). Una perspectiva sistémica para el estudio de los programas de formación de profesores de matemáticas. Proyecto doctoral aprobado
Godino, J. (2009). Categorías de análisis de los conocimientos del profesor de matemáticas. Revista Iberoamericana de Educación Matemática, 20, 13-31.
Gómez, P. (2005). Diversidad en la formación de profesores de matemáticas. La búsqueda de un núcleo común. Revista EMA, 10(1), 242-293.
Gómez, P. (2007). Desarrollo del conocimiento didáctico en un plan de formación inicial de profesores de matemáticas de secundaria (tesis doctoral). Universidad de Granada, España.
Gómez-Chacón, I. y Planchart, E. (eds.) (2005). Educación matemática y formación de profesores. Propuestas para Europa y Latinoamérica. España: Universidad de Deusto.
Hernández, I. (2004). Herbert A. Simon, 1916-2001, y el futuro de la Ciencia Económica. Revista Europea de Dirección y Economía de la Empresa, 13(2), 7-23. Recuperado de https://www.insisoc.org/wp-content/uploads/2017/06/SIMONMONOG.pdf
Koban, N. (2008). Los sesgos cognitivos en la toma de decisiones. International Journal of Psychological Research, 1(1), 68-73. DOI: https://doi.org/10.21500/20112084.968
León, O. (2005). Experiencia figural y procesos semánticos para la argumentación en geometría (tesis doctoral). Universidad del Valle, Cali, Colombia.
León, O. (ed.) (2014). Referentes curriculares con incorporación de tecnologías para la formación del profesorado de matemáticas en y para la diversidad. Bogotá: Universidad Distrital Francisco José de Caldas.
Lupiáñez, J. (2009). Expectativas de aprendizaje y planificación curricular en un programa de formación inicial de profesores de matemáticas de secundaria (tesis doctoral). Universidad de Granada, España.
Marcelo, C. (1995). Formación del profesorado para el cambio educativo. Barcelona: Ediciones Universitarias de Barcelona.
Marcelo, C. y Vaillant, D. (2009). Desarrollo profesional docente. ¿Cómo se aprende a enseñar? Madrid: Narcea S. A.
Martínez, M. (2003). Concepciones sobre la enseñanza de la resta: un estudio en el ámbito de la formación permanente del profesorado (tesis doctoral). Universidad Autónoma de Barcelona, Bellaterra.
Merieu, P. (2002). Formación de profesores y aprendizajes. En Cátedra Emblemática “Alvaro Pio Valencia” (pp. 13-36). Universidad Santiago de Cali.
Oliveras, M. (1996). Etnomatemáticas. Formaciónde profesores e Innovación curricular. Granada, España: Universidad de Granada.
Papanastasiou, E., Tatto, M. y Neophytou, L. (2011). Programme Theory, Programme Documents and State Standards in Evaluating Teacher Education. Assessment & Evaluation in Higher Education, 37-41. DOI: https://doi.org/10.1080/02602938.2010.534760
Pérez, Á. (1996). La función y formación del profesorado en la enseñanza para la comprensión. Diferentes perspectivas. En: J. Gimeno y Á. Pérez (eds.), Comprender y transformar la enseñanza (pp. 398-429). Madrid: Ediciones Morata.
Poster, G. (2004). Análisis del currículo. México: McGraw-Hill.
Radford-Hernández, L. (2011). La evolución de paradigmas y perspectivas en la investigación. El caso de la didáctica de las matemáticas. En J. Vallés, D. Álvarez, & R. Rickenmann del Castillo (eds.), L’activitat docente. Intervenció, innovació, investigación. Girina (España): Documenta universitaria, 33-49.
Saldarriaga, J. (2008). Una experiencia pedagógica, formativa y editorial: la revista Educación y Pedagogía. Entrevista al profesor Jesús Alberto Echeverri Sánchez (director). Revista Educación y Pedagogía, 10(50), 13-29. Recuperado de http://aprendeenlinea.udea.edu.co/revistas/index.php/revistaeyp/article/viewFile/9923/9121.
Salinas, E. y Jail, A. (2014). Herramientas teórico-conceptuales para el análisis de la toma de decisiones en comités de economía pública. Revista Análisis Político, 27(80). DOI: https://doi.org/10.15446/anpol.v27n80.45619
Simon, H. (2003). Racionalidad, historicidad y predicción en Herbert A. Simon. Filosofía y metodología de la ciencia. Netbiblo S.I. Coruña. Teacher Education and Development Study in Mathematics (TEDS-M) (2012). Estudio internacional sobre la formación inicial en matemáticas de los maestros. Informe español. España: Secretaría General Técnica, Subdirección General de Documentación y Publicaciones.
Vaillant, D. (2004). Construcción de la profesión docente en América Latina. Tendencias, temas y debates: Programa de Promoción de la Reforma Educativa en América Latina. Santiago de Chile, Chile: Preal.
Vidal, J. (2012). Teoría de la decisión: proceso de interacciones u organizaciones como sistemas de decisiones. Cinta de Moebio, 44, 136-152. https://dx.doi.org/10.4067/S0717-554X2012000200004
WordReference (s.f.). Núcleo. Recuperado de http://www.wordreference.com/definicion/n%C3%BAcleo.
Zambrano, A. (2007). Formación, experiencia y saber. Bogotá: Cooperativa Editorial Magisterio.
Zuluaga, O. y Herrera, S. (2009). La configuración de campos conceptuales como posibilidad para estudiar las culturas pedagógicas. En: A. Martínez y F. Peña (eds.), Instancias y estancias de la pedagogía. La pedagogía en movimiento (pp. 25-44). Bogotá: Bonaventuriana.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de junio de 2018; Aceptado: de diciembre de 2018
Resumen
En este artículo se presenta, como uno de los resultados del desarrollo de la investigación, el diseño de la estructura del sistema para el estudio de los programas de formación de profesores de Matemáticas. El propósito central de la investigación consistió en el diseño y aplicación de un sistema de relaciones entre los campos: formación de profesores de Matemáticas, currículo y didáctica de las Matemáticas. Este sistema de relaciones se construyó a partir del estudio de tres aspectos al interior de cada uno de los campos. El primer aspecto es el estudio de los sentidos y posibles significaciones (subcampo conceptual) de cada campo. El segundo aspecto es el estudio de los intelectuales que organiza las producciones de otros intelectuales (subcampo intelectual) en cada uno de los tres campos. Y el tercer aspecto es el estudio de los problemas y del proceso de toma de decisiones (subcampo decisional) en los programas de formación, en especial las situaciones en las que se hace referencia a alguno de los tres campos. Las conclusiones están enfocadas en el diseño de unas herramientas caracterizadoras y diferenciadoras que permitan el estudio de los programas de formación de profesores de Matemáticas desde estos tres campos presentes y necesarios para la existencia de estos programas.
Palabras clave:
campo, currículo, didáctica de las Matemáticas, formación.Abstract
This article presents the design of the structure of the system for the study of the mathematics teacher training program, as one of the results of the development of the research. The central purpose of the research consisted of the design and application of a system of relations between the fields: teacher training in mathematics, curriculum, and mathematics teaching. This system of relationships was built from the study of three aspects within each of the fields. The first aspect, the study of the senses and possible meanings (conceptual subfield) of: the training of teachers of mathematics, the curriculum for the training of teachers and the didactics of mathematics. The second aspect, the study of the intellectuals that organizes the productions of other intellectuals (intellectual subfield) in each of the three fields. And the third aspect, the study of the problems and the decision-making process (decisional subfield) in the training programs, especially the situations in which one of the three fields is referred to. The conclusions are focused on the design of characterizing and differentiating tools that allow the study of mathematics teacher training programs from three fields present and necessary for the existence of any mathematics teacher training program.
Keywords:
field, curriculum, didactics of mathematics, training.Resumo
Este artigo apresenta o desenho da estrutura do sistema para o estudo do programa de treinamento de professores de matemática, como um dos resultados do desenvolvimento da pesquisa. O objetivo central da pesquisa consistiu na concepção e aplicação de um sistema de relações entre os campos: formação de professores em matemática, currículo e ensino de matemática. Esse sistema de relacionamentos foi construído a partir do estudo de três aspectos dentro de cada um dos campos. O primeiro aspecto, o estudo dos sentidos e possíveis significados (subáconos conceituais) de: a formação de professores de matemática, o currículo para a formação de professores e a didática da matemática. O segundo aspecto, o estudo dos intelectuais que organiza as produções de outros intelectuais (subcampo intelectual) em cada um dos três campos. E o terceiro aspecto, o estudo dos problemas e o processo de tomada de decisão (subcampo decisório) nos programas de treinamento, especialmente as situações em que um dos três campos é referido. As conclusões centram-se na concepção de ferramentas de caracterização e diferenciação que permitem o estudo de programas de formação de professores de matemática a partir de três domínios presentes e necessários para a existência de qualquer programa de formação de professores de matemática.
Palavras-chaves:
campo, currículo, didática da matemática, formação.Introducción
La investigación doctoral en desarrollo Una perspectiva sistémica para el estudio de los programas de formación de profesores de matemáticas centra su estudio en la comprensión y caracterización de los programas de formación de profesores de matemáticas. La palabra “programa” viene del griego (prógamma), de pró que significa delante de todos y grámma que significa letra, escritura; y del latín, que significa inscripción, cartel (Faquineto, 1887). Estas características etimológicas del término son reflejadas en todo programa de formación, puesto que se elabora con anticipación a todo proceso y, por otra parte, está soportado en documentos escritos.
Los programa de formación de profesores tiene varias acepciones entre las que podemos encontrar que algunos países de Europa, Estados Unidos y América Latina y el Caribe reconocen la existencia de tres tipos de programas: los programas de formación inicial, los programas de formación en servicio o continuada y los programas de formación avanzada o pos gradual, las especializaciones, las maestrías, los doctorados y los posdoctorados (León, 2014; Marcelo, 1995; Marcelo y Vaillant, 2004; Dussel, 2001). Cuando algunos investigadores hacen mencionan programas de formación de profesores de matemáticas se refieren a una asignatura relacionada con algún aspecto de la didáctica (Lupiáñez, 2009; Martínez, 2003; Gómez, 2005 y 2007). Para otros, se trata más de un plan de estudio que otorga al final un título o certificación para ejercer como profesor de Matemáticas (Papanastasiou, Tatoo y Neophytou, 2011; TEDS-M, 2012; Gómez-Chacón y Planchart, 2005).
Por lo anterior, la investigación se enfoca en el estudio de los programas de formación de profesores de Matemáticas a nivel de pregrado o formación inicial. Para esto, la indagación consistió en crear y aplicar un sistema de relaciones entre los campos formación de profesores, currículo y didáctica de las matemáticas. Esto, a partir de sus campos internos conceptual, intelectual y decisional, con el fin de identificar y caracterizar programas de formación de profesores desde una perspectiva sistémica y proveniente del campo de la educación.
En la primera parte de este artículo se muestra la estrategia metodológica desarrollada para el logro del propósito de la investigación y se presentan algunos de los resultados que el desarrollo de esta metodología permite identificar y comprender de tres programas de formación de profesores de Matemáticas en Colombia, los cuales fueron participantes en la investigación.
Metodología
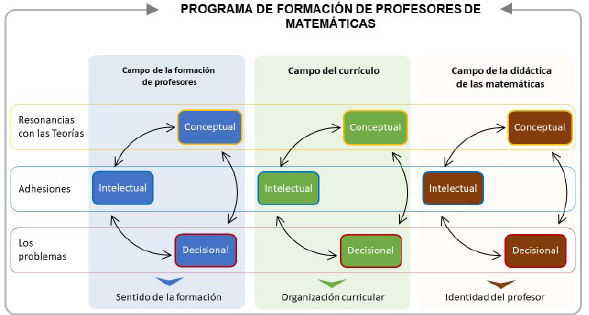
El tejido conceptual y relacional que se elaboró para el estudio y comprensión de los programas de formación de profesores de Matemáticas tuvo en cuenta desde el ámbito de la educación un sistema de relaciones entre los campos: formación de profesores, currículo y didáctica de las matemáticas para el estudio, análisis y comprensión de un programa de formación de profesores de matemáticas en el contexto colombiano (figura 1).
Figura 1: Estructura metodológica para el estudio de los programas de formación de profesores de Matemáticas.
La investigación consideró dos grandes focos de reflexión. El primero, fundamentado en la teoría general de procesos (TGP) y la teoría general de sistemas (TGS), en tanto posibilitaron epistemológica y metodológicamente la construcción del sistema de relaciones para el estudio de los programas. El otro foco de reflexión es la noción de campo, la cual permitió la organización y selección de los elementos constitutivos del sustrato del sistema que brindaron los elementos (categorías de análisis) y las relaciones para la estructura del sistema desde la identificación de relaciones al interior de los campos: formación de profesores, currículo y didáctica de la matemática (Gil-Chaves, 2016).
El punto de inicio se dio al reconocer la existencia de un campo en el que se evidencia la presencia de diferentes teorías, conceptos, prácticas y modos de producir conocimiento (Bolívar, 2008; Marcelo, 1995; Echeverri y Zambrano, 2013; Saldarriaga, 2008). Además, se reconoce la existencia de corpus discursivos, personas, instituciones, intereses o juegos de poder, comunidades académicas y sociales que reconocen y ponen en evidencia las contradicciones, las tensiones, las incoherencias, las relaciones, los apoyos, las exclusiones, las diferencias y los encuentros entre prácticas y teorías (Bourdieu, 2002; Díaz, 1995; Bernstein, 1990; Zuluaga y Herrera, 2009).
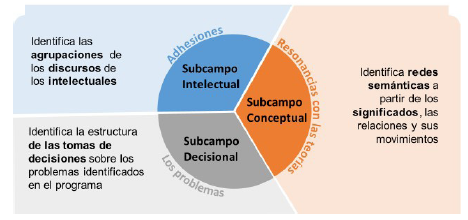
Entonces, ¿cómo abordar metodológicamente el estudio de un campo? Algunos autores han optado por el estudio del campo intelectual de la educación, como es el caso de Díaz (1995); otros estudian el campo conceptual y narrativo de la pedagogía (Echeverri y Zambrano, 2013). En este mismo sentido, este estudio, como estrategia metodológica, opta por considerar que para abordar el estudio de tres campos que se encuentran presentes en todo programa (la formación de profesores, el currículo y el de la didáctica de las matemáticas), es necesario tener en cuenta los siguientes subcampos (figura 2).
Figura 2: Esquema de la estrategia metodológica para abordar los campos: formación de profesores, currículo y didáctica de las matemáticas.
Estrategias iniciales y generales para la identificación de los elementos del sistema
Para la identificación de los elementos del sistema se utilizaron las siguientes estrategias:
Taller de vocablos. Búsqueda de la significación etimológica de los términos esenciales: formación de profesores, currículo y didáctica de las matemáticas. Esta actividad permitió la exploración de los campos semánticos a los que pertenecen y relacionarlos con el estudio de los programas de formación de profesores de matemáticas.
Estado del arte. Considerado como la compilación, el análisis y el estudio de documentos existentes sobre los campos de estudio.
La prueba de expertos. Consistió en la validación de los focos de significación, identificados para cada uno de los subcampos internos de los campos, mediante la consulta a expertos reconocidos en cada uno de estos. Fueron seleccionados docentes de reconocida trayectoria académica e investigativa en su campo de estudio1. Se recibieron los aportes para cada uno de los subcampos y se sistematizó la información obtenida.
Estrategias para la identificación del sentido de la formación de profesores, el currículo y la didáctica de las matemáticas
El subcampo conceptual se caracteriza por sus significados nodulares, redes conceptuales, relaciones de significación, movimiento de los conceptos a través del desplazamiento por diferentes paradigmas. La herramienta metodológica para el estudio de este subcampo es la red semántica. Como instrumento de investigación esta permite, a través de sus formas de representación, evidenciar la organización, identificación y transformación de los significados de las palabras o los vocablos, las frases, los enunciados, etc. Lo más importante de una red semántica son los significados que la van constituyendo y las relaciones que se pueden establecer.
El estudio del significado se sitúa en el desarrollo que el lenguaje alcanza a partir de las lenguas y no puede ser ajeno a la presencia de las funciones discursivas de ellas (Duval, 1999 citado en Calderón, 2012; León, 2005). Para esta investigación se tomó como fuente para los criterios de identificación de las redes semánticas tres funciones discursivas propias de una lengua: la función referencial, que permite la instauración (al quién del habla), mediante la determinación (nombres); la función apofántica, que permite la identificación de enunciados de significación con atribuciones y valores sociales, esto es la producción de predicados sobre los objetos y de puntos de vista sobre ellos y sus relaciones; la función de la expansión discursiva, la cual permite el establecimiento de la continuidad temática entre significados nodulares.
En particular para la investigación, está técnica permitirá el análisis del subcampo conceptual de los campos a estudiar a partir de la identificación, organización y transformación de las unidades de significado que conforman la red y que muestran la ampliación, desarrollo y evolución de la red.
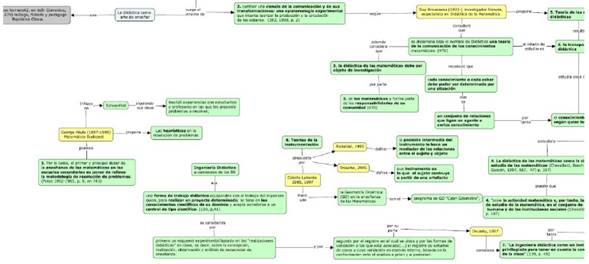
La elaboración de las redes semánticas (figura 3) parte de la identificación de las unidades de significado en cada uno de los campos formación de profesores, currículo y didáctica de las matemáticas, con los siguientes criterios:
Figura 3: Toma parcial de una de las redes semánticas de didáctica de las Matemáticas.
El criterio cronológico, como su nombre lo establece, es una organización y ubicación de los nodos personas y nodos enunciados de significación al interior de cada uno de los campos siguiendo una línea de tiempo. Con la aplicación de este criterio se genera una forma particular de representar la red semántica, en la que es importante ubicar un año como punto de partida de la red (que puede ser el año de publicación de un libro o la fecha de existencia de algún autor), para luego ir colocando en orden cronológico las unidades de significación y algunos aspectos relevantes que hacen parte de la comprensión de la red semántica. Esto hace que visualmente la red semántica se presente como un tejido y no se vea una organización lineal. En la parte izquierda se presentan los nodos que provienen del primer corte de tiempo considerado para la red y a la derecha se ubiquen los nodos más actuales; esto implica que la lectura, el estudio y el análisis de la red semántica va del pasado al presente (izquierda a derecha).
El criterio de referencia, es un aspecto que permite la identificación de las unidades básicas de información de la red semántica que se llaman nodos. La presencia de la función referencial lleva a considerar el tipo de nodo que describe al quién del habla, que llamaremos nodos tipo personas (subcampo intelectual); y la presencia de la función apofántica lleva a considerar el tipo de nodo que refiere a enunciados que hacen la expansión semántica, que llamaremos nodos tipo enunciación (subcampo conceptual).
El criterio de resonancia2 es un aspecto que permite identificar la expansión o limitación de las rutas en la red. Este criterio reconoce que los nodos enunciados son unidades de significación (o unidades de significado, es decir, los indicadores de cada una de las redes semánticas) que hacen expansión al significado nodular y los nodos personas señalan quién hace la resonancia que genera la expansión del significado nodular de la red semántica. Esto corresponde con la función expansiva de la lengua.
El proceso anterior permitió la construcción y consolidación de las redes semánticas. Para el campo de la formación de profesores se identificaron tres redes semánticas, para el campo del currículo tres redes semánticas y para el campo de la didáctica de las matemáticas cuatro redes semánticas (tabla 1).
Fuente: elaboración propia de la autora.
Tabla 1: Nombres de las redes semánticas identificadas en cada uno de los campos y las unidades de significado.

Este subcampo conceptual será estudiado en los documentos de los programas a partir de la identificación de las resonancias que se establecen entre los enunciados que se encuentran en los documentos de los programas de formación de profesores de matemáticas y las unidades de significado propias de cada una de las redes semánticas de los campos. Este subcampo permitirá conocer y caracterizar el sentido y significado que cada programa de formación de profesores de matemáticas le otorga a la formación de profesores de matemáticas, currículo y didáctica de las matemáticas desde la identificación de las resonancias del programa con las teorías que refieren.
Estrategias para la identificación de los estudios y agrupaciones sobre el sentido de la formación de profesores, currículo y didáctica de las matemáticas
El subcampo intelectual se caracteriza por estar constituido por sujetos, discursos y prácticas que describen las tensiones, valoraciones, oposiciones e interacciones propias de los campos formación de profesores, currículo y didáctica de las matemáticas. La herramienta metodológica para el estudio de este subcampo es la identificación de algunos intelectuales3 que reconocen y analizan las producciones discursivas de otros intelectuales y generan agrupaciones, a partir de un foco caracterizador que se convierte en un aspecto esencial para el análisis del subcampo intelectual pues este evidencia las contradicciones, las valoraciones oposiciones dentro de este subcampo.
Para la selección de los intelectuales y las producciones discursiva, se tuvieron en cuenta los siguientes criterios:
Fuente acreditada de que hayan realizado estudios del tipo estados del arte en los campos de este estudio. Para identificar los intelectuales que hacen revisión y estudio del discurso en cada uno de los campos. Como resultado, se obtiene a los intelectuales que realizaron análisis de producciones discursivas y formulan estructuras tipo modelos, enfoques, tipologías, paradigmas, etc.
Presencia de una pauta de estudio y organización. Para identificar la pauta de estudio y organización o núcleo4 caracterizador de los enfoques, tipos, paradigmas, orientaciones, perspectivas, modelos, teorías y experiencias en los que se organizan los discursos de los intelectuales. Como resultado se identifican las diferentes pautas de estudio y sus respectivas tipologías en cada uno de los campos.
Presencia del intelectual en las tipologías seleccionadas en los campos. Para reconocer a los intelectuales en los discursos de los campos con los que se establece una conexión que puede ser de identificación (cuando se reconoce que existe y se analizan sus planteamientos); alineación (cuando se reconoce que existe y se manifiesta que se comparte algunos aspectos); y de afiliación (cuando se reconoce que existe conexión por identificación con los planteamientos). Como resultado, se obtuvieron agrupaciones realizadas por intelectuales en cada uno de los campos.
Este subcampo intelectual será estudiado en los documentos de los programas de formación de profesores de matemáticas, a partir de la identificación de las adhesiones que hacen los enunciados de los documentos del programa con las características de cada uno de los tipos que corresponden a cada tipología según su foco de organización para los campos de formación de profesores, currículo y didáctica de las matemáticas. Este subcampo permitirá conocer qué intelectuales, agrupaciones y características se identifica en cada programa de formación de profesores en los campos estudiados.
Estrategias para la identificación de los problemas y la toma de decisiones en los programas de la formación de profesores de matemáticas
A diferencia de los sub-campos conceptual e intelectual, que tienen mayores desarrollos, hay evidencias que indican la presencia de un tercer sub-campo al que se propone llamar sub-campo decisional. La configuración de este subcampo requiere del reconocimiento de teorías de las decisiones; conceptualizaciones como la toma de decisión; objetos de estudio como el proceso de la toma de decisiones; líneas y perspectivas de investigación; identificación de tensiones entre teorías y metodologías vinculadas a las decisiones sus procesos y sus efectos. Sin embargo, no sobra mencionar que en literatura revisada ya hay alusiones explicitas a la existencia del campo; Hansson (1994, citado en Salinas y Jalil, 2014) reconoce no solo la existencia del campo de la teoría de la toma de decisión, sino también el estudio interdisciplinario sobre la toma de decisión desde distintas áreas del saber.
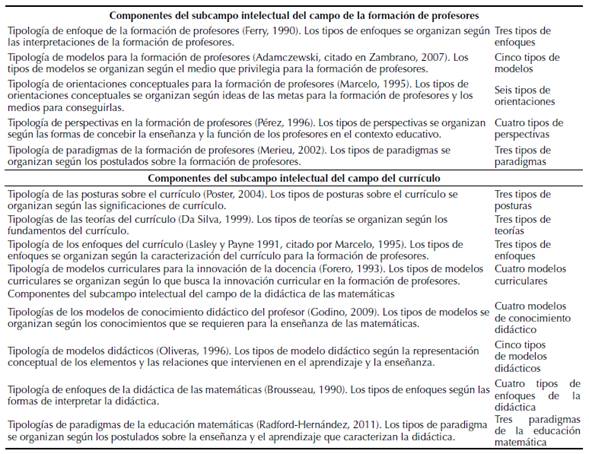
Fuente: elaboración propia de la autora.
Tabla 2: Las agrupaciones identificadas en los campos formación de profesores de matemáticas, currículo y didáctica de las matemáticas.
En la fundamentación de la emergencia de este campo hay que reconocer:
-
Sus objetos de estudio: la decisión como un proceso institucional, las decisiones, la función de las decisiones, la diferencia y relación entre decisión y acción, el proceso decisorio, proceso de toma de decisiones, condiciones en las que se toman las decisiones. Otro de los objetos de investigación de este campo a nivel educativo y específicamente en el contexto de la educación matemática es la toma de decisiones de los profesores en el aula de clase de matemáticas (Stockero y Van Zoest, 2013 citado en Garzón, 2017). La vigencia y trayectoria de sus objetos de estudio se evidencia en dos premios nobel, el primero para Herbert Simon en 1977 y el segundo para el psicólogo Daniel Kahneman en el 2002 (Koban, 2008).
-
La producción de conceptualizaciones. Por ejemplo, las decisiones pueden ser definidas como: una selección de medios alternativos para perseguir un objetivo (McDonald, 1978), las opciones tomadas entre dos o más alternativas para maximizar un resultado (Robbins, 1999), o como el proceso de resolución de incertidumbre para seleccionar la mejor alternativa o medio (Gast, 1978). Todos citados en Salinas y Jalil (2014), entre otras.
-
La presencia de tensiones y fuerzas en el reconocimiento de las perspectivas teóricas para abordar el estudio de las decisiones. Una perspectiva denominada “la decisión de la incertidumbre” reconoce la teoría crítica de la multirracionalidad lineal, la sociología fenomenológica y la etnometodología. En esta se considera que la decisión es un proceso de interacciones sociales en la que la libertad del sujeto tiene gran importancia (Sfez, 2005, citado en Vidal, 2012; Anzola, 2016). La otra perspectiva, llamada “la decisión multicriterio”, reconoce la teoría de sistemas autorreferenciales, teoría de la integración y entorno al debate estructural-funcional; “interpreta las organizaciones como sistemas de decisiones y entiende el concepto de decisión en su especificidad puramente epistemológica, al abstraer de la decisión todos los elementos y variables organizacionales relacionados con ella (Niklas Luhmann)” (Vidal, 2012, p. 136).
-
La presencia de diferentes áreas de conocimiento en la delimitación de los objetos de estudio, como es el caso del proceso de la toma de decisiones, pues ha sido estudiado en diferentes momentos desde perspectivas cualitativas y cuantitativas por la economía (Bonomem citado en Simon, 2003; Hernández, 2004) la administración (Anzola, 2016), la psicología (Koban, 2008) y la sociología (Vidal, 2012).
-
La presencia de diversidad enfoques para el estudio de sus objetos como los de tipo:
-
[…] descriptivos que privilegian el análisis de lo que hace el sujeto en el proceso (Lenis y Mann, 1977), los normativos que dan cuenta de lo que el sujeto debería hacer (Luce y Von Winterfeld, 1994), y los prescriptivos (Dillon, 1997) referidos a lo que el sujeto debe hacer y hace al tomar decisiones. (Anzola, 2016, p. 114)
-
La emergencia de modelos para representar las relaciones entre teorías y objetos de estudio como: el modelo de elección racional que se caracteriza por considerar que el proceso de toma de decisiones es prescriptivo y simple. Los aspectos fundamentales para este proceso son: la información completa y disponible para saber la relación entre los medios y los fines que tiene la persona o las personas que toman las decisiones, lo que les permite, de forma racional, tomar la mejor opción. El modelo de la racionalidad limitada de Herbert A. Simon (2003) se caracteriza por reconocer que el proceso de toma de decisiones es una acción humana. Los aspectos que intervienen en el proceso son: las motivaciones, las emociones, la capacidad cognitiva, la intuición, el sentido común, las experiencias y otros propios de la persona o las personas decisoras. El modelo de las anarquías organizadas (March, 1994, citado en Anzola, 2016), se caracteriza por reconocer que el proceso de toma de decisiones es una forma de mostrar y comunicar significados. Son considerados como elementos de la toma de decisiones: la oportunidad, la confusión, la complejidad, el simbolismo y la ambigüedad. El modelo de análisis que incorpora la emoción y la subjetividad (Lowenstein y Lerner, 2003, citado en Anzola, 2016; Koban, 2008), se caracteriza por reconocer que en el proceso de toma de decisiones está presente la ambigüedad de diferentes formas. Este modelo demuestra que en el proceso de toma de decisiones se incorporan aspectos como: las emociones, los afectos, las intuiciones, los prejuicios, las expectativas, en ocasiones en conflicto y muchos otros aspectos propios de las subjetividades de los que intervienen en este proceso.
Todo lo anterior evidencia la emergencia del sub-campo decisional en el panorama de la educación. Como opción metodológica para indagar la presencia de este sub-campo en los programas de formación de profesores de matemáticas, se utiliza el proceso de la toma de decisiones teniendo en cuenta que desde diferentes disciplinas ha sido considerado como un proceso necesario para la comprensión de dinámicas propias de las mismas. En disciplinas como en la economía (Bonome, citado en Simon, 2003; Hernández, 2004), la psicología (Koban, 2008), la sociología (Vidal, 2012), la administración (Anzola, 2016) y la educación (Garzón, 2017), entre otras. En la formulación de los indicadores de este proceso se optó por el modelo de la racionalidad limitada, específicamente en lo que concierne a la identificación de este proceso con un proceso de solución de problemas. En cuanto a los métodos de recolección de datos se privilegia la “extracción de información sobre procesos de decisión a partir de documentos escritos” (Simon, 2003, p. 107).
Los indicadores provienen, como se mencionó, de una estructura de solución de problemas que se presenta a continuación:
Identificar un problema. Este aspecto hace referencia a la determinación que toman los decisores de considerar como prioridad una situación y no otra. Es decir, se selecciona entre varias posibles situaciones problemas. Una vez hecho esto, se define el problema complejo a ser estudiado (Bonome, citado en Simon, 2003; Hernández, 2004; Anzola, 2016).
Construcción de procedimientos para abordar el problema. Este aspecto hace referencia a la forma en que el grupo de personas decisoras aborda el problema. Esto se puede dar, entre otros, al comparar la situación actual con la situación ideal a la que se quiere llegar; o dividir el problema en sub-problemas, con lo que se selecciona una sola parte del problema para ser abordado (Bonome, citado en Simon, 2003; Anzola, 2016).
Generación de posibles alternativas. Este aspecto se refiere al momento en que el grupo de decisores reconoce una serie (más de dos) de posibilidades de actuación para la resolución del problema. Estas alternativas pueden surgir a partir de elaboraciones realizadas por los decisores, experiencia de otros ante el mismo problema, la combinación de la experiencia de otros y las construcciones de los decisores (Bonome, citado en Simon, 2003; Hernández, 2004; Anzola, 2016).
Evaluación de las distintas opciones. Este aspecto hace referencia a la valoración que da el grupo de personas decisoras a cada una de las posibilidades de actuación para resolver el problema (Bonome, citado en Simon, 2003; Hernández, 2004; Anzola, 2016).
Con este sub-campo decisional se busca identificar en cada uno de los programas de formación de profesores de Matemáticas los problemas e indagar sobre el proceso de toma de decisiones. Con ello se busca identificar decisiones, como producto de este proceso, relacionadas con la formación de profesores, la organización curricular y la presencia de la didáctica de las matemáticas en los programas.
Fuente: elaboración propia de la autora.
Tabla 3: Aspectos en el proceso de toma de decisiones y sus respectivos indicadores.

Conclusiones
Todo lo anterior permite afirmar que la investigación, hasta el momento, ofrece un sistema como herramienta de identificación y caracterización de los programas de formación de profesores de Matemáticas. Para ponerlo en funcionamiento, este sistema requiere de tres acciones fundamentales. Primero, consultar a las comunidades educativas de los programas (docentes, egresados, estudiantes, administrativos) para seleccionar los documentos que mejor describen o dan cuenta del programa. Segundo, hacer un análisis de contenido de cada uno de los documentos seleccionados para identificar las resonancias (sentidos, subcampo conceptual), las adhesiones (identificación con significados, subcampo intelectual), los problemas y los procesos de toma de decisiones. Tercero, analizar y estudiar los resultados con la comunidad educativa de cada uno de los programas de formación de profesores. Esta última etapa se encuentra en proceso de desarrollo dentro de la presente investigación.
Referencias
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.