La solución de un problema matemático no convencional por estudiantes universitarios

Introducción

Aunque la resolución de problemas matemáticos es un tema que ha sido ampliamente estudiado (Armella y Santos-Trigo, 2013), esta investigación tiene el propósito de reflexionar en torno a la implementación un problema matemático, al que Schoenfeld (1985) denomina “problema no rutinario”, con la intención de realizar una valoración cualitativa de los argumentos que los estudiantes exponen durante su proceso de resolución (Calderón, 2006). Este tipo de problema no rutinario se caracteriza por plantear situaciones que no tienen estructura convencional a los que presentan usualmente en un curso de matemáticas; caso contrario, estos emplean un contexto amplio y, en ocasiones, la información no aparece del todo explícita, por lo que se requiere hacer interpretaciones, inferencias e, incluso, realizar una reflexión previa para identificar una cuestión central. Cuando los estudiantes se enfrentan a este tipo de problemas suelen tener dificultades, ya que no se parecen a los típicos problemas escolares en los que los datos aparecen bien identificados y que para resolverlos basta con elegir la fórmula, realizar la operación y escribir el resultado. La introducción de problemas no convencionales al aula puede constituir un recurso natural para motivar la discusión, la exposición de conjeturas, contraejemplos y aproximaciones (Santos, 2007), así como el intercambio y enfrentamiento de puntos de vista.

De acuerdo con Cerbin (1998), la actividad de resolver problemas se apoya de las argumentaciones para justificar procedimientos y resultados, pero esta relación se vuelve más estrecha cuando se abordan problemas con una estructura abierta o problemas no convencionales (Cho y Jonassen, 2002), ya que este tipo de problemas admiten diversas interpretaciones y procedimientos de solución. Los típicos problemas matemáticos con una estructura definida no ofrecen un amplio margen para explorar, discutir o proponer estrategias debido a lo predecible y mecánico que resulta su proceso de solución, por lo que los argumentos en estos casos suelen fundamentarse únicamente en los algoritmos que le dan una validez al procedimiento y a la solución. En cambio, la introducción de problemas no rutinarios permite que los estudiantes se involucren en una amplia reflexión sobre los elementos planteados, no solo respecto a la información matemática en juego, sino también los aspectos del contexto del propio problema.

Dado que la resolución de problemas plantea un contexto de aprendizaje en el cual los argumentos contribuyen a formular ideas y repensar los problemas (Lester, 2013; Cerbin, 1988), se planteó el estudio de la implementación de un problema matemático no rutinario, así como el análisis de los argumentos que exponen estudiantes universitarios durante su solución (Schoenfeld, 1985), el propósito es distinguir las características de los argumentos particularmente cuando establecen el procedimiento de solución.

Marco conceptual

De acuerdo con Schoenfeld (1985), la definición de problema admite diversas interpretaciones debido a que se trata de algo relativo; lo que para una persona requiere de un esfuerzo significativo, para otra puede representar un ejercicio de rutina. Pero, afirma que un problema es una relación particular entre el individuo y la tarea, específicamente cuando la tarea representa un desafío y no se conoce el esquema de solución. El individuo debe emplear sus recursos matemáticos para establecer un posible procedimiento a partir de la información proporcionada en el problema, esto implica reconocer su estado inicial e identificar las condiciones y características del resultado final.

La habilidad para resolver problemas es reconocida como una forma de razonamiento de alto nivel (Santos, 2007) que involucra el uso y desarrollo de un pensamiento no algorítmico (Arcavi y Friedlander, 2002), así como la articulación de una variedad de acciones cognitivas que involucran conocimientos y habilidades específicas, algunas de ellas no rutinarias, tales como elegir las representaciones apropiadas, establecer conjeturas, coordinar experiencias y conocimientos previos, incluso desarrollar una intuición matemática para generar procedimientos e integrar algoritmos (Lester, 2013).

En este sentido, Lester propone un modelo para describir el proceso de resolución de problemas en el que se destaca el tránsito entre dos mundos, el cotidiano de problemas y el abstracto de conceptos, símbolos y operaciones matemáticas. Así, los elementos más importantes son las relaciones entre el proceso matemático (mundo matemático) y las acciones sobre los elementos particulares del problema (mundo cotidiano). En su modelo, Lester (2013) describe los momentos por los que transita un individuo que trabaja en la solución de un problema matemático, el cual es entrelazado y multifase, ya que considera que el actuar de un individuo en el proceso de solución, puede requerir de una constante comparación y esta se puede presentar en las diversas fases, modificando su actuar en el proceso de solución que desarrolla el individuo.

Este esquema inicia con un contexto en el cual se le propone al estudiante a trabajar en la resolución de un problema (A), se le plantea una consigna específica que debe atender (flecha sólida entre A y B). El estudiante simplifica el planteamiento al identificar conceptos y procesos que soportan al problema (B). El estudiante vuelve al contexto inicial para reinterpretar en sentido del problema (flecha punteada entre B y A). A continuación, viene la fase de abstracción (flecha sólida entre B y C) la cual introduce conceptos matemáticos y notaciones (idiosincrásicas). Esta fase de abstracción involucra la selección de conceptos matemáticos que representen las características esenciales del modelo. Una vez que el estudiante ha generado una representación matemática de la situación original, este problema matemático adquiere un significado propio, volviéndose un problema matemático aislado, bien definido (cuadro C). La tercera fase del proceso (de C a D) involucra la manipulación de la representación matemática y la deducción de algunas conclusiones matemáticas (señaladas como la flecha sólida de cálculos). Por último, la fase, que puede ser de D a A, D a B, y D a C, implica la comparación de las conclusiones o resultados con el problema en su contexto original o con su representación matemática. Esta etapa no implica necesariamente la conclusión del ciclo, ya que se trata de un proceso de continuo de monitoreo, la cual es definida por Lester como una actividad metacognitiva de reflexión continua, que representa un elemento clave para el éxito en tareas matemáticas complejas. Lester afirma que el grado con el cual un individuo compara el estado actual del problema con estados anteriores denota la complejidad de la tarea, permitiendo distinguir así tareas rutinarias o no rutinarias. Esta investigación pone especial atención a lo que ocurre en el momento de la “abstracción” en el modelo anterior, ya que en esta fase el estudiante elige e introduce conceptos matemáticos, notaciones esenciales para resolver el problema y aparecen argumentaciones que conducen a la solución de problema.

Figura 1: Modelo de actividad matemática de resolución de problemas.

Fuente: traducción propia a partir de Lester (2013).

Argumentación

Metaxas, Potari y Zachariades (2016) señalan que la argumentación contribuye a la construcción de conocimiento, pues implica el uso de habilidades para justificar, desafiar, contraponer o conceder ideas respecto de un conocimiento. No obstante, como lo afirman Inglis y Mejía-Ramos (2005), es común que los estudiantes universitarios presenten dificultades al formular y sustentar sus argumentos en el contexto de una actividad matemática. Determinar el origen de esas dificultades ha motivado el estudio y análisis de las argumentaciones para describir la naturaleza de los argumentos, los elementos que los sustentan, así como su función en el desarrollo de una actividad matemática. El aula de clase representa el contexto idóneo para realizar observaciones de los procesos argumentativos. En este ámbito se puede analizar el trabajo de los alumnos para identificar el papel que tienen las explicaciones, afirmaciones, cuestionamientos en el estudio de conceptos matemáticos. Tal como lo señalan De Gamboa, Planas y Edo (2010), la argumentación es un discurso que se dirige a un receptor con el fin de justificar una opinión a partir de hechos, razonando los criterios sobre los que se decide la adecuación de la opción elegida. Sin embargo, no todas las actividades que se realizan en clase permiten a los alumnos exponer públicamente los argumentos, heurísticas y conjeturas que elaboran durante en sus actividades matemáticas. Pedirle a un estudiante exponer explícitamente sus argumentos no siempre resulta fácil debido a la ausencia de la actividad metareflexiva en los procesos matemáticos que realiza; además, como afirman Kidron y Dreyfus (2010), incluso los estudiantes de nivel universitario carecen de la claridad conceptual para formular o enunciar un argumento matemático. Esta situación alentó el desarrollo de este trabajo, al proponer un problema para el cual los estudiantes se involucren en el diálogo, debate y puedan exponer sus puntos de vista, sostener sus ideas y construir argumentos. De Gamboa, Planas y Edo (2010) señalan que la argumentación se desarrolla como parte de la actividad matemática en donde las “razones” se proponen como “justificación” entre los datos y la conclusión, aunque estas proposiciones deben ser de naturaleza deductiva y no solo semántica. De esta forma, el estudiante podría reconocer el poder que tienen sus argumentos en el desarrollo de sus propias conclusiones, las cuales contribuyen a fundamentar su aprendizaje.

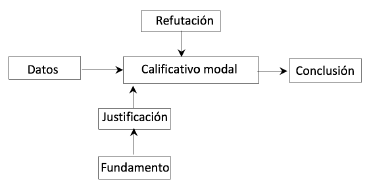
La identificación de argumentos matemáticos se puede realizar utilizando el esquema argumentativo de Toulmin (Inglis, Mejía-Ramos y Simpson, 2007), el cual está conformado por seis tipos de declaraciones y cada una de estas cumple un papel diferente en el argumento. Inglis y Mejía-Ramos (2005) plantean el modelo en la figura 2.

Figura 2: Esquema del modelo de Toulmin.

Fuente: traducción propia a partir de Inglis y Mejía-Ramos (2005).

Inglis y Mejía-Ramos (2005) señalan que la conclusión (C) es la tesis que se invoca; el dato (D) es la información en la cual se basa la conclusión que está formada por hechos o condiciones que son observables; la justificación (J) es una declaración que justifica la conexión entre el dato y la conclusión, haciendo referencia, por ejemplo, a una regla, definición, analogía, que brinda la lógica para la transición del dato a la conclusión, además, justifica la importancia del dato. La “justificación” es el apoyo o respaldo que puede ser un estudio, un código, una estadística o incluso una creencia. El calificador (Q) determina la fuerza de la conclusión, en dicha declaración se expresa el grado de confianza en la tesis. Y la refutación (R) presenta las excepciones de la conclusión, es decir, las condiciones en las cuales no es posible sostener la tesis del argumento.

Inglis y Mejía-Ramos señalan que no todos estos tipos de declaraciones son necesariamente verbalizados de manera explícita por los estudiantes durante una actividad matemática, lo que dificulta su identificación. Dado que la resolución de problemas es un tipo de actividad matemática que demanda la puesta en funcionamiento de diversos recursos matemáticos, habilidades, estrategias de solución y que, además, favorece un contexto de diálogo, debate y argumentación, esta investigación postula plantear una extensión del modelo de Lester (2013) e integrar al momento de “abstracción” el modelo argumentativo de Toulmin, ya que en ese momento los estudiantes también elaboran argumentos, implícitos o explícitos, y es donde justifican sus decisiones y procedimientos.

Metodología

Para llevar a cabo la investigación, primero se formuló un problema no rutinario (Schoenfeld, 1985) distinto a los resueltos comúnmente en clase de matemáticas, ya que, como señalan Alvarado y González (2009), el proceso habitual de instrucción en matemáticas no ofrece oportunidades para que los alumnos expresen verbalmente sus impresiones; además de que los problemas que se ponen en marcha son muy estructurados, con información precisa, reglas claras y criterios definidos para resolverlos (Simon, 1973). En cambio, los problemas no rutinarios admiten varios procedimientos de solución, en el que se requiere, en conjunto conlas reglas, fórmulas y algoritmos, el uso de conjeturas, contraejemplos y aproximaciones (Santos, 2007). Considerando lo planteado por Schoenfeld (1985), se formuló un problema denominado “Vuelo a Madrid”, que está inspirado en un itinerario real de viaje. El problema plantea determinar el tiempo de viaje y la diferencia de horarios entre las dos ciudades, en el problema se indican los horarios de salida y llegada en la hora local de la ciudad correspondiente.

La actividad se aplicó en tres grupos de estudiantes universitarios en la modalidad de trabajo en equipo, uno de primer semestre (grupo 1) que cursaban la materia Introducción a las matemáticas; un grupo de estudiantes de tercer semestre que cursaban la materia Cálculo diferencial e integral (grupo 2); y otro de séptimo semestre que cursaban la materia Métodos numéricos (grupo 3), con un total de 58 estudiantes, todos eran alumnos de la carrera de ingeniería en sistemas computacionales en una universidad pública de la ciudad de San Luis Potosí, en el estado del mismo nombre en México. La selección de estos grupos atendió al criterio de integrar una muestra con estudiantes de cursos básicos, intermedios y avanzados. El profesor titular del curso (el mismo en los tres grupos) fue el responsable de poner en marcha la actividad durante el horario escolar. Los estudiantes del primer grupo (básico) habían cursado asignaturas de matemáticas básicas, como álgebra y trigonometría. Los estudiantes del segundo grupo (intermedios) habían cursado geometría analítica, álgebra lineal, probabilidad, estadística. Los estudiantes del tercer grupo (avanzados) habían cursado variable compleja y ecuaciones diferenciales.

En la primera fase, los estudiantes trabajaron en equipo en la solución del problema, después se realizó una sesión grupal para analizar los resultados. Durante las jornadas de trabajo se utilizó un equipo de filmación para recuperar las interacciones verbales y se recopilaron los registros escritos de cada estudiante con el propósito de analizar e interpretar los planteamientos matemáticos.

Problema “Vuelo a Madrid”

Procedimientos de solución esperados

Existen al menos tres procedimientos para resolver el problema: empleando operaciones aritméticas, a través de un sistema de ecuaciones de 2x2 o través de una ecuación lineal de primer grado. Presentamos a continuación la solución del problema empleando un sistema de ecuaciones.

En cualquier viaje, el tiempo de duración se determina a través de una diferencia entre la hora de salida y llegada al destino. En el problema identificamos como elemento central la hora de salida y llegada en cada ciudad, ya que a partir de estos datos es posible determinar el tiempo de vuelo aparente, es decir, el tiempo de vuelo sin considerar las horas de diferencia entre las ciudades. El vuelo de la Ciudad de México a Madrid sale el lunes a las 6:25 pm y llega el martes a las 12:40 pm, existe una diferencia de 18 horas 15 minutos, es decir, 1095 minutos en el tiempo aparente de vuelo. El vuelo de Madrid a la Ciudad de México sale el lunes a las 2:40 pm y llega el lunes a las 7:20 pm, existe una diferencia de 4 horas con 40 minutos, es decir, una diferencia de 280 minutos en el tiempo aparente de vuelo. Se observa que existe una diferencia considerable entre los tiempos de vuelo calculados anteriormente, la cual puede ser explicada por la diferencia de horarios. En el primer viaje se agrega al tiempo aparente de vuelo, las horas de la diferencia horaria; por el contrario, al regreso el tiempo de vuelo se restan las horas de diferencia horaria. En el vuelo de la Ciudad de México a Madrid, representamos con v el tiempo aparente de vuelo y d las horas de diferencia entre estas ciudades, tenemos:

v + d = 1095

Sabemos que en el vuelo de Madrid a la Ciudad de México duró 25 minutos más, por lo que el tiempo de vuelo lo representamos como v + 25 y las horas de diferencia d se restan, entonces tenemos:

v + 25 - d = 280

Esto conduce a un sistema de dos ecuaciones con dos variables:

v + d = 1095

v + 25 - d = 280

Aplicando eliminación por suma o resta tenemos:

2v + 25 = 1375

v = 675

Por lo cual:

d = 420

Con lo cual concluimos que existen siete horas de diferencia entre ambas ciudades.

Cómo resolvieron el problema

Discusión de resultados: los momentos en los que aparecen los argumentos

Para determinar la duración de los vuelos la mayoría de los estudiantes del grupo 2 planteó la diferencia entre el horario de salida y de llegada. Esto los llevó a concluir que el tiempo de duración de ambos vuelos no es igual y ante este hecho aparecen dos tipos de argumentos: aquellos que atribuyen situaciones propias del contexto del problema que no están explícitas en el problema, como suponer una demora de uno de los vuelos; o bien, aquellos que señalan un error en el planteamiento. A continuación, se presenta el análisis realizado a tres diálogos que se desarrollaron en el primer momento de trabajo en equipo con estudiantes del grupo 2. Como se ha señalado, los estudiantes trabajaron en equipo y estuvieron acompañados por el profesor en breves periodos de tiempo, debido a que el docente tenía que recorrer todos los equipos del grupo. En las intervenciones, el profesor tuvo el papel de orientar el diálogo y motivar la exposición de argumentos.

Para realizar este análisis se utilizó el modelo de Toulmin descrito en Inglis y Mejía-Ramos (2005). La secuencia de la argumentación consiste en demostrar la conclusión a partir de los datos. Esta relación se expresa en la línea principal del trazado y puede referirse a la inferencia del argumento, pero esa inferencia requiere una legitimidad (respaldos), que representan fundamentos básicos indiscutibles (justificación, fundamentos). Como lo señalan Teixeira, Freire y Greca (2015), la estructura de un argumento se puede resumir de la siguiente forma: J, una vez aprobado por F, autoriza a C, obtenida a partir de D, siendo considerado Q, a menos que haya R.

Los argumentos pueden ser encadenados de tal manera que una conclusión puede funcionar de nuevo como dato para un nuevo argumento posterior (Krummheuer, 2015). En nuestro caso, los argumentos se refieren al planteamiento del proceso de solución y esto concluye con un resultado obtenido, sea correcto o incorrecto. De acuerdo con Inglis y Mejía-Ramos (2005), no todos los tipos de declaraciones son necesariamente verbalizados de manera explícita, de ahí la importancia de la intervención del profesor para motivar a los estudiantes a exponer sus ideas.

Para este reporte se presentan tres diálogos, que fueron seleccionados considerando la amplitud y claridad de las declaraciones de los estudiantes. Los dos primeros desarrollados entre el profesor (P) y los estudiantes del equipo 4, Bernardo (B), Karina (K) y Anahí (A). El tercer diálogo se establece entre P con el equipo 3 conformado por Martín (M), Ludivina (L) y Semiramis (S). Al momento de realizar esta conversación los estudiantes ya habían superado la fase de abstracción, así que ya habían acordado el procedimiento que desarrollarían en la fase de representación matemática. El primer diálogo se refiere a la conclusión “el problema se resuelve con una derivada” expuesta por Bernardo.

Episodio 1: Bernardo y el profesor

• P: Y bien ¿cómo se resuelve el ejercicio?

• B: Yo creo que el tiempo… de la hora de salida de México a la hora de llegada, es algo así como una resta es igual a x, y después la hora de salida de Madrid a la hora de llegada igual una resta... pero sería equis más veinticinco (x + 25) minutos que es lo que dice que demoró.

• P: ¿Y usaste ese razonamiento para la solución?, o lo estás pensando ahora.

• B: No, pues yo le puse que se hacía con una derivada, porque es una razón de cambio las horas... de México y de Madrid.

• P: ¿Qué está cambiando?

• B: Pues es diferente la hora de aquí (México) a la de allá (Madrid), ¿no?

• P: ¿Es un variable?

• B: (asiente).

• P: ¿Y la otra? en la razón de cambio involucramos dos variables, ¿verdad?

• B: Pues el tiempo.

• P: ¿Es la hora?

• B: (asiente).

• P: Ok, pero tú dices que tienes esa incógnita que es la equis x, ¿es el tiempo verdad?, y de regreso equis más veinticinco x+25.

• B: Sí, pero podría ser una ecuación.

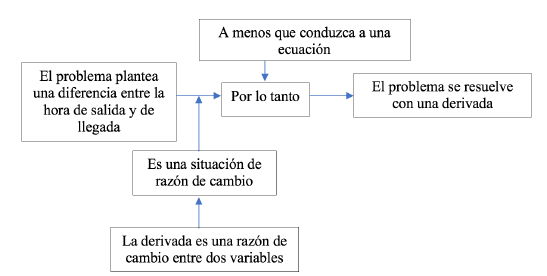
A partir de este diálogo se construyó el esquema de la figura 3, en el que se observa que la idea de “diferencia” fue la que motivó la asociación con la derivada y, por lo tanto, afirmó que se trataba de un tema de cálculo diferencial. El argumento expuesto por Bernardo estuvo influido por un contrato didáctico (en el sentido de Brousseau), ya que en días previos a la aplicación de la actividad se abordó el tema de “derivada” en el curso de cálculo.

Figura 3: Esquema para el argumento de Bernardo

Fuente: elaboración propia.

Episodio 2: Anahí y el profesor

El segundo diálogo se refiere a la conclusión “el problema no se puede resolver” que expone Anahí.

• P: La primera pregunta que les voy a hacer es ¿cómo se resuelve el problema?

• A: Bueno a mí se me hizo un problema muy difícil porque yo sentía que nos faltaban datos para poderlo resolver.

• P: De acuerdo, ¿qué fue lo que pensaste, Anahí?

• A: Bueno pues yo empecé restando como si fueran las horas iguales, las de aquí (México) a las horas de allá (Madrid) yo puse que en el primero eran 18 horas y 15 minutos y en el segundo eran 4 horas y 40 minutos, entonces yo concluí que no era posible, por razonamiento lógico no era posible determinar el tiempo ya que los datos no eran los... que ocupábamos para poder resolver, pues cuando uno viaja el tiempo de viaje es lo primero que se sabe.

• P: ¿Qué concluyes?

• A: No se puede resolver, está mal planteado.

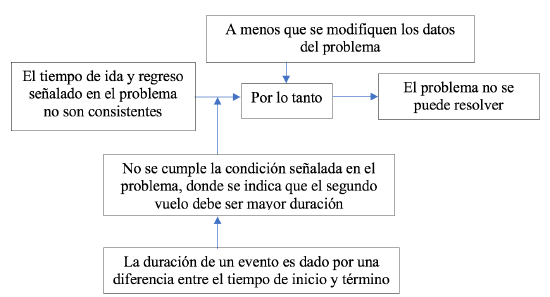
A partir de este diálogo se construyó el esquema de la figura 4. Anahí señala que la diferencia obtenida en los vuelos no era congruente, ya que, de acuerdo con su experiencia de viaje, esos datos son precisos, por lo tanto, no es posible resolver el problema.

Figura 4: Esquema de argumentos de Anahí.

Fuente: elaboración propia.

Episodio 3: Martín, Ludivina, Semiramis y el profesor

El tercer diálogo se refiere a la conclusión “el problema se resuelve a través de un sistema de ecuaciones”.

• P: ¿Con los datos que tienen es posible determinar el tiempo de viaje de México a Madrid?

• L: Sí.

• P: ¿Cómo se podría hacer eso?

• L: Mediante una ecuación.

• P: De acuerdo.

• S: Ya lo intentamos.

• M: Un sistema de ecuaciones.

• P: ¿Y con eso será posible determinar la diferencia de horarios?

• M: Sí

• L: Yo digo que no, pero...

• P: Ella dice que no, tú dices que sí, ¿por qué lo afirmas Martín?

• M: Porque nos da dos datos diferentes, antes pensaba diferente, pero ahora que lo analizo de esta manera nos conduce a un sistema de ecuaciones. Entonces podemos determinar algo, ya sea que encontremos las horas que tarda en viajar o la diferencia de horario si hacemos correctamente el sistema de ecuaciones podemos encontrar uno de estos.

• P: Tú dices que si encuentras una variable después ya puedes encontrar la otra.

• M: En el sistema de ecuaciones, ese es ahí donde yo creo que está, nos está faltando definir.

• P: ¿Qué opinan ustedes muchachas?, ¿será correcto lo que dice su compañero?, ¿están de acuerdo?

• L: Bueno sí, sí ya encontramos una variable ya nada más sería de despejar y ya podríamos encontrar la otra.

A partir del diálogo anterior se elaboró una línea argumentativa en la figura 5. En este episodio, Martín señala que el problema tiene dos incógnitas, por lo que esto puede dar lugar al planteamiento de un sistema de ecuaciones. Conociendo el valor de una de las variables, entonces se puede determinar la otra. El problema es establecer esta relación de variables y emplear un método para resolver el sistema.

Figura 5: Esquema de argumentos de Martín.

Fuente: elaboración propia.

El profesor encargado de la implementación recorrió todos los equipos para entablar conversación, con el propósito de obtener información sobre la forma en que cada equipo planteó la solución del problema. Esta se organizó y se formularon cuatro categorías atendiendo a la forma en que cada equipo planteó la solución al problema, estas categorías se describen a continuación.

1. El problema no se puede resolver debido a que faltan de datos (C). Los estudiantes identifican en el problema las horas de salida y llegada (D) y plantean operaciones para calcular la diferencia de tiempo (F), y determinar el tiempo de vuelo de cada viaje (J), pero al realizar las operaciones obtienen resultados que no se ajustan a las condiciones del problema y admiten que son inconsistentes por lo que (Q) no se puede resolver a menos que se agreguen información adicional (R) al problema para subsanar los huecos de información, por ejemplo, aclarar cuántas escalas hizo el avión o la velocidad del avión en cada viaje.

2. No se puede resolver el problema debido a errores en la redacción (C), los estudiantes identifican las horas de salida y llegada (D) y determinan que el problema se resuelve con una resta (F), lo que permite determinar la duración del tiempo de vuelo (J), pero al plantear y resolver sus operaciones obtienen resultados que no concuerdan con la situación planteada y admiten que sus resultados son inconsistentes y no son lógicos con lo que ocurre en la vida real. A menos que se modifique el planteamiento y establezcan correctamente los datos (R).

3. El problema se puede resolver a través de una operación o ecuación (C). Los estudiantes identifican la hora de salida y de llegada (D) y establecen operaciones o plantean ecuaciones (F) que permitirán determinar el tiempo de vuelo (J). Después de efectuar el procedimiento matemático señalado, se obtiene un resultado equivocado, que no se confrontan con el planteamiento y se acepta como válido. No emplean un procedimiento para verificar sus resultados y confían en el resultado de la operación. Las excepciones (R) son de dos tipos. La primera referida a la posibilidad de plantear o usar una operación o ecuación incorrecta. La segunda, la posibilidad de un error de cálculo que conduzca a un resultado equivocado.

4. Homólogo al anterior, con la diferencia de que las operaciones o ecuaciones planteadas conducen a la solución correcta, sin que necesariamente todos hayan llegado a ella. En el caso de aquellos estudiantes que obtuvieron un resultado, lo validan al sumar la diferencia horaria al tiempo de vuelo de cada viaje.

Estas categorías antes descritas ponen de manifiesto que los datos del problema establecen el punto de partida para el proceso de solución y definen la conclusión a partir de tres referentes matemáticos: 1) los conocimientos que han abordado o estudiado previamente en su curso de matemáticas, bajo la idea de que el problema planteado es un ejercicio de “aplicación”; (2) el planteamiento y ejecución de cálculos matemáticos y ecuaciones simples, sin una reflexión previa sobre el uso de esos recursos matemáticos y asumiendo que los problemas se resuelven aplicando ciertas operaciones; y 3) la identificación de variables en el problema y la asociación inmediata a la formulación de ecuaciones para determinar su relación, tanto en ecuaciones lineales como sistemas de ecuaciones. Las categorías a y b exponen los casos donde se afirma que el problema no se puede resolver, en estos, la “excepción” permite a los estudiantes justificar una modificación al problema: ajustar su redacción para eliminar inconsistencias o bien para agregando información complementaria para hacerlo más preciso.

La categoría c se refiere al caso en el que los estudiantes no realizan una reflexión sobre el sentido del problema durante la fase de la abstracción, y continúan con la solución sin preguntar la coherencia de sus resultados. La justificación se sostiene en la idea de diferencia entre horarios como forma de determinar la duración del viaje, y el fundamento en las operaciones aritméticas. Así, los estudiantes no expresan ninguna dificultad y confían en que su procedimiento los llevará a la solución correcta del problema. Este fenómeno, denominado “contrato didáctico”, se refiere a comportamientos específicos de los estudiantes cuando responden a un planteamiento matemático para cumplir con lo que, creen, se espera de ellos (Education Committee of the European Mathematical Society, 2012). Uno de estos casos es un problema que se presenta bajo el nombre de “la edad del capitán”, el cual enuncia: “en un barco hay 26 ovejas y 10 cabras, ¿Cuál es la edad del capitán?”, las investigaciones que exploraron las respuestas de este problema (como la de Verschaffel, Greer y de Corte, 2000) señalan que la gran mayoría de los alumnos realizan cálculos para determinar un valor a través de alguna operación como suma o resta, sin que sea cuestionada la estructura del problema. Es decir, confían en que el profesor ha asignado un problema correctamente ya que sería extraño que un ejercicio no tuviera solución.

Conclusiones

Una de las características de los problemas “no convencionales” es que los datos no son explícitos, están incompletos y en ocasiones no hay una respuesta única al problema. Ante esto, los estudiantes dedican más tiempo a la interpretación de la situación, la deducción de datos y a la construcción de procedimientos para resolver el problema. Esto suele generar incertidumbre ya que los estudiantes deben tomar decisiones sobre todas las etapas en la solución del problema, no obstante, esto representa un importante potencial didáctico al permitir a los estudiantes poner en juego sus recursos matemáticos, explorar diferentes rutas de solución y propiciar la comunicación de información matemática con sus compañeros.

Usualmente, los libros de texto abordan muy pocos problemas de este tipo, y más bien se enfocan en plantear problemas que asocien o favorezcan el uso de ciertos procedimientos, técnicas o métodos.

Sin embargo, es importante enfatizar que esta distinción en los tipos de problemas no es del todo absoluta pues, como lo señala Schoenfeld (1985), existe la posibilidad de que un mismo planteamiento implique diferente esfuerzo aún para estudiantes con los mismos antecedentes matemáticos. Postulamos la idea de que los problemas “no convencionales” tienen ciertos rasgos distintivos que posibilitan la creación de un ambiente para explorar, debatir y justificar los procedimientos de solución. No obstante, esto debe tomarse con cautela pues en esta investigación se observó que algunos estudiantes, incluso trabajando en equipo, no cuestionaron ni reflexionaron sobre el sentido de sus operaciones y los resultados obtenidos. Este grupo de estudiantes presentó sus resultados sin que realizaran un enfrentamiento con el contexto y las condiciones señaladas en el problema. Otro grupo de estudiantes (avanzados), no reveló ninguna dificultad la solución del problema pues, para ellos, resultó muy sencillo. Tampoco se generó mucha interacción ya que planteamiento surgió rápidamente y no hubo conflictos. Otro grupo de estudiantes consiguió abordar el problema como un desafío, en él apareció una constante reflexión sobre el sentido del problema y, aunque no todos llegaron a la solución completa, sí hubo justificaciones correctas sobre los planteamientos matemáticos elegidos. Este grupo fue el elegido para profundizar en el análisis de sus argumentos.

El problema creado para esta investigación tuvo la característica de emplear consignas abiertas, lo que permitió la formulación de diversas interpretaciones, que, incluso, pusieron en duda la estructura y coherencia del problema. Por otra parte, permitió el uso de cualquier recurso matemático para su solución, lo cual ofreció libertad a los estudiantes en la elección del procedimiento. Estas dos características, aunado a un esquema de trabajo colectivo para favorecer la interacción, motivaron que en la fase de “abstracción” se identificaran al menos cuatro diferentes conclusiones (C) asociadas a la solución del problema.

Este trabajo ofrece dos contribuciones al campo de la educación matemática, el primero al profundizar en la compresión y origen de los argumentos o razones lógicas de los estudiantes, a través del modelo argumentativo de Toulmin, durante la fase de “abstracción” en el modelo de resolución de problemas de Lester (2013). La conjunción de estas dos unidades teóricas resultó muy favorable pues permitió ordenar los recursos matemáticos y procedimientos que pusieron en juego los estudiantes para la solución del problema (observados en la fase de “abstracción”) e identificar el origen de las conclusiones que formulan los estudiantes. La segunda contribución se refiere a una serie de reflexiones sobre las características de los procedimientos que eligieron los estudiantes para la solución del problema, directamente asociados a sus antecedentes matemáticos, pero también influidos por la interpretación del problema. Como se pudo observar, los estudiantes más jóvenes atribuyeron una supuesta inconsistencia del problema que limitó el trabajo matemático.