DOI:
https://doi.org/10.14483/23448350.15601Published:
05/03/2020Issue:
Vol. 38 No. 2 (2020): May-August 2020Section:
Science and EngineeringT-overlap T-migrative Functions: a generalization of migrativity in t-overlap functions
Funciones t-migrativas t-overlap: una generalización de migratividad en funciones t-overlap
Keywords:
migrative function, overlap function, t-norm (en).Keywords:
función migrativa, función overlap, normas triangulares (es).Downloads
References
Alcala-Fdez, J., Alcala, R., Herrera, F. (2011). A fuzzy association rule-based classification model for high-dimensional problems with genetic rule selection and lateral tuning. IEEE Transactions on Fuzzy Systems, 19(5), 857-872.https://doi.org/10.1109/TFUZZ.2011.2147794
Bandler, W., Kohout, L. (1980). Fuzzy power sets and fuzzy implication operators. Fuzzy Sets and Systems, 4(1), 13-30. https://doi.org/10.1016/0165-0114(80)90060-3
Bustince, H., Fernandez, J., Mesiar, R., Montero, J., Orduna, R. (2010). Overlap functions. Nonlinear Analysis: Theory, Methods & Applications, 72(3-4), 1488-1499. https://doi.org/10.1016/j.na.2009.08.033
Bustince, H., Montero, J., Mesiar, R. (2009). Migrativity of aggregation functions. Fuzzy Sets and Systems, 160(6), 766-777. https://doi.org/10.1016/j.fss.2008.09.018
Durante, F., Sarkoci, P. (2008). A note on the convex combinations of triangular norms. Fuzzy Sets and Systems, 159(1), 77-80. https://doi.org/10.1016/j.fss.2007.07.005
Fodor, J., Rudas, I. J. (2007). On continuous triangular norms that are migrative. Fuzzy Sets and Systems, 158(15), 1692-1697. https://doi.org/10.1016/j.fss.2007.02.020
Grabisch, M., Marichal, J. L., Mesiar, R., Pap, E. (2009). Aggregation Functions. Encyclopedia of Mathematics and its Applications, Cambridge University, New York. https://doi.org/10.1017/CBO9781139644150
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de noviembre de 2019; Aceptado: de abril de 2020
Abstract
This paper introduces a generalization of migrative functions by extending the conditions of the product operation applied in the variables. We operate a number with the variables according to a t-norm instead of multiplying the variable x by this number. Such generalization, whenever it occurs, is called a t-migrative function with respect to such t-norm. Furthermore, we analyse the main properties of t-migrative and t-overlap functions. We introduce some interesting methods of construction of such functions.
Keywords:
Migrative function, overlap function, t-norm..Resumen
Este artículo introduce una generalización de funciones migrativas por extensión de la condición de la operación producto aplicada en las variables. Más específicamente, en lugar de exigir multiplicar la variable x por un número real _; en este trabajo se trabaja este número _ con las variables de acuerdo a una t-norma. Se denomina a esta generalización función t-migrativa con respecto a tal t-norma. Luego se analizan las propiedades principales de funciones t-migrativas en funciones t-overlap y se introducen algunos métodos de construcción de este tipo de funciones.
Palabras clave:
función migrativa, función overlap, normas triangulares..Resumo
Este artigo apresenta uma generalização das funções migratórias estendendo as condições da operação do produto aplicada nas vari´veis. Mais especificamente, em vez de exigir a multiplicação da vari´vel x por um número real _; neste trabalho operamos isso _ número com as variáveis de acordo com a norma t. Chamamos essa generalização de uma função t-migrative em relação a essa norma t. Em seguida se analiza as principais propiedades das funções t-sobreposição migratórias e introduzimos alguns métodos de construoção.
Palavras-chaves:
função migratória, função de sobreposição,norma t.Introduction
The purpose of this paper is to generalize the notion of migrative functions by relaxing one of the conditions of product operators applied in the variables. The notion of migrative function was introduced and studied in (Bustince, Montero and Mesiar, 2009). We follow a different approach. Rather than multiplying the variables of the function by a real number a, we operate this number with a t-norm.We allow it some kind of threshold, defined in terms of a t-norm T. We call such generalization a t-migrative function with respect to T and here after, we apply the migrativity to t-overlap functions. We observed that, this simple generalization allows us to state several interesting properties, which can be applied in fuzzy rule-based systemto eliminated bad rules when computing the compatibility degree. Section 1 presents some preliminary concepts. In Section 2, we propose some method of construction of such function. We also study the main properties of the generalized functions.
Preliminaries
Triangular Norms
One of the basic concepts of the fuzzy theory is triangular norms or t-norms. In this paper, these functions are frequently used. We begin with the basic definition of t-norms.
Definition 1 (See Bustince, Burillo, and Soria (2003)) A triangular norm or t-norm is an aggregation function

We then present some examples of t-norms which are of great interest.
Example 1 The function T : [0,1]2 - [0,1], defined by T(x, y) = mín {x,y} is a t-norm.
Definition 2 A t-norm function is strict if it is strictly increasing for its two variables, that is to say if x1 < x2 and y ¹ 0 then T(x1, y) < T(x2, y):
Definition 3 A t-norm function is positive if T(x, y) = 0 iff xy = 0:
Migrativity
The concept of _-migrativity was introduced by Durante and Sarkoci (2008) . A bivariate operation’s class having a property previously presented by Mesiar and Novak (1996) which was later studied by Fodor and Rudas (2007) .
Definition 4 (Durante and Sarkoci 2008) Let α ? [0; 1] be fixed. A bivariate operation
G : [0, 1]2 ?[0; 1] is α ?migrative if G(αx, y) = G(x, α y), for all x, y ? [0, 1].
From the definition above, we can easily observed that all function G : [0, 1]2 - [0, 1] is 1-migrative, as G(x, y) = G(1.x, y) = G(x, 1:y). This definition is referred to as a predetermined α. We generalized the concept of α-migrativity the next form,
Definition 5 (SeeBustince, Montero and Mesiar (2009)) A function G : [0, 1]2 -[0, 1] is called migrative if and only if G(αx, y) = G(x, αy) for all x; y ? [0; 1] and for all α? [0, 1].
Example 2 The function h : [0, 1]2 - [0, 1]; defined by h(x, y) = xy; is migrative.
Example 3 La function G : [0; 1]2 - [0, 1]; defined by
 shows that
shows that
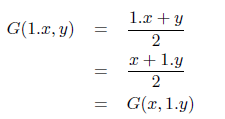
thus G is a 1-migrative function, but if you take
 it shows that
it shows that
 .This is easy to see, in particular if it is done x = 1 and
.This is easy to see, in particular if it is done x = 1 and

The following lemma is the characterization of the main migrative functions.
Lemma 1 (Bustince, et al., 2010) A function

is migrative if and only if G(x, y) = G(1, xy); for all x; y ? [0; 1].
From the lemma (Bandler and Kohout, 1980), we deduce the following corollary, in which a characterization of bivariate migrative function is seen as a function of a variable.
Corollary 1 (Bustince, et al., 2010) A function G : [0, 1]2 - [0, 1] is migrative if and only if ther exists a function g : [0, 1] - [0, 1] such that G(x, y) = g(xy) for all X, y ? [0; 1].
Overlap and T-Overlap Functions
In this section, we present the definition of overlap function as well as some of its properties. This type of functions constitutes one of the most important pillars in this work.
Definition 6 (Bustince, et al., 2010) A function GS: [0, 1]2 -[0, 1] is an overlap function, if it satisfies the following conditions:
-
(Gs 1) Gs is symmetrical,
-
(Gs 2) Gs(x; y) = 0 if and only if xy = 0,
-
(Gs 3) Gs(x; y) = 1 if and only if xy = 1;
-
(Gs 4) Gs is not decreasing,
-
(Gs 5) Gs is continuous.
Example 4 An example of an overlap function is the product function h(x, y) = xy, with x, y ? [0, 1].
Example 5 The function G(x, y) = sin
 is an overlap function.
is an overlap function.
Example 6 Other example of overlap function is

The concept of the generalization of the overlap function, is obtained by changing the condition (Gs2) given in (Alcala-Fdez, Alcala and Herrera, 2011). This property requires that given an overlap function GS, then GS(x; y) = 0 , xy = 0. In this generalization, the product operation is replaced by a t-norm
T : [0, 1]2 - [0, 1].
Definition 7 Let T : [0, 1]2 - [0, 1] be a t-norm. A function GT: [0, 1]2 - [0, 1] is said to be a t-overlap function with respect to T if the following conditions holds:

T-Migrativity
We then present a generalization of the migrativity concept where the multiplication operation is replaced by a t-norm.
Definition 8 A two-dimensional G function is said to be t-migrative with respect to a t-norm T if for all α ? [0, 1] we have that G(x; T(α, y)) = G(T(x, α), y) for all x, y ? [0, 1].
Traditionally, a migrativity property is given for the particular case in which α= 0.
Proposition 1 A function G : [0, 1] - [0, 1] is 0-tmigrative if and only if G(x, 0) = G(0, y)
Proof 1 If G is 0-t-migrative then G(x, 0) = G(x, T(0, y)) = G(T(x, 0), y) = G(0, y) If G(x, 0) = G(0, y) then as for all t-norm T(0, x) = 0 then G(x, T(0, y)) = G(T(x, 0), y).
The following theorem broadly generalizes theorem 1
Theorem 1 A function G : [0, 1]2 - [0; 1] is t-migrative with respect to a t-norm T if and only if there exists a function g : [0, 1] - [0, 1] such that G(x, y) = g(T(x, y)).
Proof 2 Let G(x, y) = g(T(x, y)), then
G(x, T(y, z)) = g(T(x, T(y; z))) = g(T(T(x, y), z)) = G(T(x, y), z):
If G is t-migrative with respec to a t-norm T, then
G(x, y) = G(T(x, 1), y) = G(1, T(x, y))
for all x, y ? [0; 1], if G(x, y) = G(u, v) then G(1, T(x, y)) = G(1, T(u, v)) where T(x, y) = T(u, v) thus g is well defined
The next corollary is a generalization of corollary 1
Corollary 2 G is t-migrative with respec to a t-norm T if and only if
G(x, y) = G(1, T(x, y))
The following corollary shows an obvious consequence of t-migrativity.
Corollary 3 If G is t-migrative with respect to a t-norm T then G is symmetrical.
Proof 3 G(x, y) = G(1, T(x, y)) = G(1, T(y, x)) = G(y, x).
Below is a list of some of the properties of t-migrative functions.
Theorem 2 Let G : [0, 1]2 - [0, 1] be a t-migrative function, then:
-
G is non-decreasing if and only if g is nondecreasing.
-
G is strictly increasing in [0; 1]2 if and only if g and T are strictly increasing.
-
G(1; 1) = 1 if and only if g(1) = 1
-
G(0; 0) if and only if g(0).
-
G is continuous if and only if g and T are continuous.
Proof 4
-
Suppose that G is a non-decreasing function. Let x, y ? [0, 1] such that x ? y; then G(x, 1) ? G(y, 1); thus g(T(x, 1)) ? g(T(y, 1)); therefore g(x) ? g(y): Suppose that g is a nondecreasing function and x, y ? [0, 1] such that x ? y then for all z ? [0, 1] is true that T(x, z) ? T(y, z); therefore g(T(x, z)) ? g(T(y, z)) thus G(x, z) ? G(y, z).
-
Analogous.
-
G(1, 1) ? g(T(1, 1)) = 1 , g(1) = 1
-
G(0, 0) ? g(T(0, 0)) = 0 , g(0) = 0
-
G is continuous if and only if g and T are continuous.
One of the most important aspects of this work is the generalization of the migratives of overlap functions. One of the results of this generalization is shown.
Theorem 3 If GT is a t-overlap function with respect to the continuous t-norm T, then
G(x, y) = GT (1, T(x, y))
is a t-overlap t-migrative function with respect to T.
Proof 5
-
Evidently G is Symmetrical.
-
G(x, y) = 0 ? GT (1, T(x, y)) = 0 ? T(x, y) =0.
-
G(x, y) = 1 ? GT (1; T(x, y)) = 1 ? T(x, y) =1 ? x = y = 1.
-
G is continuous.
-
G is no decreasing.
G(T(x, y), z) = GT (1, T(T(x, y), z)) = GT (1; T(x, T(y, z))) = G(x, T(y, z)).
The following theorem shows that the convex sum of t-overlap t-migrative functions with respect to a continuous t-norm is also t-overlap t-migrative function.
Theorem 4 If

are overlap functions and T is a t-norm continuous, then

is t-overlap t-migrative function with respect to T.
Proof 6
-
G is symmetrical
.

-
G is continuous.
-
G is non-decreasing.
Theorem 5 If T1 and T2 are continuous and GT is a overlap function, then
G(x, y) = GT (T1(x; y); T2(x; y))
is a t-overlap t-migrative function with respect to T1 or T2:
Proof 7
-
1. G is symmetrical.
-
2. G(x, y) = 0 ?.GT (T1(x, y); T2(x, y)) = 0 ? T1(x, y) = 0 ? T2(x, y) = 0.
-
3. G(x, y) = 1 ?.GT (T1(x, y); T2(x, y)) = 1 ? T1(x, y) = 1 ? T2(x, y) = 1?x = y = 1.
-
4. G is continuous.
-
5. G is non-decreasing.
Corollary 4 If G is given as in the previous theorem and T1 = T2 then G is t-migrative.
Proof 8 G(x, T(y, z)) = GT (T1(x; T(y, z)); T2(x, T(y; z))) = GT (T1(T(x, y); z), T2(T(x; y); z)) = G(T(x; y); z):
Corollary 5 If T is a t-norm and a strong negation n, then

is a t-overlap t-migrative function with respect to T.
Theorem 6 If GT is an overlap function and T is a continuous t-norm, then

is a t-overlap t-migrative function.
Proof 9
-
1. G is symmetrical
.

-
4. G is non-decreasing.
-
5. G is continuous.
Theorem 7 Let M be a continuous and increasing function such that M(x) = 0? x = 0 and M(x) = 1?x = 1. If GT is an overlap function and T is a continuous t-norm, then
G(x, y) = M(GT (1, T(x, y)))
is a t-overlap t-migrative function.
Theorem 8 Let M be a n-dimensional function, nondecreasing, continuous such that

is a t-overlap t-migrative function if Gi is an overlap function for all i ? 1; : : : ; n and continuous t-norm T.
Proof 10
-
1. G is symmetrical

-
4. G is non-decreasing.
-
5. G is continuous.
Theorem 9 Let M be an n-dimensional and continuous function, such that M(x1; : : : ; xn) = 0 , xi = 0 for some i 2 f1; : : : ; ng y M(x1; : : : ; xn) = 1 , xi = 1 for some i 2 f1; : : : ; ng: Then

is a t-overlap function with respect to some t-norm Tk where Ti are continuous t-norms and Gi are overlap functions.
Theorem 10 A function GS: [0, 1]2 - [0, 1] is an overlap t-migrative function if and only if GS(x, y) = g(T(x, y)) for all x, ? [0, 1] holds for some non-decreasing function g : [0, 1] - [0, 1] such that g(0) = 0 y g(1) = 1.
Proof 11 Let GS be an overlap t-migrative function, then there exists a non-decreasing function g such that GS(x, y) = g(T(x, y)): Now g(0) = g(T(0, 0)) =GS(0, 0) = 0: Besides g(1) = g(T(1, 1)) = GS(1, 1) =1 If GS(x, y) = g(T(x, y)) then GS(x, T(y, z)) =GS(T(x, T(y, z))) = g(T(T(x, y); z)) = GS(T(x, y), z).
Theorem 11 If T is a continuous t-norm and n is a strong negation then
 is a t-overlap tmigrative function with respect to T.
is a t-overlap tmigrative function with respect to T.
Proof 12 By corollary it can be said that G is a toverlap function with respect to the t-norm T. On the

Theorem 12 Let G1; : : : ;Gn be t-migrative overlap functions with respect to T.

is a t-migrative overlap function with respect the t-norm T.
Proposition 2 If GT is a t-overlap function with respect to t-norm T, then GT is t-migrative with respect to T.
Conclusions
In this article we present a generalization of the concept of migrativity applied to overlap function, this generalization expands and allow the migrativity and the applications of the overlap functions on the topics about artificial intelligence and we present how we can generate new migrative functions.
References
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.



