DOI:
https://doi.org/10.14483/23448350.16211Published:
05/01/2020Issue:
Vol. 38 No. 2 (2020): May-August 2020Section:
Scientific and technological educationCompetencia Científica y Resolución de Problemas de Física
Physics problems and development of scientific competence
Keywords:
physics problem, scientific competence, problem solving (en).Keywords:
problemas de física, competencia científica, resolución de problemas (es).Downloads
References
Alonso Sánchez, M.; Carrascosa Alís, J.; Martínez Sala, S. Problemas de Física. Cinemática relativista. Dinámica relativista. Problemas de Física y Química como investigación. Problemas de hidrostática. Problemas de estática. 2019. didacticafisicaquimica.es Acceso en: 1 de enero de 2020
Becerra Labra, C., Gil Pérez, D., Guisasola, J., Martínez Torregrosa, J. (2005). ¿Podemos mejorar la enseñanza de la resolución de problemas de lápiz y papel en las aulas de Física y Química?. Educación química, 16(2), 230-245. https://doi.org/10.22201/fq.18708404e.2005.2.66116
Furió, C. J., Iturbe, J., Reyes, J. V. (1995). ¿Cuánto contaminará una central térmica que funciona con fuel?: Un ejemplo de resolución de problemas como investigación. Alambique, 5, 27-36.
Furió, C.; Reyes, J.V. (1990). O Modelo de Resoluçao de Problemas como Investigaçao. Sua aplicaçao à Quîmica. Boletim da Sociedade Portuguesa de Química, 41(2), 11-16.
Gil Pérez, D.; Carrascosa, J.; Furió, C.; Martínez Torregrosa, J. La enseñanza de las ciencias en la educación secundaria. ICE/ Universidad de Barcelona. Barcelona: Horsori, 1991. cap. 2, p. (41-54).
Gil Pérez, D.; Martínez Torregrosa, J.; Ramírez De Castro, L. (1994). La resolución de pro-blemas de Física y de Química como investigación. Madrid: Centro de publicaciones del Ministerio de Educación y Ciencia CIDE.
Marchesi, A., Martín, E., Casas, E., Ibáñez, A., Monguillot, I., Riviere, V., Romero, F. Tecno-logía y aprendizaje. Investigación sobre el impacto del ordenador en el aula. Madrid: Ediciones SM, 2005.
Martínez Torregrosa, J., Sifredo, C. ¿Cómo convertir los problemas de lápiz y papel en autén-ticos desafíos de interés? En: Gil- Pérez, D., Macedo, B., Martínez Torregrosa, J., Si-fredo, C., Valdés, P., Vilches, A. (Eds.). ¿Cómo promover el interés por la cultura científica? Una propuesta didáctica fundamentada para la educación científica de jóvenes de 15 a 18 años. Santiago: OREALC/UNESCO, 2005. cap. 5, p. 103-121.
National Academies of Sciences, Engineering, and Medicine. Science Teachers Learning: En-hancing Opportunities, Creating Supportive Contexts. Washington, DC: The National Academies Press. https://www.nap.edu/catalog/21836/science-teachers-learning-enhancing-opportunities-creating-supportive-contexts Acceso en 24 dic. 2019.
National Research Council. A framework for K–12 science education: Practices, crosscutting concepts, and core ideas. Washington, DCE: National Academies Press, 2010.
Niaz, M. (2016). History and Philosophy of Science as a Guide to Understanding Nature of Science. Revista Científica, 1(24), 7-16. https://doi.org/10.14483/udistrital.jour.RC.2016.24.a1
Pérez, D. G., Furió-Mas, C., Castro, P. V., Salinas, J., Torregrosa, J. M., Aranzabal, J. G., de Carvalho, A. M. P. (1999). ¿Tiene sentido seguir distinguiendo entre aprendizaje de conceptos, resolución de problemas de lápiz y papel y realización de prácticas de laboratorio?. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 17(2), 311-320.
Pérez, D. G., Martínez-Torregrosa, J., Ramírez, L., Carrée, A. D., Gofard, M., de Carvalho, A. M. P. (1992). Questionando a didática de resolução de problemas: elaboração de um modelo alternativo. Caderno Brasileiro de Ensino de Física, 9(1), 7-19. https://doi.org/10.1080/0140528830050408
Pérez, D. G., Torregrosa, J. M. (1983). A model for problem‐solving in accordance with scien-tific methodology. European Journal of Science Education, 5(4), 447-455.
Rocard, M., Csermely, P., Jorde, D., Lenzen, D., Walberg-Henriksson, H., Hemmo, V. (2007). Science Education Now: A renewed pedagogy for the future of Europe, European Commission Directorate-General for Research Science. Economy and Society, Infor-mation and Communication Unit. Brussels. http://ec.europa.eu/research/sciencesociety/document_library/pdf_06/report-rocard-on-science-education_en.pdf. Acceso en 24 dic. 2019.
Sánchez-Robayo, B. J., Torres-Duarte, J. (2016). Aprender a investigar investigando. Realiza-ción de una propuesta de formación. Revista Científica, 1(28), 17-31. https://doi.org/10.14483/udistrital.jour.RC.2017.28.a2
Solbes-Matarredona, J., Torres-Merchán, N. Y. (2015). Alternativas para reflexionar aspectos críticos de la ciencia en el aula. Revista Científica, 2(22), 31-44. https://doi.org/10.14483/10.14483/udistrital.jour.RC.2015.22.a3
Vilches, A., Pérez, D. G. (2013). Investigación e innovación en la enseñanza de las ciencias. Necesidad de una mayor vinculación. Tecné Episteme y Didaxis: TED, (34). https://doi.org/10.17227/01213814.34ted15.27
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de enero de 2020; Aceptado: de abril de 2020
Resumen
Impulsar y desarrollar la competencia científica entre los estudiantes que cursan materias como la Física, es un objetivo contemplado actualmente de forma explícita en la mayoría de los currículos escolares y es compartido por muchos expertos en Didáctica de las Ciencias Experimentales. Sin embargo, cuando se trata este tema con el profesorado de ciencias, suele hacerse ignorando los contenidos concretos de la materia a enseñar, con lo cual, los profesores difícilmente pueden trasladar a sus clases aquello que les ha sido expuesto en términos demasiado generales o abstractos. En nuestra opinión, si realmente se quiere impulsar y desarrollar la competencia científica, ello ha de hacerse de forma conjunta a través de contenidos claves para la enseñanza y aprendizaje de las ciencias, como son: la introducción de conceptos, la resolución de problemas y los trabajos prácticos. El problema es que la mayor parte del profesorado de ciencias admite que muchos de los aspectos metodológicos inherentes a la competencia científica, como la emisión de hipótesis, la elaboración de estrategias para su contrastación, el análisis de resultados, etc., se pueden incorporar con relativa facilidad a los trabajos experimentales, pero no lo ven tan claro cuando nos referimos a la introducción de conceptos teóricos o a la resolución de problemas de lápiz y papel. En este trabajo se intenta mostrar, a través de la resolución de un problema de Física concreto, cómo se pueden contemplar esos aspectos esenciales de la competencia científica, en la resolución de problemas. También se plantea la posibilidad de incorporar a la resolución, de manera funcional, elementos prácticos y nuevas tecnologías.
Palabras clave:
problemas de física, competencia científica, resolución de problemas.Abstract
Boosting and developing scientific competence among students studying subjects such as Physics, is an objective currently contemplated in an explicit way in most school curricula and is shared by many experts in Science education. However, when this topic is discussed with science teachers, it is usually done by ignoring the specific contents of the subject to be taught, so that teachers can hardly transfer to their classes what has been exposed to them in terms that are too general. In our opinion, if to promote and develop scientific competence is really wanted, this must be done jointly through key content for the teaching and learning of science, such as the introduction of concepts, problem solving and laboratory experiments. The problem is that most science teachers admit that many of the methodological aspects inherent in scientific competence, such as the issuance of hypotheses, the development of strategies for their contrast, the analysis of results, etc., can be incorporated with relative ease to the experimental works, but they do not see it so clear when it concerns the introduction of theoretical concepts or the resolution of pencil and paper problems. This paper attempts to show, through the resolution of a specific Physics problem, how these essential aspects of scientific competence can be contemplated in problem solving. In addition, the possibility of incorporating practical elements and new technologies, in a functional way, into the resolution is also considered.
Keywords:
physics problem, scientific competence, problem solving.Resumo
Aumentar e desenvolver a competência científica entre os alunos que cursam disciplinas como Física, é um objetivo atualmente explicitamente contemplado na maioria dos currículos escolares e é compartilhado por muitos especialistas em Didática das Ciências Experimentais. No entanto, quando esse tópico é discutido com professores de ciências, geralmente é feito ignorando o conteúdo específico da matéria a ser ensinado, o que significa que os professores dificilmente podem transferir para suas aulas o que lhes foi explicado em termos muito gerais ou abstratos. Em nossa opinião, se você realmente deseja promover e desenvolver competência científica, isso deve ser feito em conjunto por meio de conteúdo essencial para o ensino e aprendizagem de ciências, como: introdução de conceitos, resolução de problemas e trabalhos práticos. O problema é que a maioria dos professores de ciências admite que muitos dos aspectos metodológicos inerentes à competência científica, como a emissão de hipóteses, a elaboração de estratégias para seus testes, a análise de resultados etc., podem ser incorporados com relativa facilidade ao trabalho experimental, mas não o vêem tão claramente quando nos referimos à introdução de conceitos teóricos ou à resolução de problemas de lápis e papel. Este trabalho tenta mostrar, através da resolução de um problema específico de Física, como esses aspectos essenciais da competência científica podem ser contemplados na solução de problemas. Também é considerada a possibilidade de incorporar na resolução, de forma funcional, elementos práticos e novas tecnologias.
Palavras-chaves:
problemas de física, competência científica, resolução de problemas..Impulsar y desarrollar la competencia científica en la enseñanza de las ciencias
Dentro del cuerpo de conocimientos de la Didáctica de las Ciencias Experimentales (DCE), la competencia científica en una materia determinada (como, por ejemplo, la Física) se puede entender como: saber (sus contenidos teóricos), saber hacer (relacionado con aspectos procedimentales y metodológicos) y, también, saber ser y estar (relacionado con aspectos axiológicos tales como una actitud positiva, un mayor interés hacia la materia y su aprendizaje, trabajar bien en equipo, etc.).
Una conclusión ampliamente aceptada entre los investigadores en DCE es la necesidad de impulsar estrategias de indagación e investigación en el alumnado, dentro de lo que es la competencia científica. Así se enfatiza, por ejemplo, en un amplio y documentado estudio sobre la formación del profesorado de ciencias, realizado en Estados Unidos (National Academies of Sciencies, Engineering, and Medicine, 2015), en el que se afirma:
"Research has shown that students best understand scientific ideas when they actively apply their knowledge while engaging in the practices of science, for example, modeling, developing explanations or solutions, and arguing about evidence…"
En el mismo sentido hay que interpretar las llamadas de atención realizadas para cambiar la práctica educativa más habitual y extendida, basada en la simple transmisión-recepción de conocimientos, hacia metodologías que se inspiren, dentro de lo que sea posible en cada nivel, en el proceso de investigación científica (Rocard et al., 2007; National Research Council., 2012).
Las propuestas anteriores se pueden sintetizar en el objetivo de impulsar y desarrollar la competencia científica entre el alumnado. El profesorado de ciencias ha de apropiarse de dicho objetivo, y ello no solo porque este se contempla ya de forma explícita en la mayoría de los currículos actuales, sino también, y, sobre todo, porque avanzar hacia él es la mejor forma de aprender ciencias (con todo lo que ello conlleva). En cuanto a la metodología esto implica, al menos:
-
Plantear problemas de interés y saber precisarlos
-
Enunciar hipótesis teóricamente fundamentadas
-
Elaborar posibles diseños con los que poder contrastar las hipótesis
-
Llevar a cabo los diseños elaborados
-
Realizar análisis críticos, interpretar, argumentar, modelizar, búsqueda de coherencia y globalidad
-
Considerar las perspectivas abiertas por la investigación realizada.
Todo ello supone un cambio metodológico muy importante, que ha de romper con hábitos de pensamiento fuertemente enraizados, fruto de la forma ordinaria de abordar e interpretar las situaciones de la vida cotidiana. Sin embargo, es necesario tener en cuenta que dicho cambio conlleva unos determinados requerimientos y que no es posible avanzar en el mismo dejando de lado la adquisición de unos contenidos conceptuales que presenten una cierta amplitud, globalidad y coherencia interna. El problema es que cuando se habla acerca de la competencia científica, a menudo se hace de forma genérica, desligada de unos contenidos conceptuales específicos, con lo cual es muy probable que los profesores y las profesoras a quienes nos dirigimos no sean capaces de trasladar a la enseñanza de su materia aquello que les ha sido expuesto en términos demasiado generales. En otras palabras: No se puede enseñar nada de la competencia científica en abstracto, de igual forma que tampoco es posible llevar a cabo ninguna investigación científica fuera de un marco teórico determinado, el cual desempeña un papel muy importante desde el mismo inicio hasta el final de esta.
La mayor parte del profesorado de ciencias de enseñanza secundaria admite que todas esas actividades citadas anteriormente (hipótesis, diseños, análisis de resultados, etc.), se pueden incorporar y desarrollar con relativa facilidad en los trabajos experimentales, sin plantearse ir más allá. Pero lo cierto es que, si realmente se quiere impulsar y desarrollar la competencia científica de forma eficaz, es preciso extender también dichas actividades a otros aspectos claves para la enseñanza y aprendizaje de materias científicas como la Física, tales como la introducción de conceptos teóricos o la resolución de problemas de lápiz y papel. Es justamente en este último aspecto, considerado por la mayoría del profesorado como una herramienta privilegiada de aprendizaje y de evaluación de lo aprendido, en el que se centra este trabajo.
Los problemas de Física y el desarrollo de la competencia científica
De acuerdo con las consideraciones anteriores, en este trabajo se intenta responder la siguiente cuestión: ¿Con qué características y cómo deberían plantearse los problemas de lápiz y papel en Física, para que contribuyan realmente a desarrollar la competencia científica en el alumnado?
Como ya se ha indicado anteriormente, impulsar y desarrollar la competencia científica implica, entre otras cosas, utilizar estrategias de enseñanza coherentes con aspectos esenciales del trabajo científico. En el caso que nos ocupa (resolución de problemas de lápiz y papel), los detalles concretos al respecto ya fueron expuestos hace mucho tiempo (Gil et al., 1992) y siguen vigentes en la actualidad (Martínez-Torregrosa, et al., 2018). Concretamente, de acuerdo con estos autores, la utilización de dichas estrategias supone, entre otros aspectos, admitir que:
-
Los problemas científicos son, en general, inicialmente “situaciones problemáticas confusas”. Los problemas no vienen “dados”, son situaciones que tienen interés (por distintas causas) pero que requieren ser simplificadas, modelizadas, definidas (operativizándolas, precisando cuál es el problema, qué es lo que se busca), partiendo, por supuesto, de los conocimientos que se poseen en el campo específico en el que se ubique la investigación.
-
Es necesario “dar forma” a las situaciones problemáticas de interés, tomando decisiones para transformarlas en “investigables”.
-
El avance en el problema está guiado por hipótesis, por “tentativas de respuesta”, que deben ser puestas a prueba lo más rigurosamente posible.
-
No se razona en términos de certeza, ni tampoco el conocimiento científico se descubre “mirando directamente a la Naturaleza”. Por el contrario, se procura avanzar de un modo tentativo, que conlleva dudar sistemáticamente de los resultados obtenidos y de todo el proceso de resolución. Ello obliga a interpretar y contrastar los resultados, mediante su consistencia con las hipótesis formuladas, a probar caminos distintos para ver si se obtiene lo mismo, a revisar la coherencia global con lo conocido en ese campo, o a ver si lo hecho abre y/o permite avanzar en nuevos problemas de interés. Esto puede conducir a revisar las hipótesis, la estrategia de resolución y/o, incluso, a reformular el problema de forma distinta.
-
A menudo un problema abre y/o permite avanzar en nuevos problemas de interés
Para poder contemplar aspectos como los anteriores en la resolución de problemas en materias como la Física, es necesario abandonar el modelo tradicional de enseñanza en el que estos se tratan al final como meros ejercicios de aplicación y manejo de unos contenidos teóricos previamente expuestos por el profesor, y cambiar a otro modelo de resolución, más coherente con la naturaleza de la ciencia y el trabajo científico en la que los problemas se traten como pequeñas investigaciones que realizan grupos de alumnos con la ayuda del profesor. Para ello es necesario tener muy en cuenta las investigaciones e innovaciones previas más relevantes realizadas en este campo (Gil-Pérez y Martínez Torregrosa, 1983; Gil et al., 1991; Martínez Torregrosa y Sifredo, 2005), en las que se basa el modelo didáctico de resolución propuesto.
En este trabajo se comentan las orientaciones didácticas más importantes que se derivan de dicho modelo en la actualidad, a través de la resolución de un problema de Física concreto (acompañado de una cuestión previa), tratando así de alejarnos de la retórica excesivamente abstracta, que, con frecuencia, se utiliza en las llamadas de atención sobre la necesidad de impulsar y desarrollar la competencia científica en el alumnado. Para a ello se han seguido las mismas pautas que otros autores desarrollaron ya en otros trabajos similares (Martínez-Torregrosa, et al., 2018). No obstante, queremos destacar algunas aportaciones novedosas importantes que hemos intentado plasmar en este ejemplo. Concretamente, hemos tenido en cuenta que la separación clásica entre contenidos puramente teóricos, actividades experimentales y problemas de lápiz y papel no guarda paralelismo con la actividad científica real (Gil-Pérez, et al., 1999) por lo que, si realmente se quiere desarrollar la competencia científica entre los estudiantes, se deberían aprovechar todas las ocasiones posibles para tratar todos esos contenidos de forma conjunta. Por ello, en el problema que se muestra a continuación, no solo se manejan contenidos teóricos básicos de gran importancia (principio de acción y reacción, concepto de la fuerza peso, fuerza de empuje...) tratando explícitamente de salir al paso de algunas confusiones y errores conceptuales frecuentes, sino que también se incluye una sencilla actividad experimental, que se presenta como otra posible estrategia de resolución y se integra perfectamente en el desarrollo del problema. Esta actividad experimental puede desempeñar, en su caso, el papel de un verdadero conflicto cognoscitivo, cuando los estudiantes comprueban que la realidad contradice sus ideas previas. Además, se ha extendido esta integración entre contenidos, incluyendo también en el desarrollo del problema, la utilización funcional de las nuevas tecnologías como una parte fundamental del mismo.
Enunciado y desarrollo del problema
A continuación, se procede a enunciar, resolver y comentar el problema, de acuerdo con las consideraciones realizadas hasta aquí.
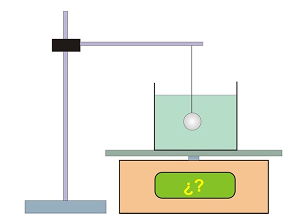
Sobre una balanza electrónica se coloca un recipiente con agua para a continuación, introducir una bola de acero que cuelga mediante un hilo de un soporte fijo, tal y como se muestra en la figura 1.
Figura 1: En la situación descrita, la balanza marcará (señala la propuesta que se estime más correcta, razonando nuestra elección): a) Más que antes de introducir la bola b) Igual que antes de introducir la bola c) Menos que antes de introducir la bola
Una vez contestada la cuestión anterior, proceda a resolver el problema siguiente y utilizad el resultado obtenido por distintas vías, para confirmar o cambiar vuestra respuesta.
Sobre una balanza electrónica se coloca un recipiente con agua, observando que la balanza señala entonces 264 g. Una vez hecho esto, se introduce en el agua una bola de 1’25 cm de radio y una masa de 64’5 g que cuelga mediante un hilo de un soporte fijo externo, tal y como se muestra en la figura anterior. Se pide: En la situación descrita ¿qué marcará la balanza?
(Datos: densidad del agua da = 1g/cm3, g = 9’81 N/kg).
Estudio cualitativo de la situación planteada
Comenzar por un análisis cualitativo de la situación, planteando con claridad qué es concretamente lo que se pide en el problema, aquello que se busca, qué interés puede tener, precisando las condiciones que se consideran imperantes en la situación abordada, y apoyándose, siempre que sea posible, en representaciones o esquemas gráficos apropiados.
Para poder resolver la cuestión planteada hay que reflexionar antes acerca de si por el hecho de introducir la bola en el vaso con agua, varía de alguna forma la fuerza vertical y hacia abajo que se ejerce sobre el plato de la balanza. En principio podría tenerse la tentación de pensar que no, dado que la bola está sujeta por el hilo. Pero, si se analiza la situación con cuidado, hay que concluir que sí varía, porque, de acuerdo con el Principio de Arquímedes, al sumergir la bola en el agua comienza a actuar sobre ella una fuerza de empuje hacia arriba. Dicha fuerza no afecta directamente a la fuerza normal que el conjunto vaso-agua ejerce sobre el plato de la balanza; no obstante, no se puede olvidar que, de acuerdo con el principio de acción-reacción, las fuerzas siempre se ejercen por parejas, de manera que, al igual que el agua empuja la bola hacia arriba, la bola empujará simultáneamente el agua hacia abajo con otra fuerza del mismo valor, pero de sentido contrario. Es razonable pensar, pues, que la presencia de esta última fuerza se traduzca, de alguna manera, en un aumento del valor de la fuerza total (vertical y de sentido descendente) que se ejerce sobre el plato de la balanza.
El problema queda, pues, precisado como:
¿En cuánto se incrementa la fuerza normal que se ejerce sobre el plato de la balanza una vez que hemos introducido la bola totalmente en el agua?
Es importante resaltar la posibilidad de cuestionar de manera funcional alguna idea alternativa. Concretamente la de identificar fuerza peso de un objeto con la fuerza que se ejerce sobre la superficie horizontal en la que se encuentre. La existencia de esta idea alternativa, junto con un aprendizaje no significativo del principio de acción y reacción, lleva a considerar a muchos alumnos que la balanza marca lo mismo antes y después de introducir la bola. Este problema permite mostrar lo incorrecto de esa identificación, ya que, como se podrá constatar por distintas vías, el peso del conjunto vaso-agua es el mismo antes que después de introducir la bola, pero no sucede lo mismo con la fuerza normal que se ejerce sobre el plato de la balanza, que es la fuerza que realmente miden este tipo de balanzas en cualquier situación.
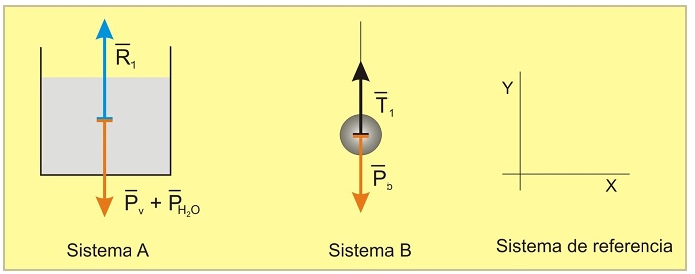
En el ejemplo propuesto, para una resolución rigurosa del problema conviene analizar, en primer lugar, todas las fuerzas que actúan en cada caso, con objeto de comparar la fuerza normal que se ejerce sobre el plato de la balanza antes y después de sumergir totalmente la bola en el agua. Para ello consideraremos como sistema “A” el conjunto agua-vaso y como sistema “B” la bola. Supondremos que el hilo del que cuelga dicha bola es inextensible y de masa despreciable y trabajaremos en un sistema de coordenadas cartesianas en el plano.
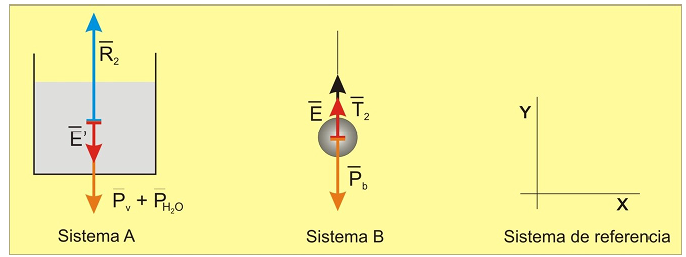
En los esquemas (Figura 2 y 3) se han representado las fuerzas que actúan sobre ambos sistemas, antes (1) y después (2) de introducir la bola en el agua:
Figura 2: Fuerzas antes de sumergir la bola en el agua.
Figura 3: Fuerzas después de sumergir la bola en el agua.
En el esquema anterior,
 representa el peso de la bola,
representa el peso de la bola,
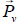 el peso del vaso,
el peso del vaso,
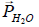 el peso del agua,
el peso del agua,
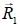 la tensión del hilo del que cuelga la bola y
la tensión del hilo del que cuelga la bola y
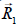 la fuerza que ejerce el plato de la balanza sobre el vaso (igual y de sentido contrario a la fuerza
la fuerza que ejerce el plato de la balanza sobre el vaso (igual y de sentido contrario a la fuerza
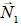 que ejerce el vaso sobre el plato de la balanza y que no se ha representado en el esquema).
que ejerce el vaso sobre el plato de la balanza y que no se ha representado en el esquema).
En este segundo esquema
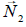 representa la fuerza vertical y hacia arriba que ejerce el plato de la balanza sobre el vaso después de haber introducido la bola (igual y de sentido contrario a la fuerza
representa la fuerza vertical y hacia arriba que ejerce el plato de la balanza sobre el vaso después de haber introducido la bola (igual y de sentido contrario a la fuerza
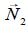 que ejerce el vaso sobre el plato de la balanza y que no se ha representado en el esquema). Como puede verse, aparece también una nueva fuerza que no existía en el anterior esquema, antes de introducir la bola dentro del vaso con agua. Se trata de la fuerza de empuje que, de acuerdo con el Principio de Arquímedes, actúa sobre la bola sumergida empujándola hacia arriba y que hemos designado como
que ejerce el vaso sobre el plato de la balanza y que no se ha representado en el esquema). Como puede verse, aparece también una nueva fuerza que no existía en el anterior esquema, antes de introducir la bola dentro del vaso con agua. Se trata de la fuerza de empuje que, de acuerdo con el Principio de Arquímedes, actúa sobre la bola sumergida empujándola hacia arriba y que hemos designado como
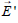 . Dicha fuerza tiene su correspondiente pareja (acción-reacción) en otra fuerza del mismo módulo, pero de sentido contrario a ella, que actúa sobre el agua y que hemos designado como
. Dicha fuerza tiene su correspondiente pareja (acción-reacción) en otra fuerza del mismo módulo, pero de sentido contrario a ella, que actúa sobre el agua y que hemos designado como
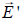 .
.
A la derecha de ambos esquemas se incluye también el sistema de referencia de coordenadas cartesianas a utilizar.
Resolver este ejercicio supone comprender previamente que lo que indica la balanza viene determinado por el valor de la fuerza
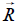 que se ejerce sobre el plato de esta hacia abajo. Esta fuerza no hay que confundirla con el peso de lo que hay sobre dicho plato (aunque su valor numérico pueda coincidir en muchos casos) y, de acuerdo con el principio de acción-reacción, su módulo será siempre igual al de la fuerza hacia arriba
que se ejerce sobre el plato de esta hacia abajo. Esta fuerza no hay que confundirla con el peso de lo que hay sobre dicho plato (aunque su valor numérico pueda coincidir en muchos casos) y, de acuerdo con el principio de acción-reacción, su módulo será siempre igual al de la fuerza hacia arriba
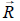 que simultáneamente ejerce el plato sobre el vaso. Por tanto, una forma de resolver el problema será determinar los valores (módulo) de en
que simultáneamente ejerce el plato sobre el vaso. Por tanto, una forma de resolver el problema será determinar los valores (módulo) de en
 las dos situaciones planteadas, que designaremos como R1 (antes de introducir la bola) y R2 (después de introducir la bola) para compararlos.
las dos situaciones planteadas, que designaremos como R1 (antes de introducir la bola) y R2 (después de introducir la bola) para compararlos.
Emisión de hipótesis
Emitir hipótesis fundadas sobre los factores de los que puede depender la magnitud buscada y sobre la forma de dicha dependencia, imaginando, en particular, posibles casos límite de fácil interpretación física.
La emisión de hipótesis es una de las actividades más importantes en cualquier investigación y en la enseñanza de las ciencias supone una excelente ocasión para poner de manifiesto, de manera funcional, la existencia de posibles ideas alternativas, que habrán de ser valoradas y contrastadas. Los datos necesarios para la resolución del problema vendrán marcados precisamente por aquellos factores que se hayan considerado en las hipótesis emitidas (estos serán los datos o parámetros del problema). El hecho de aventurar de qué forma pueden influir dichos factores y analizar algún caso límite evidente, contribuye especialmente a poder realizar después un mejor análisis crítico del resultado, lo cual es otro aspecto fundamental del trabajo científico. Finalmente, conviene tener en cuenta que los alumnos, al elaborar hipótesis y considerar casos límite, profundizan en su conocimiento físico acerca de los contenidos manejados en la situación planteada, lo que favorece un aprendizaje realmente significativo.
Puesto que hemos planteado que la diferencia en la lectura de la balanza se ha de deber a la existencia de la fuerza de empuje, hemos de usar el principio de Arquímedes y considerar que la variación producida en la fuerza que se ejerce sobre el plato de la balanza dependerá de los factores que determinan el valor de dicho empuje, es decir: el radio r de la bola, la densidad da del agua, y la gravedad, g.
Más concretamente:
-
El valor del empuje (y el de la correspondiente lectura de la balanza) aumentará en el caso de que (a igualdad de los restantes factores), aumente el radio de la bola, r, ya que dicho aumento supone un aumento del volumen de la bola, Vb, que, como sabemos, al estar totalmente sumergida, será igual al volumen de agua desalojada.
-
Del mismo modo, si varía la densidad del agua, da, (podríamos, por ejemplo, sustituir agua dulce por agua salada, o, más en general, por cualquier otro líquido), el resultado del problema también debe variar. Si da aumenta se incrementará el valor de la lectura y si da disminuye, disminuirá dicho valor.
-
Finalmente, si aumentase el valor de la gravedad también debería aumentar el valor del empuje (puesto que aumentaría el peso del agua desalojada) y el correspondiente incremento en el valor de la lectura de la balanza.
El resultado también debería contemplar algún caso límite evidente como, por ejemplo, que, si el radio de la bola tiende a 0, lo mismo deberá ocurrir con el empuje, y la lectura de la balanza sería cada vez más parecida a la inicial (antes de introducir la bola).
En la situación descrita, la masa de la bola, mb, no debe influir en el resultado. Y ello por dos razones: En primer lugar, porque (a igualdad de los demás factores) ninguna modificación del valor de dicha masa afectará al peso del agua desalojada por la bola (y, por tanto, tampoco afectará al empuje). En segundo lugar, porque la bola pende de un hilo sujeto a un soporte exterior y, por ello, es indiferente que pese más o pese menos, puesto que no descansa sobre ninguna parte del recipiente.
Estrategias de resolución
Elaborar y exponer de manera clara y concisa, una posible estrategia para la resolución del problema antes de proceder a esta, evitando recurrir al simple ensayo y error. Se trata de que los estudiantes, utilizando sus conocimientos de partida, elaboren de manera fundamentada una estrategia que pueda conducir a la resolución del problema y la expongan de forma resumida argumentando sobre ella y los pasos a seguir. Esta etapa sería equivalente a lo que en una investigación científica se considera como la elaboración de diseños para la contrastación de las hipótesis emitidas y es una actividad excelente para favorecer el desarrollo de la imaginación y la creatividad.
Hacer referencia cuando sea posible a otros métodos alternativos de resolución. La búsqueda de distintas vías para la resolución de un mismo problema y el debate sobre ellas es algo que no solo posibilita una mejor contrastación de los resultados obtenidos, sino que, además, puede contribuir decisivamente a que los alumnos se den cuenta de la coherencia global y la validez del cuerpo de conocimientos que se va construyendo. Por otra parte, contribuye a desarrollar una imagen de la ciencia más cercana a la realidad, ya que las contrastaciones por distintas vías desempeñan un papel fundamental en el trabajo científico.
Tanto antes como después de sumergir la bola en el agua, los dos sistemas A y B considerados (véanse los esquemas anteriores) se encuentran en equilibrio. Por tanto, la fuerza resultante sobre cada uno de dichos sistemas ha de ser nula. Podemos, pues, aplicar esa condición de equilibrio antes y después de introducir la bola, para tratar de hallar los valores de R1 y R2 que buscamos.
Otra posible estrategia para resolver este problema es optar por la vía experimental. Ello, además, es una forma de someter a prueba el resultado obtenido teóricamente (y también la respuesta dada a la cuestión previa). En este caso concreto, es posible realizar una contrastación experimental de forma rápida y sencilla en la propia aula. De hecho, los datos numéricos del enunciado provienen de la contrastación experimental realizada por un grupo de profesores en formación durante el curso 2019-20 en un taller sobre resolución de problemas. Basta con utilizar una balanza electrónica y realizar el montaje que se muestra en el mismo enunciado, para apreciar (y medir) el aumento que señala la balanza en cuanto se introduce la bola dentro del agua. Llevar a cabo esta estrategia no solo aumenta la coherencia con la actividad científica (en la que, como se ha señalado, no tiene sentido separar problemas, teoría y actividad experimental) sino que hace también el problema más interesante y motivador.
Resolución propiamente dicha
Proceder a la resolución del problema de acuerdo con la estrategia escogida, razonando lo que se hace y por qué se hace, sin caer en operativismos precipitados y carentes de significado. Se trata, esencialmente, de que se haga referencia a la información teórica disponible, se justifiquen las expresiones que se van a utilizar comprobando, por ejemplo, que su campo de validez es el adecuado según las condiciones que se consideran imperantes en la situación planteada y de que, sobre todo, se evite una resolución meramente mecánica o mimética del problema.
Siempre que sea factible, es importante efectuar una resolución literal, evitando la tendencia a trabajar desde el principio con los valores numéricos. Conviene tener en cuenta que no se trata de que los alumnos no manejen datos cuantitativos y obtengan un resultado final expresado numéricamente sino, más bien, de que hagan esto cuando corresponde. En muchos casos (como se podrá ver en este ejemplo), es posible efectuar dicha resolución literal antes de sustituir los valores numéricos. Aunque para algunos estudiantes, acostumbrados a operar con los números de forma inmediata, puede resultar un paso difícil, es perfectamente superable y conviene trabajar sobre ello, ya que se trata de algo esencial para conseguir, entre otras cosas, que se pueda realizar un buen análisis crítico del resultado (otro aspecto fundamental de la metodología científica).
Dado que todas las fuerzas se ejercen en la dirección vertical, es posible trabajar únicamente con las componentes escalares de los vectores según el eje Y de coordenadas, con lo que siguiendo la primera de las estrategias de resolución propuestas, en el equilibrio, antes de introducir la bola (véase esquema 1), se ha de cumplir:
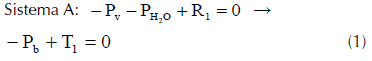
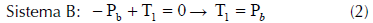
Siguiendo la misma estrategia para determinar R2, en el equilibrio, después de sumergir totalmente la bola colgada del hilo (ved esquema 2), se tendrá que:
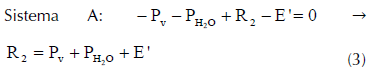
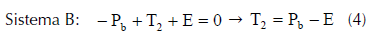
Teniendo en cuenta (1), la ecuación (3) queda como:
R R E' 2 1 = + (5)
Por tanto, se concluye que, tal y como se había avanzado, después de introducir la bola en el agua, la balanza señalará un valor más alto que antes de introducirla y que la diferencia es justamente igual al valor del empuje sobre la bola.
Estamos ahora en condiciones de obtener el valor de R2, que es la magnitud buscada. Dado que se conoce R1 (es un dato del enunciado) y que sabemos que E’ = E, obtener R2 pasa por determinar el valor de la fuerza de empuje E que el agua ejerce sobre la bola. Como E coincide con el peso del agua desalojada Pad por la bola, utilizaremos esta igualdad (en módulos de fuerzas) para obtener dicho valor:

Y si ahora tenemos en cuenta que E = E’ podemos sustituir (6) en (5) y obtener finalmente:
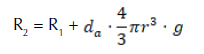
Sustituyendo ahora los valores propuestos por el enunciado (en unidades internacionales), se obtiene el valor de R2:
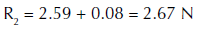
Lo que implica una nueva lectura (en gramos) de 272.45 en lugar de los 264 que indicaba la balanza antes de sumergir la bola.
Análisis de resultados
Analizar el o los resultados obtenidos mediante resolución literal, a la luz de las hipótesis elaboradas y, en particular, de los casos límites considerados. Realizar también un sencillo análisis dimensional.
El análisis de los resultados de un problema se puede realizar cuando estos vienen dados en forma de una expresión literal, ya que entonces es posible comprobar (de acuerdo con las hipótesis y casos límite de partida), la influencia de las magnitudes que aparecen en ellos. Además, conviene tener presente que es aquí, precisamente, donde se puede producir algún conflicto cognoscitivo (por ejemplo, cuando en el resultado no aparece alguna magnitud que sí había sido considerada como influyente durante el planteamiento cualitativo), convirtiéndose así los problemas en poderosos instrumentos para un desarrollo realmente efectivo de la competencia científica.
Analizar también el resultado cuantitativo, viendo si los valores encontrados son lógicos o no. A veces es posible que un resultado numérico se desvíe tanto que se convierta en absurdo y, sin embargo, no suponga ninguna inquietud en alumnos que no están acostumbrados a este tipo de análisis. Este es el caso de quienes, ante un problema determinado, obtienen, por ejemplo, que un átomo de oxígeno tiene una masa de 16 g, o que el periodo de la Luna en su giro alrededor de la Tierra es de millones de años y aceptan el resultado sin más.
En nuestro caso, la expresión literal obtenida contempla todas las hipótesis consideradas y, además, es dimensionalmente homogénea (F en ambos lados). Por otra parte, el aumento obtenido en la lectura de la balanza por el hecho de introducir la bola en el agua (8.45 gramos) es una cantidad perfectamente razonable, comparada con el resto de los valores que se están manejando.
Como ya se indicó anteriormente, R2 coincide con el valor de N2 o fuerza normal que se ejerce sobre el plato de la balanza (no representada en el esquema), que es la fuerza que realmente mide siempre la balanza. Así, pues, el hecho de introducir la bola en la forma que se muestra en el enunciado implica que la balanza señale inmediatamente una fuerza mayor que antes, siendo el aumento producido justamente igual al valor del empuje sobre la bola.
Consideración de nuevas perspectivas abiertas
Considerar las perspectivas abiertas tras la resolución del problema. Contemplar, por ejemplo, la posibilidad de abordarlo con un mayor nivel de complejidad, estudiando sus implicaciones teóricas (profundización en la comprensión de algún concepto), prácticas (situaciones similares de interés técnico), etc.
Además de las orientaciones anteriores, en nuestra opinión, conviene contemplar también (en la medida de lo posible), otros aspectos:
Uno de ellos será la posible utilización de elementos de las nuevas tecnologías para mejorar el aprendizaje derivado de la resolución del problema. Se puede, por ejemplo, utilizar applets u otras aplicaciones informáticas que refuercen, complementen o amplíen elementos del problema, etc. Ahora bien, hay que asegurar que el uso de estas tecnologías se haga de forma coherente con el modelo de resolución de problemas que estamos desarrollando, poniendo especial cuidado en evitar antiguas metodologías, que pudieran, incluso, ser antagónicas a dicho modelo (Marchesi, et al., 2005). Aquí hemos incorporado este aspecto, elaborando una animación sobre el problema, con la que, como veremos más adelante, los estudiantes pueden poner a prueba sus hipótesis acerca de la influencia de los parámetros del problema, probar casos límite, introducir los datos del enunciado y/o los datos reales manejados (en su caso) en la actividad experimental propuesta como otra posible estrategia de resolución, etc.
Otro elemento a incorporar, será conectar el problema con aspectos prácticos, científico-tecnológicos, históricos, sociales o del medio natural. Siempre que la naturaleza de la situación lo permita conviene incluir, como mínimo, algunas reflexiones sobre su posible interés científico-tecnológico o sus implicaciones en la vida de las personas y en la naturaleza. Con ello se contribuye no solo a una toma más fundamentada de decisiones sino también a poner en cuestión una imagen descontextualizada de la Ciencia y del trabajo científico. En este caso se puede plantear un trabajo bibliográfico (podría ser a través de internet, lo que nos remite otra vez al uso de las nuevas tecnologías), sobre la balanza hidrostática, cuya invención se atribuye a Galileo, y su importancia histórica. La balanza hidrostática utiliza provechosamente el hecho, aprendido en este problema, de la influencia concreta que tiene el empuje de los cuerpos sumergidos en la lectura de la balanza, para así poder medir experimentalmente las densidades de dichos cuerpos.
Los problemas muchas veces pueden sugerir otras situaciones próximas, cuyo estudio o consideración también puede interesar incorporar con objeto de profundizar en algunos de los conceptos involucrados. En este problema, se ha reforzado la idea de que la balanza electrónica no indica ni el peso ni la masa del objeto que se coloca encima de su plato, sino la fuerza normal ejercida sobre la superficie de dicho plato. En la mayoría de las situaciones cotidianas, el valor (módulo) de dicha fuerza normal, coincide con el de la fuerza peso y, por este motivo, las balanzas suelen calibrarse de forma que indican directamente en su pantalla la masa del objeto. Pues bien, si queremos reforzar el concepto citado, podemos plantear otros supuestos en los que ocurra lo mismo que aquí, es decir, en los que la lectura de la balanza no coincida con el peso. Por ejemplo, se puede plantear el uso de una balanza dentro de un ascensor, ya que la lectura de esta no coincidirá con el peso si se efectúa la medida cuando dicho ascensor comienza a descender o cuando frena para pararse (sólo se dará esa coincidencia mientras el ascensor esté descendiendo con velocidad constante, que es la única de las tres situaciones propuestas en la que el valor de la fuerza normal sobre la balanza coincide con el valor del peso de la persona u otro objeto que se coloque encima de ella).
Finalmente, conviene referirse a una de las propiedades más inherentes al trabajo científico, que también ha de incorporarse a los problemas planteados como investigación: el hecho de que la bondad de toda investigación depende, no solo de las cuestiones que resuelve o ayuda a resolver, sino que también se valora por su capacidad para generar nuevas preguntas o promover nuevas investigaciones. Concretamente en este problema, podemos plantearnos, entre otras muchas, las siguientes cuestiones:
¿Qué ocurre con la tensión del hilo?
Si se compara la ecuación (4) con la (2), puede verse que el hilo está menos tenso y que la diferencia es justamente el valor de la fuerza de empuje.
¿Qué ocurre si se rompe el hilo y la bola queda en reposo en el fondo del vaso? ¿Qué marcaría entonces la balanza?
Si se considera ahora como único sistema el vaso junto con el agua y la bola sobre el fondo y que dicho sistema se encuentra en equilibrio, se puede expresar la fuerza resultante sobre el mismo como:
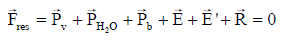
En la ecuación anterior, representa la fuerza normal que el plato de la balanza ejerce sobre el vaso (igual y de sentido contrario a la que realmente buscamos). Dado que todos los vectores se encuentran sobre el eje Y de coordenadas, es posible trabajar con esta única componente, con lo que, teniendo en cuenta que las fuerzas E y E’ son iguales y de sentido contrario, la ecuación anterior se puede expresar como:
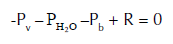
Y despejando, obtenemos
 Teniendo en cuenta que:
Teniendo en cuenta que:
Pb = mb·g = 64’5 10-3 9’81 = 0’63 N, y que Pv+= R1 = 2’59 N podemos sustituir estos valores y obtener finalmente: R = 2’59 + 0’63 = 3’22 N. Como puede verse, un valor más alto que cuando la bola pendía del hilo.
En esta situación, la fuerza normal ejercida sobre el plato de la balanza sí que coincide numéricamente con el peso de lo que hay encima de ella, pero, naturalmente, siguen siendo fuerzas distintas, que responden a interacciones distintas y que se ejercen sobre cuerpos distintos.
Utilización funcional de las nuevas tecnologías
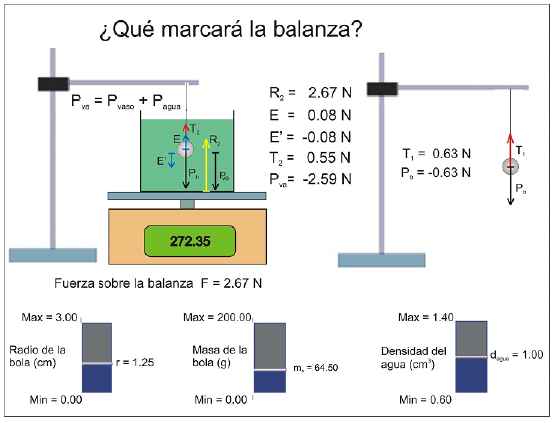
Para reforzar algunos de los conceptos involucrados en este problema hemos creado una animación Modellus. En la pantalla se muestra el montaje, incluyendo la lectura de la balanza (en gramos).
La animación es interactiva, de tal forma que los alumnos pueden modificar cualquiera de los parámetros del problema entrando en la ventana de las condiciones iniciales. Adicionalmente disponen en la propia pantalla de tres controladores manuales para modificar ahí directamente, si lo desean, el radio de la bola, la densidad del agua y la masa de la bola. Al intervenir sobre estos parámetros, pueden poner a prueba sus hipótesis y los casos límite. Por ejemplo: pueden constatar que, si modifican la masa de la bola, no se altera la lectura de la balanza (pero sí el peso de la bola y la tensión del hilo). En cambio, si modifican la densidad del agua y/o el radio de la bola, constatarán que sí se altera la lectura de la balanza. El profesor les puede pedir que, antes de manipular la animación, adelanten estos resultados en términos cualitativos. También se pueden considerar otras situaciones interesantes e instructivas. Por ejemplo, se puede hacer que disminuya paulatinamente el radio de la bola, lo que equivale a hacer que también lo haga la fuerza de empuje y que, por tanto, se tienda a que no haya una diferencia de lecturas, por estar el cuerpo sumergido; también se pueden introducir datos reales, obtenidos experimentalmente, etc. La imagen (figura 4) corresponde a la situación planteada con los datos del enunciado.
Figura 4: Situación planteada con los datos del enunciado. La animación y el programa para hacerla correr están disponibles en la página “Web de Materiales para la Enseñanza y la Divulgación de la Física”, de la Sección Local de Alicante de la Real Sociedad Española de Física (RSEF). http://rsefalicante.umh.es/fisica.htm
Conclusiones
En este trabajo, a través de un ejemplo, se ha intentado mostrar los aspectos u orientaciones concretas a tener en cuenta para conseguir que los problemas de Física puedan contribuir de una forma más eficaz al desarrollo de la competencia científica entre el alumnado de enseñanza secundaria (aunque el modelo también es aplicable con estudiantes de ciencias universitarios y en la formación didáctica del profesorado).
Se ha visto la potencialidad de este ejemplo para cuestionar algunas ideas alternativas, como la idea de que la fuerza peso de un objeto es la fuerza normal que se ejerce sobre cualquier plataforma horizontal en la que se halle dicho objeto, así como para profundizar en algunos principios importantes como el de acción-reacción y el principio de Arquímedes.
También se ha mostrado que es posible integrar actividades que aparecen estrechamente ligadas en el trabajo científico pero que se suelen tratar como aspectos totalmente separados en la enseñanza tradicional, donde los problemas se utilizan como simples actividades de manejo de los conceptos y principios previamente introducidos y las prácticas como una comprobación de leyes y expresiones que ya se han tratado anteriormente. Por el contrario, en este ejemplo se han tratado conjuntamente, contenidos teóricos, problema, actividad experimental y nuevas tecnologías. Otros ejemplos muy similares a este, elaborados por nosotros, se pueden encontrar en la web: didacticafisicaquimica.es, así como en la página “Web de Materiales para la Enseñanza y la Divulgación de la Física”, de la Sección Local de Alicante de la RSEF. http://rsefalicante.umh.es/fisica.htm
Conviene tener en cuenta que las orientaciones precedentes no pretenden ser ninguna receta cuyo seguimiento paso a paso garantice el éxito asegurado en la resolución de problemas. Se trata, por el contrario, de indicaciones muy generales que alertan contra determinados vicios metodológicos que impiden tratar los problemas como tales (algo para lo cual, de entrada, no se dispone de una solución evidente) y que permiten que la resolución de problemas se pueda convertir en una herramienta más eficaz con la que impulsar y desarrollar la competencia científica.
Para que las orientaciones anteriores se puedan contemplar en una programación y, lo que es más importante, para que el profesorado pueda apropiarse de ellas como punto de partida en el que apoyarse, es absolutamente necesario disponer de colecciones de problemas, acordes con dichas orientaciones. Desgraciadamente, los ejemplos de estos materiales educativos innovadores son escasos y, sobre todo, poco conocidos por la mayoría del profesorado. Esta situación se debe a diversas causas. Vilches y Gil-Pérez (2013) , se refieren a este respecto a la existencia, entre algunos investigadores en DCE, de una concepción según la cual los trabajos deberían centrarse en estudiar problemas relativos a la enseñanza y aprendizaje de las ciencias, pero sin descender a la elaboración de propuestas de actuación concretas en el aula (lo que sería ya calificado como "simple" innovación). Esta situación es coherente, por otra parte, con que en algunas revistas de investigación didáctica a menudo se rechacen aquellos trabajos que se consideren de innovación, por muy fundamentados que puedan estar. No se tiene en cuenta el hecho de que, análogamente a como ocurre en otros campos de la investigación científica como la Física o la Química, tampoco pueden darse realmente por válidos los análisis críticos o las explicaciones a los problemas estudiados en una investigación didáctica, hasta que no vayan acompañados de pruebas sólidas que muestren cómo al incidir sobre las supuestas causas, se producen resultados coherentes con las hipótesis manejadas. Por otra parte, desde la propia administración educativa, tampoco se facilita la edición y difusión de este tipo de materiales.
Es necesario tener en cuenta que no todos los problemas se pueden plantear del mismo modo, ni tampoco se pueden contemplar siempre en un problema todas las orientaciones comentadas anteriormente. No obstante, aunque la mayor parte de los problemas planteados como investigación se han venido desarrollando principalmente en el cuerpo de conocimientos correspondiente a la mecánica newtoniana, también se ha mostrado la viabilidad de la propuesta aplicada, con sus oportunas variantes, en otros temas de Física (Gil-Pérez, Martínez-Torregrosa y Ramírez de Castro, 1994) y también de Química (Furió y Reyes, 1990; Furió, Iturbe y Reyes, 1995). Por nuestra parte (Alonso, Carrascosa y Martínez, 2018), hemos puesto a libre disposición del profesorado sendas colecciones de problemas de cinemática relativista y dinámica relativista junto con otra de más de 30 problemas en la que se involucran diferentes temas de Física y de Química del currículum español de Enseñanza Secundaria (alumnado de 12 a 17 años).
Modestamente, abogamos por que se supere la “amnesia crónica” que con frecuencia afecta a la Didáctica de las Ciencias Experimentales y se ponga de nuevo el foco en el diseño, experimentación y evaluación de propuestas concretas con las que desarrollar la competencia científica entre el alumnado a través de los contenidos específicos de las asignaturas que el profesorado imparte.
Nota final: La cuestión cualitativa propuesta en el problema fue presentada por la profesora Wanda Kaminski -Université Paris 7- en un taller desarrollado en el III Congreso Internacional sobre Didáctica de las Ciencias y de las Matemáticas, realizado en Santiago de Compostela (España) en 1989.
Referencias
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.