DOI:
https://doi.org/10.14483/23448350.7694Published:
10/21/2014Issue:
Vol. 20 No. 3 (2014): September-December 2014Section:
Research ArticlesPerspectivas para formar profesores de matemáticas: disminuyendo la brecha entre la teoría y la práctica-Prospects for training teachers of mathematics: brinding the breach between theory and practice
Keywords:
formación de profesores, formación inicial, desarrollo profesional, tutoría entre pares, comunidad de práctica. (es).Downloads
References
Alsina, Á. (2010). El aprendizaje reflexivo en la formación inicial del profesorado: un modelo para aprender a enseñar matemáticas. Educación Matemática, 22(1), 149-166.
Azcárate, P. y Cardeñoso, J. (1998). La formación inicial de profesores de matemáticas, finalidades, limitaciones y obstáculos. Investigación en la Escuela, (35), 76-85.
Ball, D. L., Hill, H. C. and Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, Fall.
Botello y Parada (2013) Tutorías entre pares: una oportunidad de formación para futuros profesores de matemáticas. Revista Científica, (Edición especial) 135-139. Universidad Distrital. Bogotá, Colombia. D.C.
Buysse, V., Sparkman, K. and Wesley, P. (2003). Communities of practice: Connecting what we know with what we do. Exceptional Children, 69(3), 263-278.
Chapman, O. (2005). Stories of Practice: A Tool in Preservice Secondary Mathematics Teacher Education. En The Fifteenth ICMI Study, Águas de Lindóia.
Fennema, E. y Loef, M. (1992). Los conocimientos de los profesores y su impacto. En D.A. Grows (Ed.), Handbook of Research on Mathematics Teaching and Learning. New York, USA: Macmillan Publishing Company.
Flores, P. (2007). Profesores de Matemáticas Reflexivos: Formación y Cuestiones de Investigación. Revista de Investigación en Didáctica de la Matemática, 1(4), 139-159.
Font, V. (2002). Una propuesta dialógica sobre la formación inicial en matemáticas de los maestros de educación primaria. En G. Perafán, y A. Adúriz (Eds), Pensamiento y conocimiento de los profesores. Debate y perspectivas contemporáneas. Bogotá: Universidad Pedagógica Nacional.
Gómez, P. (2004). Diversidad en la formación inicial de profesores de matemáticas en la búsqueda de un núcleo común. Revista EMA, 10(1), 242-293.
González, F. (2010). Un modelo didáctico para la formación inicial de profesores de de Investigación, 11(1), 47-59.
Grossman, P., Wilson, S. y Shulman, L. (2005). Profesores de sustancia: El conocimiento de la materia para la enseñanza. Profesorado. Revista de Currículo y Formación de Profesorado, 9(2), 1-24.
Harris, Ch. (2008.) Learning & Innovation in communities of practice. Access: mayo de 2009. Available: http://www.pyramidodi.com/papers/CoPs.pdf.
Jaworski, B. (2008). Building and Sustaining Inquiry Communities in Mathematics Teaching Development. In K. Krainer, T. Woods (Eds.), Participants in Mathematics Teachers Education Rotterdam/Taipei: Sense Publishers.
Kosheleva, O., Medina, A. and Ioudina, V. (2007). Pre-service teacher training in mathematics using tablet PC technology. Institute of Mathematics and Informatics, 6(2), 231-334.
Kwon, N.Y. and Orrill, Ch. H. (2008). A comparison study of a teacher’s reflection. In O. Figueras, J.L. Cortina, S. Alatorre, T. Rojano y A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of the 32nd Conference of the International Group for the Psychology of Mathematics Education and XXXth Annual Meeting of the North American Chapter of PME, 1.
Lave, J. and Wenger (1991). Situated learning: Legitimate peripherical participation. Cambridge: Cambridge University Press.
Llinares, S (2000). Intentando comprender la práctica del profesor de matemáticas. En J.P. da Ponte, J.P. y Serrazina, L. (Coord.), Educação matemática em Portugal, Espanha e Italia. Lisboa: Secção de Educação Matemática da Sociedade Portuguesa de Ciências da Educação.
Llinares, S. and Krainer, K. (2006). Mathematics (students) teachers and teacher educators as learners. In A. Gutierrez y P. Boero (Eds.), Handbook of Research on the Psychology of Mathematics Education. Rotherdam/Taipei: Sense Publichers.
Llinares, S. (2007). Formación de profesores de matemáticas. Desarrollando entornos de aprendizaje para relacionar la formación inicial y el desarrollo profesional. Memorias de la XIII Jornadas de Aprendizaje y Enseñanza de las Matemáticas, Granada, Universidad de Alicante. Ministerio de Educación Colombia. (1998). Lineamientos Curriculares. Bogotá, Colombia.
Ministerio de Educación Colombia. (2006). Estándares Básicos de Competencias. Bogotá, Colombia.
Parada, S. (2009). Reflexión sobre la práctica profesional: actividad matemática promovida por el profesor en su salón de clases. Tesis de maestría inédita. México: Centro de Investigaciones y Estudios Avanzados del IPN.
Parada (2011). Reflexión y acción en comunidades de práctica: Un modelo de desarrollo profesional. Tesis de doctorado inédita. México: Centro de Investigaciones y Estudios Avanzados del IPN.
Parada, S. (2013 )Alternativas curriculares para atender la problemática relacionada con el curso de cálculo diferencial de la Universidad Industrial de Santander. En Roa, S., Fiallo, J. y Parada, S. (Eds), Memoria del 4o Seminario Taller en Educación Matemática: La enseñanza del cálculo y las componentes de su investigación. Universidad Industrial de Santander. Bucaramanga.
Ponte, J. P. e Serrazina, L. (2004). Práticas profissionais dos professores de Matemática. Quadrante,13(2), 51-74.
Recio, T. (2004). Seminario: Itinerario Educativo de la Licenciatura de Matemáticas. Documento de conclusiones y propuestas. La gaceta de la RSME, 7(1), 33-36.
Rico, L. (2004). Reflexiones sobre la formación inicial del profesor de matemáticas de secundaria. Revista de currículum y formación del profesorado, 8,(1) 1-15.
Shulman, L. (1987). Knowledge and teaching: foundations of the New Reform. Harvard Educational Review, 57(1), 1-21.
Suárez, R. y Parada (2013) Actividades de refuerzo para estudiantes de once grado alrededor de sus habilidades comunicativas en matemáticas: una alternativa de preparación para el ingreso a la universidad. Revista Científica. (Edición especial) Universidad Distrital. Bogotá,.
Thompson, A. (1992). Teachers´ beliefs and conceptions: a synthesis of the research. In Grows, D.A. (Ed.), International Handbook of Research on Mathematics Teaching and Learning. New York, USA: Macmillan Publishing Company.
Treffers, A. (1987). Three dimensions: A model of goal and theory description in mathematics education. The Wiskobas project. Dordrecht: Kluwer Academic Publishers.
Trouche, L. (2004) Managing Complexity of Human/Machine Interactions in Computerized Learning Environments: Guiding Student's Command Process Through Instrumental Orchestrations. International Journal of Computers for Mathematical Learning, 9(3) 281- 307.
Vega, M. (1990). Introducción a la psicología cognitiva. Madrid: Alianza.
Wenger, E. (1998). Communities of Practice: Learning, Meaning, and Identity. Cambridge: Cambridge University Press.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Perspectivas para formar profesores de matemáticas: disminuyendo la brecha entre la teoría y la práctica1
Prospects for training teachers of mathematics: brinding the breach between theory and practice
Perspectivas para formar professores de ,matematicas: diminuindo a infraçao entre a teoria e a práctica
Sandra Evely Parada Rico2
Jorge Enrique Fiallo Leal2
1Artículo de investigación
2Universidad Industrial de Santander. Contacto: sparada@matematicas.uis.edu.co
3Universidad Industrial de Santander. Contacto: jfiallo@uis.edu.co
Fecha de recepción: febrero 2014, Fecha de aceptación: julio de 2014
Resumen
En este artículo se analizan algunas acepciones sobre la problemática de la formación inicial y continuada de profesores de matemáticas. Se plantea la necesidad de posibilitar experiencias y espacios de aprendizaje en los programas de formación y de actualización de docentes, en los que se reflexione sobre las prácticas del aula y problemáticas educativas reales, esto con el fin de disminuir la brecha entre las teorías y las prácticas profesionales. A partir de resultados de investigación se proponen alternativas de formación como: 1) en la formación inicial las tutorías académicas universitarias como práctica docente pueden aportar en el desarrollo del pensamiento reflexivo de los futuros maestros; así mismo, la vinculación de estos en investigaciones los puede proyectar como educadores matemáticos, y 2) para el desarrollo profesional, se plantea la necesidad de construir espacios de trabajo colaborativo como puede ser al interior de comunidades de práctica.
Palabras clave: formación de profesores, formación inicial, desarrollo profesional, tutoría entre pares, comunidad de práctica.
Abstract
In this paper exhibit some meanings on the problems related to the initial and continuing training of mathematics teachers, this raised the need for training programs and educational update enable experiences and learning spaces which reflect on the practices of classroom and real educational problems, this in order to reduce the gap between theories and practices.From research results proposed training alternatives such as: i) in the initial training teaching practice through academic tutoring university can contribute to the development of reflective thinking (in terms of Parada, 2011) of prospective teachers, also linking of these investigations can be projected as the mathematics educators, and ii) for professional development, there is a need to build collaborative work spaces such as within communities of practice.
keywords: teacher training, training, professional development, peer mentoring, community of practice.
Resumo
Este trabalho apresentam alguns significados sobre os problemas relacionados com a formação inicial e continuada de professores de matemática, este levantou a necessidade de programas de capacitação e atualização educacional permitir experiências e espaços de aprendizagem que refletem sobre as práticas sala de aula e os problemas educacionais reais, isso a fim de reduzir o fosso entre teorias e práticas. Para este fim os resultados de alternativas de formação em investigação são propostos: i) na formação inicial e prática docente universitário tutoria acadêmica pode contribuir para o desenvolvimento do pensamento reflexivo (em termos de Parada, 2011) de futuros professores , da mesma forma que liga estas investigações podem ser projetadas como os educadores matemáticos , e ii) para o desenvolvimento profissional , há uma necessidade de construir espaços de
trabalho colaborativos , como no seio das comunidades de prática.
Palavras-chave: formação de professores, formação inicial, desenvolvimento profissional, tutela entre pares, Comunidade de prática.
Introducción
La formación de profesores en matemática es un campo en el que se ha centrado la atención en los últimos tiempos, esto obedece a que la comunidad académica precedió investigaciones de tipo: curricular, cognitivo, didáctico entre otros; para interiorizar y comprender que, en los resultados de las líneas antes mencionadas, es el maestro quien lleva la “batuta” en los procesos de enseñanza y aprendizaje del área.
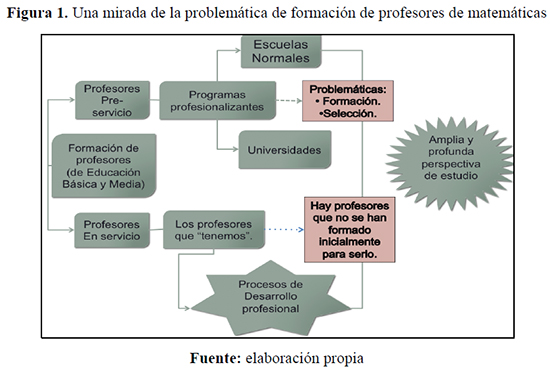
La formación de profesores de matemáticas se constituye en un amplio y profundo campo de estudio que necesita pensarse desde sus dos grandes ejes: 1) el de la formación inicial de profesionales que van a ser maestros; y 2) el desarrollo profesional de quienes ya están desempeñándose como docentes del área. En la figura 1 se presenta un esquema de la problemática relacionada con la formación de docentes de matemáticas en Colombia. Lo que vislumbra la necesidad de un estudio consciente sobre currículos que respondan a las necesidades básicas para que el futuro maestro pueda enfrentar diversas situaciones en sus clases de matemáticas. Desde el desarrollo profesional se requiere de una amplia reflexión de las instituciones u organizaciones —oficiales, privadas y de ciencias— que promueven permanentemente la actualización de los profesores que ya están desempeñándose como docentes de matemáticas, aún cuando pudieron no haberse formado profesionalmente para ello.
BUSCANDO DISMINUIR LA BRECHA ENTRE LA TEOR�A Y LA PR�CTICA EN LA FORMACI�N INICIAL DE PROFESORES
En los programas de formación inicial de docentes en matemáticas se han empleado diferentes modelos. Por ejemplo, Rico (2004) dice que, en España, los planes de formación no consideran las necesidades de formación propias de los profesores de matemáticas, además faltan criterios sobre los conocimientos necesarios y el marco teórico adecuado para ejercer satisfactoriamente la profesión. Por su parte Azcárate y Cardeñoso (1998) hablan de cómo las concepciones de los profesores en formación pueden convertirse en obstáculos, por lo que sugieren que los formadores deben incidir en aquellas concepciones elaboradas por los estudiantes para el profesor a partir de sus experiencias propias, las cuales, en algunos casos no permiten evolucionar hacia formas más complejas de comprensión e intervención en la realidad educativa.
Modelos de formación inicial de profesores de matemáticas
Son diferentes los reportes que tratan sobre los modelos o programas de formación inicial, en los cuales se vislumbra una preocupación permanente por la relación e integración entre el conocimiento matemático, el conocimiento pedagógico y el conocimiento didáctico (Gómez, 2004). Se encuentran diversos trabajos para referirse a la práctica, el uso de relatos y el uso de las tecnologías digitales. El trabajo de Chapman (2005) sugiere que la escritura de relatos e historias sobre la enseñanza y el aprendizaje de las matemáticas, y las reflexiones que el profesor en formación realice contribuyen a la formación. De modo que emplea los relatos para que los profesores en formación realicen una diferenciación entre lo que habían previsto para la clase y lo que observaron en ella.
En Gónzalez (2010) se encuentra un modelo didáctico para formación inicial que se fundamenta en: el modelo conceptual sobre el aula, los principios didácticos, los fines educativos y la práctica escolar. Mientras Alsina (2010) plantea un modelo de formación inicial que se fundamenta en la aplicación del aprendizaje reflexivo para aprender a enseñar matemática. En tanto que Kosheleva, Medina, e Ioudina (2007) proponen un modelo donde los profesores en formación incorporan en su formación las tabletas y las tecnologías digitales para el aprendizaje y la enseñanza de las matemáticas.
Competencias a desarrollar en los futuros profesores de matemáticas
Para algunos investigadores es esencial que los estudiantes que se preparan para ser profesores de matemáticas posean competencias que les permitan tener un buen desarrollo en el ejercicio de su profesión. No obstante, como lo expresa Llinares (2007) algunas de esas competencias no logran alcanzarse durante sus estudios universitarios, puede que se alcancen después de empezar a ejercer la enseñanza o cuando se realicen estudios de actualización docente. Por ello, el desarrollo profesional es una acción complementaria a la formación inicial, para que así se realice una actualización permanente de los profesores de matemáticas y puedan mejorar la calidad de la enseñanza.
Recio (2004) describe las competencias generales que deben desarrollarse desde la formación inicial, estas son:
i) Dominio de los contenidos matemáticos de educación secundaria desde una perspectiva matemática superior y su conocimiento como objetos de enseñanza-aprendizaje; ii) la organización curricular y planificación de estos contenidos matemáticos para su enseñanza; iii) el análisis, interpretación y evaluación de los conocimientos matemáticos de los alumnos a través de sus actuaciones y producciones matemáticas; y iv) la capacidad de gestión del contenido matemático en el aula (p.35).
Otras competencias generales del profesor de matemáticas que propone Rico (2004) son: 1) organizar el contenido matemático para enseñarlo; 2) analizar e interpretar las producciones matemáticas de los alumnos; y 3) gestionar el contenido matemático en el aula. De dichas competencias se determinan competencias específicas las cuales se enuncian a continuación:
i) Conectar los contenidos matemáticos de la educación secundaria con los fenómenos que los originan (de situaciones cotidianas y de ámbitos multidisciplinares; ii) conocer diversas teorías de aprendizaje del conocimiento matemático; iii) analizar críticamente y evaluar propuestas curriculares; iv) reconocer los tipos de razonamiento de los estudiantes, proponer tareas que los orienten; v) seleccionar y secuenciar actividades para el aprendizaje escolar; vi) diseñar, seleccionar y analizar unidades didácticas, textos y recursos; vii) disponer de criterios, técnicas e instrumentos específicos para la evaluación del conocimiento matemático; viii) reconocer recursos y materiales (computacionales, audiovisuales, manuales, bibliográficos, etc.) y emplearlos adecuadamente en la enseñanza; ix) utilizar técnicas de comunicación para dotar de significado los conceptos matemáticos; y x) favorecer las potencialidades matemáticas de los estudiantes.
Socialmente, el aula de matemáticas delimita un ambiente complejo lleno de diversas interacciones promotoras del aprendizaje, por ello, es importante que los profesores iniciales sepan qué saber matemático deben enseñar en cada nivel bajo la directriz de los Lineamientos Curriculares (MEN, 1998) y los Estándares Básicos de Competencias en Matemáticas (MEN, 2005) en el contexto colombiano. Además, deben tener claro por qué enseñar unos contenidos y destrezas y no otros, qué secuencia seguir, cómo distribuir el tiempo; debe tener criterios para ser agentes críticos y reflexionar sobre su quehacer docente en pos de autoevaluarse para que elija estrategias de cambio que le permitan mejorar.
En Colombia las universidades que tienen programas de licenciatura en matemáticas o enseñanza de las matemáticas cuentan con dos grandes líneas de estudio: la línea de las matemáticas y la línea de las didácticas —incluyendo aquí materias sobre pedagogía, psicología, currículo y evaluación—, estas además se conjugan al final del plan de estudios en prácticas docentes, que en ocasiones construyen sobre procesos artificiales, alejándolos así de las prácticas reales del aula.
Tutorías entre pares como puente entre la práctica artificial y la práctica real de maestros en formación
Con el interés de establecer un puente entre la práctica real y la práctica artificial que viven los profesores en formación, Botello y Parada (2013) presentan una propuesta en la que los alumnos-maestros funjan como tutores en cursos de los primeros niveles universitarios. En dicho estudio se postulan los programas de tutorías como un laboratorio académico, en el cual los alumnos-docentes pueden desarrollar su pensamiento didáctico y su pensamiento matemático escolar, en términos de Parada (2011).
Del trabajo experimental realizado por Botello y Parada (2013) con tutores y los estudiantes de cálculo diferencial, se ha encontrado que el programa de tutorías es una oportunidad para que los tutores confronten y mejoren sus conocimientos adquiridos. Además, identifican aprendizajes que pueden emerger de este proceso tanto desde el pensamiento matemático como el didáctico, entre ellos:
- Del pensamiento matemático
- a) Posibilita recordar contenidos del cálculo.
- b) Posibilita reaprender contenidos del cálculo diferencial que no habían quedado completamente claros o estaban mal aprendidos.
- c) Posibilita aprender contenidos que nunca se vieron o aprendieron en su formación matemática.
- Del pensamiento pedagógico y didáctico
- a) Aporta experiencia para identificar problemas de aprendizaje de los contenidos del curso.
- b) Aporta experiencia para identificar problemas de enseñanza de los contenidos del curso.
- c) Aporta experiencia en el dominio grupal y en la atención a estudiantes.
Aunque las tutorías representan una responsabilidad mayor para los alumnos-docentes pues les implica trabajar con estudiantes universitarios y con una asignatura compleja —como lo es el cálculo diferencial—, éstos manifiestan que su experiencia es tanto de enseñanza-aprendizaje del cálculo, y que ésta les permitió vislumbrar un poco de lo que será su práctica real.
Proyección hacia una formación investigativa
Font (2002) plantea que la formación de los futuros profesores debe examinar los resultados de investigaciones en Educación Matemática, este autor menciona que por medio de las reflexiones sobre la enseñanza de la matemática se les permite a los profesores en formación a:
i) Tomar conciencia sobre la existencia de parámetros y variables que condicionan las situaciones de enseñanza; ii) conocer la existencia de concepciones, representaciones en los alumnos, y conocer los efectos de estas concepciones; iii) saber que los obstáculos en el aprendizaje no provienen todos de los propios alumnos, sino frecuentemente del propio concepto a enseñar, o de las elecciones didácticas llevadas a cabo por el propio profesor; iv) concientizarse de sus propias
representaciones y concepciones y de su posible influencia en la enseñanza; v) conocer, o al menos tratar de aproximarse, a la explicación de los errores de los alumnos, acercarse a lo que estos errores muestran sobre la estructura cognitiva de los alumnos; vi) saber lo que se puede pedir a los investigadores en didáctica. (p. 3)
Desde esta perspectiva, se pudo desarrollar un estudio por Suárez y Rojas (2013) en el que ellas, como profesoras en formación, se involucraron en una investigación de tipo curricular desarrollada por Parada (2013) en la que se analizan —entre otros aspectos— las competencias matemáticas con las que ingresan los estudiantes a la Universidad. En dicho estudio, estas futuras maestras desarrollaron una investigación cualitativa que tuvo como objetivo diseñar experiencias que posibilitaron el desarrollo de habilidades comunicativas en estudiantes de once grado, y analizar como dichas habilidades contribuyen en el progreso de su pensamiento algebraico. Entendiendo por habilidades comunicativas la capacidad que tienen las personas de expresar sus ideas hablando y escribiendo, de comprender, de interpretar y de sustentar ideas; además de formular preguntas, y producir argumentos persuasivos y convincentes (MEN, 1998).
Para la consecución de dicho objetivo se diseña e implementa un plan de intervención alrededor de la habilidad para interpretar y la habilidad para explicar con estudiantes de once grado de una institución pública. Las reflexiones resultantes de la aplicación de las actividades posibilitaron un avance en el desarrollo de dichas habilidades en los estudiantes que participaron del plan de intervención, donde ellos reconocieron la importancia de la traducción de expresiones en sus diferentes representaciones para la resolución de problemas.
Pero ¿qué caminos abren estas perspectivas para los futuros maestros?, específicamente, esta perspectiva de formación docente:
- Posibilita espacios para fortalecer las herramientas docentes —matemáticas y didácticas— para los procesos de enseñanza y aprendizaje de su práctica actual y futura.
- Abre caminos para continuar con el “perfeccionamiento” docente —postgrados en profundización—, para que coadyuven en procesos de construcción y no de reproducción de la labor docente.
- La participación en estudios educativos les permite comprender fenómenos en los que se ver inmersos como docentes.
- Aporta herramientas para participar en futuros proyectos curriculares y de desarrollo.
- Abre perspectivas y plantea interrogantes para continuar la formación como investigadores —postgrados de investigación—.
PROCESO DE DESARROLLO PROFESIONAL
A pesar del reconocimiento de la gran relevancia que tiene en el desarrollo profesional de los docente en ejercicio, tanto en los procesos de profundización o actualización, es de conocimiento consensual que, aunque la mayoría de los programas de desarrollo profesional —diplomados, especializaciones, maestrías en educación— son planeados para atender las necesidades actuales de los maestros, éstos se encuentran limitados por tiempo, programas y evaluaciones. Es por ello, que muchos programas formales de desarrollo profesional dejan ciertos vacíos, tanto de conocimientos de la matemática escolar, como de conocimientos pedagógicos y didácticos, por lo que no logran satisfacer las necesidades reales de los profesores.
En la literatura relacionada con la formación de profesores de matemáticas, se puede observar que varios de los estudios en esta área se enfocan en el análisis de los conocimientos matemáticos y concepciones de los profesores, así como en el estudio de sus actitudes y creencias, debido a la relación que algunos investigadores establecen entre cómo se comprende y enseña la matemática, y el aprendizaje de los estudiantes. Por ejemplo, Thompson (1992) estudió las relaciones entre los conocimientos, concepciones y creencias de los maestros. Investigadores como Fennema y Loef (1992), Grossman, Wilson y Shulman (2005), Llinares y Krainer (2006), entre otros, han centrado su interés en conocer y comprender los conocimientos matemáticos con los que cuentan los maestros.
Otras investigaciones sugieren que, para mejorar la comprensión del profesor, son útiles las experiencias de reflexión de, y con, profesores; entre ellas se pueden mencionar las de Flores (2007)) y Kwon y Orrill (2008) que muestran evidencias de que la reflexión sobre la experiencia profesional, como podría darse dentro de comunidades de práctica —ver abajo—, contribuye al desarrollo de los conocimientos matemáticos y pedagógicos de los profesores en servicio.
Algunas investigaciones presentan una perspectiva sociocultural para situar los aprendizajes adquiridos a través de prácticas profesionales y de interacciones sociales. Muchas de ellas se enfocan en los aprendizajes construidos por los profesores a través de su participación en una comunidad de práctica o CoP. Entre ellas, las de Llinares (2000), Jaworski (2008) y Parada (2009) mencionan que las discusiones entre maestros, o maestros en formación, favorecen una mayor comprensión de la experiencia profesional de quienes participan y apoyan su crecimiento profesional. Asimismo, Parada señala la importancia de los procesos de seguimiento y acompañamiento permanente dentro del desarrollo profesional de los profesores de matemáticas.
También, Lave y Wenger (1991) hablan de lo que representa aprender en función de la participación en comunidades de práctica (CoP), en la que se comparten e intercambian conocimientos y experiencias. Así mismo, para Harris (2008), en la formación de profesionales en general, no se logran abarcar los conocimientos necesarios para resolver los problemas propios de la práctica —en nuestro caso, de la práctica
docente—, creándose vacíos cognitivos que él considera se pueden llenar mediante participación en las CoP: los profesionales en las CoP pueden hacer conexiones rápidamente para conseguir respuestas a preguntas que necesitan contestar.
Comunidades de práctica y desarrollo profesional
Parada (2011) presenta un modelo de desarrollo profesional —modelo R-y-A, de Reflexión-y-Acción— en el que se propone el trabajo colaborativo al interior de comunidades de práctica (CoP) como espacios permanentes y favorables para la reflexión sobre la práctica docente y por ende para el mejoramiento del desempeño del profesor en el aula. En dicho modelo retomó la definición de comunidades de práctica de Wenger (1998), quien dice que éstas están conformadas por un grupo de personas que comparten preocupaciones e intereses comunes, y que profundizan y construyen de manera colaborativa conocimiento. Para este autor, una CoP se caracteriza por tener un compromiso mutuo; y por ser una empresa conjunta y compartir un repertorio.
En el modelo R-y-A (Parada, 2011) se plantea la conformación de CoP de educadores matemáticos —profesores de matemáticas, investigadores, autoridades educativas y otros interesados en el mejoramiento de la educación matemática— asumiendo que en el desarrollo profesional de los docentes se debe propiciar la concurrencia de conocimientos —científicos, técnicos, pedagógicos, entre otros— y experiencias. Así, si los maestros exponen sus vivencias de enseñanza y en el aula, a investigadores y colegas con mayor experiencia, es posible que desarrollen ideas, conocimientos y alternativas concretas para mejorar su práctica docente.
Modelo de Reflexión-y-Acción en una CoP de Educadores Matemáticos
El modelo Reflexión-y-Acción (R-y-A) de Parada (2011) pretende ser una guía metodológica para impulsar y favorecer el desarrollo profesional de profesores que participan en CoP de educadores matemáticos. Wenger (1998) sustenta que una CoP se caracteriza por: 1) el compromiso mutuo, 2) la empresa conjunta y 3) el repertorio compartido. En este estudio, se enfoca el análisis de los datos desde la perspectiva del desarrollo de un repertorio compartido, con el cual los profesores tienen la oportunidad de participar en la actividad matemática propuesta. Buysse, Sparkman y Wesley (2003) definen una CoP como un grupo de profesionales y otros interesados que buscan una empresa de aprendizaje compartido, normalmente centrado en un tema en particular. Es este el caso de estudio presente, pues se conforman las CoP entre diferentes actores interesados en la educación matemática. Se incluyeron a las autoridades educativas, ya que éstas necesitan conocer los fenómenos de estudio y comprenderlos para que apoyen las alternativas generadas por los profesores.
Pensamiento reflexivo del profesor de matemáticas.
Según Vega (1990), el pensamiento es una actividad global del sistema cognitivo que ocurre siempre que el humano se enfrenta a una tarea o problema, con un objetivo y un cierto nivel de incertidumbre sobre la forma de realizarla. El modelo R-y-A enfatiza en que la formación de profesores debe apuntar al desarrollo de un pensamiento reflexivo, en el que se privilegien los saberes adquiridos por cada maestro en el trayecto de su práctica y en las maneras como usen dichos saberes para resolver los problemas cognitivos, didácticos, tecnológicos, sociales y de otro tipo, que suelen darse en el aula. No obstante, se reconoce la complejidad de la labor y, como ya se ha mencionado, se descompone dicho pensamiento en tres partes:
- 1) Pensamiento matemático escolar. Al respecto Shulman (1987) enfatiza que para enseñar, en primer lugar, hay que comprender críticamente el conjunto de ideas que van a enseñarse. El modelo R-y-A establece una diferencia entre el pensamiento matemático y el conocimiento matemático, para explicar que, más allá de que el profesor sea un experto en el área, éste necesta usar sus saberes matemáticos para conducir la actividad matemática en el aula.
- 2) Pensamiento didáctico de la matemática escolar. Ball, Hill y Bass (2005) destacan la necesidad de trabajar las relaciones entre el conocimiento matemático y pedagógico en la formación de docentes de matemáticas. Desde esta perspectiva, el pensamiento didáctico del profesor de matemáticas se da cuando éste cuestiona las diferentes maneras de acercar los estudiantes a los contenidos matemáticos, buscando las formas más útiles de representar los contenidos mediante analogías, ilustraciones, ejemplos, explicaciones, y demostraciones que permitan hacerla más comprensible a los alumnos.
- 3) Pensamiento orquestal. Inspirados por Trouche (2004) y su idea de orquestación, se plantea como metáfora la idea de que el maestro necesita hacer las veces del conducir su clase como lo hace el director de una orquesta. El modelo R-y-A caracteriza el pensamiento orquestal del profesor de matemáticas en torno a la conducción de su clase —reflexión-en-la acción—, y en torno a las maneras como usa los recursos que ha seleccionado para favorecer la actividad matemática que tiene prevista.
Actividad matemática.
La matemática como actividad de resolución de problemas introduce en muchos casos un componente fundamental: la matematización. Matematizar, según Treffers (1987), es organizar y estructurar la información que aparece en un problema, identificando los aspectos matemáticos relevantes, descubriendo regularidades, relaciones y estructuras. El interés de analizar la actividad matemática del profesor es identificar las condiciones necesarias del pensamiento reflexivo de éste, para que logre conducir la apropiación por parte de los estudiantes.
Procesos de reflexión.
El modelo también considera tres procesos de reflexión, y estos son: 1) reflexión-para-la acción, la cual se hace presente en la relación de la matemática escolar y el profesor, cuando éste planifica la actividad matemática esperada por parte de los estudiantes en la clase; 2) reflexión-en-la acción, ésta se da en la clase, en los intercambios entre el profesor y los estudiantes en torno al contenido matemático de estudio y; 3) reflexión-sobre-la acción, la cual se da después de la clase cuando el maestro evalúa la actividad matemática que había planeado comparada con la actividad matemática que logró.
¿Cómo influyen los aprendizajes construidos en CoP en los profesores en ejercicio?
En el transcurso de la investigación realizada por Parada (2011) se pudo ver cómo los significados negociados en las CoP influyeron en las prácticas profesionales, especialmente de los profesores y autoridades educativas que participaron frecuentemente en las actividades de la comunidad. De acuerdo a las prácticas profesionales que redefinieron a a partir de los ejercicios propios de la actividad docente que proponen Ponte y Serrazina (2004), se puede señalar que:
- Los aprendizajes pueden influir en las maneras de proponer tareas por parte de los profesores participantes, pues para la mayoría de los maestros no es una costumbre planear sus clases. Los maestros a través del trabajo en comunidad valoran la selección y diseños de actividades para lograr la actividad matemática esperada.
- En la práctica de seleccionar, usar y diseñar recursos, los maestros construyen significados críticos sobre los recursos con los que cuentan.
- Se fortalece la interpretación crítica de los materiales oficiales y se logran adaptaciones o modificaciones curriculares.
- Las actividades de análisis sobre las maneras de comunicación en el aula sugirieren la autorreflexión de los maestros en dicho aspecto.
- En relación a la evaluación, las actividades en las CoP ayudan a los maestros a asumirla de manera más formativa, tanto para ellos como para sus estudiantes.
- La práctica de colaboración se ve favorecida pues los maestros más participativos terminan fungiendo como formadores de otros colegas.
- El modelo R-y-A se puede convertir en una alternativa o complemento para la práctica de profesionalización, fueron evidentes los significados negociados y cosificados a través del proceso.
REFLEXIONES FINALES
Es importante destacar la importancia de que los estudios sobre formación de profesores cuenten con amplias y conscientes lecturas de los fenómenos de estudio desde la matemática educativa, para evitar emitir juicios arriesgados de los docentes o plantear propuestas “milagrosas” que amplíen la brecha entre la teoría y la práctica.
La formación de profesores va más allá de aportar un cúmulo de conocimientos teóricos, una lista de estrategias de enseñanza o una serie de “nuevos” recursos didácticos. La actualización y desarrollo profesional requiere aprovechar los conocimientos adquiridos por los profesores a través de su experiencia docente y posibilitar espacios de acompañamiento y seguimiento permanente, en los que se promuevan procesos de reflexión sobre sus acciones docentes.
Las investigaciones que ha desarrollado Parada (2009, 2011) alrededor de los procesos de reflexión-acción —antes durante y después de la clase— han mostrado que éstos favorecen el entendimiento y concientización de los maestros sobre sus prácticas y la actividad matemática que promueven en sus aulas. Asimismo, el proceso individual de reflexión de los profesores se ve enriquecido a través de la comunicación y socialización de experiencias. Es por ello que deben fortalecerse proyectos curriculares en las instituciones formadoras de profesores en los que los futuros maestros puedan experimentar prácticas reales. Además, la conformación de comunidades de práctica pueden ser espacios de aprendizaje de los maestros, en los cuales las reflexiones personales y colectivas pueden provocar “un efecto de palanca” elevando y fortaleciendo sus procesos de desarrollo profesional, así como su confianza y competencias docentes.
REFERENCIAS
Alsina, Á. (2010). El aprendizaje reflexivo en la formación inicial del profesorado: un modelo para aprender a enseñar matemáticas. Educación Matemática, 22(1), 149-166.
Azcárate, P. y Cardeñoso, J. (1998). La formación inicial de profesores de matemáticas, finalidades, limitaciones y obstáculos. Investigación en la Escuela, (35), 76-85.
Ball, D. L., Hill, H. C. and Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, Fall.
Botello y Parada (2013) Tutorías entre pares: una oportunidad de formación para futuros profesores de matemáticas. Revista Científica, (Edición especial) 135-139. Universidad Distrital. Bogotá, Colombia. D.C.
Buysse, V., Sparkman, K. and Wesley, P. (2003). Communities of practice: Connecting what we know with what we do. Exceptional Children, 69(3), 263-278.
Chapman, O. (2005). Stories of Practice: A Tool in Preservice Secondary Mathematics Teacher Education. En The Fifteenth ICMI Study, Águas de Lindóia.
Fennema, E. y Loef, M. (1992). Los conocimientos de los profesores y su impacto. En D.A. Grows (Ed.), Handbook of Research on Mathematics Teaching and Learning. New York, USA: Macmillan Publishing Company.
Flores, P. (2007). Profesores de Matemáticas Reflexivos: Formación y Cuestiones de Investigación. Revista de Investigación en Didáctica de la Matemática, 1(4), 139-159.
Font, V. (2002). Una propuesta dialógica sobre la formación inicial en matemáticas de los maestros de educación primaria. En G. Perafán, y A. Adúriz (Eds), Pensamiento y conocimiento de los profesores. Debate y perspectivas contemporáneas. Bogotá: Universidad Pedagógica Nacional.
Gómez, P. (2004). Diversidad en la formación inicial de profesores de matemáticas en la búsqueda de un núcleo común. Revista EMA, 10(1), 242-293.
González, F. (2010). Un modelo didáctico para la formación inicial de profesores de matemática. Sapiens. Revista Universitaria de Investigación, 11(1), 47-59.
Grossman, P., Wilson, S. y Shulman, L. (2005). Profesores de sustancia: El conocimiento de la materia para la enseñanza. Profesorado. Revista de Currículo y Formación de Profesorado, 9(2), 1-24.
Harris, Ch. (2008.) Learning & Innovation in communities of practice. Access: mayo de 2009. Available: http://www.pyramidodi.com/papers/CoPs.pdf.
Jaworski, B. (2008). Building and Sustaining Inquiry Communities in Mathematics Teaching Development. In K. Krainer, T. Woods (Eds.), Participants in Mathematics Teachers Education Rotterdam/Taipei: Sense Publishers.
Kosheleva, O., Medina, A. and Ioudina, V. (2007). Pre-service teacher training in mathematics using tablet PC technology. Institute of Mathematics and Informatics, 6(2), 231-334.
Kwon, N.Y. and Orrill, Ch. H. (2008). A comparison study of a teacher’s reflection. In O. Figueras, J.L. Cortina, S. Alatorre, T. Rojano y A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of the 32nd Conference of the International Group for the Psychology of Mathematics Education and XXXth Annual Meeting of the North American Chapter of PME, 1.
Lave, J. and Wenger (1991). Situated learning: Legitimate peripherical participation. Cambridge: Cambridge University Press.
Llinares, S (2000). Intentando comprender la práctica del profesor de matemáticas. En J.P. da Ponte, J.P. y Serrazina, L. (Coord.), Educação matemática em Portugal, Espanha e Italia. Lisboa: Secção de Educação Matemática da Sociedade Portuguesa de Ciências da Educação.
Llinares, S. and Krainer, K. (2006). Mathematics (students) teachers and teacher educators as learners. In A. Gutierrez y P. Boero (Eds.), Handbook of Research on the Psychology of Mathematics Education. Rotherdam/Taipei: Sense Publichers.
Llinares, S. (2007). Formación de profesores de matemáticas. Desarrollando entornos de aprendizaje para relacionar la formación inicial y el desarrollo profesional. Memorias de la XIII Jornadas de Aprendizaje y Enseñanza de las Matemáticas, Granada, Universidad de Alicante. Ministerio de Educación Colombia. (1998). Lineamientos Curriculares. Bogotá, Colombia.
Ministerio de Educación Colombia. (2006). Estándares Básicos de Competencias. Bogotá, Colombia.
Parada, S. (2009). Reflexión sobre la práctica profesional: actividad matemática promovida por el profesor en su salón de clases. Tesis de maestría inédita. México: Centro de Investigaciones y Estudios Avanzados del IPN.
Parada (2011). Reflexión y acción en comunidades de práctica: Un modelo de desarrollo profesional. Tesis de doctorado inédita. México: Centro de Investigaciones y Estudios Avanzados del IPN.
Parada, S. (2013 )Alternativas curriculares para atender la problemática relacionada con el curso de cálculo diferencial de la Universidad Industrial de Santander. En Roa, S., Fiallo, J. y Parada, S. (Eds), Memoria del 4o Seminario Taller en Educación Matemática: La enseñanza del cálculo y las componentes de su investigación. Universidad Industrial de Santander. Bucaramanga.
Ponte, J. P. e Serrazina, L. (2004). Práticas profissionais dos professores de Matemática. Quadrante,13(2), 51-74.
Recio, T. (2004). Seminario: Itinerario Educativo de la Licenciatura de Matemáticas. Documento de conclusiones y propuestas. La gaceta de la RSME, 7(1), 33-36.
Rico, L. (2004). Reflexiones sobre la formación inicial del profesor de matemáticas de secundaria. Revista de currículum y formación del profesorado, 8,(1) 1-15.
Shulman, L. (1987). Knowledge and teaching: foundations of the New Reform. Harvard Educational Review, 57(1), 1-21.
Suárez, R. y Parada (2013) Actividades de refuerzo para estudiantes de once grado alrededor de sus habilidades comunicativas en matemáticas: una alternativa de preparación para el ingreso a la universidad. Revista Científica. (Edición especial) Universidad Distrital. Bogotá.
Thompson, A. (1992). Teachers´ beliefs and conceptions: a synthesis of the research. In Grows, D.A. (Ed.), International Handbook of Research on Mathematics Teaching and Learning. New York, USA: Macmillan Publishing Company.
Treffers, A. (1987). Three dimensions: A model of goal and theory description in mathematics education. The Wiskobas project. Dordrecht: Kluwer Academic Publishers.
Trouche, L. (2004) Managing Complexity of Human/Machine Interactions in Computerized Learning Environments: Guiding Student's Command Process Through Instrumental Orchestrations. International Journal of Computers for Mathematical Learning, 9(3) 281- 307.
Vega, M. (1990). Introducción a la psicología cognitiva. Madrid: Alianza.
Wenger, E. (1998). Communities of Practice: Learning, Meaning, and Identity. Cambridge: Cambridge University Press.
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.