Razonamiento algebraico elemental: propuestas para el aula-Elementary Algebraic Reasoning: Classroom Proposals

Razonamiento algebraico elemental: propuestas para el aula¹

Razonamiento algebraico elemental: propuestas para el aula

Raciocínio algébrico Fundamental: propostas para a sala de aula

Walter F. Castro G²

¹Artículo de investigación

²Profesor. Universidad de Antioquia, Colombia. Contacto: wfcastro82@gmail.com

Fecha de recepción: enero 2014, Fecha de aceptación: julio de 2014

Resumen

En este artículo se aborda el problema de la enseñanza de álgebra en la escuela primaria. Se discute lo que se entiende como “early álgebra” y se presentan varios enfoques sobre la introducción del álgebra en la escuela elemental. En correspondencia con los enfoques, se discuten tanto algunas tareas de razonamiento algebraico elemental que pueden ser implantadas en el aula, como algunas de las características algebraicas atribuidas. Finalmente, se presenta una propuesta para asignar niveles o grados de algebrización a algunas tareas.

Palabras clave: razonamiento algebraico elemental, análisis epistémico, álgebra elemental, currículo, naturaleza algebraica.

Abstract

IThe problem of teaching algebra in elementary school is discussed. It discusses what is meant by "early algebra" and various approaches to the introduction of algebra in elementary school are presented. In correspondence with the approaches, both some elementary algebraic reasoning tasks that can be implemented in the classroom, as some of the characteristics attributed algebraic discussed. Finally a proposal to assign levels or degrees of algebraization some tasks is presented.

keywords: Algebraic Reasoning Elemental, epistemic analysis, elementary algebra curriculum, algebraic nature.

Resumo

O problema de álgebra de ensino na escola primária é discutida. Ele discute o que se entende por "álgebra precoce" e várias abordagens para a introdução da álgebra na escola primária são apresentados. Em correspondência com as abordagens, tanto algumas tarefas de raciocínio algébricas elementares que podem ser implementadas em sala de aula, como algumas das características atribuídas algébrica discutido. Finalmente, uma proposta para atribuir níveis ou graus de algebraization algumas tarefas é apresentada.

Palavras-chave: Raciocínio Algébrica Elementais, análise epistêmica, currículo álgebra elementar, natureza algébrica.

ANTECEDENTES

El álgebra ha sido considerada como un “guardián” que impide el acceso de los estudiantes a niveles superiores de estudio y reflexión en matemáticas. Kaput (2000) hizo una propuesta denominada “algebra for all” en la que sugiere tomar acción para promover al álgebra como facilitadora de una mejor comprensión de las matemáticas en lugar de ser inhibidora.

Para lograr que la formación en álgebra alcance a una población mayor, algunos investigadores han propuesto incluir el razonamiento algebraico desde los niveles inferiores de la educación primaria (Davis, 1985). Esta propuesta ha sido denominada “la algebrización” del currículo (Kaput, 2000), lo cual se conoce también como “early algebra” —algebra temprana—. Los resultados de diversas investigaciones longitudinales sobre la inclusión del razonamiento algebraico desde la escuela elemental (Derry, Wilsman y Hackbarth, 2007) animan a iniciar la enseñanza del álgebra en la escuela primaria para preparar a los niños para asumir el álgebra de la escuela secundaria. Ante los informes sobre la introducción del álgebra en la escuela se formula la pregunta ¿pueden los niños aprender álgebra? (Carraher y Schlieman, 2007, p. 675).

ENFOQUES DE INTRODUCCIÓN DEL ÁLGEBRA

No existe una autoridad ni una organización que determine con certeza que ha de entenderse como “álgebra” y por ello, ha de entenderse como álgebra en la escuela elemental. Sin embargo diversos autores han señalado características del álgebra. Entre tales caracterizaciones se encuentran las siguientes:

• Usiskin (1988), propone cuatro concepciones del álgebra: Aritmética generalizada; el conjunto de procedimientos usados para resolver ciertos problemas; el estudio de las relaciones entre cantidades, y finalmente, el estudio de la estructura.

• Kaput (1998), identificó cinco aspectos propios del álgebra: Generalización y formalización; El estudio de las funciones, relaciones y la variación conjunta; y la modelación.

• La NCTM (1998; p. 161), propuso cuatro organizadores curriculares para el álgebra escolar: Funciones y relaciones; modelación; estructura, y finalmente, lenguaje y representación. En el año 2000 la NCTM afirma que el álgebra en la escuela primaria “enfatiza las relaciones entre cantidades, que incluye a las funciones, formas de representar las relaciones matemáticas, y el análisis del cambio” (p. 37).

• Bass (1998), adoptó una definición más tradicional del álgebra, como la totalidad del sistema numérico, las operaciones aritméticas, el ordenamiento lineal y las ecuaciones.

• Kieran (1996), propuso categorizar el álgebra escolar de acuerdo con las actividades que se pueden proponer a los niños: Actividades generativas, transformacionales, y actividades globales de meta-nivel.

• La Joint Mathematical Council of the United Kingdom (1996), reconoce actividades que considera precursoras del álgebra y que pueden ser trabajadas tanto en la escuela primaria como en la secundaria. Afirma que “hay una necesidad de enfatizar aspectos de meta-razonamiento en el trabajo algebraico y hacerlo parte de la enseñanza” (p. 14).

• Kaput (1998), amplió su propuesta del año 1995 e identificó cinco formas interrelacionadas del pensamiento algebraico: álgebra como una forma de generalizar y formalizar patrones y regularidades, en particular el álgebra como una aritmética generalizada; como una forma de manipulación simbólica, sintácticamente guiada; como el estudio de la estructura y los sistemas, abstraídos de los cálculos y las relaciones; como el estudio de las funciones, las relaciones, y la variación conjunta y finalmente, álgebra como modelación.

• Burkhardt (2001), propuso una taxonomía para lo que significa hacer álgebra, que comprende quince aspectos. Es una propuesta amplia de inclusión del álgebra en el currículo matemático de la escuela primaria y secundaria.

Este amplio conjunto de caracterizaciones da una idea sobre los aspectos fundamentales, sugeridos por los investigadores, que subyacen y conectan muchos principios matemáticos básicos.

Se ha argumentado que el álgebra puede apoyar a estructurar los conocimientos matemáticos de los estudiantes; adicionalmente, se ha reportado el efecto positivo en la enseñanza del álgebra de la secundaria como resultado de la introducción temprana del álgebra en la escuela primaria (Smith, 1996, Strother, 2010). Otros estudios han mostrado que los estudiantes pueden usar los conceptos algebraicos fundamentales en los primeros niveles de la escuela primaria (Schifter y otros, 2008; Brizuela y Earnest, 2008). Estos resultados favorables han animado a los maestros y a los funcionarios educativos a incluir el álgebra en el currículo de la escuela primaria (Cai, 2004; CCSSI, 2010).

Sin embargo, no se trata de introducir un curso formal de álgebra en el currículo de la escuela primaria, ni de proponer a los escolares tareas tipo “álgebra de Baldor”. La propuesta (Kaput, 2000) es “algebrizar” tareas matemáticas para resaltar los aspectos algebraicos que tales tareas puedan tener. Aún en tales casos no se podría afirmar que los niños estén trabajando con álgebra de manera amplia y conscientemente, sólo que están usando algunas características algebraicas, aún así es recomendable ofrecer a los niños oportunidades de usar algunas características del álgebra.

PROPUESTAS DE INTRODUCCIÓN DEL ÁLGEBRA

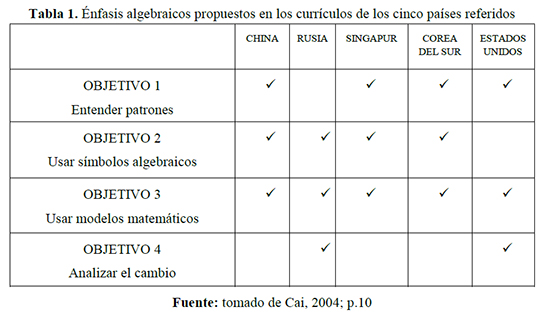
Los enfoques sobre lo que ha de considerarse como álgebra son diversos, así mismo lo son las propuestas curriculares de introducción del álgebra en diversos países. En lo que sigue se hará un compendio de propuestas de introducción curricular del álgebra, en el cual se mencionarán algunos de los elementos algebraicos y el enfoque que tienen en el currículo de los países referenciados. Estos países son: China, Rusia, Corea, Estados Unidos, y la ciudad estado, Singapur. Para el caso de Estados Unidos y Rusia, las propuestas discutidas son válidas en algunos de sus estados o provincias.

• Álgebra en el currículo chino: el propósito de la introducción del álgebra en el currículo es “ayudar a los estudiantes a representar y a comprender relaciones cuantitativas numérica y simbólicamente” (Cai, 2004, p.7). Las variables se introducen por medio del recurso de “espacios para completar” con números, se ven como “representaciones de un rango de valores” y se hace uso de palabras, en lugar de letras, para ayudar a los estudiantes a comprender las fórmulas. Así mismo, se enfatizan tres “hábitos mentales”: examen de relaciones cuantitativas desde diferentes perspectivas; uso de operaciones inversas para resolver ecuaciones; y finalmente la generalización a partir de casos específicos. El álgebra, desde esta perspectiva, se introduce desde el primer grado.

• Álgebra en el currículo ruso: desde la propuesta de Davydov, los niños desarrollan el razonamiento algebraico al explorar y comparar cantidades. Esto se hace antes del estudio de la aritmética. El proceso se inicia mediante el uso de letras para expresar relaciones parte-todo, para hallar números faltantes, se continúa hacia la medición. Los niños usan modelos para analizar y expresar relaciones cuantitativas, y manipular simbólicamente estas relaciones. El álgebra se introduce desde el primer grado.

• Álgebra en el currículo coreano: el estudio “formal” del álgebra se inicia en séptimo grado. El álgebra es mucho más que el dominio de técnicas y procedimientos. Durante la educación matemática precedente se provee a los estudiantes con oportunidades para fundamentar el estudio del álgebra. Algunas de estas actividades son: generalización, pensamiento analítico, pensamiento dinámico, modelación y organización.

• Álgebra en el currículo de Estados Unidos: si bien, dada la estructura organizativa del sistema educativo de los Estados Unidos, no existe una propuesta unificada de introducción del álgebra en la escuela primaria. Existen propuestas
  de actividades que orientan tal introducción. Ejemplos de actividades se pueden localizar en el sitio http://investigations.terc.edu/. De tales actividades se resaltan dos características: el estudio del cambio y, estudio de relaciones cuantitativas y cualitativas.

• Álgebra en el currículo de Singapur: algunos conceptos formales se introducen en grado seis. En este grado, se enseña a construir, simplificar y evaluar expresiones algebraicas de una variable. El currículo matemático de la primaria ofrece oportunidades para que se desarrolle el pensamiento algebraico: generalización, resolución de problemas y conocimiento de funciones como modelos de ciertos problemas. Las operaciones aritméticas resaltan el proceso de “hacer y deshacer”. Se enfatiza en los procesos de pensamiento, más que en las técnicas. Se reconocen varias “grandes” ideas en álgebra: la incógnita; patrones numéricos; y uso de letras como variables. Los niños trabajan problemas en los cuales se enfatizan “hábitos mentales”: hacer, deshacer, construcción de reglas para representar funciones.

La tabla 1 muestra los énfasis algebraicos propuestos en los currículos de los cinco países referidos

A MANERA DE EJEMPLO

A continuación se ilustran dos tareas y las soluciones, dadas por niños de quinto grado de escuela primaria, a tareas algebraicas.
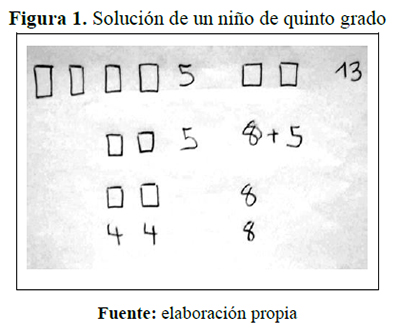
Tarea 1. Se sabe que cuatro bolsitas de caramelos más cinco caramelos tiene el mismo número de caramelos que dos bolsas más trece caramelos. Todas las bolsas tienen el mismo número de caramelos. ¿Cuántos caramelos tiene la bolsa?

El niño ha representado cada bolsa de caramelos mediante un rectángulo. Este rectángulo representa tanto la bolsa de caramelos como el número desconocido de caramelos que contiene. La similitud entre el uso de un “rectángulo” para representar a la bolsa y al número de caramelos que contiene y el uso de una letra “x”, que podría usarse formalmente, para denotar lo mismo es notable.

A continuación, se aprecia un procedimiento “algebraico” que conduce a una reducción de la ecuación. Las operaciones “físicas” o “numéricas” que el niño utiliza corresponden a operaciones matemáticas bien reconocidas por los maestros.

Nótese la descomposición que el niño hace del número trece como “8 +5” cuya intención es “eliminar” el cinco de ambos lados de la expresión. Finalmente, encuentra una expresión que se puede leer como “la cantidad de caramelos contenidos en dos
bolsas es 8”, la condición sobre el mismo número de caramelos en cada bolsa es claramente tenido en cuenta por el niño, quien descompone 8 como “4+4”, de donde se obtiene la solución al problema. La presencia del concepto de “igualdad” como relación de equivalencia es manifiesta a lo largo del proceso. Aceptar esta solución como algebraica o no algebraica depende de la postura epistémica de cada uno.

Tarea 2. Se muestra en la figura 2, la cual se tomó de Positive Algebra: A Collection of Productive Exercises (2004, p. 66).

Resalta en esta tarea el uso de representaciones visuales en el enunciado. El uso de las mismas en la resolución de tareas matemáticas es controversial pues, a pesar que ha sido usado durante siglos y considerado indispensable en el trabajo de los matemáticos (Rival, 1987), fue relegado por los matemáticos del siglo pasado por considerarlo informal. Para Stylianou (2002) “se ha hecho poco trabajo empírico que conduzca hacia una mayor comprensión de los procesos relacionados con el uso de representaciones visuales” (p. 304).

En esta tarea se reconoce la importancia a los elementos gráficos y se asumen en su papel de “elementos lingüísticos” que están sujetos a asignación de significados por parte de los niños a quienes se les propone la solución de la tarea. A continuación, se enumeran algunos objetos y significados de carácter algebraico que están presentes o surgen cuando se resuelve la tarea. Los elementos lingüísticos en esta tarea son de dos tipos: los escritos y los pictóricos. Estos últimos tienen gran presencia e importancia en esta tarea, en tanto que comunican significados que no están explícitamente expresados en la redacción de la tarea ni en la pregunta. Algunos investigadores han indagado sobre las representaciones gráficas y su uso por los niños (Goldenberg, 1988; Juraschek y Angle, 1986). Goldenberg concluyó que las gráficas tienen convenciones y ambigüedades propias y pueden ser poco accesibles a los niños que se inician en el estudio del álgebra.

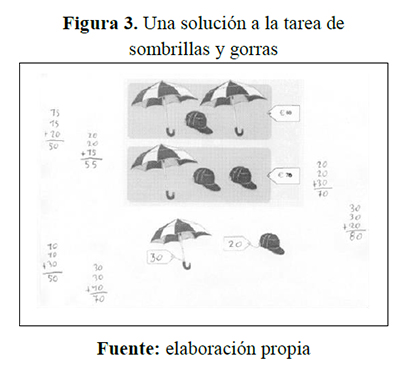
La presencia de elementos pictóricos en el enunciado de esta tarea y la asignación de significados que convocan, es determinante para su solución. La pregunta ¿cuánto vale una sombrilla y una gorra?, establece la pregunta en la tarea. Indica que la respuesta que corresponde al valor numérico correspondiente al precio de una sombrilla y de una gorra.

La suma de los precios de dos sombrillas y una gorra es de 80€; el precio de cada sombrilla es el mismo. Las suma de los precios de dos gorras de características similares y de una sombrilla es de 70€; el precio de cada gorra es el mismo.

Los conceptos de incógnita suma e igualdad son básicos en una propuesta de solución de la tarea, ya sea de carácter algebraica o aritmética, como se describen a continuación:

• Incógnitas: valores desconocidos que deben ser hallados. Tales valores están sujetos a condiciones establecidas gráficamente.

• Suma: la suma de los precios desconocidos.

• Igualdad: relación establecida entre precios desconocidos y los valores de sus sumas.

El reconocimiento de dos valores desconocidos que pueden ser hallados a partir de la información provista en el problema es crucial en el carácter algebraico de la tarea, con independencia del método de solución del mismo. Se resalta el carácter relacional que el signo igual tiene en esta tarea y que es asumido como tal por los niños sin ninguna instrucción al respecto. Algunos de los procedimientos que se resaltan en una posible solución de la tarea son:

• Procedimiento numérico de ensayo y error: los estudiantes asignan diversos valores numéricos para los precios de las sombrillas y de las gorras, los suman y comprueban si cumplen simultáneamente las dos condiciones.

• Procedimiento gráfico: consiste en escribir (dibujar) dos sombrillas y una gorra, más dos sombrillas y una gorra, y luego asociar dos sombrillas y una gorra y reemplazarlas por el precio combinado de ellas. De tal manera se puede obtener una gráfica en donde figuran dos gorras con un precio de 84, y como el precio de cada gorra es el mismo, se obtiene así el precio combinado de dos gorras, de donde se puede obtener el precio de una sola.

• Procedimiento algebraico: se asignan incógnitas para los precios desconocidos de sombrillas y gorras, y se procede a resolver un sistema lineal de dos ecuaciones por dos incógnitas.

Algunas propiedades que podrían ser usadas en una solución a la tarea son:

• El precio de cada sombrilla es el mismo: el precio de una sombrilla es el mismo en ambas condiciones de la tarea, lo cual reduce el número de incógnitas.

• El precio de cada gorra es el mismo: los estudiantes asignan diversos valores numéricos para las sombrillas y las gorras, los suman y comprueban si cumplen simultáneamente las dos condiciones.

• El precio de una sombrilla y una gorra, respectivamente, es el mismo en ambas condiciones de la tarea, lo cual reduce el número de incógnitas.

• La tarea tiene solución única: la tarea tiene solución y puede ser hallada.

NIVELES DE ALGEBRIZACIÓN

Las experiencias enumeradas (Cai, 2004) ilustran alternativas de introducción curricular del álgebra en la escuela primaria. Adicionalmente, diversas investigaciones reportan los logros de niños de escuela primaria cuando trabajan con tareas propias del razonamiento algebraico elemental (Amit y Neria, 2008; Becker y Rivera, 2008, Britt y Irwin, 2008).

reconocer niveles o grados de algebrización de las tareas matemáticas que se proponen en el currículo establecido. Estos niveles deberían considerar las diversas características asociadas al razonamiento algebraico elemental de una manera progresiva a lo largo de toda la educación primaria. La identificación de niveles de algebrización podría ayudar a los maestros a reconocer características algebraicas infusas en las tareas y a promover el desarrollo del pensamiento algebraico. Para Blanton y Kaput (2005, p. 414): “la mayoría de los profesores de escuela elemental tienen poca experiencia con los aspectos ricos y conexos del razonamiento algebraico elemental” y agregan “debemos proveer formas apropiadas de apoyo profesional que produzca cambio en las prácticas curriculares” (p. 414).

A partir de consideraciones sobre la naturaleza del álgebra (Godino, Castro, Ake y Wilhelmi, 2012) se pueden proponer niveles de algebrización (Godino, Ake, Gonzato, Wilhelmi, 2012). A modo de resumen se enumeran los niveles de algebrización y las características asociadas a tales niveles. Para un estudio más detallado, tanto de la naturaleza algebraica como de los niveles, se referencian los dos artículos mencionados anteriormente.

Las actividades se consideran “algebraicas” en tanto que exhiben algunas características algebraicas y que los estudiantes utilicen estas características para resolver tareas matemáticas, abordables en educación primaria. El nivel se asigna, no a la tarea en sí misma, sino a la actividad matemática que se realiza, por lo que dependiendo de la manera en que se resuelve una tarea, la actividad matemática puede ser clasificada en un nivel u otro.

A continuación se describen los cuatro niveles de algebrización propuestos por Godino, Ake, Gonzato, Wilhelmi (2012). Las definiciones se citan literalmente del texto referido.

• Ausencia del razonamiento algebraico (Nivel 0). Intervienen objetos extensivos (particulares) expresados mediante lenguajes natural, numérico, icónico o gestual. Pueden intervenir símbolos que refieren a un valor desconocido, pero dicho valor se obtiene como resultado de operaciones sobre objetos particulares. En tareas de generalización el mero reconocimiento de la regla recursiva que relaciona un término con el siguiente, en casos particulares, no es indicativa de generalización.

• Nivel incipiente de algebrización (Nivel 1). Intervienen objetos intensivos cuya generalidad se reconoce de manera explícita mediante lenguajes natural, numérico, icónico o gestual. Pueden intervenir símbolos que refieren a los intensivos reconocidos, pero sin operar con dichos objetos. En tareas estructurales se aplican relaciones y propiedades de las operaciones y pueden intervenir datos desconocidos expresados simbólicamente. En tareas funcionales se reconoce la generalidad aunque expresada en un lenguaje diferente al simbólico-literal.

• Nivel intermedio de algebrización (Nivel 2). Intervienen indeterminadas o variables expresadas con lenguaje simbólico – literal para referir a los intensivos reconocidos, aunque ligados a la información del contexto espacial temporal. En tareas estructurales las ecuaciones son de la forma Ax±B=C. En tareas funcionales se reconoce la generalidad, pero no se opera con las variables para obtener formas canónicas de expresión.

Estos niveles favorecen la atribución de niveles o grados de algebrización a tareas matemáticas escolares. Adicionalmente, pueden contribuir a sistematizar la introducción del razonamiento algebraico elemental desde los primeros niveles de la escolaridad. Esta sistematización apoya la propuesta de Kaput (2000) de algebrizar el currículo matemático escolar.

REFERENCIAS

Amit M., Neria D. (2008). Rising to the challenge: using generalization in pattern problems to unearth the algebraic skills of talented pre-algebra students. ZDM.

The International Journal on Mathematics Education, 40(1), 11-119.

Bass, H. (1998). Algebra with integrity and reality. In M. S. E. Board (Ed.), The nature and role of algebra in the K-14 curriculum: Proceedings of the National Research Council Symposium. Washington DC: National Research Council.

Blanton, M. L., and Kaput, J. (2005). Characterizing a classroom practice that promotes algebraic reasoning. Journal for Research in Mathematics Education, 36(5): 412-446.

Becker, J. R. and Rivera, F. D. (2008). Generalization in algebra: The foundation of algebraic thinking and reasoning across the grades. ZDM The international Journal on Mathematics Education, 40(1), 1.

Britt, M. and Irwin, K. (2008). Algebraic thinking with and without algebraic representation: a three-year longitudinal study. Zentralblatt fuer Didaktik der Mathematic, 40(1), 39-53.

Brizuela, B. M. and Earnest, E. (2008). Multiple notational systems and algebraic understandings: The case of the "Best Deal" problem. In J. J. Kaput, D. W. Carraher and M. L. Blanton (Eds.), Algebra in the early grades. New York: Routledge.

Burkhardt, H. (2001). Algebra for all: What does it mean? How are we doing? In H. Chick, K. Stacey, J. Vincent & J. Vincent (Eds.), The future of the teaching and learning of algebra (Vol. 1). Melbourne: University of Melbourne, Australia.

Cai, J. (2004). Developing algebraic thinking in the earlier grades: A case study of the chinese elementary school curriculum. The Mathematics Educator, 8(1), 107-130.

Carraher, D. W. and Schlieman, A. (2007). Early Algebra and Algebraic Reasoning. In F. Lester y K. Jr (Eds.), Second Handbook of Research on Mathematics Teaching and Learning (Vol. 2). NCTM.

Common Core State Standards Initiative. (2010). Common Core State Standards for mathematics. Access: December 2010. Available: http://www.corestandards.orgiassets/CCSSI_Math%20Standards.pdf

Davis, R. B. (1985). ICME-5 Report: Algebraic thinking in the early grades. Journal of Mathematical Behavior, 4, 195-208.

Derry, S. J., Wilsman, M. J. and Hackbarth, A. J. (2007). Using Constrasting Case Activities to Deepen Teacher Understanding of Algebraic Thinking and Teaching. Mathematical Thinking and Learning, 9(3), 305-329.

Godino, J; Castro, W.F; Ake Lilia y Wilhelmi, M. (2012). Naturaleza del Razonamiento Algebraico Elemental. Bolema (Boletín de Educación Matemática, Revista Brasileña), 26, (42B),559-588

Godino, J.D., Aké, L.P., Gonzato, M. y Wilhelmi, M.R. (2012). Niveles de razonamiento algebraico elemental. En A. Estepa, Á. Contreras, J. Deulofeu, M. C. Penalva, F. J. García y L. Ordóñez (Eds.), Investigación en Educación Matemática XVI. Jaén: SEIEM

Goldenberg, E. P. (1988). Mathematics, metaphors and human factors: Mathematical, technical and pedagogical challenges in the educational use of graphical representations of functions. Journal of Mathematical Behavior, 7, 135-173.

Joint Mathematical Council of the United Kingdom. (1996). Teaching and learning algebra pre-19. London: Royal Society/JMC Working Group.

Juraschek, B. and Angle, N. S. (1986). The binomial grid. Mathematics Teacher, 5, 337-339.

Kaput, J. (2000). Transforming algebra from an engine of inequity to an engine of mathematical power by algebrafying the K-12 curriculum: National Center of Improving Student Learning and Achievement in Mathematics and Science. Dartmouth, MA.

Kaput, J. (Ed.). (1998). Transforming algebra from an engine of inequity to an engine of mathematical power by algebrafying the K-12 curriculum. Washington D.C: National Academy Press.

Kieran, C. (1996). The changing face of school algebra. In C. Alsina, J. Alvarez, C. Hodgson, C. Laborde and A. Pérez (Eds.), 8 th International Congress on Mathematical Education: Selected lectures. Seville, Spain: S.A.E.M. Thales.

NCTM. (1998). Principles and standards in school mathematics: Discussion draft. Reston (Virginia): NCTM.

Rival, I. (1987). Picture puzzling:mathematicians are rediscovering the power of pictorial reasoning. Sciences, 27(1): 40-46.

Schifter, D., Monk, S., Russell, S. J. and Bastable, V. (2008). Early algebra: What does understanding the laws of arithmetic mean in the elementary grades? In J. Kaput, D. Carraher and M. Blanton (Eds.), Algebra in the early grades. Mahwah, NJ: Lawrence Erlbaum Associates.

Smith, J. B. (1996). Does an extra year make any difference? The impact of early access to algebra on long-term gains in mathematics achievement. Educational Evaluation and Policy Analysis, 18(2), 141-153.

Strother, S.A. (2011). Algebra knowledge in early elementary school supporting later mathematics ability. University of Louisville. Tesis Doctoral.

Stylianou, D. A. (2002). On the interaction of visualization and analysis: the negotiation of a visual representation in expert problem solving. Journal of Mathematical Behavior, 21, 303-317

Usiskin, Z. (1988). Conceptions of school algebra and uses of variables. In A. F. Coxford (Ed.), The Ideas of Algebra K-12,. Reston, VA: NCTM.