DOI:
https://doi.org/10.14483/23448393.11976Published:
2017-09-12Issue:
Vol. 22 No. 3 (2017): September - DecemberSection:
Complex SystemsAlgoritmo de Encriptación de Imágenes Utilizando el Atractor Caótico de Lorenz
Images Encryption Algorithm Using the Lorenz´s Chaotic Attractor
Keywords:
sincronización, caos, criptografía de imágenes, atractor de Lorenz (es).Keywords:
synchronization, chaos, images cryptography, Lorenz’s attractor. (en).References
Y. Yan, Song, Cryptanalytic Attacks on RSA. Springer US, 2008, pp. 91-110.
Louis M. Pecora y Thomas L. Carroll, “Synhronization in chaotic systems”. Physical Review Letters, Volumen 64, 8, 1990, pp. 821- 824.
Jian Zhang, An Image Encryption Scheme Based on Cat Map and Hyperchaotic Lorenz System. International Conference on Computational Intelligence & Communication Technology. IEEE. 2015.
Chong Fu, Wen Jing Li, Zhao-yu Meng, Tao Wang, Pei-xuan Li, A Symmetric Image Encryption Scheme Using Chaotic Baker map and Lorenz System, Ninth International Conference on Computational Intelligence and Security, IEEE 978-1-4799-2548-3/13. 2013.
Yulling Luo, Lvchen Cao, Senhui Qiu, Hui Lin, Jim Harkin, Junxlu Liu, “A Chaotic map- control-based and the image-related cryptosystem”. Nonlinear Dyn, Volumen 83 Springer, 2016. pp. 2293-2310.
Yannick Abanda & Alain Tiedeu, Image encryption by chaos mixing. Journal the Institution of Engineering and Technology IET.
Buhalqam Awdun, Guodong Li, “The Color Image Encryption Technology Based on DNA Encoding & Sine Chaos”.
International Conference on Smart City and Systems Engineering, 978-1-5090-5530-2/16 IEEE, 2016.
Guodong Ye, Haiqing Zhao, Huajin Chai, “Chaotic image encryption algorithm using wave-line permutation. and block diffusion”. Nonlinear Dyn, 83 Springer, 2016, pp. 2067–2077.
Jiangang Zhang, Li Zhang, Xinlei An, Hongwei Luo & Kutorzi Edwin Yao, “Adaptive Coupled Synchronization Among Three Coupled Chaos Systems and Its Application to Secure Communications”. EURASIP Journal on Wireless Communications and Networking V, 134, 2016.
Mariela Rodríguez, María González, Juan Estrada, Lúa Acosta y Octavio Florez, “Secure Point-To-Point Communication Using Chaos”. DYNA, [S.l.], v. 83, n. 197, p. 180-186, may, 2016.
Wang Zhen, Huang Xia, Li Yu-Xia and Song Xiao-Na, “A New Image Encryption Algorithm Based on The Fractional-Order Hyperchaotic Lorenz System”. Chin. Phys. B., vol. 13, no. 3, 2012, pp. 1441–1450.
H. Alsafasfeh and, Arfoa, “Image Encryption Based on the General Approach for Multiple Chaotic System”. Journal of Signal and Information Processing, vol. 2, no. 3, 2011, pp. 238-244.
L. Kocarev, “Chaos-based cryptography: A brief overview”. IEEE Circuits and Systems Magazine, 2001, 1(2): pp. 6-21.
Steven H. Strogatz, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering. Perseus Books, Reading, Estados Unidos, 1994, pp. 301-347.
José Moreno, Fabio Parra, Rafael Huérfano, César Suárez y Isabel Amaya, “Modelo de Encriptación Simétrica basada en atractores caóticos”. Ingeniería, Vol. 21 No. 3, 2016. pp. 378-390.
Guodong,Ye., K.W ,Wong, “An Efficient Chaotic Image Encryption Algorithm Based on a Generalized Arnold Map”. Nonlinear Dyn. 69 Springer, 2012, pp. 2079– 2087.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Images Encryption Algorithm Using the Lorenz’s Chaotic Attractor
Algoritmo de Encriptación de Imágenes Utilizando el Atractor Caótico de Lorenz
Hugo Ernesto Gutierrez Vanegas
TIVIT. Bogotá D.C. - Colombia,
hugoegutierrezv@gmail.com
Miguel Alberto Melgarejo Rey
Universidad Distrital Francisco José de Caldas, LAMIC. Bogotá D.C. - Colombia,
mmelgarejo@udistrital.edu.co
Recibido: 30/01/2017. Modificado: 17/06/2017. Aceptado: 31/07/2017.
Abstract
Context: With the increasing volumes of information generated in real time, novel mechanisms area needed to ensure security so as to prevent access to unauthorized people. The conventional encryption methods are not appropriate for images, because they are prone to statistical attacks due to the strong correlation between adjacent pixels and the analysis of color gamut histograms, which can help to identify them within the image; with this aim in mind, in this paper an algorithm for image encryption using chaotic attractors is proposed.
Method: Chaotic synchronization is used for the key management, the diffusion stage is made by means of ergodic sequences generated from the numerical solution of the Lorenz’s attractor and the permutation stage is accomplished with the wave line technique.
Results: The proposed algorithm was tested using a set of gray-scale images obtaining suitable performance in segurity and speed, the pixel correlation is almost null and the entropy is similar to that presented in recent works with the same approach
Conclusions: Chaotic methods are an alternative to improve the security levels in the cryptography of images due to their properties of unpredictability and sensitivity to the initial conditions. For future work the approach presented could be applied to the encryption of color images and using different chaotic attractors.
Keywords:Synchronization, chaos, images cryptography, Lorenz’s attractor..
Language: Spanish
Resumen
Contexto: Con el creciente volumen de información generada en tiempo real, nuevos mecanismos son necesarios para garantizar su seguridad, evitando el acceso a personas no autorizadas. Los métodos convencionales de criptografía no son apropiados para imágenes por su debilidad a ataques estadísticos, debido a la fuerte correlación entre píxeles adyacentes y el análisis de los histogramas de gamas de colores, lo que puede ayudar a identificarlos dentro de la imagen; con este objetivo en mente, se propone un algoritmo para el cifrado de imágenes utilizando atractores caóticos.
Método: La sincronización caótica se utiliza para la gestión de la clave, la etapa de difusión se realiza mediante secuencias ergódicas generadas a partir de la solución numérica del atractor de Lorenz y la etapa de permutación se realiza con la técnica de línea de onda.
Resultados: Se probó el algoritmo propuesto utilizando un conjunto de imágenes en escala de grises, obteniendo un desempeño adecuado en seguridad y velocidad, la correlación de píxeles es casi nula y la entropía es similar a la presentada en trabajos recientes con el mismo enfoque.
Conclusiones: Los métodos caóticos son una buena alternativa para mejorar los niveles de seguridad en la criptografía de imágenes debido a sus propiedades de imprevisibilidad y sensibilidad a las condiciones iniciales. Para trabajos futuros el enfoque presentado podría aplicarse a la encriptación de imágenes a color y utilizando diferentes atractores caóticos.
Palabras clave: Atractor de Lorenz, Caos, Criptografía de imágenes, Sincronización.
Idioma: Español
1. Introduction
La transferencia de información de manera segura es una prioridad que exige el interés de las comunidades académicas interesadas en el área de la criptografía para explorar, diseñar y proponer esquemas de seguridad eficientes. Desde hace décadas existen diferentes técnicas de cifrado que se basan principalmente en métodos iterativos y en la factorización de números primos. La seguridad de estos métodos se encuentra soportada en que no existen procedimientos computacionalmente eficientes para factorizar números de gran cantidad de dígitos; particularmente se dificulta la factorización cuando el número a factorizar es el producto de dos números primos de aproximadamente la misma cantidad de dígitos. Sin embargo, con el desarrollo acelerado de la computación es posible que pronto puedan ser vulnerables este tipo de criptosistemas [1].
Motivados por esta posible vulnerabilidad, una alternativa para encriptar imágenes es utilizar los sistemas dinámicos que generan caos, ya que las propiedades de dependencia sensitiva a las condiciones iniciales, mezcla y ergodicidad se pueden aprovechar para garantizar la no predictibilidad de los mecanismos de seguridad.
Por lo general, en los esquemas de comunicación caótica que utilizan sincronización se toma un sistema caótico como transmisor y la señal de información se mezcla con el transmisor para generar una señal de transmisión caótica, la cual se transmite al receptor. El mecanismo receptor es básicamente un sistema dinámico caótico construido sobre la base de la estructura del transmisor. Cuando los mecanismos transmisor y receptor se sincronizan la información es recuperada por el receptor [2]. Recientemente, se han publicado diferentes propuestas que utilizan este enfoque, algunas de las cuales se analizan a continuación.
En [3] se propone un esquema de encriptación de imágenes, utilizando la función cat de Arnold para el proceso de permutación y un sistema hipercaótico de Lorenz para el proceso de difusión. Los autores hacen un análisis Marco teórico estadístico de seguridad que involucra la longitud y la sensibilidad de la clave, lo cual les permite asegurar el buen nivel de seguridad de su propuesta. Además, en el artículo se resalta el potencial de los sistemas hipercaótico para mejorar la seguridad de los criptosistemas basados en caos; porque comparándolos con sistemas caóticos de un número menor de dimensiones tienen un comportamiento dinámico más complejo y manejan un mayor número de variables. Lo anterior permite inferir que los criptosistemas basados en sistemas hipercaóticos son más impredecibles y con un espacio de claves más amplio.
En el año 2013 se desarrolló un sistema de encriptación simétrica para imágenes basado en caos, utilizando para el proceso de difusión el atractor caótico de Lorenz y para el proceso de permutación la función del panadero. Los autores hacen un análisis estadístico del desempeño de seguridad del algoritmo propuesto, mostrando una alta seguridad en su esquema [4].
En [5] se presenta un algoritmo de encriptación de imágenes utilizando el sistema caótico provisto por la función tienda para los procesos de difusión y permutación. Al analizar los histogramas de escala de grises de las imágenes real y cifrada, la distribución uniforme que presenta el histograma de la imagen cifrada permite garantizar una buena seguridad del algoritmo. Además, mediante el cálculo de los coeficientes de correlación entre píxeles adyacentes, se evidencia que estos tienden a 1, para los píxeles de la imagen original y a 0 para los píxeles correspondientes a la imagen cifra- da; lo anterior significa que se logra eliminar la correlación entre los pixeles adyacentes durante el proceso de cifrado.
En [6] se propone un esquema de encriptación de imágenes en escala de grises y a color de tipo simétrico utilizando los atractores caóticos provistos por el sistema autónomo de Colpitts y el sistema no autónomo de Duffing, los cuales son resueltos por medio del método numérico para la solución de ecuaciones diferenciales Runge Kutta 4 y aprovechados para generar una matriz del tamaño de la imagen original. Por medio de esta matriz, se cifra cada uno de los píxeles de la imagen original; la clave secreta está construida por los valores de las condiciones iniciales de los dos sistemas utilizados. Los autores realizan análisis de espacio de clave, análisis de sensibilidad de la clave e histograma de la imagen cifrada; el espacio de clave utilizado es 2448 = 7,26*1013 y el histograma de escala de grises de la imagen cifrada presenta una distribución uniforme. También hacen un análisis de correlación entre los coeficientes de pixeles adyacentes en las direcciones horizontal, vertical y diagonal para varias imágenes encriptadas encontrando que estos tienden a cero. Los resultados experimentales muestran la robustez, eficiencia y el buen nivel de seguridad del algoritmo.
En el trabajo desarrollado en [7], se presenta un algoritmo que fusiona un atractor caótico provisto por una función senoidal con algunos principios de la codificación genética. Los autores indican que, si utilizan únicamente el atractor caótico, el algoritmo es sencillo pero débil en seguridad y genera distorsión de la imagen. Separan la imagen en tres capas de color: verde, azul y roja; utilizando los principios del caos y de la genética, codifican cada capa de manera independiente en base decimal, base binaria y en código ADN (código generado a partir de principios de la genética), obteniendo tres matrices, una por cada color, que luego adicionan según las reglas del código ADN con tres matrices que generan de aplicar la función caótica senoidal sobre las matrices anteriores, Como se ejecutan tres procesos independientes utilizan programación paralela para reducir el tiempo de ejecución. El algoritmo permite obtener una imagen cifrada con muy baja correlación entre píxeles adyacentes y demuestra ser eficiente para la encriptación de archivos de gran volumen debido al uso de la programación paralela.
En el año 2015 en [8], los autores diseñan un esquema de codificación de imágenes en escala de grises basado en un proceso de permutación vertical y horizontal en forma circular utilizando la función de Arnold con parámetros positivos e implementan la función hash SHA-3 para el proceso de difusión. Realizan un análisis de sensibilidad aplicado a las claves, un análisis estadístico y análisis de aleatoriedad mediante el test NIST 800-22. Concluyen que el algoritmo tiene un buen rendimiento en procesamiento y una capacidad de resistir a ataques como el ataque de texto elegido.
En [9] los autores proponen un método adaptable de sincronización acoplando tres sistemas caóticos idénticos y muestran mediante dos ejemplos que el acoplamiento puede ser unidireccional o bidireccional. Para mostrar la sincronización con acoplamiento unidireccional consideran tres sistemas caóticos de Rössler y utilizan tres sistemas caóticos de Lorenz para mostrar la sincronización con acoplamiento bidireccional. Basados en esta nueva forma de sincronización proponen un método de encriptación caótica diferente a los criptosistemas tradicionales; empleando tres sistemas caóticos para el proceso de la sincronización y encriptación, utilizando dos sistemas caóticos emisores que se encargan de la encriptación y el tercer sistema caótico como receptor para desencriptar; la idea básica que sustentan es que después de cifrar dos veces en dos transmisores y un receptor, el receptor puede recuperar de manera fidedigna la señal enviada.
En [10] se presenta una alternativa para resolver una vulnerabilidad existente en los sistemas de enmascaramiento caóticos mediante el proceso de sincronización de atractores caóticos. El sistema evita la detección de parámetros utilizando dos claves de cifrado que se emplean para la modificación continua de las condiciones iniciales del atractor de Rössler. El autor destaca su técnica mostrando resistencia a ataques estadísticos y evitando que el atacante obtenga los valores iniciales de los atractores.
En el trabajo propuesto en [11], se utiliza el sistema de Lorenz hipercaótico de orden fraccional, que es un sistema que maneja cuatro componentes , empleando una de estas para generar una máscara caótica, del tamaño de la imagen que se desea cifrar, la cual utilizan para enmascarar la imagen mediante la operación OR, entre cada uno de los valores de las posiciones de la máscara y de la imagen; las demás componentes las utilizan para generar una sucesión caótica, que permite reordenar la matriz difundida y finalmente obtener la imagen cifrada, como resultados destacan la simpleza del procedimiento de enmascaramiento, también la mejora del desempeño en cuanto a seguridad.
En [12] se propone una técnica de cifrado de imágenes, en escala de grises, basada en un sistema caótico múltiple que es el resultado de la suma de los sistemas caóticos de Rössler y Lorenz. El esquema de encriptación propuesto consiste en un algoritmo iterativo que mezcla los valores de los píxeles mediante operaciones XOR y cambia los valores de la escala de grises usando el sistema caótico múltiple. Mediante los resultados de las pruebas se puede apreciar que las bondades de esta propuesta son: buen nivel de seguridad, gran espacio de clave y un algoritmo con alta velocidad de ejecución.
En el presente artículo se propone el desarrollo de un algoritmo de encriptación de imágenes en escala de grises aprovechando las características de sincronización del sistema caótico de Lorenz. El artículo está organizado de la siguiente forma: en la sección 2, se presentan los fundamentos teóricos sobre sistemas caóticos y la sincronización de estos. En la sección 3, se describe y se implementa el algoritmo propuesto que involucra los procesos de sincronización, permutación y difusión utilizando el atractor caótico de Lorenz y se presentan las pruebas realizadas con diferentes imágenes clásicas. En la sección 4, se hace el análisis estadístico de desempeño y se compara con los algoritmos propuestos en [5] y [8]. Finalmente, se resaltan las conclusiones y se dan algunas indicaciones para trabajos futuros en esta misma dirección.
2. Marco Teórico
El área de los sistemas dinámicos surge del intento de estudiar el comportamiento de un sistema que evoluciona en el tiempo, tiene aplicación en diferentes campos del conocimiento tales como biología, medicina e ingeniería. Los sistemas dinámicos de tipo no lineal son los que pue- den presentan comportamientos complejos, lo cual los hace atractivos para utilizarlos en sistemas criptográficos, buscando aumentar su seguridad. La seguridad de la información secreta que se transmita a través de la red es algo imperante en la actualidad, ya que se debe impedir que personas no autorizadas modifiquen o accedan a la información. Se han propuesto varios trabajos en este sentido, inicialmente utilizando sistemas dinámicos caóticos unidimensionales, los cuales posibilitan generar algoritmos sencillos pero un poco lentos y débiles contra ataques, situación que ha hecho fortalecer la línea de trabajo mediante el uso de sistemas dinámicos de más de una dimensión [13]
2.1. Sistema caótico de Lorenz
La teoría del caos surge con el estudio de los sistemas dinámicos de tipo no lineal que se modelan por medio de ecuaciones diferenciales en el caso continuo y ecuaciones en diferencias finitas en el caso discreto; es de gran utilidad tanto a nivel de la matemática como en el ámbito de las aplicaciones a otra áreas del conocimiento, ya que generalmente son impredecibles, presentan una dependencia sensible a las condiciones iniciales, es decir, que para dos condiciones iniciales próximas, se genera un comportamiento dinámico totalmente diferente. Además, suelen presentar atractores extraños que involucran propiedades de auto similitud, generando imágenes con naturaleza fractal, lo cual permite obtener técnicas para disminuir la correlación entre los pixeles adyacentes en el cifrado de imágenes [14].
Una de las razones que dio origen al estudio cualitativo de los sistemas dinámicos tiene que ver con el problema de Lorenz, quien formulo´ un modelo tridimensional para realizar predicciones climáticas, y se dio cuenta que si este se alimentaba de la observación anterior aplicando un pro- ceso de redondeo de cifras, aunque inicialmente se comportaba de forma similar, rápidamente se empezaban a trazar trayectorias totalmente diferentes a las generadas sin aplicar ningún redondeo, lo que mostraba resultados erróneos en el momento de hacer predicciones.
En la literatura matemática se han mostrado y caracterizado varios sistemas dinámicos caóticos. En la ecuación (1) se describe el modelo formulado por Lorenz:
Donde, (x, y, z) describen una condición atmosférica, σ, b y r, son parámetros. Este sistema describe un comportamiento caótico para varios valores de los parámetros, los más utilizados han sido σ = 10, b = 8/3 y r = 28.
2.2. Sincronización
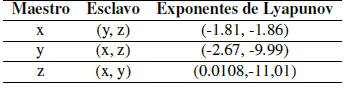
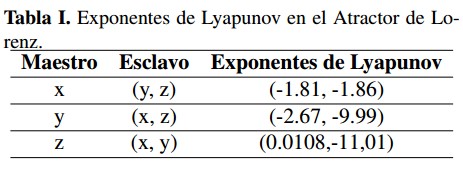
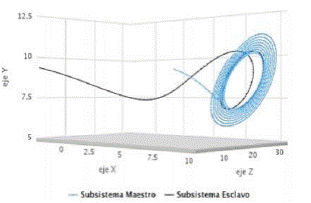
Consiste en enlazar dos sistemas caóticos mediante una o varias señales comunes para obligar a que sus trayectorias a largo plazo converjan a los mismos valores. El tipo de sincronización que se utiliza en este trabajo es unidireccional, propuesto por Pecora y Carrol [2], que consiste en dividir el sistema caótico en dos subsistemas denominados maestro y esclavo, el maestro conduce al sistema esclavo a seguir su trayectoria. Una de las condiciones para que se presente este tipo de sincronización es que los exponentes de Lyapunov de los subsistemas a sincronizar sean negativos, este hecho provee la estabilidad en el sistema esclavo. Una de las razones por las cuales se utiliza la sincronización para la seguridad de la información que se transmite en la red es la facilidad que ofrece para cifrar y descifrar la información, cuyo cifrado se basa en el comportamiento impredecible de los sistemas caóticos. Para el caso de estudio alusivo al sistema de Lorenz con los parámetros anteriormente mencionados, Pecora y Carrol calcularon los exponentes de Lyapunov encontrando que estos son negativos cuando se seleccionan como maestro las componentes x o y, como se muestra en la Tabla I.
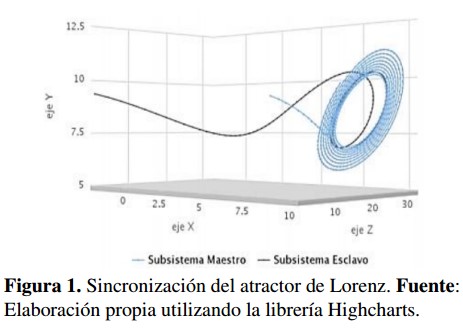
Se puede verificar que cuando se elige x o y como variable sincronizante los dos subsistemas se sincronizan, como se muestra en la Figura 1, siendo la línea negra la trayectoria del subsistema esclavo y la línea azul la trayectoria del subsistema maestro.
El mecanismo de sincronización en el algoritmo que se propone se utiliza para encriptar la clave que se envía al receptor, considerando el sistema caótico de Lorenz y dos subsistemas de este y utilizando “y” como variable sincronizante, a través de la cual se envía la clave que permitirá desencriptar la imagen [15].
3. Esquema de encriptación propuesto
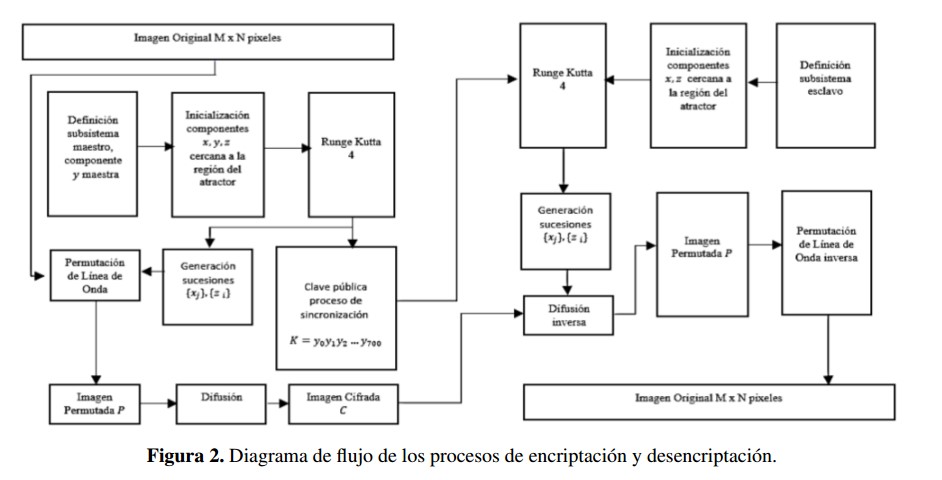
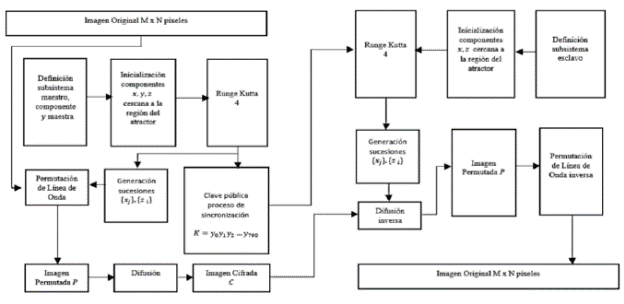
Se presenta un algoritmo para encriptación de imágenes en escala de grises, de tamaño M X N píxeles. El proceso de permutación se realiza mediante la permutación de línea de onda y para el proceso de difusión se utilizan sucesiones ergódicas generadas a partir de la solución numérica del atractor caótico de Lorenz, utilizando el método Runge Kutta 4. El diagrama de flujo del algoritmo se presenta en la Figura 2.
Las fases del proceso de encriptación comprenden los siguientes pasos:
- El atractor de Lorenz se divide en dos subsistemas maestro y esclavo, utilizando como variable sincronizante ”y”, debido a que sus exponentes de Lyapunov son los más negativos, recordando que entre más negativos sean estos, más rápida será´ la convergencia.
- Se inicializan los subsistemas con condiciones iniciales aleatorias que estén cercanas a la región del atractor.
- Se sincronizan los atractores enviando la componente maestra hacia el esclavo. Se generan los 700 primeros valores del atractor maestro utilizando Runge Kutta 4 con un incremento de tiempo h = 0,01 (centésimas de segundo) y se env´ıan los resultados de la componente “y” como clave pública K hacia el atractor esclavo en el instante de tiempo ti, como se indica en la ecuación (2).
Donde yi corresponde a la salida del atractor en valor absoluto, considerando solamente una cifra decimal multiplicada por 10 en el instante de tiempo tj definido por la ecuación (3).
Se debe actualizar ti a tj, debido a que cada vez que se codifica un mensaje, existe un corrimiento de (M + N ) h unidades de tiempo, con el fin de no perder la sincronía entre los subsistemas maestros y esclavo, como se muestra en la ecuación (4).
- Se utiliza el proceso de permutación de línea de onda [16], primero se construyen dos sucesiones (xj) y (zi), i = 1, . . . , N , y j = 1, . . . M , a partir de los valores obtenidos para las variables x, z del atractor, mediante método numérico Runge Kutta 4; se consideran los últimos tres dígitos de dichos valores y se utiliza una matriz de M X N que tiene en cada una de sus posiciones los valores en escala de gris de la imagen original. El valor xj se asocia con la columna j de la matriz, e indica el número de posiciones que se deben desplazar las entradas de esa columna “verticalmente”, consiguiendo una nueva matriz, luego, la fila i de esta última matriz se asocia con el valor zi el cual indica las posiciones que se deben desplazar sus entradas “horizontalmente”, obteniéndose otra matriz y finalizando un ciclo de permutación. El desplazamiento horizontal de las entradas de la fila i es hacia la derecha si zi es menor que el umbral (M/2) y el desplazamiento vertical de las entradas de la columna j es hacia abajo si xj es menor que N/2. El proceso anterior se ejecuta cuatro veces para completar la fase de permutación que se conoce como permutación circular [8], obteniendo la matriz permutada P.
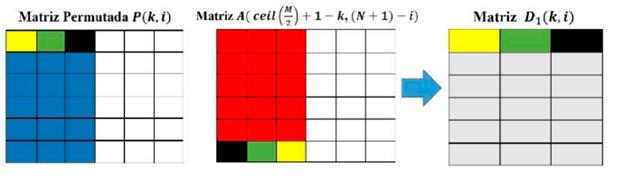
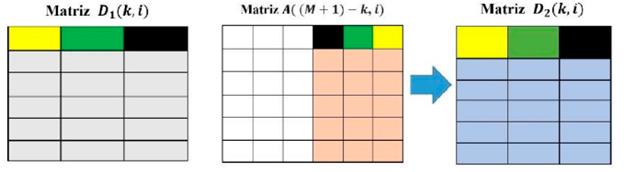
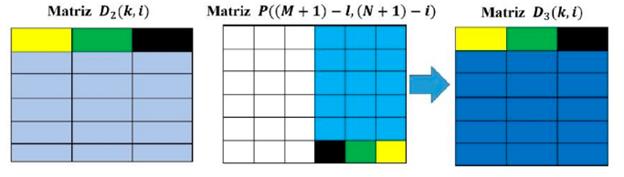
- Con los datos obtenidos por Runge Kutta 4, para los componentes z y x del atractor, se genera una matriz de A de tamaño M X N, considerando los valores numéricos obtenidos de los últimos tres dígitos, la cual se suma con la matriz obtenida en el ítem 4, luego se aplica la operación módulo 256 a cada entrada de la matriz resultante, como se ilustra en la Figuras 3, 4 y 5.
Siendo P (k, i) el valor que va de 0 a 256 en la posición (k, i) de la matriz que resulta del proceso completo de permutación de línea de onda, las matrices D1 , D2 ,D3 se obtienen de acuerdo con las ecuaciones (5),(6) y (7).
Con i = 1, 2, . . . , N ; l = 1, 2, . . . , floor ( M/L ); k = 1, 2, . . . , ceil ( M/K ), donde floor( M/L) representa el mayor número entero menor o igual que el número racional M/L y ceil( M/L ) representa el menor número entero mayor o igual que el número racional M.
Como primer paso se toma una parte de la matriz A, de tamaño ceil( M/L )XN y también una parte de la matriz permutada P de tamaño ceil( M/2 )×N, asociando, como se ve en la Figura 1, los colores con la posición en la que los valores de ambas matrices se operan, como se muestra en la en la ecuación (1), generando la matriz D1.
Para el segundo paso se toma la matriz D1 y una segunda parte de la matriz A de tamaño ceil( M/L ) X N , asociando, como se ve en la Figura 2, los colores con la posición de los valores de ambas matrices, describiendo la forma en que operará la difusión representada en la ecuación (2), generando la matriz D2.
En el tercer paso, se utiliza una parte de la matriz D2 de tamaño floor( M/L ) X N , y una segunda parte de la matriz permutada P de tamaño floor( M/L ) X N , cuyo proceso se ilustra en la Figura 3, de manera similar al paso anterior la Figura 3 asocia los colores con la posición de los valores a los que se les se aplicará la difusión descrita en la ecuación (3), generando la matriz D3.
Por último, se concatenan las matrices D2 y D3, es decir todas las filas de la matriz D2 se unen a las filas de la matriz D3 en su respectivo orden, dejando una única matriz C correspondiente a la imagen cifrada.
El proceso descrito anteriormente mejora la aleatoriedad de la imagen cifrada C, es decir, si todos los colores en escala de grises en la imagen cifrada C tienden repetirse un número igual o cercano a (M X N )/256 veces el grado de incertidumbre aumenta y por ende la impredecibilidad de la imagen cifrada.
En el desarrollo del esquema de encriptación se tuvo en cuenta la relación existente entre los procesos de permutación y difusión; por ejemplo, el proceso de difusión descrito en [5] des- taca por su simpleza, pero su proceso de permutación es más complejo, lo cual exige mayores recursos computacionales, pero ofrece resultados interesantes en cuanto a la aleatoriedad en su cifrado; en [8] el proceso de difusión utiliza más recursos y el de permutación en este caso es el proceso sencillo, sin embargo tiene menor aleatoriedad en las imágenes cifradas que en [5]; por lo tanto tener un buen desarrollo en la permutación contribuye en gran medida al proceso de difusión para aumentar la aleatoriedad de las imágenes cifradas, razón por la cual en este trabajo se realizan más rondas de permutación que en [8], adicionalmente se buscó un mejor desarrollo en la fase de difusión sin utilizar demasiados recursos en ambas fases.
La adición de una permutación simple que se le aplica a la matriz A, utilizada para difundir, permite a la imagen cifrada C no poseer patrones reconocibles, como grupos de píxeles cercanos con colores que tengan similar valor o valores con diferencias muy grandes. Similar estrategia se puede evidenciar en [8] con la matriz utilizada para difundir, la cual se construye con valores que se obtienen iterando el mapa de Arnold, consiguiendo completar la matriz en (M×N )/2 iteraciones si M × N es par o ceil((M×N)/2 ) iteraciones si M × N es impar, tomando dichos valores de las componentes del sistema de Arnold e intercalándolos en la matriz, teniendo efectividad en disolver patrones reconocibles en la imagen cifrada ; en [11], la estrategia es más simple ya que utilizan M X N iteraciones para generar una matriz, solo con los valores de una única componente del sistema caótico, que permite difundir mediante la operación OR, resultando en un desempeño menor a [8]; en [12] el proceso es más complejo que en [11] para la generación de la matriz, aquí utilizan una matriz de M X N que repetidas veces se opera con la matriz que representa a la imagen original mediante la operación XOR hasta conseguir la imagen cifrada, resultando en un buen desempeño.
Hay que destacar la importancia de realizar tratamiento a la matriz A, por su implicación en la reducción de patrones, es decir , lo que se busca en esta matriz es que sea lo suficientemente aleatoria; por ejemplo, en [5] optan por evitar tomar algunos de valores generados por el sistema caótico para obtener dichas matrices, en otros casos como en [8], [11] y [12], iteran muchas veces para obtener dichos valores, esto quiere decir que utilizan bastantes recursos para mejorar la aleatoriedad de la matriz y del sistema en general; en el esquema propuesto no se requieren muchas iteraciones, ya que particularmente el sistema de Lorenz es suficientemente aleatorio; en este caso se utilizan M + N valores para generar la matriz A y se realizan M iteraciones, una ventaja, ya que si existiesen aproximaciones y un número alto de iteraciones, la degradación dinámica puede dañar el comportamiento caótico del sistema.
Para el proceso de desencriptación se aplican los pasos 4 y 5 en forma inversa.
Para verificar la funcionalidad del algoritmo se realizaron varias pruebas con diferentes imágenes, tomadas de las referencias consultadas, algunas de estas se muestran en las Figuras 6,7,8 y 9.
En las Figuras 6,7,8 y 9 se evidencia el buen funcionamiento del algoritmo para encriptar y desencriptar imágenes; las imágenes decodificadas son iguales a las originales.
4. Resultados
Se presenta aquí los resultados del estudio comparativo de clasificación de avance de proyectos mediante ANN y SVM en los escenarios generados a partir de la base de datos.
4. Análisis estadístico
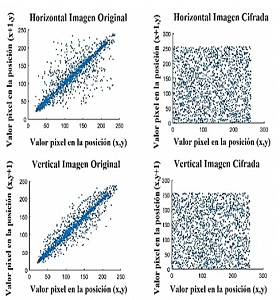
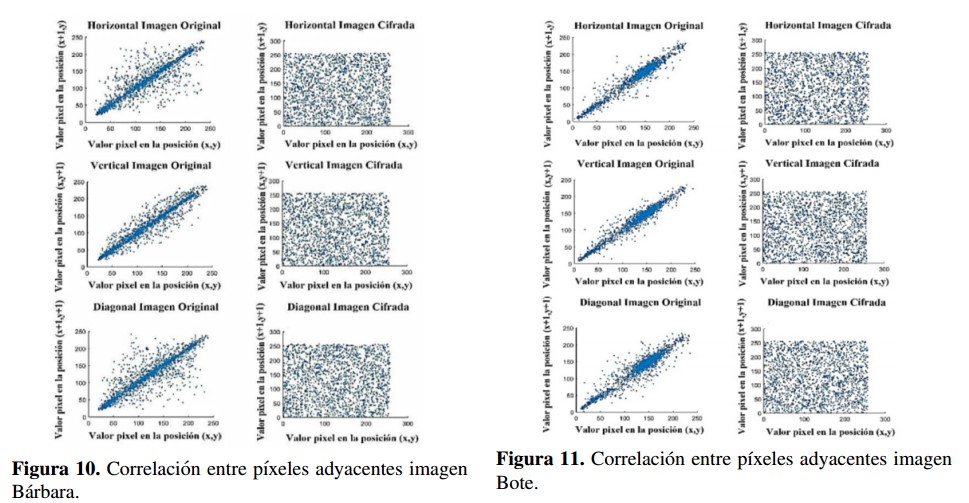
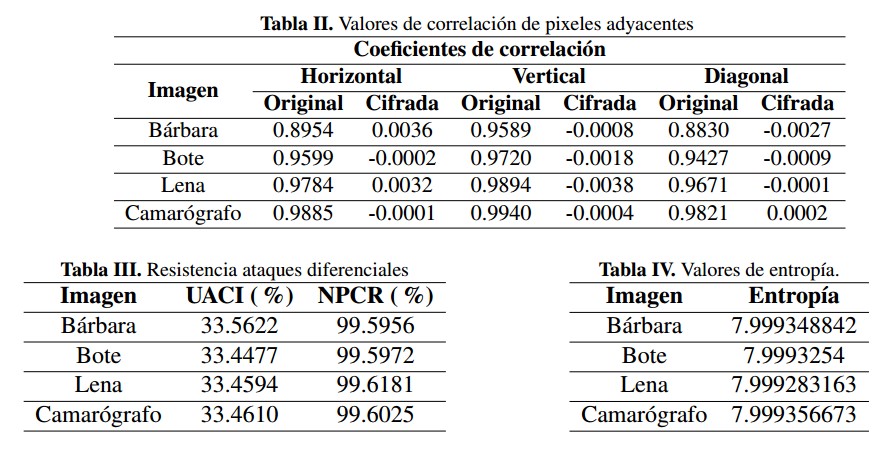
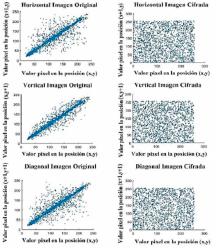
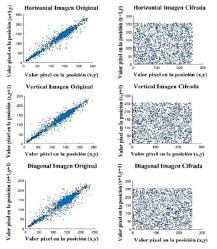
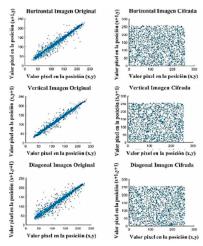
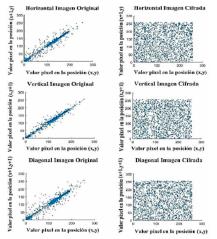
Para evaluar el desempeño del algoritmo propuesto se analizó la correlación entre los pixeles adyacentes en forma horizontal, vertical y diagonal, tanto para la imagen original como para la cifrada, obteniendo que la correlación tiende a desaparecer en la encriptación, como se muestra en las las Figuras 10, 11,12 y 13
A continuación, se presenta el análisis de sensibilidad del proceso de encriptación frente al cambio de un único bit de la imagen original en las Figuras 14 y 15, y el cambio de un único bit en la condición inicial del sistema de Lorenz en la componente ”x”, es un numero de 15 dígitos entre 0 y 1; en las figuras Figuras 16 y 17, evidenciando una imagen cifrada totalmente diferente.
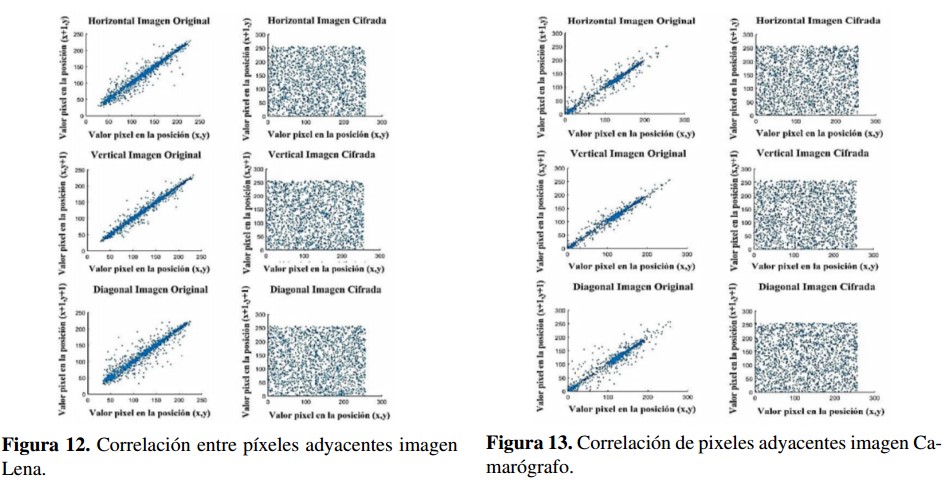
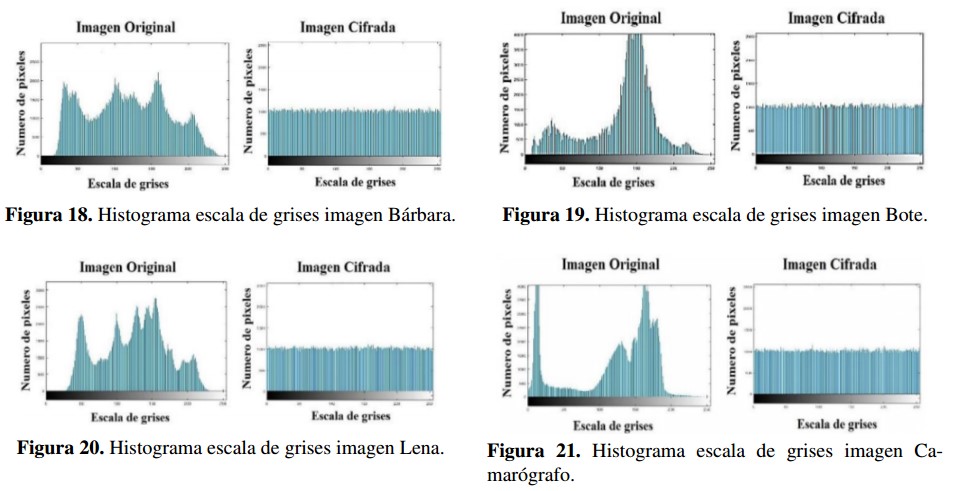
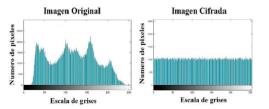
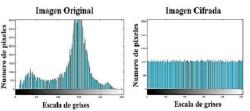
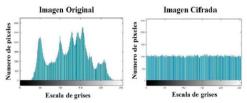
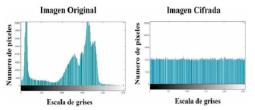
En las Figuras 18, 19, 20 y 21 se muestran los histogramas de la distribución de la escala de grises en la imagen original comparada con la imagen cifrada encontrando uniformidad en la imagen cifrada; donde se pueden resaltar las distribuciones uniformes presentes en los histogramas de las imágenes cifradas.
Para las cuatro imágenes presentadas se hallaron los coeficientes de correlación agrupados en la Tabla II, las medidas que evalúan la resistencia a ataques diferenciales UACI (promedio unificado de intensidad de cambio, sus siglas en ingles) y NPCR (razón de cambio de pixeles, sus siglas en inglés), además de la entropía correspondiente, los cuales se presentan en las TablaS III y IV. La expresión matemática para UACI esta´ dada por la ecuación (9).
Siendo M X N el tamaño de la imagen, E1(i,j) el valor del pixel en la posición del (i, j) de la imagen cifrada E1 y E2(i,j) el valor del pixel en la posición del (i, j) de la imagen cifrada E2, donde la imagen E1 corresponde al cifrado de la imagen original sin modificaciones y E2 corresponde al cifrado de la imagen original modificada en un pixel o también en la modificación de un bit en la condición inicial y 2n es el valor máximo que puede tomar cada pixel.
La fórmula que define NPCR esta´ dada en la ecuación (10).
Siendo, p0 la probabilidad de que un pixel (i, j) en la imagen cifrada C1 , sea igual al pixel (i, j) en la imagen C2 y p1 la probabilidad de que un pixel en la imagen cifrada C1(i, j), sea diferente al pixel (i, j) de la imagen cifrada C2, es decir son las probabilidades de obtener 0 o 1, respectivamente en la distribución de probabilidad D(i, j).
El valor de la entropía es un indicador muy importante, ya que muestra el nivel de aleatoriedad de los pixeles en las imágenes cifradas, lo cual significa que entre mayor sea el valor de la entropía la aleatoriedad es mejor. Para las imagines en estudio se logró obtener valores muy próximos a 8 calculado por:
donde N es la cantidad de símbolos, en este caso la cantidad de valores en escala de grises y P(si) la probabilidad de ocurrencia del símbolo si , si la probabilidad de ocurrencia de todos los símbolos es de 1/256 el valor de la entropía es de 8; luego este es el valor ideal de entropía en los procesos de encriptación de imagines cuando se trabaja con 256 tonalidades de grises.
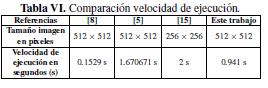
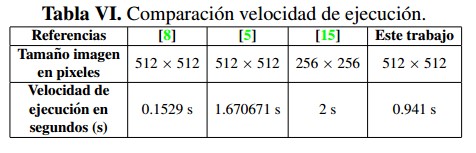
El algoritmo propuesto se ejecutó´ en un equipo Intel(R) Core(TM) i5-2410M, 2.30GHz CPU; los resultados de su desempeño y la comparación con los resultados obtenidos en [5], [8] y [15] se resumen en las Tablas V y VI; como se puede ver el algoritmo propuesto presenta desempeños muy similares a los presentados en las referencias consideradas en los indicadores UACI, NPCR y la entropía, logra mejores coeficientes de correlación entre píxeles adyacentes y un buen desempeño en velocidad de ejecución. Sin embargo en cuanto a indicadores como el UACI y NPCR es difícil saber cuál trabajo es más seguro, si bien se busca que el NPCR tienda a 100 %, es decir, que no exista ningún pixel con el mismo valor en la misma posición para dos imagines cifradas, es más difícil acercarse a dicho valor ideal a medida que las imágenes son más grandes; para el UACI que evalúa que tan diferente son dos imágenes cifradas, no es lógico pensar que este valor tenga que ser muy grande ya que se perdería desempeño en la entropía, o que sea muy pequeño puesto que las imágenes cifradas no serían lo suficientemente diferentes la una de la otra.
En la Tablas V, en los coeficientes de correlación, se puede observar que la referencia [8] presenta un mejor desempeño que la referencia [5], ya que a pesar de presentar correlaciones positivas mayores en las imágenes originales logra menores valores de correlaciones vertical y horizontal de las imágenes cifradas. La razón del mejor desempeño de la referencia [8] se puede atribuir a su buen proceso de permutación, tener un proceso de difusión iterativo e incorporar mayor aleatoriedad a la máscara que se utilizan para difundir la imagen permutada. En el caso de la entropía, la referencia [5] posee mejor desempeño que la [8], que segura- mente se debe al uso de un proceso de permutación más complejo, puesto que en [5] el trabajo para la obtención de las sucesiones caóticas es bastante exhaustivo.
En este trabajo se buscó equilibrio entre seguridad y velocidad de ejecución, es decir, lograr un algoritmo con buen nivel de seguridad sin perder velocidad de ejecución.
6. Conclusiones
La propiedad de no predictibilidad generada por el sistema de Lorenz fue aprovechada para generar un sistema de encripta miento eficiente, el cual, como lo demuestra el análisis estadístico, evidencia una alta resistencia a ataques estadísticos conservando un alto nivel de entropía, sin la necesidad de mantener un constante cambio de las condiciones iniciales del atractor. Esto significa un uso eficiente de las propiedades de sincronización y entropía del sistema caótico de Lorenz.
El uso inapropiado de los parámetros mostrados en este artículo puede generar una codificación no adecuada de la imagen. Al usar un incremento de tiempo muy pequeño del atractor, la variabilidad del estado anterior y siguiente no es significativa, volviendo el sistema vulnerable a ataques estadísticos; así, el atractor debe tener incrementos de tiempo grandes para generar mayor entropía.
Aunque en el presente trabajo se utiliza únicamente el atractor de Lorenz, para trabajos futuros se sugiere explorar con otros atractores caóticos buscando obtener mejores medidas de desempeño y con mayor espacio de clave. Por otra parte, el algoritmo presentado está diseñado para codificar imágenes en escala de grises, se espera que el trabajo desarrollado en este artículo pueda contribuir en el desarrollo de algoritmos para codificar imágenes a color.
References
[1] Y. Yan, Song, Cryptanalytic Attacks on RSA. Springer US, 2008, pp. 91-110. 397
[2] Louis M. Pecora y Thomas L. Carroll, “Synhronization in chaotic systems”. Physical Review Letters, Volumen 64, 8, 1990, pp. 821- 824. 397, 401
[3] Jian Zhang, An Image Encryption Scheme Based on Cat Map and Hyperchaotic Lorenz System. International Conference on Computational Intelligence & Communication Technology. IEEE. 2015. 398
[4] Chong Fu, Wen Jing Li, Zhao-yu Meng, Tao Wang, Pei-xuan Li, A Symmetric Image Encryption Scheme Using Chaotic Baker map and Lorenz System, Ninth International Conference on Computational Intelligence and Secu- rity, IEEE 978-1-4799-2548-3/13. 2013. 398
[5] Yulling Luo, Lvchen Cao, Senhui Qiu, Hui Lin, Jim Harkin, Junxlu Liu, “A Chaotic map- control-based and the image-related cryptosystem”. Nonlinear Dyn, Volumen 83 Springer, 2016. pp. 2293-2310. 398, 400, 405, 410
[6] Yannick Abanda & Alain Tiedeu, Image encryption by chaos mixing. Journal the Institution of Engineering and Technology IET. 398
[7] Buhalqam Awdun, Guodong Li, “The Color Image Encryption Technology Based on DNA Encoding & Sine Chaos”. International Conference on Smart City and Systems Engineering, 978-1-5090-5530-2/16 IEEE, 2016. 398
[8] Guodong Ye, Haiqing Zhao, Huajin Chai, “Chaotic image encryption algorithm using wave-line permutation. and block diffusion”. Nonlinear Dyn, 83 Springer, 2016, pp. 2067–2077. ↑ 399, 400, 403, 405, 410
[9] Jiangang Zhang, Li Zhang, Xinlei An, Hongwei Luo & Kutorzi Edwin Yao, “Adaptive Coupled Synchronization Among Three Coupled Chaos Systems and Its Application to Secure Communications”. EURASIP Journal on Wireless Communications and Networking V, 134, 2016. 399
[10] Mariela Rodríguez, María González, Juan Estrada, Lúa Acosta y Octavio Flórez, “Secure Point-To-Point Com- munication Using Chaos”. DYNA, [S.l.], v. 83, n. 197, p. 180-186, may, 2016. 399
[11] Wang Zhen, Huang Xia, Li Yu-Xia and Song Xiao-Na, “A New Image Encryption Algorithm Based on The Fractional-Order Hyperchaotic Lorenz System”. Chin. Phys. B., vol. 13, no. 3, 2012, pp. 1441–1450. 399, 405
[12] H. Alsafasfeh and, Arfoa, “Image Encryption Based on the General Approach for Multiple Chaotic System”.Journal of Signal and Information Processing, vol. 2, no. 3, 2011, pp. 238-244. 399, 405
[13] L. Kocarev, “Chaos-based cryptography: A brief overview”. IEEE Circuits and Systems Magazine, 2001, 1(2): pp. 6-21. 400
[14] Steven H. Strogatz, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engi- neering. Perseus Books, Reading, Estados Unidos, 1994, pp. 301-347. 400
[15] Jose´ Moreno, Fabio Parra, Rafael Huérfano, César Suárez y Isabel Amaya, “Modelo de Encriptación Simétrica basada en atractores caóticos”. Ingeniería, Vol. 21 No. 3, 2016. pp. 378-390. 401, 410
[16] Guodong,Ye., K.W ,Wong, “An Efficient Chaotic Image Encryption Algorithm Based on a Generalized Arnold Map”. Nonlinear Dyn. 69 Springer, 2012, pp. 2079– 2087.↑ 403
Recibido: 24 de mayo de 2017; Revisión recibida: 5 de julio de 2017; Aceptado: 22 de agosto de 2017
Resumen
Contexto:
Con el creciente volumen de information generada en tiempo real, nuevos mecanismos son necesarios para garantizar su seguridad, evitando el acceso a personas no autorizadas. Los metodos convencionales de criptografia no son apropiados para imagenes por su debilidad a ataques estadisticos, debido a la fuerte correlation entre pixeles adyacentes y el analisis de los histogramas de gamas de colores, lo que puede ayudar a identificarlos dentro de la imagen; con este objetivo en mente, se propone un algoritmo para el cifrado de imafgenes utilizando atractores caof ticos .
Metodo:
La sincronizacion caotica se utiliza para la gestion de la clave, la etapa de difusion se realiza mediante secuencias ergof dicas generadas a partir de la soluciof n numefrica del atractor de Lorenz y la etapa de permutaciofn se realiza con la tefcnica de lfinea de onda.
Resultados:
Se probof el algoritmo propuesto utilizando un conjunto de imafgenes en escala de grises, obteniendo un desempeno adecuado en seguridad y velocidad, la correlation de pixeles es casi nula y la entropia es similar a la presentada en trabajos recientes con el mismo enfoque.
Conclusiones:
Los metodos caoticos son una buena alternativa para mejorar los niveles de seguridad en la criptografia de imagenes debido a sus propiedades de imprevisibilidad y sensibilidad a las condiciones iniciales. Para trabajos futuros el enfoque presentado podria aplicarse a la encriptacion de imafgenes a color y utilizando diferentes atractores caof ticos.
Palabras clave:
Atractor de Lorenz, Caos, Criptografia de imagenes, Sincronizacion, Idioma: Español.Abstract
Context:
With the increasing volumes of information generated in real time, novel mechanisms area needed to ensure security so as to prevent access to unauthorized people. The conventional encryption methods are not appropriate for images, because they are prone to statistical attacks due to the strong correlation between adjacent pixels and the analysis of color gamut histograms, which can help to identify them within the image; with this aim in mind, in this paper an algorithm for image encryption using chaotic attractors is proposed.
Method:
Chaotic synchronization is used for the key management, the diffusion stage is made by means of ergodic sequences generated from the numerical solution of the Lorenz’s attractor and the permutation stage is accomplished with the wave line technique.
Results:
The proposed algorithm was tested using a set of gray-scale images obtaining suitable performance in segurity and speed, the pixel correlation is almost null and the entropy is similar to that presented in recent works with the same approach.
Conclusions:
Chaotic methods are an alternative to improve the security levels in the cryptography of images due to their properties of unpredictability and sensitivity to the initial conditions. For future work the approach presented could be applied to the encryption of color images and using different chaotic attractors.
Keywords:
Synchronization, chaos, images cryptography, Lorenz’s attractor., Language: Spanish.1.Introduction
La transferencia de information de manera segura es una prioridad que exige el interns de las comunidades academicas interesadas en el area de la criptograffa para explorar, disenar y proponer esquemas de seguridad eficientes. Desde hace decadas existen diferentes tecnicas de cifrado que se basan principalmente en metodos iterativos y en la factorization de mimeros primos. La seguridad de estos metodos se encuentra soportada en que no existen procedimientos computacionalmente eficientes para factorizar ntimeros de gran cantidad de dfgitos; particularmente se dificulta la factorization cuando el ntimero a factorizar es el producto de dos mimeros primos de aproximadamente la misma cantidad de digitos. Sin embargo, con el desarrollo acelerado de la computation es posible que pronto puedan ser vulnerables este tipo de criptosistemas [1].
Motivados por esta posible vulnerabilidad, una alternativa para encriptar imafgenes es utilizar los sistemas dinamicos que generan caos, ya que las propiedades de dependencia sensitiva a las condiciones iniciales, mezcla y ergodicidad se pueden aprovechar para garantizar la no predictibilidad de los mecanismos de seguridad.
Por lo general, en los esquemas de comunicacion caotica que utilizan sincronizacion se toma un sistema caotico como transmisor y la sefial de information se mezcla con el transmisor para generar una senal de transmision caotica, la cual se transmite al receptor. El mecanismo receptor es basicamente un sistema dinamico caotico construido sobre la base de la estructura del transmisor. Cuando los mecanismos transmisor y receptor se sincronizan la informaciofn es recuperada por el receptor [2]. Recientemente, se han publicado diferentes propuestas que utilizan este enfoque, algunas de las cuales se analizan a continuacion.
En [3] se propone un esquema de encriptacion de imagenes, utilizando la funcion cat de Arnold para el proceso de permutation y un sistema hipercaotico de Lorenz para el proceso de difusion. Los autores hacen un analisisMarco teorico estadfstico de seguridad que involucra la longitud y la sensibilidad de la clave, lo cual les permite asegurar el buen nivel de seguridad de su propuesta. Ademas, en el artfculo se resalta el potencial de los sistemas hipercaoticos para mejorar la seguridad de los criptosistemas basados en caos; porque comparandolos con sistemas caoticos de un numero menor de dimensiones tienen un comportamiento dinamico mas complejo y manejan un mayor numero de variables. Lo anterior permite inferir que los criptosistemas basados en sistemas hipercaoticos son mas impredecibles y con un espacio de claves mas amplio.
En el ano 2013 se desarrollo un sistema de encriptacion simetrica para imagenes basado en caos, utilizando para el proceso de difusion el atractor caotico de Lorenz y para el proceso de permutation la funcion del panadero. Los autores hacen un analisis estadfstico del desempeno de seguridad del algoritmo propuesto, mostrando una alta seguridad en su esquema [4].
En [5] se presenta un algoritmo de encriptacion de imagenes utilizando el sistema caotico provisto por la funcion tienda para los procesos de difusion y permutation. Al analizar los histogramas de escala de grises de las imagenes real y cifrada, la distribution uniforme que presenta el histograma de la imagen cifrada permite garantizar una buena seguridad del algoritmo. Ademas, mediante el calculo de los coeficientes de correlation entre pfxeles adyacentes, se evidencia que estos tienden a 1, para los pixeles de la imagen original y a 0 para los pfxeles correspondientes a la imagen cifrada; lo anterior significa que se logra eliminar la correlation entre los pixeles adyacentes durante el proceso de cifrado.
En [6] se propone un esquema de encriptacion de imagenes en escala de grises y a color de tipo simetrico utilizando los atractores caoticos provistos por el sistema autonomo de Colpitts y el sistema no autonomo de Duffing, los cuales son resueltos por medio del metodo numerico para la solution de ecuaciones diferenciales Runge Kutta 4 y aprovechados para generar una matriz del tamano de la imagen original. Por medio de esta matriz, se cifra cada uno de los pfxeles de la imagen original; la clave secreta estaf construida por los valores de las condiciones iniciales de los dos sistemas utilizados. Los autores realizan anaflisis de espacio de clave, anaflisis de sensibilidad de la clave e histograma de la imagen cifrada; el espacio de clave utilizado es 2448 = 7,26 * 10134 y el histograma de escala de grises de la imagen cifrada presenta una distribution uniforme. Tambiefn hacen un anaflisis de correlaciofn entre los coeficientes de pixeles adyacentes en las direcciones horizontal, vertical y diagonal para varias imafgenes encriptadas encontrando que estos tienden a cero. Los resultados experimentales muestran la robustez, eficiencia y el buen nivel de seguridad del algoritmo.
En el trabajo desarrollado en [7], se presenta un algoritmo que fusiona un atractor caotico provisto por una funcion senoidal con algunos principios de la codification genetica. Los autores indican que, si utilizan unicamente el atractor caotico, el algoritmo es sencillo pero debil en seguridad y genera distorsion de la imagen. Separan la imagen en tres capas de color: verde, azul y roja; utilizando los principios del caos y de la geneftica, codifican cada capa de manera independiente en base decimal, base binaria y en codigo ADN (codigo generado a partir de principios de la geneti-
ca), obteniendo tres matrices, una por cada color, que luego adicionan segun las reglas del codigo ADN con tres matrices que generan de aplicar la funcion caotica senoidal sobre las matrices anteriores, Como se ejecutan tres procesos independientes utilizan programacion paralela para reducir el tiempo de ejecucion. El algoritmo permite obtener una imagen cifrada con muy baja correlation entre pfixeles adyacentes y demuestra ser eficiente para la encriptaciofn de archivos de gran volumen debido al uso de la programacion paralela.
En el ano 2015 en [8], los autores disenan un esquema de codification de imagenes en escala de grises basado en un proceso de permutation vertical y horizontal en forma circular utilizando la funcion de Arnold con parametros positivos e implementan la funcion hash SHA-3 para el proceso de difusion. Realizan un analisis de sensibilidad aplicado a las claves, un analisis estadfstico y analisis de aleatoriedad mediante el test NIST 800-22. Concluyen que el algoritmo tiene un buen rendimiento en procesamiento y una capacidad de resistir a ataques como el ataque de texto elegido.
En [9] los autores proponen un metodo adaptable de sincronizacion acoplando tres sistemas caoticos identicos y muestran mediante dos ejemplos que el acoplamiento puede ser unidireccional o bidireccional. Para mostrar la sincronizacion con acoplamiento unidireccional consideran tres sistemas caoticos de Rossler y utilizan tres sistemas caoticos de Lorenz para mostrar la sincronizacion con acoplamiento bidireccional. Basados en esta nueva forma de sincronizacion proponen un metodo de encriptacion caotica diferente a los criptosistemas tradicionales; empleando tres sistemas caoticos para el proceso de la sincronizacion y encriptacion, utilizando dos sistemas caoticos emisores que se encargan de la encriptacion y el tercer sistema caotico como receptor para desencriptar; la idea basica que sustentan es que despues de cifrar dos veces en dos transmisores y un receptor, el receptor puede recuperar de manera fidedigna la senal enviada.
En [10] se presenta una alternativa para resolver una vulnerabilidad existente en los sistemas de enmascaramiento caoticos mediante el proceso de sincronizacion de atractores caoticos. El sistema evita la detection de parametros utilizando dos claves de cifrado que se emplean para la modification continua de las condiciones iniciales del atractor de Rossler. El autor destaca su tecnica mostrando resistencia a ataques estadfisticos y evitando que el atacante obtenga los valores iniciales de los atractores.
En el trabajo propuesto en [11], se utiliza el sistema de Lorenz hipercaotico de orden fraccional, que es un sistema que maneja cuatro componentes , empleando una de estas para generar una mascara caotica, del tamano de la imagen que se desea cifrar, la cual utilizan para enmascarar la imagen mediante la operation OR, entre cada uno de los valores de las posiciones de la mascara y de la imagen; las demafs componentes las utilizan para generar una sucesiofn caoftica, que permite reordenar la matriz difundida y finalmente obtener la imagen cifrada, como resultados destacan la simpleza del procedimiento de enmascaramiento, tambien la mejora del desempeno en cuanto a seguridad.
En [12] se propone una tecnica de cifrado de imagenes, en escala de grises, basada en un sistema caotico multiple que es el resultado de la suma de los sistemas caoticos de Rossler y Lorenz. El esquema de encriptacion propuesto consiste en un algoritmo iterativo que mezcla los valores de los pfxeles mediante operaciones XOR y cambia los valores de la escala de grises usando el sistema
caotico multiple. Mediante los resultados de las pruebas se puede apreciar que las bondades de esta propuesta son: buen nivel de seguridad, gran espacio de clave y un algoritmo con alta velocidad de ejecuciofn.
En el presente artículo se propone el desarrollo de un algoritmo de encriptacion de imagenes en escala de grises aprovechando las caracterfsticas de sincronizacion del sistema caotico de Lorenz. El artfculo esta organizado de la siguiente forma: en la seccion 2, se presentan los fundamentos teoricos sobre sistemas caoticos y la sincronizacion de estos. En la seccion 3, se describe y se implementa el algoritmo propuesto que involucra los procesos de sincronizacion, permutacion y difusion utilizando el atractor caotico de Lorenz y se presentan las pruebas realizadas con diferentes imagenes clasicas. En la seccion 4, se hace el analisis estadfstico de desempeno y se compara con los algoritmos propuestos en [5] y [8] . Finalmente, se resaltan las conclusiones y se dan algunas indicaciones para trabajos futuros en esta misma direction.
2.Marco teorico
El area de los sistemas dinamicos surge del intento de estudiar el comportamiento de un sistema que evoluciona en el tiempo, tiene aplicacion en diferentes campos del conocimiento tales como biologfa, medicina e ingenierfa. Los sistemas dinamicos de tipo no lineal son los que pueden presentan comportamientos complejos, lo cual los hace atractivos para utilizarlos en sistemas criptograficos, buscando aumentar su seguridad. La seguridad de la information secreta que se transmita a traves de la red es algo imperante en la actualidad, ya que se debe impedir que personas no autorizadas modifiquen o accedan a la information. Se han propuesto varios trabajos en este sentido, inicialmente utilizando sistemas dinamicos caoticos unidimensionales, los cuales posibilitan generar algoritmos sencillos pero un poco lentos y debiles contra ataques, situation que ha hecho fortalecer la linea de trabajo mediante el uso de sistemas dinamicos de mas de una dimension [13]
2.1. Sistema caotico de Lorenz
La teorfa del caos surge con el estudio de los sistemas dinamicos de tipo no lineal que se modelan por medio de ecuaciones diferenciales en el caso continuo y ecuaciones en diferencias finitas en el caso discreto; es de gran utilidad tanto a nivel de la matematica como en el ambito de las aplicaciones a otra areas del conocimiento, ya que generalmente son impredecibles, presentan una dependencia sensible a las condiciones iniciales, es decir, que para dos condiciones iniciales proximas, se genera un comportamiento dinamico totalmente diferente. Ademas, suelen presentar atractores extranos que involucran propiedades de auto similitud, generando imagenes con naturaleza fractal, lo cual permite obtener tecnicas para disminuir la correlation entre los pixeles adyacentes en el cifrado de imagenes [14].
Una de las razones que dio origen al estudio cualitativo de los sistemas dinafmicos tiene que ver con el problema de Lorenz, quien formulo un modelo tridimensional para realizar predicciones climaticas, y se dio cuenta que si este se alimentaba de la observation anterior aplicando un proceso de redondeo de cifras, aunque inicialmente se comportaba de forma similar, rapidamente se empezaban a trazar trayectorias totalmente diferentes a las generadas sin aplicar ningifn redondeo,
lo que mostraba resultados erroneos en el momento de hacer predicciones.
En la literatura matematica se han mostrado y caracterizado varios sistemas dinamicos caoticos. En la ecuacion (1) se describe el modelo formulado por Lorenz:

donde, (x, y, z) describen una condition atmosferica, a, b y r, son patimetros. Este sistema describe un comportamiento caotico para varios valores de los parametros, los mas utilizados han sido a =10, b = 8/3 y r = 28.
2.2.Sincronizacion
Consiste en enlazar dos sistemas caoticos mediante una o varias senales comunes para obligar a que sus trayectorias a largo plazo converjan a los mismos valores. El tipo de sincronizacion que se utiliza en este trabajo es unidireccional, propuesto por Pecora y Carrol [2], que consiste en dividir el sistema caotico en dos subsistemas denominados maestro y esclavo, el maestro conduce al sistema esclavo a seguir su trayectoria. Una de las condiciones para que se presente este tipo de sincronizacion es que los exponentes de Lyapunov de los subsistemas a sincronizar sean negativos, este hecho provee la estabilidad en el sistema esclavo. Una de las razones por las cuales se utiliza la sincronizacion para la seguridad de la information que se transmite en la red es la facilidad que ofrece para cifrar y descifrar la information, cuyo cifrado se basa en el comportamiento impredecible de los sistemas caoticos. Para el caso de estudio alusivo al sistema de Lorenz con los parametros anteriormente mencionados, Pecora y Carrol calcularon los exponentes de Lyapunov encontrando que estos son negativos cuando se seleccionan como maestro las componentes x o y, como se muestra en la Tabla I.
Tabla I: Exponentes de Lyapunov en el Atractor de Lorenz.
Se puede verificar que cuando se elige x o y como variable sincronizante los dos subsistemas se sincronizan, como se muestra en la Figura 1, siendo la linea negra la trayectoria del subsistema esclavo y la linea azul la trayectoria del subsistema maestro.
El mecanismo de sincronizacion en el algoritmo que se propone se utiliza para encriptar la clave que se envia al receptor, considerando el sistema caotico de Lorenz y dos subsistemas de este y utilizando “y” como variable sincronizante, a traves de la cual se envia la clave que permitira desencriptar la imagen [15].
Figura 1: Sincronizacion del atractor de Lorenz.
3.Esquema de encriptacion propuesto
Se presenta un algoritmo para encriptacion de imagenes en escala de grises, de tamafio M x N pixeles. El proceso de permutacion se realiza mediante la permutacion de linea de onda y para el proceso de difusion se utilizan sucesiones ergodicas generadas a partir de la solution numerica del atractor caotico de Lorenz, utilizando el metodo Runge Kutta 4. El diagrama de flujo del algoritmo se presenta en la Figura 2.
Figura 2: Diagrama de flujo de los procesos de encriptacion y desencriptacion.
Las fases del proceso de encriptacion comprenden los siguientes pasos:
1. El atractor de Lorenz se divide en dos subsistemas maestro y esclavo, utilizando como variable sincronizante ”y”, debido a que sus exponentes de Lyapunov son los mas negativos, recordando que entre mas negativos sean estos, mas rapida sera la convergencia.
2. Se inicializan los subsistemas con condiciones iniciales aleatorias que esten cercanas a la region del atractor.
3. Se sincronizan los atractores enviando la componente maestra hacia el esclavo. Se generan los 700 primeros valores del atractor maestro utilizando Runge Kutta 4 con un incremento de tiempo h = 0,01 (centesimas de segundo) y se envlan los resultados de la componente “y” como clave publica K hacia el atractor esclavo en el instante de tiempo ti, como se indica en la ecuacion (2).

Donde yi corresponde a la salida del atractor en valor absoluto, considerando solamente una cifra decimal multiplicada por 10 en el instante de tiempo tj definido por la ecuacion (3).

Se debe actualizar ti a tj, debido a que cada vez que se codifica un mensaje, existe un corrimiento de (M + N) * h unidades de tiempo, con el fin de no perder la sincronia entre los subsistemas maestros y esclavo, como se muestra en la ecuacion (4).

4. Se utiliza el proceso de permutacion de linea de onda [16], primero se construyen dos sucesiones (xj) y (zi), i = 1,..., N, y j = 1,... M, a partir de los valores obtenidos para las variables x, z del atractor, mediante metodo numerico Runge Kutta 4; se consideran los ultimos tres digitos de dichos valores y se utiliza una matriz de M x N que tiene en cada una de sus posiciones los valores en escala de gris de la imagen original. El valor xj se asocia con la columna j de la matriz, e indica el numero de posiciones que se deben desplazar las entradas de esa columna “verticalmente”, consiguiendo una nueva matriz, luego, la fila i de esta ultima matriz se asocia con el valor zi el cual indica las posiciones que se deben desplazar sus entradas “horizontalmente”, obteniendose otra matriz y finalizando un ciclo de permutacion. El desplazamiento horizontal de las entradas de la fila i es hacia la derecha si zi es menor que el umbral (M/2) y el desplazamiento vertical de las entradas de la columna j es hacia abajo si Xj es menor que N/2. El proceso anterior se ejecuta cuatro veces para completar la fase de permutacion que se conoce como permutacion circular [8], obteniendo la matriz permutada P.
5. Con los datos obtenidos por Runge Kutta 4, para los componentes z y x del atractor, se genera una matriz de A de tamano M x N, considerando los valores numericos obtenidos de los ultimos tres digitos, la cual se suma con la matriz obtenida en el item 4, luego se aplica la operation modulo 256 a cada entrada de la matriz resultante, como se ilustra en la Figuras 3, 4 y 5.
Figura 3: Primer paso para la difusion de la imagen permutada.
Figura 4: Segundo paso para la difusion de la imagen permutada.
Figura 5: Tercer paso para la difusion de la imagen permutada.
Siendo P(k, i) el valor que va de 0 a 256 en la position (k, i) de la matriz que resulta del proceso completo de permutation de linea de onda, las matrices D1 , D2 ,D3 se obtienen de acuerdo con las ecuaciones (5), (6) y (7).
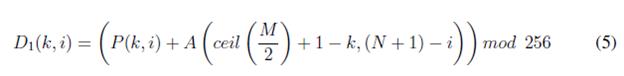
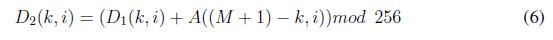
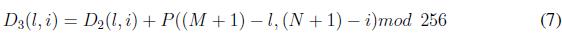
Con i = 1; 2,…,N; l = 1; 2;…, 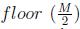 ; k = 1, 2;…,
; k = 1, 2;…, 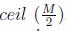 , donde
, donde 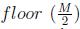 representa el mayor numero entero menor o igual que el numero racional
representa el mayor numero entero menor o igual que el numero racional 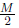 y
y 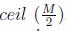 representael menor numero entero mayor o igual que el numero racional
representael menor numero entero mayor o igual que el numero racional 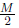 .
.
Como primer paso se toma una parte de la matriz A, de tamaño 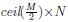 y tambien unaparte de la matriz permutada P de tamaño
y tambien unaparte de la matriz permutada P de tamaño 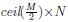 , asociando, como se ve en la Figura 1, los colores con la posici´on en la que los valores de ambas matrices se operan, como se muestra en la en la ecuacion (1), generando la matriz D1.
, asociando, como se ve en la Figura 1, los colores con la posici´on en la que los valores de ambas matrices se operan, como se muestra en la en la ecuacion (1), generando la matriz D1.
Para el segundo paso se toma la matriz D1 y una segunda parte de la matriz A de tamano 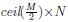 , asociando, como se ve en la Figura 2, los colores con la posicion de los valores de ambas matrices, describiendo la forma en que operara la difusion representada en la ecuacion (2), generando la matriz D2.
, asociando, como se ve en la Figura 2, los colores con la posicion de los valores de ambas matrices, describiendo la forma en que operara la difusion representada en la ecuacion (2), generando la matriz D2.
En el tercer paso, se utiliza una parte de la matriz D2 de tamaño 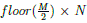 , y una segunda parte de la matriz permutada P de tamaño
, y una segunda parte de la matriz permutada P de tamaño 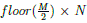 , cuyo proceso se ilustra en la Figura 3, de manera similar al paso anterior la Figura 3 asocia los colores con la posicion de los valores a los que se les se aplicar´a la difusi´on descrita en la ecuacion (3), generando lamatriz D3.
, cuyo proceso se ilustra en la Figura 3, de manera similar al paso anterior la Figura 3 asocia los colores con la posicion de los valores a los que se les se aplicar´a la difusi´on descrita en la ecuacion (3), generando lamatriz D3.
Por ultimo, se concatenan las matrices D2 y D3 , es decir todas las filas de la matriz D2 se unen a las filas de la matriz D3 en su respectivo orden, dejando una unica matriz C correspondiente a la imagen cifrada.
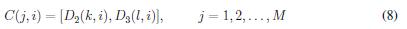
El proceso descrito anteriormente mejora la aleatoriedad de la imagen cifrada C, es decir, si todos los colores en escala de grises en la imagen cifrada C tienden repetirse un numero igual o cercano a (M x N)/256 veces el grado de incertidumbre aumenta y por ende la impredecibilidad de la imagen cifrada.
En el desarrollo del esquema de encriptacion se tuvo en cuenta la relation existente entre los procesos de permutacion y difusion; por ejemplo, el proceso de difusion descrito en [5] destaca por su simpleza, pero su proceso de permutacion es mas complejo, lo cual exige mayores recursos computacionales, pero ofrece resultados interesantes en cuanto a la aleatoriedad en su cifrado; en [8] el proceso de difusion utiliza mas recursos y el de permutacion en este caso es el proceso sencillo, sin embargo tiene menor aleatoriedad en las imagenes cifradas que en [5]; por lo tanto tener un buen desarrollo en la permutacion contribuye en gran medida al proceso de difusion para aumentar la aleatoriedad de las imagenes cifradas, razon por la cual en este trabajo se realizan mas rondas de permutacion que en [8], adicionalmente se busco un mejor desarrollo en la fase de difusion sin utilizar demasiados recursos en ambas fases.
La adicion de una permutacion simple que se le aplica a la matriz ti, utilizada para difundir, permite a la imagen cifrada C no poseer patrones reconocibles, como grupos de pixeles cercanos con colores que tengan similar valor o valores con diferencias muy grandes. Similar estrategia se puede evidenciar en [8] con la matriz utilizada para difundir, la cual se construye con valores que se obtienen iterando el mapa de Arnold, consiguiendo completar la matriz en 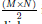 iteraciones si M x N es par o
iteraciones si M x N es par o 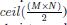 iteraciones si M x N es impar, tomando dichos valores de las componentes del sistema de Arnold e intercalandolos en la matriz, teniendo efectividad en disolver patrones reconocibles en la imagen cifrada ; en [11], la estrategia es mas simple ya que utilizan M x N iteraciones para generar una matriz, solo con los valores de una unica componente del sistema caotico, que permite difundir mediante la operation OR, resultando en un desempefio menor a [8]; en [12] el proceso es mas complejo que en [11] para la generation de la matriz, aqui utilizan una matriz de M x N que repetidas veces se opera con la matriz que representa a la imagen original mediante la operation XOR hasta conseguir la imagen cifrada, resultando en un buen desempefio.
iteraciones si M x N es impar, tomando dichos valores de las componentes del sistema de Arnold e intercalandolos en la matriz, teniendo efectividad en disolver patrones reconocibles en la imagen cifrada ; en [11], la estrategia es mas simple ya que utilizan M x N iteraciones para generar una matriz, solo con los valores de una unica componente del sistema caotico, que permite difundir mediante la operation OR, resultando en un desempefio menor a [8]; en [12] el proceso es mas complejo que en [11] para la generation de la matriz, aqui utilizan una matriz de M x N que repetidas veces se opera con la matriz que representa a la imagen original mediante la operation XOR hasta conseguir la imagen cifrada, resultando en un buen desempefio.
Hay que destacar la importancia de realizar tratamiento a la matriz ti, por su implication en la reduction de patrones, es decir, lo que se busca en esta matriz es que sea lo suficientemente aleatoria; por ejemplo, en [5] optan por evitar tomar algunos de valores generados por el sistema caotico para obtener dichas matrices, en otros casos como en [8], [11] y [12], iteran muchas veces para obtener dichos valores, esto quiere decir que utilizan bastantes recursos para mejorar la aleatoriedad de la matriz y del sistema en general; en el esquema propuesto no se requieren muchas iteraciones, ya que particularmente el sistema de Lorenz es suficientemente aleatorio; en este caso se utilizan M + N valores para generar la matriz ti y se realizan M iteraciones, una ventaja, ya que si existiesen aproximaciones y un numero alto de iteraciones, la degradation dinamica puede danar el comportamiento caotico del sistema.
Para el proceso de desencriptacion se aplican los pasos 4 y 5 en forma inversa.
Para verificar la funcionalidad del algoritmo se realizaron varias pruebas con diferentes imagenes, tomadas de las referencias consultadas, algunas de estas se muestran en las figuras 6, 7, 8 y 9.
Figura 6: Imagen “Barbara”, tamano 512x512.
Figura 7: Imagen Bote, tamano 512x512.
Figura 8: Imagen “Lena”, tamano 512x512.
Figura 9: Imagen Camarografo, tamano 512x512.
En las figuras 6, 7, 8 y 9, se evidencia el buen funcionamiento del algoritmo para encriptar y desencriptar imagenes; las imagenes decodificadas son iguales a las originales.
4.Analisis estadistico
Para evaluar el desempefio del algoritmo propuesto se analizo la correlation entre los pixeles adyacentes en forma horizontal, vertical y diagonal, tanto para la imagen original como para la cifrada, obteniendo que la correlation tiende a desaparecer en la encriptacion, como se muestra en las figuras 10, 11, 12 y 13.
Figura 10: Correlation entre pixeles adyacentes imagen Barbara.
Figura 11: Correlation entre pixeles adyacentes imagen Bote.
Figura 12: Correlation entre pixeles adyacentes imagen Lena.
Figura 13: Correlation de pixeles adyacentes imagen Camarografo.
A continuation, se presenta el analisis de sensibilidad del proceso de encriptacion frente al cambio de un unico bit de la imagen original en las figuras 14 y 15, y el cambio de un unico bit en la condition inicial del sistema de Lorenz en la componente ”x”, es un numero de 15 digitos entre 0 y 1; en las figuras 16 y 17, evidenciando una imagen cifrada totalmente diferente.
Figura 14: Analisis sensibilidad imagen Barbara.
Figura 15: Analisis sensibilidad imagen bote.
Figura 16: Analisis sensibilidad imagen Lena.
Figura 17: Analisis sensibilidad imagen Camarografo.
En las figuras 18, 19, 20 y 21 se muestran los histogramas de la distribution de la escala de grises en la imagen original comparada con la imagen cifrada encontrando uniformidad en la imagen cifrada; donde se pueden resaltar las distribuciones uniformes presentes en los histogramas de las imagenes cifradas.
Figura 18: Histograma escala de grises imagen Barbara.
Figura 19: Histograma escala de grises imagen Bote.
Figura 20: Histograma escala de grises imagen Lena.
Figura 21: Histograma escala de grises imagen Camarografo.
Para las cuatro imagenes presentadas se hallaron los coeficientes de correlation agrupados en la Tabla II, las medidas que evaluan la resistencia a ataques diferenciales UACI (promedio unificado de intensidad de cambio, sus siglas en ingles) y NPCR (razon de cambio de pixeles, sus siglas en ingles), ademas de la entropia correspondiente, los cuales se presentan en las tablas III y IV. La expresion matematica para UACI esta dada por la ecuacion (9).
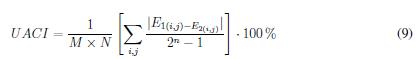
Siendo M x N el tamano de la imagen, E^j el valor del pixel en la position del (i, j) de la imagen cifrada E1 y E^j el valor del pixel en la position del (i, j) de la imagen cifrada E2, donde la imagen E1 corresponde al cifrado de la imagen original sin modificaciones y E2 corresponde al cifrado de la imagen original modificada en un pixel o tambien en la modification de un bit en la condition inicial y 2n es el valor maximo que puede tomar cada pixel.
La formula que define NPCR esta dada en la ecuacion (10).
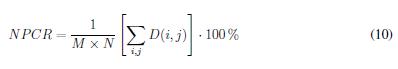
Donde:
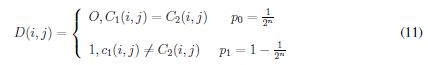
Siendo, Po la probabilidad de que un pixel (i, j) en la imagen cifrada C1 , sea igual al pixel (i, j) en la imagen C2 y p1 la probabilidad de que un pixel en la imagen cifrada C1(i, j), sea diferente al pixel (i, j) de la imagen cifrada C2, es decir son las probabilidades de obtener 0 o 1, respectivamente en la distribution de probabilidad D(i, j).
Tabla II: Valores de correlation de pixeles adyacentes
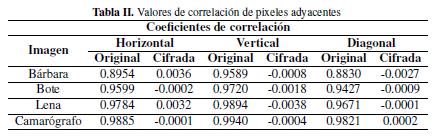
Tabla III: Resistencia ataques diferenciales
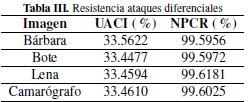
Tabla IV: Valores de entropia.
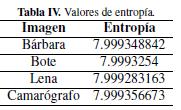
El valor de la entropia es un indicador muy importante, ya que muestra el nivel de aleatoriedad de los pixeles en las imagenes cifradas, lo cual significa que entre mayor sea el valor de la entropia la aleatoriedad es mejor. Para las imagenes en estudio se logro obtener valores muy proximos a 8 calculado por:
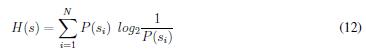
donde N es la cantidad de slmbolos, en este caso la cantidad de valores en escala de grises y P(si) la probabilidad de ocurrencia del slmbolo si , si la probabilidad de ocurrencia de todos los slmbolos es de 1/256 el valor de la entropia es de 8; luego este es el valor ideal de entropia en los procesos de encriptacion de imagenes cuando se trabaja con 256 tonalidades de grises.
El algoritmo propuesto se ejecuto en un equipo Intel(R) Core(TM) i5-2410M, 2.30GHz CPU; los resultados de su desempeno y la comparacion con los resultados obtenidos en (5), (8) y (15) se resumen en las tablas V y VI; como se puede ver el algoritmo propuesto presenta desempenos muy similares a los presentados en las referencias consideradas en los indicadores UACI, NPCR y la entropia, logra mejores coeficientes de correlation entre pixeles adyacentes y un buen desempeno en velocidad de ejecucion. Sin embargo en cuanto a indicadores como el UACI y NPCR es dificil saber cual trabajo es mas seguro, si bien se busca que el NPCR tienda a 100 %, es decir, que no exista ningun pixel con el mismo valor en la misma position para dos imagenes cifradas, es mas diflcil acercarse a dicho valor ideal a medida que las imagenes son mas grandes; para el UACI que evalua que tan diferente son dos imagenes cifradas, no es logico pensar que este valor tenga que ser muy grande ya que se perderia desempeno en la entropia, o que sea muy pequeno puesto que las imagenes cifradas no senan lo suficientemente diferentes la una de la otra.
Tabla V: Comparacion Indicadores de desempefio.

En la Tabla V, en los coeficientes de correlation, se puede observar que la referencia (8) presenta un mejor desempeno que la referencia (5), ya que a pesar de presentar correlaciones positivas mayores en las imagenes originales logra menores valores de correlaciones vertical y horizontal de las imagenes cifradas. La razon del mejor desempefio de la referencia (8) se puede atribuir a su buen proceso de permutacion, tener un proceso de difusion iterativo e incorporar mayor aleatoriedad a la mascara que se utilizan para difundir la imagen permutada.
En el caso de la entropia, la referencia (5) posee mejor desempeno que la (8), que seguramente se debe al uso de un proceso de permutacion mas complejo, puesto que en (5) el trabajo para la obtencion de las sucesiones caoticas es bastante exhaustivo.
Tabla VI: Comparacion velocidad de ejecucion.
En este trabajo se busco equilibrio entre seguridad y velocidad de ejecucion, es decir, lograr un algoritmo con buen nivel de seguridad sin perder velocidad de ejecucion.
5.Conclusiones
Con el desarrollo del presente algoritmo se evidencia que gracias a la complejidad en el comportamiento del sistema caotico de Lorenz y su propiedad de sincronizacion, se logra obtener un sistema de encriptacion de imagenes a escala de grises con buen desempeno en cuanto a seguridad y velocidad de ejecucion comparable con los resultados obtenidos en trabajos recientes.
La propiedad de no predictibilidad generada por el sistema de Lorenz fue aprovechada para generar un sistema de encriptamiento eficiente, el cual, como lo demuestra el analisis estadfstico, evidencia una alta resistencia a ataques estadfsticos conservando un alto nivel de entropia, sin la necesidad de mantener un constante cambio de las condiciones iniciales del atractor. Esto significa un uso eficiente de las propiedades de sincronizacion y entropfa del sistema caotico de Lorenz.
El uso inapropiado de los parametros mostrados en este artfculo puede generar una codification no adecuada de la imagen. Al usar un incremento de tiempo muy pequeno del atractor, la variabilidad del estado anterior y siguiente no es significativa, volviendo el sistema vulnerable a ataques estadfsticos; asf, el atractor debe tener incrementos de tiempo grandes para generar mayor entropfa.
Aunque en el presente trabajo se utiliza unicamente el atractor de Lorenz, para trabajos futuros se sugiere explorar con otros atractores caoticos buscando obtener mejores medidas de desempeno y con mayor espacio de clave. Por otra parte, el algoritmo presentado esta disenado para codificar imafgenes en escala de grises, se espera que el trabajo desarrollado en este artficulo pueda contribuir en el desarrollo de algoritmos para codificar imagenes a color.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

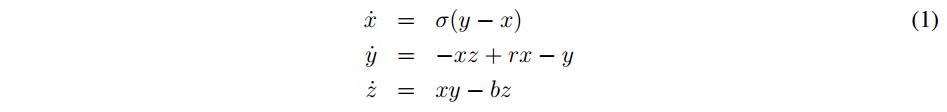
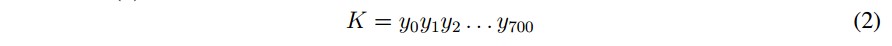
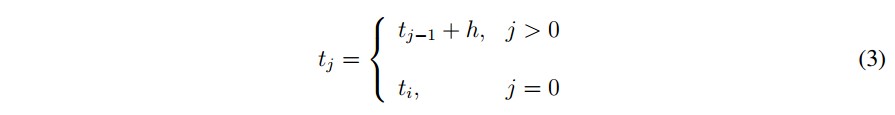
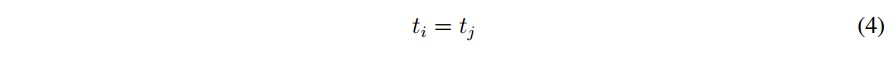
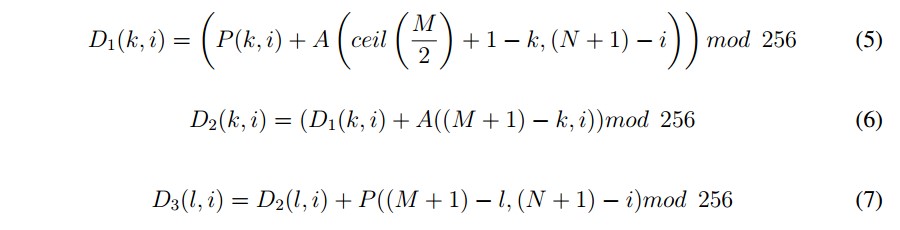
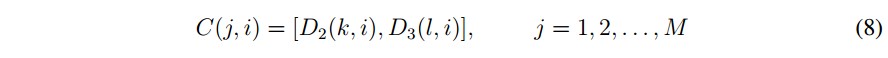



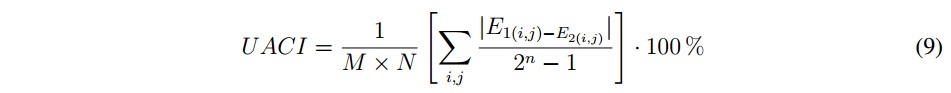
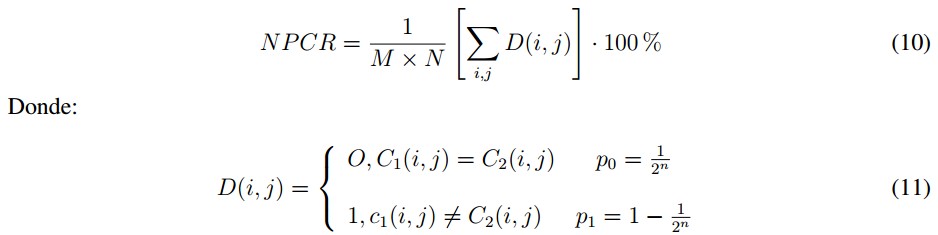
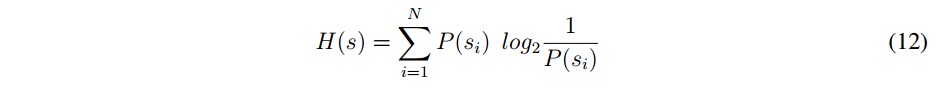










2.jpg)










