DOI:
https://doi.org/10.14483/23448393.2847Published:
2008-11-30Issue:
Vol. 8 No. 1 (2003): January - JuneSection:
Science, research, academia and developmentDeterminación de la predecibilidad de trazas de tráfico mediante análisis de recurrencia
Keywords:
Tráfico autosimilar, Análisis de Recurrencia, Graficas de recurrencia, Teoría del caos. (es).Downloads
References
M. Arlitt and C. Williamson. Web Server Workload Characterization: The search for Invariants. IEEE/ACM Trans. Networking, 5(5):631-645, 1997.
J. Beran, R. Sherman, M. Taqqu and W. Willinger. Long-Range Dependence in VBR video traffic. IEEE. Trans. Commun. 43:1566-1579, 1995.
M. Crovella, M. Taqqu and A. Betsavros. Heavy-Tailed Probability Distributions in the WWW, In "A practical guide to Heavy Tails", Adler, Feldman and Taqqu, editors. Birkhauser, 1998.
M. Crovella and A. Bestavros. Self-similarity in WWW traffic. IEEE/ACM Trans. Networking, 5:835-846, 1997.
A. Feldman, A. Gilbert, P. Huang and W. Willinger. Dynamics of IP Traffic: A Study of the Role of Variability and the Impact of Control. Proc. ACM SIGCOM'99, 1999.
W. Leland, M. Taqqu, W. Willinger and D. Wilson. On the selfsimilar nature of Ethernet Traffic. IEEE/ACM Trans. Networking, 2:1-15, 1994.
J. Baras. Control Problems in Modern Communication Networks. ENEE769 syllabus, University of Maryland, Spring 2001.
W. Willinger and J. Doyle. Robustness and the Internet: Design and Evolution. Caltech, Pasadena, 2002.
A.Veres and M.Boda. The Chaotic nature of TCP congestion control. IEEE Infocom'2000.
P. Ranjan, E. Abed and R. La. Nonlinear Instabilities in TCPRED. IEEE Infocom'2002.
Takens, F. Detecting strange attractors in fluid turbulence. In Dynamical Systems and Turbulence, Berlin: Springer-Verlag. 1981.
Fraser A.M. Information Entropy in strange attractor. IEEE Transaction on Information Theory, Vol 35 N 2, 1989
Eckmann J, Kamphorst S. Recurrence plots of dynamical sustems. Europhysucs Letters 5, 1987.
Eckmann J. Oliffson K, Ruelle D, Ciliberto S. Liapunov exponents from time series. Physical Review A, Vol 34, Num 6, 1986.
Zbilut J. P, Webber C.L Jr: Embeddings and delays as derived from quantification of recurrence plots. Physics Letters A 171 (3-4) 1992.
Kennel M. B, Brown R, Abarbanel H.D.I, Determining embedding dimension for phase-space reconstruction using a geometrical construction, Phys. Rev. A 45, 3403 (1992).
Williams Garnett. Chaos theory tamed. Joseph Henry press. Washington 1997.
Packard N., Crutchfield N. H., Farmer J. D., Shaw R. S.: Geometry from a time series, Phys. Rev. Lett., Vol. 45, 1980, pp. 712-716.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:1 pág:19-28
Determinación de la predecibilidad de trazas de tráfico mediante análisis de recurrencia
José Félix Vega Stavro
Miembro Grupo de investigación en DPS y en Telecomunicaciones.
Marco Aurelio Alzate Monroy
Miembro Grupo de investigación en DPS y en Telecomunicaciones.
Resumen
Este artículo hace parte de una serie de artículos acerca de la caracterización de tráfico fractal o autosemejante, publicados en esta revista. En él se presenta la aplicación de las técnicas de análisis de recurrencia en series de tiempo autosemejantes con el objetivo de determinar la predecibilidad de tales series. Este es un resultado preliminar dentro de un trabajo de investigación en progreso sobre complejidad, caos y fractalidad en redes de comunicaciones.
Palabras clave: Tráfico autosimilar, Análisis de Recurrencia, Graficas de recurrencia, Teoría del caos.
Abstract
This is one of a series of papers, appearing on this journal, about self-similar traffic characterization. This time we present recurrence analysis techniques their predictability. This is a preliminary result of an ongoing research work on complexity, chaos and fractality in communication networks.
Key words: Self-similar traffic, Recurrence analysis, Chaos theory.
INTRODUCCIÓN
Tradicionalmente, las redes de comunicaciones se han estudiado como un sistema determinístico (los recursos de la red y los protocolos con que se asignan dichos recursos) sometido a unas entradas aleatorias (las demandas de los usuarios). Esta visión, que ha tenido más de cien años de exitosa aplicación, condujo a un impresionante desarrollo de la teoría de colas, la más importante rama de las matemáticas en cuanto a su aplicación a las redes de comunicaciones. Sin embargo, la teoría de colas se ve seriamente limitada cuando en los procesos de tráfico no se pueden identificar modelos markovianos [1]. La proliferación de aplicaciones multimedios con complejas estructuras de correlación y el incremento de las velocidades de transmisión de algunos kbps a 10 Gbps y más, revelan un amplio rango de escalas de tiempo donde se descubren fenómenos fractales en el tráfico, los cuales se presentan con una ubicuidad abrumadora [2,3,4,5,6].
En consecuencia, muchos de los problemas técnicos actuales como el control de admisión, el control de flujo, el control de congestión, el control de la memoria en las colas, la asignación de recursos, el enrutamiento dinámico adaptable, la recuperación automática ante fallas, etc., se han reformulado exitosamente en términos de la teoría de control y la optimización [7]. Más interesante aún, este tipo de sistemas se han estudiado en muy diferentes contextos como la mecánica estadística, la biología y la economía, entre otros, donde han conducido a la teoría de sistemas complejos [8]. De hecho, al empezar a estudiar los problemas de asignación de recursos y control de congestión en redes IP desde el punto de vista de la teoría de control, se han venido descubriendo comportamientos dinámicos sorprendentes de los protocolos de la red. En particular, variando algunos pocos parámetros dentro de los protocolos de control de flujo entre extremos con gestión activa de colas (TCP/RED, por ejemplo), se descubren diferentes fenómenos de bifurcación que conducen a órbitas periódicas de período arbitrario e, inclusive, al caos [9-10]. Este descubrimiento tiene muchas implicaciones no sólo en cuanto a la posibilidad de introducir a las redes de comunicaciones la reciente teoría del control del caos, sino como una manera misma de explicar el fenómeno de la fractalidad en los patrones medidos de tráfico. En efecto, se sabe que las trayectorias de sistemas caóticos suelen ser de naturaleza fractal y, de hecho, suelen usarse como generadores de estructuras fractales.
Dentro de este contexto general, en este artículo nos interesa modelar las redes de comunicaciones como sistemas dinámicos, para lo cual usamos una herramienta llamada Análisis Cuantitativo de Recurrencia. Hasta donde sabemos, esta técnica no ha sido aplicada antes al estudio de fenómenos de tráfico. Nuestro objetivo es validar las conclusiones presentadas en [9] repitiendo los experimentos allí citados, pero a la luz de esta novedosa herramienta.
El artículo esta organizado de la siguiente forma: en la primera parte se presenta la teoría de la reconstrucción en el Pseudo Espacio de Fases. En seguida se introducen los Gráficos de Recurrencia y se aplica el Análisis Cuantitativo de Recurrencia para evaluar predecibilidad en series de datos autosemejantes. Finalmente se caracteriza una red de comunicaciones como un sistema caótico mostrando la sensibilidad del sistema a las condiciones iniciales.
I. GRÁFICOS DE RECURRENCIA
El Gráfico de Recurrencia (GR) es una herramienta de análisis que revela la existencia de patrones recurrentes e intermitentes en series de tiempo. Propuesto por primera vez por Eckman [13], ha tenido gran aplicación en la caracterización de sistemas dinámicos.
El objetivo del gráfico de recurrencia es encontrar la repetición de un patrón dentro del espacio de estados de un sistema. Aunque un proceso no sea periódico en sentido estricto es posible que muestre comportamientos repetitivos o "recurrentes". Una de las formas de caracterizar esta recurrencia consiste en comparar la diferencia entre todos los estados de la trayectoria que describe la evolución del sistema.
A continuación ampliaremos y precisaremos el contexto de aplicación de conceptos como: espacio de estados, espacio de estados reconstruido, trayectoria y recurrencia. Finalmente aplicaremos estos conceptos a series de datos autosimilares.
1.1 ESPACIO DE ESTADOS
Un sistema dinámico puede describirse por sus variables de estado.
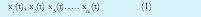
El conjunto de m variables de estado forma un vector x(t) en un espacio m-dimensional, espacio conocido como espacio de fases. La evolución en el tiempo de este vector forma una trayectoria u órbita en el espacio de fases y la evolución de la trayectoria indica la dinámica del sistema.
Usualmente no es posible obtener todas las variables de estado que caracterizan un sistema. Algunas veces sólo se dispone de una de ellas. Sin embargo, existe un método para reconstruir la dinámica m-dimensional del sistema a partir del conocimiento de una sola de las variables del mismo. Esto es posible gracias al acoplamiento interno del sistema, que proyecta la dinámica de las variables una sobre la otra. Las consecuencias de ésta propiedad de los sistemas dinámicos son bastante profundas. Por ejemplo, en teoría se podría conocer la dinámica de los océanos de la tierra observando un centímetro de playa.
1.2 MÉTODO DE TAKENS
Un método usado con frecuencia para reconstruir la trayectoria del espacio de fases fue propuesto por Takens [11] y Packard [18], es llamado método de retardos en el tiempo. Dado un sistema dinámico de dimensión m, del cual sólo se conoce la serie u= u1, u2 ,....., un que representa la evolución temporal de una de las variables de estado del sistema, es posible construir un Pseudo espacio de fases del sistema, que sea topológicamente equivalente. Es necesario que tal sistema dinámico (de origen) sea determinístico de la forma xt+1 = F(xt, µ). La reconstrucción es aplicable sólo en una región A suave de dimensión dA con un número finito de puntos de equilibrio sin órbitas periódicas de período entre τ y 2τ, pero con un número finito de órbitas periódicas de período nτ para n entre 3 y m y τ entero
El vector de estados de tal reconstrucción estaría dado por:
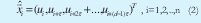
Donde τ es un retardo en el tiempo aplicado a u, y d es la dimensión del Pseudo espacio de fases o dimensión reconstruida.
El teorema de Takens [11] garantiza que si d ≥ 2m+1 la estructura topológica de la trayectoria original será preservada en la trayectoria reconstruida; es decir, para obtener un sistema dinámico equivalente al original, se debe cumplir una condición obvia: el pseudo espacio de fases debe tener, por lo menos, la misma complejidad del espacio original. Volviendo a la observación anterior sobre la dinámica oceánica, el espacio de fases reconstruido tendría tantas variables de estado que sería impracticable tal reconstrucción.
La selección de la dimensión de reconstrucción y del retardo en el tiempo es crucial en la generación de ^xi. Expondremos a continuación los métodos ^ para determinar correctamente tales valores.
1.3 VECINOS PRÓXIMOS FALSOS Y DIMENSIÓN DE RECONSTRUCCIÓN
Un método para determinar el número de dimensiones en las que se desenvuelve el proceso es conocido como el método de los Vecinos Próximos Falsos [16]. Supóngase que Ad de dimensión d es el pseudo espacio de fases correspondiente al espacio de fases Bm de dimensión m, tal que d=2m + 1. Tómese un punto b ∈ Bm que tiene como correspondencia a No ∈ Xd en el espacio reconstruido. Como vimos anteriormente, ambos espacios tienen las mismas propiedades topológicas, así que los puntos que estén cercanos a b deben tener sus equivalentes en la cercanía de No. Si la condición d ≥ 2m + 1 no se cumple, los puntos vecinos de b serán proyectados muy lejos de No y la estructura topológica no se preservará.
Si no se conoce de antemano la dimensión menor en que puede ser observada la dinámica del sistema es necesario estimarla construyendo los posibles espacios
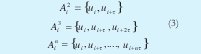
La dimensión de reconstrucción será d=2 si los puntos que se son vecinos en A2 siguen siéndolo en A3. Si la condición no se cumple significa que los puntos que están próximos en esta dimensión son vecinos falsos. Pasaríamos a observar si se cumple entre A3 y A4, hasta encontrar el espacio de dimensión d=n donde se cumpla que los puntos vecinos An en sigan siéndolo en An+1 .
En resumen: Sea un par de puntos vecinos en An

Si se cumple que:
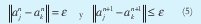
Entonces αkn y αjn son vecinos próximos verdaderos en An. De lo contrario son vecinos próximos falsos. El test se aplica a todos los puntos pertenecientes al espacio. Si en la dimensión n hay un gran porcentaje de puntos que sean vecinos falsos, entonces n no es una dimensión de reconstrucción adecuada y habría que hacer el test en una dimensión mayor.
1.4 RETARDO EN EL TIEMPO E INFORMACIÓN MUTUA
El siguiente parámetro a elegir es el retardo τ. La idea a la hora de elegir el retardo de la serie u es bastante sencilla. Supóngase que graficamos un sistema con d=2, tendríamos una gráfica u(t) Vs u(t+τ). Si τ = 0 , evidentemente esta gráfica no aportaría información alguna acerca del comportamiento del sistema., pues sería una línea recta con pendiente 45º. En la medida en que τ sea pequeño, las series en los ejes de la gráfica serán muy parecidas y la gráfica obtenida seguirá brindando poca información. El retardo ideal será aquel que maximice la independencia entre u(t) y u(t+τ). Una forma de estimar el retardo que produzca esta independencia, sugerida por Fraser [12], se llama Test de Información Mutua.
La Información mutua en función del retardo esta expresada como:
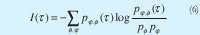
Donde:
p φ, Φ es la probabilidad de que ui = φ y ui + τ = Φ.
p φ es la probabilidad de que ui = φ
p Φ es la probabilidad de que ui + τ= Φ
El valor óptimo de τ será aquel que minimice a I (τ). Cuando esto suceda, las dos series serán lo más independiente posible una de la otra. Por lo general se escoge el retardo que produzca el primer mínimo.
1.5 RECONSTRUCCIÓN DE DOS ATRACTORES CONOCIDOS
Veamos un par de ejemplos tomados de un texto tradicional de Teoría del Caos [17]. Se trata de la reconstrucción del Atractor de Lorenz, y de las ecuaciones de Henon. El primer atractor se construye a partir de la integración numérica del sistema de ecuaciones:
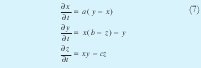
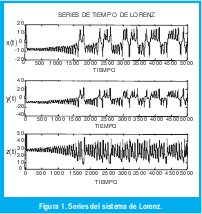
En este sistema, las variables de estado son x, y, z. La figura 1 ha sido obtenida a partir de la integración numérica del sistema de ecuaciones anterior.
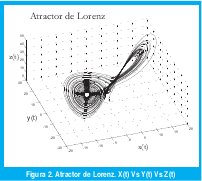
Las variables de estado mencionadas constituyen un atractor en 3 dimensiones que se muestra en la figura 2.
El segundo ejemplo es el atractor de Henon obtenido a partir de la iteración de las ecuaciones
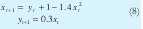
La iteración se hace eligiendo un par de valores iniciales arbitrarios y0, x0 , en el rango (-1.3,1.3) y calculando sucesivamente x1, y1, x2 ,.....etc
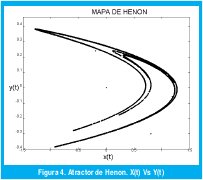
La figura 3 presenta las series temporales generadas a partir de las ecuaciones (8). Y la figura 4 presenta el diagrama de fases x(t) Vs y (t).

En ambos casos podemos apreciar la existencia de una regularidad u orden en los diagramas. Vemos que, aunque el sistema evoluciona y no se detiene en un punto fijo del espacio de fases, tiende a ocupar una región muy definida dentro de este espacio. Ambos son ejemplos de Atractores Caóticos.
Apliquemos el procedimiento de reconstrucción antes mencionado al sistema de Lorenz, y al de Henon, escogiendo la serie x(t) como origen de la reconstrucción en ambos casos. El cálculo de la dimensión de reconstrucción d se obtiene a partir del porcentaje de vecinos falsos, mostrado en la tabla 1.
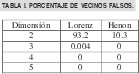

Se concluye que la dimensión de reconstrucción óptima es d=2 para el atractor de Henon y d=3 para el atractor de Lorenz
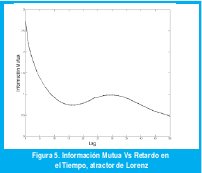
El retardo óptimo es aquél donde se encuentra el primer mínimo en la información mutua. En la figura 5 se aprecia que el primer mínimo se obtiene para un retardo temporal igual a 17. En la figura 6 se observa que no hay un mínimo relativo, pues la gráfica es monótonamente decreciente, en este caso la teoría recomienda escoger un retardo igual a 2. Las figuras 7 y 8 muestran los atractores reconstruidos en cada caso.
1.6 GRÁFICO DE RECURRENCIA
Como se mencionó inicialmente, el objetivo del GR es encontrar la recurrencia de los estados del sistema, para lo cual se propone analizar las trayectorias del sistema a partir de la reconstrucción en el espacio de estados.

Para la construcción del gráfico pueden seguirse dos procedimientos. El primero, llamado Gráfico de Recurrencia sin Umbral, se resume a continuación:

Sea Zt la serie de datos unidimiensional que describe una de las dimensiones del proceso a analizar:
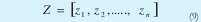
Sea Y la serie de datos reconstruida en la dimensión dE con un retardo τ
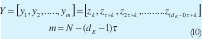
La matriz de recurrencia X se define como:
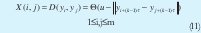
Donde
Θ es la función de Heaviside.
dE es la dimensión de reconstrucción.
u es el umbral de recurrencia.
Cada punto dentro de la matriz de recurrencia define si la distancia o norma entre los puntos de Y cae dentro del umbral u.
A partir de la matriz de recurrencia se usan dos colores (blanco y negro por ejemplo) para codificar la recurrencia de los estados. Si el valor X(i,j) es mayor que determinado umbral, entonces el punto en X(i,j) en un espacio bidimensional, es negro, de lo contrario el punto se colorea como blanco. Evidentemente, la elección del valor del umbral u es crítica, puesto que con un umbral muy pequeño el gráfico quedaría saturado y, con un umbral muy grande, el gráfico quedaría prácticamente sin puntos.
El segundo tipo de gráficos son los gráficos sin umbral. La matriz de recurrencia se define como:
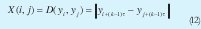
En este procedimiento, el valor de X(i,j) se codifica en una escala graduada en colores. Si se usara una escala de grises, un valor alto de X(i,j) sinificaría un punto de color cercano al negro en la posición (i,j) de un gráfico bidimensional. Un valor cercano a cero de X(i,j), significaría un punto de color cercano al blanco en esta misma posición.
En las figuras 9 y 10 pueden apreciarse los GR con umbral y sin umbral, correspondientes a una serie de datos senoidal.

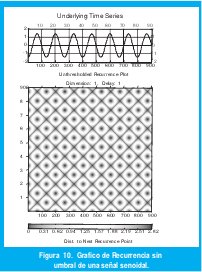
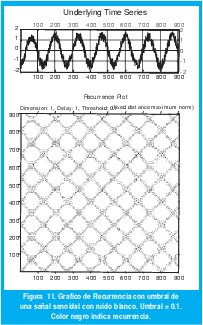
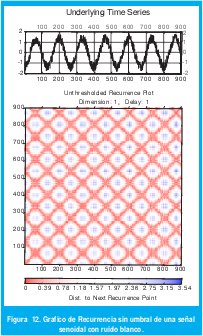
La figuras 11 y 12 muestran los mismos gráficos para la misma señal contaminada con ruido.
1.7 CUANTIFICACIÓN DE LOS RESULTADOS DEL GR (RQA)
Los resultados de los GR se cuantifican por un procedimiento llamado RQA (Recurrent Quantification Analysis), desarrollado por Zbilut y Webber [15]. A continuación describiremos algunos de los parámetros del RQA aplicados a los GR con umbral.
El primero, denominado Porcentaje de Recurrencia (%REC), es simplemente el número de puntos que hay en el GR, es decir puntos cuyo valor cae dentro de los límites del umbral. Este parámetro se usa para calcular la Dimensión de Correlación (DC) del espacio de fases reconstruido. La DC está definida como la pendiente de la regresión lineal de la relación entre %REC y el valor del umbral de decisión; es lógico suponer que entre mayor sea el umbral habrá un % de REC menor, y viceversa. La Dimensión de Correlación caracteriza esta relación.
El siguiente parámetro es el Porcentaje de Determinismo (%DET), el cual está definido como el porcentaje de los puntos del gráfico de recurrencia que se encuentran organizados en líneas paralelas a la diagonal principal, excluyendo la diagonal principal. Estas líneas revelan las semejanzas existentes en el valor de datos cercanos en el tiempo. El %DET, entonces, informa la presencia de interacciones estables en la serie, así como la aparición de órbitas o comportamientos periódicos [13]. El %DET indica entonces, qué tan organizado es el proceso bajo observación.
El siguiente parámetro que tiene en cuenta el RQA se denomina Entropía (ENT). Se calcula agrupando las líneas diagonales definidas anteriormente, de acuerdo a sus longitudes y usando la siguiente fórmula:
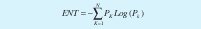
donde N es el número de grupos formados y Pk es el porcentaje de líneas de longitud k. El parámetro ENT está ligado con el %DET, pues la Teoría de la Información demuestra que la predecibilidad disminuye con el aumento de la entropía.
El último de los parámetros que consideraremos es el inverso de la línea máxima (1 / LMAX), donde la línea máxima (LMAX) es la línea más larga paralela a la diagonal principal. Se dice en [15] que éste parámetro está directamente relacionado con el inverso del máximo exponente positivo de Lyapunov. Valores pequeños de LMAX indican comportamiento caótico, valores grandes indican comportamiento periódico.
Estas medidas pueden aplicarse a la serie de datos completa, lo que daría una idea de comportamiento global, o pueden aplicarse de manera local a ventanas de la serie, para observar la evolución de la misma.
II. ANÁLISIS CUALITATIVO DE RECURRENCIA DE SERIES DE DATOS AUTOSEMEJANTES
Realizaremos a continuación el análisis de recurrencia de series de datos con diferentes grados de autosemejanza con el fin de establecer qué relación existe entre el grado de autosemejanza y el porcentaje de determinismo de la serie. Las figuras 13, 14 y 15 presentan los GR de tres series de datos con parámetro H= 0.5, H= 0.7, H= 0.9 respectivamente.
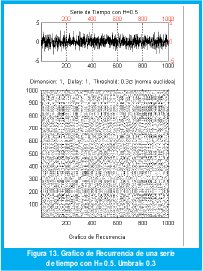
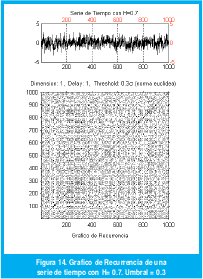
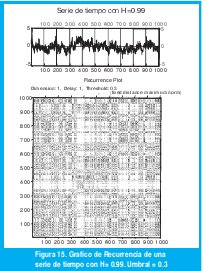
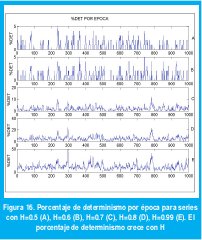
Para cada gráfico de recurrencia se ha calculado el %DET de manera local, tomando 1000 zonas o "épocas" dentro de la serie total. En el resultado, que se presenta en la figura 16, puede observarse el aumento del %DET local con el aumento de H.
El RQA muestra que las series de datos autosemejantes tienen una estructura determinística local, que aumenta con H. Este resultado es coherente con la memoria a largo plazo de las series autosemejantes y confirma, además, que es posible realizar predicciones a corto plazo en tales procesos, obteniendo mayor precisión en la predicción a medida que H aumenta.
III. CAOS Y TCP
En [9], András Veres demuestra que el protocolo de control de congestión de TCP puede inducir un comportamiento caótico y que existe fuerte dependencia de las condiciones iniciales. En esta sección se reproducen las simulaciones que dieron origen a estas conclusiones y se usan las herramientas estudiadas anteriormente para contrastar tales resultados.
El experimento realizado en NS-2 por Vères se basó en la topología propuesta en la figura 17.
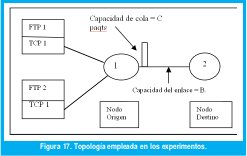
Tal red consiste en un par de fuentes TCP/Tahoe compartiendo un enlace de datos con capacidad C y longitud de cola B. Las variables de estado del sistema son el tamaño de la ventana de congestión de los protocolos TCP1 y TCP2 (las que llamaremos CWND1 y CWND2 respectivamente), que son fuentes de datos corriendo en el mismo nodo y compartiendo el mismo enlace. Cabe anotar que la ventana de congestión no es la única variable de estado que podría observarse para establecer la sensibilidad a las condiciones iniciales del sistema
Se dice que un sistema es sensible a las condiciones iniciales si la evolución del sistema en el espacio de fases es radicalmente diferente ante un cambio sutil en las condiciones iniciales del mismo. Es lógico que tal efecto no se presente en un sistema lineal, donde un cambio en las condiciones iniciales del mismo se verá reflejado en un cambio proporcional de su comportamiento.
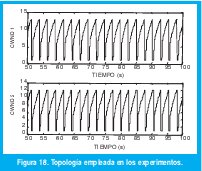
Veamos cómo se comporta nuestro sistema ante cambios sutiles en las condiciones iniciales. El primer ambiente de simulación tiene las siguientes características: C=0.5Mbps, capacidad de la cola del enlace = 20 paquetes, retardo del enlace = 10ms. Se muestra en la figura 18 evolución de las variables de estado del sistema respecto al tiempo entre 50 y 60 seg.
Se puede ver cómo ambos protocolos alcanzan un estado estable consistente en arranque lento cada vez que en la cola que hay entre los dos nodos se pierde un paquete, generando un comportamiento periódico.
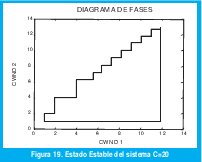
La figura 19 muestra el espacio de fases de este sistema, y en ella también se puede observar el comportamiento periódico.
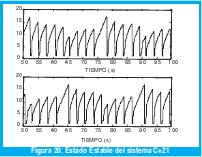
Ahora observemos el mismo sistema con un ligero cambio: la capacidad de la cola se ha incrementado en un paquete, para un total de 21 paquetes como máximo. En la figura 20 se muestra la evolución en el tiempo de las variables de estado del sistema y en la figura 21 se muestra el diagrama de fases.
Un pequeño cambio en el tamaño de la cola produjo un comportamiento completamente diferente en el sistema. Aunque no estemos en presencia de un atractor caótico, pues de nuevo el sistema sigue una trayectoria cerrada, la diferencia en la trayectoria del espacio fases es bastante notable.

Como se mencionó inicialmente, estos resultados ya han sido obtenidos por Vères en trabajos anteriores. De aquí en adelante aplicaremos el análisis de recurrencia a este sistema con el ánimo de caracterizar la dependencia a las condiciones iniciales.
Lo primero es observar las gráficas de recurrencia de cada serie. En este caso tomaremos como serie origen para la reconstrucción el valor de CWND1.
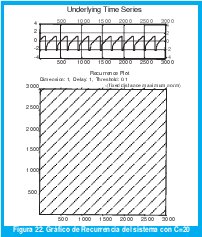

Las figuras 22, 23, 24, 25, 26 y 27 muestran el análisis de recurrencia para los casos en que la cola es igual a 20 y 21 paquetes. La serie se ha dividido en épocas o secciones de 40 puntos cada una.
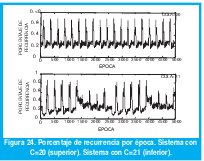
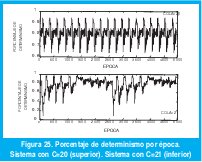
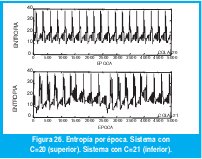
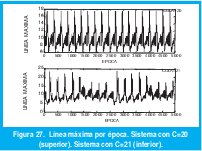
IV. CONCLUSIONES
Las graficas y el análisis de recurrencia permiten comprobar que los procesos autosemejantes son predecibles y que la predecibilidad de los mismos aumenta con el aumento de H. Mediante técnicas de Análisis de recurrencia se pudieron comprobar los resultados de los experimentos de Veres en [9], obtenidos mediante otros métodos tradicionales ligados al de los coeficientes de Lyapunov.
Quedan abiertos varios caminos en esta investigación Uno de ellos consiste en plantear el trabajo en términos de la teoría de la bifurcación, y encontrar el diagrama de bifurcación del sistema en términos de los parámetros del mismo.
El parámetro más destacable en este análisis de recurrencia es la Línea Máxima. En la figura 27 puede observarse que éste parámetro es menor en la fuente de datos donde la cola es 21 paquetes. Zbilut & Webber [15] afirman que una longitud de la línea máxima es inversamente proporcional al valor del coeficiente de Lyapunov máximo. Quiere decir esto que hay un coeficiente de Lyapunov mayor para el segundo caso, que para el primero, resultado que coincide con el encontrado por Veres.
V. AGRADECIMIENTOS
Agradecemos al Doctor Norbert Marwan, de la Universidad de Postdam, por habernos facilitado el uso del Matlab® Toolbox Cross Recurrente Plot 4.5, herramienta con la que se realizaron las Gráficas de Recurrencia.
REFERENCIAS BIBLIOGRÁFICAS
[1] M. Arlitt and C. Williamson. Web Server Workload Characterization: The search for Invariants. IEEE/ACM Trans. Networking, 5(5):631-645, 1997.
[2] J. Beran, R. Sherman, M. Taqqu and W. Willinger. Long-Range Dependence in VBR video traffic. IEEE. Trans. Commun. 43:1566-1579, 1995.
[3] M. Crovella, M. Taqqu and A. Betsavros. Heavy-Tailed Probability Distributions in the WWW, In "A practical guide to Heavy Tails", Adler, Feldman and Taqqu, editors. Birkhauser, 1998.
[4] M. Crovella and A. Bestavros. Self-similarity in WWW traffic. IEEE/ACM Trans. Networking, 5:835-846, 1997.
[5] A. Feldman, A. Gilbert, P. Huang and W. Willinger. Dynamics of IP Traffic: A Study of the Role of Variability and the Impact of Control. Proc. ACM SIGCOM'99, 1999.
[6] W. Leland, M. Taqqu, W. Willinger and D. Wilson. On the selfsimilar nature of Ethernet Traffic. IEEE/ACM Trans. Networking, 2:1-15, 1994.
[7] J. Baras. Control Problems in Modern Communication Networks. ENEE769 syllabus, University of Maryland, Spring 2001.
[8] W. Willinger and J. Doyle. Robustness and the Internet: Design and Evolution. Caltech, Pasadena, 2002.
[9] A.Veres and M.Boda. The Chaotic nature of TCP congestion control. IEEE Infocom'2000.
[10] P. Ranjan, E. Abed and R. La. Nonlinear Instabilities in TCPRED. IEEE Infocom'2002.
[11] Takens, F. Detecting strange attractors in fluid turbulence. In Dynamical Systems and Turbulence, Berlin: Springer-Verlag. 1981.
[12] Fraser A.M. Information Entropy in strange attractor. IEEE Transaction on Information Theory, Vol 35 N 2, 1989
[13] Eckmann J, Kamphorst S. Recurrence plots of dynamical sustems. Europhysucs Letters 5, 1987.
[14] Eckmann J. Oliffson K, Ruelle D, Ciliberto S. Liapunov exponents from time series. Physical Review A, Vol 34, Num 6, 1986.
[15] Zbilut J. P, Webber C.L Jr: Embeddings and delays as derived from quantification of recurrence plots. Physics Letters A 171 (3-4) 1992.
[16] Kennel M. B, Brown R, Abarbanel H.D.I, Determining embedding dimension for phase-space reconstruction using a geometrical construction, Phys. Rev. A 45, 3403 (1992).
[17] Williams Garnett. Chaos theory tamed. Joseph Henry press. Washington 1997.
[18] Packard N., Crutchfield N. H., Farmer J. D., Shaw R. S.: Geometry from a time series, Phys. Rev. Lett., Vol. 45, 1980, pp. 712-716.
Jose Felix Vega Stavro
Ingeniero Electrónico de la Universidad Distrital en 1998. Magíster en Teleinformática Universidad Distrital 2003. Fue asesor en el área de Telecomunicaciones del Ministerio de Agricultura entre 1998 y 2000. Coordinó el proyecto curricular de electrónica en la Universidad Pedagógica Nacional durante 2002. Actualmente se desempeña como docente en la Facultad de Ingeniería Electrónica de la Universidad Central.
Marco Aurelio Alzate Monroy
Ingeniero Electrónico de la Universidad Distrital en 1989 y Master en Ingeniería Electrica en la Universidad de los Andes 1991. Entre 1989 y 1992 fue docente-investigador en la División de Investigación del ITEC Telecom y luego se vinculó a la Facultad de Ingeniería de la Universidad Distrital donde actualmente se desempeña como profesor. En este momento adelanta su disertación doctoral en Ingeniería Electrica y de Computadores en la Universidad de Maryland USA.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










