DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.3.a08Published:
2016-10-09Issue:
Vol. 21 No. 3 (2016): September - DecemberSection:
Dossier "Complexity and Engineering"Modelo de encriptación simétrica basada en atractores caóticos
Symmetric Encryption Model Based on Chaotic Attractors
Keywords:
sincronización, caos, encriptación, atractor de Lorenz, comunicaciones digitales (es).Keywords:
Chaos, chaotic attractors, digital communications, encryption, security, synchronization (en).Downloads
References
P. Anghelescu, S. Ionita and E. Sofron, "Block Encryption Using Hybrid Additive Cellular Automata". 7th Interna-tional Conference on Hybrid Intelligent Systems (HIS 2007), Kaiserlautern, 2007, pp. 132-137.
R. S. Vignesh, S. Sudharssun and K. J. J. Kumar, "Limitations of Quantum & the Versatility of Classical Cryptog-raphy: A Comparative Study". Environmental and Computer Science, 2009. ICECS '09. Second International Confer-ence on, Dubai, 2009, pp. 333-337.
Louis M. Pecora y Thomas L. Carroll, “Synhronization in chaotic systems”. Physical Review Letters, Volumen 64, Número 8, Febrero 1990, pp. 821- 824.
Li S., Alvarez G., Li Z. y Halang W. A., 2007. Analog chaos-based secure communications and cryptanalysis: a brief survey. PhysCon.
L. Kocarev, “Chaos-based cryptography: A brief overview”. IEEE Circuits and Systems Magazine, 2001, 1(2): 6-21.
K. M. Cuomo, A. V. Oppenheim, y Steven H. Strogatz, “Synchronization of Lorenz-Based Chaotic Circuits with Applications to Communications”. IEEE transactions on circuits and systems-II: analog and digital signal processing, Volumen 40, Número 10, Octubre 1993, pp. 626-633.
V. Milanovic and M.E. Zaghloul, “Improved masking algorithm for chaotic Communication systems”. Electronic Letters, 1996, 32(1): 11-12.
M. S. Azzaz, C. Tanougast, et al., “Real-time FPGA implementation of Lorenz's chaotic generator for ciphering telecommunications”. IEEE North-East Workshop on Circuits and Systems and TAISA Conference, 2009, pp. 1-4.
Camilo A. Ramírez, “Enmascaramiento de Información Mediante Sistemas Caóticos Sincronizados”, Tesis de ma-gister, Departamento de matemáticas, Universidad Nacional de Colombia, Bogotá D.C., Colombia, 2011.
N.K. Pareek, Vinod Patidar y K.K. Sud. “Image encryption using chaotic logistic map”. Image and Vision Compu-ting, 2006, 24(9): 926-934.
M.S. Baptista, “Cryptography with chaos”. Physics Letters A. Vol 240, 1998, pp 50-54.
Murillo-Escobar M.A. y Cruz-Hernández C. “Cifrado caótico de plantilla de huella dactilar en sistemas biomé-tricos”. Congreso Latinoamericano de Control Automático, 2014, 18-23.
Yuling Luo, Lvchen Cao, Senhui Qiu, Hui Lin, Jim Harkin y Junxiu Liu, “A chaotic map-control-based and the plain image-related cryptosystem”. 2016. Nonlinear Dynamics. Volume 83, Issue 4, pp 2293-2310.
A. Akgül, S. Kaçar, B. Aricıoğlu and İ Pehlivan, "Text encryption by using one-dimensional chaos generators and nonlinear equations". Electrical and Electronics Engineering (ELECO), 2013 8th International Conference on, Bursa, 2013, pp. 320-323.
Steven H. Strogatz, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engi-neering. Perseus Books, Reading, Estados Unidos, 1994, pp. 301-347.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.3.a08
Modelo de Encriptación Simétrica Basada en Atractores Caóticos
Symmetric Encryption Model Based on Chaotic Attractors
José Moreno
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. jdmorenop@udistrital.edu.co
Fabio Parra
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. faparraf@correo.udistrital.edu.co
Rafael Huérfano
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. rehuerfanoo@correo.udistrital.edu.co
Cesár Suarez
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. casuarezp@udistrital.edu.co
Isabel Amaya
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. iamaya@udistrital.edu.co
Recibido: 04-12-2015. Modificado: 15-05-2016. Aceptado: 28-07-2016
Resumen
Contexto: El aumento en la capacidad de procesamiento de las máquinas y los desarrollos en los algoritmos de búsqueda combinatoria disminuyen el tiempo necesario para descifrar fraudulentamente la información; por esta razón se plantea la necesidad de generar nuevas formas de codificar la información para su transmisión segura.
Método: En este artículo se presenta un modelo de encriptación simétrico extensible para comunicaciones digitales, aprovechando el caos generado por sistemas dinámicos no lineales.
Resultados: El modelo desarrollado demostró estar en la capacidad de encriptar mensajes en tiempos de sincronización, encriptación y desencriptación inferiores a 1 ms con una entropía superior a 6 usando el atractor de Rössler para su implementación.
Conclusiones: El algoritmo se presenta como una alternativa a los algoritmos tradicionales de combinatoria demostrando una mayor eficiencia en la gestión de recursos computacionales y plantea las bases para su continuar con su estudio en la comunidad académica interesada, debido a la variedad de los sistemas dinámicos no lineales.
Palabras claves: Atractores caóticos, caos, comunicaciones digitales, encriptación, seguridad, sincronización.
Idioma: Español
Abstract
Context: The increase in the processing capacity of machines and developments in combinatorial search algorithms reduces the time required to decipher the information fraudulently. Bear in mind this, there is a need to generate new ways of encoding information for secure transmission.
Method: In this paper a symmetrical and extensible model for digital communications encryption is presented, taking advantage of the chaos generated by nonlinear dynamic systems.
Results: The developed model proved to encrypt messages in time synchronization, encryption and decryption less than 1 ms with an entropy higher than 6 using the Rössler attractor for its implementation.
Conclusions: The algorithm is presented as an alternative to traditional algorithms demonstrating greater efficiency in the management of computing resources and raises the groundwork for continuing their study on the interested academic community due to the variety of dynamical systems nonlinear.
Keywords: Chaos, chaotic attractors, digital communications, encryption, security, synchronization.
1. Introducción
Los sistemas dinámicos estudian el comportamiento de fenómenos físicos en el tiempo, los cuales se modelan matemáticamente por medio de ecuaciones diferenciales o en diferencias finitas, según se trate de fenómenos de tipo continuo o discreto, respectivamente. El propósito es, antes que hallar la solución analítica, analizar el comportamiento del sistema a largo plazo y determinar si al realizar pequeños cambios en las condiciones iniciales del modelo, se generan cambios trascendentales con el paso del tiempo; en caso afirmativo, se trata de una situación en la que aparece el caos, que está ligado a fenómenos de tipo no lineal, en los cuales el comportamiento es impredecible a largo plazo. En el año 1963, el meteorólogo Edward Lorenz estudió el comportamiento de la atmósfera y quiso proponer un modelo matemático para realizar predicciones del clima, formuló lo que en la actualidad se conoce como ecuaciones de Lorenz, pero, curiosamente, por medio de simulaciones computacionales se dio cuenta de que, ante pequeñas perturbaciones de los datos iniciales, el sistema cambiaba su comportamiento, lo cual impedía hacer predicciones.
Por otra parte, la criptografía es una disciplina muy antigua y tiene como fin proteger información confidencial, ha sido utilizada desde su origen en entornos políticos, militares, religiosos, entre otros. El intercambio de información juega un papel trascendental en la actualidad y gracias al progreso de la tecnología existen prometedores resultados con respecto a la evolución y mejora de la seguridad en su transmisión. Según el número de claves utilizadas, los sistemas criptográficos se clasifican en simétricos y asimeétricos, en los sistemas simétricos el emisor y el receptor utilizan la misma clave y en los sistemas asimétricos el emisor y el receptor utilizan claves distintas.
Los algoritmos convencionales de encriptación se basan en factorización de enteros y en el problema de logaritmo discreto, pero continuamente se están desarrollando nuevos algoritmos, como los basados en los principios de la mecánica cuántica, los algoritmos que implementan autómatas celulares y los que utilizan la teoría del caos.
Los autómatas celulares corresponden a modelos matemáticos idealizados de sistemas físicos en los cuales el espacio y el tiempo se consideran discretos y evolucionan mediante reglas de iteración de tipo local. Este principio es aprovechado para el enmascaramiento de información, un mensaje es enmarcado dentro de una vecindad y esta lo encripta a medida que evoluciona. En [1] se muestra una aplicación de autómatas celulares para la encriptación de datos médicos enviados a través de internet. El problema que presenta este método corresponde a la complejidad de las reglas utilizadas, ya que a mayor complejidad no es posible predecir el comportamiento futuro del sistema de encriptación; sin embargo, si las reglas no son lo suficientemente complejas el sistema de encriptación se vuelve vulnerable.
La criptografía cuántica fue propuesta en 1984 por Brennet y Brassard y está basada en el teorema de la no clonación de la mecánica cuántica. Aunque los sistemas de criptografía cuántica no son de fácil acceso por la construcción del ordenador cuántico, se advierte que estos serían una amenaza a los sistemas de criptografía convencional debido a que se podría factorizar a una velocidad superior a la de los ordenadores actuales [2].
Este artículo se centra en los algoritmos basados en caos, estos aparecieron en 1990 como una aplicación novedosa de los sistemas dinámicos no lineales y en las últimas décadas han tomado mucha fuerza en el diseño de algoritmos de encriptación [3] - [15], lo que ha generado una nueva línea de investigación denominada criptografía caótica.
El caos ha sido utilizado para diseñar comunicaciones seguras de forma análoga y digital, ya que existen propiedades similares, como por ejemplo, la sensibilidad de los sistemas caóticos a las condiciones iniciales se asemeja a la propiedad de difusión en los sistemas de criptografía. La baja sensibilidad a la clave secreta y la posibilidad latente de ataques basados en la estimación de los parámetros de encriptación son considerados los dos mayores problemas en casi todos los sistemas de comunicación análoga basados en caos, cuya seguridad se fundamenta en la teoría de sincronizació de los atractores caóticos propuesta por Pecora y Carroll. [3], [4].
En [5] el autor describe las fortalezas que aportan los sistemas caóticos en términos de la seguridad de la información, aunque advierte que los algoritmos basados en caos que incluyen los principios de difusión y confusión, no se pueden comparar con los algoritmos criptográficos tradicionales, debido a que usualmente presentan debilidades en términos de seguridad y rapidez de convergencia. Además, hace analogías entre los fundamentos de los sistemas dinámicos y los de la criptografía; la interrelación básicamente la plantea bajo la premisa que los algoritmos de encriptación de bloques pueden ser reescritos como sistemas dinámicos en tiempo discreto, donde la condición inicial es el texto plano que se va a encriptar y el estado final es el texto encriptado.
Por otra parte, el autor resalta que los parámetros de la función caótica pueden representar la clave del algoritmo de encriptación, y que el sistema debe satisfacer la propiedad de mezcla la cual permite generar el princi- pio de difusión, que significa esparcir un dígito del texto original en muchos dígitos del texto cifrado. También, señala que el futuro de la criptografía basada en caos depende de si la solución del problema es computacionalmente impredecible, es decir, que no pueda ser resuelto por máquinas de tiempo polinómico probabilístico.
En el año 1993 Kevin Cuomo y Alan Oppenhein, utilizaron la propiedad de sincronización para ocultar comunicaciones análogas implementando las ecuaciones de Lorenz en los circuitos electrónicos de emisión y recepción. Ellos propusieron dos estrategias para el encriptamiento de la información, la primera adicionando al mensaje el enmascaramiento caótico de la señal común en el emisor y luego restándolo en el receptor, la segunda consistió en utilizar la modulación de las señales caóticas para adicionar el mensaje en el circuito emisor y luego hacer la detección del error en el circuito receptor [6].
En 1996 en [7] los autores propusieron un método de sincronización robusta, basado en un sistema de realimentación, para esquemas de comunicación caótica. Este método permite que, en ausencia de ruido, múltiples señales en un solo canal logren una perfecta sincronización de los receptores con sus respectivos transmisores.
M.S. Azzaz, C. Tankougast, S. Sadoudi y Adandach, de la Universidad Paul Verlaine de Metz en Francia, realizaron la implementación de una llave aleatoria, para encriptar y desencriptar información , basada en el atractor caótico de Lorenz, sobre compuertas programables FPGA (Field Programing Gates Array), con lo cual lograron, según lo indican, una arquitectura de hardware compacta y con alta velocidad de desempeño. La arquitectura se diseño con base en la solución numérica de las ecuaciones de Lorenz por el método Runge Kutta 4 [8].
En el año 2011, se realizó una tesis de maestría, en la Universidad Nacional de Colombia Sede Bogotá, alusiva al enmascaramiento de información mediante sistemas caóticos sincronizados, en la que se aplicó la propiedad de sincronismo de algunos sistemas caóticos para simular numéricamente el enmascaramiento de información, la transmisión y recuperación de ésta, utilizando la técnica de enmascaramiento Chaotic Shift Keying (CSK) con los modelos de Lorenz, Rössler y Sprott [9].
En [10], se propone un nuevo enfoque para la encriptación de imágenes en tiempo real utilizando dos funciones logísticas y empleando una clave de 80 bits, la llave secreta es dinámica y se cambia cada 16 pixeles. Aprovechando las propiedades caóticas de las funciones logísticas demuestran la alta sensibilidad de la clave secreta.
En [11] se presenta un algoritmo para encriptar texto plano por medio de la función logística, pero se genera un sistema de encriptación débil y lento ya que el mensaje es encriptado con el número entero de iteraciones realizadas por esta función.
En [12], se describe una aplicación de un algoritmo de encriptación caótico para cifrar plantillas de huella dactilar con base en la generación de sucesiones caóticas utilizando la función logística y un proceso de permutación y difusión para evitar el robo de identidad. La encriptación basada en caos ha demostrado ser mejor debido a las propiedades inherentes de ergodicidad, sensibilidad, parámetros de control, pseudo-aleatoriedad y mezcla, todos estos útiles para mejorar la seguridad de la transmisión de la información.
En [13] se propone un algoritmo de encriptación de imágenes utilizando la función lineal a trozos conocida en la literatura de los sistemas dinámicos como función tienda. El valor de los pixeles de la imagen plana y la clave inicial son calculados mediante un algoritmo de cuantificación dando como resultado un valor decimal, el cual se utiliza como valor inicial de la función tienda. El algoritmo de cuantificación está basado en operaciones de multiplicación, por lo que pequeños cambios en la imagen plana generan una alta sensibilidad en los resultados de cuantificación. Con el decimal obtenido en el proceso de cuantificación se generan dos sucesiones ergódicas, usadas para el proceso de permutación, se aplica también difusión, en el cual los valores de los pixeles son modificados basados en la división y operación módulo utilizando ocho valores caóticos especiales. Los autores muestran que el método de encriptación es robusto y seguro, por lo tanto, es apropiado para utilizar como herramienta de cifrado de imágenes.
En [14] se desarrolla un modelo factible de encriptación caótico utilizando las propiedades que presentan tres funciones generadoras de caos, la función logística, la función de Pinchers y Sinecircle, los autores logran tiempos de encriptación por debajo de 1.5 milésimas de segundo, para desencriptar un tiempo inferior a 61.3 milésimas de segundo y una entropía superior a 7.4, que garantiza un alto nivel de eficiencia y seguridad.
En la literatura existen desarrollos de algoritmos de encriptación basados en caos utilizando un único sistema dinámico caótico, en este artículo se desarrolla un algoritmo de encriptación genérico, es decir, un algoritmo extensible a cualquier sistema caótico sincronizable como lo plantea Pecora & Caroll en [3]. Una vez sincronizados ambos subsistemas, cada mensaje se encripta superponiendo una de las componentes del atractor con la representación en ASCII del mensaje. Como caso de estudio, se implementó el algoritmo desarrollado con los sistemas caóticos de Lorenz y Rössler.
2. Marco Teórico
2.1. Generalidades de los sistemas dinámicos caóticos
Un sistema dinámico es una representación matemática de un sistema físico, que busca predecir su comportamiento a medida que transcurre el tiempo; la representación matemática involucra ecuaciones diferenciales o ecuaciones en diferencias finitas, según sea de tipo continuo o discreto respectivamente. Cuando no se satisface el principio de superposición se está ante la presencia de un sistema no lineal para lo cual se hace un estudio fundamentalmente de tipo cualitativo para caracterizar su dinámica en el tiempo, la no linealidad abre la posibilidad de que se genere caos.
En este artículo se entiende que el caos ocurre cuando el sistema presenta un comportamiento aperiódico a largo plazo, es decir, existen trayectorias que con el paso del tiempo no convergen a órbitas periódicas, cuasi periódicas, o puntos fijos y exhibe una dependencia sensible a pequeñas variaciones en las condiciones iniciales; lo que significa que dos trayectorias cercanas, a medida que transcurre el tiempo se separan de forma exponencial. Los sistemas dinámicos caóticos sincronizables son caracterizados por los exponentes de Lyapunov negativos, una entropía y complejidad algorítmica positiva, y tienen otras propiedades tales como mezcla y preservación de medida en las transformaciones [5].
Lorenz formuló un modelo tridimensional para realizar predicciones climatológicas y notó que, si el modelo se alimentaba de la observación anterior con cifras redondeadas, en lugar de las cifras reales, este se comportaba inicialmente de la misma forma, pero rápidamente comenzaban a trazarse trayectorias totalmente distintas a las seguidas cuando las cifras eran las reales, lo cual generaba predicciones erróneas en las condiciones climatológicas [15].
El modelo de Lorenz se describe en la ecuación (1).
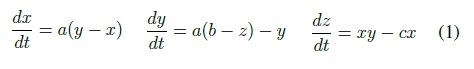
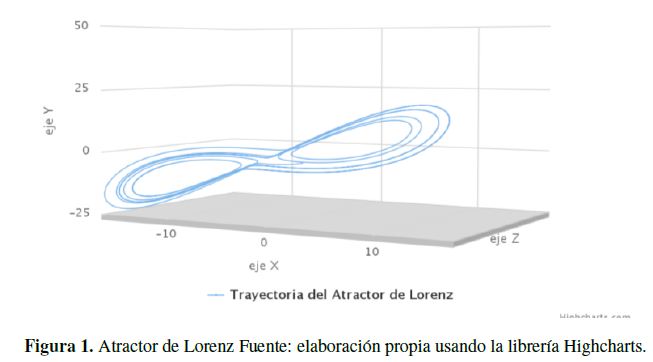
Donde cada punto (x; y; z) representa un estado de la atmósfera y, a,b y c son parámetros. Para analizar su evolución se debe seguir un campo de vectores, dicho sistema presenta comportamiento caótico para varios valores de los parámetros y originó todo un desarrollo en la teoría de los sistemas dinámicos caóticos. La Figura 1, muestra una trayectoria descrita por el atractor de Lorenz.
2.2 Sincronización de sistemas dinámicos caóticos
La sincronización es el proceso en el que dos o más sistemas caóticos logran un comportamiento dinámico común después de un estado transitorio [5]. En 1989, Louis M. Pécora y Thomas L. Carroll, descubrieron el sincronismo que se puede presentar en atractores caóticos, descomponiendo los sistemas en por lo menos dos subsistemas y encadenándolos con señales comunes; si los exponentes de Lyapunov de los subsistemas son todos negativos, ellos demostraron que los subsistemas se sincronizarán, es decir, la trayectoria de un subsistema convergerá hacia la del otro, a medida que el tiempo transcurre [3].
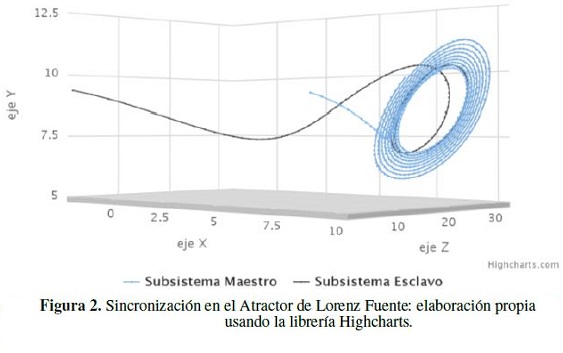
La sincronización de sistemas se ha utilizado para encriptar información, gracias a la impredictibilidad en el comportamiento de los sistemas caóticos. Para realizar la sincronización se requieren dos sistemas, uno llamado maestro, que es el sistema caótico original, y el otro denominado esclavo, el cual se construye de subsistemas obtenidos a partir del sistema original y seleccionando la variable que se desee como enlace, llamada variable sincronizante o conductora. La Figura 2 muestra el proceso de sincronización, siendo la trayectoria del subsistema esclavo la línea negra y la del maestro la línea azul.
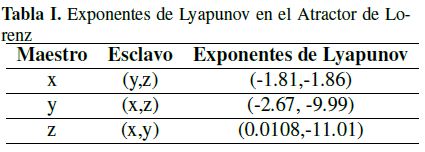
Particularmente, en el caso del atractor de Lorenz, Pécora formuló 3 formas de dividir el sistema de acuerdo con la componente x, y o z que se escoja como maestra y las dos restantes como esclavos respectivamente. Por cada una de estas posibles divisiones se debe calcular los sub exponentes de Lyapunov como se muestra en la Tabla I. El sistema de Lorenz presenta exponentes de Lyapunov negativos, como lo calculó Pécora & Carroll, cuando la componte x ó y se seleccionan como maestros.
3. Algoritmo de encriptación propuesto
En el esquema de encriptación desarrollado se toma un sistema caótico y se divide en dos subsistemas autónomos llamados maestro y esclavo. El subsistema maestro es asignado al emisor y el esclavo al receptor. Tanto el emisor como el receptor inicializaran sus sistemas caóticos en condiciones iniciales diferentes. Posteriormente, el maestro envía la componente conductora hacia el receptor hasta que los dos subsistemas estén sincronizados. Una vez sincronizados los dos subsistemas, se representa el mensaje en ASCII y se suma cada carácter con una de las componentes del atractor obtenidas en una unidad de tiempo ti. La unidad de tiempo va aumentando a medida que se codifica cada carácter. Finalmente, se convierte el mensaje encriptado utilizando la tabla ASCII y se envía al receptor.
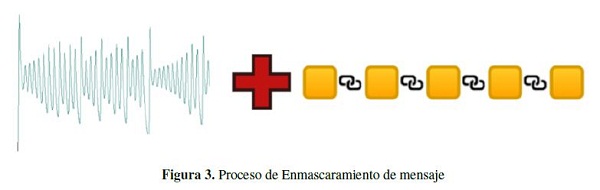
El receptor toma el mensaje, lo representa en ASCII y resta cada digito con una de las componentes del atractor obtenidas en la misma unidad de tiempo ti. La unidad de tiempo va aumentando a medida que se decodifica cada caracter. El mensaje desencriptado se convierte a caracteres utilizando la tabla ASCII. En la Figura 3, se esquematiza el proceso anterior, los cuadrados amarillos representan el mensaje en código ASCII y se muestra la superposición del caos con el mensaje.
Se deben tener presentes las siguientes consideraciones:
- Se pueden generar las condiciones iniciales de forma aleatoria, pero si los valores se alejan demasiado de la región ocupada por el atractor, el proceso de sincronización tomará más tiempo.
- La convergencia de la sincronización será más rápida entre más pequeña sea la unidad de tiempo y menor la cantidad de dígitos decimales utilizados para la aproximación.
- En caso de obtener valores negativos durante el proceso de encriptación, se debe tomar el valor absoluto de estos y sumarlo al valor en ASCII con el fin de evitar números negativos en el mensaje encriptado.
- Los dígitos del mensaje encriptado no pueden ser superiores a 255.
- Se deben tomar unidades de tiempo grandes con el fin de generar la mayor entropía posible durante el proceso de encriptaci'on, el cual se inicia una vez los atractores estén sincronizados.
Con el fin de ilustrar el algoritmo de encriptación desarrollado, se toma como caso de estudio el
atractor de Lorenz con los parámetros 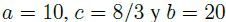 . A continuación, se describen las
fases de desarrollo:
. A continuación, se describen las
fases de desarrollo:
- Se divide el sistema en dos subsistemas maestro - esclavo, en este caso se utilizó como maestro debido a que sus exponentes de Lyapunov son los más negativos, recordando que entre más negativos sean los exponentes de Lyapunov, más rápida será la convergencia.
- Se inicializan los subsistemas con condiciones iniciales aleatorias que esén cercanas a la región del atractor.
- Se sincronizan los atractores enviando la componente maestra hacia el esclavo. Se generan los 700 primeros valores del atractor maestro utilizando Runge Kutta 4 con un salto h = 0;01(centésimas de segundo) y se envían los resultados de la componente como clave pública K hacia el atractor esclavo. Este proceso se representa en la ecuación 2.
- Se determina la longitud del mensaje, que corresponde al número n de caracteres que éste posee. Por ejemplo, el mensaje "Hola" tiene cuatro caracteres, por lo tanto n = 4.
- Como se muestra en la ecuación 4, se convierte cada dígito del mensaje m en su representación numérica según la tabla ASCII.
- Se calcula la salida del atractor para n iteraciones. Utilizando Runge Kutta 4 con un salto h = 0;1(décimas de segundo) se generan n valores del atractor representados como se muestra en (5).
- Se debe actualizar ti a tj , debido a que cada vez que se codifica un mensaje, existe un corrimiento de n * h unidades de tiempo, con el fin de no perder la sincronía entre los subsistemas maestro y esclavo.
- Se suma cada salida del vector e con los caracteres del mensaje m representados en la tabla ASCII, para superponer el mensaje con el caos generado por el atractor obteniendo el mensaje encriptado me, como se muestra en (7).
- Se convierte el mensaje codificado me en caracteres ASCII.

Siendo yi el número obtenido en la iteración , en el instante de tiempo ti definido como se muestra en 3

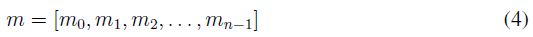
Tomando el ejemplo anterior, el mensaje "Hola" representado en ASCII corresponde a m = [72; 111; 108; 97].

Donde ei corresponde a la salida del atractor en valor absoluto, aproximada a un dígito y multiplicada por 10. En un instante de tiempo tj definido en (6) .
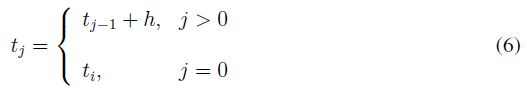
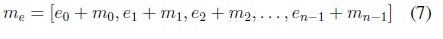
Para el proceso de desencriptación se generan los valores obtenidos desde el emisor en el receptor tomando el mismo instante tj , como la longitud del mensaje encriptado es la misma que la del mensaje original, basta con repetir los pasos 4, 5, 6 y 7 en el sistema esclavo. Finalmente, el mensaje desencriptado md se calcula utilizando la fórmula mostrada en (8).
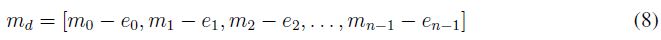
Aunque el algoritmo de encriptación descrito anteriormente utiliza el atractor de Lorenz, conviene precisar que este algoritmo puede extenderse reemplazando el sistema de Lorenz por otro sistema dinámico caótico que cumpla las condiciones descritas anteriormente; particularmente en la sección 4 se ejemplifica con el atractor de Rössler.
4. Implementación del algoritmo
Con el propósito de mostrar la validez y viabilidad del algoritmo propuesto, se realizaron pruebas cifrando un texto utilizando los atractores de Rössler y Lorenz en el lenguaje de programación JavaScript 1.8.
La Tabla II muestra el resumen del proceso de encriptación y desencriptación para un mensaje especifico usando el atractor de Lorenz como caso de prueba para el algoritmo desarrollado. Debido a que las condiciones iniciales son aleatorias en cada ejecución y al desplazamiento en el tiempo cada vez que se codifica un mensaje, se genera una codificación diferente para un mismo mensaje en instantes de tiempo diferente. Si se hace una segunda ejecución, con el mismo atractor y el mismo mensaje se genera una nueva codificación.
En la Tabla III, se muestra el mismo texto, pero encriptándolo mediante el atractor de Rössler, siguiendo el algoritmo propuesto.
En todos los casos se desencriptó el mensaje sin ningún tipo de inconveniente y con tiempos buenos de ejecución, como se evidencia en el análisis de seguridad.
5. Anális de seguridad
Para analizar el desempeño del algoritmo propuesto se midió el tiempo de sincronización, el tiempo de encriptación, el tiempo de desencriptación y la entropía para diez ejecuciones del algoritmo y posteriormente se calculó el promedio de estos, ya que los tiempos de ejecución varían debido a la naturaleza de los sistemas dinámicos no lineales y las condiciones iniciales aleatorias en cada ejecución. Estas pruebas fueron realizadas en una máquina con 8 GB de memoria RAM y un procesador Intel R Core(TM) i5-4210U CPU @ 1.70HGz 2.40 GHz. A continuación, se describen las métricas utilizadas para evaluar el desempeño del algoritmo sobre los atractores de Rössler y Lorenz:
- El tiempo de sincronización corresponde al tiempo requerido para que la trayectoria del atractor esclavo se sincronice con la del maestro. Este tiempo comienza a medirse después de la generación de la clave pública y su recepción por parte del emisor.
- El tiempo de encriptación se cuenta a partir del instante en que finaliza la sincronización, se mide desde el momento que se recibe el mensaje hasta que este se encripta.
- El tiempo de desencriptación se mide desde el momento en que se recibe el mensaje encriptado hasta que este se desencripta.
Finalmente, para la medición de la entropía se utilizó la fórmula de Shannon mostrada en la ecuación (9).
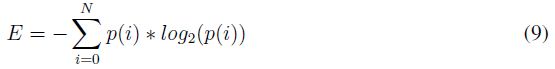
Donde pi denota la probabilidad de obtener el caracter i del mensaje codificado y N la longitud del mensaje. A medida que el valor de la entropía aumente, mayor va a ser la fiabilidad del método de encriptación.
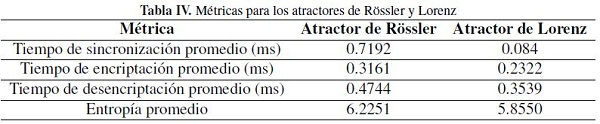
En la Tabla IV se sintetizan los resultados de las métricas tomadas sobre los atractores extraños. Se evidencia que los tiempos de sincronización, encriptación y desencriptación están por debajo de 1 milisegundo (ms), presentando un mejor desempeño para el atractor de Lorenz, sin embargo la entropía tiene un mejor desempeño con el atractor de Rössler.
5.1 Análisis de sensibilidad
Debido a la propiedad de alta sensibilidad que tienen los sistemas caóticos y la imposibilidad de sincronización cuando no se envían los resultados de las trayectorias del atractor maestro, un solo cambio en la clave pública K impediría la sincronización del sistema esclavo y su posterior desencriptación del mensaje. En la Figura 4 se muestra un intento fallido de desencriptación al sumar 0.1 a la salida del atractor de Lorenz en K700.
6. Conclusiones
Se logró formular un algoritmo eficiente de encriptación basado en atractores caóticos. Aunque solo se utilizaron los atractores de Lorenz y Rössler, se pueden emplear otros atractores caóticos que cumplan con las condiciones descritas en este documento, los cuales podrían aumentar la variabilidad y por ende la seguridad del algoritmo, hecho que debe motivar a la comunidad académica interesada en el tema a seguir explorando la interacción entre el caos y la seguridad.
Se destaca que, en el proceso de sincronización y encriptación, se cambian los valores de h con el fin de obtener un equilibrio entre tiempo de sincronización y entropía del mensaje a encriptar. Se recomienda usar valores de h pequeños al momento de la sincronización, ya que valores muy grandes generan una llave más grande y valores más grandes para la encriptación y desencriptación, con el fin de generar mayor entropía.
En este artículo se utilizó una sola componente del atractor caótico para realizar la encriptación, pero en el futuro se podría pensar en usar todas las componentes del atractor en instantes de tiempo diferentes con el fin de aumentar la entropía del mensaje encriptado. Además, se recomienda proteger la clave pública para evitar la sincronización de otro sistema intruso esclavo, lo cual se puede lograr aprovechando un sistema de encriptación asimétrico.
Con la implementación del algoritmo propuesto y basados en los resultados de las métricas obtenidas se logró evidenciar un tiempo bastante corto en el proceso de encriptación, desencriptación y sincronización, además de un valor de entropía alto, por lo cual se puede recomendar como un método viable y seguro de cifrado. Según los resultados obtenidos se aconseja usar el atractor de Rössler, ya que a pesar de que sus tiempos de ejecución son mayores que los de Lorenz, son infinitesimales en ambos casos, mientras que su entropía es mayor, lo que garantiza un mejor nivel de seguridad.
Con los resultados de las métricas tomadas, se evidencia que el algoritmo desarrollado tiene un buen desempeño en términos de tiempo inferiores a 1 ms, al ser comparado con el propuesto en [14], se muestra que existe una mejora en términos de tiempo de ejecución, aunque, cabe recalcar que los autores no especifican las características del recurso utilizado para la ejecución de tales pruebas, ni la cantidad de pruebas realizadas.
Referencias
[1] P. Anghelescu, S. Ionita and E. Sofron, "Block Encryption Using Hybrid Additive Cellular Automata". 7th International Conference on Hybrid Intelligent Systems (HIS 2007), Kaiserlautern, 2007, pp. 132-137.
[2] R. S. Vignesh, S. Sudharssun and K. J. J. Kumar, "Limitations of Quantum & the Versatility of Classical Cryptography: A Comparative Study". Environmental and Computer Science, 2009. ICECS '09. Second International Conference on, Dubai, 2009, pp. 333-337.
[3] Louis M. Pecora y Thomas L. Carroll, "Synhronization in chaotic systems". Physical Review Letters, Volumen 64, Número 8, Febrero 1990, pp. 821- 824.
[4] Li S., Alvarez G., Li Z. y Halang W. A., 2007. Analog chaos-based secure communications and cryptanalysis: a brief survey. PhysCon.
[5] L. Kocarev, "Chaos-based cryptography: A brief overview". IEEE Circuits and Systems Magazine, 2001, 1(2): 6-21.
[6] K. M. Cuomo, A. V. Oppenheim, y Steven H. Strogatz, "Synchronization of Lorenz-Based Chaotic Circuits with Applications to Communications". IEEE transactions on circuits and systems-II: analog and digital signal processing, Volumen 40, Número 10, Octubre 1993, pp. 626-633.
[7] V. Milanovic and M.E. Zaghloul, "Improved masking algorithm for chaotic Communication systems".Electronic Letters, 1996, 32(1): 11-12.
[8] M. S. Azzaz, C. Tanougast, et al., "Real-time FPGA implementation of Lorenz's chaotic generator for ciphering telecommunications". IEEE North-East Workshop on Circuits and Systems and TAISA Conference, 2009, pp. 1-4.
[9] Camilo A. Ramírez, "Enmascaramiento de Información Mediante Sistemas Caóticos Sincronizados", Tesis de magister, Departamento de matemáticas, Universidad Nacional de Colombia, Bogotá D.C., Colombia, 2011.
[10] N.K. Pareek, Vinod Patidar y K.K. Sud. "Image encryption using chaotic logistic map".Image and Vision Computing, 2006, 24(9): 926-934.
[11] M.S. Baptista, "Cryptography with chaos". Physics Letters A. Vol 240, 1998, pp 50-54.
[12] Murillo-Escobar M.A. y Cruz-Hernández C. "Cifrado caótico de plantilla de huella dactilar en sistemas biométricos". Congreso Latinoamericano de Control Automático, 2014, 18-23.
[13] Yuling Luo, Lvchen Cao, Senhui Qiu, Hui Lin, Jim Harkin y Junxiu Liu, "A chaotic map-control-based and the plain image-related cryptosystem". 2016. Nonlinear Dynamics. Volume 83, Issue 4, pp 2293-2310.
[14] A. Akgül S. Kacar, B. Aricioglu and .I Pehlivan, "Text encryption by using one-dimensional chaos generators and nonlinear equations". Electrical and Electronics Engineering (ELECO), 2013 8th International Conference on, Bursa, 2013, pp. 320-323.
[15] Steven H. Strogatz, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering. Perseus Books, Reading, Estados Unidos, 1994, pp. 301-347.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.







2.jpg)










