DOI:
https://doi.org/10.14483/23448393.16719Published:
2020-12-19Issue:
Vol. 26 No. 1 (2021): January-AprilSection:
Electrical and Electronic EngineeringDiseño de un controlador lineal cuadrático gaussiano y un controlador autosintonizado por asignación de polos para el control del voltaje de un generador CD
Design of a Linear Quadratic Gaussian Controller and a Self-Tuning Regulator Based on Pole Placement to Control the Voltage of a DC Generator
Keywords:
Kalman filter, LQR controller, STR controller, cost function (en).Keywords:
filtro de Kalman, controlador LQR, controlador STR, función de costo (es).Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 7 de agosto de 2020; Revisión recibida: 30 de octubre de 2020; Aceptado: 27 de noviembre de 2020
Resumen
Contexto:
En este artículo se presenta el diseño de un controlador lineal cuadrático gaussiano para regular el voltaje de un generador CD y se compara su desempeño con el de un regulador autoajustable sintonizado por asignación de polos.
Método:
Para implementar estas estrategias de control, se utiliza el prototipo de un generador CD y se obtiene el modelo matemático del sistema utilizando identificación no paramétrica, se presentan las bases teóricas y el diseño de las dos estrategias de control y se realiza la comparación del desempeño de los dos controladores utilizando métricas de la integral del error y respuesta temporal.
Resultados:
Las métricas de la integral del error y las de respuesta temporal muestran que, aunque el desempeño del controlador lineal cuadrático gaussiano es ligeramente superior al presentado por el controlador autoajustable por asignación de polos, con las dos estrategias de control las respuestas del sistema son estables, con buena velocidad de respuesta y error de estado estable igual a cero.
Conclusiones:
Las estrategias de control lineal cuadrático gaussiano y el control autosintonizado son una buena alternativa al control convencional y generan un adecuado control del proceso, acorde con los requerimientos del sistema.
Palabras clave:
filtro de Kalman, controlador LQR, controlador STR, función de costo..Abstract
Context:
This paper presents the design of a Linear Quadratic Gaussian controller to regulate the voltage of a DC generator, and its performance is compared with that of a self-tuning regulator based on pole placement.
Method:
To implement these control strategies, a prototype DC generator is used, and the mathematical model of the system is obtained by means of non-parametric identification. The theoretical bases and the design of the two control strategies are presented, and the performance comparison of the two controllers is performed by using metrics from their integral error and time response.
Results:
Integral error and time response metrics show that, although the performance of the Linear Quadratic Gaussian controller is slightly higher than that presented by the self-tuning controller, system responses are stable with both control strategies, as well as with a good speed response and a steady-state error equal to zero.
Conclusions:
A Linear Quadratic Gaussian controller and self-tuned control strategies are a good alternative to conventional control and generate an adequate process control that is in line with system requirements.
Keywords:
Kalman filter, LQR controller, STR controller, cost function.Introducción
La aplicación intensiva de las técnicas del control automático de procesos se basa en la evolución de las tecnologías de medición y control aplicadas al ambiente industrial. El crecimiento en la complejidad de los procesos industriales ha traído como consecuencia que el control automático de los mismos se haya desarrollado a gran velocidad, y que los modos de control convencional estén siendo reemplazados por controladores óptimos como una estrategia clave para mejorar la competitividad de la empresa y alcanzar objetivos que de otro modo difícilmente podrían conseguirse.
En la literatura se encuentran diferentes publicaciones que hacen referencia al control óptimo y específicamente al control lineal cuadrático gaussiano (LQG). En [1] se describe la implementación de un controlador LQG y de un regulador lineal cuadrático (LQR) para controlar la dinámica del vuelo lateral y longitudinal en la simulación de vuelo de una aeronave con el fin de lograr una estabilidad robusta. En el trabajo realizado por [2] se presenta el diseño de dos estrategias de control, un controlador LQG y un controlador DMPC (Discrete Time Model Predictive Control) para regular la velocidad de una turbina de vapor acoplada a un generador CD, con el fin de mantener constante la velocidad ante variaciones de presión en la tubería de vapor. Rodríguez, Murilo y Silva [3] investigan el comportamiento de un sistema de dirección eléctrica asistida al aplicar un controlador LQG discreto; implementan este controlador debido a su estabilidad y robustez aun cuando el sistema se encuentra sometido a ruidos y perturbaciones. En [4] se implementa una plataforma experimental de un helicóptero de dos grados de libertad pivotado, se estima el modelo matemático que describe el comportamiento del sistema y se diseña un controlador PID y un controlador LQR. Finalmente, se realiza la comparación de los controladores para determinar su desempeño frente a perturbaciones, en [5] hace referencia al diseño de un algoritmo de control óptimo para el sistema HVAC de un edificio e introduce un algoritmo de control jerárquico que se compone de controladores PID y un controlador LQR. El controlador LQR minimiza una función de coste cuadrático que tiene dos términos cuadráticos: uno tiene en cuenta el nivel de confort y el otro representa el esfuerzo de control, es decir la cantidad de energía consumida. En [6] se propone un controlador LQG de velocidad para suprimir las vibraciones torsionales en el sistema de accionamiento de un motor con una carga de dos masas giratorias. Debido a la dificultad de medir la velocidad de la carga y el par del eje, se utiliza el filtro de Kalman como un estimador de orden completo. Se realizan simulaciones para comparar el desempeño del controlador LQG con un controlador PI convencional. [7] presenta un artículo en el cual realiza el diseño de un algoritmo de control basado en la optimización de los parámetros del controlador LQG mediante el uso de algoritmos genéticos (GA) para controlar la velocidad del motor de CD. Los resultados obtenidos muestran que el enfoque seleccionado utilizado en la elección de la matriz Q y R logra un muy buen rendimiento y refleja la eficiencia y la accesibilidad a los requisitos de diseño del enfoque propuesto.
El objetivo de este trabajo es diseñar un controlador LQG y un controlador STR para el voltaje producido por una planta prototipo constituida por un sistema de un motor y un generador CD, y comparar el desempeño de los dos controladores, utilizando diferentes métricas.
Con este artículo se busca incentivar a otros académicos para que se interesen por esta línea de trabajo del área de la Ingeniería de Control y se pretende demostrar que es posible, utilizando prototipos de bajo costo, implementar técnicas avanzadas de control con buenos resultados, acordes a las exigencias impuestas por el avance y desarrollo de sistemas de control.
Metodológicamente el artículo inicia con la descripción del sistema a controlar y la obtención de su modelo matemático utilizando identificación no paramétrica, a continuación, se plantean los conceptos básicos de los controladores STR y LQG, se estiman sus parámetros y, finalmente, se implementan en la planta prototipo, para comparar su desempeño y analizar los resultados obtenidos.
Materiales y métodos
Descripción del sistema
La Figura 1 muestra la planta prototipo objeto de estudio, la cual está compuesta por: la unidad electromecánica, encargada de la generación del voltaje que se desea controlar en el sistema, está constituida por dos motores CD de 24 V, uno de ellos trabajando como motor propiamente dicho y el otro, unido al primer motor mediante un acople flexible, cumpliendo la función de generador; la unidad de medición, encargada de adecuar el valor de la variable a controlar, formada por un divisor de voltaje que convierte la salida proveniente del generador CD en una señal de 0 a 4,5 voltios; el sistema de adquisición de datos y control basado en una tarjeta Arduino UNO®, un módulo driver dual L298N para motores CD, el cual maneja la potencia mediante la modulación del ancho de pulso (PWM), cuya amplitud depende de la señal de control proveniente del computador en el cual se implementan los algoritmos de control en la plataforma Labview® y, finalmente, una fuente de alimentación con salida de 24VCD a 10 A.
Figura 1: Prototipo del generador CD utilizado en el trabajo
La Figura 2 muestra el diagrama eléctrico que interconecta las unidades de funcionamiento que conforman el sistema.
Figura 2: Diagrama eléctrico del prototipo
Obtención del modelo matemático del prototipo del generador CD
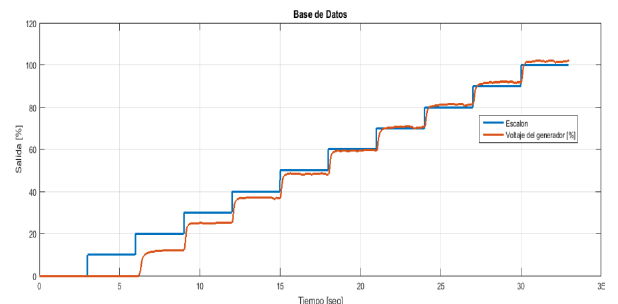
La identificación de sistemas permite obtener el modelo matemático que describe la dinámica del sistema a partir de datos experimentales [8]. El prototipo del generador CD se sometió a diferentes señales de entrada de tipo escalón, en un rango del 0 al 100 %, con incrementos de 10% como se muestra en la Figura 3.
Figura 3: Base de datos para la identificación del sistema
Por las características de la respuesta y las del prototipo del generador CD, su dinámica se aproximó a un modelo de segundo orden con retardo (SOR) [9], [10], se utilizó el método de Stark, también llamado método de los tres puntos [11], que corresponden a los tiempos requeridos para que la respuesta, ante una señal en forma de escalón, alcance el 15 %, el 45% y el 75% del valor final. El método se aplicó a cada uno de los escalones y luego se promediaron los resultados, la función de transferencia estimada se da en la ecuación (1).
Controlador STR por asignación de polos Sea la planta definida por la función de transferencia dada en la ecuación (2):
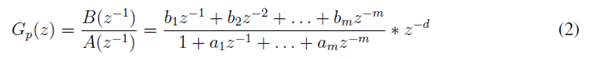
Para dicha planta, es posible obtener un controlador representado por la ecuación (3).
De modo que sus polos de lazo cerrado queden ubicados en el lugar deseado [12]. El orden del numerador y del denominador de la función de transferencia del controlador deben ser: v = m y u = m+d respectivamente. La ecuación característica deseada para el sistema en lazo cerrado está dada por:
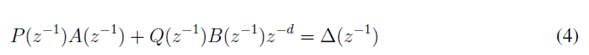
En donde:
La ecuación característica deseada Δ(z-1) se determina a partir de las especificaciones de diseño establecidas, el orden l de la misma está dado por: l = 2m + d. Los parámetros del controlador se obtienen al resolver la ecuación (4) aplicando la ecuación (6).
Por último, los parámetros hallados en la ecuación (6) se reemplazan en la ecuación (3) obteniendo así la función de transferencia del controlador STR.
Regulador lineal cuadrático LQG
Para diseñar el controlador LQG se aplica el principio de separación que permite calcular en forma independiente la matriz de realimentación de ganancia K del regulador lineal cuadrático (LQR) y un estimador de estados tipo Kalman, que posteriormente se combinan para formar el controlador [13], [14]. Para calcular la matriz de ganancia K se utiliza una función de costo cuadrática que minimiza el índice de desempeño presentado en la ecuación (7)[15]:
En donde Q y R son matrices de peso positivas definidas y se seleccionan para penalizar a algunos estados o a algunas entradas más que a otras [16], [17]. S es una matriz semidefinida positiva. Para calcular el control LQR, se parte del sistema definido por la ecuación (8) y la ecuación (9):
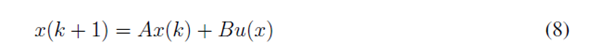
El objetivo es encontrar la señal del control u(k) que lleve al sistema dado por la ecuación (8), del estado inicial x(k) = x(0) al estado final x(N) = x(f) minimizando la función de coste cuadrática definida por la ecuación (7). Utilizando un procedimiento iterativo se puede obtener el paso del estado k al estado N [18], lo que da como resultado:
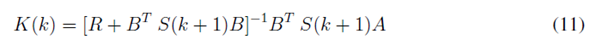
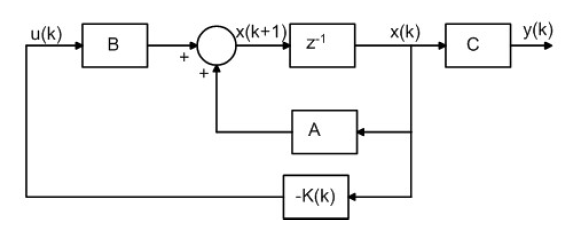
Las ecuaciones (10), (11) y (12) generan el controlador LQR para el sistema discreto descrito por la ecuación (8). La ecuación (12) se conoce como la ecuación de Riccati. En la Figura 4 se presenta un diagrama de bloques del sistema de control LQR.
Filtro de Kalman
El filtro de Kalman es un algoritmo óptimo recursivo basado en el modelo de espacio de estados y su objetivo es estimar los estados de una manera óptima y, dada su función de filtro, eliminar el ruido; de manera que se minimice el índice del error cuadrático medio [19]. Si se considera el sistema discreto:
En donde v(k) y w(k) son el ruido del proceso y de la medición respectivamente. Para obtener el filtro de Kalman se parte de la ecuación del observador de estados normal, pero teniendo en cuenta los efectos del ruido para el cálculo de la matriz de ganancia L. Esta matriz debe elegirse de forma que dé la mejor estimación del estado del sistema y que rechace los efectos de los ruidos. Esta elección define el observador óptimo conocido como filtro de Kalman dado por la ecuación (15) 20
En donde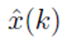 
es la variable de estado estimada y L es la matriz de ganancia de Kalman.
El filtro de Kalman estima el estado del proceso en un instante de tiempo y posteriormente obtiene una realimentación de las medidas. Por eso las ecuaciones del filtro de Kalman se pueden dividir en dos partes: actualización en el tiempo (conocida como predicción) y actualización en las medidas (conocida como corrección) [21]. En la fase de predicción, se realiza el cálculo del estado y de la covarianza del error actual P(k) a partir de la covarianza del error en el instante anterior, es decir:
En la fase de corrección, se actualiza la ganancia de Kalman, se corrige la estimación del estado calculado en la etapa de predicción y, finalmente, se actualiza la covarianza del error, o sea:
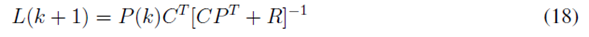
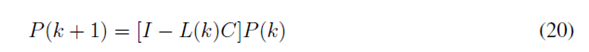
La implementación del controlador utilizando el filtro de Kalman es similar a la utilizada con el observador tipo predictor diseñado, utilizando la técnica de asignación de polos (21), es decir:
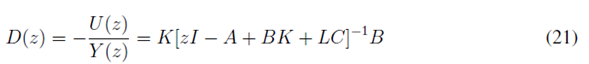
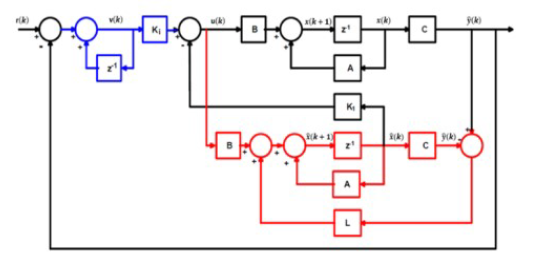
Como el sistema anterior no considera una entrada de referencia, se puede presentar error en estado estable; para evitar este problema, se utiliza un sistema de seguimiento con un integrador en el camino directo entre el comparador de error y la planta [21], [ 22 ], tal como se observa en la Figura 5.
Figura 5: Sistema LQR con filtro de Kalman e integrador
La ley de control del sistema de la Figura 5 está dada por la ecuación (22), formada por el integrador, la matriz de ganancia de realimentación óptima y el estimador de estados del sistema (filtro de Kalman) [21], [23]
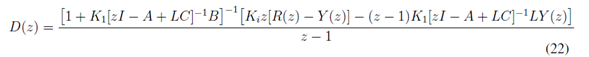
Para el cálculo de K1 y Ki se utiliza la ecuación (23):
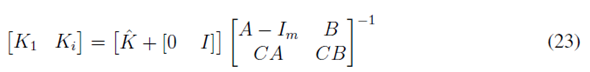
En donde 
es la matriz de ganancia del estimador óptimo LQR obtenida con las matrices ampliadas:
Resultados
Diseño del controlador STR por asignación de polos para el prototipo del generador CD
Utilizando como periodo de muestreo T = 0; 0335 s, la función de transferencia discreta de la planta es:
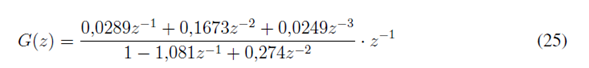
De la ecuación (24), se obtiene: m = 3, d = 1, por tanto para el controlador resulta: v = 3, u = 4 y el orden de la ecuación característica deseada es l = 7.
Se definen como parámetros de diseño para el sistema en lazo cerrado: factor de amortiguamiento de 0,8 y tiempo de establecimiento 20% menor al correspondiente en lazo abierto. Así, los polos de lazo cerrado dominantes están ubicados en z = 0,687±j 0;18. Se deben agregar cinco polos no dominantes para completar el orden de la ecuación característica. Si se ubican en z = 0, se obtiene la ecuación (26):
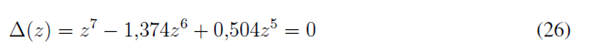
Utilizando la ecuación (6) se estiman los parámetros del controlador:
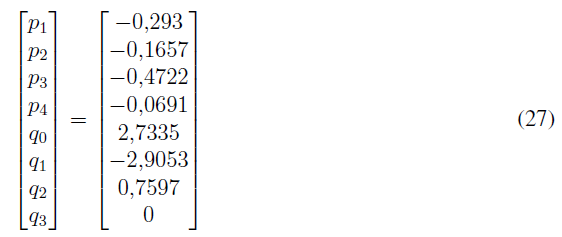
La función de transferencia del controlador es, según la ecuación (3):
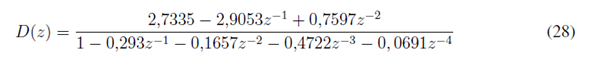
Diseño del controlador LQG para el prototipo del generador CD
La representación del sistema en el espacio de estados en su forma canónica observable está dada por:
Haciendo uso del software Matlab® se realiza el cálculo de la matriz de ganancia del observador L, ingresando como parámetros de entrada las matrices A y B del sistema y como ruidos para el proceso y para la medición v = 0,02 y w = 0,008 respectivamente. La matriz de ganancia del observador está dada por:
Para el cálculo de la ganancia K del controlador LQR se utilizaron las matrices ampliadas A 1 y B 1 , dadas en la ecuación (24), debido a la inclusión del integrador. La matriz S inicial se tomó como una matriz identidad y las matrices Q y R se estimaron con el criterio de Bryson [16]:
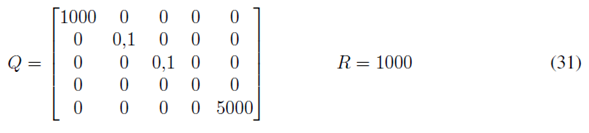
El resultado obtenido, utilizando recursivamente las ecuaciones (10), (11) y (12), se da en la ecuación (31):
Análisis de Resultados
Resultados obtenidos con el controlador STR
La Figura 6 muestra la respuesta del sistema de control STR simulada con el software Matlab®, ante escalones del 20 %, 30% y 40% respectivamente aplicados en la referencia. En la Figura 7 se presenta la respuesta del sistema real ante las mismas señales de entrada. Se observa coincidencia en las dos respuestas: máximo sobreimpulso menor del 10 %, buena velocidad de respuesta, error de estado estable igual a cero y la ley de control produce una salida bastante fuerte al inicio de la respuesta del sistema de control, llevando rápidamente el sistema a estabilidad en el punto de referencia establecido para cada caso.
Figura 6: Simulación del controlador STR
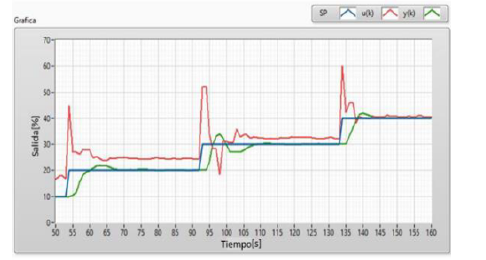
Figura 7: Control STR con el prototipo del generador CD
La Figura 8 muestra la respuesta del sistema real ante una perturbación: se añade una carga al generador en t=14s y se suspende en t=20s, se observa que el controlador STR responde de manera eficiente ante el cambio de carga, presentando una respuesta rápida en presencia de la misma y retornando el sistema al punto de referencia, tanto al conectar la carga como al desconectarla.
Figura 8: Respuesta del control STR ante una carga
Resultados obtenidos del controlador LQG
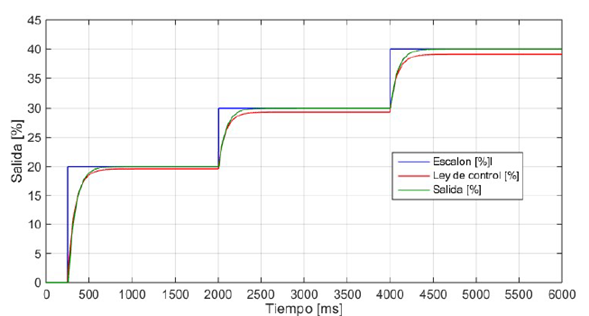
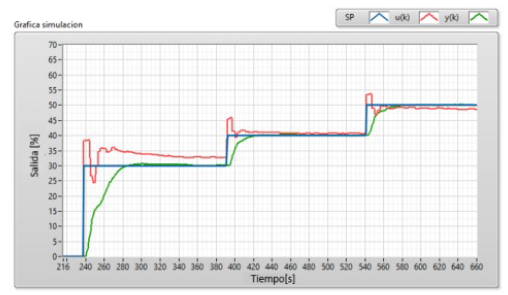
La Figura 9 muestra la respuesta del sistema con el controlador LQG, simulada con el software Matlab®, para entradas en forma de escalón del 20 %, 30% y 40 %, y en la Figura 10 se aprecia la respuesta del sistema real ante las mismas señales de entrada. En los dos casos el sistema presenta buena velocidad de respuesta, error de estado estable igual a cero, sobreimpulso no significativo, y la ley de control no es tan agresiva como la generada por el STR en las mismas condiciones.
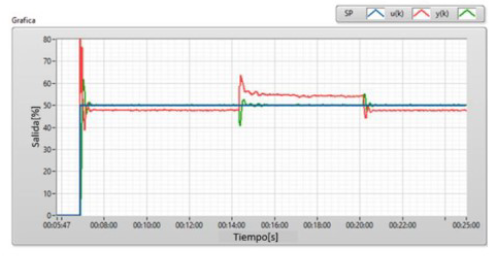
Finalmente, en la Figura 11 se ve la respuesta del sistema ante una carga aplicada al generador, igual que la utilizada para el STR; se observa que el controlador LQG responde rápidamente ante la presencia de la carga y el sistema retorna al punto de consigna tanto al aplicar la carga como al desconectarla.
Figura 9: Simulación del controlador LQG
Figura 10: Control LQG del prototipo del generador CD
Figura 11: Respuesta del control LQG ante una carga
Comparación del desempeño de las dos estrategias de control para el prototipo del generador CD
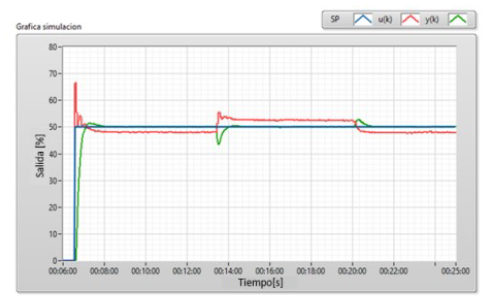
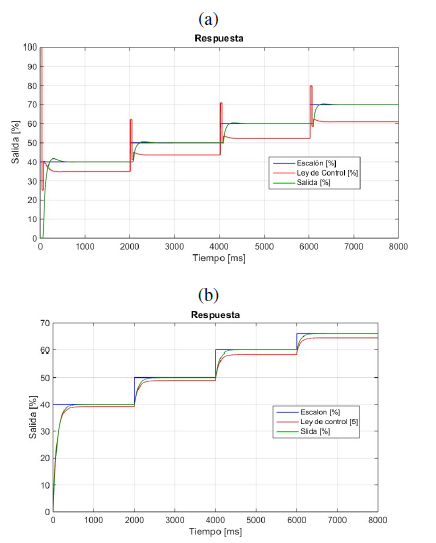
Para comparar las dos estrategias de control, se utilizaron métricas de respuesta temporal y de la integral evaluadas bajo las mismas condiciones de señal de entrada y de carga aplicadas al sistema real. Para la respuesta temporal se utilizaron: el máximo sobreimpulso (Mp), el tiempo de establecimiento (ts) y el error de estado estable (eee). En las métricas de la integral se utilizaron, entre otras, la integral del valor absoluto del error (IAE), la integral del valor del cuadrado del error (ICE) y el trabajo sobre la variable manipulada (TVM). Se considera una zona de operación entre el 40% y 70% con incrementos del 10% en la referencia, en la Figura 12a se observa la respuesta del sistema de control STR y en la Figura 12b se muestra la del sistema de control LQG ante el mismo estímulo.
Figura 12: a) Respuesta con el control STR. b) Respuesta con el controlador LQG
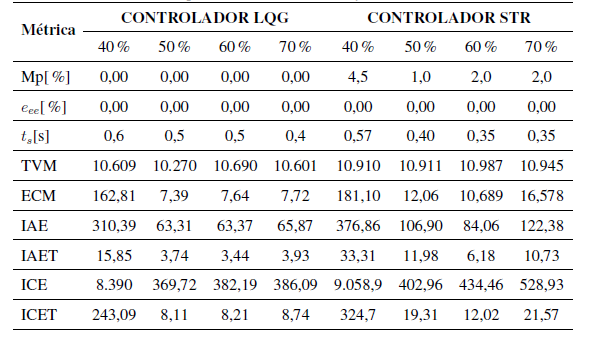
En la Tabla I se presentan los resultados obtenidos con cada una de las métricas para el controlador LQG y para el STR respectivamente. Los resultados muestran que las diferencias en el desempeño de las dos estrategias de control no presentan diferencias muy significativas, inclinándose a favor del controlador LQG, en algunos aspectos como la no presencia de sobreimpulso y menores valores en los criterios de la integral del error y a favor del STR en cuanto a menor tiempo de establecimiento. Los resultados de las pruebas indican que para incrementos en el set-point del 10 %, el controlador LQG presentó, en todos los casos, menor sobreimpulso que el STR. Sin embargo, el tiempo de establecimiento con el controlador LQG fue mayor al presentado por el controlador STR. En los experimentos realizados, los dos controladores presentan error de estado estable igual a cero. Analizando los resultados de las métricas de la integral del error y el TVM, se deduce que el desempeño del controlador LQG, en términos generales, fue mejor que el presentado por el controlador STR.
Fuente: elaboración propia
Tabla I: Desempeño del Controlador LQG y del controlador STR
Conclusiones
Se realizó el diseño de dos estrategias de control para el voltaje generado por una planta prototipo formada por la combinación de dos motores de 24 V, uno trabajando como motor propiamente dicho y el otro como generador. Para el diseño de los controladores la planta se aproximó a un sistema de segundo orden con retardo. Al realizar las pruebas sobre el sistema real se observó que las dos estrategias de control mostraron buen desempeño ante cambios en la señal de referencia y en presencia de perturbaciones. El tiempo de establecimiento del sistema con el controlador STR fue menor que el del sistema con el LQG pero, como resultado, el controlador STR presentó mayor sobreimpulso y una ley de control más agresiva que la del sistema con el LQG, haciéndose evidente la relación entre el esfuerzo de control y los parámetros de desempeño de sobreimpulso y el tiempo de establecimiento. También se observó que las variaciones en la carga no afectaron la estabilidad del sistema y los dos controladores compensaron los cambios en la misma, lo cual demuestra que las dos estrategias son robustas ante la presencia de perturbaciones, notándose, en general, un mejor desempeño del controlador LQG. Finalmente, y a diferencia de otros trabajos en los cuales se analiza el desempeño de controladores mediante métricas de la integral y de la respuesta temporal en un solo punto de trabajo, en este trabajo se proporcionó un criterio de evaluación basado en la respuesta en diferentes zonas de trabajo del proceso, evaluación útil en sistemas no lineales con multiplicidad de estados.
A futuro, el trabajo motiva a utilizar en el prototipo otros algoritmos de control, incluyendo el uso de algoritmos genéticos, redes neuronales y control Fuzzy con miras a contribuir desde lo académico a soluciones que puedan ser aplicables en ambientes reales de control de procesos.
Referencias
License
Copyright (c) 2020 Luis Edo Garcia Jaimes
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
2.jpg)
