DOI:
https://doi.org/10.14483/udistrital.jour.reving.2014.2.a01Published:
2014-08-11Issue:
Vol. 19 No. 2 (2014): July - DecemberSection:
ArticleModelos de Inventarios con Productos Perecederos: Revisión de la Literatura
Inventory Models with Deteriorating Items: A Literature Review
Keywords:
inventory control, perishability, deteriorating items, review (en).Keywords:
control de inventario, productos perecederos, deterioro, revisión de literatura. (es).Downloads
References
Harris, F.W., How many parts to make at once. Factory, The Magazine of Management Science, 1913. 10(2): p. 135–136, 152.
Nahmias, S., Perishable Inventory Theory: A Review. Operations Research, 1982. 30(4): p. 680–708.
Goyal, S.K. and B.C. Giri, Recent trends in modeling of deteriorating inventory. European Journal of Operational Research, 2001. 134(1): p. 1–16.
Raafat, F., Survey of Literature on Continuously Deteriorating Inventory Models. Journal of the Operational Research Society, 1991. 42(1): p. 27-37.
Nahmias, S., Perishable Inventory Systems. International Series in Operations Research & Management Science. 2011: Springer US. 80.
Bakker, M., J. Riezebos, and R.H. Teunter, Review of inventory systems with deterioration since 2001. European Journal of Operational Research, 2012. 221(2): p. 275-284.
Amorim, P., et al., Managing perishability in production-distribution planning: a discussion and review. Flexible Services and Manufacturing Journal, 2013. 25(3): p. 389-413.
Masters, J.M., A Note on the Effect of Sudden Obsolescence on the Optimal Lot Size. Decision Sciences, 1991. 22(5): p. 1180.
Song, Y. and H.C. Lau, A periodic-review inventory model with application to the continuous-review obsolescence problem. European Journal of Operational Research, 2004.
(1): p. 110-120.
Hadley, G. and T.M. Whitin, Analysis of Inventory Systems. 1963, Englewood Cliffs, N.J.
David, I., E. Greenshtein, and A. Mehrez, A dynamic-programming approach to continuous-review obsolescent inventory problems. Naval Research Logistics (NRL), 1997. 44(8):
p. 757-774.
David, I. and A. Mehrez, An Inventory Model with Exogenous Failures. Operations Research, 1995. 43(5): p. 902-903.
Joglekar, P. and P. Lee, An exact formulation of inventory costs and optimal lot size in face of sudden obsolescence. Operations Research Letters, 1993. 14(5): p. 283-290.
Pahl, J. and S. Voß, Integrating deterioration and lifetime constraints in production and supply chain planning: A survey. European Journal of Operational Research, 2014(0).
Karaesmen, I., A. Scheller–Wolf, and B. Deniz, Managing Perishable and Aging Inventories: Review and Future Research Directions, in Planning Production and Inventories in
the Extended Enterprise, K.G. Kempf, P. Keskinocak, and R. Uzsoy, Editors. 2011, Springer US. p. 393-436.
Liu, L. and Z. Lian, (s, S) Continuous Review Models for Products with Fixed Lifetimes. Operations Research, 1999. 47(1): p. 150-158.
Pentico, D.W. and M.J. Drake, A survey of deterministic models for the EOQ and EPQ with partial backordering. European Journal of Operational Research, 2011. 214(2): p.
-198.
Chakraborty, N., S. Mondal, and M. Maiti, A deteriorating multi-item inventory model with price discount and variable demands via fuzzy logic under resource constraints.
Computers & Industrial Engineering, 2013. 66(4): p. 976-987.
Kumar, S.D., P.K. Kundu, and A. Goswami, An economic production quantity inventory model involving fuzzy demand rate and fuzzy deterioration rate. Journal of Applied
Mathematics and Computing, 2003 12(1-2): p. 251–260.
Mahata, G.C. and A. Goswami, An EOQ model for deteriorating items under trade credit financing in the fuzzy sense. Production Planning & Control, 2007. 18(8): p. 681-692.
Mahata, G.C. and P. Mahata, Analysis of a fuzzy economic order quantity model for deteriorating items under retailer partial trade credit financing in a supply chain. Mathematical
and Computer Modelling, 2011. 53(9-10): p. 1621-1636.
Taleizadeh, A.A., H.-M. Wee, and F. Jolai, Revisiting a fuzzy rough economic order quantity model for deteriorating items considering quantity discount and prepayment.
Mathematical and Computer Modelling, 2013. 57(5-6): p. 1466-1479.
Wee, H.-M., C.-C. Lo, and P.-H. Hsu, A multi-objective joint replenishment inventory model of deteriorated items in a fuzzy environment. European Journal of Operational
Research, 2009. 197(2): p. 620-631.
Sarkar, B., A production-inventory model with probabilistic deterioration in two-echelon supply chain management. Applied Mathematical Modelling, 2013. 37(5): p. 3138-3151.
Sarkar, M. and B. Sarkar, An economic manufacturing quantity model with probabilistic deterioration in a production system. Economic Modelling, 2013. 31: p. 245-252.
Cai, X., et al., Optimization and coordination of fresh product supply chains with freshness-keeping effort. Production and Operations Management, 2009. 19(3): p. 261–278.
Chen, Y.-R. and C.-Y. Dye, Application of particle swarm optimisation for solving deteriorating inventory model with fluctuating demand and controllable deterioration rate.
International Journal of Systems Science, 2013. 44(6): p. 1026-1039.
Dye, C.-Y., The effect of preservation technology investment on a non-instantaneous deteriorating inventory model. Omega, 2013. 41(5): p. 872-880.
Dye, C.-Y. and T.-P. Hsieh, An optimal replenishment policy for deteriorating items with effective investment in preservation technology. European Journal of Operational Research,
218(1): p. 106-112.
Hsieh, T.-P. and C.-Y. Dye, A production–inventory model incorporating the effect of preservation technology investment when demand is fluctuating with time. Journal of
Computational and Applied Mathematics, 2013. 239: p. 25-36.
Hsu, P.H., H.M. Wee, and H.M. Teng, Preservation technology investment for deteriorating inventory. International Journal of Production Economics, 2010. 124(2): p. 388-394.
Lee, Y.-P. and C.-Y. Dye, An inventory model for deteriorating items under stock-dependent demand and controllable deterioration rate. Computers & Industrial Engineering,
63(2): p. 474-482.
Shah, N., D. Shah, and D. Patel, Optimal Preservation Technology Investment, Retail Price and Ordering Policies for Deteriorating Items under Trended Demand and Two Level
Trade Credit Financing. Journal of Mathematical Modelling and Algorithms in Operations Research, 2014: p. 1-12.
Abad, P.L., Optimal pricing and lot-sizing under conditions of perishability, finite production and partial backordering and lost sale. European Journal of Operational Research,
144(0 ): p. 677–685.
Abdul, I. and A. Murata, A fast-response production-inventory model for deteriorating seasonal products with learning in set-ups. International Journal of Industrial Engineering
Computations, 2011. 2(4): p. 715-736.
Abdul, I. and A. Murata, Optimal production strategy for deteriorating items with varying demand pattern under inflation. International Journal of Industrial Engineering Computations,
2(3): p. 449-466.
Alamri, A.A., Theory and methodology on the global optimal solution to a General Reverse Logistics Inventory Model for deteriorating items and time-varying rates. Computers
& Industrial Engineering, 2011. 60(2): p. 236-247.
Alshamrani, A.M., Optimal control of a stochastic production-inventory model with deteriorating items. Journal of King Saud University - Science, 2012.
Balkhi, Z.T., On a finite horizon production lot size inventory model for deteriorating items: an optimal solution. European Journal of Operational Research, 2001. 132(4): p.
–223.
Baten, M.A., A.A. Kamil, and H. Lateh, Inventory-Production Control Systems with Gumbel Distributed Deterioration. AASRI Procedia, 2012. 2: p. 93-105.
Bhowmick, J. and G.P. Samanta, A Deterministic Inventory Model of Deteriorating Items with Two Rates of Production, Shortages, and Variable Production Cycle. ISRN Applied
Mathematics, 2011. 2011: p. 1-16.
Bhunia, A.K., et al., An application of tournament genetic algorithm in a marketing oriented economic production lot-size model for deteriorating items. International Journal of
Production Economics, 2009. 119(1): p. 112-121.
Bukhari, F.A. and A. El-Gohary, Optimal control of a production-maintenance system with deteriorating items. Journal of King Saud University - Science, 2012. 24(4): p. 351-357.
Cai, X., et al., Fresh-product supply chain management with logistics outsourcing. Omega, 2013. 41(4): p. 752-765.
Chakraborty, T. and B.C. Giri, Joint determination of optimal safety stocks and production policy for an imperfect production system. Applied Mathematical Modelling, 2012.
(2): p. 712-722.
Chen, J.-M. and L.-T. Chen, Pricing and production lot-size/scheduling with finite capacity for a deteriorating item over a finite horizon. Computers & Operations Research, 2005.
(11): p. 2801-2819.
Chen, L.-T. and C.-C. Wei, Multi-period channel coordination in vendor-managed inventory for deteriorating goods. International Journal of Production Research, 2012. 50(16):
p. 4396-4413.
Chung, C.J. and H.M. Wee, An integrated production-inventory deteriorating model for pricing policy considering imperfect production, inspection planning and warranty-periodand
stock-level-dependant demand. International Journal of Systems Science, 2008. 39(8): p. 823-837.
Chung, C.-J. and H.-M. Wee, Short life-cycle deteriorating product remanufacturing in a green supply chain inventory control system. International Journal of Production Economics,
129(1): p. 195-203.
Chung, C.-J., G.A.Widyadana, and H. MingWee, Economic production quantity model for deteriorating inventory with random machine unavailability and shortage. International
Journal of Production Research, 2011. 49(3): p. 883-902.
Chung, K.-J., L. Eduardo C´ardenas-Barr´on, and P.-S. Ting, An inventory model with non-instantaneous receipt and exponentially deteriorating items for an integrated three layer
supply chain system under two levels of trade credit. International Journal of Production Economics, (0).
Dalfard, V. and N. Nosratian, A new pricing constrained single-product inventory-production model in perishable food for maximizing the total profit. Neural Computing and
Applications, 2012: p. 1-9.
Das, B.C., B. Das, and S.K. Mondal, Integrated supply chain model for a deteriorating item with procurement cost dependent credit period. Computers & Industrial Engineering,
64(3): p. 788-796.
Das, D., et al., Two-warehouse production model for deteriorating inventory items with stock-dependent demand under inflation over a random planning horizon. Central European
Journal of Operations Research, 2012. 20(2): p. 251-280.
Das, D., et al., Two-warehouse production inventory model for a deteriorating item with time-varying demand and shortages: a genetic algorithm with varying population size
approach. Optimization and Engineering, 2013: p. 1-19.
Duan, Q. and T.W. Liao, Optimization of blood supply chain with shortened shelf lives and ABO compatibility. International Journal of Production Economics, (0).
Feng, L., J. Zhang, and W. Tang, Optimal control of production and remanufacturing for a recovery system with perishable items. International Journal of Production Research,
51(13): p. 3977-3994.
Gaur, N.K., S. Kumar, and S.R. Singh, An Integrated Production-Inventory Model for Deteriorating Items under the effect of Inflation. International Transactions in Applied
Sciences, 2011. 3(3): p. 543-562.
Ghosh, S.K., S. Khanra, and K.S. Chaudhuri, Optimal price and lot size determination for a perishable product under conditions of finite production, partial backordering and lost
sale. Applied Mathematics and Computation, 2011. 217(13): p. 6047-6053.
Giri, B.C. and A. A. Chakraborty, Supply chain coordination for a deteriorating product under stock-dependent consumption rate and unreliable production process. International
Journal of Industrial Engineering Computations, 2011. 2(2): p. 263-272.
Giri, B.C. and T. Maiti, Supply chain model for a deteriorating product with time-varying demand and production rate. Journal of the Operational Research Society, 2011. 63(5):
p. 665-673.
Guchhait, P., M. Kumar Maiti, and M. Maiti, Production-inventory models for a damageable item with variable demands and inventory costs in an imperfect production process.
International Journal of Production Economics, 2013. 144(1): p. 180-188.
He, Y. and S. Wang, Analysis of production-inventory system for deteriorating items with demand disruption. International Journal of Production Research, 2012. 50(16): p.
-4592.
He, Y., S.-Y. Wang, and K.K. Lai, An optimal production-inventory model for deteriorating items with multiple-market demand. European Journal of Operational Research, 2010.
(3): p. 593-600.
Konstantaras, I. and K. Skouri, A note on a production-inventory model under stock-dependent demand,Weibull distribution deterioration, and shortage. International Transactions
in Operational Research, 2011. 18(4): p. 527-531.
Lee, C.C. and S.-L. Hsu, A two-warehouse production model for deteriorating inventory items with time-dependent demands. European Journal of Operational Research, 2009.
(3): p. 700-710.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Modelos de inventarios con productos perecederos: revisión de literatura
Inventory models with deteriorating items: A literature review
Freddy Andrés Pérez Mantilla, Universidad de los Andes, fa.perez10@uniandes.edu.co
Fidel Torres; Universidad de los Andes, ftorres@uniandes.edu.co
Recibido: 27-11-2013. Modificado: 09-08-2014. Aceptado: 11-12-2014
Resumen
En el presente artículo se lleva a cabo una revisión de las principales características estudiadas por la comunidad científica en el desarrollo de modelos matemáticos que buscan definir una política de inventario óptima para productos que se deterioran. De este modo, se referencian 390 artículos publicados a partir del año 2001 en revistas de gran impacto, teniendo en cuenta: el tipo de demanda y deterioro representado en los modelos matemáticos, el estudio de una política de precio óptima, la inclusión de faltantes y/o valor del dinero en el tiempo, el estudio de múltiples productos y/o dos o más eslabones de la cadena de suministro, y la utilización de parámetros o variables difusas. Finalmente, se identifican oportunidades de investigación que a la fecha no han sido abordadas por la comunidad científica en este campo del conocimiento.
Palabras claves: control de inventario, productos perecederos, deterioro, revisión de literatura.
Abstract
This paper presents a review of the main characteristics of the mathematical models developed by the scientific community in order to determine an optimal inventory policy for deteriorating items. Thus, a classified bibliography of 390 articles published from 2001 to 2014 in high-impact journals is submitted while considering the type of demand and deterioration, the integration of inventory and pricing decisions, the inclusion of shortage and/or the time value of money, the consideration of multiple items and/or multi-echelon systems, and the incorporation of uncertain parameters other than demand. Finally, research questions not yet addressed by the research community in the field of inventory control for deteriorating items are pointed out.
1. Introducción
La teoría de inventarios tiene sus raíces en el modelo de Cantidad Económica de Pedido (EOQ, por sus siglas en inglés), propuesto por Harris [1] y en donde se asumió entre otros supuestos que los productos tienen vida útil ilimitada. A la fecha, dicho modelo permite obtener una buena aproximación de la política óptima de inventarios en varias situaciones de la vida real. No obstante, en sistemas de inventarios donde el deterioro tiene un impacto económico significativo, asumir que los productos tienen vida útil ilimitada conduce a la adopción de políticas de inventarios muy alejadas a la óptima. La disminución de la calidad de los productos agrega una penalización adicional en el mantenimiento del inventario, y, por tanto, un desafío importante en la gestión de inventarios con productos perecederos es determinar una manera eficiente de mantener la disponibilidad de los artículos mientras que se evitan excesivas pérdidas por productos vencidos.
Cuando se habla de los tipos de deterioro que sufren los productos cuando se mantienen como inventario, en la literatura se pueden observar diferentes tipos de clasificaciones. Nahmias [2], Goyal & Giri [3] hacen una distinción entre productos perecederos con vida útil fija (3 días, 1 mes, etc) y productos cuya vida útil es una variable aleatoria con distribución conocida (random lifetime perishability). Raafat [4] distingue entre productos con vida útil fija y productos con deterioro continuo (continuous decay or random lifetime), sin embargo, también se sugiere una clasificación de acuerdo con el valor o la utilidad de los productos respecto al tiempo (constant-utility, decreasing-utility, increasing utility). En otro trabajo, Nahmias [5] primero define decay, exponential decay, y age-independent perishability como el deterioro que se presenta en los sistemas de inventarios cuando se asume que una fracción fija del inventario a la mano se pierde durante cada periodo de tiempo; luego introduce el término perishability para aquellos productos que tienen un valor o utilidad constante durante un periodo de caducidad conocido o desconocido. Por su parte, Bakker et al. [6] clasifican el deterioro de los productos como fixed lifetime, age dependent deterioration rate y time or inventory (but not age) dependent deterioration rate, implicando en la segunda categoría que la vida útil de los productos siguen una distribución de probabilidad. Finalmente, Amorim et al. [7] clasifican el perecimiento de los productos de acuerdo con su regulación externa (fijada o libre) y el valor percibido por los clientes (constante o decreciente).
Si bien en la última década la mayoría de investigadores han adoptado alguna de estas clasificaciones, en el presente artículo se utiliza una clasificación más acorde con el modelo matemático desarrollado. Por ejemplo, en muchas publicaciones se afirma que el deterioro de los productos sigue una distribución de probabilidad Weibull; no obstante, al observar en los modelos matemáticos que el deterioro con distribución de Weibull no es más que una función respecto al tiempo sin ninguna variable aleatoria, sería incorrecto definir la tasa de deterioro como una variable incierta o aleatoria.
Por otra parte, cuando se trata de inventarios constituidos por componentes electrónicos, celulares, artículos de moda, etc., se dice que dicho inventario está sujeto a obsolescencia debido a la entrada de productos sustitutos y/o el desarrollo de nuevas tecnologías. En este contexto, es claro que el margen de utilidad de los productos inventariados se hace cero o disminuye considerablemente a partir de un instante de tiempo desconocido o aleatorio. Es decir, que contrario a los productos que están sujetos a deterioro, no existe ningún interés en hacer nuevos pedidos de productos que ya están obsoletos. Los lectores interesados en diferentes enfoques utilizados por los investigadores en modelos de inventario sujeto a obsolescencia pueden consultar los varios trabajos en [8], [9]-[13].
Al igual que Goyal & Giri [3] y Bakker et al. [5], en el presente artículo se da una visión general sobre las principales contribuciones científicas en sistemas de inventario sujeto a deterioro. No obstante, se discuten nuevas características no tenidas en cuenta en dichas revisiones, al igual que nuevos hallazgos encontrados en los últimos dos años. De este modo, el presente artículo se centra en investigaciones que hacen referencia al desarrollo de modelos de inventario con productos que se deterioran, haciendo énfasis en los principales supuestos adoptados y las especificaciones de los modelos matemáticos desarrollados. En la sección 2 se resume la metodología utilizada para la selección de los artículos con los que se desarrolla el presente trabajo. En la sección 3 se discuten las principales características de los sistemas de inventario sujeto a deterioro. La sección 4 presenta la clasificación de la literatura revisada y en la sección 5 se da a conocer la conclusión del estudio llevado a cabo. Para el lector interesado en modelos de inventario para productos perecederos, y enfocados hacia la planeación de la producción en una cadena de suministro se sugiere ver la revisión de literatura realizada en [14]. Para el lector interesado en revisiones de literatura enfocadas en modelos de inventario para productos que tienen una vida útil fija (finite shelf-life) se sugiere ver los trabajos en [15, 16]. Para los lectores interesados en revisiones donde sólo se incluyen modelos determinísticos con la inclusión de faltantes se sugiere ver [17].
2. Método
La búsqueda de los artículos de investigación se realizó en las bases de datos EbscoHost, Informs Journals, Jstors, Proquest, Sciencedirect, Springerlink, Taylor & Francis Group, y WileyOnlineLibrary. En cada una de éstas, las palabras deteriorat*, perish*, decay*, shelf life y lifetime fueron ingresadas junto a la palabra AND inventory para obtener coincidencias a nivel de Title, Abstract y Keywords, con artículos disponibles desde enero del 2001 a diciembre del 2013. Nótese que el asterisco (*) es utilizado con el fin de incluir dentro de la búsqueda todas las formas posibles de hacer referencia al deterioro (deteriorating, deteriorate, perishable, perishability, etc). Nótese también que la búsqueda incluye todos los artículos en donde los autores mencionan tanto el deterioro como la palabra Inventory, pero en campos de búsqueda diferentes (title, abstract o keywords). Los artículos fueron juzgados en primera medida de acuerdo con el título, y de ser necesario según el resumen o el desarrollo del tema, para verificar que efectivamente se trataba de un modelo matemático para optimizar el control de inventarios de productos que se deterioran. Los artículos enfocados hacia los modelos de inventario sujeto a obsolescencia fueron descartados a menos que simultáneamente determinaran políticas óptimas de reabastecimiento para la gestión de inventario de productos sujeto a deterioro. Finalmente, como resultado de esta búsqueda, y del proceso de clasificación llevado a cabo mediante el programa EndNote, se obtuvieron 390 artículos de investigación relevantes para la presente revisión de literatura.
3. Principales características de sistemas de inventario sujeto a deterioro
Teniendo en cuenta las diferentes características que se presentan en el control de inventarios con productos que se deterioran, estos se pueden clasificar principalmente de acuerdo con el tipo de demanda con la que interactúa el sistema o el tipo de deterioro que sufren los artículos cuando se mantienen en inventario.
Dependiendo del tipo de demanda, se puede hablar de modelos de inventarios con demanda determinista (conocida) o incierta: si la demanda es determinista, la variación del inventario respecto al tiempo durante cada ciclo de inventario puede verse afectada por una predicción de demanda constante (e.g,∂I(t)/∂t = −D1), o por el efecto combinado de una demanda constante D1 y una fracción fija D2 sobre el nivel de inventario en un instante dado (e.g,∂I(t)/∂t = −D1 − D2I(t)). En modelos de inventarios más elaborados, el consumo del inventario puede también ocurrir mediante una demanda que depende del tiempo y/o de uno o varios parámetros de la mercadotecnia (e.g. precio de venta, frecuencia de publicidad, facilidades de pago, servicios posventa, etc.). Por su parte, si la demanda es incierta, entonces ésta podría estar representada por medio de una distribución de probabilidad conocida, o podría estar representada por medio de una función aditiva o multiplicativa con componentes aleatorios. Cuando no es posible obtener una distribución de probabilidad confiable para representar la demanda, la consideración de una demanda fuzzy o híbrida [18-23] suele ser útil para manejar este tipo de incertidumbre.
Como se mencionó en la introducción, no existe un consenso de las anteriores revisiones para clasificar el tipo de deterioro que se manifiesta en los sistemas de inventario. No obstante, en la presente revisión de literatura se usan tres categorías para representar exactamente la forma en que el deterioro fue definido y modelado por la mayoría de los autores que publicaron sus trabajos en revistas de gran impacto. La primera categoría, modelos de inventario con una vida útil fija y conocida, es utilizada para referirse a productos con un periodo de caducidad conocido (e.g, 2 días, 1 mes, etc.). La segunda categoría, modelos de inventario con una tasa de deterioro constante, es utilizada para referirse a modelos donde la variación del inventario en cada periodo o instante de tiempo t se ve afectada por una fracción constante θ sobre el nivel de inventario en un instante de tiempo dado (e.g,∂I(t)/∂t = D1 − θ I(t)). La tercera categoría, modelos de inventarios con tasa de deterioro variable, es utilizada para referirse a aquellos modelos en donde la variación del inventario en cada periodo o instante de tiempo t está afectada por un deterioro θ(t) que sigue cualquier función del tiempo (e.g,∂I(t)/∂t = D1 − θ(t)I(t)).
Nótese que investigaciones en las que se refieren a productos cuyo deterioro sigue alguna distribución de probabilidad, son clasificadas en la segunda categoría si se asume que la tasa de deterioro θ es igual a la esperanza matemática de la función de distribución de probabilidad [24, 25]. Contribuciones como [26-33] en la que la tasa de deterioro se puede reducir a una tasa m(ξ) mediante la inversión de ξ unidades monetarias en alguna tecnología de preservación, pueden ser clasificadas en la segunda o tercera categoría (C2 y C3) dependiendo de la variabilidad o no de la tasa de deterioro en el modelo matemático resultante. (e.g,∂I(t)/∂t = D1 − [θ − m(ξ)]I(t) → C2; ∂I(t)/∂t = −[1 − m(ξ)]θ(t)I(t) → C3). Mientras que modelos de inventario en donde los productos pueden expirar aleatoriamente
antes de su fecha de caducidad máxima, son clasificados en la categoría tres debido a que la cantidad de productos que se deterioran no es uniforme respecto al tiempo, i.e., la cantidad de productos que se deterioran de un mismo lote o pedido explícitamente varía respecto al tiempo.
Como se ha podido observar, el nivel de inventario respecto al tiempo puede verse disminuido por el efecto combinado de la demanda y la cantidad de productos que se deterioran. No obstante, dicha disminución puede ser contrarrestada ya sea por una tasa finita de producción [19, 24-26, 30, 34-116], o bien por una reproducción del inventario como el que se presenta en el sector ganadero, en donde los inventarios son ganados que decrecen debido a la demanda y el deterioro, pero que también crecen por la reproducción del mismo [117-119].
Ahora bien, es importante observar que, aunque en la mayoría de los modelos de inventarios el modelamiento del deterioro y la demanda más que representar una situación particular son definidos como un supuesto del modelo matemático que se desarrolla, todas estas encajan bien en situaciones de la vida real. Por ejemplo, en algunas industrias el consumidor podría verse atraído por productos que se exhiben en los almacenes en grandes cantidades, o bien, una empresa podría interactuar en un mercado en el que la demanda esperada es incierta, y en donde además el consumidor es permisivo o castiga fuertemente periodos de desabastecimiento. Por ende, una adecuada aplicación de los modelos de inventarios con productos que se deterioran dependerá en gran medida del buen juicio del profesional.
Entre las demás interacciones, supuestos y/o restricciones que han de tenerse cuenta en mayor o menor medida para el buen desarrollo y/o aplicación de los modelos de inventario sujeto a deterioro se encuentran principalmente el tiempo de entrega (lead time con distribución conocida, desconocida, cero o constante), la política de control de inventario (con revisión periódica o continua), la inclusión de faltantes (acumulación total o parcial de la demanda o con ventas perdidas), la inclusión de múltiples productos (productos sustitutos o complementarios), tasa de producción (finita, infinita o incierta), el precio de venta (fijo, variable o incierto), el valor del dinero en el tiempo, la cantidad de eslabones dentro de la cadena de abastecimiento, la inclusión de políticas de ventas del proveedor (fija o condicionada) y/o el conjunto de parámetros inciertos o difusos.
4. Clasificación de modelos de inventario sujeto a deterioro
En la presente sección se clasifican y analizan 390 artículos científicos, cuyo aporte principal fue el desarrollo de un modelo de inventario con productos que se deterioran. En la sección 4.1 se clasifican las investigaciones desarrolladas entre el año 2001 y 2013 de acuerdo con el tipo de demanda y deterioro asumido, y en la sección 4.2 se clasifican los diferentes trabajos referenciados de acuerdo con las siguientes características distintivas en los sistemas de inventarios: variación en el precio de venta (determinación de una política de precio óptima); existencia de faltantes; inclusión de múltiples productos; existencia de más de un depósito para el almacenamiento de los inventarios; inclusión de más de un nivel dentro de la cadena de suministro; existencia de una política de crédito del proveedor; inclusión del valor del dinero en el tiempo y/o inflación; y utilización de parámetros/variables difusas/híbridas.
4.1. Clasificación de acuerdo con la demanda y el deterioro asumido en los modelos de inventarios
En la Tabla I se muestra el tipo de demanda y deterioro modelado por los diferentes autores de acuerdo con las características mencionadas en la sección 3. De aquí, 331/390 de los trabajos consultados entre el año 2001 y 2013 estudian una demanda determinista y 62/390, una demanda incierta. Así mismo, en 265/390 artículos se consideró un deterioro con tasa constante; en 81/390 se consideró un deterioro con una tasa variable; y en 44/390, un deterioro con vida útil fija. Nótese que de todos los artículos en donde se consideró una vida útil fija, 33/44 tuvieron en cuenta una demanda incierta, y que de todos los trabajos en donde se consideró una demanda determinista, 318/381 no incluyeron ninguna de las estrategias de mercado que generalmente usan las empresas para influenciar la demanda, tales como la publicidad, facilidades de pago, servicios postventas etc.
Cuando se utilizan estrategias de mercadotecnia para estimular el consumo de los clientes, la integración de decisiones de mercadotecnia con la gestión de inventario resulta importante para maximizar el beneficio mutuo y evitar conflictos potenciales entre departamentos de una misma compañía. De 331 modelos de inventario con demanda determinística, en donde se buscó tanto una decisión óptima para el departamento de mercadotecnia como para la administración de inventario, sólo 13 artículos han considerado que la demanda depende de factores diferentes al precio: en [328, 355, 357], la demanda es influenciada por facilidades de pago (trade credit period) que le ofrece un minorista al consumidor; en [312, 224], la demanda además de depender del precio, también depende del nivel de inventario a la vista de los consumidores y de la frecuencia con que se publicitan los productos; en [254, 42], la demanda depende del precio de venta, de la frecuencia con que se publicitan los productos y del costo de mercadotecnia asociado; en [48], el consumo de los clientes depende del nivel de inventario disponible, y de la duración del periodo de garantía ofrecido a los clientes; en [291, 326, 327], la demanda es sensible al precio de venta y la calidad instantánea (freshness) de los productos, expresada como el tiempo que le queda a los productos para su vencimiento en un periodo o instante de tiempo dado; en [252], la tasa de la demanda depende del precio de venta, del nivel de inventario y de la frescura de los productos que sigue una distribución de Weibull; y en [108] se considera que la demanda depende tanto del precio como del nivel de servicio postventa ofrecido a los clientes.
Ahora bien, cuando factores externos tales como la economía de un país y las tendencias de consumo de un mercado cambian durante el horizonte de planeación, y tienen además un efecto importante sobre la demanda, podría ser incorrecto asumir que la demanda durante cada periodo de planeación es una variable aleatoria independiente de factores externos diferentes al tiempo. Para tales situaciones prácticas, un enfoque basado en las cadenas de Markov provee una alternativa flexible para el modelamiento del proceso de la demanda [361, 366, 370, 376, 379, 380, 388, 395, 397, 400, 401, 404-407] y no sólo generaliza un comportamiento de la demanda que sigue un proceso de Poisson [56, 358, 370, 372, 381, 384, 387, 392-394, 402], sino que es una herramienta conveniente para el modelamiento de procesos de renovación o no de la demanda. Sin embargo, a pesar de este hecho, el correcto modelamiento de la demanda mediante el enfoque de las cadenas de Markov sólo se mantiene para procesos de demanda con coeficientes de variación relativamente bajos, debido a que cuando se observan altas variaciones de la demanda, periodos estándares de longitud constante pueden introducir memoria y generar una distribución de la demanda correlacionada entre periodos. De los modelos de inventario con demanda estocástica que explícitamente tienen en cuenta parámetros de mercadotecnia, solo los modelos desarrollados en [26, 44, 359, 361, 363-365, 370, 373, 378, 379, 398] definen tanto un precio óptimo de venta como políticas de control de inventario. Por su parte, modelos de inventario en [26] [44] [73] [369] [378] [382] [383] tienen en cuenta que la demanda es aleatoria y sensible a la frescura de los productos, pero solo Cai et al. [26] estudian los esfuerzos para mantener la frescura de los productos como variable de decisión.
De investigaciones que tienen en cuenta una demanda determinista y una tasa de deterioro variable: en los modelos de inventario [28, 39, 69, 92, 96, 262, 263, 266, 267, 270, 272, 275, 279, 341, 343-347, 354], la tasa de deterioro se estudia como una función general o arbitraria respecto al tiempo θ(t); en los modelos desarrollados en [58, 190, 268, 281, 284, 285, 325, 349], la tasa de deterioro se estudia como una fracción del tiempo θ(t) = θ ·t; en los artículos [189, 192, 193, 264, 273, 282, 342, 353], la tasa de deterioro sigue una distribución de Weibull de tres parámetros θ(t) = α · β (t − γ)β−1; en los modelos [35, 36, 48, 65, 74, 85, 87, 97, 115, 119, 187, 265, 271, 276, 278, 280, 286, 287, 289, 290, 292-294, 324, 348, 350-352, 356], la tasa de deterioro sigue una distribución de Weibull de dos parámetros θ(t) = α · β (t)β−1; y en los modelos desarrollados en [188, 191, 277, 283, 355, 357], los productos se deterioran a una tasa θ(t) = 1/(1 + m − t), donde m representa la vida útil máxima de los productos. En otros trabajos particulares: Mahapatra & Maiti [74] presentan una tasa deterioro como función tanto del nivel de frescura o calidad como del tiempo mediante una función que sigue la distribución de Weibull de dos parámetros.; Baten et al. [40] y Chen & Lin [269] estudian un deterioro que sigue una distribución de Gumbel y una distribución normal respectivamente; y Wang & Li [291] introducen una tasa de deterioro que depende del tiempo y la temperatura de almacenamiento al cual los productos son expuestos.
Respecto a los modelos de inventarios con demanda incierta, es interesante resaltar que la mayoría de estos han tenido en cuenta una vida útil fija conocida, y con la excepción de Ketzenberg et al. [406], Gürler & özkaya [405], y Lian et al. [407] nadie más ha incluido modelos de inventario en donde los productos pueden expirar aleatoriamente antes de su fecha de caducidad máxima. De hecho, considerando artículos previos de revisión que abarcan publicaciones antes del año 2001 [2, 4, 16], sólo se encuentra un artículo, de Nahmias [408]. De acuerdo con la clasificación para el deterioro usada en el presente artículo, el deterioro asumido en [405-407] es clasificado como tasa de deterioro variable. No obstante, modelos como el desarrollado por Cai et al. [44], en donde la tasa de deterioro es modelada como la cantidad de productos que sobreviven mediante una función arbitraria o general del tiempo y con rango de [0,1] puede ser incluida en esta categoría también. Por su lado, de los modelos de inventarios con demanda incierta y tasa de deterioro constante, la vida útil de los productos en [388, 392, 393, 395-397, 400-404] es considerada mediante una distribución exponencial negativa con parámetro γ(> 0); y el deterioro de los productos en [18-23, 81, 387, 389-391, 394, 398, 399] es considerado como una fracción constante θ entre [0-1] sobre el nivel de inventario en una instante dado.
En casi todos los modelos de inventarios se asume de una manera implícita que los productos mantenidos como inventarios son entregados inmediatamente al consumidor con su llegada. No obstante, cuando los productos son entregados al cliente mediante un tiempo de servicio, que generalmente es aleatorio, los administradores de inventario necesitan considerar políticas de reabastecimiento que tengan en cuenta la formación de colas, con el fin de implementar políticas adecuadas de servicio. Manuel et al. [396, 397] y Yadavalli et al. [404] analizan un sistema de inventario con tiempo de servicio y productos que siguen una distribución exponencial, asumiendo que el tiempo entre llegada de los consumidores sigue un proceso markoviano; pero el primero considera un solo servidor, y el segundo considera un sistema con múltiples servidores. En [400, 401] y [403], la vida útil de los productos también sigue una distribución exponencial; pero en [400] [401] se tiene en cuenta una distribución cuasialeatoria; y en [403], un proceso de Poisson.
4.2. Clasificación según otras características distintivas en los sistemas de inventarios
Como se puede observar en la Tabla II, entre las características de los sistemas de inventario estudiadas por los autores referenciados en esta sección, 206/390 artículos permiten periodos de desabastecimiento (categoría 1), 86/390 tienen en cuenta políticas de ventas que ofrecen los proveedores (característica 2), 72/390 consideran la determinación de una política óptima de precio (categoría 3), 61/390 estudian sistemas multiniveles (categoría 4), 62/390 desarrollan un modelo de inventario considerando el valor del dinero en el tiempo (categoría 5), 31/390 estudian la existencia de más de una instalación para el almacenamiento de los productos (categoría 6), 20/390 tienen en cuenta la existencia de múltiples productos (categoría 7), y 31/390 estudian la inclusión de parámetros difusos o la inclusión de parámetros estocásticos diferente a la demanda (categoría 8).
De 206 investigaciones que permiten periodos con faltantes: 18, 33, 21, 43, 19, 12 y 17 artículos incluyen la categoría C2, C3, C4, C5, C6, C7 y C8, respectivamente. De 86 investigaciones que consideran políticas de pago a los proveedores: 10, 6, 17, 7, 1 y 6 artículos han considerado la categoría C3, C4, C5, C6, C7, y C8, respectivamente. De 72 investigaciones que determinan una política de precios óptima: 9, 8, 2, 3 y 6 artículos consideran la categoría C4, C5, C6, C7 y C8, respectivamente. De 61 modelos de inventario para un sistema multinivel: 6, 5, 4, y 4 incluyen la categoría C5, C6, C7 y C8, respectivamente. De 62 investigaciones que consideran el efecto del valor del dinero en el tiempo: 12 y 3 artículos incluyen la categoría C6 y C8, respectivamente. De 31 investigaciones que consideran un sistema con más de una instalación para el almacenamiento de los productos: 2 y 3 artículos han incluido la categoría C7 y C8, respectivamente. Finalmente, de 20 artículos que incluyen la existencia de múltiples productos, 5 consideran la categoría C8.
4.2.1. Modelos de inventarios que incluyen periodos de desabastecimiento (faltantes)
Cuando la demanda es mayor que lo previsto y ésta no se puede satisfacer inmediatamente con las existencias en bodega, se dice que hay exceso de demanda o faltantes. Dependiendo del tipo de relación cliente-empresa, el exceso de demanda (faltantes) podría perderse y penalizarse [45, 50, 102-104, 205, 232], o acumularse y penalizarse de diferentes maneras, incluyendo un costo por faltante. Por tanto, la forma en que se ve afectado el sistema de inventario durante periodos de desabastecimiento puede variar de un modelo a otro.
Como se puede observar en la Tabla III, de 331 artículos que desarrollan un modelo de inventario para productos con demanda determinista y en donde además se incluye la existencia de periodos de desabastecimiento, 65/331 asumen que toda la demanda en exceso se mantiene para ser satisfecha en el futuro con la llegada de nuevos pedidos, 18/331 asumen que una parte fija del exceso de demanda durante los periodos de faltantes se acumula y la otra parte se pierde, y 80/331 consideran que el consumo del inventario durante periodos de desabastecimiento depende de alguna función δ(τ) respecto al tiempo τ para la llegada de nuevos pedidos (e.g., 0 ≤ δ(τ) ≤ 1, con δ(τ) = e−σ·τ = 1 (ó 0) indicando que los faltantes son completamente satisfechos al inicio del próximo periodo de reabastecimiento (o perdidos).
Respecto a los modelos de inventarios que estudian una demanda incierta y la existencia de faltantes, casi todos los autores asumen que la demanda durante periodos de desabastecimiento se pierde [56, 73, 358, 360, 366, 367, 374, 376, 378, 384-386, 390, 392, 393, 402, 406], o bien se satisface al inicio del periodo de reaprovisionamiento más cercano [22, 23, 81, 361, 362, 364, 368, 370-372, 375, 377, 379-381, 387, 388, 391, 393, 395, 405, 407]. No obstante, en [56, 369, 383, 398, 399] pueden encontrarse modelos de inventario con demanda incierta en los que sólo una fracción fija de los faltantes se satisfacen con la llegada del pedido más cercano; y en [401, 404] se estudian sistemas de inventario en donde la demanda que se presenta durante periodos de desabastecimiento reitera su intento de compra de acuerdo con un tiempo aleatorio y hasta encontrar existencias del producto (retrial demand). Es importante notar que contrario al caso en que los faltantes se penalizan, el último caso es más aplicable a casos en los que la compañía no se ve afectada significativamente por el mantenimiento de demanda no satisfecha.
Wu et al. [255], por ejemplo, propusieron un modelo para productos que comienzan a deteriorarse después de cierto tiempo (deterioro no instantáneo), en donde la demanda está en función del inventario y, además, se acumula o pierde en función del tiempo de espera. Olsson & Tydesjö [381] tienen en cuenta un modelo de inventario con demanda estocástica, pero asumen que el exceso de ésta se acumula totalmente indistintamente del tiempo de espera. Por su parte, Agrawal et al. [195] estudian un modelo de inventario con la flexibilidad de operar con uno o dos almacenes, en los que la tasa de deterioro es constante pero diferente y en donde los faltantes se acumulan a una tasa constante.
4.2.2. Modelos de inventarios que consideran políticas de pago a proveedores
En el modelo tradicional EOQ fue tácitamente asumido que el valor total de los pedidos era pagado tan pronto como éste fuera entregado. No obstante, es común encontrar proveedores que conceden un determinado plazo de pago sin el cobro de intereses (trade credit period), más allá del cual el valor total o parcial del pedido puede ser también cancelado, pero con el cargo de intereses.
Los modelos de inventarios en donde se otorga sólo un plazo de pago para pedidos mayores o iguales a un valor predeterminado por el proveedor pueden consultarse en [127, 128, 139, 146, 156, 207, 350]. Los modelos de inventarios en donde un plazo de pago es otorgado por el proveedor para cualquier tamaño de pedido pueden encontrarse en [71, 80, 86, 126, 133-135, 137, 141, 144, 148, 155, 158, 168, 173, 177, 185, 187, 188, 192, 213, 228, 229, 231, 235, 236, 240, 250, 263, 265-267, 282, 287, 317, 319, 320, 335, 336]. Mientras que los autores que consideran un plazo de pago pero como variable de decisión pueden consultarse en [53, 180, 198, 253, 340, 355, 357].
Los modelos de inventario desarrollados en [20, 21, 33, 51, 75, 76, 130, 138, 152, 157, 161, 179, 198, 216, 219, 299, 318, 322, 328, 344, 357, 389] no sólo tienen en cuenta la concesión de un plazo de pago entre un proveedor y un comprador, sino de este último al consumidor. En estos modelos se asume que el plazo concedido por el proveedor al minorista es mayor que el ofrecido por el minorista al consumidor. No obstante, Chang et al. [130] relajan este supuesto. Por otra parte, los modelos desarrollados en [136, 142, 147, 166, 209, 226] tienen en cuenta situaciones en las que el proveedor no sólo ofrece un plazo de pago M3 sin el cobro de intereses, sino que también ofrece un descuento por pronto pago si el valor total del pedido se paga dentro de otro plazo M1 (con M3 > M1). Ouyang et al. [167] y Guchhait et al. [305] no sólo tienen en cuenta situaciones en las que el proveedor ofrece un plazo de pago sin el cobro de intereses M3 para tamaños de pedidos iguales o mayores a una cantidad predeterminada W, sino que ofrece también un plazo de pago sin el cobro de intereses para una parte del valor total del pedido cuando la cantidad que se compre sea menor que W. Al respecto, si la cantidad de pedido Q es menor que W, entonces el minorista debe pagar una fracción 0 ≤ β ≤ 1 sobre el total de la compra c · Q cuando la orden es entregada, y pagar el resto c · Q(1 − β) durante un plazo M2 sin el cobro de intereses. Estos casos también son estudiados por Chung et al. [385] y Liao et al. [394]. Pero el minorista puede seleccionar entre un periodo de descuento M1 por pronto pago y un plazo de pago sin el cobro de intereses para una parte del valor total del pedido si Q < W, o puede elegir entre un periodo de descuento M1 por pronto pago y un plazo de pago M3 sin el cobro de intereses para el valor total del pedido si Q ≥ W.
Taleizadeh et al. [22] consideran una situación en la que el proveedor ofrece diferentes descuentos en función del tamaño del pedido bajo la condición de que una parte del valor total del pedido sea cancelada inmediatamente y el resto dentro de un plazo acordado. Por su parte, Sarkar [283] considera tres tipos de descuentos sobre el valor total del pedido realizado a un proveedor de acuerdo con el plazo de pago sin el cobro de intereses seleccionado.
4.2.3. Modelos de inventarios que buscan determinar una política de precio óptima
En ambientes competitivos es común variar el precio de los productos para estimular la demanda y disminuir de este modo el nivel de deterioro de los productos almacenados: en este contexto, la política de precios que se debería adoptar juega un papel importante dentro del horizonte de planeación y por ende es importante tenerla en cuenta.
El precio de venta como variable de decisión fue considerado por primera vez en 1996 para productos perecederos por Eilon & Mallya [409]. Más adelante, Kang & Kim [410] y Aggarwal & Jaggi [411] reformularían y extenderían dicho modelo para abrir paso a investigaciones adicionales en donde se determina tanto una política de precios óptima [26, 33, 34, 42, 44, 46, 48, 52, 59, 93, 96, 108, 112, 164, 194, 198, 202, 205, 216, 231, 232, 245, 251, 302, 305, 306, 330, 331, 334-346, 348, 349, 351-354, 356, 365, 378, 379] como una política de descuento o rebajas óptima [18, 210, 221, 313, 325]. En los artículos [121] [132] se consideran escenarios en los que se ofrece un descuento en el precio de venta para estimular la demanda, pero dicho descuento en lugar de ser una variable de decisión es un parámetro.
Tradicionalmente, una práctica común llevada a cabo por las empresas es la de mantener un precio constante en los bienes o servicios ofrecidos y aplicar descuentos, ya sea cuando los productos o servicios ofrecidos están cerca de caducar o bien en periodos en los que la demanda es baja. No obstante, en compañías tales como hoteles y agencias de viajes, una estrategia en la que los precios varían en diferentes periodos (precios dinámicos) ha demostrado tener mejores beneficios. Los modelos de inventarios que consideran una política con precios dinámicos pueden consultarse en [47, 237, 250, 291, 321, 326, 327, 329, 333, 359, 361, 363, 364, 370, 373, 398].
4.2.4. Modelos de inventarios multiniveles
En la literatura estudiada, 43/61 de los modelos de inventarios que consideran más de un nivel dentro de la cadena de abastecimiento están restringidos a las interacciones que se presentan entre un proveedor o productor y un minorista [24, 26, 47, 48, 53, 56, 58, 60, 61, 67, 68, 72, 94, 98, 100, 108, 110, 114, 115, 124, 150, 151, 162, 163, 178-181, 183, 184, 210, 217, 220, 253, 304, 328, 340, 357, 373, 374, 376, 391, 399]. Sin embargo, los modelos en los que se considera un sistema de múltiples minoristas y un proveedor se estudian en [106, 112, 113, 116, 154, 241]. De los modelos que consideran un vendedor y múltiples compradores, Yang & We [113] y Wu & Sarker [106] consideran una política integrada de producción e inventario; Yu et al. [116] consideran un sistema en el que el inventario es manejado por el proveedor (Vendor Managed Inventory, VMI); y Li et al. [154] estudian el impacto de una estrategia de aplazamiento (postponement strategy), que consiste en retrasar procesos de diferenciación de productos tanto como sea posible hasta que el costo de la cadena de suministro sea eficiente.
Los modelos que analizan tres eslabones de la cadena de abastecimiento pueden encontrarse en [44, 67, 83, 84, 99, 107, 120, 222, 383, 394]; y los modelos que tienen en cuenta el flujo de productos debido a la logística inversa (cadena de suministro de ciclo cerrado) pueden consultarse en [37, 49, 57, 112, 181]. Seyedhosseini et al. [383] estudian un sistema de múltiples proveedores-compradores-consumidores en un tiempo de horizonte finito con múltiples productos. Cai et al. [44] estudian un sistema en el que un productor le provee los productos a un distribuidor a través de un outsourcing con el fin de determinar la cantidad óptima de pedido tanto para el productor como del comprador y el precio óptimo de las tres partes involucradas. Wee et al. [181] consideran un proveedor y un comprador teniendo en cuenta un sistema logístico con productos remanufacturados debido a la logística inversa bajo un sistema VMI. Chung & Wee [49] y Yang et al [112] también tienen en cuenta la logística inversa, pero en un sistema conformado por un productor y un comprador, y un productor y múltiples minoristas, respectivamente. Por su parte Feng et al. [57] y Alamri [37] consideran productos remanufacturados, pero desde la perspectiva de un productor con una y dos instalaciones respectivamente para las operaciones concernientes a la logística inversa.
4.2.5. Modelos de inventarios que consideran el valor del dinero en el tiempo y/o la inflación
El efecto del valor del dinero y la inflación es otra importante extensión del modelo tradicional EOQ que hace a los modelos de inventario aplicables a situaciones de la vida real. El valor del dinero en el tiempo juega un rol importante en los sistemas empresariales, y especialmente en países con doble dígito en el Producto Interno Bruto [270]. Teniendo en cuenta esto, en la Tabla IV se muestran los artículos de investigación que han sido desarrollados para tener en cuenta el efecto del dinero en el tiempo junto a otras características de los sistemas de inventario. Obsérvese que ningún trabajo ha sido desarrollado para tener en cuenta simultáneamente el efecto del dinero en el tiempo y la existencia de múltiples productos, y sólo pocas investigaciones han sido abordadas para incluir el valor del dinero en el tiempo en ambientes difusos.
Hou & Lin [306] desarrollaron un modelo de inventario en donde la demanda está representada como función de la cantidad de inventario disponible y en donde los faltantes de cada ciclo de inventario se satisfacen en su totalidad al inicio de cada ciclo. Chern et al. [270] propusieron un modelo con una demanda representada mediante una función del tiempo, y en donde sólo una parte de la demanda en exceso (faltantes) se acumula o se satisface al inicio de cada ciclo. Mientras que Taleizadeh & Nematollahi [177] investigan el efecto de la inflación y del valor del dinero en el tiempo sobre un modelo de inventario con un horizonte de planeación finito y en donde se permite tanto faltantes como políticas de crédito ofrecidas por el proveedor.
En la mayoría de los modelos de inventario que consideran el efecto del dinero en el tiempo, la tasa de inflación es considerada como un valor constante y conocido. No obstante, Mirzazadeh et al. [81] tienen en cuenta una demanda incierta que depende linealmente de la tasa interna y externa de inflación mediante variables aleatorias que siguen una distribución de probabilidad conocida sobre un horizonte de planeación finito. En este modelo, la demanda durante los periodos de desabastecimiento se satisface completamente con la llegada de nuevos pedidos, y una fracción constante sobre el inventario a la mano se deteriora por unidad de tiempo.
4.2.6. Modelos de inventarios con más de un almacén
En la mayoría de los modelos de inventarios se supone que todos los productos se almacenan en una sola instalación. No obstante, en algunos casos las organizaciones cuentan con otros almacenes en los que varía tanto la tasa de deterioro de los productos como su estructura de costos. Por ejemplo, podría darse la situación en la que existe una capacidad limitada y en la que la empresa opta por rentar una bodega adicional. Otro caso podría ser el de un minorista que posee un punto de venta para vender productos frescos a un precio estándar y otro punto de venta para ofrecer descuentos en los productos que no se hayan vendido dentro de un tiempo determinado (productos próximos a caducar). Los modelos de inventario para productos perecederos en donde se tiene en cuenta más de una instalación para el almacenamiento de los productos junto a otras características de los sistemas de inventario se presentan en la Tabla V. Nótese que modelos que consideran tanto el valor del dinero en el tiempo como dos instalaciones para el almacenamiento de productos que se deterioran se incluyeron dentro de la Tabla IV.
Bhunia et al. [201] estudian un modelo determinista bajo condiciones de inflación y emplea la metaheurística PSO (Particle Swarm Optimization) para mostrar que se obtiene un mayor costo si se consideraran los faltantes al final del ciclo en lugar que al inicio. Guchhait et al. [305], en cambio, combinan las características del PSO con las del algoritmo genético en una heurística híbrida PSGA (Particle Swarm-Genetic Algorithm) para demostrar que el desempeño de ésta es mejor en comparación al FGA (Fuzzy Genetic Algorithm) y el PSGA tradicional en un sistema de inventario en el que la demanda es sensible al precio de venta y los costos son conocidos o inciertos.
4.2.7. Modelos de inventarios con la inclusión de múltiples productos
Pese a que en la mayoría de los sistemas empresariales se manejan diferentes clases de productos, son muy pocos los estudios llevados a cabo en este contexto en comparación con los modelos que tienen en cuenta una misma clase de productos (single ítem). La razón se debe tal vez a la complejidad que supone la inclusión de dicho factor, ya que a diferencia de los modelos de inventarios con un solo tipo de producto, el espectro de solución asociado a los modelos de inventarios con múltiples productos se aumenta considerablemente y más aún cuando se tienen en cuenta otras implicaciones tales como la complementariedad y/o sustitución entre los productos.
Los modelos de inventarios con la incorporación de múltiples productos y periodos de faltantes se tienen en cuenta en [22, 23, 56, 74, 109, 154, 334, 364, 368, 369, 383, 402]. Los modelos de inventarios que determinan una política óptima de precio en un sistema con múltiples productos pueden consultarse en [18, 334, 364]. Los modelos de inventarios con múltiples productos y parámetros difusos se estudian en [18, 23, 74, 171]. De éstos, Gumasta et al. [369] y Frank et al [368] desarrollaron un modelo de inventario de revisión periódica y demanda incierta. El primero considerando una longitud de ciclo arbitrario pero fijo y el segundo teniendo en cuenta un sistema de producción en el que los productos son fabricados por medio de un componente que se deteriora y otro que no. Maity & Maiti [309] y Shavandi et al. [334] presentan un modelo de inventario que tiene en cuenta la presencia de productos sustitutos y complementarios con una tasa de deterioro constante. Shavandi et al. [334] estudian una política de producción e inventario y de precios que permite maximizar el beneficio neto en un modelo en el que la demanda es sensible al precio de productos sustitutos, complementarios e independientes y en donde se permiten faltantes que se acumulan en función del tiempo de espera. Mientras que en [309] se consideran productos sustitutos y complementarios, pero la demanda es sensible al nivel del inventario y no se permiten faltantes. Finalmente, en artículos de investigación más recientes, Chew et al. [364] y Duan & Liao [56] consideran un sistema con demanda incierta y productos con fecha de caducidad conocida de múltiples periodos, y en donde se presenta sustitución entre productos de diferente edad. Duan & Liao [56] toman en cuenta la substitución en una cadena de suministro con bancos de sangre humana; y Chew et al. [364] consideran la sustitución en un contexto en que la demanda de los productos de diferente edad depende tanto de su propio precio como del precio de productos sustitutos.
4.2.8. Modelos de inventarios que incluyen parámetros inciertos
En la mayoría de los modelos de inventario con demanda estocástica, el tiempo de entrega (lead time) es considerado como cero o insignificante [81, 361, 364-366, 368, 369, 371, 373, 378-380, 383, 386, 389, 390, 395, 398, 405, 407] o bien como una constante fija y positiva [56, 358, 360, 372, 374, 376-378, 380, 381, 384, 386, 387, 393, 399, 405]. Sin embargo, en la literatura también se encuentran modelos de inventario que consideran el tiempo de entrega como variable de decisión [107, 391], o como un parámetro incierto que sigue una distribución de probabilidad general o arbitraria [44, 388, 392, 400], o bien que sigue una distribución exponencial [397, 401, 402, 404]. Adicionalmente, aunque el estudio del tiempo de entrega usualmente se relaciona con modelos que estudian una demanda incierta, un modelo con demanda conocida y tiempo de entrega incierto se desarrolla en [123, 222], y un modelo de inventario en donde se determina el límite inferior y superior óptimo para el tiempo de entrega se estudia en [212].
En algunos modelos que consideran una demanda estocástica, el inventario es controlado explícitamente mediante un sistema de revisión periódica [56, 360, 361, 363, 364, 366-369, 372-374, 376, 378, 379, 386, 389, 393, 394, 398, 406], mientras que en otros es controlado mediante un sistema de revisión continua [358, 371, 374, 377, 380, 381, 384, 387, 388, 392, 395, 397, 400-402, 404, 405, 407]. La mayoría de modelos de inventario encontrados desde el año 2001 y que consideran un sistema de revisión continua han estudiado una política (s,S) que consiste en realizar un pedido de tamaño S − s cada vez que el inventario llega al nivel s [371, 374, 380, 388, 395, 397, 400-402, 404, 405, 407], con la excepción de [358, 377, 381, 384, 387, 392]: una política (S − 1,S) en la que se solicita una unidad de producto cada vez que el inventario cae en una unidad, ya sea por la demanda o bien por el efecto combinado de la demanda y el perecimiento de los productos se estudia en [387, 392] y [381] respectivamente; una política de control de inventario (Q,r) en la que un pedido de tamaño Q es solicitado cada vez la posición del inventario llega a r (o por debajo debido al perecimiento de los productos) puede encontrarse en [358, 377]; y una política (Q,r,T) en la que se ordena un pedido de tamaño Q cada vez que el inventario alcanza el nivel r, o bien cuando T unidades de tiempo transcurren, lo primero que ocurra primero, puede encontrarse en [384].
Por su parte, la mayoría de modelos de inventario que estudian un sistema de revisión periódica ha estudiado la determinación de políticas de control de inventario en la que se solicita una orden de pedido al inicio de cada periodo [361, 363, 364, 366, 368, 369, 373, 376, 378, 385, 398, 406], con la excepción de [56, 360, 366, 367, 374, 386, 389, 393, 394]: una política (R,S) en la que el nivel de inventario es observado en intervalos de tiempo R y las unidades de productos son ordenadas de tal manera que la posición de inventario alcance el nivel S se estudia en [374, 386, 389, 393, 394]; una política de control de inventario (s,S,q,Q), la cual consiste en una política (s,S), pero con tiempos de revisión de un día y órdenes de pedido restringidos entre [q,Q] se introduce en [372]; y nuevas políticas de control de inventario basada en la edad de los productos, Old Inventory Ratio y EWA, se estudian en [56, 367] y [360] respectivamente.
Por otra parte, en el desarrollo de los modelos de inventario usualmente se asume que todos los parámetros del sistema son conocidos y/o fijos. No obstante, en algunas aplicaciones prácticas, la obtención de algunos de éstos (costos, demanda, tasa de producción, inflación, etc.) puede ser vaga e imprecisa o inclusive imposible de tener con exactitud. Al respecto, con la excepción de [18, 22, 308, 335], casi todos los artículos que consideran un modelo de inventario en ambientes difusos, incorporan un número difuso en lugar de una variable difusa [19-21, 23, 74, 85, 133, 144, 171, 210, 233, 245, 305, 314, 332, 375]. Téngase en cuenta que una variable difusa puede estudiarse como una variable difusa aleatoria, como una variable aleatoria difusa o como una variable híbrida. Una variable aleatoria difusa puede ser vista como una variable aleatoria cuyos valores son difusos en lugar de números reales, y una variable difusa aleatoria puede ser vista como una variable difusa que toma valores aleatorios. Para el lector interesado en afianzar estos y otros conceptos básicos sobre la teoría difusa (Fuzzy theory) se recomienda consultar los artículos en [413-415].
Kumar et al. [19] consideran como un número difuso tanto la demanda como la tasa de deterioro. Chen & Ouyang [133] y Soni & Patel [335] consideran simultáneamente el costo de mantener inventarios y los intereses pagados y ganados como difuso en un modelo donde se permite el retraso en el pago de los pedidos, pero [133] como números difusos y [335] como variables difusas. Taleizadeh et al. [22] consideran la demanda como una variable difusa en un sistema que sigue una política de compra con descuento y faltantes. Katagiri & Ishii [375] consideran el costo de faltante y el costo de salvamento de los productos deteriorados (shortage and outdating cost) como valores difusos. Roy et al. [314] estudian la inflación como un valor difuso en un modelo en donde el horizonte de planeación sigue una distribución de probabilidad exponencial con media conocida.
5. Conclusiones
En el presente artículo se ha mostrado la manera en que han sido abordadas las diferentes características que se presentan en los sistemas de inventarios con productos que se deterioran. Es notoria la cantidad de modelos desarrollados asumiendo una demanda determinista en lugar de una demanda incierta. No obstante, un análisis más detallado sobre modelos de inventarios que incluyen una demanda determinista revela que las estrategias habituales de los sistemas empresariales para influenciar la demanda escasamente han sido incluidas. Al respecto, entre el año 2001 y 2013, de 331 artículos de investigación (ver sección 4.1), sólo 13 han tenido en cuenta que la demanda depende de otros factores diferentes al precio, del nivel de inventario y/o del tiempo con el fin de determinar tanto políticas óptimas de inventarios como políticas para la inversión en estrategias de mercadotecnia [42, 48, 108, 291, 312, 324, 326-328, 352, 354, 355, 357].
En cuanto al tipo de deterioro incluido en los diferentes modelos encontrados en la literatura, solo ocho contribuciones científicas [26-33] estudian políticas de inventario óptimas teniendo en cuenta la inversión en tecnologías de preservación para la reducción de la tasa de deterioro de los productos; sólo tres modelos de inventario [19, 144, 308] han considerado una tasa de deterioro difusa; y sólo cinco modelos de inventarios con demanda estocástica (incluyendo revisiones de artículos antes del año 2001) han sido encontrado considerando que la cantidad de un mismo tipo de producto perecedero no es uniforme respecto al tiempo.
En cuanto al tipo de deterioro incluido en los diferentes modelos encontrados en la literatura, solo ocho contribuciones científicas [26-33] estudian políticas de inventario óptimas teniendo en cuenta la inversión en tecnologías de preservación para la reducción de la tasa de deterioro de los productos; sólo tres modelos de inventario [19, 144, 308] han considerado una tasa de deterioro difusa; y sólo cinco modelos de inventarios con demanda estocástica (incluyendo revisiones de artículos antes del año 2001) han sido encontrado considerando que la cantidad de un mismo tipo de producto perecedero no es uniforme respecto al tiempo.
Ahora bien, una revisión de características distintivas en los sistemas de inventario, diferentes al de la demanda y del deterioro, revela que varias de estas se encuentran muy bien representadas en la actual literatura, mientras que otras han sido muy poco estudiadas (ver sección 4.2). Sin embargo, aún hay oportunidades de investigación dentro de cada una de las características discutidas. Por ejemplo, aunque la inclusión de faltantes ha sido ampliamente abordada en modelos de inventario para productos perecederos, y se ha puesto considerable atención en estudios de sistemas con formación de colas, el supuesto de que los clientes durante los periodos de faltantes persisten en su requerimiento de una manera aleatoria introduce una alternativa natural para los modelos en donde los faltantes se consideran como ventas pérdidas o se satisfacen totalmente o parcialmente con la llegada de nuevos pedidos. Al respecto, basado en nuestro conocimiento, sólo los artículos en [401] y [404] han sido desarrollados para considerar esta característica en sistemas de inventario para productos perecederos.
De igual forma, un análisis cruzado de cada una las anteriores características distintivas en los sistemas de inventario muestra también que son escasas las investigaciones que han tenido en cuenta las diferentes políticas de precios que podría adoptar una empresa en un sistema con más de un depósito para el almacenamiento de los productos y/o en donde se tenga en cuenta el valor del dinero del tiempo. Por otra parte, un análisis sobre la evolución de las características mencionadas en la sección 4.2 muestra que la cantidad de modelos de inventario desarrollados entre el año 2011 a 2013, y que estudian un sistema multinivel, superó en número a los desarrollados entre el año 2001 y 2010 (i.d. 20 artículos entre el año 2001-2010 y 41 entre 2011 y 2013). No obstante, los modelos de inventarios que integren varios eslabones de la cadena de suministro a través de un adecuado sistema de información y la inclusión de múltiples productos sustitutos y/o complementarios contribuirían aún más con el marco teórico y práctico de los sistemas de inventario sujeto a deterioro. De los pocos artículos donde se considera una política óptima de inventario para múltiples productos que son sustitutos y/o complementarios entre sí, sólo Duan & Liao [56] han tenido en cuenta un sistema multinivel con productos sustitutos. Por tanto, deberían llevarse a cabo investigaciones futuras para cubrir cada uno de los anteriores aspectos señalados en el presente artículo.
Referencias
-
Harris, F.W., How many parts to make at once. Factory, The Magazine of Management Science, 1913. 10(2): p. 135–136, 152.
-
Nahmias, S., Perishable Inventory Theory: A Review. Operations Research, 1982. 30(4): p. 680–708.
-
Goyal, S.K. and B.C. Giri, Recent trends in modeling of deteriorating inventory. European Journal of Operational Research, 2001. 134(1): p. 1–16.
-
Raafat, F., Survey of Literature on Continuously Deteriorating Inventory Models. Journal of the Operational Research Society, 1991. 42(1): p. 27-37.
-
Nahmias, S., Perishable Inventory Systems. International Series in Operations Research & Management Science. 2011: Springer US. 80.
-
Bakker, M., J. Riezebos, and R.H. Teunter, Review of inventory systems with deterioration since 2001. European Journal of Operational Research, 2012. 221(2): p. 275-284.
-
Amorim, P., et al., Managing perishability in production-distribution planning: a discussion and review. Flexible Services and Manufacturing Journal, 2013. 25(3): p. 389-413.
-
Masters, J.M., A Note on the Effect of Sudden Obsolescence on the Optimal Lot Size. Decision Sciences, 1991. 22(5): p. 1180.
-
Song, Y. and H.C. Lau, A periodic-review inventory model with application to the continuous-review obsolescence problem. European Journal of Operational Research, 2004. 159(1): p. 110-120.
-
Hadley, G. and T.M. Whitin, Analysis of Inventory Systems. 1963, Englewood Cliffs, N.J.
-
David, I., E. Greenshtein, and A. Mehrez, A dynamic-programming approach to continuous-review obsolescent inventory problems. Naval Research Logistics (NRL), 1997. 44(8): p. 757-774.
-
David, I. and A. Mehrez, An Inventory Model with Exogenous Failures. Operations Research, 1995. 43(5): p. 902-903.
-
Joglekar, P. and P. Lee, An exact formulation of inventory costs and optimal lot size in face of sudden obsolescence. Operations Research Letters, 1993. 14(5): p. 283-290.
-
Pahl, J. and S. Voß, Integrating deterioration and lifetime constraints in production and supply chain planning: A survey. European Journal of Operational Research, 2014(0).
-
Karaesmen, I., A. Scheller–Wolf, and B. Deniz, Managing Perishable and Aging Inventories: Review and Future Research Directions, in Planning Production and Inventories in the Extended Enterprise, K.G. Kempf, P. Keskinocak, and R. Uzsoy, Editors. 2011, Springer US. p. 393-436.
-
Liu, L. and Z. Lian, (s, S) Continuous Review Models for Products with Fixed Lifetimes. Operations Research, 1999. 47(1): p. 150-158.
-
Pentico, D.W. and M.J. Drake, A survey of deterministic models for the EOQ and EPQ with partial backordering. European Journal of Operational Research, 2011. 214(2): p. 179-198.
-
Chakraborty, N., S. Mondal, and M. Maiti, A deteriorating multi-item inventory model with price discount and variable demands via fuzzy logic under resource constraints. Computers & Industrial Engineering, 2013. 66(4): p. 976-987.
-
Kumar, S.D., P.K. Kundu, and A. Goswami, An economic production quantity inventory model involving fuzzy demand rate and fuzzy deterioration rate. Journal of Applied Mathematics and Computing, 2003 12(1-2): p. 251–260.
-
Mahata, G.C. and A. Goswami, An EOQ model for deteriorating items under trade credit financing in the fuzzy sense. Production Planning & Control, 2007. 18(8): p. 681-692.
-
Mahata, G.C. and P. Mahata, Analysis of a fuzzy economic order quantity model for deteriorating items under retailer partial trade credit financing in a supply chain. Mathematical and Computer Modelling, 2011. 53(9-10): p. 1621-1636.
-
Taleizadeh, A.A., H.-M. Wee, and F. Jolai, Revisiting a fuzzy rough economic order quantity model for deteriorating items considering quantity discount and prepayment. Mathematical and Computer Modelling, 2013. 57(5-6): p. 1466-1479.
-
Wee, H.-M., C.-C. Lo, and P.-H. Hsu, A multi-objective joint replenishment inventory model of deteriorated items in a fuzzy environment. European Journal of Operational Research, 2009. 197(2): p. 620-631.
-
Sarkar, B., A production-inventory model with probabilistic deterioration in two-echelon supply chain management. Applied Mathematical Modelling, 2013. 37(5): p. 3138-3151.
-
Sarkar, M. and B. Sarkar, An economic manufacturing quantity model with probabilistic deterioration in a production system. Economic Modelling, 2013. 31: p. 245-252.
-
Cai, X., et al., Optimization and coordination of fresh product supply chains with freshness-keeping effort. Production and Operations Management, 2009. 19(3): p. 261–278.
-
Chen, Y.-R. and C.-Y. Dye, Application of particle swarm optimisation for solving deteriorating inventory model with fluctuating demand and controllable deterioration rate. International Journal of Systems Science, 2013. 44(6): p. 1026-1039.
-
Dye, C.-Y., The effect of preservation technology investment on a non-instantaneous deteriorating inventory model. Omega, 2013. 41(5): p. 872-880.
-
Dye, C.-Y. and T.-P. Hsieh, An optimal replenishment policy for deteriorating items with effective investment in preservation technology. European Journal of Operational Research, 2012. 218(1): p. 106-112.
-
Hsieh, T.-P. and C.-Y. Dye, A production–inventory model incorporating the effect of preservation technology investment when demand is fluctuating with time. Journal of Computational and Applied Mathematics, 2013. 239: p. 25-36.
-
Hsu, P.H., H.M. Wee, and H.M. Teng, Preservation technology investment for deteriorating inventory. International Journal of Production Economics, 2010. 124(2): p. 388-394.
-
Lee, Y.-P. and C.-Y. Dye, An inventory model for deteriorating items under stock-dependent demand and controllable deterioration rate. Computers & Industrial Engineering, 2012. 63(2): p. 474-482.
-
Shah, N., D. Shah, and D. Patel, Optimal Preservation Technology Investment, Retail Price and Ordering Policies for Deteriorating Items under Trended Demand and Two Level Trade Credit Financing. Journal of Mathematical Modelling and Algorithms in Operations Research, 2014: p. 1-12.
-
Abad, P.L., Optimal pricing and lot-sizing under conditions of perishability, finite production and partial backordering and lost sale. European Journal of Operational Research, 2003. 144(0 ): p. 677–685.
-
Abdul, I. and A. Murata, A fast-response production-inventory model for deteriorating seasonal products with learning in set-ups. International Journal of Industrial Engineering Computations, 2011. 2(4): p. 715-736.
-
Abdul, I. and A. Murata, Optimal production strategy for deteriorating items with varying demand pattern under inflation. International Journal of Industrial Engineering Computations, 2011. 2(3): p. 449-466.
-
Alamri, A.A., Theory and methodology on the global optimal solution to a General Reverse Logistics Inventory Model for deteriorating items and time-varying rates. Computers & Industrial Engineering, 2011. 60(2): p. 236-247.
-
Alshamrani, A.M., Optimal control of a stochastic production-inventory model with deteriorating items. Journal of King Saud University Science, 2012.
-
Balkhi, Z.T., On a finite horizon production lot size inventory model for deteriorating items: an optimal solution. European Journal of Operational Research, 2001. 132(4): p. 210–223.
-
Baten, M.A., A.A. Kamil, and H. Lateh, Inventory-Production Control Systems with Gumbel Distributed Deterioration. AASRI Procedia, 2012. 2: p. 93-105.
-
Bhowmick, J. and G.P. Samanta, A Deterministic Inventory Model of Deteriorating Items with Two Rates of Production, Shortages, and Variable Production Cycle. ISRN Applied Mathematics, 2011. 2011: p. 1-16.
-
Bhunia, A.K., et al., An application of tournament genetic algorithm in a marketing oriented economic production lot-size model for deteriorating items. International Journal of Production Economics, 2009. 119(1): p. 112-121.
-
Bukhari, F.A. and A. El-Gohary, Optimal control of a production-maintenance system with deteriorating items. Journal of King Saud University Science, 2012. 24(4): p. 351-357.
-
Cai, X., et al., Fresh-product supply chain management with logistics outsourcing. Omega, 2013. 41(4): p. 752-765.
-
Chakraborty, T. and B.C. Giri, Joint determination of optimal safety stocks and production policy for an imperfect production system. Applied Mathematical Modelling, 2012. 36(2): p. 712-722.
-
Chen, J.-M. and L.-T. Chen, Pricing and production lot-size/scheduling with finite capacity for a deteriorating item over a finite horizon. Computers & Operations Research, 2005. 32(11): p. 2801-2819.
-
Chen, L.-T. and C.-C. Wei, Multi-period channel coordination in vendor-managed inventory for deteriorating goods. International Journal of Production Research, 2012. 50(16): p. 4396-4413.
-
Chung, C.J. and H.M. Wee, An integrated production-inventory deteriorating model for pricing policy considering imperfect production, inspection planning and warranty-periodand stock-level-dependant demand. International Journal of Systems Science, 2008. 39(8): p. 823-837.
-
Chung, C.-J. and H.-M. Wee, Short life-cycle deteriorating product remanufacturing in a green supply chain inventory control system. International Journal of Production Economics, 2011. 129(1): p. 195-203.
-
Chung, C.-J., G.A. Widyadana, and H. Ming Wee, Economic production quantity model for deteriorating inventory with random machine unavailability and shortage. International Journal of Production Research, 2011. 49(3): p. 883-902.
-
Chung, K.-J., L. Eduardo Cárdenas-Barrón, and P.-S. Ting, An inventory model with non-instantaneous receipt and exponentially deteriorating items for an integrated three layer supply chain system under two levels of trade credit. International Journal of Production Economics, (0).
-
Dalfard, V. and N. Nosratian, A new pricing constrained single-product inventory-production model in perishable food for maximizing the total profit. Neural Computing and Applications, 2012: p. 1-9.
-
Das, B.C., B. Das, and S.K. Mondal, Integrated supply chain model for a deteriorating item with procurement cost dependent credit period. Computers & Industrial Engineering, 2013. 64(3): p. 788-796.
-
Das, D., et al., Two-warehouse production model for deteriorating inventory items with stock-dependent demand under inflation over a random planning horizon. Central European Journal of Operations Research, 2012. 20(2): p. 251-280.
-
Das, D., et al., Two-warehouse production inventory model for a deteriorating item with time-varying demand and shortages: a genetic algorithm with varying population size approach. Optimization and Engineering, 2013: p. 1-19.
-
Duan, Q. and T.W. Liao, Optimization of blood supply chain with shortened shelf lives and ABO compatibility. International Journal of Production Economics, (0).
-
Feng, L., J. Zhang, and W. Tang, Optimal control of production and remanufacturing for a recovery system with perishable items. International Journal of Production Research, 2013. 51(13): p. 3977-3994.
-
Gaur, N.K., S. Kumar, and S.R. Singh, An Integrated Production-Inventory Model for Deteriorating Items under the effect of Inflation. International Transactions in Applied Sciences, 2011. 3(3): p. 543-562.
-
Ghosh, S.K., S. Khanra, and K.S. Chaudhuri, Optimal price and lot size determination for a perishable product under conditions of finite production, partial backordering and lost sale. Applied Mathematics and Computation, 2011. 217(13): p. 6047-6053.
-
Giri, B.C. and A. A. Chakraborty, Supply chain coordination for a deteriorating product under stock-dependent consumption rate and unreliable production process. International Journal of Industrial Engineering Computations, 2011. 2(2): p. 263-272.
-
Giri, B.C. and T. Maiti, Supply chain model for a deteriorating product with time-varying demand and production rate. Journal of the Operational Research Society, 2011. 63(5): p. 665-673.
-
Guchhait, P., M. Kumar Maiti, and M. Maiti, Production-inventory models for a damageable item with variable demands and inventory costs in an imperfect production process. International Journal of Production Economics, 2013. 144(1): p. 180-188.
-
He, Y. and S. Wang, Analysis of production-inventory system for deteriorating items with demand disruption. International Journal of Production Research, 2012. 50(16): p. 4580-4592.
-
He, Y., S.-Y. Wang, and K.K. Lai, An optimal production-inventory model for deteriorating items with multiple-market demand. European Journal of Operational Research, 2010. 203(3): p. 593-600.
-
Konstantaras, I. and K. Skouri, A note on a production-inventory model under stock-dependent demand, Weibull distribution deterioration, and shortage. International Transactions in Operational Research, 2011. 18(4): p. 527-531.
-
Lee, C.C. and S.-L. Hsu, A two-warehouse production model for deteriorating inventory items with time-dependent demands. European Journal of Operational Research, 2009. 194(3): p. 700-710.
-
Lee, C.-F. and C.-P. Chung, An Inventory Model for Deteriorating Items in a Supply Chain with System Dynamics Analysis. Procedia Social and Behavioral Sciences, 2012. 40: p. 41-51.
-
Lee, S. and D. Kim, An optimal policy for a single-vendor single-buyer integrated production–distribution model with both deteriorating and defective items. International Journal of Production Economics, 2014. 147: p. 161-170.
-
Li, S., Optimal control of the production–inventory system with deteriorating items and tradable emission permits. International Journal of Systems Science, 2013: p. 1-12.
-
Li, S., Optimal control of production-maintenance system with deteriorating items, emission tax and pollution R&D investment. International Journal of Production Research, 2014. 52(6): p. 1787-1807.
-
Liao, J.-J., On an EPQ model for deteriorating items under permissible delay in payments. Applied Mathematical Modelling, 2007. 31(3): p. 393-403.
-
Lin, Y.S., J.C.P. Yu, and K.-J. Wang, An efficient replenishment model of deteriorating items for a supplier–buyer partnership in hi-tech industry. Production Planning & Control, 2009. 20(5): p. 431-444.
-
Lodree, E.J. and B.M. Uzochukwu, Production planning for a deteriorating item with stochastic demand and consumer choice. International Journal of Production Economics, 2008. 116(2): p. 219-232.
-
Mahapatra, N.K. and M. Maiti, Decision process for multiobjective, multi-item production-inventory system via interactive fuzzy satisficing technique. Computers & Mathematics with Applications, 2005. 49(5-6): p. 805-821.
-
Mahata, G.C., A Production Lot-Size Model for Perishable Items Under Two Level Trade Credit Policy for a Retailer with a Powerful Position in a Supply Chain System. Journal of Mathematical Modelling and Algorithms, 2011. 10(4): p. 323-340.
-
Mahata, G.C., An EPQ-based inventory model for exponentially deteriorating items under retailer partial trade credit policy in supply chain. Expert Systems with Applications, 2012. 39(3): p. 3537-3550.
-
Maity, A.K., et al., A Chebyshev approximation for solving the optimal production inventory problem of deteriorating multi-item. Mathematical and Computer Modelling, 2007. 45(1-2): p. 149-161.
-
Manna, S.K. and K.S. Chaudhuri An economic order quantity model for deteriorating items with time-dependent deterioration rate, demand rate, unit production cost and shortages. International Journal of Systems Science, 2001 32(8): p. 1003–1009.
-
Manna, S.K. and K.S. Chaudhuri, An EOQ model with ramp type demand rate, time dependent deterioration rate, unit production cost and shortages. European Journal of Operational Research, 2006. 171(2): p. 557-566.
-
Min, J., et al., An EPQ model for deteriorating items with inventory-level-dependent demand and permissible delay in payments. International Journal of Systems Science, 2012. 43(6): p. 1039-1053.
-
Mirzazadeh, A., M.M. Seyyed Esfahani, and S.M.T. Fatemi Ghomi, An inventory model under uncertain inflationary conditions, finite production rate and inflation-dependent demand rate for deteriorating items with shortages. International Journal of Systems Science, 2009. 40(1): p. 21-31.
-
Nasr, W.W., M.K. Salameh, and L. Moussawi-Haidar, Integrating the economic production model with deteriorating raw material over multi-production cycles. International Journal of Production Research, 2014. 52(8): p. 2477-2489.
-
Rau, H., M.Y. Wu, and H.M. Wee, Deteriorating item inventory model with shortage due to supplier in an integrated supply chain. International Journal of Systems Science, 2004. 35(5): p. 293-303.
-
Rau, H., M.-Y. Wu, and H.-M. Wee, Integrated inventory model for deteriorating items under a multi-echelon supply chain environment. International Journal of Production Economics, 2003. 86(2): p. 155-168.
-
Roy, A., S. kar, and M. Maiti, A volume flexible production-policy for randomly deteriorating item with trended demand and shortages. International Journal of Production Economics, 2010. 128(1): p. 188-199.
-
Roy, A. and G.P. Samanta, Inventory model with two rates of production for deteriorating items with permissible delay in payments. International Journal of Systems Science, 2011. 42(8): p. 1375-1386.
-
Roy, T. and K.S. Chaudhuri, A production-inventory model under stock-dependent demand, Weibull distribution deterioration and shortage. International Transactions in Operational Research, 2009. 16(3): p. 325-346.
-
Sana, S., K.S. Chaudhuri, and B. Mahavidyalaya, On a volume flexible production policy for a deteriorating item with time-dependent demand and shortages. Advanced Modeling & Optimization, 2004. 6(1): p. 57–74.
-
Sana, S., S.K. Goyal, and K.S. Chaudhuri, A production–inventory model for a deteriorating item with trended demand and shortages. European Journal of Operational Research, 2004. 157(2): p. 357-371.
-
Shen, Z., M. Dessouky, and F. Ordonez, Perishable inventory management system with a minimum volume constraint. The Journal of the Operational Research Society, 2011. 62(12): p. 2063-2082.
-
Skouri, K. and S. Papachristos, Optimal stopping and restarting production times for an EOQ model with deteriorating items and time-dependent partial backlogging. International Journal of Production Economics, 2003. 81-82(0): p. 525–531.
-
Tadj, L., M. Bounkhel, and Y. Benhadid, Optimal control of a production inventory system with deteriorating items. International Journal of Systems Science, 2006. 37(15): p. 1111-1121.
-
Teng, J.-T. and C.-T. Chang, Economic production quantity models for deteriorating items with priceand stock-dependent demand. Computers & Operations Research, 2005. 32(2): p. 297-308.
-
Tsai, D.-M., An optimal production and shipment policy for a single-vendor single-buyer integrated system with both learning effect and deteriorating items. International Journal of Production Research, 2011. 49(3): p. 903-922.
-
Tyagi, V.K., S. Singh, and S.R. Singh, Probabilistic Inventory Model for Deteriorating Items with Non-Linear Production Rate Depending on Linear Demand Rate. International Transactions in Applied Sciences, 2011. 3(3): p. 313-322.
-
Valliathal, M. and R. Uthayakumar, Simple approach of obtaining the optimal pricing and lot-sizing policies for an EPQ model on deteriorating items with shortages under inflation and time-discounting. Istanbul University Journal Of The School Of Business Administration, 2011. 40(2): p. 304-320.
-
Valliathal, M. and R. Uthayakumar, Designing and computing optimal policies on a production model for non-instantaneous deteriorating items with shortages. International Journal of Production Research, 2013. 51(1): p. 215-229.
-
Wang, K.-J. and Y.-S. Lin, Optimal inventory replenishment strategy for deteriorating items in a demand-declining market with the retailer’s price manipulation. Annals of Operations Research, 2012. 201(1): p. 475-494.
-
Wang, K.-J., Y.S. Lin, and J.C.P. Yu, Optimizing inventory policy for products with time-sensitive deteriorating rates in a multi-echelon supply chain. International Journal of Production Economics, 2011. 130(1): p. 66-76.
-
Wang, S.P., W. Lee, and C.Y. Chang, Modeling the consignment inventory for a deteriorating item while the buyer has warehouse capacity constraint. International Journal of Production Economics, 2012. 138(2): p. 284-292.
-
Wang, T.-Y. and L.-H. Chen, A production lot size inventory model for deteriorating items with time-varying demand. International Journal of Systems Science, 2001. 32(6): p. 745-751.
-
Wee, H.M. and G.A. Widyadana, Economic production quantity models for deteriorating items with rework and stochastic preventive maintenance time. International Journal of Production Research, 2012. 50(11): p. 2940-2952.
-
Wee, H.M. and G.A. Widyadana, A production model for deteriorating items with stochastic preventive maintenance time and rework process with FIFO rule. Omega, 2013. 41(6): p. 941-954.
-
Widyadana, G.A. and H.M. Wee, Optimal deteriorating items production inventory models with random machine breakdown and stochastic repair time. Applied Mathematical Modelling, 2011. 35(7): p. 3495-3508.
-
Widyadana, G.A. and H.M. Wee, An economic production quantity model for deteriorating items with multiple production setups and rework. International Journal of Production Economics, 2012. 138(1): p. 62-67.
-
Wu, B. and B.R. Sarker, Optimal manufacturing and delivery schedules in a supply chain system of deteriorating items. International Journal of Production Research, 2013. 51(3): p. 798-812.
-
Xiao, T., et al., Ordering, wholesale pricing and lead-time decisions in a three-stage supply chain under demand uncertainty. Computers & Industrial Engineering, 2010. 59(4): p. 840-852.
-
Xiao, T. and T. Xu, Coordinating price and service level decisions for a supply chain with deteriorating item under vendor managed inventory. International Journal of Production Economics, 2013.
-
Xu, Y. and B.R. Sarker, Models for a family of products with shelf life, and production and shortage costs in emerging markets. Computers & Operations Research, 2003. 30(6): p. 925–938.
-
Yan, C., A. Banerjee, and L. Yang, An integrated production–distribution model for a deteriorating inventory item. International Journal of Production Economics, 2011. 133(1): p. 228-232.
-
Yang, H.-L., A partial backlogging production-inventory lot-size model for deteriorating items with time-varying production and demand rate over a finite time horizon. International Journal of Systems Science, 2011. 42(8): p. 1397-1407.
-
Yang, P.C., et al., Collaboration for a closed-loop deteriorating inventory supply chain with multi-retailer and price-sensitive demand. International Journal of Production Economics, 2013. 143(2): p. 557-566.
-
Yang, P.C. and H.M. Wee, A single-vendor and multiple-buyers production inventory policy for a deteriorating item. European Journal of Operational Research, 2002. 143(3): p. 570–581.
-
Yang, P.-C. and H.-M. Wee, An integrated multi-lot-size production inventory model for deteriorating item. Computers & Operations Research, 2003. 30(5 ): p. 671–682.
-
Yu, J.C.P., Y.-S. Lin, and K.-J. Wang, Coordination-based inventory management for deteriorating items in a two-echelon supply chain with profit sharing. International Journal of Systems Science, 2013. 44(9): p. 1587-1601.
-
Yu, Y., Z. Wang, and L. Liang, A vendor managed inventory supply chain with deteriorating raw materials and products. International Journal of Production Economics, 2012. 136(2): p. 266-274.
-
Mishra, S., et al., Optimal control of an inventory system for weibull ameliorating, deteriorating items under the influence of inflation. Bulletin of Pure & Applied SciencesMathematics, 2011. 30E(1): p. 85-94.
-
Moon, I., B.C. Giri, and B. Ko, Economic order quantity models for ameliorating/deteriorating items under inflation and time discounting. European Journal of Operational Research, 2005. 162(3): p. 773-785.
-
Wee, H.-M., et al., An inventory model for ameliorating and deteriorating items taking account of time value of money and finite planning horizon. International Journal of Systems Science, 2008. 39(8): p. 801-807.
-
Coelho, L.C. and G. Laporte, Optimal joint replenishment, delivery and inventory management policies for perishable products. Computers & Operations Research, 2014. 47: p. 42-52.
-
Ferguson, M., V. Jayaraman, and G.C. Souza, Note: An application of the EOQ model with nonlinear holding cost to inventory management of perishables. European Journal of Operational Research, 2007. 180(1): p. 485-490.
-
Kishore, R.A., et al., N-Period Dynamic Deterministic Inventory Model for Perishable Goods. IUP Journal of Operations Management, 2011. 10(1): p. 7-17.
-
Sazvar, Z., A. Baboli, and M. Akbari Jokar, A replenishment policy for perishable products with non-linear holding cost under stochastic supply lead time. The International Journal of Advanced Manufacturing Technology, 2013. 64(5-8): p. 1087-1098.
-
Zanoni, S. and L. Zavanella, Single-vendor single-buyer with integrated transport-inventory system: Models and heuristics in the case of perishable goods. Computers & Industrial Engineering, 2007. 52(1): p. 107-123.
-
Atici, F.M., A. Lebedinsky, and F. Uysal, Inventory model of deteriorating items on non-periodic discrete-time domains. European Journal of Operational Research, 2013. 230(2): p. 284-289.
-
Bhunia, A.K., et al., A two-warehouse inventory model for deteriorating items under permissible delay in payment with partial backlogging. Applied Mathematics and Computation, 2014. 232: p. 1125-1137.
-
Chang, C.-T., An EOQ model with deteriorating items under inflation when supplier credits linked to order quantity. International Journal of Production Economics, 2004. 88(3): p. 307-316.
-
Chang, C.-T., L.-Y. Ouyang, and J.-T. Teng, An EOQ model for deteriorating items under supplier credits linked to ordering quantity. Applied Mathematical Modelling, 2003. 27(12): p. 983-996.
-
Chang, C.-T., et al., Optimal ordering policies for deteriorating items using a discounted cash-flow analysis when a trade credit is linked to order quantity. Computers & Industrial Engineering, 2010. 59(4): p. 770-777.
-
Chang, C.-T., J.-T. Teng, and M.-S. Chern, Optimal manufacturer’s replenishment policies for deteriorating items in a supply chain with up-stream and down-stream trade credits. International Journal of Production Economics, 2010. 127(1): p. 197-202.
-
Chang, H.-J. and W.-F. Lin, A Simple Solution Method for the Finite Horizon Eoq Model for Deteriorating Items with Cost Changes. Asia-Pacific Journal of Operational Research, 2011. 28(06): p. 689-704.
-
Chang, H.-J., W.-F. Lin, and J.-F. Ho, Closed-form solutions for Wee’s and Martin’s EOQ models with a temporary price discount. International Journal of Production Economics, 2011. 131(2): p. 528-534.
-
Chen, L.-H. and L.-Y. Ouyang, Fuzzy inventory model for deteriorating items with permissible delay in payment. Applied Mathematics and Computation, 2006. 182(1): p. 711-726.
-
Chung, K.-J., A complete proof on the solution procedure for non-instantaneous deteriorating items with permissible delay in payment. Computers & Industrial Engineering, 2009. 56(1): p. 267-273.
-
Chung, K.-J., Using the convexities of total annual relevant costs to determine the optimal cycle times of inventory models for deteriorating items with permissible delay in payments. Computers & Industrial Engineering, 2010. 58(4): p. 801-808.
-
Chung, K.-J., Some improved algorithms to locate the optimal solutions for exponentially deteriorating items under trade credit financing in a supply chain system. Computers & Mathematics with Applications, 2011. 61(9): p. 2353-2361.
-
Chung, K.-J., S.-L. Chang, and W.-D. Yang, The Optimal Cycle Time for Exponentially Deteriorating Products under Trade Credit Financing. The Engineering Economist, 2001. 46(3): p. 232-242.
-
Chung, K.-J. and T.-S. Huang, The optimal retailer’s ordering policies for deteriorating items with limited storage capacity under trade credit financing. International Journal of Production Economics, 2007. 106(1): p. 127-145.
-
Chung, K.-J. and J.-J. Liao, Lot-sizing decisions under trade credit depending on the ordering quantity. Computers & Operations Research, 2004. 31(6): p. 909-928.
-
Chung, K.-J. and C.-N. Lin, Optimal inventory replenishment models for deteriorating items taking account of time discounting. Computers & Operations Research, 2001. 28(1): p. 67–83.
-
Chung, K.-J. and S.-D. Lin, The inventory model for trade credit in economic ordering policies of deteriorating items in a supply chain system. Applied Mathematical Modelling, 2011. 35(6): p. 3111-3115.
-
Chung, K.-J., S.-D. Lin, and H.M. Srivastava, The complete solution procedures for the mathematical analysis of some families of optimal inventory models with order-size dependent trade credit and deterministic and constant demand. Applied Mathematics and Computation, 2012. 219(1): p. 142-157.
-
Chung, K.-J., S.-D. Lin, and H.M. Srivastava, The Inventory Models for Deteriorating Items in the Discounted Cash-Flows Approach Under Conditional Trade Credit and Cash Discount in a Supply Chain System. Applied Mathematics & Information Sciences, 2014. 8(5): p. 2103-2111.
-
De, S.K. and A. Goswami, An EOQ model with fuzzy inflation rate and fuzzy deterioration rate when a delay in payment is permissible. International Journal of Systems Science, 2006. 37(5): p. 323-335.
-
Hou, K.-L., An inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting. European Journal of Operational Research, 2006. 168(2): p. 463-474.
-
Huang, K.-N. and J.-J. Liao, Bounds on the Optimum Order Quantity of the EOQ Model with Deteriorating Items under Supplier Credit Linked to Order Quantity. International Journal of Information and Management Sciences, 2006 17(3): p. 105–116.
-
Huang, K.-N. and J.-J. Liao, A simple method to locate the optimal solution for exponentially deteriorating items under trade credit financing. Computers & Mathematics with Applications, 2008. 56(4): p. 965-977.
-
Jaggi, C.K., S.K. Goel, and M. Mittal, Economic order quantity model for deteriorating items with imperfect quality and permissible delay on payment. International Journal of Industrial Engineering Computations, 2011. 2(2): p. 237-248.
-
Jaggi, C.K. and M. Mittal, Economic order quantity model for deteriorating items with imperfect quality. Investigación Operacional, 2011. 32(2): p. 107-113.
-
Kawakatsu, H., A Wholesaler’s Optimal Ordering and Quantity Discount Policies for Deteriorating Items. Engineering Letters, 2011. 19(4): p. 339-345.
-
Kawakatsu, H., An Optimal Quantity Discount Pricing Policy for Deteriorating Items. Australian Journal of Basic & Applied Sciences, 2011. 5(3): p. 11-19.
-
Kumar, A., K.K. Kaanodiaya, and R.R. Pachauri, Retailer’s inventory policy for deteriorating items under partial trade credit policy. International Journal of Industrial Engineering Computations, 2011: p. 699-714.
-
Lee, C.C., Two-warehouse inventory model with deterioration under FIFO dispatching policy. European Journal of Operational Research, 2006. 174(2): p. 861-873.
-
Li, J., T.C. Edwin Cheng, and S. Wang, Analysis of postponement strategy for perishable items by EOQ-based models. International Journal of Production Economics, 2007. 107(1): p. 31-38.
-
Liang, Y. and F. Zhou, A two-warehouse inventory model for deteriorating items under conditionally permissible delay in payment. Applied Mathematical Modelling, 2011. 35(5): p. 2221-2231.
-
Liao, J.-J., A note on an EOQ model for deteriorating items under supplier credit linked to ordering quantity. Applied Mathematical Modelling, 2007. 31(8): p. 1690-1699.
-
Liao, J.-J., An EOQ model with noninstantaneous receipt and exponentially deteriorating items under two-level trade credit. International Journal of Production Economics, 2008. 113(2): p. 852-861.
-
Liao, J.-J., K.-J. Chung, and K.-N. Huang, A deterministic inventory model for deteriorating items with two warehouses and trade credit in a supply chain system. International Journal of Production Economics, 2013. 146(2): p. 557-565.
-
Liao, J.-J., K.-N. Huang, and K.-J. Chung, Lot-sizing decisions for deteriorating items with two warehouses under an order-size-dependent trade credit. International Journal of Production Economics, 2012. 137(1): p. 102-115.
-
Liao, J.-J., K.-N. Huang, and Y.-F. Huang, A note on the optimal order and payment policies for deteriorating items in discount cash flows analysis under the alternatives of conditionally permissible delay in payments and cash discount. Journal of Statistics and Management Systems, 2012. 15(1): p. 21-27.
-
Liao, J.-J., K.-N. Huang, and P.-S. Ting, Optimal strategy of deteriorating items with capacity constraints under two-levels of trade credit policy. Applied Mathematics and Computation, 2014. 233: p. 647-658.
-
Lin, C. and Y. Lin, A cooperative inventory policy with deteriorating items for a two-echelon model. European Journal of Operational Research, 2007. 178(1): p. 92-111.
-
Lin, Y.-H., C. Lin, and B. Lin, On conflict and cooperation in a two-echelon inventory model for deteriorating items. Computers & Industrial Engineering, 2010. 59(4): p. 703-711.
-
Mishra, S.S. and P.P. Mishra, Price determination for an EOQ model for deteriorating items under perfect competition. Computers & Mathematics with Applications, 2008. 56(4): p. 1082-1101.
-
Niu, B. and J. Xie, A note on “Two-warehouse inventory model with deterioration under FIFO dispatch policy”. European Journal of Operational Research, 2008. 190(2): p. 571-577.
-
Ouyang, L.Y., C.T. Chang, and J.T. Teng, An EOQ model for deteriorating items under trade credits. Journal of the Operational Research Society, 2005. 56(6): p. 719-726.
-
Ouyang, L.-Y., et al., An economic order quantity model for deteriorating items with partially permissible delay in payments linked to order quantity. European Journal of Operational Research, 2009. 194(2): p. 418-431.
-
Ouyang, L.-Y., K.-S. Wu, and C.-T. Yang, A study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments. Computers & Industrial Engineering, 2006. 51(4): p. 637-651.
-
Pattnaik, M., An EOQ model for perishable items with constant demand and instant deterioration. Decision (0304-0941), 2012. 39(1): p. 55-61.
-
Purohit, G.N. and H. Rathore, Multi-Item Inventory Control Model with Space Constraints for Perishable Items. IUP Journal of Operations Management, 2012. 11(1): p. 35-41.
-
Roy, A., S. Kar, and M. Maiti, A deteriorating multi-item inventory model with fuzzy costs and resources based on two different defuzzification techniques. Applied Mathematical Modelling, 2008. 32(2): p. 208-223.
-
Sazvar, Z., M.R. Akbari Jokar, and A. Baboli, A new order splitting model with stochastic lead times for deterioration items. International Journal of Systems Science, 2013: p. 1-19.
-
Song, X. and X. Cai, On optimal payment time for a retailer under permitted delay of payment by the wholesaler. International Journal of Production Economics, 2006. 103(1): p. 246-251.
-
Taleizadeh, A.A., An EOQ model with partial backordering and advance payments for an evaporating item. International Journal of Production Economics, (0).
-
Taleizadeh, A.A., An economic order quantity model for a deteriorating item in a purchasing system with multiple prepayments. Applied Mathematical Modelling, 2014.
-
Taleizadeh, A.A., et al., An EOQ model for perishable product with special sale and shortage. International Journal of Production Economics, 2013. 145(1): p. 318-338.
-
Taleizadeh, A.A. and M. Nematollahi, An inventory control problem for deteriorating items with back-ordering and financial considerations. Applied Mathematical Modelling, 2014. 38(1): p. 93-109.
-
Tat, R., A.A. Taleizadeh, and M. Esmaeili, Developing economic order quantity model for non-instantaneous deteriorating items in vendor-managed inventory (VMI) system. International Journal of Systems Science, 2013: p. 1-12.
-
Thangam, A., Optimal price discounting and lot-sizing policies for perishable items in a supply chain under advance payment scheme and two-echelon trade credits. International Journal of Production Economics, 2012. 139(2): p. 459-472.
-
Uthayakumar, R. and P. Parvathi, A two-stage supply chain with order cost reduction and credit period incentives for deteriorating items. The International Journal of Advanced Manufacturing Technology, 2011. 56(5-8): p. 799-807.
-
Wee, H.-M., et al., Optimal replenishment policy for a deteriorating green product: Life cycle costing analysis. International Journal of Production Economics, 2011. 133(2): p. 603-611.
-
Widyadana, G.A., L.E. Cárdenas-Barrón, and H.M. Wee, Economic order quantity model for deteriorating items with planned backorder level. Mathematical and Computer Modelling, 2011. 54(5-6): p. 1569-1575.
-
Yang, H.-L., Two-warehouse inventory models for deteriorating items with shortages under inflation. European Journal of Operational Research, 2004. 157(2): p. 344-356.
-
Yang, H.-L., Two-warehouse partial backlogging inventory models for deteriorating items under inflation. International Journal of Production Economics, 2006. 103(1): p. 362-370.
-
Yang, H.-L. and C.-T. Chang, A two-warehouse partial backlogging inventory model for deteriorating items with permissible delay in payment under inflation. Applied Mathematical Modelling, 2013. 37(5): p. 2717-2726.
-
Yang, H.-L., J.-T. Teng, and M.-S. Chern, Deterministic inventory lot-size models under inflation with shortages and deterioration for fluctuating demand. Naval Research Logistics, 2001. 48(2): p. 144–158.
-
Chauhan, S.S. and R. Kumari, Optimal Policy for Deteriorating Inventory with Permissible Delay in Payments Under Inflation. International Transactions in Applied Sciences, 2011. 3(4): p. 615-636.
-
Chen, S.-C. and J.-T. Teng, Retailer’s optimal ordering policy for deteriorating items with maximum lifetime under supplier’s trade credit financing. Applied Mathematical Modelling, 2014.
-
Sanni, S.S. and W.I.E. Chukwu, An Economic order quantity model for Items with Three-parameter Weibull distribution Deterioration, Ramp-type Demand and Shortages. Applied Mathematical Modelling, 2013.
-
Sarkar, B. and S. Sarkar, An improved inventory model with partial backlogging, time varying deterioration and stock-dependent demand. Economic Modelling, 2013. 30: p. 924-932.
-
Sarkar, B. and S. Sarkar, Variable deterioration and demand—An inventory model. Economic Modelling, 2013. 31: p. 548-556.
-
Tripathy, C.K. and L.M. Pradhan, An EOQ model for three parameter Weibull deterioration with permissible delay in payments and associated salvage value. international journal of industrial engineering computations, 2012. 3(2): p. 115-122.
-
Yang, H.-L., Two-warehouse partial backlogging inventory models with three-parameter Weibull distribution deterioration under inflation. International Journal of Production Economics, 2012. 138(1): p. 107-116.
-
Avinadav, T., A. Herbon, and U. Spiegel, Optimal inventory policy for a perishable item with demand function sensitive to price and time. International Journal of Production Economics, 2013. 144(2): p. 497-506.
-
Agrawal, S., S. Banerjee, and S. Papachristos, Inventory model with deteriorating items, ramp-type demand and partially backlogged shortages for a two warehouse system. Applied Mathematical Modelling, 2013.
-
Ahmed, M.A., T.A. Al-Khamis, and L. Benkherouf, Inventory models with ramp type demand rate, partial backlogging and general deterioration rate. Applied Mathematics and Computation, 2013. 219(9): p. 4288-4307.
-
Ali, S.S., et al., Inventory management of perishable products: a time decay linked logistic approach. International Journal of Production Research, 2013. 51(13): p. 3864-3879.
-
Arcelus, F.J., N.H. Shah, and G. Srinivasan, Retailer’s pricing, credit and inventory policies for deteriorating items in response to temporary price/credit incentives. International Journal of Production Economics, 2003. 81-82(0): p. 153–162.
-
Balkhi, Z.T. and L. Benkherouf, On an inventory model for deteriorating items with stock dependent and time-varying demand rates. Computers & Operations Research, 2004. 31(2): p. 223-240.
-
Balkhi, Z.T. and L. Tadj, A generalized economic order quantity model with deteriorating items and time varying demand, deterioration and costs. International Transactions in Operational Research, 2008. 15(4): p. 509–517.
-
Bhunia, A.K., A.A. Shaikh, and R.K. Gupta, A study on two-warehouse partially backlogged deteriorating inventory models under inflation via particle swarm optimisation. International Journal of Systems Science, 2013: p. 1-15.
-
Chang, H.-J., et al., Retailer’s optimal pricing and lot-sizing policies for deteriorating items with partial backlogging. European Journal of Operational Research, 2006. 168(1): p. 51-64.
-
Cheng, M. and G. Wang, A note on the inventory model for deteriorating items with trapezoidal type demand rate. Computers & Industrial Engineering, 2009. 56(4): p. 1296-1300.
-
Cheng, M., B. Zhang, and G. Wang, Optimal policy for deteriorating items with trapezoidal type demand and partial backlogging. Applied Mathematical Modelling, 2011. 35(7): p. 3552-3560.
-
Chung, C.-J., H.-M. Wee, and Y.-L. Chen, Retailer’s replenishment policy for deteriorating item in response to future cost increase and incentive-dependent sale. Mathematical and Computer Modelling, 2013. 57(3-4): p. 536-550.
-
Chung, K.-J., The correct process of arguments of the solution procedure on the inventory model for deteriorating items with trapezoidal type demand rate in supply chain management. Applied Mathematics Letters, 2012. 25(11): p. 1901-1905.
-
Chung, K.-J. and J.-J. Liao, The optimal ordering policy in a DCF analysis for deteriorating items when trade credit depends on the order quantity. International Journal of Production Economics, 2006. 100(1): p. 116-130.
-
Chung, K.-J. and S.-F. Tsai, Inventory systems for deteriorating items with shortages and a linear trend in demand-taking account of time value. Computers & Operations Research, 2001. 28(9): p. 915–934.
-
Darzanou, G. and K. Skouri, An Inventory System for Deteriorating Products with Ramp-Type Demand Rate under Two-Level Trade Credit Financing. Advances in Decision Sciences, 2011. 2011: p. 1-15.
-
Das, K., T.K. Roy, and M. Maiti *, Buyer–seller fuzzy inventory model for a deteriorating item with discount. International Journal of Systems Science, 2004. 35(8): p. 457-466.
-
Deng, P.S., R.H.J. Lin, and P. Chu, A note on the inventory models for deteriorating items with ramp type demand rate. European Journal of Operational Research, 2007. 178(1): p. 112-120.
-
Dey, J.K., S.K. Mondal, and M. Maiti, Two storage inventory problem with dynamic demand and interval valued lead-time over finite time horizon under inflation and time-value of money. European Journal of Operational Research, 2008. 185(1): p. 170-194.
-
Dye, C.-Y. and H.-J. Chang, A replenishment policy for deteriorating items with linear trend demand and shortages when payment periods are offered. International Journal of Information and Management Sciences, 2003. 14(2): p. 31–45.
-
Dye, C.-Y., H.-J. Chang, and J.-T. Teng, A deteriorating inventory model with time-varying demand and shortage-dependent partial backlogging. European Journal of Operational Research, 2006. 172(2): p. 417-429.
-
Dye, C.-Y., H.-J. Chang, and C.-H. Wu, Purchase-inventory decision models for deteriorating items with a temporary sale price. International Journal of Information and Management Sciences, 2007. 18(1 ): p. 17–35.
-
Dye, C.-Y. and L.-Y. Ouyang, A particle swarm optimization for solving joint pricing and lot-sizing problem with fluctuating demand and trade credit financing. Computers & Industrial Engineering, 2011. 60(1): p. 127-137.
-
Dye, C.-Y., L.-Y. Ouyang, and T.-P. Hsieh, Deterministic inventory model for deteriorating items with capacity constraint and time-proportional backlogging rate. European Journal of Operational Research, 2007. 178(3): p. 789-807.
-
Ghosh, S.K. and K.S. Chaudhuri, An EOQ model with a quadratic demand, time-proportional deterioration and shortages in all cycles. International Journal of Systems Science, 2006. 37(10): p. 663-672.
-
Hsieh, T.-P., et al., Optimal lot size under trade credit financing when demand and deterioration are fluctuating with time. International Journal of Information and Management Sciences, 2009. 20(2): p. 191–204.
-
Hsieh, T.-P., C.-Y. Dye, and L.-Y. Ouyang, Determining optimal lot size for a two-warehouse system with deterioration and shortages using net present value. European Journal of Operational Research, 2008. 191(1): p. 182-192.
-
Hsu, P.H. and H.M. Wee, Discounting decision for enterprises with high fixed cost and low variable cost. International Transactions in Operational Research, 2006 13(2): p. 111–124.
-
Hsu, P.-H., H.M. Wee, and H.-M. Teng, Optimal ordering decision for deteriorating items with expiration date and uncertain lead time. Computers & Industrial Engineering, 2007. 52(4): p. 448-458.
-
Hung, K.-C., An inventory model with generalized type demand, deterioration and backorder rates. European Journal of Operational Research, 2011. 208(3): p. 239-242.
-
Jaggi, C.K., K.K. Aggarwal, and S.K. Goel, Optimal order policy for deteriorating items with inflation induced demand. International Journal of Production Economics, 2006. 103(2): p. 707-714.
-
Jaggi, C.K., A. Khanna, and P. Verma, Two-warehouse partial backlogging inventory model for deteriorating items with linear trend in demand under inflationary conditions. International Journal of Systems Science, 2011. 42(7): p. 1185-1196.
-
Jain, D. and K.K. Aggarwal, The effect of inflation-induced demand and trade credit on ordering policy of exponentially deteriorating and imperfect quality items. International Transactions in Operational Research, 2012. 19(6): p. 863-889.
-
Khanra, S. and K.S. Chaudhuri, A note on an order-level inventory model for a deteriorating item with time-dependent quadratic demand. Computers & Operations Research, 2003. 30(12): p. 1901-1916.
-
Khanra, S., S.K. Ghosh, and K.S. Chaudhuri, An EOQ model for a deteriorating item with time dependent quadratic demand under permissible delay in payment. Applied Mathematics and Computation, 2011. 218(1): p. 1-9.
-
Liao, J.-J. and K.-N. Huang, Deterministic inventory model for deteriorating items with trade credit financing and capacity constraints. Computers & Industrial Engineering, 2010. 59(4): p. 611-618.
-
Lin, S.-W., Inventory models with managerial policy independent of demand. European Journal of Operational Research, 2011. 211(3): p. 520-524.
-
Maihami, R. and I.N.K. Abadi, Joint control of inventory and its pricing for non-instantaneously deteriorating items under permissible delay in payments and partial backlogging. Mathematical and Computer Modelling, 2012. 55(5-6): p. 1722-1733.
-
Maihami, R. and I. Nakhai Kamalabadi, Joint pricing and inventory control for non-instantaneous deteriorating items with partial backlogging and time and price dependent demand. International Journal of Production Economics, 2012. 136(1): p. 116-122.
-
Maity, K. and M. Maiti Numerical approach of multi-objective optimal control problem in imprecise environment. Fuzzy Optimization and Decision Making, 2005 4(4): p. 313–330.
-
Mandal, N.K., T.K. Roy, and M. Maiti, Inventory model of deteriorated items with a constraint: A geometric programming approach. European Journal of Operational Research, 2006. 173(1): p. 199-210.
-
Musa, A. and B. Sani, Inventory ordering policies of delayed deteriorating items under permissible delay in payments. International Journal of Production Economics, 2012. 136(1): p. 75-83.
-
Pal, M. and H.K. Maity, An Inventory Model for Deteriorating Items with Permissible Delay in Payment and Inflation Under Price Dependent Demand. Pakistan Journal of Statistics & Operation Research, 2012. 8(3): p. 583-592.
-
Panda, S., S. Saha, and M. Basu, Optimal pricing and lot-sizing for perishable inventory with price and time dependent ramp-type demand. International Journal of Systems Science, 2013. 44(1): p. 127-138.
-
Panda, S., S. Senapati, and M. Basu, Optimal replenishment policy for perishable seasonal products in a season with ramp-type time dependent demand. Computers & Industrial Engineering, 2008. 54(2): p. 301-314.
-
Sarkar, B., S. Saren, and H.-M. Wee, An inventory model with variable demand, component cost and selling price for deteriorating items. Economic Modelling, 2013. 30: p. 306-310.
-
Shah, N.H., Inventory model for deteriorating items and time value of money for a finite time horizon under the permissible delay in payments. International Journal of Systems Science, 2006. 37(1): p. 9-15.
-
Shah, N.H., A.S. Gor, and C. Jhaveri, An integrated inventory policy with deterioration for a single vendor and multiple buyers in supply chain when demand is quadratic. Investigaciones Operacionales, 2011. 32(2): p. 95-106.
-
Sicilia, J., et al., An inventory model for deteriorating items with shortages and time-varying demand. International Journal of Production Economics, (0).
-
Skouri, K. and I. Konstantaras, Order Level Inventory Models for Deteriorating Seasonable/Fashionable Products with Time Dependent Demand and Shortages. Mathematical Problems in Engineering, 2009. 2009: p. 1-25.
-
Skouri, K. and S. Papachristos, Four inventory models for deteriorating items with time varying demand and partial backlogging: A cost comparison. Optimal Control Applications and Methods, 2003. 24(6): p. 315-330.
-
Soni, H.N. and K.A. Patel, Joint pricing and replenishment policies for non-instantaneous deteriorating items with imprecise deterioration free time and credibility constraint. Computers & Industrial Engineering, 2013. 66(4): p. 944-951.
-
Tan, Y. and M.X. Weng, A discrete-in-time deteriorating inventory model with time-varying demand, variable deterioration rate and waiting-time-dependent partial backlogging. International Journal of Systems Science, 2013. 44(8): p. 1483-1493.
-
Teng, J.T. and H.L. Yang, Deterministic economic order quantity models with partial backlogging when demand and cost are fluctuating with time. Journal of the Operational Research Society, 2004. 55(5): p. 495-503.
-
Teng, J.-T., et al., An optimal replenishment policy for deteriorating items with time-varying demand and partial backlogging. Operations Research Letters, 2002. 30(6): p. 387–393.
-
Teng, J.-T., L.-Y. Ouyang, and M.-C. Cheng, An EOQ model for deteriorating items with power-form stock-dependent demand. International Journal of Information and Management Sciences, 2005 16(1): p. 1–16.
-
Tsao, Y.-C. and G.-J. Sheen, Dynamic pricing, promotion and replenishment policies for a deteriorating item under permissible delay in payments. Computers & Operations Research, 2008. 35(11): p. 3562-3580.
-
Valliathal, M. and R. Uthayakumar, Optimal pricing and replenishment policies of an EOQ model for non-instantaneous deteriorating items with shortages. The International Journal of Advanced Manufacturing Technology, 2010. 54(1-4): p. 361-371.
-
Wang, S.-P., An inventory replenishment policy for deteriorating items with shortages and partial backlogging. Computers & Operations Research, 2002. 29(14): p. 2043–2051.
-
Wu, C. and Q. Zhao, Supplier–retailer inventory coordination with credit term for inventory-dependent and linear-trend demand. International Transactions in Operational Research, 2013: p. n/a-n/a.
-
Wu, K.-S., Discounted-cash-flow EOQ model for a deteriorating item. International Journal of Information and Management Sciences, 2002 13(4): p. 55–67.
-
Wu, K.-S., L.-Y. Ouyang, and C.-T. Yang, An optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlogging. International Journal of Production Economics, 2006. 101(2): p. 369-384.
-
Wu, K.-S., L.-Y. Ouyang, and C.-T. Yang, Retailer’s optimal ordering policy for deteriorating items with ramp-type demand under stock-dependent consumption rate. International Journal of Information and Management Sciences, 2008. 19(2): p. 245–262.
-
Yang, C.-T., et al., An optimal replenishment policy for deteriorating items with stock-dependent demand and relaxed terminal conditions under limited storage space. Central European Journal of Operations Research, 2009. 19(1): p. 139-153.
-
Yang, H.-L., A comparison among various partial backlogging inventory lot-size models for deteriorating items on the basis of maximum profit. International Journal of Production Economics, 2005. 96(1): p. 119-128.
-
Yang, H.-L., A Partial Backlogging Inventory Model for Deteriorating Items with Fluctuating Selling Price and Purchasing Cost. Advances in Operations Research, 2012. 2012: p. 1-15.
-
Yang, H.-L., J.-T. Teng, and M.-S. Chern, An inventory model under inflation for deteriorating items with stock-dependent consumption rate and partial backlogging shortages. International Journal of Production Economics, 2010. 123(1): p. 8-19.
-
Bai, Q.-G., Y.-Z. Zhang, and G.-L. Dong, A note on an economic lot-sizing problem with perishable inventory and economies of scale costs: Approximation solutions and worst case analysis. International Journal of Automation and Computing, 2010. 7(1): p. 132-136.
-
Balkhi, Z.T., An optimal solution of a general lot size inventory model with deteriorated and imperfect products, taking into account inflation and time value of money. International Journal of Systems Science, 2004. 35(2): p. 87-96.
-
Balkhi, Z.T., Optimal economic ordering policy with deteriorating items under different supplier trade credits for finite horizon case. International Journal of Production Economics, 2011. 133(1): p. 216-223.
-
Banerjee, S. and S. Agrawal, A two-warehouse inventory model for items with three-parameter Weibull distribution deterioration, shortages and linear trend in demand. International Transactions in Operational Research, 2008 15(6): p. 755–775.
-
Chang, H.-J. and C.-Y. Dye, An inventory model for deteriorating items with partial backlogging and permissible delay in payments. International Journal of Systems Science, 2001. 32(3): p. 345-352.
-
Chang, H.-J., C.-H. Hung, and C.-Y. Dye, An inventory model for deteriorating items with linear trend demand under the condition of permissible delay in payments. Production Planning & Control, 2001. 12(3): p. 274-282.
-
Chang, H.-J., C.-H. Hung, and C.-Y. Dye, A finite time horizon inventory model with deterioration and time-value of money under the conditions of permissible delay in payments. International Journal of Systems Science, 2002. 33(2): p. 141-151.
-
Chaudhary, R., S.R. Singh, and A. Chauhan, An inventory model with time dependent demand and deterioration under partial backlogging. International Transactions in Applied Sciences, 2011. 3(1): p. 55-62.
-
Chen, J.-M. and C.-S. Lin, An optimal replenishment model for inventory items with normally distributed deterioration. Production Planning & Control, 2002. 13(5): p. 470-480.
-
Chern, M.-S., et al., Partial backlogging inventory lot-size models for deteriorating items with fluctuating demand under inflation. European Journal of Operational Research, 2008. 191(1): p. 127-141.
-
Deng, P.S., Improved inventory models with ramp type demand and weibull deterioration. International Journal of Information and Management Sciences, 2005 16(4 ): p. 79–86.
-
Dye, C.-Y., A note on an EOQ model for items with weibull distributed deterioration, shortages and power demand pattern. International Journal of Information and Management Sciences, 2004 15(2 ): p. 81–84.
-
Giri, B.C., A.K. Jalan, and K.S. Chaudhuri Economic order quantity model with Weibull deterioration distribution, shortage and ramp-type demand. International Journal of Systems Science, 2003 34(4): p. 237–243.
-
Goyal, S.K. and B.C. Giri, The production–inventory problem of a product with time varying demand, production and deterioration rates. European Journal of Operational Research, 2003. 147(3): p. 549-557.
-
Jung, S.-T., J.S.-J. Lin, and J.P.C. Chuang, A note on an EOQ model for items with weibull distributed deterioration, shortages and power demand pattern. International Journal of Information and Management Sciences, 2008 19(4): p. 667–672.
-
Kaushal, P., A.P. Singh, and D. Singh, An Inventory Model with Shortages, with Time Dependent Deterioration and the Demand Rate as Stock Dependent Over a Finite Planning Horizon. International Transactions in Applied Sciences, 2011. 3(4): p. 727-742.
-
Kumar Sett, B., B. Sarkar, and A. Goswami, A two-warehouse inventory model with increasing demand and time varying deterioration. Scientia Iranica, 2012. 19(6): p. 1969-1977.
-
Lee, W.-C. and J.-W. Wu, An EOQ model for items with Weibull distributed deterioration, shortages and power demand pattern.pdf¿. International Journal of Information and Management Sciences, 2002. 13(2 ): p. 19–34.
-
Lin, K.-P., An extended inventory models with trapezoidal type demands. Applied Mathematics and Computation, 2013. 219(24): p. 11414-11419.
-
Mishra, U. and C.K. Tripathy, An EOQ model for time dependent Weibull deterioration with linear demand and shortages. LogForum, 2012. 8(2): p. 123-136.
-
Mishra, V., L. Singh, and R. Kumar, An inventory model for deteriorating items with time-dependent demand and time-varying holding cost under partial backlogging. Journal of Industrial Engineering International, 2013. 9(1): p. 1-5.
-
Pradhan, L.M. and C.K. Tripathy, An EOQ model for Weibull deteriorating item with ramp type demand and salvage value under trade credit system. LogForum, 2014. 10(1): p. 61-72.
-
Sarkar, B., An EOQ model with delay in payments and time varying deterioration rate. Mathematical and Computer Modelling, 2012. 55(3-4): p. 367-377.
-
Sarkar, T., S.K. Ghosh, and K.S. Chaudhuri, An optimal inventory replenishment policy for a deteriorating item with time-quadratic demand and time-dependent partial backlogging with shortages in all cycles. Applied Mathematics and Computation, 2012. 218(18): p. 9147-9155.
-
Sharma, S., An Inventory Model for Deteriorating Products with Inflation, Lost Sales and Stock and Time Dependent Demand. International Transactions in Applied Sciences, 2011. 3(4): p. 695-708.
-
Singh, J., B.B. Singh, and S.R. Singh, Optimal Inventory Replenishment Model for Deteriorating Items Taking Account of Time Discounting. International Transactions in Applied Sciences, 2011. 3(4): p. 791-812.
-
Singh, T., S.K. Sahu, and A.K. Nayak, An EOQ Model for a Deteriorating Item with Time Dependent Quadratic Demand and Weibull Distribution Deterioration under Permissible Delay in Payment. Advances in Theoretical & Applied Mathematics, 2012. 7(3): p. 295-307.
-
Skouri, K., et al., Inventory models with ramp type demand rate, time dependent deterioration rate, unit production cost and shortages. Annals of Operations Research, 2011. 191(1): p. 73-95.
-
Skouri, K., et al., Inventory models with ramp type demand rate, partial backlogging and Weibull deterioration rate. European Journal of Operational Research, 2009. 192(1): p. 79-92.
-
Tripathy, C.K. and U. Mishra, An EOQ model with time dependent Weibull deterioration and ramp type demand. International Journal of Industrial Engineering Computations, 2011. 2(2): p. 307-318.
-
Wang, X. and D. Li, A dynamic product quality evaluation based pricing model for perishable food supply chains. Omega, 2012. 40(6): p. 906-917.
-
Wu, K.-S., An EOQ inventory model for items with Weibull distribution deterioration, ramp type demand rate and partial backlogging. Production Planning & Control, 2001. 12(8): p. 787-793.
-
Wu, K.-S., EOQ inventory model for items with Weibull distribution deterioration, time-varying demand and partial backlogging. International Journal of Systems Science, 2002. 33(5): p. 323-329.
-
Yang, G.K., et al., Note on inventory models with Weibull distribution deterioration. Production Planning & Control, 2011. 22(4): p. 437-444.
-
Zhou, Y.W. and S.L. Yang, An optimal replenishment policy for items with inventory-level-dependent demand and fixed lifetime under the LIFO policy. Journal of the Operational Research Society, 2003. 54(6): p. 585-593.
-
Bhattacharya, D.K., On multi-item inventory. European Journal of Operational Research, 2005. 162(3): p. 786-791.
-
Chang, C.-T., J.-T. Teng, and S.K. Goyal, Optimal replenishment policies for non-instantaneous deteriorating items with stock-dependent demand. International Journal of Production Economics, 2010. 123(1): p. 62-68.
-
Chu, P. and P.S. Chen, A note on inventory replenishment policies for deteriorating items in an exponentially declining market. Computers & Operations Research, 2002 29(13): p. 1827–1842.
-
Chung, K.-J. and L.E. Cárdenas-Barrón, The simplified solution procedure for deteriorating items under stock-dependent demand and two-level trade credit in the supply chain management. Applied Mathematical Modelling, 2013. 37(7): p. 4653-4660.
-
Disney, S.M. and R.D.H. Warburton, On the Lambert W function: Economic Order Quantity applications and pedagogical considerations. International Journal of Production Economics, 2012. 140(2): p. 756-764.
-
Duan, Y., et al., Inventory models for perishable items with inventory level dependent demand rate. Applied Mathematical Modelling, 2012. 36(10): p. 5015-5028.
-
Dye, C.-Y. and T.-P. Hsieh, Deterministic ordering policy with priceand stock-dependent demand under fluctuating cost and limited capacity. Expert Systems with Applications, 2011. 38(12): p. 14976-14983.
-
Dye, C.-Y. and L.-Y. Ouyang, An EOQ model for perishable items under stock-dependent selling rate and time-dependent partial backlogging. European Journal of Operational Research, 2005. 163(3): p. 776-783.
-
Ghiami, Y., T. Williams, and Y. Wu, A two-echelon inventory model for a deteriorating item with stock-dependent demand, partial backlogging and capacity constraints. European Journal of Operational Research, 2013. 231(3): p. 587-597.
-
Guchhait, P., M.K. Maiti, and M. Maiti, Two storage inventory model of a deteriorating item with variable demand under partial credit period. Applied Soft Computing, 2013. 13(1): p. 428-448.
-
Hou, K.L. and L.C. Lin, An EOQ model for deteriorating items with priceand stock-dependent selling rates under inflation and time value of money. International Journal of Systems Science, 2006. 37(15): p. 1131-1139.
-
Hsieh, T.-P. and C.-Y. Dye, Optimal replenishment policy for perishable items with stock-dependent selling rate and capacity constraint. Computers & Industrial Engineering, 2010. 59(2): p. 251-258.
-
Jana, D.K., B. Das, and M. Maiti, Multi-item partial backlogging inventory models over random planninghorizon in random fuzzy environment. Applied Soft Computing, 2014. 21: p. 12-27.
-
Maity, K. and M. Maiti, Optimal inventory policies for deteriorating complementary and substitute items. International Journal of Systems Science, 2009. 40(3): p. 267-276.
-
Min, J. and Y.-W. Zhou, A perishable inventory model under stock-dependent selling rate and shortage-dependent partial backlogging with capacity constraint. International Journal of Systems Science, 2009. 40(1): p. 33-44.
-
Ouyang, L.-Y., et al., An Inventory Model for Deteriorating Items with Stock-Dependent Demand under the Conditions of Inflation and Time-Value of Money. The Engineering Economist, 2003. 48(1): p. 52-68.
-
Pal, A.K., A.K. Bhunia, and R.N. Mukherjee, Optimal lot size model for deteriorating items with demand rate dependent on displayed stock level (DSL) and partial backordering. European Journal of Operational Research, 2006. 175(2): p. 977-991.
-
Panda, S., S. Saha, and M. Basu, An EOQ model for perishable products with discounted selling price and stock dependent demand. Central European Journal of Operations Research, 2009. 17(1): p. 31-53.
-
] Roy, A., et al., An inventory model for a deteriorating item with displayed stock dependent demand under fuzzy inflation and time discounting over a random planning horizon. Applied Mathematical Modelling, 2009. 33(2): p. 744-759.
-
Singh, M. and P. Sharma, An Inventory Model for Deteriorating Items With Two-Level Storage Under Inflation. International Transactions in Applied Sciences, 2011. 3(4): p. 683-694
-
Singh, S.R. and A.K. Malik, Two Warehouses Inventory Model for Non-Instantaneous Deteriorating Items With Stock-Dependent Demand. International Transactions in Applied Sciences, 2011. 3(4): p. 911-920.
-
Skouri, K., et al., Supply chain models for deteriorating products with ramp type demand rate under permissible delay in payments. Expert Systems with Applications, 2011. 38(12): p. 14861-14869.
-
Soni, H.N., Optimal replenishment policies for deteriorating items with stock sensitive demand under two-level trade credit and limited capacity. Applied Mathematical Modelling, 2013. 37(8): p. 5887-5895.
-
Soni, H.N., Optimal replenishment policies for non-instantaneous deteriorating items with price and stock sensitive demand under permissible delay in payment. International Journal of Production Economics, 2013. 146(1): p. 259-268.
-
Teng, J.-T., et al., A comprehensive extension of optimal ordering policy for stock-dependent demand under progressive payment scheme. European Journal of Operational Research, 2011. 215(1): p. 97-104.
-
Tripathy, P.K., M. Pattnaik, and P. Tripathy, The finite horizon trended continuous inventory replenishment and pricing problems for deteriorating items with stock and price sensitive demand. Investigaciones Operacionales, 2012. 33(1): p. 1-12.
-
Urban, T.L., An extension of inventory models incorporating financing agreements with both suppliers and customers. Applied Mathematical Modelling, 2012. 36(12): p. 63236330.
-
Uthayakumar, R. and M. Rameswari, Economic order quantity for deteriorating items with time discounting. The International Journal of Advanced Manufacturing Technology, 2011. 58(5-8): p. 817-840.
-
Bhunia, A.K. and A.A. Shaikh, A deterministic model for deteriorating items with displayed inventory level dependent demand rate incorporating marketing decisions with transportation cost. International Journal of Industrial Engineering Computations, 2011. 2(3): p. 547-562.
-
Vaish, B. and G. Garg, Optimal Price Discount Policy for Non-instantaneous Deteriorating Items with Stock-dependent and Time Decreasing Demand. Journal of Mathematics Research, 2011. 3(3).
-
Herbon, A., Dynamic pricing vs. acquiring information on consumers’ heterogeneous sensitivity to product freshness. International Journal of Production Research, 2014. 52(3): p. 918-933.
-
7] Herbon, A., E. Levner, and T.C.E. Cheng, Perishable inventory management with dynamic pricing using time–temperature indicators linked to automatic detecting devices. International Journal of Production Economics, 2014. 147: p. 605-613.
-
Annadurai, K. and R. Uthayakumar, Two-echelon inventory model for deteriorating items with credit period dependent demand including shortages under trade credit. Optimization Letters, 2013. 7(6): p. 1227-1249.
-
Cai, X., et al., Optimal pricing policy for a deteriorating product by dynamic tracking control. International Journal of Production Research, 2013. 51(8): p. 2491-2504.
-
Dye, C.-Y. and T.-P. Hsieh, Joint pricing and ordering policy for an advance booking system with partial order cancellations. Applied Mathematical Modelling, 2013. 37(6): p. 3645-3659.
-
Neetu and A.K. Tomer, Deteriorating inventory model with linear demand, quantity discount, constant deterioration and partial backordering. International Transactions in Applied Sciences, 2011. 3(1): p. 141-148.
-
Rong, M., N.K. Mahapatra, and M. Maiti, A two warehouse inventory model for a deteriorating item with partially/fully backlogged shortage and fuzzy lead time. European Journal of Operational Research, 2008. 189(1): p. 59-75.
-
Sankar Sana, S., Price-sensitive demand for perishable items – an EOQ model. Applied Mathematics and Computation, 2011. 217(13): p. 6248-6259.
-
Shavandi, H., H. Mahlooji, and N.E. Nosratian, A constrained multi-product pricing and inventory control problem. Applied Soft Computing, 2012. 12(8): p. 2454-2461.
-
Soni, H.N. and K.A. Patel, Optimal pricing and inventory policies for non-instantaneous deteriorating items with permissible delay in payment: Fuzzy expected value model. international journal of industrial engineering computations, 2012. 3(3): p. 281-300.
-
Teng, J.-T., C.-T. Chang, and S.K. Goyal, Optimal pricing and ordering policy under permissible delay in payments. International Journal of Production Economics, 2005. 97(2): p. 121-129
-
Teng, J.-T., L.-Y. Ouyang, and L.-H. Chen, A comparison between two pricing and lot-sizing models with partial backlogging and deteriorated items. International Journal of Production Economics, 2007. 105(1): p. 190-203.
-
Tsao, Y.-C. and G.-J. Sheen, Joint pricing and replenishment decisions for deteriorating items with lot-size and time-dependent purchasing cost under credit period. International Journal of Systems Science, 2007. 38(7): p. 549-561.
-
Wu, K.-S., L.-Y. Ouyang, and C.-T. Yang, Coordinating replenishment and pricing policies for non-instantaneous deteriorating items with price-sensitive demand. International Journal of Systems Science, 2009. 40(12): p. 1273-1281.
-
Yu, J.C.P., A collaborative strategy for deteriorating inventory system with imperfect items and supplier credits. International Journal of Production Economics, 2013. 143(2): p. 403-409.
-
Abad, P.L., Optimal price and order size for a reseller under partial backordering. Computers & Operations Research, 2001. 28(1): p. 53–65.
-
Begum, R., R.R. Sahoo, and S.K. Sahu, A replenishment policy for items with price-dependent demand, time-proportional deterioration and no shortages. International Journal of Systems Science, 2012. 43(5): p. 903-910.
-
Dye, C.-Y., Joint pricing and ordering policy for a deteriorating inventory with partial backlogging. Omega, 2007. 35(2): p. 184-189.
-
Dye, C.-Y., A finite horizon deteriorating inventory model with two-phase pricing and time-varying demand and cost under trade credit financing using particle swarm optimization. Swarm and Evolutionary Computation, 2012. 5: p. 37-53.
-
Dye, C.-Y., T.-P. Hsieh, and L.-Y. Ouyang, Determining optimal selling price and lot size with a varying rate of deterioration and exponential partial backlogging. European Journal of Operational Research, 2007. 181(2): p. 668-678.
-
Dye, C.-Y., L.-Y. Ouyang, and T.-P. Hsieh, Inventory and pricing strategies for deteriorating items with shortages: A discounted cash flow approach. Computers & Industrial Engineering, 2007. 52(1): p. 29-40.
-
Kar, S., A.K. Bhunia, and M. Maiti, Inventory of multi-deteriorating items sold from two shops under single management with constraints on space and investment. Computers & Operations Research, 2001 28(12 ): p. 1203–1221.
-
Mukhopadhyay, S., R.N. Mukherjee, and K.S. Chaudhuri *, An EOQ model with two-parameter Weibull distribution deterioration and price-dependent demand. International Journal of Mathematical Education in Science and Technology, 2005. 36(1): p. 25-33.
-
Mukhopadhyay, S., R.N. Mukherjee, and K.S. Chaudhuri, Joint pricing and ordering policy for a deteriorating inventory. Computers & Industrial Engineering, 2004. 47(4): p. 339-349.
-
Neetu and A.K. Tomer, A Deteriorating Inventory Model Under Variable Inflation When Supplier Credits Linked to Order Quantity. Procedia Engineering, 2012. 38: p. 1241-1263.
-
Papachristos, S. and K. Skouri, An inventory model with deteriorating items, quantity discount, pricing and time-dependent partial backlogging. International Journal of Production Economics, 2003. 83(3): p. 247-256.
-
Qin, Y., J. Wang, and C. Wei, Joint pricing and inventory control for fresh produce and foods with quality and physical quantity deteriorating simultaneously. International Journal of Production Economics, (0).
-
Shah, N.H., H.N. Soni, and J. Gupta, A note on ‘a replenishment policy for items with price-dependent demand, time-proportional deterioration and no shortages’. International Journal of Systems Science, 2012: p. 1-5.
-
Shah, N.H., H.N. Soni, and K.A. Patel, Optimizing inventory and marketing policy for non-instantaneous deteriorating items with generalized type deterioration and holding cost rates. Omega, 2013. 41(2): p. 421-430.
-
Wang, W.-C., J.-T. Teng, and K.-R. Lou, Seller’s optimal credit period and cycle time in a supply chain for deteriorating items with maximum lifetime. European Journal of Operational Research, 2014. 232(2): p. 315-321.
-
Wee, H.-M. and S.-T. Law, Replenishment and pricing policy for deteriorating items taking into account the time-value of money. International Journal of Production Economics, 2001. 71(1-3): p. 213–220.
-
Wu, J., et al., Optimal credit period and lot size for deteriorating items with expiration dates under two-level trade credit financing. European Journal of Operational Research, 2014(0).
-
Berk, E. and U. Gurler, Analysis of the (Q, r) Inventory Model for Perishables with Positive Lead Times and Lost Sales. Operations Research, 2008. 56(5): p. 1238-1246.
-
Berk, E., ü. Gürler, and G. Yıldırım, On pricing of perishable assets with menu costs. International Journal of Production Economics, 2009. 121(2): p. 678-699.
-
Broekmeulen, R.A.C.M. and K.H. van Donselaar, A heuristic to manage perishable inventory with batch ordering, positive lead-times, and time-varying demand. Computers & Operations Research, 2009. 36(11): p. 3013-3018.
-
Chande, A., et al., Perishable inventory management and dynamic pricing using RFID technology. Sadhana, 2005 30((2-3)): p. 445–462.
-
Cheong, T., Joint inventory and transshipment control for perishable products of a two-period lifetime. The International Journal of Advanced Manufacturing Technology, 2012. 66(9-12): p. 1327-1341.
-
Chew, E.P., C. Lee, and R. Liu, Joint inventory allocation and pricing decisions for perishable products. International Journal of Production Economics, 2009. 120(1): p. 139-150.
-
Chew, E.P., et al., Optimal dynamic pricing and ordering decisions for perishable products. International Journal of Production Economics, (0).
-
Chun, Y.H., Optimal pricing and ordering policies for perishable commodities. European Journal of Operational Research, 2003 144(1): p. 68–82.
-
Cooper, W.L., Pathwise properties and performance bounds for a perishable inventory system. Operations Research, 2001 49(3): p. 455–466.
-
Duan, Q. and T.W. Liao, A new age-based replenishment policy for supply chain inventory optimization of highly perishable products. International Journal of Production Economics, 2013. 145(2): p. 658-671.
-
Frank, K.C., H.-S. Ahn, and R.Q. Zhang, Inventory policies for a make-to-order system with a perishable component and fixed ordering cost. Naval Research Logistics, 2009. 56(2): p. 127-141.
-
Gumasta, K., F.T.S. Chan, and M.K. Tiwari, An incorporated inventory transport system with two types of customers for multiple perishable goods. International Journal of Production Economics, 2012. 139(2): p. 678-686.
-
Guo, P., Z. Lian, and Y. Wang, Pricing Perishable Products with Compound Poisson Demands. Probability in the Engineering and Informational Sciences, 2011. 25(03): p. 289-306.
-
Gürler, ü. and B.Y. özkaya, A note on continuous review perishable inventory systems: models and heuristics. IIE Transactions, 2003. 35(3): p. 321–323.
-
Haijema, R., A new class of stock-level dependent ordering policies for perishables with a short maximum shelf life. International Journal of Production Economics, 2013. 143(2): p. 434-439.
-
Jia, J. and Q. Hu, Dynamic ordering and pricing for a perishable goods supply chain. Computers & Industrial Engineering, 2011. 60(2): p. 302-309.
-
Kanchanasuntorn, K. and A. Techanitisawad, An approximate periodic model for fixed-life perishable products in a two-echelon inventory–distribution system. International Journal of Production Economics, 2006. 100(1): p. 101-115.
-
Katagiri, H. and H. Ishii, Fuzzy inventory problems for perishable commodities. European Journal of Operational Research, 2002 138(3): p. 545–553.
-
Ketzenberg, M. and M.E. Ferguson, Managing Slow-Moving Perishables in the Grocery Industry. Production and Operations Management, 2008. 17(5): p. 513-521.
-
Kouki, C., et al., Assessing the impact of perishability and the use of time temperature technologies on inventory management. International Journal of Production Economics, 2013. 143(1): p. 72-85.
-
Li, Y., B. Cheang, and A. Lim, Grocery Perishables Management. Production and Operations Management, 2012. 21(3): p. 504-517.
-
Li, Y., A. Lim, and B. Rodrigues, Note–Pricing and Inventory Control for a Perishable Product. Manufacturing & Service Operations Management, 2008. 11(3): p. 538-542.
-
Lian, Z. and L. Liu, Continuous review perishable inventory systems: models and heuristics. IIE Transactions, 2001. 33(9): p. 809-822.
-
Olsson, F. and P. Tydesjö, Inventory problems with perishable items: Fixed lifetimes and backlogging. European Journal of Operational Research, 2010. 202(1): p. 131-137.
-
Piramuthu, S. and W. Zhou, RFID and perishable inventory management with shelf-space and freshness dependent demand. International Journal of Production Economics, 2013. 144(2): p. 635-640.
-
Seyedhosseini, S.-M., B. Elahi, and A. Akhlaghy, Proposing a non-linear mathematical model for order splitting in a supply chain with perishable products: solving by genetic algorithm. International Journal of Business Research, 2011. 11(4): p. 104-111.
-
Tekin, E., ü. Gürler, and E. Berk, Age-based vs. stock level control policies for a perishable inventory system. European Journal of Operational Research, 2001. 134(2): p. 309–329.
-
Yun, Y., S. Osako, and T. Nakai, Optimal inventory control for deteriorative goods considering delays of deliveries. Journal of Information and Optimization Sciences, 2012. 33(1): p. 103-114.
-
6] Zhou, D., L.C. Leung, and W.P. Pierskalla, Inventory Management of Platelets in Hospitals: Optimal Inventory Policy for Perishable Products with Regular and Optional Expedited Replenishments. Manufacturing & Service Operations Management, 2011. 13(4): p. 420-438.
-
] Alizadeh, M., H. Eskandari, and S.M. Sajadifar, A modified (S−1,S) inventory system for deteriorating items with Poisson demand and non-zero lead time. Applied Mathematical Modelling, 2014. 38(2): p. 699-711.
-
Chakravarthy, S.R. and J.K. Daniel, A Markovian inventory system with random shelf time and back orders. Computers & Industrial Engineering, 2004. 47(4): p. 315-337.
-
De, L.N. and A. Goswami, Probabilistic EOQ model for deteriorating items under trade credit financing. International Journal of Systems Science, 2009. 40(4): p. 335-346.
-
Huang, M.-G., Economic ordering model for deteriorating items with random demand and deterioration. International Journal of Production Research, 2013. 51(18): p. 5612-5624.
-
Huang, Y.-S., W.-J. Su, and Z.-L. Lin, A study on lead-time discount coordination for deteriorating products. European Journal of Operational Research, 2011.
-
Kalpakam, S. and S. Shanthi, A perishable inventory system with modified (S-1,S) policy and arbitrary processing times. Computers & Operations Research, 2001 28(5): p. 453–471.
-
Kouki, C., et al., Analysis of a periodic review inventory control system with perishables having random lifetime. International Journal of Production Research, 2014. 52(1): p. 283-298.
-
Lan, H., et al., Study on the inventory control of deteriorating items under VMI model based on bi-level programming. Expert Systems with Applications, 2011. 38(8): p. 9287-9295.
-
Lian, Z., X. Liu, and N. Zhao, A perishable inventory model with Markovian renewal demands. International Journal of Production Economics, 2009. 121(1): p. 176-182.
-
Manuel, P., B. Sivakumar, and G. Arivarignan, A perishable inventory system with service facilities, MAP arrivals and PH — Service times. Journal of Systems Science and Systems Engineering, 2007. 16(1): p. 62-73.
-
Manuel, P., B. Sivakumar, and G. Arivarignan, A perishable inventory system with service facilities and retrial customers. Computers & Industrial Engineering, 2008. 54(3): p. 484-501.
-
Pang, Z., Optimal dynamic pricing and inventory control with stock deterioration and partial backordering. Operations Research Letters, 2011. 39(5): p. 375-379.
-
Sazvar, Z., et al., A bi-objective stochastic programming model for a centralized green supply chain with deteriorating products. International Journal of Production Economics, 2014. 150: p. 140-154.
-
Shophia Lawrence, A., B. Sivakumar, and G. Arivarignan, A perishable inventory system with service facility and finite source. Applied Mathematical Modelling, 2013. 37(7): p. 4771-4786.
-
Sivakumar, B., A perishable inventory system with retrial demands and a finite population. Journal of Computational and Applied Mathematics, 2009. 224(1): p. 29-38.
-
Sivakumar, B., N. Anbazhagan, and G. Arivarignan, Two commodity continuous review perishable inventory system. International Journal of Information and Management Sciences, 2006. 17(3 ): p. 47–64.
-
Sivakumar, B. and G. Arivarignan, A Perishable Inventory System at Service Facilities with Negative Customers. Journal of Information and Management Sciences, 2006. 17(2): p. 1-18.
-
Yadavalli, V.S.S., et al., A multi-server perishable inventory system with negative customer. Computers & Industrial Engineering, 2011. 61(2): p. 254-273.
-
Gürler, ü. and B.Y. özkaya, Analysis of the (s,S) policy for perishables with a random shelf life. IIE ransactions, 2008. 40(8): p. 759-781.
-
Ketzenberg, M., J. Bloemhof, and G. Gaukler, Managing Perishables with Time and Temperature History. Production and Operations Management, 2014: p. n/a-n/a.
-
Lian, Z., L. Liu, and M.F. Neuts, A Discrete-Time Model for Common Lifetime Inventory Systems. Mathematics of Operations Research, 2005. 30(3): p. 718-732.
-
Nahmias, S., On Ordering Perishable Inventory when Both Demand and Lifetime are Random. Management Science, 1977. 24(1): p. 82-90.
-
Eilon, S. and R.V. Mallya. Issuing and pricing policy of semi-perishables. 1966. New York: Wiley-Interscience.
-
Kang, S. and I.-T. Kim, A study on the price and production level of the deteriorating inventory system. International Journal of Production Research, 1983. 21(6): p. 899-908.
-
Aggarwal, S.P. and C.K. Jaggi, Ordering policy for decaying inventory. International Journal of Systems Science, 1989. 20(1): p. 151-155.
-
] Li, G., et al., Dynamic pricing for perishable products with hybrid uncertainty in demand. Applied Mathematics and Computation, 2013. 219(20): p. 10366-10377.
-
Kwakernaak, H., Fuzzy random variables—I. definitions and theorems. Information Sciences, 1978. 15(1): p. 1-29.
-
Liu, B., Uncertainty Theory. 2004, Springer Berlin Heidelberg.
-
Liu, B., A survey of credibility theory. Fuzzy Optimization and Decision Making, 2006. 5(4): p. 387-408.
Freddy Andrés Pérez Mantilla
Nació en Barranquilla, Colombia. Es ingeniero industrial de la Universidad del Atlántico, de Barranquilla, Colombia. Actualmente es estudiante de doctorado en ingeniería en la Universidad de los Andes, de Bogotá, Colombia, y se desempeña como investigador del grupo PYLO, donde realiza estudios sobre la gestión de inventarios para productos perecederos.
e-mail: fa.perez10@uniandes.edu.co
Fidel Torres
Nació en Bogotá, Colombia. Es ingeniero eléctrico y matemático de la Universidad de los Andes, de Bogotá, Colombia. Obtuvo su título de Maestría en Ingeniería Eléctrica en la Universidad de los Andes de Bogotá, Colombia. Obtuvo su Magíster y PhD en Automática Informática Industrial en la Universidad Toulouse lII-Paul Sabatier, de Toulouse, Francia. Actualmente se desempeña como profesor en el área de Logística, producción y simulación en la Universidad de los Andes de Bogotá, Colombia, y es investigador del grupo PYLO.
e-mail: ftorres@uniandes.edu.co
Anexo: clasificación consolidada
Se presenta de manera tabulada y consolidada el resumen de los modelos revisados en la sección 4, conforme a la siguiente nomenclatura
-
Ref = número de la referencia bibliográfica
-
θ = tipo deterioro (F= vida útil fija conocida,C= tasa constante;V= tasa variable)
-
λ = tipo de demanda (C = constante, T = en función del tiempo, I = sensible al nivel de inventario,M= en función de estrategias de mercado,S= estocástica F= fuzzy)
-
σ = determinación de una política de precio de venta (R = con descuentos, S = con precios óptimos,D= con precios dinámicos)
-
Φ = inclusión de faltantes (T = con acumulación total, F = con acumulación parcial pero fija, I = con acumulación parcial pero en función del tiempo de espera, L = con venta perdidas,R=retrial)
-
Σ = inclusión de múltiples productos (M)
-
W = inclusión de más de un depósito para el almacenamiento (w)
-
X = estudios de sistemas multiniveles (S = un proveedor- un comprador, M = un proveedor/productor-múltiples compradores, T = tres eslabones, L = con logística inversa)
-
Π = Determinación de políticas de pago a proveedores (F =con un plazo de pago sin interés para cualquier tamaño de pedido, G = con plazo de pago en sin intereses para pedidos mayores a “q” ,B=con plazo de pago entre proveedor/comprador/consumidor, D = con plazo de pago y descuento por pronto pago, V = con plazo de pago como variable de decisión,Q= con plazo de pago parcial)
-
ρ = inclusión del valor del dinero en el tiempo e inflación (I)
-
H = utilización de variables/constantes híbridas/difusas, o parámetros estocásticos diferente a la demanda (F)
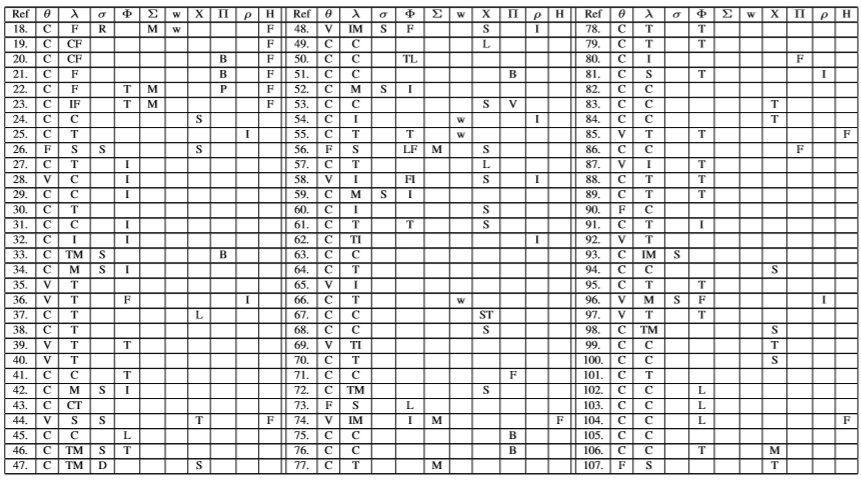
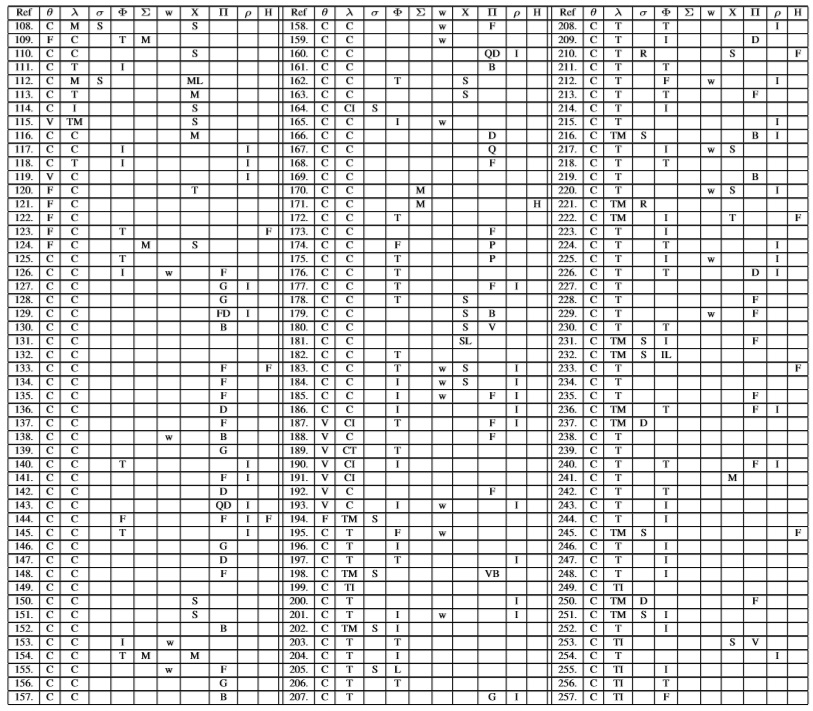
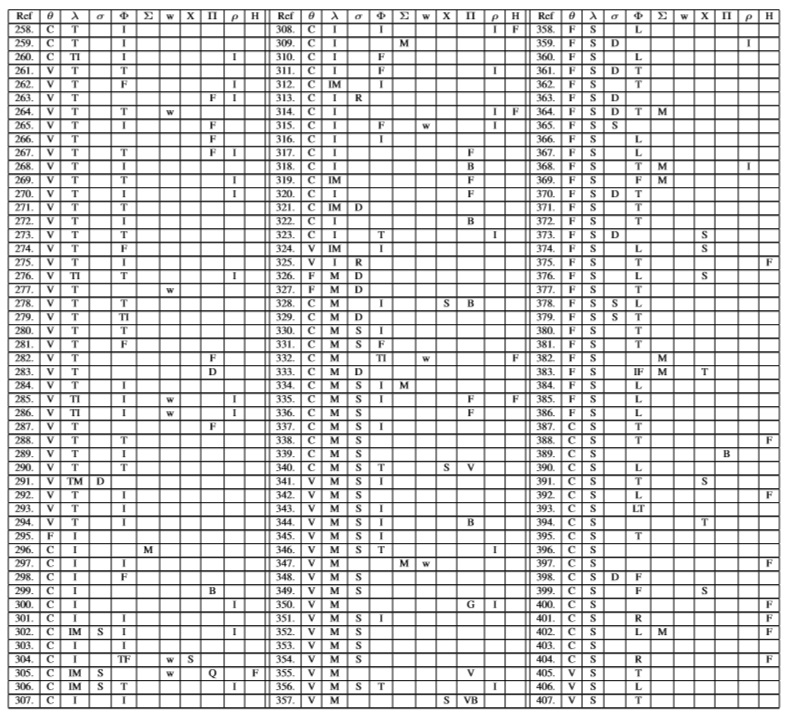

Este trabajo está autorizado por una Licencia Attribution-NonCommercial-NoDerivs CC BY-NC-ND.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.


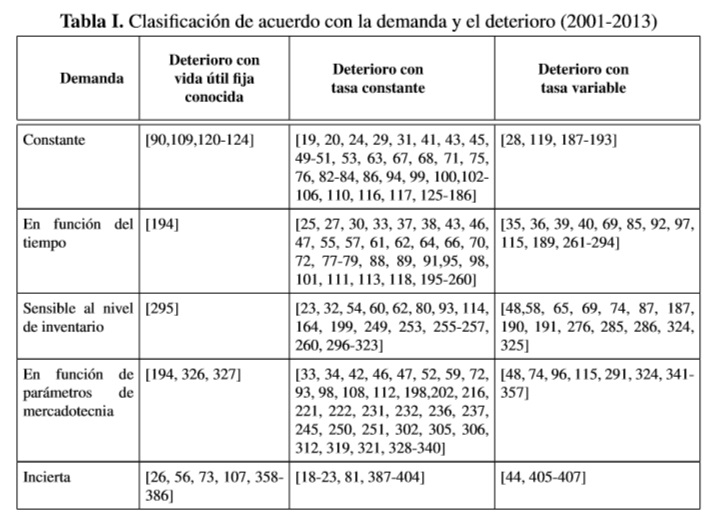
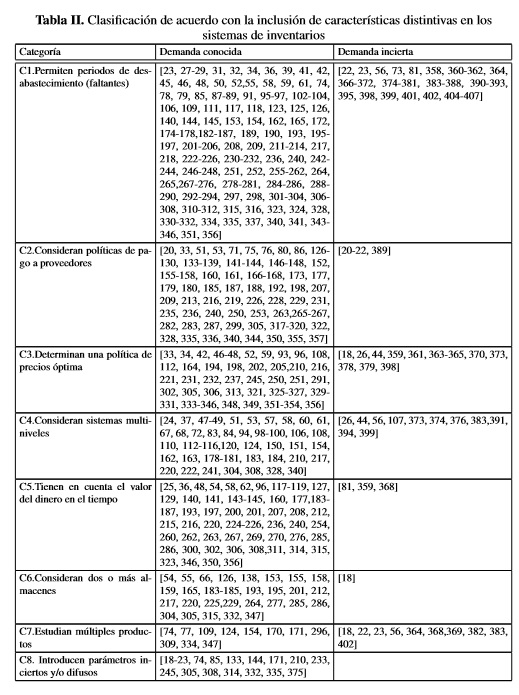
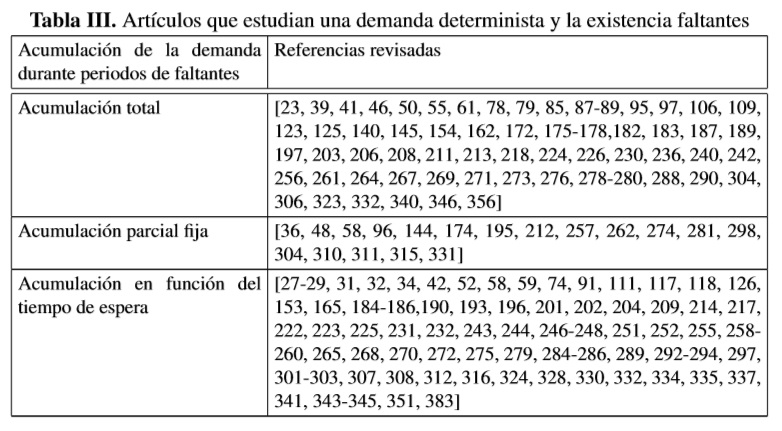
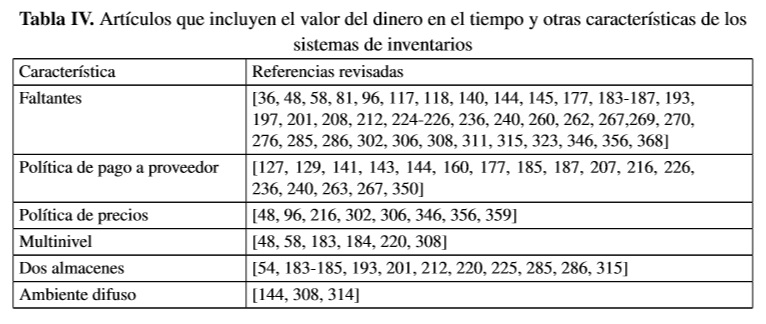
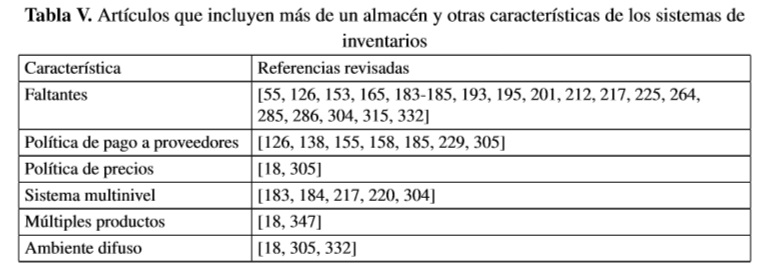



2.jpg)










