DOI:
https://doi.org/10.14483/23448393.15620Published:
2020-03-12Issue:
Vol. 25 No. 1 (2020): January - AprilSection:
Special Section: Best Extended Articles - WEA 2019FRand: MATLAB Toolbox for Fuzzy Random Number Simulation
FRand: Toolbox de MATLAB para Simulación de Números Aleatorios Difusos
Keywords:
Fuzzy random numbers, Random number generation, MATLAB (en).Keywords:
N´umeros aleatorios difusos, generaci´on de variable aleatoria, MATLAB (es).Downloads
References
Figueroa-García, J.C.: Mixed production planning under fuzzy uncertainty: A cumulative membership function approach. In: IEEE (ed.) Workshop on Engineering Applications (WEA). vol. 1, pp. 1–6. IEEE (2012), https://doi.org/10.1109/WEA.2012.6220081
Figueroa-García, J.C., López, C.A.: Linear programming with fuzzy joint parameters: A cumulative membership function approach. In: 2008 Annual Meeting of the IEEE North American Fuzzy Information Processing Society (NAFIPS). pp. 1–6. IEEE (2008), https://doi.org/10.1109/NAFIPS.2008.4531293
Figueroa-García, J.C., Lopez, C.A.: Pseudo-optimal solutions of FLP problems by using the cumulative mem- bership function. In: Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS). vol. 28, pp. 1–6. IEEE (2009), https://doi.org/10.1109/NAFIPS.2009.5156464
Grimmet, G., Stirzaker, D.: Probability and Random Processes. Oxford University Press (2001)
Johnson, L.A., Montgomery, D.C.: Operations Research in Production Planning, Scheduling and Inventory Control. John Wiley & Sons (1974)
Klir, G.J., Folger, T.A.: Fuzzy Sets, Uncertainty and Information. Prentice Hall (1992)
Klir, G.J., Yuan, B.: Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall (1995)
Kolmogorov, A.N.: Foundations of the Theory of Probability. Chelsea Publishing New York (1956)
Law, A., Kelton, D.: Simulation Modeling and Analysis. Mc Graw Hill (2000)
Monahan, J.F.: Numerical Methods of Statistics. Cambridge Press (2001)
Mood, A.M., Graybill, F.A., Boes, D.C.: Introduction to the Theory of Statistics. Mc Graw Hill Book Company (1974)
Pulido-López, D.G., García, M., Figueroa-García, J.C.: Fuzzy uncertainty in random variable generation: a cumulative membership function approach. Communications in Computer and Information Science 742(1), 398– 407 (2017), https://doi.org/10.1007/978-3-319-66963-2_36
Ross, S.M.: Stochastic Processes. John Wiley and Sons (1996)
Varon-Gaviria, C.A., Barbosa-Fontecha, J.L., Figueroa-García, J.C.: Fuzzy uncertainty in random variable generation: an α-cut approach. Lecture Notes in Artificial Intelligence 10363(1), 1–10 (2017)
Wilks, A.: Mathematical Statistics. John Wiley and Sons, New York (1962)
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 27 de noviembre de 2019; Revisión recibida: 10 de marzo de 2020; Aceptado: 12 de marzo de 2020
Abstract
Context:
This paper presents a MATLAB code implementation and the GUI (General User Interface) for fuzzy random variable generation. Based on previous theoretical results and applications, a MATLAB toolbox has been developed and tested for selected membership functions.
Method:
A two-step methodology was used: i) a MATLAB toolbox was implemented to be used as interface and ii) all .m functions are available to be used as normal code. The main goal is to provide graphical and code-efficient tools to users.
Results:
The main obtained results are the MATLAB GUI and code. In addition, some experiments were ran to evaluate its capabilities and some randomness statistical tests were successfully performed.
Conclusions:
Satisfactory results were obtained from the implementation of the MATLAB code/toolbox. All randomness tests were accepted and all performed experiments shown stability of the toolbox even for large samples (>10.000). Also, the code/toolbox are available online.
Keywords:
Fuzzy random numbers, Random number generation, MATLAB..Resumen
Contexto:
Este trabajo presenta una implementación de código de MATLAB y un GUI (interfaz de usuario) para la generación de variable aleatoria difusa. Basados en resultados teóricos y aplicación previos, un toolbox de MATLAB fué desarrollado y validado para diferentes funciones de pertenencia.
Método:
Una metodología de dos pasos ha sido implementada: i) un toolbox de MATLAB es implementado para usarse como interfaz y ii) todas las funciones .m están disponibles para usarse como código normal. La meta principal es proveer herramientas gráficas y de código a los usuarios
Resultados:
Los resultados principales de este trabajo son el MATLAB GUI y el código subyacente. Adicionalmente, algunos experimentos fueron realizados para evaluar las capacidades del toolbox, y algunas pruebas estadísticas de aleatoriedad fueron realizadas con éxito.
Conclusiones:
Resultados satisfactorios de la implementación del código/toolbox de MATLAB fueron obtenidos. Todos los tests estadísticos fueron aceptados y todos los experimentos realizados mostraron que el toolbox es estable aún para tamaños de muestra grande (>10.000). Adicionalmente, el toolbox/código está disponible online.
Palabras clave:
Números aleatorios difusos, generación de variable aleatoria, MATLAB..Introduction
Random variable generation from a probabilistic point of view is based on the ideas, postulates, theorems of A.N. Kolmogorov [8] which have been widely applied to different sciences, including the theory of random processes theory (see Grimmet & Stirzaker [4] and Ross [13]). Even more, commercial simulation software packages including ARENA, ProModel, FlexSIM, MATLAB EventSIM etc. are successful commercial applications of random variable theory and methods.
Most of probabilistic methods are based on the cumulative probability function (which is monotonic non-decreasing and injective) and the idea behind is to use uniform random numbers to generate probabilistic variables. Further information about probabilistic random variable theory and methods can be found in Devroye [5], Law & Kelton[9], Monahan[10], Grimmet & Stirzaker[4], Wilks [15] and Mood et al[11].
Analogous concepts for fuzzy numbers have been proposed by Varón-Gaviria et al. [14] and Pulido-López et al. [12]who used the well known α-cuts representation of a fuzzy set and the cumulative membership function ψA(x) of A (see Figueroa-García & López-Bello[2], [3] and Figueroa-García[1]). This way, it is possible to efficiently generate random variables using uniform random numbers and fuzzy sets easy to implement in general purpose code/software like MATLAB.
This paper focuses on the implementation of two fuzzy random variable generation methods into a toolbox over MATLAB general purpose software. Some graphic analysis and statistical test are performed to verify independence and randomness of the obtained samples.
This paper is divided into six sections: Section 1 introduces the main problem. Section 2 presents a theoretical background; two methods for fuzzy random variable generation are introduced in Section 3; Section 4 presents the developed MATLAB toolbox; some experiments are presented in Section 5, and finally Section 6 shows some concluding remarks.
Theoretical background
First, we refer to well known definitions for fuzzy sets/numbers (see Klir & Folger[6], Klir & Yuan[7]) and the two implemented methods: α-cuts and cumulative membership function.
Basics on fuzzy sets
A fuzzy set is denoted by emphasized capital letters A with a membership function
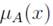over a universal set
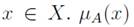measures the membership of a value
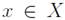regarding the concept/word/label
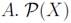is the class of all crisp sets,
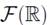is the class of all fuzzy sets,
is the class of all real-valued fuzzy sets, and
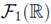is the class of all fuzzy numbers. Thus, a fuzzy set A is a set of ordered pairs of an element x and its membership degree,
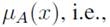
A fuzzy number is defined as follows:
Definition 1 Let
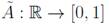be a fuzzy subset of the reals. Then
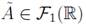is a Fuzzy Number(FN) iff there exists a closed interval
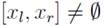with a membership function
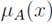such that:
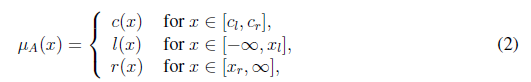
Where
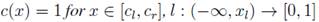is monotonic non-decreasing, continuous from the right,
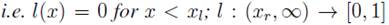is monotonic non-increasing, continuous from the left,
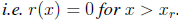
The set of elements with membership degree larger than α are called the α-cut i.e. αA
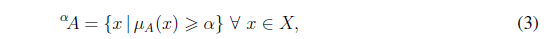
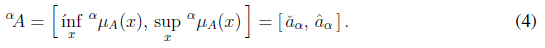
and its α-level namely Aα is the set of elements with membership degree equal to α, i.e.
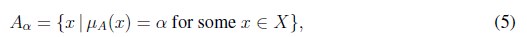
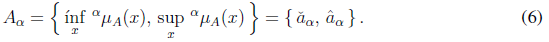
The support of
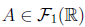, supp(A) is the set of all elements x ∈ X with nonzero membership:
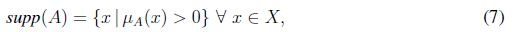
and the core of
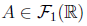is the set of elements with maximum membership degree:
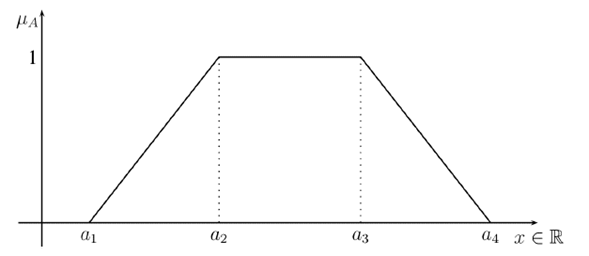
A trapezoidal fuzzy number is shown in Figure 1.
Figure 1: Fuzzy number
The Cumulative Membership Function(CMF)
The cumulative function
of a probability distribution
is defined as:
Where
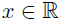Its fuzzy versión is as follows (see Figueroa-García & López-Bello[2], [3],Figueroa-García [1] and Pulido-López et.al [
12
]).
Definition 2 (Cumulative Membership Function) Let
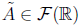be a fuzzy set and X ⊆R, then the cumulative membership function (CMF)
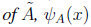is defined as:
Eq. (12) is nothing else but the possibility that all elements of X are less or equal than a value x,
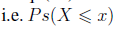In the probabilistic theory F(∞) = 1 so in the possibilistic theory 1 < ψ(∞) < Λ, where Λ is the cardinality of
:
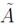A normalized ψA(x) is obtained as follows:
Clearly,
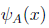is an surjection, so if we assume
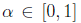then there exists one and only one value that satisfies
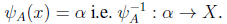
Implementation of fuzzy random generation methods
There are essentially two kinds of fuzzy numbers: Singleton-core i.e.
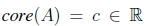and interval-corei.e. core
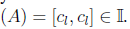The α-cuts method is adequate for single-core fuzzy numbers (triangular, Gaussian, exponential, etc), and the cumulative membership function approach is adequate for interval-core sets (trapezoidal, bell shaped, etc.). Both procedures are shown next:
α-cuts procedure
This method was proposed by Varón-Gaviria et al. [
14
]for single-core fuzzy sets. The main idea is to use the core c of
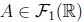to compute the partial areas namely Λ1,Λ2 around c, as follows:
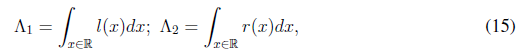
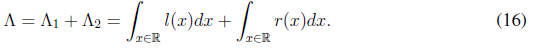
so the normalized areas
are defined as follows:
Procedure 1 show the implemented routine.
Cumulative membership procedure
For interval-core fuzzy numbers, we implement the proposal of Pulido-López et al. [ 12 ]based on Eqs. (11) and (14), as shown in Procedure 2:
MATLAB Toolbox implementation
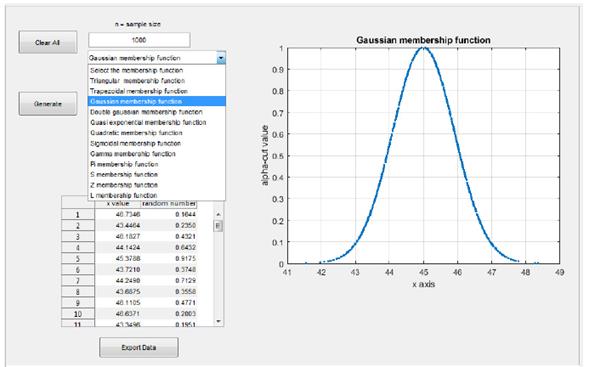
The implementation of both methods within MATLAB is divided into two parts: The code for all the implemented membership functions (useful for implementing fuzzy random variables as embedded code in other MATLAB routines/toolboxes) and the code for the GUI which are described as follows. Fig. 2 shows a screenshot of the MATLAB toolbox.
Figure 2: MATLAB Toolbox
MATLAB functions
MATLAB functions for five random generators are described below:
-
1. Triangular random generator
>> FT(a,m,b,n)
-
2. Gaussian random generator
>> FG(m,k,n)
-
3. Trapezoidal random generator
>> FTz(a,b,c,d,n)
-
4. Quasi-exponential random generator
>> FQe(m,k,n)
-
5. Double-gaussian random generator
>> FGT(m1,k1,l,r,m2,k2,n)
FRand toolbox
Basically, the toolbox contains all the previously described functions within a single file
FRand.m
that can be opened by simply writing
>> FRand
into the MATLAB command window.
Online availability
All functions have been compiled and compressed into a single file, available via the website of the Laboratory of Automation and Computational Intelligence (LAMIC) of the Universidad Distrital Francisco José de Caldas. To download the toolbox, please locate the file FRcode.zip at the URL:
https://comunidad.udistrital.edu.co/lamic/tools/
To install the functions, just copy the folder
FRand
into the path \˜\MATLAB\˜˜˜˜˜\toolbox\ e.g. for the Release 2017b:
\˜\MATLAB\R2017b\toolbox\
then add the toolbox path within MATLAB
File --> Set Path --> Add
The folder \˜\MATLAB\R2017b\toolbox\FRand\ contains the files:
FGT.m
FQe.m
FTz.m
FT.m
FG.m
After installing the folder and adding the path, the functions are ready to use and can be called from either the MATLAB command window, MATLAB SimuLink, MATLAB DiscreteEvents or any other toolbox.
Remark 1 It is important to note that our approach uses MATLAB R2017a uniform random number routines, so it may not be compatible with future MATLAB versions.
Experimentation and statistical analysis of generated data
To test the toolbox, we generated n = 1000 realizations of the following fuzzy random variables:
>> FT (44, 60, 85, 1000)
>> FTz (10, 15, 20, 22, 1000)
>> FG (50,0.3, 1000)
>> FQe (200,0.8, 1000)
>> FGT (12, 0.6, 10, 18, 14, 0.8, 1000)
Then its mean, variance, runs test, turning points test, GAP (gap test) with the Kolmogorov Smirnovtest, Chi-square test, and autocorrelation (min:↓andmax:↑) are computed to test if the obtained sequence is an independent. The results are shown in Table I.
Table I: Independence test on simulated variables(p-values)
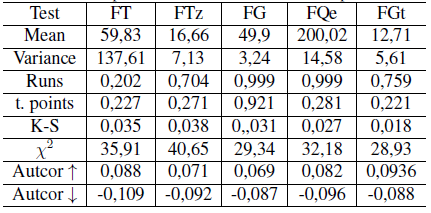
Runs and turning points tests show statistical significance of the hypothesis of independence on samples at a 95% confidence level (see Table I). The autocorrelation test shows a Pearson test on autocorrelations for the 10 first lags where autocorrelation. ↓ is the lowest observed autocorrelation and autocorrelation. ↑ is the largest observed autocorrelation (at a 95% confidence level).
The evidence shows that the generated samples are independent since the hypothesis of randomness is significant at a 95% confidence level (p-value ¿0.05), and there is no evidence autocorrelated samples since the hypothesis of existence of autocorrelation is not significant at a 95% confidence level (p-value ¡0.05). With the two gaps test, in the first case the Kolmogorov-Smirnov test is evaluated with a critical value Dα = 0,043 for each membership function, all the values are less than Dα, therefore the 1000 numbers are randomly ordered, and finally the Chi-Square test, presented a value χ2 = 44,98 with 95 % confidence level and for
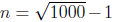. All the values obtained allow us to infer that the hypothesis that data are randomly distributed is significant for every membership function.
Figures 3-7 shows the exact location of the simulated values and their membership degree α.
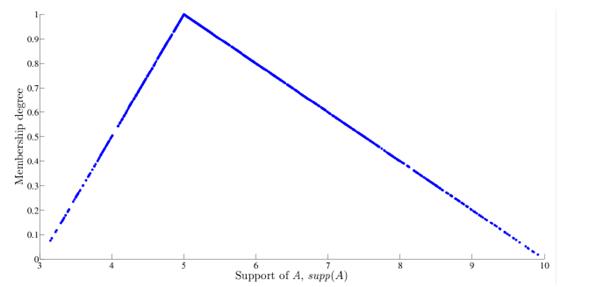
Figure 3: Simulated triangular random variables
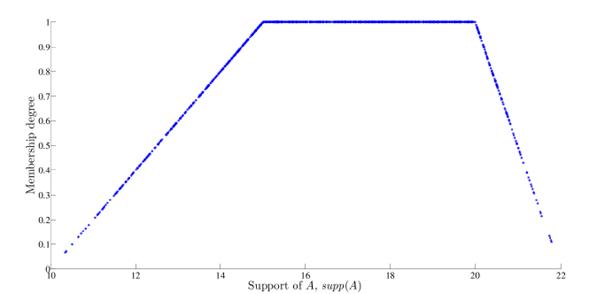
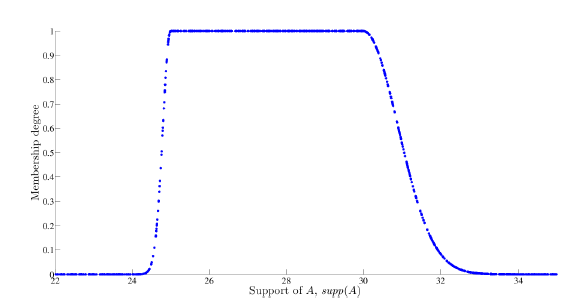
Figure 4: Simulated trapezoidal random variables
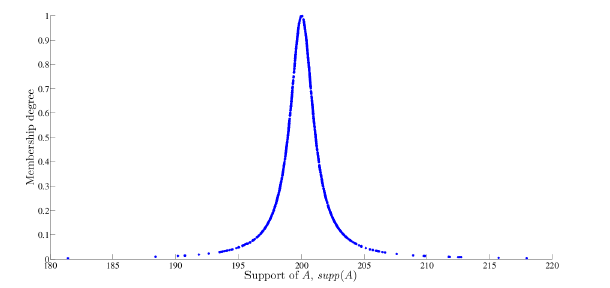
Figure 5: Simulated quasi-exponential random variables
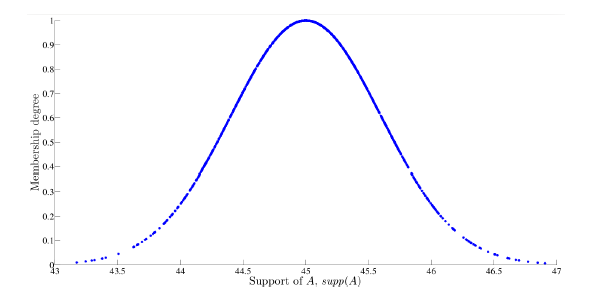
Figure 6: Simulated Gaussian random variables
Figure 7: Simulated double-exponential random variables
Note that Figs. 3-7 are good representations of each fuzzy number since the obtained shapes correspond to each membership function.
Concluding Remarks
The the oretical results of Varón-Gaviria et al. [ 14 ] and Pulido-López et al. [ 12 ]were successfully implemented as MATLAB functions. All of them are available to download for free, and the are compatible with MATLAB 9.2 R2017a and later versions.
A theoretical background has been provided to explain how to use the implemented MATLAB’s functions and toolbox. All functions are easy to understand, use, and are also complaint with MATLAB specifications for coding and compatibility.
Finally, some experiments are presented and tested using statistical tests on randomness and autocorrelation. The obtained results show generated samples to be independent and random, so the evidence supports the idea that the toolbox provides random samples.
Acknowledgements
Acknowledgements
The authors would like to thank to the Prof. M Sc. Miguel Melgarejo and Prof. José Jairo Soriano-Mendez sincerely for their interest and invaluable support, and a special gratefulness is given to all members of LAMIC.
References
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
2.jpg)
