DOI:
https://doi.org/10.14483/23448393.22049Published:
2024-11-11Issue:
Vol. 29 No. 3 (2024): September-DecemberSection:
Electrical, Electronic and Telecommunications EngineeringComparative Analysis of the Julia and AMPL Computational Tools Used in the Radial Distribution Network Optimization Problem
Análisis comparativo de las herramientas computacionales Julia y AMPL utilizadas en el problema de optimización de redes de distribución radiales
Keywords:
mathematical optimization, distribution power networks, solvers, optimal capacitor placement, optimal distributed generation allocation (en).Keywords:
optimización matemática, redes de distribución eléctrica, solucionadores, colocación óptima de condensadores, asignación óptima de generación distribuida (es).Downloads
References
R. Dos Reis Gonçalves, “Modelos de programação linear inteira Mista para resolver problemas de Otimização de sistemas de distribuição de Energia elétrica radiais,” PhD thesis, Dept. Electrical Eng., Universidade Estadual Paulista, Ilha Solteira, BRA 2013. [Online]. Available: https://repositorio.unesp.br/items/bd089af3-8e0b-4ee7-a33b-d7f7a42a4170
L. A. Gallego Pareja, J. M. Lopez Lezama, and O. Gomez Carmona, “Optimal placement of capacitors, voltage regulators, and distributed generators in electric power distribution systems,” Ingeniería, vol. 25, no. 3, pp. 334-354, Oct. 2020. https://doi.org/10.14483/23448393.16925
A. Karbowski and K. Wyskiel, “Comparative study of AMPL, Pyomo and JuMP optimization modeling languages on a flood control problem example,” Pomiary Automatyka Robotyka, vol. 25, no. 4, pp. 19-24, Dec. 2021. https://doi.org/10.14313/par_242/19
I. Dunning, J. Huchette, and M. Lubin, “JuMP: A Modeling Language for Mathematical Optimization,” SIAM Rev., vol. 59, no. 2, pp-295-320, Sep. 2017. https://doi.org/10.1137/15M1020575
M.-B. Lucioograndinetti and A. Editors, “Springer proceedings in mathematics & statistics,” 2014. [Online]. Available: http://www.springer.com/series/10533
R. Anand, D. Aggarwal, and V. Kumar, “A comparative analysis of optimization solvers,” J. Stat. Manag. Syst., vol. 20, no. 4, pp. 623-635, Jul. 2017. https://doi.org/10.1080/09720510.2017.1395182
L. A. Gallego, J. M. López-Lezama, and O. G. Carmona, “A mixed-integer linear programming model for simultaneous optimal reconfiguration and optimal placement of capacitor banks in distribution networks,” IEEE Access, vol. 10, pp. 52655-52673, 2022. https://doi.org/10.1109/ACCESS.2022.3175189
J. C. Hoyos Vallejo, “Análisis de herramientas computacionales libres utilizadas en el modelado y en la solución del problema de optimización en la ubicación de capacitores y de la generación en redes de distribución radiales,” Undergraduate Thesis, Dept. Engineering, Universidad Autónoma de Occidente, Cali, Colombia, 2023. [Online]. Available: https://red.uao.edu.co/handle/10614/15108
Norma Técnica: Calidad de la potencia de redes de distribución, Empresas Públicas de Medellín, Colombia, 2019, pp.11-12.
J. C. Hoyos, “Repositorio código AMPL - JuMP.” [Online]. Available: https://github.com/camilohoyos0499/Code
“Documentation for JuMP,” JuMP. [Online]. Available: https://jump.dev/JuMP.jl/stable/
R. Fourer, D. M. Gay, and B. W. Kernighan, “AMPL: A modeling language for mathematical programming, second edition,” 2003. [Online]. Available: https://vanderbei.princeton.edu/307/textbook/AMPLbook.pdf
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 10 de abril de 2024; Aceptado: 3 de octubre de 2024
Abstract
Context:
Research on the development of mathematical models to optimize electric power distribution systems has become increasingly important in recent years. Choosing the right optimization tools and solvers to address optimization problems in these systems has therefore become fundamental.
Method:
Nonlinear and mixed-integer nonlinear mathematical models addressing optimal capacitor placement and the allocation of distributed generation were implemented in the AMPL and Julia platforms. These models together with the Ipopt, Knitro, and Bonmin solvers, were tested and compared using 33-, 69-, and 83-bus test systems.
sults:
The comparative analysis shows that AMPL allows for a more direct and adequate implementation of this type of optimization problem, while Julia requires more elaborate constructions. The experimental results show significant reductions in system losses through optimal capacitor and distributed generation placement.
Conclusions:
AMPL offers a faster learning curve and a syntax that is more suitable for mathematical modeling. On the other hand, Julia provides superior versatility and access to a wider diversity of solvers. Although the evaluated nonlinear solvers proved to be suitable for the non-convex models and reached equivalent solutions, Knitro, a commercial solver, exhibited shorter processing times. In this sense, choosing between free or commercial alternatives involves a compromise between processing times and the available budget. Furthermore, solving the aforementioned optimization problems effectively minimized losses in the test systems. These models are basic versions that can be extended to more complex optimization problems.
Keywords:
mathematical optimization, power distribution networks, solvers, optimal capacitor placement, optimal allocation of distributed generation.Resumen
Contexto:
La investigación sobre el desarrollo de modelos matemáticos para optimizar los sistemas de distribución de energía eléctrica ha cobrado cada vez más importancia en los últimos años. La selección de las herramientas de optimización y solvers adecuados para resolver los problemas de optimización en estos sistemas se ha vuelto fundamental.
Método:
Se implementaron modelos matemáticos no lineales y no lineales de enteros mixtos para abordar la ubicación óptima de capacitores y generación distribuida en las plataformas AMPL y Julia. Estos modelos, junto con los solvers Ipop, Knitro y Bonmin, fueron evaluados y comparados utilizando sistemas de prueba de 33, 69 y 83 barras.
Resultados:
El análisis comparativo evidencia que AMPL permite una implementación más directa y adecuada para este tipo de problemas de optimización, mientras que Julia requiere construcciones más elaboradas. Los resultados experimentales evidencian reducciones significativas en las pérdidas del sistema mediante la ubicación optima de capacitores y generación distribuida.
Conclusiones:
AMPL ofrece una curva de aprendizaje más rápida y una sintaxis más adecuada para el modelado matemático. Por otro lado, Julia proporciona una versatilidad superior y acceso a una diversidad más amplia de solvers. Aunque los solvers no lineales evaluados resultaron adecuados para los modelos no convexos y alcanzaron soluciones equivalentes, Knitro, un solver comercial, presentó tiempos de procesamiento más cortos. En este sentido, elegir entre alternativas gratuitas o comerciales implica un compromiso entre los tiempos de procesamiento y el presupuesto disponible. Además, la solución de los problemas de optimización mencionados permitió minimizar de manera efectiva las perdidas en los sistemas de prueba. Estos modelos son versiones básicas que pueden ampliarse a problemas de optimización más complejos.
Palabras clave:
optimización matemática, redes de distribución eléctrica, solucionadores, colocación óptima de condensadores, asignación óptima de generación distribuida.Introduction
In recent years, research on the development of mathematical models for optimization of electrical power systems, using and solving increasingly sophisticated, complex, and realistic mathematical models through commercial or open-source solvers 1.
Within the scope of electrical distribution networks, modeling and solving optimization problems is fundamental to improving efficiency and reliability. Two areas of interest in this field are optimal capacitor placement and the allocation of distributed generation, with the goal of reducing system losses, improving voltage profiles, correcting power factors, and increasing circuit capacity 2. However, there are issues associated with both the modeling and the optimization tools used in these areas.
Regarding modeling, it is crucial to have accurate mathematical formulations that adequately represent the characteristics and constraints of electrical distribution networks. These formulations must consider the relevant input data, as well as the assumptions and limitations of the optimal capacitor and distributed generation placement problem. The lack of an adequate mathematical formulation can lead to suboptimal or unfeasible solutions in practice 1.
Secondly, the optimization tools used to solve the aforementioned mathematical models are a determining factor in the efficiency and effectiveness of the optimization process 3. In this sense, to evaluate and solve optimization problems in this field, it is critical to analyze the characteristics of the available computational tools, e.g., AMPL and Julia. These tools may offer different characteristics, such as ease of use, documentation availability, support, and flexibility.
In this work, Julia was selected as a high-performance open-source alternative to commercial systems, as well as for its JuMP library, which offers significant advances with regard to modeling and extensibility by taking advantage of several features of Julia that are unique among the programming languages used for scientific computing 4. On the other hand, AMPL was chosen because it facilitates experimenting with formulations and simplifies the use of suitable solvers in addressing optimization problems. Moreover, the notation used in AMPL is close to the typical mathematical notation of state variables, objectives, constraints, sets, and parameters 5.
The commercial and open-source solvers used to tackle optimization problems in distribution networks offer different performance characteristics concerning runtime, documentation and support, solution accuracy, and associated costs 6. Comparing and evaluating these solvers will allow determining the most efficient and suitable ones for solving the optimization problems associated with capacitor and generation placement in distribution grids.
Considering the above, this research conducted a detailed analysis of the free computational tools used to solve the studied problem, comparing the AMPL and Julia platforms with regard to mathematical modeling and optimization, as well as different commercial and open-source solvers. This comparison identified the tools’ advantages and limitations, as well as their applicability in specific situations.
Mathematical model
This section presents the mathematical models implemented in this article: 1) the power flow model adapted for distribution networks, 2) the model for the optimal placement of capacitors, and 3) the model for the optimal placement of distributed generation. The objective function of each model is presented, as well as the assumptions and constraints involved.
Power Flow
To address the optimal capacitor placement and distributed generation allocation problem, a mathematical power flow model must first be implemented, which constitutes the basis for the subsequent models. This model has the following considerations and is based on the one presented in 7, where some modifications are made to the constraints and parameters presented in 8:
-
The electric power distribution system is represented by a single-phase diagram and features a radial topology.
-
The lines’ active and reactive power losses are concentrated at the transmitting bus.
-
The loads are modeled as constant powers.
-
The power flow is unidirectional.
-
The PI model’s capacitive reactance of the transmission lines is not considered.
-
There is only one energy supply source (i.e., the substation).
The power flow optimization problem is formulated as the following nonlinear problem 7:
The objective function contains a sum representing the energy losses of the system multiplied by a cost constant K c . Thus, it is possible to determine the total cost associated with the system’s energy losses over a period of one year.
Constraints 2 to 7 are technical and operational equations that seek to replicate the limitations and behavior of the analyzed electrical system.
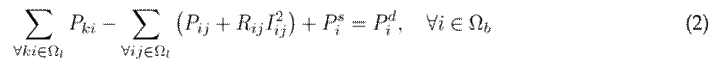
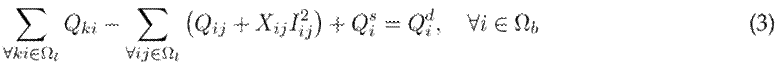
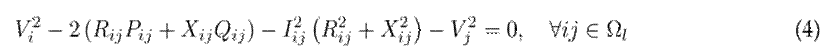
Eq. (2) represents the active power flow balance. In it, the first term denotes the active power injected by all the previous k buses that are connected to node i. The second term denotes the active power extracted towards all the subsequent buses j that are connected to node i and the active power losses of the lines ij through which bus i transmits power. The third term is the active power generated by the substation, where
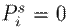for all buses
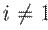, and the fourth term is the active power demand at node i.
Eq. (3) represents the reactive power flow balance. Here, the first term denotes the reactive power injected by all the previous k buses that are connected to node i. The second term denotes the reactive power extracted towards all subsequent buses j connected to node i and the reactive power losses of the lines ij through which bus i transmits power. The third term is the reactive power generated by the substation, where
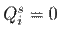for all buses
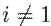, and the fourth term is the reactive power demand at node i.
Eq. (4) represents the voltage drop for each line ij of the network.
The apparent power flow constraint imposes a technical limit on the apparent power that can be transported by each conductor of the distribution network. Eq. (5) represents this constraint for each line ij.
The inequality constraints represent the permissible technical operating limits of the conductors and equipment in the distribution grid. Eq. (6) models the current constraint in each line ij of the system, aiming to prevent the conductors from overheating above their nominal capacities. Similarly, Eq. (7) defines the permissible voltage standards 9 at each node i, within which the connected equipment can operate safely and reliably.
Optimal capacitor placement
Capacitor placement optimization can be formulated as the following mixed-integer nonlinear
problem 2:
where f 1 is Eq. 1 and
The expression in 9 accounts for the installation cost of the capacitor banks K
i
. Here, the binary variable
indicates whether or not the capacitor bank is located at a node i. Eq. 10 describes the cost of each capacitor bank K
r
. The variable
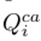indicates the reactive power injected by the capacitor at node i, thus providing the acquisition cost of the capacitor banks as a function of the reactive power injected. These two sums are multiplied by a depreciation factor D applied to the installation and acquisition costs of the capacitor banks for a period of one year, respectively.
Considering the reactive power introduced by the fixed capacitor banks in the system, the reactive power balance equation in 3 may be modified as follows:
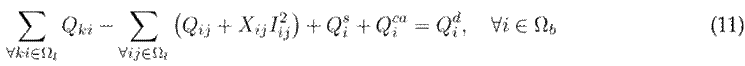
The term
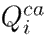in Eq. (11) denotes the reactive power injected by the fixed capacitor banks at each node i of the network.
Finally, constraints are added to the model for optimal capacitor placement.
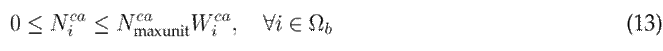
Here, Eq. (12) limits the maximum number of capacitor banks allowed in the distribution network, Eq. (13) stipulates the maximum number of capacitive units that can make up each capacitor bank at a specific node i, and Eq. (14) quantifies the reactive power injected by each capacitor bank at each specific node i.
Optimal allocation of distributed generation
The problem regarding the optimal allocation of distributed generation can be formulated as the following mixed-integer nonlinear model 2:
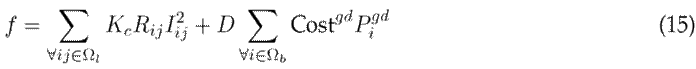
The objective function of this model contains two sums: Eq. (1) and the investment cost of distributed generation Cost gf as a function of the active power injected into the system Pi gd . An annual depreciation factor of D is applied to the investment costs, with the purpose of conducting a financial analysis in annualized terms over an evaluation period of ten years.
The following modification is made to the active and reactive power balance of Eqs. (2) and (3), respectively:
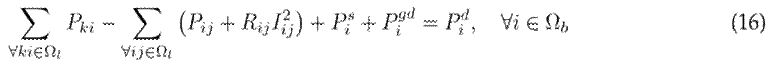
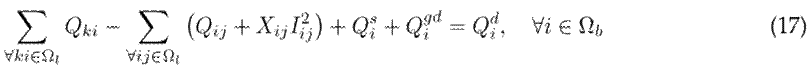
The terms Pi gd in Eq. (16) and
in Eq. (17) denote the active and reactive power injected by the distributed generators at each node i of the network. This modification expands the previous mathematical model by incorporating a new source of active and reactive power into the system.
Additionally, constraints are added to the model for the optimal allocation of distributed generation.
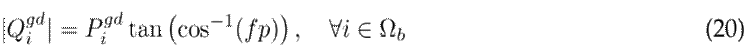
Eq. (18) limits the maximum number of distributed generation units in the network, Eq. (19) quantifies the active power injected by each distributed generation unit into each node i, and Eq. (20) quantifies the reactive power injected by each distributed generation unit into each node i.
The following values, obtained from 8, were considered in 33-, 69-, and 83-bus test systems: K
c
was equal to 168 $USD/kW-year, K
i
was 1600 $USD/bus, K
r
was 25 $USD/kvar, D was 10 %,
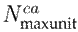was 5,
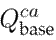was 50 kvar,
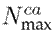and
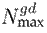were 3 for the 33- and 69-bus systems and 5 and 6 for the 83-bus feeder, Cost
gd
was 1105 $USD/kW, P
i
gd
was 100 kW, and fp was 0.92.
Computational Implementation
To computationally solve the proposed mathematical models, AMPL and Julia were used. These platforms allow translating the nonlinear equations and constraints of the models into a language that can be processed by a computer in order to find the optimal solution. The implementation process consisted of translating the mathematical formulas of each model into the specific syntax of AMPL and Julia. Due to their characteristics, and although the procedure was similar in both software platforms, some notable differences were observed for each model. The code may be accessed at (10).
Available documentation
Documentation is essential to guide the user during the implementation of a model. Julia and AMPL provide documentation but differ in approach and content. In Julia, the relevant documentation is in JuMP, a specific library for mathematical modeling, whereas, in AMPL, it is integrated. Therefore, Julia modeling requires consulting JuMP at 11 rather than the general documentation. JuMP’s documentation has a collaborative focus that encourages community participation but may cause inconsistencies between versions. AMPL, on the other hand, provides formal documentation developed by its creators. This ensures complete and reliable information, although it limits user feedback. The content focuses on using the platform 12. Moreover, JuMP focuses on language syntax and application, while AMPL also delves into mathematical optimization concepts.
Data management
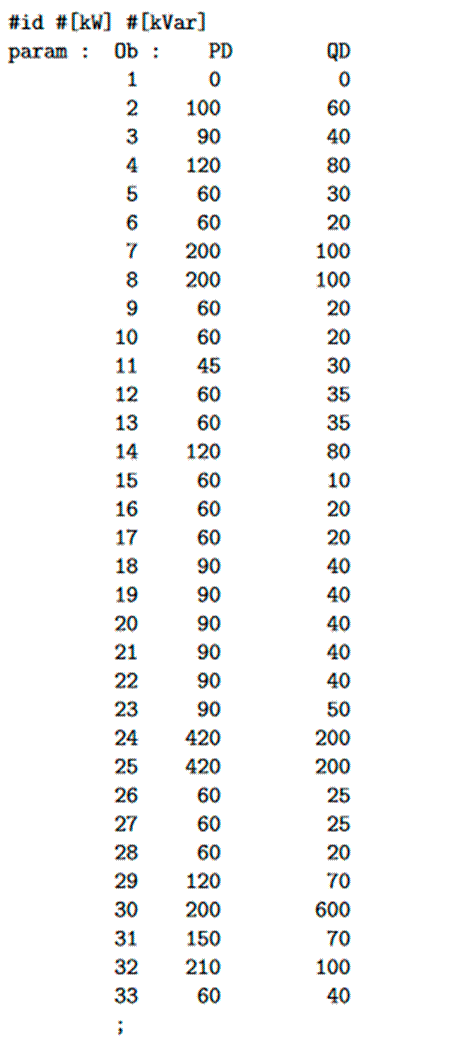
Data management in AMPL and Julia coincides in the use of sets to organize information. However, there is a relevant difference in code structuring. While Julia programming is done in a single file, AMPL uses three separate files: one for data, one for the model, and one for program execution. Both software platforms define line and bus sets with associated parameters to manage the input data of the modeled power system (Figs. 1 and 2). This helps to simplify programming in both AMPL and Julia.
Figure 1: Power demand dataset of the 33-bus test system in Julia
Programming the mathematical model
The main difference between AMPL and Julia lies in their model implementation. Julia is a general programming language with various uses, while AMPL belongs to the family of algebraic modeling and is designed for optimization and mathematical models. This is reflected in its syntax, which can directly and easily translate mathematical models. In contrast, as a complete programming language, Julia has a more complex syntax and requires solid programming foundations for effective use. Figs. 3 and 4 show an example of the computational implementation of Eq. (17) in AMPL and Julia.
Note that the translation of the mathematical model in AMPL is closer to the mathematical formulation of the model, whereas, in Julia, the implementation requires adjusting to its syntax.
Figure 2: Power demand dataset of the 33-bus test system in AMPL
Figure 3: Computational implementation of Eq. (17) in Julia
Figure 4: Computational implementation of Eq. (17) in AMP
Code length
The code length required for computational implementation is another substantial difference between AMPL and Julia. The structure of AMPL (i.e., one file for data, another for the model, and another for program execution) makes the code length increase considerably. Furthermore, in AMPL, it is mandatory to declare all parameters in an initial section before being able to use them in the data and model specifications. Julia does not have this limitation; as a programming language, it enables more compact programming, keeping all the logic in a single script, without requiring prior declarations or distribution across multiple files. Nevertheless, of required, the user also has this possibility.
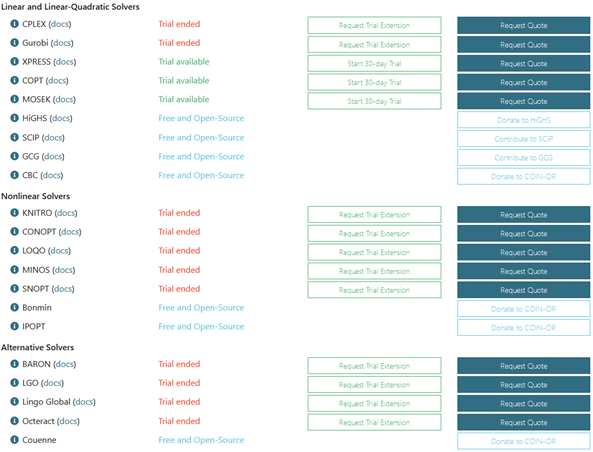
Solver installation
AMPL and Julia differ in solver management. As shown in Fig. 5, AMPL has a centralized portal to install commercial solvers according to the license type and problem, with integrated descriptions to facilitate selection by the user. Open-source solvers come by default. Julia does not have an analogous portal: commercial solvers are obtained from independent pages and open-source solvers as downloadable libraries. This decentralized diversity implies greater complexity in solver selection, as one must investigate the available alternatives online to evaluate features and limitations on an individual basis. Although the process is more complex, it provides access to a broader diversity of solvers. In AMPL, centralized management facilitates selection but limits the available options.
Figure 5: AMPL’s centralized portal
Testing and results
For computational experimentation, three optimization algorithms were selected: Knitro, which is commercial in nature, and Bonmin and Ipopt, which are open-source. This choice was based on the fact that these three solvers are available in both Julia and AMPL, and they all implement nonlinear optimization techniques. Therefore, they allow for a comparison between platforms in equivalent non-convex problems. The simulations were performed on a personal computer with an Intel Core™ i-3 1215U CPU @ 1.20 Ghz, 8GB RAM, and the default configuration of the solvers.
Comparison of results
Tables I, II, and III show the results obtained in the test systems with the selected solvers. Differences were observed in the computational time required by the models’ execution, being considerably longer in Julia. This occurs in most of the test systems and proposed optimization problems, except for the 83-bus system’s optimal capacitor placement. The above denotes the greater computational efficiency of AMPL over Julia when solving the proposed mathematical models.
Table I: Computation times for the power flow model
According to Tables IV, V and VI, across all feeders and optimization models tested for optimal capacitor and distributed generation placement, a decrease in active power losses was observed compared to the initial state of the analyzed electrical networks. Likewise, the results indicate economic viability, as reductions were observed in the total annualized costs, which consider both investment and technical losses.
Additionally, the implementation of the proposed mathematical models made it possible to improve the voltage profiles at the system buses, bringing the values closer to the nominal magnitude as well as mitigating voltage drop issues. This was achieved in both AMPL and Julia, confirming the equivalence of the selected solvers regarding operation and accuracy.
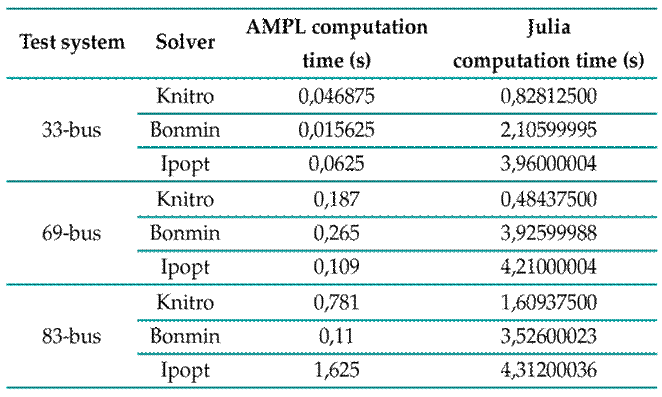
Table II: Computation times for the optimal capacitor placement model
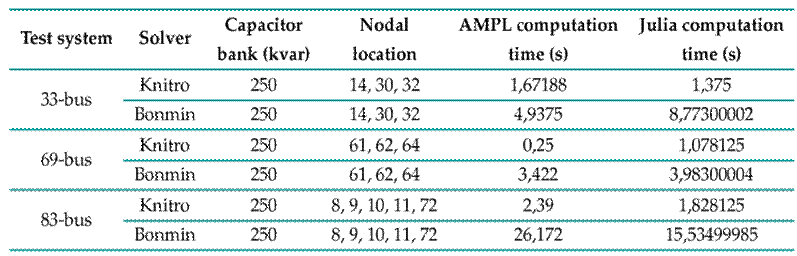
Table III: Computation times for the model concerning the optimal allocation of distributed generation
Table IV. Power losses and investment costs for the power flow model
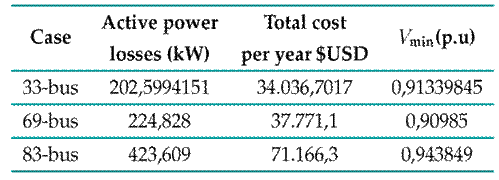
Based on the results, it should be noted that the Ipopt solver cannot solve optimization problems with binary variables, since it is designed exclusively for continuous nonlinear programming, where decision variables are continuous in nature. Given that the problems regarding optimal capacitor and distributed generation placement involve binary variables related to the installation of capacitor banks and generators, Ipopt is unable to find a feasible solution.
Conclusions
-
AMPL, as an algebraic modeling language, exhibits a faster learning curve compared to Julia, a general programming language, since its syntax is specifically designed for a direct and straightforward computational representation of mathematical models.
-
It is essential to determine the properties of mathematical models before their computational implementation, including characteristics such as linearity and convexity, among others, in order to select solvers that provide optimal and efficient solutions.
-
As the size of the test system increased, the evaluated open-source solvers (Bonmin and Ipopt) exhibited longer execution times compared to the Knitro commercial solver. This indicates the superior scalability of the latter. However, since Bonmin and Ipopt are open source, they do not incur licensing costs, unlike Knitro. This makes them viable alternatives based on the available budget, since solution accuracy was not affected. Thereupon, choosing between free or commercial solvers involves a compromise between processing times and the available economic resources.
-
The active power losses observed in the analyzed electrical systems were effectively minimized by implementing the proposed mathematical models for optimal capacitor bank placement and distributed generation allocation. It should be noted that these models can be extended to advanced complexity levels as required. In any case, the accuracy of the solutions largely depends on correctly adjusting the mathematical models according to the particularities of the analyzed electrical system.
Table V: Power losses and investment costs for the optimal capacitor placement model
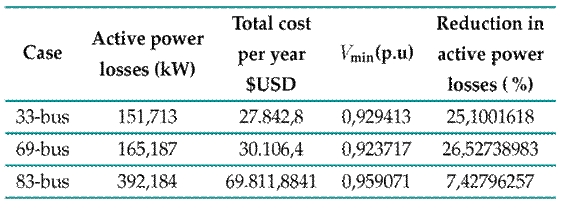
Table VI: Power losses and investment costs for the optimal distributed generation placement model
Table VII: Sets and indices of the models
Table VIII: Model parameters
Table IX: Model variables
References
License
Copyright (c) 2024 Juan Camilo Hoyos Vallejo, Jaime Quintero Restrepo
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
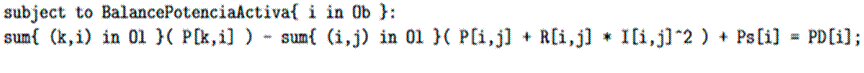
2.jpg)
