DOI:
https://doi.org/10.14483/23448393.17240Published:
2021-05-30Issue:
Vol. 26 No. 2 (2021): May - AugustSection:
Systems EngineeringRestauración de imágenes borrosas usando un modelo regularizado de programación lineal
Research Blurred Image Restoration Using a Regularized Linear Programming Model
Keywords:
Image restoration, Inverse Problems, Linear programming, L1 norm based regularization (en).Keywords:
Restauraci´on de im´agenes, problemas inversos, programaci´on lineal, regularizaci´on en norma L1 (es).Downloads
References
R. Gonzalez, R. Woods, and S. Eddins, Digital Image Processing Using MATLAB. McGraw Hill Education, 2013.
A. Zohair, and G. Sulong, “Deblurring computed tomography medical images using a novel amended landweber algorithm”, Interdisciplinary Sciences: Computational Life Sciences, 2, 2015. https://doi.org/10.1007/s12539-014-0225-x DOI: https://doi.org/10.1007/s12539-014-0225-x
J. Ye, H. Wang, and W. Yang, “Image recovery for electrical capacitance tomography based on low-rank decomposition”, IEEE Transactions on Instrumentation and Measurement, vol. 66, no. 7, pp. 1751-1759, 2017. https://doi.org/10.1109/TIM.2017.2664458 DOI: https://doi.org/10.1109/TIM.2017.2664458
Q. Qi, J. Guo, L. Jichanga, C. Li, and L. Xiao, “Blind face images deblurring with enhancement”, Multimedia Tools and Applications, vol. 80, no. 2, pp. 2975-2995, 2021. https://doi.org/10.1007/s11042-020-09460-x DOI: https://doi.org/10.1007/s11042-020-09460-x
W. Manwei, Z. Fuzhen, Z. Bing, and B. Yuyang, “An improved remote sensing image blind deblurring algorithm”, 3rd International Conference on Electronic Information Technology and Computer Engineering (EITCE), pp. 667-670, 2019. https://doi.org/10.1109/EITCE47263.2019.9094971. DOI: https://doi.org/10.1109/EITCE47263.2019.9094971
A. F. Montenegro, “Regularización de problemas inversos e imágenes borrosas”, Tesis de Maestría, Universidad Nacional de Colombia, mayo 2010.
S. Ray and P. Sahu, Novel Methods for Solving Linear and Nonlinear Integral Equations. Boca Raton, FL: Chapman and Hall/CRC, 2019. DOI: https://doi.org/10.1201/9780429431906
W. Richardson, “Bayesian-based iterative method of image restoration”, JoSA, vol. 62, no. 1, pp. 55-59, 1972. https://doi.org/10.1364/JOSA.62.000055 DOI: https://doi.org/10.1364/JOSA.62.000055
D. Liu, X. Chen, and X. Liu, “An improved richardson-lucy algorithm for star image deblurring”, IEEE International Instrumentation and Measurement Technology Conference (I2MTC), pp. 1-5, 2019. https://doi.org/10.1109/I2MTC.2019.8826905 DOI: https://doi.org/10.1109/I2MTC.2019.8826905
A. Buades, B. Coll, and J. Morel, “On image denoising methods”, tech. rep., Centre de Mathematiques et de Leurs Applications, 2004.
M. Chen, X. Zhang, M. Feng, and W. Xing, “Image deblurring method based on fourier transform”, 6th International Conference on Systems and Informatics (ICSAI), pp. 1285-1289, 2019. https://doi.org/10.1109/ICSAI48974.2019.9010430 DOI: https://doi.org/10.1109/ICSAI48974.2019.9010430
C. Cai, A. Liu, and B. Zhang, “Motion deblurring from a single image”, IEEE 20th International Conference on Computer Supported Cooperative Work in Design (CSCWD), pp. 406-410, 2016. https://doi.org/10.1109/cscwd.2016.7566023 DOI: https://doi.org/10.1109/CSCWD.2016.7566023
M. Jin, S. Roth, and P. Favaro, “Normalized blind deconvolution”, Proceedings of the European Conference on Computer Vision (ECCV), pp. 668-684, 2018. DOI: https://doi.org/10.1007/978-3-030-01234-2_41
X. Yan, G. Jing, Y. Liu, Y. Hu, L. Zhou, C. Zhang, and X.Wang Research of image deblurring based on Tikhonov regularization, vol. 11023, pp. 12 - 21, 2019. https://doi.org/10.1117/12.2515437 DOI: https://doi.org/10.1117/12.2515437
D. Krishnan, T. Tay, and R. Fergus, “Blind deconvolution using a normalized sparsity measure”, CVPR 2011, pp. 233-240, 2011. DOI: https://doi.org/10.1109/CVPR.2011.5995521
D. MacAdam, “Digital image restoration by constrained deconvolution”, Journal of the Optical Society of America, vol. 60, no. 12, pp. 1617-1628, 1970. https://doi.org/10.1364/JOSA.60.001617 DOI: https://doi.org/10.1364/JOSA.60.001617
N. Mascarenhas and W. Pratt, “Digital image restoration under a regression model”, IEEE Transactions on Circuits and Systems, vol. 22, no. 3, pp. 252-266, 1975. https://doi.org/10.1109/TCS.1975.1084026 DOI: https://doi.org/10.1109/TCS.1975.1084026
R. Mammone and G. Eichmann, “Superresolving image restoration using linear programming”, Applied optics, vol. 21, no. 3, pp. 496-501, 1982. https://doi.org/10.1364/AO.21.000496 DOI: https://doi.org/10.1364/AO.21.000496
M. Bazaraa, J. Jarvis, and H. Hanif, Linear Programming and Network Flows. Wiley-Interscience, 2004
S. Mehrotra, “On the implementation of a primal-dual interior point method”, SIAM Journal on optimization, vol. 2, no. 4, pp. 575-601, 1992. https://doi.org/10.1287/ijoc.1.2.70. DOI: https://doi.org/10.1137/0802028
R. Kress, Linear Integral Equations. Applied Mathematical Sciences 82, Springer-Verlag, 3 ed., 2014. DOI: https://doi.org/10.1007/978-1-4614-9593-2
Vicmat.com, “La conjetura de nicomaco”, 2017.
Tucarro.com, 2018. https://tucarro.com/
NASA, ESA, the Hubble Heritage Team (STScI/AURA)-ESA/Hubble Collaboration and K. Noll (STScI), NGC 6050. https://cdn.spacetelescope.org/archives/images/thumb700x/heic0810ap.jpg
R. Hanisch, R. White, and R. Gilliland, “Deconvolution of hubbles space telescope images and spectra”, in Deconvolution of images and spectra, pp. 310-360, Academic Press, 2nd ed., 1996.
D. Biggs and M. Andrews, “Acceleration of iterative image restoration algorithms”, Applied optics, vol. 36, no. 8, pp. 1766-1775, 1997. https://doi.org/10.1364/ao.36.001766 DOI: https://doi.org/10.1364/AO.36.001766
P. Hansen, J. Nagy, and D. Oleary, Society for Industrial and Applied Mathematics. 2006.
D. Krishnan, “https://dilipkay.wordpress.com/blind-deconvolution/”, 2011.
C. Hansen, J. Nagy, and D. O’Leary, “http://www.imm.dtu.dk/˜pcha/HNO/”, 2011.
U. d. G. Computer Vision Group, “Test images”, 2014. http://decsai.ugr.es/cvg/index2.php
Q. Huangfu and J. Hall), “Novel update techniques for the revised simplex method”, Computational Optimization and Applications, vol. 60, no. 3, pp. 587-608, 2014. https://doi.org/10.1007/s10589-014-9689-1 DOI: https://doi.org/10.1007/s10589-014-9689-1
F. Vitor and T. Easton, “A two dimensional search primal affine scaling interior point algorithm for linear programs”, Proceedings of the 2018 IISE Annual Conference, pp. 1961-1966, 2018.
Y. Peng, Z. Hao, and X. Yun, “Lock-free parallelization for variance-reduced stochastic gradient descent on streaming data”, IEEE Transactions on Parallel and Distributed Systems, vol. 31, no. 19, pp. 2220-2231, 2020. https://doi.org/10.1109/tpds.2020.2987867 DOI: https://doi.org/10.1109/TPDS.2020.2987867
Z. Wang, A. Bovik, H. Sheikh, and E. Simoncelli, “Image quality assessment: from error visibility to structural similarity”, IEEE transactions on image processing, vol. 13, no. 4, pp. 600-612, 2004. https://doi.org/10.1109/TIP.2003.819861 DOI: https://doi.org/10.1109/TIP.2003.819861
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 23 de noviembre de 2020; Revisión recibida: 18 de marzo de 2021; Aceptado: 26 de marzo de 2021
Resumen
Contexto:
Los problemas de minimización en el sentido de los mínimos cuadrados han sido constantemente usados en la restauración de imágenes borrosas. Estos se caracterizan por ser sensibles a valores atípicos afectando significativamente la calidad de la imagen restaurada. Teniendo en cuenta que la norma L1 es menos sensible a datos atípicos, el problema de restauración de imágenes borrosas se plantea como un problema de programación lineal.
Método:
Un método de punto interior se utiliza para la solución del problema de programación lineal. Se presenta la adaptación de técnicas de regularización al problema de programación lineal de la imagen buscada y su derivada. Se realiza un estudio comparativo con otras técnicas de restauración bajo diferentes tipos de difuminado de imágenes.
Resultados:
Se probó que el método propuesto conduce a mejoras notables en las imágenes recuperadas. Los experimentos numéricos muestran que el método de programación lineal funciona mucho mejor que los propuestos en la literatura, en términos de valores de PSNR, SSIM y en la calidad visual de las imágenes reconstruidas.
Conclusiones:
El problema de programación lineal regularizado puede utilizarse eficazmente como modelo matemático del problema de restauración de imágenes borrosas. Para trabajos futuros se plantea el estudio de la selección automática de parámetros de regularización y solución de restauración sin conocimiento previo del núcleo de difuminado.
Palabras clave:
restauración de imágenes, problemas inversos, programación lineal, regularización en norma L1..Abstract
Context:
Minimization problems in the sense of least squares have constantly been used in the restoration of blurred images. They are characterized by their sensitivity to outliers, which significantly affects affecting the quality of the restored image relevantly. Since the L1-norm is less sensitive to outliers, the image deblurring problem is posed as a linear programming problem.
Method:
An interior point method is used to solve the linear programming problem. This article presents the adaptation of regularization techniques of the image sought and its derivative to the problem of linear programming. A comparative study with other restoration methods under different types of image blurring is conducted.
Results:
The proposed method leads to remarkable improvements in the recovered images. Numerical experiments show that the linear programming method works much better than those proposed in the literature, in terms of PSNR and SSIM values, as well as in the visual quality of the reconstructed images.
Conclusions:
The regularized linear programming problem can be effectively used as a mathematical model of the image deblurring problem. For future work, there are plans to study of the automatic selection of regularization parameters and restoration solutions without prior knowledge of the blur kernel.
Keywords:
Image restoration, inverse problems, linear programming, L1 norm based regularization..Introducción
En el proceso de captura y registro de una imagen ocurren diversas anomalías que impiden una captura totalmente fiel de la realidad. Estas anomalías incluyen:
-
Factores ambientales.
-
Aquellas cosas que desean ser capturadas; por ejemplo, objetos en movimiento.
-
Errores en los dispositivos de captura, elementos dañados o mal ajustados.
-
Registro de la información.
Es muy común que estas imágenes no puedan ser tomadas de nuevo, lo que obliga a restaurarlas a su estado original para mejorar su nitidez antes de poder realizar otros pasos, como la detección, la segmentación, la clasificación [1]. En este sentido la restauración de imágenes juega un papel muy importante en áreas como: la tomografía computarizada [2], la tomografía de capacitancia y de impedancia eléctrica [3], el reconocimiento facial [4], la teledetección [5] y otras aplicaciones.
El problema de restauración de imágenes borrosas puede modelarse mediante la ecuación integral de Fredholm de primer tipo donde G es un dominio rectangular en
 representa la imagen original, E(s) describe ruido aditivo y B(s) es la imagen borrosa y ruidosa. La función K(t) núcleo del operador integral especifica como los puntos de la imagen se difuminan y es llamada función de propagación puntual o PSF por sus siglas en inglés (point spread function) [6]. Por lo tanto, dados K y B el objetivo es encontrar una aproximación de X.
representa la imagen original, E(s) describe ruido aditivo y B(s) es la imagen borrosa y ruidosa. La función K(t) núcleo del operador integral especifica como los puntos de la imagen se difuminan y es llamada función de propagación puntual o PSF por sus siglas en inglés (point spread function) [6]. Por lo tanto, dados K y B el objetivo es encontrar una aproximación de X.
Es bien conocido que la ecuación integral (1) es un problema “mal propuesto”, es decir que pequeñas perturbaciones en los datos provocan grandes cambios en los resultados [7]. Para superar esta dificultad, se han propuesto diversas técnicas que tienen el propósito de encontrar una aproximación
 de la imagen original X que solucione el problema de mínimos cuadrados
de la imagen original X que solucione el problema de mínimos cuadrados

Teniendo en cuenta este objetivo, en [8] a partir del teorema de Bayes se construye un algoritmo iterativo de deconvolución de máxima verosimilitud con un núcleo K predefinido; dicho algoritmo recibe el nombre de método de deconvolución de Lucy-Richardson [9]. También se ha propuesto usar la transformada de Fourier para multiplicar por un núcleo inverso en el dominio de la frecuencia, como se ilustra en [10] y [11]. Un método similar al método de Lucy-Richardson se presenta en [1] y [12], el filtro de Winner, en el cual se asume que la imagen borrosa es producto de una convolución con un núcleo K añadiendo ruido aditivo y busca minimizar el error cuadrático medio de este modelo con la imagen borrosa. En [13] se agregan términos adicionales al modelo para garantizar ciertas condiciones sobre el núcleo de convolución K y la solución a este problema. En [14] y [6] se usa el método de regularización de Tikhonov, planteando un error cuadrático y penalizando la norma de la solución con una constante α > 0, llamada parámetro de regularización. De manera similar a [6] en [15] se efectúa un proceso de regularización sobre la solución, salvo que el núcleo de convolución K y el cociente
 son los términos regularizados.
son los términos regularizados.
A diferencia de los trabajos mencionados, en este artículo consideramos el problema de minimización (2) en la norma L1 en vez de la norma L2, esto implica que la solución es menos sensible a valores atípicos u observaciones anormales que ocurren en el proceso de difuminado de la imagen. Este enfoque fue propuesto en [16] y posteriormente desarrollado en [17] y [18], donde el problema de restauración es visto como un problema de programación lineal (PL) y resuelto con el método Simplex, el cual no es eficiente al considerar problemas de gran tamaño [19] y las imágenes restauradas son ruidosas. El objetivo central de este trabajo es precisamente superar estas limitaciones, para ello se emplea un método de punto interior (ver [20] en la solución del problema de programación lineal y se usan técnicas de regularización numérica que permitan recuperar eficientemente imágenes más limpias. Además se realiza un estudio comparativo vía experimentación numérica de los métodos propuestos con los estudiados en la literatura.

El artículo está organizado como sigue. En la sección 2 se presenta el planteamiento del problema de restauración de imágenes borrosas como un problema de programación lineal y se comparan los métodos Simplex y de punto interior en el proceso de restauración. En la sección 3 se adapta la técnica de regularización como un problema de PL. Los experimentos numéricos se encuentran en la sección 4. Por último, se exponen las conclusiones.
Restauración de imágenes como un problema de PL
En problemas reales, las imágenes son capturadas solamente en puntos discretos dispuestos en un arreglo rectangular, cada uno de estos es denominado píxel. Por lo tanto, en la práctica se trabaja con la semidiscretización de (1)
donde N es el número de píxeles en la imagen observada. Considerando que la imagen a encontrar X(t) tiene las mismas dimensiones y es discretizada de la misma forma que la imagen borrosa, las integrales en (3) se discretizan en cada uno de los píxeles mediante la siguiente regla de cuadratura del punto medio:

Donde tanto la distancia horizontal como la vertical entre los píxeles es de 1, por lo que Δt j = 1 para cada j = 1,…, N. Ahora bien, si se consideran la matriz A cuyas entradas están dadas por A ij = K(s i - t j ), los vectores x = (X(t 1 ),…, X(t N )) T y b = (B(s 1 ) - E(s 1 ),…, B(s N ) - E(s N )) T , la ecuación (4) se convierte en el sistema de ecuaciones:

A pesar de la apariencia simple del sistema de ecuaciones (5), este es un problema mal condicionado, es decir, su solución x es muy sensible a pequeños cambios en el vector b (ver [6] y [21]). Esta característica, proviene del hecho de que el problema (5) es la discretización de la ecuación integral (1). Por lo tanto, una “buena” solución es aquella que minimiza el error residual e := Ax - b. Teniendo esto en cuenta, se propone el siguiente problema de minimización:


Donde, x ≥ y para dos vectores x, y ∈ (R N si x i ≥ y i para cada i = 1,…, N.
Para aclarar la notación e identificar cuáles son las variables, los coeficientes y hacer notoria la cantidad de restricciones, se hacen las siguientes definiciones:
N = nm, donde la imagen es una matriz de n filas y m columnas.
El vector e es descompuesto en su parte positiva e + y su parte negativa e - , esto es, e = e + + e - . Definidos como:

El vector

con ƒ ∈ R 3N es la concatenación de la imagen, la parte positiva del error y la parte negativa del error.
H ∈ R Nx3N es una matriz por bloques definida así:

c ∈ R 3N es el vector de “costos” y se define como:

Con esta nueva notación puede escribirse el problema (6) como un problema de PL en su forma canónica:

Resultados usando el modelo de PL
A continuación se presentan algunos resultados obtenidos al degradar imágenes y restaurarlas solucionando el problema de PL (11) mediante un método de punto interior [20]. Para evaluar la calidad de las restauraciones se usan las medidas de Proporción Máxima de Señal a Ruido (PSNR), el índice de similitud estructural (SSIM) y el error relativo en la norma L1. (Para las definiciones de las métricas, véase el Apéndice A). Los experimentos presentados en este artículo fueron implementados en MATLAB y ejecutados en un computador con un procesador Intel R CoreTM i5 8250u 1,60-3,40 Ghz con una memoria RAM de 4 Gb. Las imágenes y el código fuente usado en este trabajo pueden ser consultados en la siguiente dirección URL:
https://github.com/Xioeng/Restauracion-de-imagenes
En la figura 1, la imagen (c) muestra el resultado de aplicar el método de restauración de programación lineal a la imagen borrosa (b), la cual se obtuvo mediante la degradación de la imagen (a) de 236x197 píxeles por una PSF exponencial de tamaño 15x15, varianza de 16 y contaminada con un ruido blanco de 0,1%. Se observa que la imagen restaurada (c) es legible a pesar de la presencia de ruido del tipo “sal y pimienta”.
Figure 1: (Imagen degradada con 0,1% de ruido y su restauración, tomado de [22]. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada.
La tabla I muestra la diferencia entre la imagen de referencia (a) y las imágenes borrosas (b) y restaurada (c) respectivamente. Se observa la mejora en calidad, de la imagen restaurada en términos de las medidas PSNR, SSIM y el error relativo. No obstante, no debe esperarse que los errores al final de la restauración sean pequeños, debido a los grandes números de condición que presentan estas matrices; por ejemplo para la restauración de la imagen figura 1 (a), la condición de la matriz A es Cond 2 (A) = 3,66 x 10 7 .
Tabla I: Resultados de la restauración de la imagen de la Figura 1.

El algoritmo Simplex contra el algoritmo de punto interior
Un segundo experimento se ilustra en la Figura 2, en el que se evalúan y comparan los algoritmos Simplex y de punto interior en el proceso de restauración. A la imagen (a) de tamaño 194 x 259 se le aplica una PSF de desenfoque de movimiento horizontal de tamaño 51x51 y un 0,5% de ruido.
Figure 2: Imagen degradada con 0;5% de ruido y sus restauraciones. (a) Imagen original. Tomado de [23], (b) Imagen borrosa, (c) Imagen restaurada con el método Simplex, (d) Imagen restaurada con el método de punto interior.
En la figura 2 se aprecia que la imagen restaurada con el método de punto interior (d) es menos ruidosa encima de la placa que en la imagen restaurada por el método Simplex (c). Esta zona corresponde a una región homogénea y dicho efecto se ve reflejado en la medida Err. Sin embargo, los errores en cada uno de los píxeles son más grandes, como se observa en las medidas PSNR y SSIM (ver tabla II), esto se debe a lo mal condicionado del problema tratado Cond 2 (A) = 6,77 x 10 3 .
Tabla II: Resultados de la restauración de la imagen de la Figura 2.

También se encuentra que las soluciones obtenidas por los métodos de punto interior y Simplex son notoriamente diferentes, empezando por la cantidad de componentes no nulas; la menor cantidad es para el método Simplex, esto es de esperarse pues en este algoritmo las soluciones son soluciones básicas que constan de bastantes ceros. Cuantificando esta diferencia, se tiene que la norma
 de la diferencia de las soluciones es 1,08 x 106, lo que es equivalente al 20% de la norma
de la diferencia de las soluciones es 1,08 x 106, lo que es equivalente al 20% de la norma
 de la imagen original, luego estas soluciones aunque se parecen visualmente son bastante lejanas. En cuanto al tiempo de cómputo, la restauración de la imagen figura 2 (a) mediante el método Simplex tardó 66,6 segundos, mientras que el método de punto interior necesitó solo 8,7 segundos.
de la imagen original, luego estas soluciones aunque se parecen visualmente son bastante lejanas. En cuanto al tiempo de cómputo, la restauración de la imagen figura 2 (a) mediante el método Simplex tardó 66,6 segundos, mientras que el método de punto interior necesitó solo 8,7 segundos.
Modelo regularizado como un problema de PL
Con el objetivo de mejorar los resultados de la sección anterior, es decir, reducir el ruido y lograr imágenes restauradas más homogéneas, adaptamos técnicas de regularización al modelo de programación lineal. Además, puesto que las imágenes poseen cierto rango de valores: [0, 255] en el caso usual, aunque también suelen verse en el rango [0, 1]. Consideramos las restricciones de no negatividad en restricciones de caja, esto es, cambiar la desigualdad 0 ≤ x a la desigualdad 0 ≤ x ≤ u donde 0 ≤ u ∈ R N es un vector de las mismas dimensiones que x y actúa como cota superior de la solución óptima.
El problema (6) al añadir los términos de regularización y las restricciones resulta:

donde
 es la función objetivo subyacente y los términos de regularización son
es la función objetivo subyacente y los términos de regularización son
 y
y
 . Los efectos que tienen los términos de regularización en el problema de restauración son los siguientes:
. Los efectos que tienen los términos de regularización en el problema de restauración son los siguientes:
Como A es una matriz mal condicionada, la adición del término
busca mantener x de un tamaño razonable y el error residual

lo más pequeño posible. Esto remedia el problema de la aparición de píxeles con grandes valores que entorpezcan el proceso de restauración y controla también la cantidad de ceros en la imagen.

- Para tratar los casos en los que hay muchas variaciones de intensidad de la imagen se introduce el término
, el cual penaliza soluciones no suaves. Es decir, se limitan las altas frecuencias para obtener una imagen relativamente homogénea.

Para obtener una imagen lo más fiel posible a la original, los parámetros de regularización α y γ se seleccionan para alcanzar un balance entre las normas del error residual, la solución y su derivada.
En lo que sigue se transforma el problema (12) como un problema de programación lineal en forma estándar.
Abordaje
Para este propósito se usan los siguientes hechos:
1. Se puede observar que el vector x tiene componentes no negativas, entonces:

es decir, es posible obviar los valores absolutos y obtener la suma de las componentes del vector x.
2. Se puede notar que:

Es decir, se pueden separar las derivadas en la dirección horizontal y vertical de la imagen. De hecho, pueden ser calculadas de forma similar a como se calculó la matriz A. Las derivadas parciales son transformaciones lineales. Gracias a esto, se pueden calcular las matrices D h y D v , de forma que
y que

. Esto permite que


3. Al igual que en la ecuación (6), se escribe
con

. También, se separan los términos de las derivadas parciales en los vectores h+ ≥ 0, h- ≥ 0, v + ≥ 0 y v - ≥ 0, de forma que


4. Al limitar los posibles valores de la norma de la solución a un cierto rango, se obliga a que los valores de los vectores error e + , e - , h + , h - , v + y v - estén en el mismo rango. Esto se debe a que si a, b y c > 0 son tres números reales con a, b ∈ [0, c], entonces,
.

Con todas estas observaciones se puede reescribir el problema de optimización de la ecuación (12) en términos de los problemas de optimización asociados a las constantes α y γ. Para ello, se hacen las siguientes definiciones:
- El vector de variables
se define como:


Este vector es la concatenación de la imagen, la parte positiva del error y la parte negativa del error del modelo de borrado, la parte positiva y la parte negativa de las derivadas parciales.
-
es una matriz por bloques definida así:


donde cada matriz es de tamaño N x N; la matriz I es la matriz identidad y la matriz 0 es la matriz de ceros.
-
es el vector de “costos” y se define como:


- Se define el vector
como:


donde las componentes del vector b son las intensidades de los píxeles de la imagen borrosa.
- El vector
 se construye de forma que u = 255 · 1. Con 1 el vector de unos en
se construye de forma que u = 255 · 1. Con 1 el vector de unos en
 .
.
Así, la familia de problemas descritos por la ecuación (12) puede reescribirse como el problema de programación lineal

Nótese que cuando α = γ = 0 es el caso del modelo sin regularizar.
Resultados: modelo regularizado
En esta sección se presenta el resultado de emplear el método de punto interior en la solución del problema de PL (21). La restauración se realiza a imágenes degradadas con diferentes funciones PSF y con distintos niveles de ruido.
En la figura 3, la imagen (a) es degradada mediante una PSF de movimiento horizontal de tamaño 21x21 y a la imagen borrosa se le añadió 5% de ruido. Se usaron los parámetros de regularización α = 2x10-2 y γ = 8x10-2. Se observa que varias de las zonas que son homogéneas en la imagen original (a) son contaminadas con ruido en la imagen no regularizada (b). Sin embargo, en la imagen regularizada (d) es posible volverlas homogéneas de nuevo. También se observa que no se regularizó demasiado la derivada para no perder ciertos detalles de la imagen (como lo son los tornillos y pernos en la placa y cerca de ella). Por otra parte, hay que tener cuidado de no regularizar demasiado la derivada ya que detalles importantes como lo puede ser la palabra “Colombia” pueden verse afectados.
Figure 3: Imagen degradada con 5% de ruido y sus restauraciones usando el algoritmo de punto interior. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con el modelo sin regularizar, (d) Imagen restaurada con el modelo regularizado.
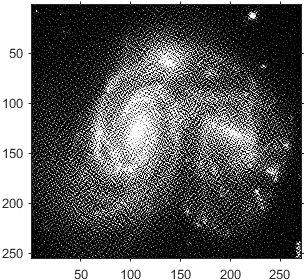
En la figura 4, la imagen (a) de tamaño 255x271 píxeles es degradada con una PSF exponencial con varianza de 16, un coeficiente q = 3 y de tamaño 11x11. Esta imagen fue contaminada con 0,5% de ruido. Se usaron los parámetros de regularización α = 1 x 10-2 y γ = 2,5x10-2.
Figure 4: Imagen degradada con 0,5% de ruido y sus restauraciones usando el algoritmo de punto interior. Tomado de [24] . (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con el modelo sin regularizar, (d) Imagen restaurada con el modelo regularizado.
En la imagen figura 4 (d) se observa que al regularizar la norma y su derivada se evita la aparición del ruido artificial que se aprecia en la imagen que no fue regularizada (figura 4 (c)), esto permite recuperar zonas que verdaderamente son homogéneas, al igual que el caso anterior. Sin embargo, dada la naturaleza de la imagen, en la que se presentan varios detalles que pueden ser interpretados como ruido (los puntos blancos que son polvo estelar o estrellas), es necesario regularizar menos la derivada de la solución para no eliminarlos. En este ejemplo, se observa que es indispensable un compromiso entre la cantidad de ruido admisible y la cantidad de detalles permitidos que puedan parecer ruido, esto se refleja en la selección de los parámetros de regularización α y γ.
En las tablas III y IV se compara la calidad de las imágenes restauradas obtenidas de solucionar el problema de PL (11) y el problema de PL regularizado (21). Como podemos ver, aplicar la técnica regularización propuesta da un mejor resultado de restauración en las tres métricas.
Tabla III: Comparación de la calidad las restauraciones de la imagen de la Figura 3.

Tabla IV: Comparación de la calidad las restauraciones de la imagen de la Figura 4.

Comparación contra otros métodos de restauración
En esta sección se estudia el desempeño de nuestra propuesta con respecto a los siguientes métodos formulados por otros autores:
-
Método de deconvolución de Lucy-Richardson propuesto en [8].
-
Método de deconvolución de Wiener propuesto en [1].
-
Algoritmo propuesto en [15] llamado “Blind Deconvolution Using a Normalized Sparsity Measure” (BDNSM).
-
Método de regularización de Tikhonov desarrollado en [27] y [6].
-
Método propuesto en el que se usa PL.
La implementación de estos métodos como: el algoritmo de Lucy-Richardson, el algoritmo de Wiener y el algoritmo de blind deconvolution son funciones implementadas por defecto en MATLAB. La implementación del algoritmo (BDNSM) fue tomada de la web del autor [28] y la implementación del método de regularización de Tikhonov fue tomada del sitio web de los autores [29].
A continuación se presentan varios experimentos de restauración a diversos tipos de imágenes [30] con diferentes tipos de PSF, así como los resultados cuantitativos de dichas restauraciones (ver Tabla V). Para cada uno de los experimentos todos los algoritmos fueron provistos con la misma PSF y fueron usados con los parámetros que tienen por defecto. Para los casos de los métodos de regularización de Tikhonov y el propuesto se usó el mismo valor de α para ambos.
Experimento 1
En la figura 5 se presenta el estudio comparativo. Inicialmente se desenfoca la imagen (a) usando una PSF de movimiento vertical de tamaño 31x31 y luego contaminada con 3% de ruido blanco. Para la restauración se usaron los valores de parámetros α = 1x10-2 y γ = 7x10-2. En la figura 5(h) se observa la efectividad del modelo propuesto al restaurar imágenes con regiones homogéneas, como se ha visto antes. En los otros métodos tienden a aparecer líneas horizontales que originalmente no estaban en la imagen, esto puede ser visto como ruido adicional en la imagen. En particular, las restauraciones logradas con los métodos de Wiener figura 5(d) y de regularización de Tikhonov figura 5(g) contienen muchos puntos blancos (el ruido del que se habló en la sección 2.1). Esto puede deberse tanto a la ausencia de la regularización en la derivada, como a la norma usada en la optimización que se realiza en estas dos técnicas.
Figura 5: Imagen degradada con 3% de ruido y sus restauraciones. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con método de Lucy-Richardson, (d) Imagen restaurada con método de deconvolución de Wiener, (e) Imagen restaurada con el método blind deconvolution, (f) Imagen restaurada con método BDNSM, (g) Imagen restaurada con método de regularización de Tikhonov, (h) Imagen restaurada con método propuesto.
Experimento 2
En este experimento se difumina la imagen original figura 6 (a) mediante una PSF exponencial con varianza igual a 7 y luego es contaminada con un ruido blanco del 1%. En la figura 6 se aprecia que las restauraciones de los diferentes métodos apuntan a recuperar los detalles generales de la imagen, aunque en algunas de ellas (figura 6 (d), (e) y (f)) se nota aún la presencia de efectos borrosos sobre esta. En cambio, el método propuesto restaura con mayor nitidez características locales de la imagen, por ejemplo: el portarretratos y los números del reloj (ver figura 6(h)).
Figura 6: Imagen degradada con 1% de ruido y sus restauraciones. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con método de Lucy-Richardson, (d) Imagen restaurada con método de deconvolución de Wiener, (e) Imagen restaurada con el método blind deconvolution, (f) Imagen restaurada con método BDNSM, (g) Imagen restaurada con método de regularización de Tikhonov, (h) Imagen restaurada con método propuesto.
Experimento 3
La imagen de la figura 7(b) ha sido generada por la convolución de la imagen original (figura 7(a)), con una PSF de degradado atmosférico y la adición de un ruido blanco del 1%. Se aprecia en la imagen de la figura 7(h) cómo el método propuesto recupera los bordes de las figuras geométricas, evitando que aparezcan líneas de contorno alrededor de ellas o ruido en el fondo de la imagen, a diferencia de lo que se observa en las imágenes 7 (c), (e) y (g). Se nota que el método de Wiener no arroja resultados satisfactorios, esto debido a su sensibilidad con respecto al ruido de fondo.
Figura 7: Imagen degradada con una PSF de degradado atmosférico, 1% de ruido y sus restauraciones. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con método de Lucy-Richardson, (d) Imagen restaurada con método de deconvolución de Wiener, (e) Imagen restaurada con el método blind deconvolution, (f) Imagen restaurada con método BDNSM, (g) Imagen restaurada con método de regularización de Tikhonov, (h) Imagen restaurada con método propuesto.
Experimento 4
En este experimento se restaura la imagen borrosa 8(b) la cual se obtuvo al aplicar un PSF de desenfoque y un ruido blanco del 1% a la imagen 8(a). Observamos una mejor calidad de reconstrucción al emplear el método propuesto (figura 8(h)). Se recuperan los caracteres degradados evitando, de nuevo, que haya ruido que degrade el fondo. Este efecto es resultado de penalizar la norma kxk1.
Figura 8: Imagen degradada con una PSF de desenfoque, 1% de ruido y sus restauraciones. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con método de Lucy-Richardson, (d) Imagen restaurada con método de deconvolución de Wiener, (e) Imagen restaurada con el método blind deconvolution, (f) Imagen restaurada con método BDNSM, (g) Imagen restaurada con método de regularización de Tikhonov, (h) Imagen restaurada con método propuesto.
Experimento 5
A continuación se presenta una imagen de resonancia magnética (figura 9(a)) que fue alterada mediante una PSF de movimiento en una dirección de 300 grados de tamaño 31x31 y contaminada con ruido blanco del 1%. En la figura 9(h) se aprecia el potencial del método propuesto en el procesamiento de imágenes médicas. Se recupera la imagen manteniendo los detalles de la misma sin añadir ruido al fondo, el cual podría ser nocivo para un posprocesamiento. Además, se restaura la escala de grises con mayor fidelidad que la de las otras técnicas.
Figura 9: Imagen degradada con una PSF de movimiento, 1% de ruido y sus restauraciones. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con método de Lucy-Richardson, (d) Imagen restaurada con método de deconvolución de Wiener, (e) Imagen restaurada con el método blind deconvolution, (f) Imagen restaurada con método BDNSM, (g) Imagen restaurada con método de regularización de Tikhonov, (h) Imagen restaurada con método propuesto.
Una evaluación más objetiva de nuestro método se ilustra en la tabla V. En esta se presentan las medidas de error relativo, PSNR y SSIM de las imágenes restauradas por los diferentes métodos y los tipos de difuminado. Los mejores resultados están en negrita. Se puede observar que los valores de error relativo, PSNR y SSIM del método propuesto son superiores a los de otros métodos, excepto en el caso de la restauración de las figuras geométricas (figura 7) en el que el método de deconvolución ciega BDSNM muestra un mejor valor de SSIM. Esto se debe a que la eliminación de ruido de fondo es mejor que la producida por el método propuesto (véase figura 7(f)). Por otra parte, es de recalcar que el método de PL con regularización contrarresta el efecto amplificador de los errores por el mal condicionamiento del problema de restauración. Obsérvese el error relativo de la última columna de la tabla V.
Tabla V: Comparación de la calidad de las restauraciones de la imagen de las Figuras 6, 7, 8 y 9.

Conclusiones
Se exploró y se probó un método alternativo para la restauración de imágenes borrosas, visto y solucionado como un problema de programación lineal tomando en cuenta las propiedades particulares de la norma
 . La adaptación de la técnica de regularización en el problema de programación lineal, para tratar con el mal condicionamiento procedente de la ecuación integral (1) conduce a la obtención de resultados óptimos en la restauración de las imágenes difuminadas por diferentes funciones PSF. Es así, que la penalización de la solución en la norma L1 reduce el ruido en las áreas homogéneas de la imagen y la penalización del gradiente permite preservar mejor los bordes de la imagen obteniendo mejores resultados que con otros métodos usualmente empleados en la literatura. Se observa que para obtener resultados óptimos en la restauración de las imágenes es necesario un criterio de selección de los parámetros de regularización α y γ que discrimine de la mejor manera los detalles de la imagen que pueden parecer ruido. En este trabajo no se consideraron imágenes de gran tamaño; sin embargo, en vista del rendimiento superior del método propuesto, puede ser interesante investigar el desempeño de otros esquemas numéricos para la solución de problemas de PL de gran tamaño, como una implementación basada en la actualización de soluciones básicas de Forrest-Tomlin [31] o métodos de búsqueda multidimensional [32]. Además, dado el carácter convexo del problema aquí tratando, es posible emplear métodos incrementales y de reducción de la varianza para el descenso del gradiente estocástico [33], especialmente usados en problemas de aprendizaje de máquina. Otro trabajo futuro es explorar la selección automática de parámetros de regularización y la incorporación de la estimación del núcleo de borrado en el marco de un problema de programación lineal.
. La adaptación de la técnica de regularización en el problema de programación lineal, para tratar con el mal condicionamiento procedente de la ecuación integral (1) conduce a la obtención de resultados óptimos en la restauración de las imágenes difuminadas por diferentes funciones PSF. Es así, que la penalización de la solución en la norma L1 reduce el ruido en las áreas homogéneas de la imagen y la penalización del gradiente permite preservar mejor los bordes de la imagen obteniendo mejores resultados que con otros métodos usualmente empleados en la literatura. Se observa que para obtener resultados óptimos en la restauración de las imágenes es necesario un criterio de selección de los parámetros de regularización α y γ que discrimine de la mejor manera los detalles de la imagen que pueden parecer ruido. En este trabajo no se consideraron imágenes de gran tamaño; sin embargo, en vista del rendimiento superior del método propuesto, puede ser interesante investigar el desempeño de otros esquemas numéricos para la solución de problemas de PL de gran tamaño, como una implementación basada en la actualización de soluciones básicas de Forrest-Tomlin [31] o métodos de búsqueda multidimensional [32]. Además, dado el carácter convexo del problema aquí tratando, es posible emplear métodos incrementales y de reducción de la varianza para el descenso del gradiente estocástico [33], especialmente usados en problemas de aprendizaje de máquina. Otro trabajo futuro es explorar la selección automática de parámetros de regularización y la incorporación de la estimación del núcleo de borrado en el marco de un problema de programación lineal.
Medidas cuantitativas de la calidad de la restauración
Para evaluar la calidad de las restauraciones se usan tres medidas, dos de ellas son muy usadas en la literatura correspondiente a imágenes. Sean I y R dos matrices que representan a dos imágenes en sus arreglos como píxeles y donde se busca medir que tanto se parece la imagen I a la imagen de referencia R:
Proporción Máxima de Señal a Ruido (PSNR) por sus siglas en inglés (Peak Signal to Noise Ratio). Esta medida se basa en el error cuadrático medio (ECM), calculado como

y tiene en cuenta el mayor valor de intensidad que puede tomar la imagen Max. Si se tienen b bits para representar la imagen entonces
, y el PSNR se calcula como


En este caso la calidad de la restauración es mejor a medida que PSNR(I,R) se hace cada vez más grande.
- Índice de similitud estructural o SSIM por sus siglas en inglés (Structural Similarity Index): este índice evalúa la similitud entre dos imágenes, varía de cero a uno, donde uno significa que las imágenes son la misma y cero que las imágenes no tienen estructuras comunes (ver [34])

donde:
-
son los promedios de las intensidades de Im y Ref respectivamente.

-
son las varianzas de las intensidades de Im y Ref respectivamente.

-
es la covarianza de las intensidades de intensidades de Im y Ref.

- c1 y c2 son parámetros de estabilización.
- Error relativo: en este caso se define

Donde A es una matriz de n x m y sus entradas están dadas por los números a ij con i = 1,…, n y j = 1,…, m. Entonces se define el error relativo como

Acknowledgements
Agradecimientos
Los autores agradecen a los árbitros anónimos por sus valiosos comentarios y sugerencias que contribuyeron para mejorar el manuscrito.
Referencias
License
Copyright (c) 2021 Jorge Mauricio Ruiz Vera

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

![(Imagen degradada con 0,1% de ruido y su restauración, tomado de [22]. (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada.](https://revistas.udistrital.edu.co/index.php/reving/article/download/17240/version/12943/17667/108914/0121-750X-inge-26-02-254-gf1.png)
![Imagen degradada con 0;5% de ruido y sus restauraciones. (a) Imagen original. Tomado de [23], (b) Imagen borrosa, (c) Imagen restaurada con el método Simplex, (d) Imagen restaurada con el método de punto interior.](https://revistas.udistrital.edu.co/index.php/reving/article/download/17240/version/12943/17667/108915/0121-750X-inge-26-02-254-gf2.png)

![Imagen degradada con 0,5% de ruido y sus restauraciones usando el algoritmo de punto interior. Tomado de [24] . (a) Imagen original, (b) Imagen borrosa, (c) Imagen restaurada con el modelo sin regularizar, (d) Imagen restaurada con el modelo regularizado.](https://revistas.udistrital.edu.co/index.php/reving/article/download/17240/version/12943/17667/108917/0121-750X-inge-26-02-254-gf4.png)








2.jpg)










