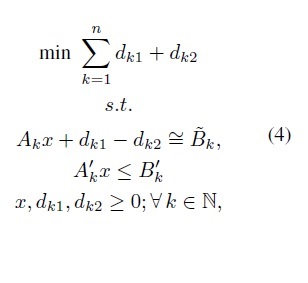
DOI:
https://doi.org/10.14483/23448393.8300Published:
2015-08-10Issue:
Vol. 20 No. 2 (2015): July - DecemberSection:
ArticleAn Approach for Solving Goal Programming Problems using Interval Type-2 Fuzzy Goals
Un Enfoque para Resolver Problemas de Programación de Metas utilizando Intervalo Tipo-2 Objetivos difusos
Keywords:
Fuzzy programming, Type-2 Fuzzy sets, Goal programming (en).Downloads
References
A Charnes and WW Cooper. Management models and industrial applications of linear programming, vol. i, 1961.
Abraham Charnes and William Wager Cooper. Goal programming and multiple objective optimizations: Part 1. European Journal of Operational Research, 1(1):39–54, 1977.
Liang-Hsuan Chen and Feng-Chou Tsai. Fuzzy goal programming with different importance and priorities. European Journal of Operational Research, 133(3):548–556, 2001.
Ting-Yu Chen. An electre-based outranking method for multiple criteria group decision making using interval type-2 fuzzy sets. Information Sciences, 263:1–21, 2014.
Edward L Hannan. On fuzzy goal programming*. Decision Sciences, 12(3):522–531, 1981.
Chaofang Hu, Shaokang Zhang, and Na Wang. Enhanced interactive satisficing method via alternative tolerance for fuzzy goal programming with progressive preference. Applied Mathematical Modelling, 38(19):4673–4685, 2014.
Kaveh Khalili-Damghani, Soheil Sadi-Nezhad, and Madjid Tavana. Solving multi-period project selection problems with fuzzy goal programming based on topsis and a fuzzy preference relation. Information Sciences, 252:42–61, 2013.
George Klir and Bo Yuan. Fuzzy sets and fuzzy logic, volume 4. Prentice Hall New Jersey, 1995.
Gang Li. Fuzzy goal programming–a parametric approach. Information Sciences, 195:287–295, 2012.
Jerry M Mendel. Uncertain rule-based fuzzy logic system: introduction and new directions. Prentice Hall PTR, 2001.
Ram Narasimhan. Goal programming in a fuzzy environment. Decision sciences, 11(2):325–336, 1980.
Jindong Qin and Xinwang Liu. Multi-attribute group decision making using combined ranking value under interval type-2 fuzzy environment. Information Sciences, 297:293–315, 2015.
Turgay Safiye and Tas¸kın Harun. Fuzzy goal programming for health-care organization. Computers & Industrial Engineering, 2014.
Abolfazl Doostparast Torshizi and Mohammad Hossein Fazel Zarandi. A new cluster validity measure basedon general type-2 fuzzy sets: Application in gene expression data clustering. Knowledge-Based Systems, 64:81–93, 2014.
Taeyong Yang, James P Ignizio, and Hyun-Joon Kim. Fuzzy programming with nonlinear membership functions: piecewise linear approximation. Fuzzy sets and systems, 41(1):39–53, 1991.
Zhiming Zhang and Shouhua Zhang. A novel approach to multi attribute group decision making based on trapezoidal interval type-2 fuzzy soft sets. Applied Mathematical Modelling, 37(7):4948–4971, 2013.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
An approach for solving Goal Programming problems using Interval Type-2 fuzzy goals
An approach for solving Goal Programming problems using Interval Type-2 fuzzy goals
Juan Sebastian Patiño-Callejas
Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. juansebastianpatinoc@gmail.com
Krisna Yoel Espinosa-Ayala
Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. joespinosa1018@gmail.com
Juan Carlos Figueroa-García
Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. jcfigueroag@udistrital.edu.co
Recibido:24-03-2015 Modificado:17-06-2015 Aceptado:08-08-2015
Abstract
This paper presents a proposal for solving goal problems involving multiple experts opinions and perceptions. In goal programming problems where no statistical data about their goals exist, the use of information coming from experts becomes the last reliable source. This way, we propose an approach to model this kind of goals using Interval Type-2 fuzzy sets, and a simple method for finding an optimal solution based on previous methods that have been proposed for classical fuzzy sets.
Key words: fuzzy linear programming, Interval Type-2 fuzzy sets, Goal programming
Resumen
Este trabajo presenta un acercamiento a la solución de problemas de programación por metas que incluyen la opinión y percepión de múltiples expertos. En problemas de metas que no tienen información estadística adecuada para definir los valores meta, el uso de información proveniente de expertos se convierte en la última fuente confiable de información. Así pues, proponemos una aproximación al modelado de este tipo de problemas utilizando conjuntos difusos de Intervalo Tipo-2, y un método sencillo para encontrar soluciones usando métodos propuestos por otros autores para conjuntos difusos clásicos.
Palabras claves:Programación lineal difusa, Conjuntos difusos Tipo-2 de intervalo, Programación por metas.
1 Introduction
Decision making in practical applications faces multiple issues, including human being interaction and social behavior. Some problems are built over the base of having multiple goals involving multiple experts that try to solve the same problem with different objectives. To solve this kind of situations, goal programming provides a first tool to find crisp solutions.
To handle the problem of having both multiple experts and uncertainty around the exact value of a desired goal, fuzzy sets appear as a useful tool for handling numerical uncertainty coming from experts. fuzzy goal programming has been proposed by Narasimhan [15], and later developed by Yang [20], Turgay & Takin [18], Li & Gang [12],Hu, Zhang & Wang [9], Khalili-Damghani & Sadi-Nezhad [10], in both theoretical and practical situations.
In decision making, Qin & Liu [17], Zhang & Zhang[21], and Chen&Ting[4]have already used Type-2 fuzzy systems to handle uncertainty coming from multiple experts, so its use in goal programming seems to be feasible.
Based on the model of Narasimhan [15], Yang [20] has proposed a model with fewer variables which obtains the same solution, so what we propose in this paper is to extend their results to a case where multiple experts deal with multiple goals by using Interval Type-2 fuzzy sets to handle linguistic/numerical uncertainty coming from experts and Linear Programming (LP) methods for handling goal programming.
The paper is organized as follows:Section 1 introduces the main problem. Section 2 presents some basics on fuzzy sets. In Section 3, goal programming LP model is referred. Section 4 presents the Yang [20] proposal for fuzzy goal programming. Section 5 contains the proposal; Section 6 shows an application example; and finally Section 7 presents the concluding remarks of the study.
2 Basic on fuzzy sets
According to Klir & Yuan [11], the membership function of a fuzzy set A is denoted by μA :X → [0, 1]. P is the class of all crisp sets, F1 is the class of all fuzzy sets, and F2 is the class of all Type-2 fuzzy sets.
2.1 Interval Type-2 fuzzy Sets (IT2FS)
In general, a Type-2 fuzzy set is simply a function that transforms a set A into the set of fuzzy sets defined over [0, 1], this is à :X → F[0, 1], where F[0, 1] is also known as the secondary membership function of Ã. An Interval Type-2 fuzzy set (see Mendel [13]) is an ordered pair {(x, μà (x)) :x ∈ X }, where A is a linguistic label à that represents uncertainty about the word A. Its mathematical definition is:
where u ∈ Jx ⊆[0, 1] is the domain of uncertainty around A.
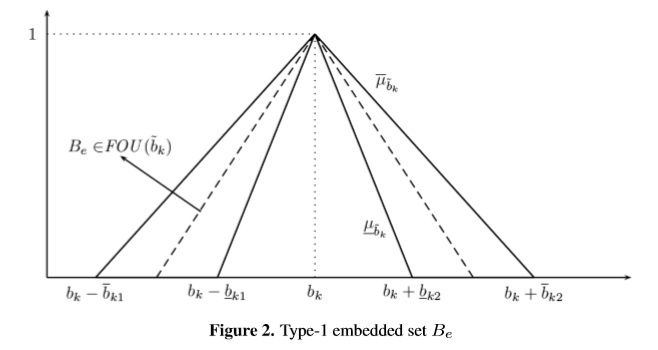
Alternatively, an IT2FS can be fully characterized using two primary membership functions:Lower Membership function (LMF) and Upper Membership function (UMF) in which are contained all embedded fuzzy sets Ae which composes the Footprint of Uncertainty (FOU). Although there are other notations to refer to IT2FSs (see Mendel [14], Türksen [19], and Pagola et al. [16]) who recognize equivalences between Mendel and mathematical standard set notations, we use Mendel notations (see Mendel [13]) due to its interpretability and com- pleteness.
2.2 Why fuzzy Sets?
The main reason for using fuzzy sets is its ability to handle uncertainty coming from human perceptions, which is a common issue in decision making. On the other hand (numerical uncertainty), fuzzy sets can handle imprecision about X which commonly appears when no historical/statistical data is available, so the estimation of the parameters of the problem is based on approximate information coming from the experts of the problem.
3 Goal programming
The basic goal programming model proposed by Charnes, Cooper & Wagner [1], [2] tries to minimize deviations from different goals (desired objectives) through minimizing the absolute deviations dk of the constraints of the problem Akx regarding its desired value (a.k.a goal) Bk in the format min {D = ∑ nk=1|Akx-Bk|}. This model is equivalent to the following LP model (see Charnes, Cooper & Wagner [1], [2]):
where Bk ∈ R is the aspiration level, dk1,dk2 ∈ R are negative and positive deviations from the goal Bk, Ak is the set of n constraints related to goals, A'k is a set of crisp constraints of the problem, B'k is its set of boundaries, and x ∈ Rm is the set of decision variables of the problem. A negative deviation quantifies a lack of satisfaction of the desired aspiration level, and a positive deviation quantifies an excess over the desired aspiration level.
4 fuzzy Goal Programming
Although the first fuzzy goal programming has been proposed by Narasimhan [15], Narasimhan & Hanna [7], Yang [20] has proposed a model with fewer variables which obtains the same solution of [7], [15]. Yang's proposal starts by defining the membership function of the fuzzy goal Bk namely μBk, as follows:
where k ∈ N denotes the kth goal, Gk(x) is the kth constraint to be fulfilled, bk ∈ R is the aspiration level of the kth goal, and dk1 and dk2 are the maximum negative and positive deviations from bk, respectively. Its LP model is
where ∼Bk ∈ F1 the fuzzy aspiration level, dk1,dk2 ∈ R are negative and positive deviations from the goal bk, Ak is the set of n constraints related to fuzzy goals, A'k is a set of crisp constraints of the problem, B'k is its set of boundaries, and x ∈ Rm is the set of decisionvariables of the problem.
Finally, the proposal of Yang [20] is based on a simpler LP model in which G(x) ≡ Akx, as follows:
where λ ∈ [0,1] is the global satisfaction degree of all goals.
This approach uses λ as a global variable that represents the satisfaction of every fuzzy goal μBk. The first constraint represents the satisfaction degree for bk ≤ Gk(x) ≤ bk+bk2 (see Eq. (3)), and the second constraint represents the satisfaction degree for bk -bk1 ≤ Gk(x) ≤ bk (see Eq. (3)). As x is a free variable in this model, it operates over Akx and finally moves λ to its maximum value.
5 Goal programming with Interval Type-2 fuzzy aspiration levels
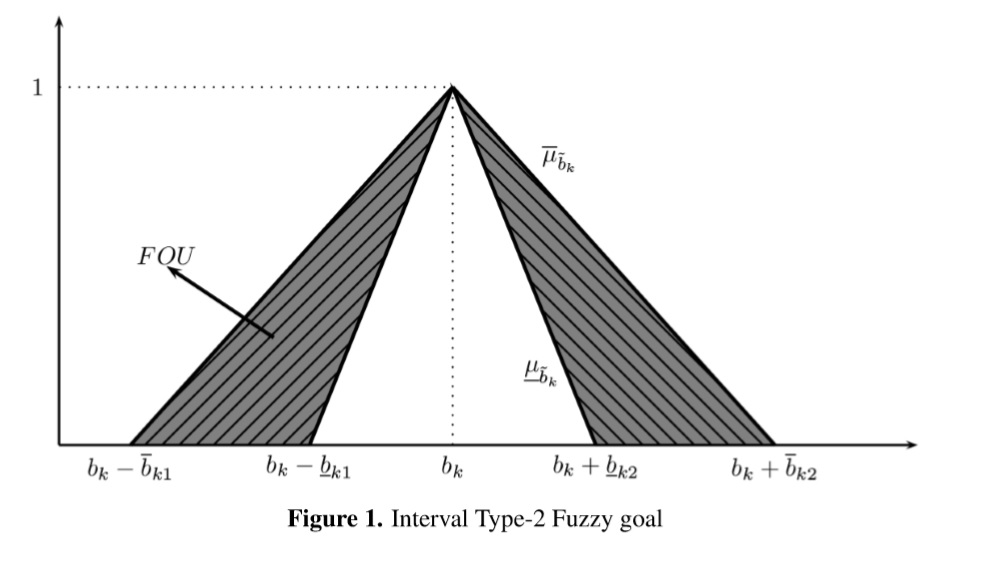
Disagreement among people who are involved into decision making is a common issue in real scenarios. Some people is pessimistic while others are optimistic about different goals. This leads to have different perceptions coming from different experts, so we handle those perceptions using two functions LMF and UMF which are defined as follows:
where ¯μ∼bk defines the UMF of the kth goal, and μ∼bk defines the LMF of the kth goal. A graphical display of a Interval Type-2 fuzzy goal is shown in Figure 1.
Based on (3) and (5), we extend its results to a Interval Type-2 fuzzy environment. Thus, we define the Interval Type-2 fuzzy aspiration level as ˜bk which leads to the following LP model:
where ∼Bk ∈ F2 is the Interval Type-2 fuzzy aspiration level, dk1,dk2 ∈ R are negative and positive deviations from the goal Bk, Ak is the set of n constraints, and x ∈ Rm is the set of decision variables of the problem.
Therefore, we extend the proposal of Yang [20] to a Interval Type-2 fuzzy model using a two-step method that finds two different λ values, one for ¯μ˜b and one for μ˜b. To do so, we have to solve the following two LPs:
where ¯λ is the overall upper satisfaction degree of the goals, and λ is the overall lower satisfaction degree of the goals. Akx is the kth technological constraint, and ¯bk1,bk1,¯bk2,bk2 are the admissible deviations from bk.
Our approach finds two values:min{λ} = λ* and max{¯λ} = ¯λ* that represent pesimistic and optimistic perceptions about bk, and also compose the interval [λ*,¯λ*] = {λ* ∈ [0,1]|λ* ≤ λ* ≤ ¯λ*}of satisfaction of all experts.
6 Experimentation and Results
6.1 Interval Type-2 fuzzy Goals
As application example we use the proposed by Narasimhan [15] and extended by Chen & Tsai [3] which is composed by three fuzzy goals, as shown as follows:
where x1 and x2 are the manufacturing quantities of two products which regard to three goals:G1 is a profitability goal, and G2 , G3 are the expected selling quantities per product. The maximum deviations from Gk = {630, 7, 4} are symmetrically handled where bk1 = bk2 = {10, 2, 2}.
We use those values as the LMF of an extended problem e.g bk1 = bk2 = {10,2,2}, and the UMF is defined using ¯bk1 = ¯bk2 = {15,3,3}. Now, their LPs are based on Eqs. (9) and (10):
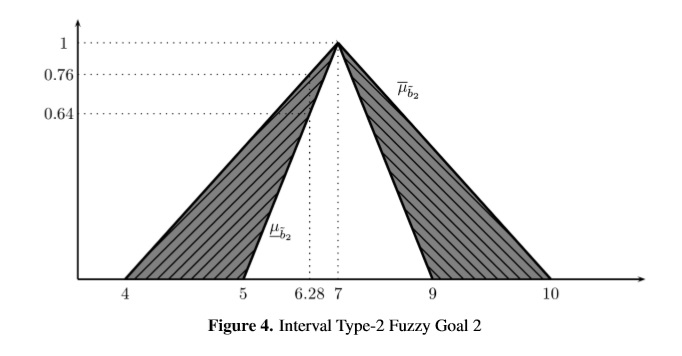
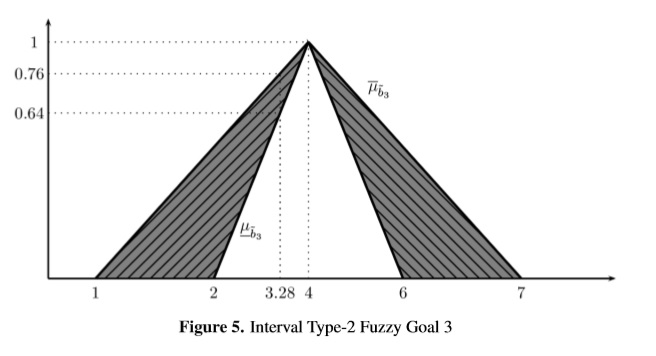
The solution of the model (12) is ¯λ* = 0.76 reached by (x1,x2) = (6.28, 3.28) and the solution of (13) is λ* = 0.64 with (x1,x2) = (6.28, 3.28). A graphical description of the results can be seen in Figures 3, 4 and 5 respectively (see Appendix 1). The optimal value of the goals 1, 2 and 3 are 633.6, 6.28 and 3.28 respectively for both ¯λ* and λ*.
Both models reach the same values of the decision variables x1 and x2 which is a logical solution since all deviations are defined as L1 distances using ¯λ and λ as linear functions of dk1 and dk2. The optimal values ¯λ* = 0.76 and λ* = 0.64 are global satisfaction degrees, which means that all three goals are satisfied at the same level.
Now, we solve another example to illustrate how an embedded Type-1 fuzzy set (Be) into FOU (∼bk ) works. To do so, we have selected the deviations for goals 1, 2 and 3 as 12.5, 2.5, 2.5 which corresponds to the middle point of the support of FOU(∼bk) as shown in Figure 2:
The LP formulation based on Eq. (5) is:
The crisp solution to the problem (14) given Type-1 fuzzy goals is λ*=0.712 which fits into the obtained range [ λ*= 0.64, ¯λ* = 0.76] obtained through (9) and (10). Also note that any Be ∈ F1 embedded into supp(∼bk) leads to an optimal satisfaction degree λ* that fits into the range [ λ, ¯λ] as described in the Appendix 2. By continuity of LP models (see Dantzig [5], Hladík [8], and Fiedler et al [6]), if ∼bk ∈ F2 is continuous then its UMF leads to an optimalsolution namely ¯λ* and every Be ∈FOU(∼bk) leads to an optimal satisfaction degree, namely λ* e ∈ [λ, ¯λ].
7 Concluding Remarks
We have presented and solved an extension of the fuzzy goal programming basic model proposed by Narasimhan [15], Yang [20] ,and Chen & Tsai [3] to a Interval Type-2 fuzzy environment, which includes linguistic uncertainty and numerical imprecision coming from multiple experts opinions and perceptions.
Our approach gives the model flexibility to find other kind of solutions in cases where the system has no the ability to fulfill all goals. As higher λ* as closer to the goal the model is. ¯λ and λ describe overall optimistic and pessimistic satisfaction degrees regarding different experts of the system.
There is a relationship among λ*, dk1 and dk2 since as wider ˜bk as higher λ* is, which means higher satisfaction values. In the first example if dk1 and dk2 are increased in a 50% then λ* is increased only in 12%, and if dk1 and dk2 are decreased in a 50% then α* is decreased in 36% (LP formulations for 50% decreased dk1 , dk2 ,¯λ and λ are shown in Appendix 2). Finally, all experts are satisfied into the range [ λ = 0.64, ¯λ = 0.76].
The second example shows an embedded set Ae into FOU(˜bk) whose optimal satisfaction degree λ* fits into the range [λ, ¯λ] as described in the Appendix 2. This helps decision making when having multiple experts and helps to see how different selections of Ae affect the problem.
References
1. A. Charnes and W. W. Cooper. Management models and industrial applications of linear programming, vol. i, 1961.
2. Abraham Charnes and William Wagner Cooper. Goal programming and multiple objective optimizations:Part 1. European Journal of Operational Research, 1(1):39-54, 1977.
3. Liang-Hsuan Chen and Feng-Chou Tsai. fuzzy goal programming with different importance and priorities. European Journal of Operational Research, 133(3):548-556, 2001.
4. Ting-Yu Chen. An electre-based out ranking method for multiple criteria group decision making using interval type-2 fuzzy sets. Information Sciences, 263:1-21, 2014.
5. George Dantzig. Linear Programming and Extensions. Princeton University Press, 1963.
6. M. Fiedler, J. Nedoma, J. Ramík, J. Rohn, and K. Zimmermann. Linear Optimization Problems with Inexact Data. Springer-Verlag, 2006.
7. Edward L Hannan. On fuzzy goal programming*. Decision Sciences, 12(3):522-531, 1981.
8. Milan Hladík.Weak and strong solvability of interval linear systems of equations and inequalities. Linear Algebra and its Applications, 438(11):4156-4165, 2013.
9. Chaofang Hu, Shaokang Zhang, and Na Wang. Enhanced interactive satisficing method via alternative toler- ance for fuzzy goal programming with progressive preference. Applied Mathematical Modelling, 38(19):4673- 4685, 2014.
10. Kaveh Khalili-Damghani, Soheil Sadi-Nezhad, and Madjid Tavana. Solving multi-period project selection problems with fuzzy goal programming based on topsis and a fuzzy preference relation. Information Sciences, 252:42-61, 2013.
11. George Klir and Bo Yuan. fuzzy sets and fuzzy logic, volume 4. Prentice Hall New Jersey, 1995.
12. Gang Li. fuzzy goal programming-a parametric approach. Information Sciences, 195:287-295, 2012.
13. Jerry M Mendel. Uncertain rule-based fuzzy logic system:introduction and new directions. Prentice Hall PTR, 2001.
14. Jerry M. Mendel. On centroid computations for Type-2 fuzzy sets. Appl. Comput. Math., 10(1):88-96, 2011.
15. Ram Narasimhan. Goal programming in a fuzzy environment. Decision sciences, 11(2):325-336, 1980.
16. M. Pagola, C. Lopez-Molina, J. Fernandez, E. Barrenechea, and H. Bustince. Interval type-2 fuzzy sets con- structed from several membership functions. application to the fuzzy thresholding algorithm. IEEE Transac- tions on fuzzy Systems, 21(2):230-244, 2013.
17. Jindong Qin and Xinwang Liu. Multi-attribute group decision making using combined ranking value under interval type-2 fuzzy environment. Information Sciences, 297:293-315, 2015.
18. Turgay Safiye and Taskin Harun. fuzzy goal programming for health-care organization. Comp. & Ind. Eng., 2014.
19. I.B. Türksen. Interval valued fuzzy sets based on normal forms. fuzzy Sets and Systems, 20(2):191-210, 1986.
20. Taeyong Yang, James P Ignizio, and Hyun-Joon Kim. fuzzy programming with nonlinear membership functions:piecewise linear approximation. fuzzy sets and systems, 41(1):39-53, 1991.
21. Zhiming Zhang and Shouhua Zhang. A novel approach to multi attribute group decision making based on trapezoidal interval type-2 fuzzy soft sets. Applied Mathematical Modelling, 37(7):4948-4971, 2013.
A Appendix 1
This appendix contains the results of the optimization process for the first Interval Type-2 fuzzy goals example.
B Appendix2
This appendix shows the model of the Type-1 example shown in Section 6 where bk1 = bk2 = {5, 1, 1} and ¯bk1 = ¯bk2 = {10, 2, 2}:
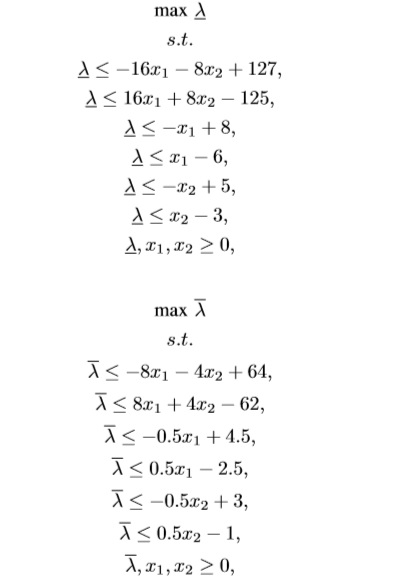
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

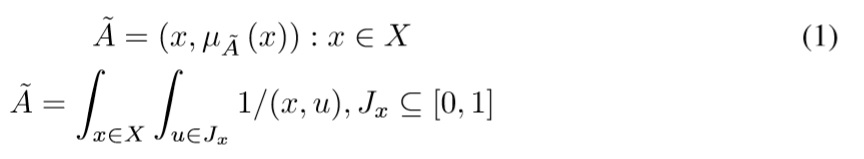
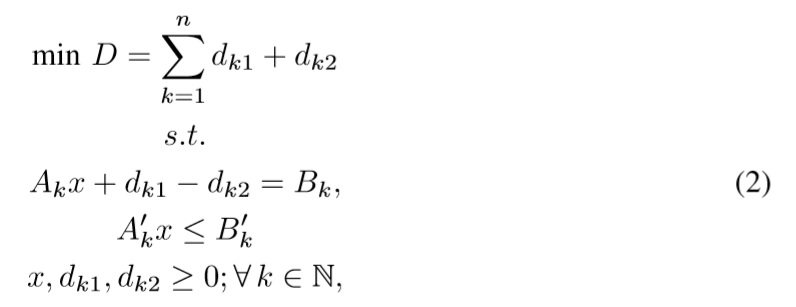
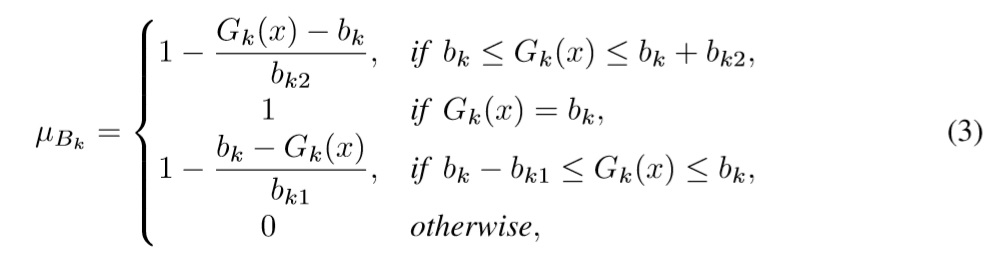
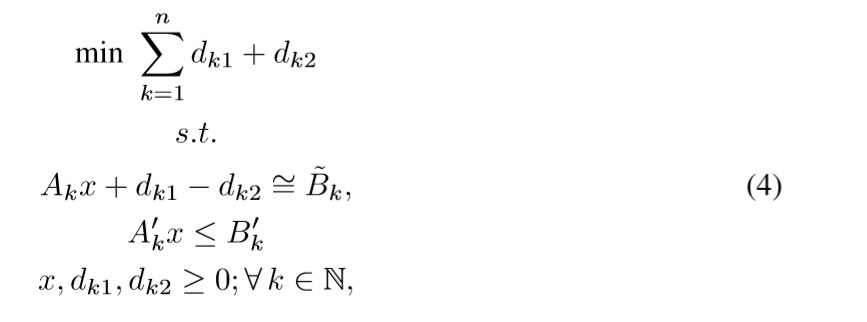
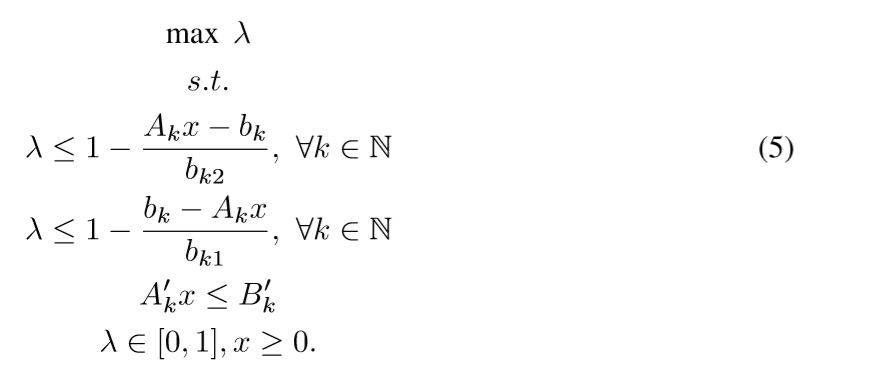
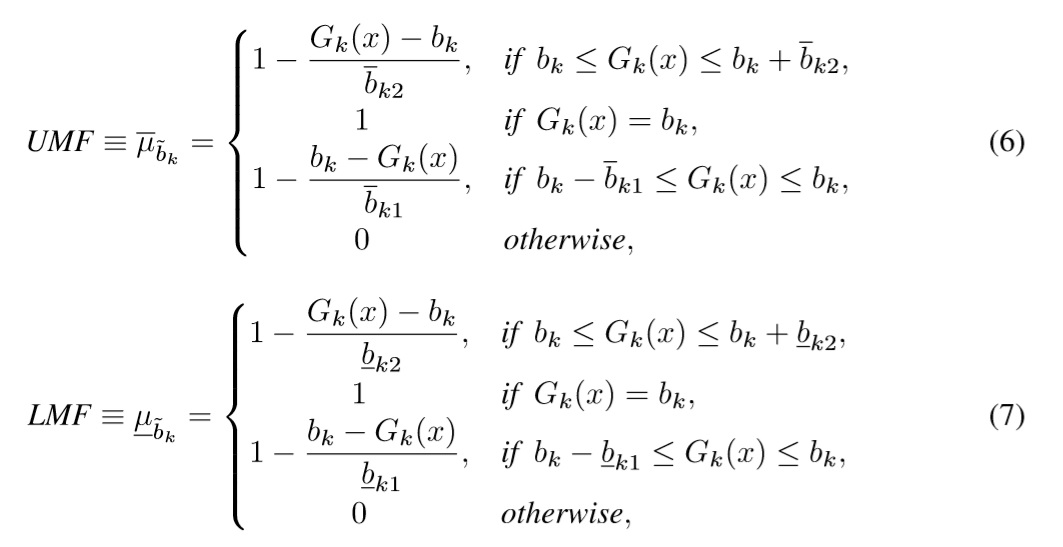
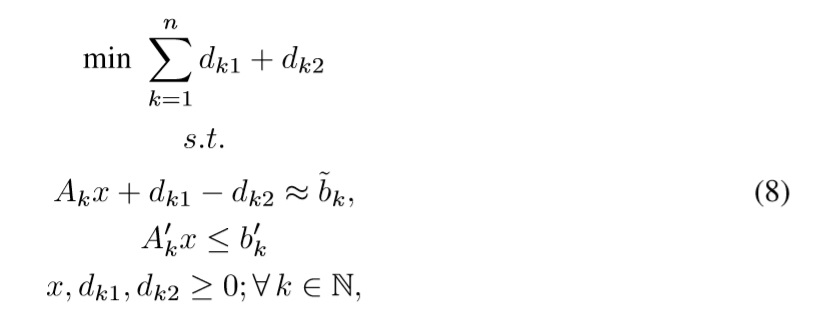
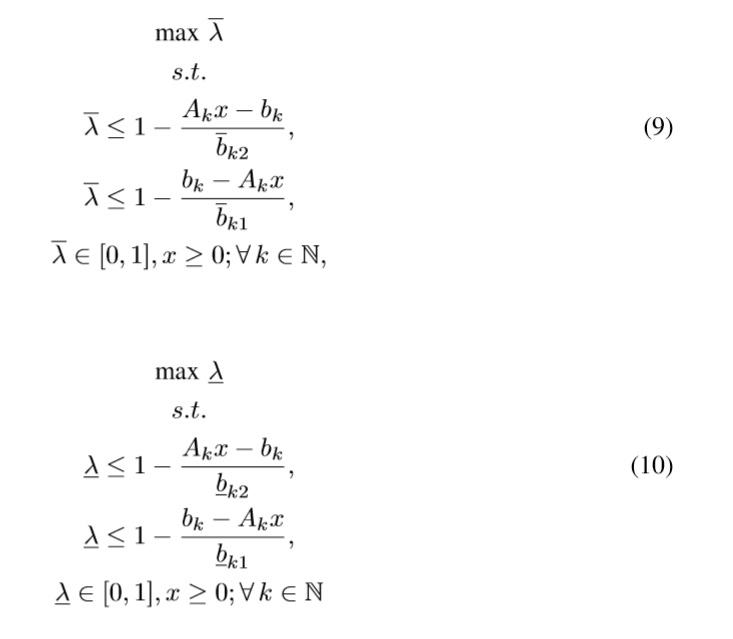
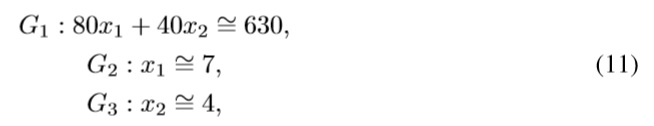

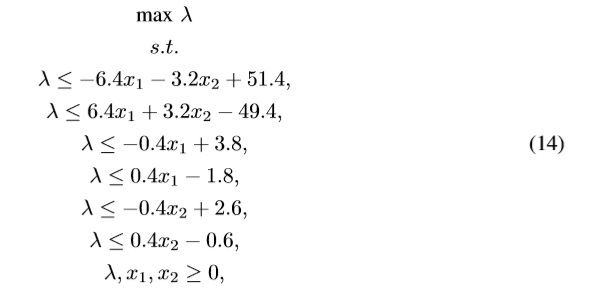




2.jpg)










