DOI:
https://doi.org/10.14483/23448393.18883Published:
2023-04-29Issue:
Vol. 28 No. 2 (2023): May-AugustSection:
Computational IntelligenceIncertidumbre epistémica y aleatoria en soft metrología: una perspectiva desde el aseguramiento de la validez de los resultados
Aleatoric and Epistemic Uncertainty in Soft Metrology: A Perspective Based on Ensuring the Validity of Results
Keywords:
soft metrology, epistemic uncertainty, random uncertainty, learning machines (en).Keywords:
soft metrología, incertidumbre epistémica, incertidumbre aleatoria, máquinas de aprendizaje (es).Downloads
References
M. Vallejo, C. de la Espriella, J. Gómez-Santamaría, A. F. Ramírez-Barrera y E. Delgado-Trejos, “Soft metrology based on machine learning: A review,” Meas. Sci. Tech., vol. 31, no. 3, pp. 1-16, 2020. https://doi.org/10.1088/1361-6501/ab4b39 DOI: https://doi.org/10.1088/1361-6501/ab4b39
L. Rossi, “Objectifying the subjective: Fundaments and applications of soft metrology,” en New Trends Developments in Metrology, L. Cocco, ed., London: IntechOpen, 2016, pp. 255-281. https://doi.org/10.5772/64123 DOI: https://doi.org/10.5772/64123
“ISO/IEC 17025:2017 General requirements for the competence of testing and calibration laboratories,” International Organization for Standardization, 2017.
“Guide to the expression of measurement uncertainty,” Joint Committee for Guides in Metrology (JCGM), 2008, pp. 1-142.
“Evaluation of measurement data — Supplement 1 to the ‘Guide to the expression of uncertainty in measurement’ — Propagation of distributions using a Monte Carlo method,” Joint Committee for Guides in Metrology (JCGM), 2008.
Y. Wang, S. Wang y C. Decès-Petit, “A Bayesian method for on-line evaluation of uncertainty in measurement of Coriolis flow meters,” Measurement, vol. 179, p. 109448, 2021. https://doi.org/10.1016/j.measurement.2021.109448 DOI: https://doi.org/10.1016/j.measurement.2021.109448
Y. Cheng, X. H. Chen, H. L. Li, Z. Y. Cheng, R. Jiang, J. Lü y H. D. Fu, “Analysis and comparison of Bayesian methods for measurement uncertainty evaluation,” Math. Prob. Eng., vol. 2018, no. 3, pp. 1-10, 2018. https://doi.org/10.1155/2018/7509046 DOI: https://doi.org/10.1155/2018/7509046
J. D. Molina-Muñoz, L. F. Giraldo-Jaramillo y E. Delgado-Trejos, “Bayesian evaluation for uncertainty of indirect measurements in comparison with GUM and Monte Carlo,” Ing. Univ., vol. 26, pp. 1-26, Jul. 2022. https://doi.org/10.11144/Javeriana.iued26.beui DOI: https://doi.org/10.11144/javeriana.iued26.beui
T. Dietz et al., “Introducing multiobjective complex systems,” Eur. J. Operat. Res., vol. 280, no. 2, pp. 581-596, Jan. 2020. https://doi.org/10.1016/j.ejor.2019.07.027 DOI: https://doi.org/10.1016/j.ejor.2019.07.027
C. Cai, J. Wang y Z. Li, “Assessment and modelling of uncertainty in precipitation forecasts from TIGGE using fuzzy probability and Bayesian theory,” J. Hydrology, vol. 577, p. 123995, Oct. 2019. https://doi.org/10.1016/j.jhydrol.2019.123995 DOI: https://doi.org/10.1016/j.jhydrol.2019.123995
S. F. dos Santos y H. S. Brandi, “Application of the GUM approach to estimate uncertainty in measurements of sustainability systems,” Clean Technol. Environ. Policy, vol. 18, no. 2, pp. 493-505, Feb. 2016. https://doi.org/10.1007/s10098-015-1029-3 DOI: https://doi.org/10.1007/s10098-015-1029-3
S. Vemulapalli y S. K. Venkata, “Soft sensor for an orifice flowmeter in presence of disturbances,” Flow Meas. Inst., vol. 86, p. 102178, 2022. https://doi.org/10.1016/j.flowmeasinst.2022.102178 DOI: https://doi.org/10.1016/j.flowmeasinst.2022.102178
J. Xu, D. Fu, L. Shao, X. Zhang y G. Liu, “A soft sensor modeling of cement rotary kiln temperature field based on model-driven and data-driven methods,” IEEE Sensors J., vol. 21, no. 24, pp. 27632-27639, 2021. https://doi.org/10.1109/JSEN.2021.3116937 DOI: https://doi.org/10.1109/JSEN.2021.3116937
H. Roh et al., “Development of the virtual metrology for the nitride thickness in multi-layer plasma-enhanced chemical vapor deposition using plasma-information variables,” IEEE Trans. Semicond. Manu., vol. 31, no. 2, pp. 232-241, 2018. https://doi.org/10.1109/TSM.2018.2824314 DOI: https://doi.org/10.1109/TSM.2018.2824314
Z. He, J. Qian, J. Li, M. Hong y Y. Man, “Data-driven soft sensors of papermaking process and its application to cleaner production with multi-objective optimization,” J. Cleaner Prod., vol. 372, p. 133803, 2022. https://doi.org/10.1016/j.jclepro.2022.133803 DOI: https://doi.org/10.1016/j.jclepro.2022.133803
P. Kadlec, B. Gabrys y S. Strandt, “Data-driven soft sensors in the process industry,” Comp. Chem. Eng., vol. 33, no. 4, pp. 795-814, 2009. https://doi.org/10.1016/j.compchemeng.2008.12.012 DOI: https://doi.org/10.1016/j.compchemeng.2008.12.012
W. Shao, W. Han, Y. Li, Z. Ge y D. Zhao, “Enhancing the reliability and accuracy of data-driven dynamic soft sensor based on selective dynamic partial least squares models,” Cont. Eng. Pract., vol. 127, p. 105292, 2022. https://doi.org/10.1016/j.conengprac.2022.105292 DOI: https://doi.org/10.1016/j.conengprac.2022.105292
L. Ren, T. Wang, Y. Laili y L. Zhang, “A data-driven self-supervised LSTM-DeepFM model for industrial soft sensor,” IEEE Tran. Ind. Inform., vol. 18, no. 9, pp. 5859-5869, 2022. https://doi.org/10.1109/TII.2021.3131471 DOI: https://doi.org/10.1109/TII.2021.3131471
J.-C. Ren, D. Liu y Y. Wan, “VMD-SEAE-TL-Based Data-Driven soft sensor modeling for a complex industrial batch processes,” Meas., vol. 198, art. 111439, 2022. https://doi.org/10.1016/j.measurement.2022.111439 DOI: https://doi.org/10.1016/j.measurement.2022.111439
Y. Liu y M. Xie, “Rebooting data-driven soft-sensors in process industries: A review of kernel methods,” J. Process Cont., vol. 89, pp. 58-73, 2020. https://doi.org/10.1016/j.jprocont.2020.03.012 DOI: https://doi.org/10.1016/j.jprocont.2020.03.012
M. J. Korczynski y A. Hetman, “A calculation of uncertainties in virtual instrument,” 2005 IEEE Inst. Meas. Technol. Conf. Proc., vol. 3, pp. 1697-1701, 2005. https://doi.org/10.1109/IMTC.2005.1604459 DOI: https://doi.org/10.1109/IMTC.2005.1604459
X. Wenjun, F. Yuguang, Q. Liang y Y. Yunfeng, “Metrological methods for virtual instrument,” 2011 IEEE Int. Conf. Comp. Sci. Autom. Eng., vol. 3, pp. 558-561, 2011. https://doi.org/10.1109/CSAE.2011.5952740 DOI: https://doi.org/10.1109/CSAE.2011.5952740
M. Mowbray et al., “Probabilistic machine learning based soft-sensors for product quality prediction in batch processes,” Chemometrics Intell. Lab. Syst., vol. 228, p. 104616, 2022. https://doi.org/10.1016/j.chemolab.2022.104616 DOI: https://doi.org/10.1016/j.chemolab.2022.104616
L. Frau, G. A. Susto, T. Barbariol y E. Feltresi, “Uncertainty estimation for machine learning models in multiphase flow applications,” Informatics, vol. 8, no. 3, Sep. 2021. https://doi.org/10.3390/informatics8030058 DOI: https://doi.org/10.3390/informatics8030058
L. Song, G. Wang y M. R. Brambley, “Uncertainty analysis for a virtual flow meter using an air-handling unit chilled water valeve,” HVAC&R Res., vol. 19, no. 3, pp. 335-345, 2013. https://doi.org/10.1080/10789669.2013.774890
H. Cheung y J. E. Braun, “A general method for calculating the uncertainty of virtual sensors for packaged air conditioners,” Int J. Refrig., vol. 63, pp. 225-236, 2016. https://doi.org/10.1016/j.ijrefrig.2015.06.022 DOI: https://doi.org/10.1016/j.ijrefrig.2015.06.022
S. Sediva y M. Havlikova, “Comparison of GUM and Monte Carlo method for evaluation measurement uncertainty of indirect measurements,” en Proc. 14th Int. Carpathian Control Conf. (ICCC), pp. 325-329, 2013.
https://doi.org/10.1109/CarpathianCC.2013.6560563 DOI: https://doi.org/10.1109/CarpathianCC.2013.6560563
E. Hüllermeier y W. Waegeman, “Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods,” Machine Learning, vol. 110, no. 3, pp. 457-506, 2021. https://doi.org/10.1007/s10994-021-05946-3 DOI: https://doi.org/10.1007/s10994-021-05946-3
A. Der Kiureghian y O. Ditlevsen, “Aleatory or epistemic? Does it matter?,” Struct. Safety, vol. 31, no. 2, pp. 105-112, 2009. https://doi.org/10.1016/j.strusafe.2008.06.020 DOI: https://doi.org/10.1016/j.strusafe.2008.06.020
M. Combalia, F. Hueto, S. Puig, J. Malvehy y V. Vilaplana, “Uncertainty estimation in deep neural networks for dermoscopic image classification,” en 2020 IEEE/CVF Conf. Comp. Vision Pattern Recog. Work. (CVPRW), 2020, pp. 3211-3220. https://doi.org/10.1109/CVPRW50498.2020.00380 DOI: https://doi.org/10.1109/CVPRW50498.2020.00380
V.-L. Nguyen, M. H. Shaker y E. Hüllermeier, “How to measure uncertainty in uncertainty sampling for active learning,” Machine Learning, vol. 11, pp. 89-122, 2021. https://doi.org/10.1007/s10994-021-06003-9 DOI: https://doi.org/10.1007/s10994-021-06003-9
A. Kendall y Y. Gal, “Kendall, A., & Gal, Y. (2017). What uncertainties do we need in Bayesian deep learning for computer vision? In 31st Conference on Neural Information Processing Systems (NIPS 2017) (Vol. 2017-Decem, pp. 5575–5585). Long Beach, CA, USA.What uncertainties do,” 31st Conf. Neural Info. Proc. Syst. (NIPS 2017), vol. 2017, pp. 5575-5585, Mar.-Dec. 2017.
N. Tagasovska y D. Lopez-Paz, “Single-model uncertainties for deep learning,” en 33rd Conf. Neural Info. Proc. Syst. (NeurIPS 2019), 2019, pp. 1-12.
H. Al Osman y S. Shirmohammadi, “Machine learning in measurement part 2: Uncertainty quantification,” IEEE Inst. Meas. Mag., vol. 24, no. 3, pp. 23-27, 2021. https://doi.org/10.1109/MIM.2021.9436102 DOI: https://doi.org/10.1109/MIM.2021.9436102
K. Posch y J. Pilz, “Correlated parameters to accurately measure uncertainty in deep neural networks,” IEEE Trans. Neural Net. Learning Syst., vol. 32, no. 3, pp. 1037-1051, 2021. https://doi.org/10.1109/TNNLS.2020.2980004 DOI: https://doi.org/10.1109/TNNLS.2020.2980004
A. Lakshminarayanan, B. Pritzel y C. Blundell, “Simple and scalable predictive uncertainty estimation using deep ensembles,” en 31st Conf. Neural Info. Proc. Syst., 2017, pp. 1-12.
E. Daxberger, A. Kristiadi, A. Immer, R. Eschenhagen, M. Bauer y P. Hennig, “Laplace redux - effortless Bayesian deep learning,” Adv. Neural Info. Proc. Syst., vol. 24, pp. 20089-20103, 2021. https://scopus.bibliotecaitm.elogim.com/inward/record.uri?eid=2-s2.0-85131861907&partnerID=40&md5=675aa0e7c27940e7c1aa25272c0fdb09
R. Neal, Bayesian Learning for Neural Networks. New York, NY, USA: Springer-Verlag, 1996. https://doi.org/10.1007/978-1-4612-0745-0 DOI: https://doi.org/10.1007/978-1-4612-0745-0
A. Olivier, M. D. Shields y L. Graham-Brady, “Bayesian neural networks for uncertainty quantification in data-driven materials modeling,” Comp. Meth. App. Mech. Eng., vol. 386, art. 114079, 2021. https://doi.org/10.1016/j.cma.2021.114079 DOI: https://doi.org/10.1016/j.cma.2021.114079
L. V. Jospin, H. Laga, F. Boussaid, W. Buntine y M. Bennamoun, “Hands-on Bayesian neural networks—A tutorial for deep learning users,” IEEE Comp. Intell. Mag., vol. 17, no. 2, pp. 29-48, May 2022. https://doi.org/10.1109/MCI.2022.3155327 DOI: https://doi.org/10.1109/MCI.2022.3155327
R. Feng, “Uncertainty analysis in well log classification by Bayesian long short-term memory networks,” J. Petrol. Sci. Eng., vol. 205, p. 108816, 2021. https://doi.org/10.1016/j.petrol.2021.108816 DOI: https://doi.org/10.1016/j.petrol.2021.108816
V. K. Kurmi, B. N. Patro, V. K. Subramanian y V. P. Namboodiri, “Do not forget to attend to uncertainty while mitigating catastrophic forgetting,” en 2021 IEEE Winter Conf. App. Comp. Vision (WACV), 2021, pp. 736-745. https://doi.org/10.1109/WACV48630.2021.00078 DOI: https://doi.org/10.1109/WACV48630.2021.00078
Y. Gal y Z. Ghahramani, “Dropout as a Bayesian approximation: Representing model uncertainty in deep learning,” Proc. 33rd Int. Conf. Machine Learning, vol. 48, pp. 1050-1059, 2016.
P. D. Wentzell, C. Giglio y M. Kompany-Zareh, “Beyond principal components: A critical comparison of factor analysis methods for subspace modelling in chemistry,” Analyt. Meth., vol. 13, no. 37, pp. 4188-4219, 2021. https://doi.org/10.1039/d1ay01124c DOI: https://doi.org/10.1039/D1AY01124C
M. S. P. B. Ayhan, “Test-time data augmentation for estimation of heteroscedastic aleatoric uncertainty in deep neural networks no title,” en 1st Conf. Med. Imaging Deep Learning, 2018, pp. 1-9.
G. Wang, W. Li, M. Aertsen, J. Deprest, S. Ourselin y T. Vercauteren, “Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks,” Neurocomp., vol. 338, pp. 34-45, 2019. https://doi.org/10.1016/j.neucom.2019.01.103 DOI: https://doi.org/10.1016/j.neucom.2019.01.103
Z. Liu y Z. Han, “Efficient uncertainty estimation for monocular 3D object detection in autonomous driving,” IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, vol. 2021-Sep., pp. 2711-2718, 2021. https://doi.org/10.1109/ITSC48978.2021.9564433 DOI: https://doi.org/10.1109/ITSC48978.2021.9564433
J. Ali, P. Lahoti y K. P. Gummadi, “Accounting for model uncertainty in algorithmic discrimination,” in AIES 2021 - Proc. 2021 AAAI/ACM Conf. AI Ethics Soc., 2021 pp. 336-345. https://doi.org/10.1145/3461702.3462630 DOI: https://doi.org/10.1145/3461702.3462630
E. Redekop and A. Chernyavskiy, “Uncertainty-based method for improving poorly labeled segmentation datasets,” in 2021 IEEE 18th Int Symp. Biomed. Imaging (ISBI), 2021, pp. 1831-1835. https://doi.org/10.1109/ISBI48211.2021.9434065 DOI: https://doi.org/10.1109/ISBI48211.2021.9434065
C. Junhwan, O. Seokmin y B. Joongmoo, “Uncertainty estimation in AVO inversion using Bayesian dropout based deep learning,” J. Petrol. Sci. Eng., vol. 208, p. 109288, 2022. https://doi.org/10.1016/j.petrol.2021.109288 DOI: https://doi.org/10.1016/j.petrol.2021.109288
“JCGM 200:2012. International vocabulary of metrology – Basic and general concepts and associated terms (VIM),” Joint Committee for Guides in Metrology (JCGM), 2012.
M. Vallejo, C. J. Gallego, L. Duque-Muñoz y E. Delgado-Trejos, “Neuromuscular disease detection by neural networks and fuzzy entropy on time-frequency analysis of electromyography signals,” Exp. Syst., vol. 35, no. 4, p. e12274, Aug. 2018. https://doi.org/10.1111/exsy.12274 DOI: https://doi.org/10.1111/exsy.12274
G. K. Nilsen, A. Z. Munthe-Kaas, H. J. Skaug y M. Brun, “Epistemic uncertainty quantification in deep learning classification by the Delta method,” Neural Net., vol. 145, pp. 164-176, Jan. 2022. https://doi.org/10.1016/j.neunet.2021.10.014 DOI: https://doi.org/10.1016/j.neunet.2021.10.014
Y. P. Paisan y J. P. Moret, “La repetibilidad y reproducibilidad en el aseguramiento de la calidad de los procesos de medición,” Tecnol. Quím., vol. 30, no. 2, Mar. 2010. https://tecnologiaquimica.uo.edu.cu/index.php/tq/article/view/994
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 7 de diciembre de 2021; Aceptado: 22 de noviembre de 2022
Resumen
Contexto:
En ingeniería, el modelado para el análisis de riesgo y confiabilidad de los procesos de medición que incluyen rutinas de cómputo exige el análisis de las fuentes y categorías de la incertidumbre, la cual, en este contexto, puede ser clasificada como aleatoria y epistémica.
Método:
Se presenta una revisión de la literatura obtenida de bases de datos como Google Scholar, IEEEXplore y ScienceDirect en cuanto a tendencias y enfoques relacionados con el concepto de incertidumbre, en el marco de la soft metrología, a fin de mejorar la comprensión cuando se tienen restricciones adicionales debido al aseguramiento de la validez de los resultados.
Resultados:
Se exponen conceptos y comparaciones que ayudan a mejorar la comprensión de la incertidumbre epistémica y aleatoria en los procesos de medición de soft metrología y su relación con el aseguramiento de la validez de los resultados, en el marco de las máquinas de aprendizaje.
Conclusiones:
Se concluye que la calidad en la representación de los sistemas de soft metrología es influenciada de manera constante por la incertidumbre aleatoria, y la incertidumbre epistémica exhibe una dinámica descendente cuanto mejor sea el ajuste del modelo con suficientes datos de entrenamiento.
Palabras clave:
soft metrología, incertidumbre epistémica, incertidumbre aleatoria, máquinas de aprendizaje..Abstract
Context:
In engineering, modeling for risk analysis and ensuring the validity of results in systems that include computational routines requires the analysis of the sources and categories of uncertainty, which, in this context, can be classified as aleatoric and epistemic.
Method:
A literature review from databases such as Google Scholar, IEEEXplore, and ScienceDirect is presented herein, analyzing trends and approaches related to the concept of uncertainty within the framework of soft metrology, in order to improve our understanding when there are additional restrictions due to the assurance of the validity of the results.
Results:
This paper presents concepts and comparisons that aid in the understanding of epistemic and random uncertainty in soft metrology measurement processes and the way in which it is related to the assurance of the validity of results within the framework of learning machines.
Conclusions:
Representation quality in soft metrology systems is constantly influenced by random uncertainty, while epistemic uncertainty exhibits descending dynamics when the fit of the model improves with sufficient training data.
Keywords:
soft metrology, epistemic uncertainty, random uncertainty, learning machines.Introducción
La soft metrología se ha definido como un conjunto de modelos y técnicas computacionales que permiten la cuantificación objetiva de magnitudes que son de naturaleza subjetiva, difíciles o costosas de medir, como aquellas de percepción humana o las derivadas de procesos dinámicos 1. La cuantificación puede llevarse a cabo experimentalmente, lo cual posibilita la obtención de uno o más valores cuantitativos, con los que se puede inferir la variable deseada mediante la correlación con otras variables del proceso cuya medición sea más factible 2.
La soft metrología requiere la medición de parámetros físicos y la construcción de un modelo para correlacionarlos con las variables que necesitan ser cuantificadas. En este sentido, existen numerosos desarrollos e implementaciones prácticas. Sin embargo, a pesar de su uso generalizado, solamente unos pocos presentan algún tipo de análisis de la incertidumbre de las variables estimadas 1, lo cual podría representar un problema desde el punto de vista del aseguramiento de la validez de los resultados. Este aseguramiento, por su parte, consiste en recurrir a distintas técnicas que facilitan la obtención de información (datos) para revisar un proceso, que a su vez equivale a una evaluación de los factores que intervienen en la medición y que, por lo general, son registrados para identificar aspectos como la detección de tendencias 3. Convencionalmente, para estimar la incertidumbre existen herramientas no estocásticas, como la Guía para la expresión de la incertidumbre en medición (GUM) 4, y estocásticas, como los métodos de Monte Carlo 5 y bayesianos 6, 7, entre otros. Sin embargo, hay situaciones propias de la soft metrología en las que no es recomendable hacer uso de estos métodos 8, por ejemplo, no linealidades muy marcadas donde se dificulta la predicción de la evolución dinámica 9, o también cuando la distribución de probabilidad de la magnitud de salida no es de tipo normal o de fácil aproximación a esta 10, o se percibe una fuerte dependencia de la naturaleza estadística de las mediciones en la serie de tiempo 11. Ante estas dificultades, es muy conveniente revisar las discusiones que se suscitan alrededor de la estimación de la incertidumbre en aplicaciones de soft metrología, lo cual es un tema abierto en la literatura que fomenta cada vez más el diseño de nuevas investigaciones.
Teniendo en cuenta que es notable la carente formalización de la estimación de la incertidumbre asociada a los espacios de representación de las máquinas de aprendizaje automático usadas en las aplicaciones de soft metrología, este artículo presenta una revisión sistemática de la literatura enfocada a la estimación de la incertidumbre en sistemas de soft metrología basados en datos, con el fin de comprender los antecedentes e identificar oportunidades de investigación relacionadas con el tamaño de los datos, los modelos de aprendizaje y la comprensión fenomenológica de las variables a medir, en el marco del aseguramiento de la validez de los resultados.
Metodología
La primera fase de la revisión de literatura se basó en una búsqueda de artículos científicos en las bases de datos de Science Direct, IEEE y Google Scholar, con el fin de conocer pruebas de laboratorios, estudios y avances científicos asociados al tema de análisis de este artículo. En síntesis, se buscaron y exploraron tendencias de investigación de soft metrología y estimación de la incertidumbre para el aprendizaje automático, de lo cual se obtuvieron los resultados que se muestran en la Tabla I. Para esta búsqueda, se emplearon las siguientes palabras claves en inglés: “soft metrology”, “soft sensor”, “uncertainty estimation”, “virtual sensor”, “machine learning”, “virtual metrology”, “epistemic uncertainty”, “aleatoric uncertainty”, “ensuring the validity of results”, solas y en combinaciones, según fuera el caso.
Tabla I: Resultados de la búsqueda bibliográfica en las principales bases de datos

La búsqueda en las bases de datos comenzó el 27 de julio de 2021 y, durante este periodo, se hizo la revisión de la documentación con enfoque en incertidumbre, máquinas de aprendizaje automático, procesamiento de datos y diseño de soft sensores, por lo que se incluyeron diferentes filtros, con el fin de hacer más específica la selección de artículos.
El criterio y justificación de la información seleccionada en este estudio se sustentó en la revisión y análisis que se hizo en el marco de las siguientes preguntas de investigación:
-
¿Qué discusiones conduce la literatura hacia el análisis de incertidumbre epistémica y aleatoria cuando se involucran los espacios de representación de las máquinas de aprendizaje automático?
-
¿Cómo aporta el tamaño de los datos, el modelo de entrenamiento y la comprensión fenomenológica al análisis general de la incertidumbre en el marco del aseguramiento de la validez de los resultados en aplicaciones de soft metrología?
-
¿En qué medida el análisis de la incertidumbre, que incluye como fuente adicional la inducida por los espacios de representación de las máquinas de aprendizaje, interviene en los procesos de medición y se proyecta a futuro para las aplicaciones de soft metrología?
Como se muestra en la Fig. 1, con estas preguntas se identificaron tendencias y enfoques en cuanto a la relación de concepto y procedimiento del análisis de incertidumbre, así como el aseguramiento de la validez de los resultados en el marco de las máquinas de aprendizaje automático y, en general, la comprensión de los procesos de soft metrología. La selección final de información quedó constituida por 54 documentos que cubrieron principalmente el periodo entre 2018 y 2022, aunque se incluyeron algunos documentos desde 2005 que resultaron relevantes por ser referentes importantes en la temática tratada.
Figura 1: Etapas de la metodología de la revisión
Resultados
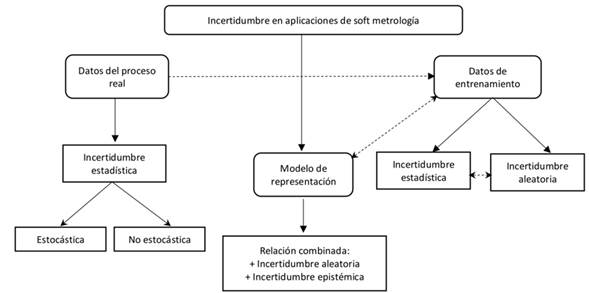
Al revisar la literatura encontrada, según los criterios explicados en la Sección 2, puede inferirse un esquema para los componentes de incertidumbre en sistemas de soft metrología, como el que se presenta en la Fig. 2 y a partir del cual se estructura el resto de la sección.
Figura 2: Diagrama de bloques del mapa conceptual
Análisis de incertidumbre en soft metrología
Hay dos enfoques importantes usados para el desarrollo de un sistema de soft metrología: el primero se establece como un enfoque basado en modelos físicos, el cual parte del conocimiento fenomenológico del proceso analizado 12, 14; el segundo es un enfoque a partir de datos que recurre a la información observada del proceso analizado (bases de datos estructuradas) para la generación del modelo 15), (18. Si bien, con las fortalezas que ofrecen los sistemas de cómputo de última generación, el enfoque derivado de los datos ha sido ampliamente investigado y probado 19, (20, el procesamiento de datos históricos mediante inteligencia computacional trae consigo diferentes retos, que actualmente siguen abiertos en la comunidad científica, para lograr cada vez mejores modelos de medición indirecta en cuanto a costo y precisión 1).
En términos del concepto de soft metrología, no es frecuente encontrar artículos cuyo foco principal sea la estimación de la incertidumbre. Algunos trabajos presentan métodos para esta, en sistemas de medición mediados por software 21, 22, pero estos no incluyen un proceso de inferencia. No obstante, lo que se ha podido observar es que el análisis es aplicable a los sistemas de soft metrología en cuanto a la parte comprendida por el sistema de adquisición de datos y los modelos de procesamiento mediante herramientas digitales. Adicionalmente, se reportan una serie de componentes que aportan a la incertidumbre del sistema, como el error de conversión, error del modelo matemático y error de cálculo (como es el redondeo). En cuanto a los sistemas de soft metrología en sí -por ejemplo, aquellos que incluyen un proceso de inferencia-, solo algunos trabajos reportan resultados relacionados con incertidumbre: algunos se concentran en la incertidumbre exclusivamente desde el punto de vista de la creación del modelo, sin considerar la propagación de las diferentes fuentes de incertidumbre 23, 24, mientras que aquellos que sí consideran una incertidumbre desde la metrología analizan solamente sistemas con enfoque basado en modelos físicos 25),(26. En 25 se presenta un análisis de incertidumbre aplicado a un caudalímetro virtual, y en 26 se reporta un método para estimar la incertidumbre de sensores virtuales para aire acondicionado. En estos dos trabajos, se encuentra que, en general, las principales fuentes de incertidumbre pueden dividirse en dos: las relacionadas con la medición de las características que serán las entradas en la medición indirecta (uso de sensores físicos) y las que surgen del modelo de inferencia de variables (uso de métodos analíticos). Debe aclararse que los enfoques basados en el modelado físico no consideran la incertidumbre asociada a la base de datos necesaria para el entrenamiento que se exige en los enfoques basados en datos, la cual debería incluirse, puesto que también afecta la incertidumbre combinada del modelo.
La incertidumbre asociada a los sensores físicos corresponde a la que típicamente debe ser estimada en los sistemas de metrología convencional. Sin embargo, los modelos matemáticos en algunos sistemas son complejos y la aplicación de la metodología GUM conlleva muchos inconvenientes. Por esta razón, los métodos estocásticos y no estocásticos a veces se combinan, dando como resultado un modelo de estimación de incertidumbre simplificado 27.
Los procedimientos en este tipo de incertidumbre están bien definidos, aunque debe aclarase que las especificidades dependen de la magnitud a medir. Con esto en mente, en el resto de este documento se enfatizará en las incertidumbres asociadas al modelo de inferencia y, por tanto, a los datos usados para entrenamiento. La literatura encontrada, y que se referenciará en adelante, muestra que dicha incertidumbre ha sido estudiada desde las perspectivas del entrenamiento de las máquinas de aprendizaje, pero no se ha formalizado desde el punto de vista metrológico con sus implicaciones en sistemas de medición indirecta.
Como en cualquier aplicación del aprendizaje de máquina, los sistemas de soft metrología buscan crear un modelo que aproxime la relación fenomenológica entre las variables de entrada y la magnitud cuyo valor quiere inferirse y, por tanto, implican las mismas incertidumbres inherentes a un modelo que es una aproximación imperfecta a la dinámica fenomenológica, debido a las múltiples suposiciones que se asumen. Entre estas incertidumbres, se pueden incluir aquellas asociadas con la inferencia inductiva o con el ruido en los datos, las derivadas de suposiciones incorrectas en la generación del modelo, entre otras 28.
Existen muchas fuentes de incertidumbre en el entrenamiento de máquinas de aprendizaje, tradicionalmente modeladas de forma probabilística. Sin embargo, la generalización del uso de sistemas basados en aprendizaje implica requerimientos de calidad y seguridad que obligan a diferenciar entre las componentes de incertidumbre que son susceptibles de ser minimizadas y aquellas que no lo son, lo que conduce a una categorización en incertidumbre epistémica y aleatoria 29.
La incertidumbre epistémica es aquella derivada de los parámetros del modelo y se relaciona con la dificultad para inferir correctamente la función generadora de los datos subyacentes 30, 31. Así, la incertidumbre epistémica se entiende como aquella derivada de la falta de conocimiento sobre la dinámica del proceso. Por consiguiente, puede afirmarse que es, por naturaleza, factible de ser reducida, ya sea mediante la consecución de una base de datos más robusta, un cambio en las hipótesis realizadas sobre la forma del modelo o, en general, un mejor ajuste de los parámetros del modelo.
En contraste, la incertidumbre aleatoria se deriva de elementos no determinísticos e inherentemente aleatorios en la dinámica del proceso. Por tanto, esta incertidumbre se considera irreducible y se ha relacionado con el ruido en las observaciones y la influencia de variables ocultas o errores de medición 32, 33.
Las incertidumbres se formalizan como distribuciones de probabilidad sobre los parámetros del modelo (para el caso de la epistémica) o las entradas del modelo (para la aleatoria) 32. Esta clasificación en las fuentes de incertidumbre se ha generalizado en la literatura sobre la incertidumbre en inteligencia computacional, y su separación es bastante evidente, aunque algunos trabajos advierten que la noción de “lo que puede ser reducible” en cuanto a la incertidumbre se puede convertir en un concepto difuso y depender fuertemente del contexto al ser analizada en detalle. En este sentido, se recomienda que el análisis se realice en cada contexto, a la luz del modelo planteado 29, en consideración de qué cambios en la estructura del modelo pueden modificar las condiciones de incertidumbre. Por ejemplo, en ejercicios de clasificación, añadir características al modelo, aumentando la dimensionalidad del espacio de representación, puede disminuir la incertidumbre aleatoria, lo que incrementa al mismo tiempo la epistémica 28.
Incertidumbre epistémica
La incertidumbre epistémica se relaciona con la densidad de los ejemplos o muestras disponibles para el entrenamiento, la elección de la forma del modelo y la falta de datos adecuados para el entrenamiento en algunas áreas del espacio de entrada 29) ,(34 ,35.
Este tipo de incertidumbre se modela colocando una distribución previa sobre las ponderaciones W del modelo y capturando cuánto varían estas ponderaciones según la dinámica de los datos 36. Por ejemplo, las redes neuronales bayesianas (BNN) proporcionan un marco de principios matemáticos para este tipo de incertidumbre 30. En efecto, sea fW (x) la salida de la red neuronal, de manera que la inferencia bayesiana es usada para calcular una distribución posterior sobre los pesos p(W|X, Y ), de acuerdo con los datos de entrenamiento (X, Y ), donde X y Y son las muestras y las etiquetas respectivamente. A partir de esta distribución posterior, se obtiene la distribución predictiva de una muestra de prueba x, con notación p(y|w, x), y se utiliza para cuantificar la incertidumbre predictiva. Sin embargo, en general, la inferencia bayesiana exacta no es computacionalmente viable para las redes neuronales. Por tanto, en la literatura se han propuesto varias alternativas, tales como la aproximación de Laplace 37, la implementación Monte Carlo de las cadenas de Markov 38 y los métodos bayesianos variacionales 39.
Otros reportes expresan el modelo de la incertidumbre epistémica, desde el método de abandono del tiempo de prueba de Monte Carlo 40, donde se entrena la red neuronal mediante deserción aleatoria (con una tasa de deserción ajustada por métodos heurísticos) para estimar la incertidumbre del modelo respecto a un ejemplo de entrenamiento x, y se usa una deserción en un tiempo de prueba con la misma probabilidad y predicciones múltiples de desempeño {pt = p(y|x, X, Y, Wt)}t=1...T , donde cada predicción es un vector de puntaje para el conjunto de etiquetas del sistema. Las técnicas de abandono se pueden configurar dentro de un esquema de regularización para reducir el sobreajuste de las redes neuronales. Particularmente, la inferencia bayesiana usa la entropía predictiva multiclase para analizar la incertidumbre epistémica del sistema 41,42.
Se han propuesto trabajos que recurren a técnicas y métricas de estimación de incertidumbre para redes neuronales profundas basadas en el muestreo de Monte Carlo y se aplican a problemas de clasificación 36 ,43. Según los resultados, las métricas de incertidumbre pueden ser utilizadas con éxito para detectar muestras fuera de distribución y de difícil integración 30. También, el análisis bayesiano ha reportado buenos resultados al modelar la incertidumbre en redes neuronales convencionales 32.
Incertidumbre aleatoria
La incertidumbre aleatoria tiene que ver, principalmente, con el ruido en las observaciones y puede categorizarse como homocedástica o heterocedástica, si se asume que el ruido es idéntico o diferente en cada una de las entradas al proceso 44,45.
La incertidumbre aleatoria no se reduce mediante un conocimiento más profundo del proceso modelado, como sí puede hacerse con la epistémica, y, como se ha mencionado, se modela mediante una distribución de probabilidades en la salida del modelo de inferencia 32.
En 45 se proponen técnicas de aumento de datos y se presenta la hipótesis de que transformaciones aleatorias simples sobre los datos permiten capturar la incertidumbre heteroscedástica en redes neuronales profundas. Para esto, se reenvían las muestras de entrenamiento varias veces a través de la red neuronal con configuraciones aleatorias de aumento de datos durante el tiempo de prueba. Para cada ejemplo de entrenamiento x, se obtiene {xt}t=1... versiones por aumento de datos, y se reenvían los ejemplos de entrenamiento para obtener un conjunto de predicciones {Pt = p(y|xt, X, Y, W)}t=1...T . En 46 también se trabajan técnicas de aumento de datos en una aplicación de imágenes médicas, donde la incertidumbre aleatoria se modela midiendo qué tan diversas son las predicciones para una imagen sometida a diferentes transformaciones geométricas, para lo cual se asumen tanto la variancia como la entropía de la distribución p(Y |X).
Una forma recurrente para estimar la incertidumbre aleatoria consiste en construir un modelo que se ajuste a la pérdida de información. Así, las predicciones con varianzas altas penalizarán las pérdidas a fin de asegurar que el modelo no se adapte a los datos asociados al ruido 47.
Otros trabajos hacen la distinción entre la incertidumbre epistémica y aleatoria, pero enfocados en identificar los errores de un modelo derivados de la incertidumbre aleatoria, para lo cual proponen que estos deben ser ignorados en el proceso de diseño 48, o re-etiquetar las bases de datos a partir de la incertidumbre aleatoria estimada 49.
Análisis conjunto de la incertidumbre epistémica y aleatoria
Como se ha mencionado, la distinción entre la incertidumbre aleatoria y epistémica puede ser difusa, está determinada por la elección del modelado y es útil para identificar fuentes de incertidumbre que se pueden reducir a corto plazo, a través de la implementación de modelos sólidos de riesgo y confiabilidad, lo cual robustece más los sistemas de toma de decisión 29.
En este sentido, algunos estudios proponen modelos en los que se asume que la incertidumbre aleatoria es conocida 39, pero otros plantean esquemas para analizar ambas incertidumbres de forma simultánea. En 32 se propone un esquema de modelado que permite el análisis, ya sea de las incertidumbres epistémica y aleatoria por separado, o de la combinación en un mismo modelo. Para esto, toman una red neuronal heteroscedástica en la cual el ruido en las observaciones se ha modelado dentro del decrecimiento de los pesos y se pone una distribución de probabilidades sobre los pesos del modelo para modelar la incertidumbre epistémica.
Es interesante encontrar trabajos, como en 50, donde se sugieren aproximaciones bayesianas con realizaciones de abandono con simulación Monte Carlo, con el fin de hacer predicciones y estimar la incertidumbre aleatoria y epistémica, donde la primera permite determinar la localización de datos ruidosos y atípicos, mientras que la segunda ayuda a cuantificar el desempeño del modelo. Además, se encontró que el conocimiento de estas incertidumbres puede reducir el riesgo en la interpretación de las predicciones.
El rol de la incertidumbre en el aseguramiento de validez de los resultados
El aseguramiento de la validez de los resultados busca que la calidad del resultado de medición sea conforme a una referencia que cumpla con los requisitos generales establecidos. Para ello, se pueden tener en cuenta los siguientes elementos 3: valores de referencia, trazabilidad de los resultados, funcionalidad de las técnicas de procesamiento, patrón de referencia, comprobaciones intermedias, repetibilidad y reproducibilidad de las pruebas con los mismos métodos u otros similares, correlación de los resultados para diferentes características, pruebas de datos que son nuevos para el sistema y comparación inter- o intralaboratorio de los resultados. Los resultados deben ser analizados bajo los requerimientos establecidos. Si el intervalo de cobertura se encuentra dentro de las especificaciones, se puede afirmar que hay elementos para establecer la conformidad del resultado de medición; en caso contrario, hay que revisar el sistema de medición y ajustarlo dentro de los criterios de aceptación para evitar el reporte de resultados incorrectos. Aquí es muy importante el concepto de regla de decisión, sobre todo para aquellos casos en que el intervalo de cobertura se encuentra parcialmente fuera de la especificación (por lo general un error máximo permitido) 3.
Los procedimientos asociados al aseguramiento de la validez de los resultados están muy bien entendidos en muchos ámbitos y magnitudes, en particular, en aquellos casos de uso convencional en los que hay riqueza normativa y reglamentos técnicos, pero se van haciendo más confusos en aquellos campos en los que la documentación no está muy bien establecida, donde es común apoyarse en artículos científicos como principal fuente de referencia. Un ejemplo es el enfoque propuesto en este artículo en relación con el análisis de incertidumbre para aplicaciones de procesos de medición en las que se vinculan las máquinas de aprendizaje computacional, donde los espacios de representación involucran incertidumbre epistémica y aleatoria.
Por consiguiente, algunos conceptos que son ampliamente discutidos en el estado del arte, y que relacionan los elementos típicos asociados al aseguramiento de la validez de los resultados, se dirigen a la importancia de contar con la trazabilidad metrológica, la cual es una propiedad de las mediciones y no de los instrumentos 51. Dentro de la cadena jerárquica de trazabilidad metrológica, las calibraciones tienen un rol importante, ya que se constituyen en cada eslabón. En este sentido, el error y la incertidumbre (tanto epistémica como aleatoria) son conceptos esenciales también allí vinculados, incluyendo aquellos procesos que contienen etapas de inferencia o clasificación soportadas en máquinas de aprendizaje y basadas en modelos interpretables profundos, inferencia aproximada y variacional, mecanismos de atención, aprendizaje por transferencia, teoría de información y rutinas de cómputo cuántico, entre otras. En particular, es importante discutir sobre el papel del análisis de relevancia para reducir dimensiones y lograr espacios de representación efectiva 52, donde típicamente se usan ortogonalizaciones basadas en componentes principales, costos basados en teoría de información, modelos generativos y variacionales, entre otros 1. También se deben considerar las técnicas de regularización y los distintos tipos de funciones de costo utilizados en la actualidad en máquinas de aprendizaje, así como su influencia en la cuantificación y mitigación de la incertidumbre.
En este sentido, se ha propuesto combinar las fortalezas de las técnicas de regularización L1 y L2 con el método delta para el análisis de la incertidumbre epistémica en aplicaciones de aprendizaje profundo 53.
Una vez que se cuenta con trazabilidad metrológica para un conjunto de resultados de medición dentro de un proceso determinado, es importante evidenciar el rol que tienen los conceptos de exactitud, veracidad y precisión, en procura de no confundirlos. Allí es importante la calidad de los espacios de representación en soft metrología.
Líneas de trabajo futuro
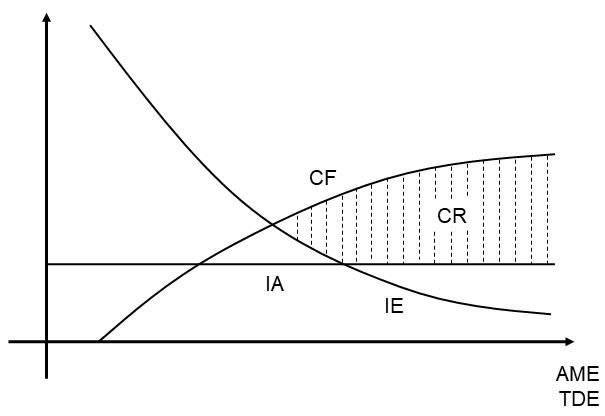
La contribución de la incertidumbre epistémica y aleatoria en la incertidumbre general o global de un proceso de medición debe continuar una línea de trabajo futuro, con enfoque en aquellos esquemas en que los espacios de representación de las máquinas de aprendizaje propagan la incertidumbre debida al ejercicio computacional, donde el valor de la medición se infiere desde estructuras de datos multivariantes. En 1 se presenta una relación entre la calidad en la representación (CR), entendida como la capacidad del modelo para representar la dinámica del sistema estudiado, con dos elementos: el tamaño de los datos de entrenamiento (TDE) y la comprensión del fenómeno (CF), esta última asociada a cómo el modelo puede ajustarse al conocimiento de los expertos sobre el sistema y los factores que afectan la dinámica. La primera relación (CR-TDE) tiene un comportamiento logarítmico directamente proporcional a la calidad en la representación, mientras que la segunda (CR-CF) exhibe un comportamiento intuitivo similar a una curva logística, aunque sigue siendo un tema abierto en la literatura. Al relacionar estos comportamientos, en la Fig. 3 se ilustra de manera conceptual el comportamiento de la incertidumbre aleatoria (IA) y epistémica (IE) en relación con la CR, el TDE y la CF. En esta figura también se hace alusión al concepto AME, que corresponde a una valoración asociada al ajuste del modelo de entrenamiento.
Figura 3: Relación entre calidad en la representación y las incertidumbres epistémica y aleatoria
La Fig. 3 indica una región correspondiente a la calidad en la representación de las máquinas de aprendizaje que soportan la soft metrología, la cual está influenciada por la incertidumbre aleatoria en un nivel constante, mientras la incertidumbre epistémica tiene una dinámica descendente. Los estudios futuros deben validar que esto se debe a que el ruido de representación intrínseco en los datos, asociado a la incertidumbre aleatoria, proviene de las perturbaciones contenidas en todas las componentes fenomenológicas, al ser parte de las dinámicas interactuantes naturales del mundo real, por lo que se considera independiente al ajuste del modelo de entrenamiento y al tamaño de los datos analizados, y por tanto es asumida como una constante en la ilustración. En cambio, queda planteado el hecho de que la incertidumbre epistémica sí se puede corregir mediante la optimización del ajuste de parámetros del modelo y mediante el aseguramiento de suficientes datos de entrenamiento, ayudado del conocimiento que se tenga del fenómeno de análisis, de manera que la cota superior de la calidad de la representación en soft metrología siempre estará dada por el acceso a ese conocimiento. Es de resaltar que, para el aseguramiento de la validez de los resultados (también aseguramiento metrológico), se requiere que la calidad de la representación asociada con la medición vincule dos tipos de precisión, a saber, la repetibilidad y la reproducibilidad (R&R) 54. La primera hace referencia a la precisión en periodos cortos de tiempo y con iguales condiciones de medición constantes, mientras la segunda consiste en la precisión cuando las condiciones de medición cambian y no necesariamente se contemplan periodos cortos de tiempo. Con frecuencia, las pruebas R&R se realizan con el propósito de asegurar la calidad de la medición según el análisis de la reproducibilidad cuando hay un cambio en el operador; aunque es un enfoque válido, se requieren nuevos estudios que profundicen y validen que la reproducibilidad se debe establecer con respecto al cambio de cualquier otra condición. Al final, se busca una compatibilidad en las mediciones, según el enfoque del Vocabulario Internacional de Metrología (VIM) 51. En consecuencia, se requiere la realización de comparaciones inter- o intralaboratorio, con el propósito de validar la competencia del laboratorio en el proceso de medición particular, donde la documentación debe formalizar los detalles experimentales, procedimentales y de análisis 3.
Conclusiones
En este artículo se discute sobre los hallazgos en la literatura relacionados con el análisis de incertidumbre en procesos de medición vinculados a aplicaciones de soft metrología, de manera que se hace la distinción entre incertidumbre epistémica y aleatoria, con el fin de aportar un mejor análisis sobre el papel de la incertidumbre en espacios de representación que están compuestos por conjuntos de variables y diferentes medidas alrededor de un fenómeno. Con esto, es posible obtener otras mediciones que son costosas o no observables en algún proceso particular. En conjunto, se busca favorecer los procesos de medición con máquinas de aprendizaje automático para la toma de decisiones con soporte en inteligencia computacional. Adicionalmente, se relaciona el tamaño de los datos, los modelos de entrenamiento y la comprensión fenomenológica con el análisis de la incertidumbre en el marco del aseguramiento de la validez de los resultados.
Si bien no es frecuente encontrar nuevas propuestas para la estimación de la incertidumbre en aplicaciones de soft metrología basadas en datos, sí existe una literatura amplia que aborda por separado cada una de los principales componentes individuales, por ejemplo, la incertidumbre derivada de los sensores físicos y la asociada a los modelos de inferencia basados en datos. Aquí toma lugar la incertidumbre epistémica y aleatoria, donde esta última hace referencia al ruido de representación que tiene su origen en las frecuencias naturales resultantes de la interacción que tienen todos los subsistemas en el proceso fenomenológico; mientras la primera se asocia a los espacios de representación con los que las máquinas de aprendizaje traducen el comportamiento fenomenológico mediante estructuras multivariadas que conforman el modelo de entrenamiento, de manera que estos espacios son sensibles a la cantidad de los datos, el ajuste adecuado de los parámetros y la selección de variables relevantes en función de una representación efectiva. Por consiguiente, los desafíos que se tienen para cuantificar y mitigar la incertidumbre epistémica en procesos en los que se incluye la inteligencia computacional deben considerar preponderantemente el tamaño de los datos, los ajustes del espacio de representación para el modelo de entrenamiento y la comprensión fenomenológica, además de tomar como factor clave el desarrollo de nuevos esquemas de optimización, regularización y análisis de relevancia orientados a una mayor confiabilidad en los procesos de medición, en el marco del aseguramiento de la validez de los resultados en la soft metrología
Debido a la necesidad de optimizar recursos y operaciones en los procesos productivos, los sistemas metrológicos han requerido el desarrollo de nuevos dispositivos de medición para el control de magnitudes asociadas a fluidos, gases, entre otros, por lo que, en los últimos años, una alta variedad de sensores y actuadores contienen microprocesadores que los convierten en herramientas basadas en datos, que a su vez requieren de una infraestructura de medición como la soft metrología para garantizar una implementación tecnológica eficiente, orientada a procesos de medición que, de forma confiable y segura, se incluyan en sistemas de tomas de decisiones en el marco de la calidad en la representación de mínimo error y concepción de distintas categorías de incertidumbre. En este sentido, las líneas de trabajo futuro se orientan a nuevas propuestas metodológicas que aseguren resultados confiables frente al tamaño de los datos de entrenamiento, robustez frente al ajuste de parámetros del modelo y el espacio de representación, y la vinculación del conocimiento experto en las rutinas de entrenamiento de las máquinas de aprendizaje.
Acknowledgements
Agradecimientos
Este artículo se presenta en el marco del proyecto P17202 y el programa Jóvenes Investigadores e Innovadores, los cuales han sido financiados por el Instituto Tecnológico Metropolitano de Medellín.
Referencias
License
Copyright (c) 2023 Valentina Agudelo-Cardona, Ingrid Natalia Barbosa, Marcela Vallejo, Nelson Bahamón-Cortés, Edilson Delgado-Trejos

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.






2.jpg)










