A Comparative Analysis between FFT, EMD, and EEMD for Epilepsy Detection

Dataset

The dataset used in the signal classification study was acquired from a freely available medical research data repository called Physionet, which contains signals collected from the scalp of intractable seizure patients at Boston Children’s Hospital. This information has been published on the Physionet website ²³.

EEG signals were captured by placing electrodes on the scalp of patients using various configurations ²⁴. The patients included both males and females in the ranges of 3-22 and 1.5-19 years old, respectively. The sampling frequency used was 256 samples per second, with a resolution of 16 bits. The nomenclature of the International 10-20 System was used to define the position of the electrodes on the scalp, with 23 channels available for each analyzed patient.

Fig. 1 shows the location of the electro desaccording to the International 10-20 System Configuration.

Figure 1: Location of electrodes according to the International 10-20 System 25

Experts in the field noted the onset and end of epileptic seizures for each of the recordings ²⁶. In total, 941.6 h of interictal activity and 3 h of ictal activity were analyzed, which corresponded to the 181 seizures described in the database. From this database, we selected the signals with epileptic seizures to perform signal decomposition, obtaining 80 samples.

Signal decomposition methods

For many years, Fourier series analysis was ideal for studying signals in different fields, and it was assumed that conventional methods were sufficient to solve a particular problem ²⁷. With the rise of new technologies, some issues emerged: the composition of signals was affected as more complex signals were being processed, which were assumed to be non-linear and non-stationary. These issues could be solved via traditional methods.

Thus, new signal decomposition methods were developed, such as the fast and the short-term Fourier transforms (FFT and STFT), which performed better but had some limitations ²⁸. Subsequently, HHT emerged as a solution to problems that could not be solved with the previous methods, and researchers were refining and perfecting new strategies that generated better solutions. In this context, EMD and EEMD, nonlinear decomposition methods each with a better response than the previous one, were created. A brief description of FFT, EMD, and EEMD is provided below.

The fast Fourier transform (FFT)

The FT is one of the most widely used tools in engineering applications where the behavior of dynamic systems and periodic signals is studied in the time domain while considering their frequency content ²⁹.

The FFT is an algorithm that allows understanding the behavior of a dataset in the frequency domain, based on the calculation of the discrete FT. Nevertheless, it has disadvantages in spectral analysis, such as aliasing and leakage, as well as with regard to the computation times needed to process data. In addition, it is difficult to detect low frequencies due to its inefficient resolution ¹⁷.

Signal processing and learning methods such as machine learning are valuable tools in EEG signal analysis, as they have been developed to diagnose seizures and epileptic attacks. The research conducted by ³⁰ allowed extracting a set of features from the original signals of two datasets to be analyzed using FT and EMD, with the purpose of classifying and evaluating EEG signals. These authors proposed a methodology to compare the behavior of signal analysis methods using classifiers in order to obtain specific features in the time domain.

The Hilbert-Huang transform (HHT)

The development of HHT arose from the need to describe distorted nonlinear waves combined with variations of the signals that naturally occur in non-stationary processes ³¹. HHT integrates EMD and HT (developed by Huang). In this case, the EMD method decomposes signals into single components called IMFs, from which it is possible to obtain the amplitude a(t) and instantaneous frequencies. This method is widely employed for extracting information from a set of nonlinear and non-stationary data (fi(t)) ³². After this procedure, HT is used to obtain the corresponding Hilbert spectrum (HS).

The HS is a 3D representation of the instantaneous amplitude and the instantaneous frequency for each IMF as a function of time. The HS is defined as follows ²²:

For a general multi-component signal, the HS is defined as the sum of the Hilbert spectra of all the IMFs, as indicated in

where Nis the total number of IMFs.

Empirical mode decomposition EMD

EMD is a tool for the analysis of nonlinear and non-stationary signals, which was proposed by Huang ³³ and aims to decompose a nonlinear and non-stationary signal into a sum of IMFs while satisfying the following criteria ^19,20:

1. In the entire data set, the number of extremes and the number of zero crossings must be equal or differ by 1 at most.

2. At any point, the mean value of the envelopes defined by the local maxima and the local minima is zero.

The second condition implies that an IMF is stationary, which simplifies its analysis. However, an IMF can exhibit changing amplitude and frequency modulation ³⁴.

EMD has some issues, such as the presence of oscillations of unequal amplitude in one or more modes and similar oscillations in different modes, a phenomenon known as mode mixing. The screening process can be summarized in the following algorithm: decompose a dataset x(t) into IMFs xn(t) and a residual r(t), such that the signal can be represented as:

EMD has been adjusted to reduce the mode mixing phenomenon and thus ensure a better identification of the different frequencies in a process or system ³⁵.

The EMDalgorithm for a signal can be summarized as follows ^32,36:

1. Identify all extremes in x(t).

2. Calculate an upper envelope e_u(t) and a lower envelope e_l(t) via interpolation.

3. Determine the local averages as m(t) = (eu(t) + e_m(l))/2.

4. Obtain the residual r(t) = x(t) + m(t).

5. Iterate until the number of zeros equals the number of zero crossings.

6. Subtract the obtained IMF from the original signal.

7. Iterate over the residual until the function becomes monotonic.

The authors of ^30), who used FFT and EMD for signal decomposition, state that it is useful to employ EMD and subsequently extract the IMFs defined by the components of amplitude modulation (AM) and frequency modulation (FM). Nonlinear and non-stationary complex signals can be decomposed into a finite number of IMFs in the spectrum of the Hilbert transform. The authors present the different decomposition modes of EMD. Different classifiers are trained and evaluated to f ind the best methodology.

Ensemble empirical mode decomposition (EEMD)

EEMD arose as an alternative to eliminate mode mixing, the main issue of the EMD. This approach consists of adding noise to the signal, known as white Gaussian noise of finite amplitude, where the real IMF is found as the average of several IMFs ³⁷. Assuming that the added noise is different for each of the IMFs, averaging them over a certain number of attempts should cancel the noise, obtaining a single part and the true IMF.

The proposed algorithm for EEMD is:

1. Add white noise to the signal.

2. Decompose the data added with white noise, using the EMD to obtain the IMFs.

3. Repeat steps 1 and 2 with different white noise in each iteration.

4. Obtain the average of the corresponding IMFs from the decomposition as the final result.

Astudy conducted by ⁶ analyzed EEG recordings using EMD and EEMD with several classifiers to identify the IMFs that best represented an original signal. After the IMF selection process, a set of features was created using IMF1, IMF2, and IMF3. According to the authors, the objective was to propose a hybrid method for IMF selection and explore the effect of these IMFs. Their work evaluated the advantages of using EEMD, decomposing versions of signals with added noise to address EMD’s modemixing issues. This approach yielded better results.

Instantaneous frequency (IF)

The concept of instantaneous frequency has become popular due to its effect on systems related to signal analysis, especially in nonlinear systems, where physical parameters derived from the signals are often characterized. Regardless of their behavior, most signals used to be analyzed via FT, which generates time-invariant frequency and amplitude values ^35,38. As per the analysis proposed by Fourier, the frequency of a signal is derived from its period. However, the frequency of a non-stationary wave is hard to define. It is also possible to define the frequency as the angular velocity associated with the phase change rate. If it is possible to define a phase for a signal, it is possible to calculate its frequency (i.e., IF) ¹⁷.

Signal decomposition using FFT

The FFT method was first implemented in MATLAB.Fig. 3 shows the results obtained after performing signal decomposition on three seizure signals in only one channel. The objective of this article is to show the frequency detected by each of the methods. Thus, three channels were selected, which allow for multiple frequencies.

Figure 3: Signal analysis using FFT

Signals 1 and 3 have several similarities; three maxima stand out at the same time instants i.e., t = 200, 1500, and 3000 s. This can be used to determine the points where seizures may be detected. After the instant t = 1500 s, the spectra does not grow as abruptly as before. Signal 2 does not exhibit notable maxima.

Signal decomposition using EMD

With the EMD method, the IMFs of each signal are obtained. EMD works as a natural filter of the original signals by separating them into frequency components, making it possible to observe the signals of interest. Fig. 4 shows the results obtained by applying EMD to the three signals.

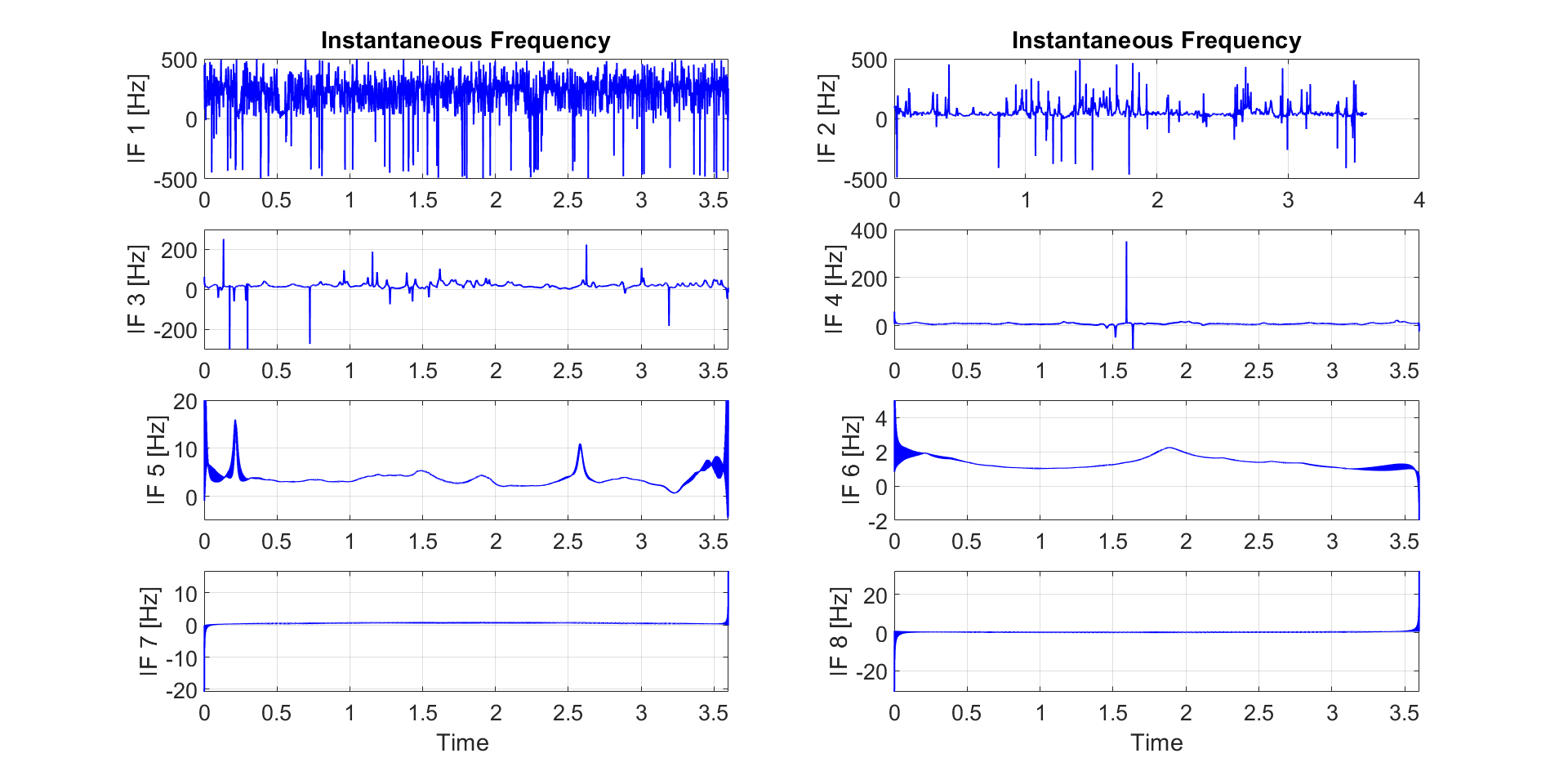
In Fig. 4, IMFs 5 and 6 of signals 1, 2, and 3 clearly show the frequencies of interest for seizure detection. IMF 5 has maximum values of 15-17 Hz, and IMF 6 has maximum values of 8-9 Hz, representing the alpha and beta bands, respectively, i.e., where seizures may occur and where seizures may be initiated. Meanwhile, IMFs 1 and 2 show noise activity, and IMF 4 shows a better separation between modes.

Subsequently, the results corresponding to the IFs of the analyzed signals are obtained. Fig. 5 shows these results.

Figure 4: Signal analysis using EMD

According to Fig. 5, the IF 5 of signals 1, 2, and 3 shows a maximum frequency value that oscillates between 10 and 15 Hz. This is in the alpha band and can be interpreted as an instance where a convulsion occurs.

Figure 5: Signal analysis with IF

Signal decomposition using EEMD

Fig. 6 shows the results obtained with EEMD, where noise is added to each of the signals to obtain a better separation of the IMFs and reduce mode mixing.

Figure 6: Signal analysis using EEM

In Fig. 6, IMFs 4 and 5 show the frequency bands where epileptic seizures may be detected, confirming the results obtained with EMD and IF in Figs. 4 and 5, respectively.

Based on the results obtained via the three signal decomposition methods, the following can be stated. Regarding the use of FFT, the results in Fig. 3 do not allow for a clear visualization of the signals of interest due to interference. Although it is possible to observe two maxima in signals 1 and 3, their meaningcannotbedetermined, whichmakesitdifficult to interpret the results and provide a conclusive answer. The analysis supports the position of ¹⁴, suggesting that each of these methodologies has both advantages and limitations. One of the disadvantages associated with decomposition is its low resolution in the time-frequency domain, which is evident in Fig. 3. In addition, the results of the FFT show alowresolution due to the non-linearity of the signal.

Furthermore, as emphasized in ¹⁵, the results demonstrate the challenges associated with interpreting signals using short time intervals due to their complex dynamics.

In this vein, FFT is not the best method to decompose non-linear and non-stationary signals where harmonic and non-harmonic components can appear. While FFT is still a valuable tool in many signal processing scenarios, its compatibility with signals exhibiting non-linearity and non-stationarity is notably sub-optimal. Thus, alternative methods that provide improved precision and adaptability to such signals should be explored.

On the other hand, when obtaining IMFs and IFs via EMD, the neuronal activity of each channel shows, in greater detail, the frequencies of interest for epileptic seizures occur. In this case, the alpha and beta frequency bands are those of greatest interest. The beta band is represented in IMF 6, and the alpha band in IMF 5. These frequency bands represent the main brain activity for our study, since they represent the onset and course of a seizure. According to the figures, the frequency increases and the amplitude decreases in IMF 5, whereas, in IMF 6, the frequency decreases and the amplitude increases.

Applying EMD has yielded notably improved results compared to the FFT method. Therefore, the authors of ³⁰ chose to employ FFT and EMD to identify the most appropriate method for detecting epileptic seizures. Upon verifying the results, it became evident that employing EMD resulted in greater clarity and improved interpretation. These findings were further corroborated in ³¹, where the acquisition of IMFs validated the significance of conducting this procedure, as it enables the decomposition of a finite number of IMFs in the spectrum of the Hilbert transform, integrating both HT and EMD.

EMD’s adaptability to non-linear and non-stationary signals provides a more accurate representation of the underlying components, enhancing the precision and interpretability of the results.

Using EEMD confirms the results obtained with the IMFs and the IFs of signals 1, 2, and 3. In IMF 5, the alpha band is of greater interest than the others because it enables the clear visualization of neuronal activity over time. Utilizing EEMD in the analysis yields better results than EMD and FFT. EEMD’s ability to address non-linear and non-stationary signal characteristics, coupled with its noise robustness, significantly improved the quality and accuracy of our findings. In comparison with EMD, EEMD’s ensemble approach introduces enhanced stability and precision with regard to mode extraction, mitigating issues such as mode mixing.

Validating the results of ⁶, we found that, by employing EMD while obtaining the IMFs, the EEMD yields results of higher reliability than those provided by EMDalone. Thesefindingsreinforcethenotion that integrating EEMD into the analysis represents a significant advance in terms of the quality and accuracyoftheresults, whichhasimportantimplicationsforthepracticalapplicationofthesetechniques in the field of epileptic seizure detection and diagnosis.

Table I showsthemostsignificant frequency values obtained using each of the signal decomposition methods for epileptic seizure detection. FFT does not allow determining specific frequency values, hindering the interpretation of the results.

Table I: Frequency values obtained with the studied decomposition methods

Finally, Table II shows the strengths and weaknesses of the decomposition methods discussed above.

Table II: Strengths and weaknesses of signal decomposition methods

This study compared the efficacy of three signal processing techniques for epileptic seizure signal analysis. FFT excels in revealing frequency components but may miss nonlinear features. EMD captures nonlinear and non-stationary characteristics but is sensitive to noise, and EEMD, as an extension of EMD, offers improved noise robustness and adaptability to non-stationary signals. This comparative assessment aims to elucidate the strengths and limitations of these methods, aiding researchers in selecting the most suitable approach for their specific epilepsy research needs.