DOI:
https://doi.org/10.14483/23448393.22852Published:
2025-08-31Issue:
Vol. 30 No. 2 (2025): May-AugustSection:
Electrical, Electronic and Telecommunications EngineeringApplying an Optimization Algorithm Based on the Cauchy Distribution for Active and Reactive Power Management with Batteries in Energy Distribution Systems
Aplicación de un algoritmo de optimización basado en la distribución de Cauchy para la gestión de potencia activa y reactiva con baterías en sistemas de distribución de energía
Keywords:
Energy dispatch model, Cauchy-based distribution optimizer, Battery energy storage, Distributed energy resources, Power system optimization (en).Keywords:
modelo de despacho de energía, optimizador basado en la distribución de Cauchy, almacenamiento de energía en baterías, recursos energéticos distribuidos, optimización de sistemas de potencia (es).Downloads
References
L. Trahey, F. R. Brushett, N. P. Balsara, G. Ceder, L. Cheng, Y.-M. Chiang, N. T. Hahn, B. J. Ingram, S.D. Minteer, J. S. Moore et al., “Energy storage emerging: A perspective from the Joint Center for Energy Storage Research,” Proc. Natl. Acad. Sci. USA, vol. 117, no. 23, pp. 12 550–12 557, 2020. https://doi.org/10.1073/pnas.182167211
Y. Yang, S. Bremner, C. Menictas, and M. Kay, “Battery energy storage system size determination in renewable energy systems: A review,” Renew. Sust. Energy Rev., vol. 91, pp. 109–125, 2018. https://doi.org/10.1016/j.rser.2018.03.047
L. F. Grisales-Noreña, B. Cortés-Caicedo, O. D. Montoya, R. I. Bolaños, and C. A. M. Moreno, “Nonlinear programming for BESS operation for the improvement of economic, technical and environmental indices by considering grid-connected and stand-alone networks: An application to the territory of Colombia,” J. Energy Stor., vol. 98, p. 112856, 2024. https://doi.org/10.1016/j.est.2024.112856
A. Valencia, R. A. Hincapie, and R. A. Gallego, “Optimal location, selection, and operation of battery energy storage systems and renewable distributed generation in medium–low voltage distribution networks,” J. Energy Stor., vol. 34, p. 102158, Feb. 2021. https://doi.org/10.1016/j.est.2020.102158
A. Eid, O. Mohammed, and H. El-Kishky, “Efficient operation of battery energy storage systems, electric-vehicle charging stations and renewable energy sources linked to distribution systems,” J. Energy Stor., vol. 55, p. 105644, 2022. https://doi.org/10.1016/j.est.2022.105644
O. D. Montoya, W. Gil-González, R. I. Bolaños, D. F. Muñoz-Torres, J. C. Hernández, and L.F. Grisales-Noreña, “Effective Power Coordination of BESUs in Distribution Grids via the Sine-Cosine Algorithm,” in 2024 IEEE Green Tech. Conf. (GreenTech). IEEE, Apr. 2024. https://doi.org/10.1109/greentech58819.2024.10520484
L. O. P. Vásquez, J. L. Redondo, J. D. Á. Hervás, V. M. Ramírez, and J. L. Torres, “Balancing CO2 emissions and economic cost in a microgrid through an energy management system using MPC and multi-objective optimization,” Appl. Energy, vol. 347, p. 120998, 2023. https://doi.org/10.1016/j.apenergy.2023.120998
J. Elio and R. J. Milcarek, “Multi-objective electricity cost and indirect CO2 emissions minimization in commercial and industrial buildings utilizing stand-alone battery energy storage systems,” J. Cleaner Prod., vol. 417, p. 137987, 2023. https://doi.org/10.1016/j.jclepro.2023.137987
A. Molina, O. D. Montoya, and W. Gil-González, “Exact minimization of the energy losses and the CO2 emissions in isolated DC distribution networks using PV sources,” DYNA, vol. 88, no. 217, pp. 178–184, May 2021. https://doi.org/10.15446/dyna.v88n217.93099
V. Suresh, P. Janik, M. Jasinski, J. M. Guerrero, and Z. Leonowicz, “Microgrid energy management using metaheuristic optimization algorithms,” Appl. Soft Comput., vol. 134, p. 109981, Feb. 2023. https://doi.org/10.1016/j.asoc.2022.109981
S. Sankarananth, M. Karthiga, S. E., S. S., and D. P. Bavirisetti, “AI-enabled metaheuristic optimization for predictive management of renewable energy production in smart grids,” Energy Rep., vol. 10, pp. 1299–1312, Nov. 2023. https://doi.org/10.1016/j.egyr.2023. 08.005
M. Barukˇci´c, T. Varga, T. Benši´c, and V. Jerkovic´ Štil, “Optimal Allocation of Renewable Energy Sources and Battery Storage Systems Considering Energy Management System Optimization Based on Fuzzy Inference,” Energies, vol. 15, no. 19, p. 6884, Sep. 2022. https://doi.org/10.3390/en15196884
T. M. Aljohani, A. F. Ebrahim, and O. Mohammed, “Hybrid Microgrid Energy Management and Control Based on Metaheuristic-Driven Vector-Decoupled Algorithm Considering Intermittent Renewable Sources and Electric Vehicles Charging Lot,” Energies, vol. 13, no. 13, p. 3423, Jul. 2020. https://doi.org/10.3390/en13133423
Y. Yang, S. Bremner, C. Menictas, and M. Kay, “Modelling and optimal energy management for battery energy storage systems in renewable energy systems: A review,” Renew. Sust. Energy Rev., vol. 167, p. 112671, Oct. 2022. https://doi.org/10.1016/j.rser.2022.112671
V. Bhattacharjee and I. Khan, “A non-linear convex cost model for economic dispatch in microgrids,” Appl. Energy, vol. 222, pp. 637–648, Jul. 2018. https://doi.org/10.1016/j.apenergy.2018.04.001
J. Montano, J. P. Guzmán, O. D. Garzón, and A. M. R. Barrera, “Techno-economic approach for energy management system: Multi-objective optimization algorithms for energy storage in standalone and grid-connected DC microgrids,” J. Energy Stor., vol. 102, p. 114069, Nov. 2024. https://doi.org/10.1016/j.est.2024.114069
O. D. Montoya, L. F. Grisales-Noreña, and W. Gil-González, “Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses,” Sustainability, vol. 16, no. 5, p. 2019, Feb. 2024. https://doi.org/10.3390/su16052019
G. Gonzales-Calienes, M. Kannangara, and F. Bensebaa, “Economic and Environmental Viability of Lithium-Ion Battery Recycling—Case Study in Two Canadian Regions with Different Energy Mixes,” Batteries, vol. 9, no. 7, p. 375, Jul. 2023. https://doi.org/10.3390/batteries9070375
L. Chen and A. P. Wemhoff, “Predicting embodied carbon emissions from purchased electricity for United States counties,” Appl. Energy, vol. 292, p. 116898, Jun. 2021. https://doi.org/10.1016/j.apenergy.2021.116898
A. González-Dumar, S. Arango-Aramburo, and C. M. Correa-Posada, “Quantifying power system flexibility for the energy transition in Colombia,” Int. J. Electr. Power Energy Syst., vol. 155, p. 109614, Jan. 2024. https://doi.org/10.1016/j.ijepes.2023.109614
C. Yang, Y. Sun, Y. Zou, F. Zheng, S. Liu, B. Zhao, M. Wu, and H. Cui, “Optimal Power Flow in Distribution Network: A Review on Problem Formulation and Optimization Methods,” Energies, vol. 16, no. 16, p. 5974, Aug. 2023. https://doi.org/10.3390/en16165974
A. Casavola, G. Franzè, D. Menniti, and N. Sorrentino, “Voltage regulation in distribution networks in the presence of distributed generation: A voltage set-point reconfiguration approach,” Electr. Power Syst. Res., vol. 81, no. 1, pp. 25–34, Jan. 2011. https://doi.org/10.1016/j.epsr.2010.07.009
J. Gomes and O. Saavedra, “A Cauchy-based evolution strategy for solving the reactive power dispatch problem,” Int. J. Electr. Power Energy Syst., vol. 24, no. 4, pp. 277–283, May 2002. https://doi.org/10.1016/s0142-0615(01)00039-4
O. D. Montoya, L. F. Grisales-Noreña, and W. Gil-González, “Simultaneous siting and sizing of PVs and D-STATCOMs in medium-voltage grids using the Cauchy-based distribution optimizer,” Results Eng., vol. 25, p. 104407, 2025. https://doi.org/10.1016/j.rineng.2025.04407
A. A. El-Fergany, “Reviews on Load Flow Methods in Electric Distribution Networks,” Arch. Comput. Methods Eng., Oct. 2024. https://doi.org/10.1007/s11831-024-10191-7
N. D. Lagaros, M. Kournoutos, N. A. Kallioras, and A. N. Nordas, “Constraint handling techniques for metaheuristics: a state-of-the-art review and new variants,” Optim. Eng., vol. 24, no. 4, pp. 2251–2298, Jan. 2023. https://doi.org/10.1007/s11081-022-09782-9
S. K. Dinkar and K. Deep, “Opposition-based antlion optimizer using Cauchy distribution and its application to data clustering problem,” Neural Comput. Appl., vol. 32, no. 11, pp. 6967–6995, Apr. 2019. https://doi.org/10.1007/s00521-019-04174-0
M. Wang, J.-S. Wang, X.-D. Li, M. Zhang, and W.-K. Hao, “Harris Hawk Optimization Algorithm Based on Cauchy Distribution Inverse Cumulative Function and Tangent Flight Operator,” Appl. Intell., vol. 52, no. 10, pp. 10 999–11 026, Jan. 2022. https://doi.org/10.1007/s10489-021-03080-0
L. Grisales-Noreña, B. Cortés-Caicedo, O. D. Montoya, J. Hernandéz, and G. Alcalá, “A battery energy management system to improve the financial, technical, and environmental indicators of Colombian urban and rural networks,” J. Energy Stor., vol. 65, p. 107199, Aug. 2023. https://doi.org/10.1016/j.est.2023.107199
W. Gil-González, O. D. Montoya, E. Holguín, A. Garces, and L. F. Grisales-Noreña, “Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model,” J. Energy Stor., vol. 21, pp. 1–8, Feb. 2019. https://doi.org/10.1016/j.est.2018.10.025
V. M. Garrido-Arévalo, O. D. Montoya, W. Gil-González, L. F. Grisales-Noreña, and J. C. Hernández, “An SDP relaxation in the complex domain for the efficient coordination of BESS and DGs in single-phase distribution grids while considering reactive power capabilities,” J. Energy Stor., vol. 90, p. 111913, Jun. 2024. https://doi.org/10.1016/j.est.2024.111913
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 5 de noviembre de 2024; Aceptado: 9 de mayo de 2025
Abstract
Context:
This study developed an energy dispatch model (EDM) using the Cauchy-based distribution optimizer (CbDO) for coordinating battery energy storage units (BESUs) and photovoltaic (PV) sources in medium-voltage distribution networks, aiming to minimize energy losses and operating costs while observing to network constraints.
Method:
The CbDO was implemented in MATLAB and benchmarked against the continuous genetic algorithm (CGA), the parallel particle swarm optimizer, the parallel vortex search algorithm, and a semidefinite programming (SDP) approach. The analyzed scenarios included unitary and variable power factor operation in order to test optimization performance.
Results:
The CbDO outperformed traditional methods, achieving lower energy losses and CO2 emissions, closely matching the SDP method’s results in variable power factor scenarios. The most significant gains were observed when all DERs operated flexibly, validating our proposal’s effectiveness in complex non-convex problems.
Conclusions:
The CbDO is a viable and efficient solution for EDM, providing near-SDP performance with a simpler implementation. BESU integration and f lexible power factor operation can notably enhance grid efficiency.
Keywords:
energy dispatch model, Cauchy-based distribution optimizer, battery energy storage, distributed energy resources, power systems optimization.Resumen
Contexto:
Este estudio desarrolló un modelo de despacho de energía (EDM) utilizando el optimizador basado en la distribución de Cauchy (CbDO) para coordinar unidades de almacenamiento de energía en baterías (BESU) y fuentes fotovoltaicas (PV) en redes de distribución de media tensión, con el fin de minimizar las pérdidas de energía y los costos de operación a la vez que se cumplen las restricciones de la red.
Método:
El CbDO fue implementado en MATLAB y comparado con el algoritmo genético continuo (CGA), el optimizador de enjambre de partículas en paralelo (PPSO), el algoritmo de búsqueda de vórtice en paralelo (PVSA) y un enfoque de programación semidefinida (SDP). Los escenarios analizados incluyeron la operación con factor de potencia unitario y variable, a fin de evaluar el desempeño de la optimización.
Resultados:
El CbDO superó a los métodos tradicionales, logrando menores pérdidas de energía y emisiones de CO2, siguiendo de cerca los resultados del método SDP en los escenarios con factor de potencia variable. Las mayores mejoras se observaron cuando todos los DERs operaban de manera flexible, validando la efectividad de nuestra propuesta en problemas no convexos complejos.
Conclusiones:
El CbDO constituye una solución viable y eficiente para el EDM, ofreciendo un desempeño cercano al del método SDP con una implementación más sencilla. La integración de BESUs y la operación con factor de potencia flexible pueden mejorar significativamente la eficiencia de la red.
Palabras clave:
modelo de despacho de energía, optimizador basado en la distribución de Cauchy, almacenamiento de energía en baterías, recursos energéticos distribuidos, optimización de sistemas de potencia.Introduction
In response to the growing demand for sustainable energy and the urgent need to reduce the carbon footprint associated with traditional power systems, the integration of energy storage systems (ESS) and renewable energy sources (RES) into electrical distribution networks has become increasingly vital 1. Among the various ESS technologies, battery energy storage units (BESUs) are the most prevalent and widely deployed solutions 2. They play a pivotal role in achieving sustainability goals, as they store surplus energy for later use and provide active power support. Additionally, with the help of power electronics, BESUs can supply reactive power to the grid, which enhances their ability to stabilize voltage and improve power quality 3.
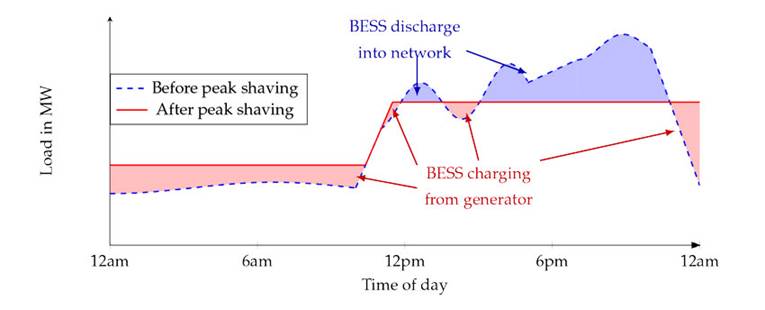
The combined management of active and reactive power through BESUs not only enhances the stability and quality of energy distribution; it also increases the resilience of distribution networks against fluctuations in renewable generation and variable demand 3. However, achieving an optimal control of these systems poses significant challenges, requiring advanced computational and technical strategies to effectively coordinate BESU operations under the dynamic conditions of distributed generation and load variability. The benefits of deploying battery energy storage systems (BESS) in distribution networks are illustrated in Fig. 1. By charging during low-demand periods and discharging during peak load intervals, BESS can effectively perform peak shaving, thereby reducing the need for additional generation capacity and alleviating stress on grid infrastructure. This operational f lexibility not only supports more efficient asset utilization but also contributes to deferring costly grid reinforcements. Moreover, such control actions allow system operators to mitigate short-term power imbalances, reduce the curtailment of renewable sources, and maintain the voltage and frequency within acceptable limits.
Figure 1: Effect of BESS peak shaving on daily load profiles
The literature presents a variety of approaches for managing RES and BESUs in distribution networks. Below are the key contributions in this field.
The authors of 4 proposed an optimal methodology for locating, selecting, and operating BESUs and renewable distributed generators (DGs) in medium- to low-voltage distribution systems. Using a mixed-integer non-linear programming(MINLP)model,theproblemwasdividedintoplanning(device location and selection) and operation (optimal BESS scheme) stages. A simulated annealing algorithm with impedance-based sensitivity analysis was used for planning, while a novel decomposition method efficiently solved the operation problem, with near-globally optimal results. Validations on a 11-node feeder, a modified IEEE 135-node test system, and a real 230-node system confirmed the robustness and effectiveness of this methodology, which was demonstrated through comparative analysis across four scenarios.
The study by (6) described a practical power coordination approach for BESUs within a leader-follower framework. Here, the leader stage determines the state of charge (SoC) of the BESUs using the sine cosine algorithm (SCA), while the follower stage employs a power flow tool based on successive approximations to solve the power balance equations. This approach leverages an equivalent fitness function for the efficient exploration and exploitation of the solution space. Targeting the minimization of carbon dioxide emissions in a distribution grid with BESUs and renewable resources, this SCA-based model demonstrated a strong performance, outperforming alternative algorithms such as the continuous genetic algorithm (CGA), the particle swarm optimizer (PSO), and the vortex search algorithm (VSA) on a 33-bus test grid.
The authors of 7 presented an energy dispatch model (EDM) for microgrids, which was aimed at meeting the energy demand while minimizing both CO2 emissions and operating costs. This EDM integrated model predictive control, a multi-objective optimization algorithm, and a decision tool. Model predictive control was used to adapt to dynamic operating conditions through a receding horizon approach, wherein optimization was recalculated at each time step based on updated data. The multi-objective optimization algorithm generated a Pareto front of trade-off solutions regarding emissions and cost, from which the decision tool selected the solution that best aligned with current operational priorities. Simulation results showed the robustness of this EDM under different forecasting accuracy conditions, highlighting the adaptability of model predictive control and the decision tool’s effectiveness in handling the Pareto front.
The study by 8 examined the optimized dispatch of lithium-ion BESUs in commercial and industrial facilities as a strategy for reducing both CO2 emissions and electricity costs. This multi-objective analysis evaluated 100 energy storage capacities, five discharge times, and two control strategies, with and without participation in event-based demand response programs. The results indicated that, unlike residential applications, standalone BESUs in large commercial settings could achieve substantial CO2 emission reductions (>31%) and cost savings (>10%). Additionally, enrollment in demand response and dispatch under load-shifting control were found to be consistently optimal for minimizing both payback periods and emissions.
Various optimization techniques have been applied to enhance power coordination in BESUs and RES, particularly to curb CO2 emissions. Among these approaches are second-order cone programming 9, ant colony optimization 10, convolutional neural networks 11, optimizers based on fuzzy logic 12, and artificial physics-based optimization 13. In addition, the comprehensive review by 14 examined EDM designs for integrating distributed energy resources into power networks. This study explored a range of solutions, including exact and probabilistic optimization methods, and highlighted the essential role of metaheuristic algorithms in the effective design and real-world application of EDM solutions.
This paper proposes an optimization approach based on Cauchy distribution to effectively manage active and reactive power, BESUs, and RES while aiming to minimize energy losses and operating costs in medium-voltage distribution networks. Unlike conventional algorithms, Cauchy-based optimization leverages the heavy-tailed nature of the Cauchy distribution to enhance the search process, enabling the exploration of more diverse regions of the search space and avoiding local optimum traps. This characteristic is particularly beneficial when dealing with complex, non-linear optimization problems, which are common in power systems.
The remainder of this document is organized as follows. Section 2 outlines the general optimization model for managing BESUs and RES in distribution networks. Section 3 describes the key components of the proposed leader-follower methodology, which employs the Cauchy-based distribution optimizer (CbDO) in the leader stage and the successive approximations method in the follower stage. Section 4 provides an overview of the modified 33-bus test system used in this study. Section 5 presents the main numerical results, and, finally, Section 6 provides some concluding remarks.
Exact problem formulation
Developing an effective EDM to coordinate BESUs and distributed energy resources (DERs) in medium-voltage distribution networks under a day-ahead planning scenario requires solving a non-linear programming (NLP) model 6. This type of model belongs to the family of non-convex optimization problems 15. Various performance indicators can be used to ensure the efficient coordination of these system components while considering technical, economic, and environmental metrics 16. This research focused on two specific objectives: a technical indicator related to daily energy losses and an environmental objective associated with carbon dioxide emissions 17. Each of these objective functions is outlined below.
Objective functions
The primary aim of an EDM for coordinating BESUs and DERs is to optimize key performance metrics for distribution companies, encompassing economic, technical, environmental, or social indicators or a combination thereof18. This study focuses on minimizing two main objectives: the expected daily energy losses (Dloss) and the daily CO2 emissions (DCO2 ), as defined by Eqs. (1) and (2) 17.
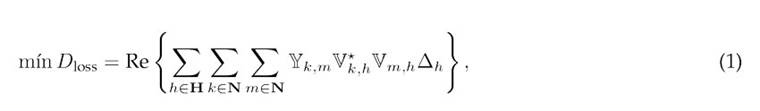
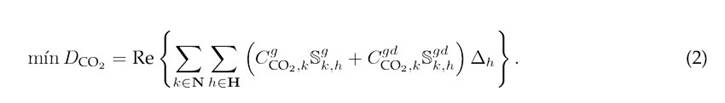
Here, Re {·} extracts the real part of the argument; H and N are the sets of analyzed time periods and network nodes, respectively; Vk,h and Vm,h denote the complex voltage at nodes k and m during time h; Yk,m represents the complex nodal admittance between nodes k and m; ∆
h
signifies the time discretization interval; and
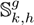 and
and
 indicate the complex power output of the conventional and renewable sources connected to node k at time h, with
indicate the complex power output of the conventional and renewable sources connected to node k at time h, with
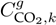 and
and
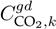 being their corresponding CO2 emission coefficients.
being their corresponding CO2 emission coefficients.
Notably, power generation using fossil fuels at medium-voltage levels is rare in urban distribution networks. Nonetheless, these systems contribute to equivalent CO2 emissions by connecting to national power grids via transmission systems. Such grids often include mixed-generation matrices composed of renewable and fossil fuel sources (19). For instance, Colombia’s electricity generation comprises approximately 67 % renewable sources (mainly hydropower), while the remaining 33 % relies on fossil fuels like coal, natural gas, and diesel (20). In this vein, the
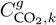 coefficient models the equivalent emissions linked to distribution network operations (17).
coefficient models the equivalent emissions linked to distribution network operations (17).
Model constraints
The challenge of achieving an efficient operation of DERs in distribution networks involves adhering to a series of constraints derived from Kirchhoff’s laws for each network node at every time interval, as well as to constraints related to the operational limits of the equipment used. Our EDM designed for the optimal coordination of DERs in medium-voltage distribution networks must consider the constraints outlined in Eqs. (3) to (18).
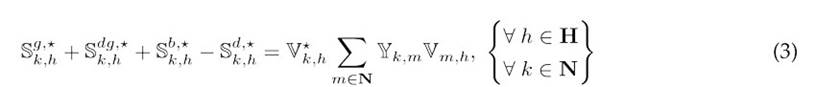
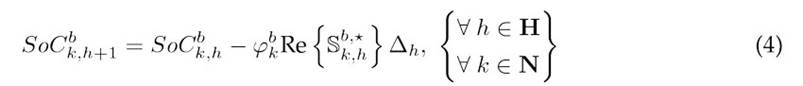
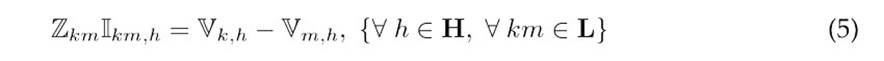
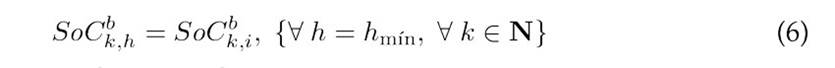
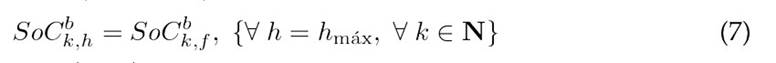
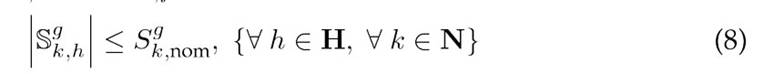
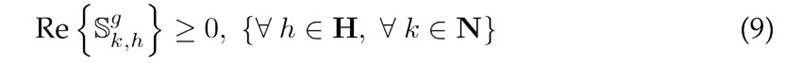
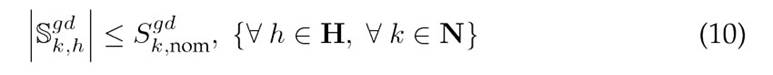
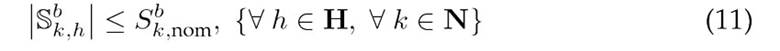

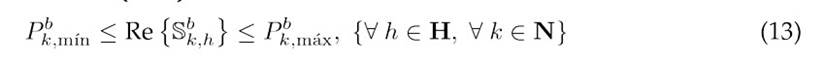
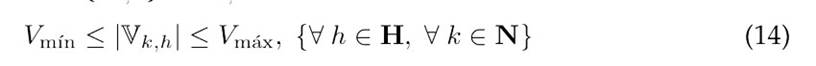
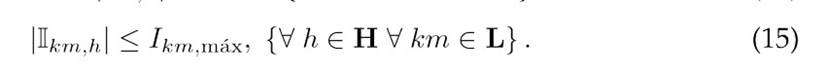
Here, S
d,⋆
k,h
denotes the complex power consumption at node k during time period h. The SoC of the type-b battery connected to bus k at times h and h + 1 is represented by SoC
k,h
b
and SoC
k,h
b
+1, respectively. The parameter/is the charge/discharge efficiency coefficient of the battery. The variables
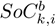 and
and
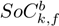 denote the initial and final SoC values expected for the type-b battery at bus k. The impedance of the branch connecting nodes k and m is expressed by Zkm, with Ikm,h representing the current that flows through this branch at time h. The symbols S
k,
g
nom and S
k,
dg
nom specify the maximum apparent power capabilities of the conventional and distributed generators at bus k. The generation availability profile for a distributed source at bus k is denoted by
denote the initial and final SoC values expected for the type-b battery at bus k. The impedance of the branch connecting nodes k and m is expressed by Zkm, with Ikm,h representing the current that flows through this branch at time h. The symbols S
k,
g
nom and S
k,
dg
nom specify the maximum apparent power capabilities of the conventional and distributed generators at bus k. The generation availability profile for a distributed source at bus k is denoted by
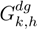 . The maximum power transfer capacity of the power electronic converter associated with the type-b battery at bus k is represented by S
k,
b
nom. The parameters P
k,
b
m´ın and P
k,
b
ma´x set the limits for active power injection or absorption for the battery at bus k. The variables V
m´ın and V
m´ax indicate the minimum and maximum voltage allowable in all network nodes at any given time, while Ima´x
km
defines the maximum current limit for the line connecting nodes k and m. Finally, the set L contains all network branches, and h
m´ın and h
m´ax represent the start and end of the period set H.
. The maximum power transfer capacity of the power electronic converter associated with the type-b battery at bus k is represented by S
k,
b
nom. The parameters P
k,
b
m´ın and P
k,
b
ma´x set the limits for active power injection or absorption for the battery at bus k. The variables V
m´ın and V
m´ax indicate the minimum and maximum voltage allowable in all network nodes at any given time, while Ima´x
km
defines the maximum current limit for the line connecting nodes k and m. Finally, the set L contains all network branches, and h
m´ın and h
m´ax represent the start and end of the period set H.
The constraints outlined in (3)-(18 can be interpreted as follows.
Eq. (3) outlines the power balance at each network node for each time interval, ensuring compliance with Kirchhoff’s current law (21). Eq. (4) details the energy storage dynamics of the batteries, modeled through the SoC for each time period (4)Eq. (5) applies Ohm’s law to each branch in the network, describing the relationship between voltage and current across branch impedances, and Eqs. (6) and (7) specify the initial and final SoC for the batteries at the start and end of the scheduling period, thereby establishing consistent energy management across the timeline 6.
Constraints 8 and 9 impose upper bounds on the power flowing from the substation and ensure that it only provides active power. Constraints 10 and 11 set the power transfer limits for the DGs and BESUs. Eq. 12 ensures that the DGs inject power only when renewable resources are available, thus preventing power absorption. Eq. (13) defines the permissible range for active power charging/discharging by the type-b battery at node k during period h. Finally, Box-Type Constraint 14 ensures that the voltage at all network nodes adheres to regulatory standards for medium-voltage systems 22, and Constraint 18 guarantees that the current flowing through any network branchremainsbelowthethermalcapacity of the conductor, thus maintaining a safe operation.
To address the challenges posed by the non-convex constraints inherent in the Optimization Model 1- 18 , this research employs a novel metaheuristic optimizer: the CbDO. The Set of Constraints 3- 18 encapsulates the technical requirements for operating a power distribution network with DERs. While many of these constraints are convex and manageable within classical optimization frameworks, critical aspects such as the Power Balance Constraint 3 and the Voltage Regulation Bounds 14 introduce significant non-convexities. These complexities arise from nonlinear relationships and inequalities, particularly due to the complex product of voltage terms and the structure of box-type constraints involving inequality conditions.
In light of these characteristics, conventional solvers often struggle to find feasible or globally optimal solutions, especially when handling non-convex, multi-modal search spaces. The aforementioned optimizer, as a metaheuristic technique inspired by the Cauchy distribution, excels in exploring such spaces efficiently 23. Its design allows for a better handling of diverse solution landscapes, leveraging the long-tailed nature of the Cauchy distribution, which promotes extensive exploration and reduces the risk of premature convergence. This is particularly valuable for solving non-convex optimization problems, where local optima may otherwise hinder traditional algorithms.
Thus, employing the CbDO for optimizing complex power system models, such as the one represented in 1- 18), provides a robust alternative that aligns with the nature of the problem. This approach facilitates the search for high-quality solutions that adhere to technical constraints while effectively navigating intricate non-convexities. The set of variables related to the Optimization Model 1- 18 is presented in Table I.
Table I: Number of variables in the Optimization Model 1- 18.

Solution methodology
Our methodology for solving the Optimization Model 1- 18 involves applying the CbDO to the active and reactive power dispatch problem while considering BESUs. The CbDO, known for its strong exploration capabilities, serves as the leader stage, while a power flow analysis tool acts as the follower stage 6,24. The leader defines the SoC of the BESUs, represented by SoC k,h b . These values are then used in the follower stage, where a power flow solver ensures compliance with the power balance constraints by determining voltage profiles and power generation values 25. The main components of the proposed methodology are outlined below.
Fitness function
In metaheuristic optimization, fitness functions are essential for managing constraints through penalty methods 6,24. For the problem under study, the fitness function Ff is defined as shown in (16):

where αk(x) denotes the penalty applied for violating the kth constraint, and C is the set of constraints considered in the fitness function. The constraints included in calculating the penalty ensure compliance with operating and technical limits, except for the constraints already handled by the follower stage, as is the case with 3. The penalty function for the current limit of the distribution branches, as expressed in 18, is given below 6:
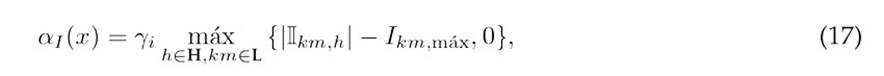
where γi is a positive penalty coefficient.
This penalty function only contributes a non-zero value if any branch current exceeds its thermal limit, thereby ensuring that the solutions remain feasible under real-world operating conditions 26.
Follower stage: power flow solution
With the aim of evaluating the solutions proposed by the CbDO, a power flow solver based on the successive approximations method is utilized to solve the nonlinear power balance constraint 3) (6. The iterative power flow update formula is presented in 18.
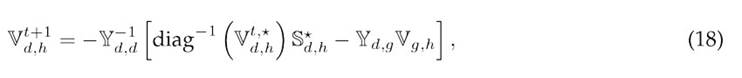
where
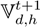 is the updated vector of demand-node voltages for time h, and Y−
d,d
1 is the inverse of the admittance matrix relating the demand nodes. The term S
⋆
d,h
represents the net power at these nodes, including the contributions of BESUs and RES.
is the updated vector of demand-node voltages for time h, and Y−
d,d
1 is the inverse of the admittance matrix relating the demand nodes. The term S
⋆
d,h
represents the net power at these nodes, including the contributions of BESUs and RES.
The iterative process converges when the stopping criterion in 19 is met.
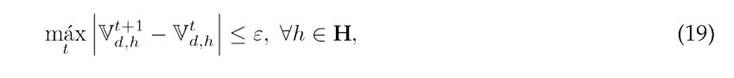
where ε is a user-defined tolerance, typically set at 1 × 10−10. Once convergence is achieved, the power injected by the conventional source is calculated as per 20.
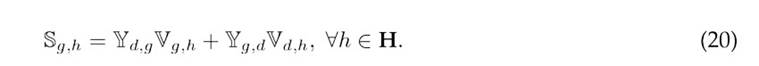
This final calculation ensures that the power dispatch observes the network constraints, allowing for an accurate evaluation of the Objective Function 1.
Leader stage: CbDO
The CbDO is a new math-inspired metaheuristic algorithm designed to explore and exploit the solution space through the properties of the Cauchy distribution 23. Below, we outline its application for the active and reactive power dispatch problem involving BESUs. The SoC of the BESUs was chosen as the set of decision variables for the algorithm. The encoding for these variables is illustrated in Eq. (21), showing the SoC values for two BESUs, one situated at bus k and the other at bus m 6.
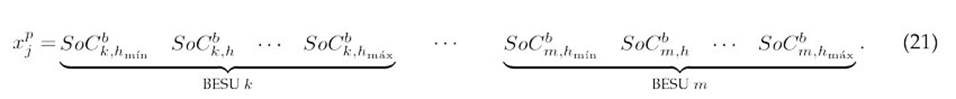
Once the SoC variables for the BESUs have been established, the CbDO determines the corresponding active and reactive power injection into the network. This step ensures compliance with all the operating constraints specified in the Optimization Model 1- 18 for the proper functioning of the BESUs.
Main parameters of the CbDO
The CbDO leverages the Cauchy distribution, which is characterized by the probability density function defined in 22) (27).
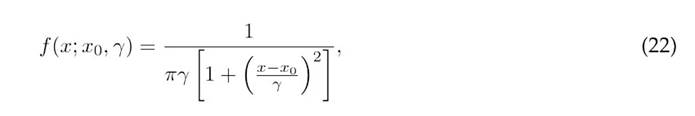
where x is the random variable, x0 is the location parameter, and ? is the scale parameter
The corresponding cumulative distribution function (CDF) is obtained as follows 22:
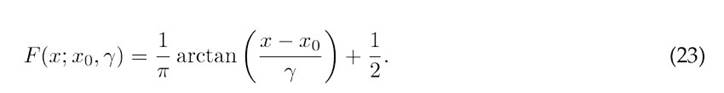
The CDF and its properties form the basis for defining the CbDO’s exploration and exploitation mechanisms 28.
Constructing the initial population
To initialize the population, the CbDO defines the center of the solution space, µ, and its standard deviation, σ:


where
 and
and
 represent the lower and upper bounds of the variables. The initial population Xt at iteration t = 0 is constructed using
represent the lower and upper bounds of the variables. The initial population Xt at iteration t = 0 is constructed using
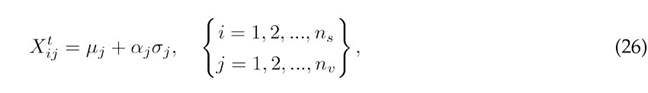
where αj is a uniformly distributed random number between 0 and 1.
Remark 1 Each position in the initial population is checked in order to ensure that it lies within the bounds
 If it does not, a correction is applied:
If it does not, a correction is applied:
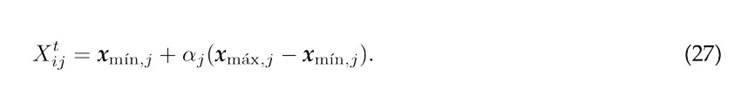
Exploration and exploitation mechanisms
The CbDO’s local exploration uses the quantile function derived from 23, which is defined as follows:
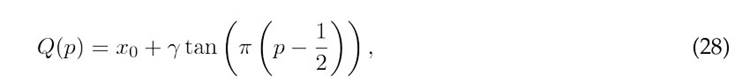
where p is a random number in the range (0, 1). This is used in the local update rule:
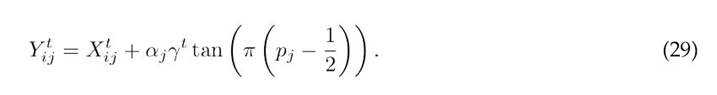
For its global exploration, the algorithm calculates the mean mt and standard deviation st of the current population:


The global update rule is as follows:
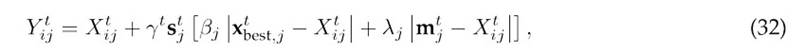
where βj and λj are uniformly distributed random numbers between-1 and 1.
Remark 2 Note that xt best represents the best solution in the population. In minimization problems, this is the solution with the lowest objective function value, whereas, in maximization problems, it corresponds to the solution with the highest value.
Population replacement and stopping criterio
Newsolutions generated by the local and global rules are checked and corrected so that they remain within the specified bounds. The replacement rule is as follows:
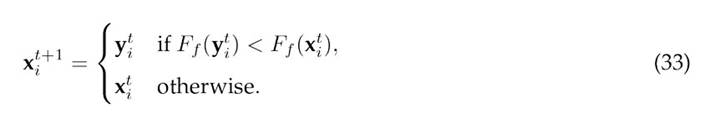
The algorithm stops when the maximum number of iterations
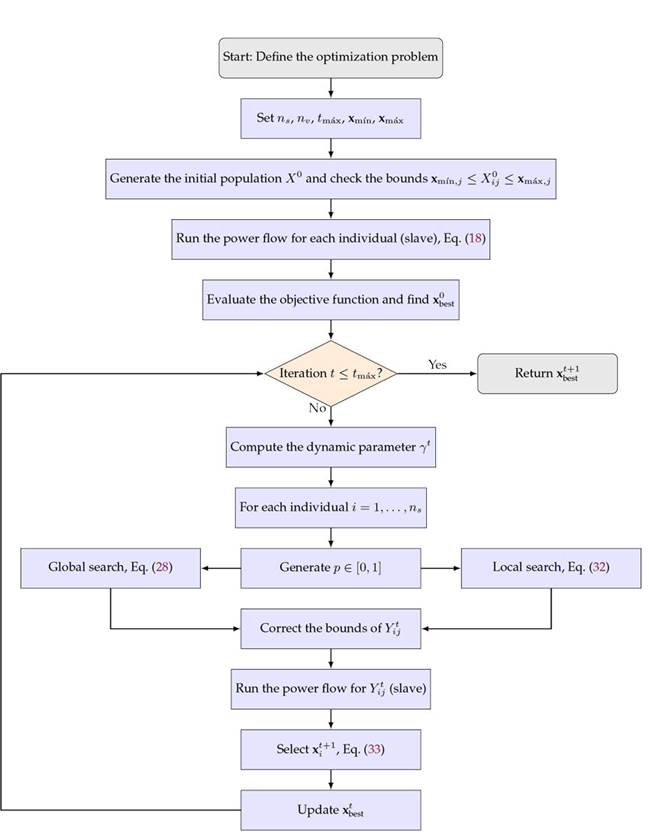
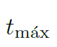 is reached. Fig. 2 presents a f lowchart of the proposed leader-follower strategy.
is reached. Fig. 2 presents a f lowchart of the proposed leader-follower strategy.
Test feeder characterization
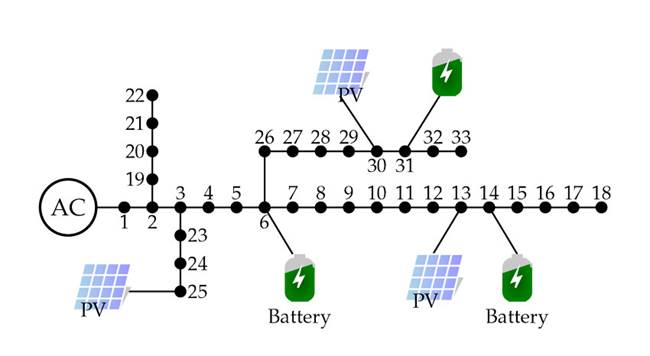
To simulate a representative urban distribution network in Colombia, we adapted a 33-bus grid by incorporating the typical demand and solar generation characteristics of Medellín (Fig. 3). This system is supplied with 12.66 kV at the substation terminals (phase-to-ground voltage). Table II presents the detailed electrical configuration, peak demand values, and conductor thermal constraints of the 33-bus grid. This information was taken from 29.
In this adaptation, renewable generation through PV systems and energy storage provided by lithium-ion BESUs were included in order to study their daily operation within the network. Additional specifics are available in 29. Three PV units were strategically positioned at nodes 13, 25, and 30, with nominal capacities of 1125, 1320, and 999 kW, respectively. Moreover, BESUs (types C, A, and B) were placed at nodes 6, 14, and 31. The voltage regulation parameters for the system allowed for deviations of ±10%.Toensure the proper operation of the BESUs, the allowable range for the SoC was set between 10 and 90%, with initial and final SoC levels of 50%.
Figure 2: Detailed flowchart of the proposed CbDO-based leader-follower strategy
Table II.: Main parameters for the 33-node test system
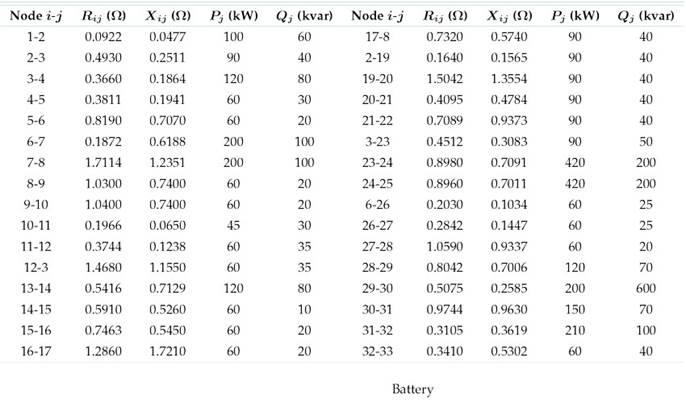
Figure 3: Adaptation of the 33-bus grid for emulating an urban network
Further insights into the classification and characteristics of the different BESU types can be obtained by consulting (30). For a comprehensive view of the hourly daily generation and demand profiles utilized in this study, please refer to (29). Additionally, the CO2 emissions factor for the PV generators was assumed to be zero (denoted as
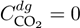 ), while the emissions factor associated with conventional power generation from the substation (
), while the emissions factor associated with conventional power generation from the substation (
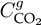 ) was set as 0.16438 g/Wh, according to data from(29).
) was set as 0.16438 g/Wh, according to data from(29).
Numerical validations, analysis, and discusión
For the computational implementation of our proposal, we employed the MATLAB programming environment (version 2022b). The simulations were performed on a PC equipped with an AMDRyzen7 3700 processor at 2.3 GHz and 16.0 GB of RAMrunninga64-bit version of Microsoft Windows 10 Single Language. The optimization of the semidefinite programming (SDP) model was also conducted in the MATLAB software, using the CbDO to solve the studied problem.
Computational validation against literature reports
A comparative analysis against a recent metaheuristic approach demonstrated that the proposed CbDO method can solve the problem regarding the effective coordination of BESUs and solar generation systems. For the sake of comparison, we conducted two analyses of the proposed optimization approach:
-
A distribution network analysis considering a unitary power factor for the BESUs and PV generators, in order to compare our approach against the continuous genetic algorithm (CGA) and the parallel versions of the particle swarm optimizer (PPSO) and the vortex search algorithm (PVSA). Here,
was defined as 0,16438 kg/kWh, and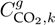
was assumed to be zero since solar generation, in its operation stage, is regarded as a green energy technology.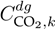
-
An evaluation of the effectiveness of the proposed SDP relaxation in managing DERs in medium-voltage distribution networks with a variable power factor, considering three simulation scenarios. The first scenario (S1) involved the daily dispatch of PV sources operating with a unitary power factor and BESUs with a variable power factor. In the second scenario (S2), the PV sources were dispatched on a daily basis with a variable power factor, while the BESUs maintained a unitary power factor. Finally, in the third scenario (S3), all DERs operated with a variable power factor. These scenarios were designed to provide a thorough assessment of the approach under different operating conditions.
Unitary power factor análisis
Applying the CbDO to solve the EDM developed for dispatching BESUs and PVs in distribution networks while considering a unitary power factor yielded the results presented in Table III.
Table III: Comparison of results regarding both objective functions analyzed
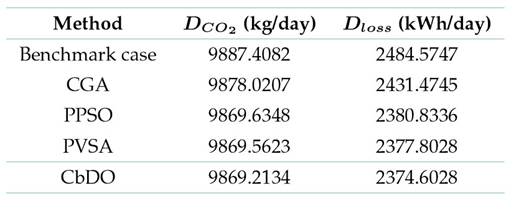
Based on these numerical results, the following can be stated:
-
The CbDO performs better than the other metaheuristic methods (CGA, PPSO, and PVSA) in relation to both objective functions. Specifically, regarding the expected daily energy losses, CbDO reports a reduction of 3.2000 kWh/day compared to PVSA. As for CO2 emissions, the CbDO shows a decrease of 0.3489 kg/day with respect to PVSA. Although these improvements may appear modest, they underscore CbDO’s ability to effectively explore the solution space and avoid local optima, wherein other metaheuristics might exhibit some limitations.
-
In comparison with the benchmark case (i.e., grid operation with PVs but without BESUs), the CbDO shows significant reductions in both metrics. The daily energy losses are lowered by approximately 4.4261%, while the CO2 emissions are reduced by about 0.1840% This confirms the potential benefits of integrating BESUs into distribution networks for optimal energy management, as it yields notable improvements in terms of technical efficiency and environmental sustainability.
Variable power factor análisis
To validate the effectiveness of the proposed optimization approach regarding a variable power factor operation of DERs, the objective function related to energy losses was analyzed in comparison with the results reported in 31, which employed an SDP approach.
In this analysis, the benchmark case corresponds to the numerical results reported in Table IV, which pertain to the unitary power factor operation of the PVs and BESS. Here, the CbDO results are labeled as S0.
Table IV: Comparative analysis considering a variable power factor operation for minimizing energy losses
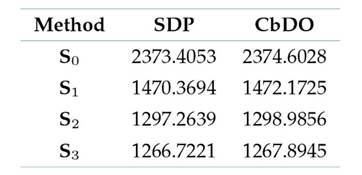
This comparison aids in evaluating the performance of the proposed CbDO and the SDP approach under various operating scenarios regarding DERs with variable power factor capabilities. Here, the energy losses function serves as the primary metric for assessing the effectiveness of the aforementioned optimization methods. For context, S0 represents the benchmark case where the PVs and BESUs operate with a unitary power factor.
-
Benchmark comparison (S0). The baseline S0 scenario, wherein the PVs and BESUs are dispatched withaunitarypowerfactor,providestheinitial energylosses. According totheresults, the SDP approach outperforms the CbDO in this case, with a value of 2373.4053 kWh/day vs. our proposal’s 2374.6028 kWh/day. The marginal difference between these results suggests that, while both optimization methods are effective, the SDP approach has a slight edge in this specific configuration.
-
Variable power factor for the BESUs (S1). In scenario S1, the BESUs are operated with a variable power factor, while the PVs continue to function at a unitary power factor. Here, both the SDP approach and CbDO demonstrate significant improvements in reducing energy losses compared to the benchmark case. The SDP approach achieves energy losses of 1470.3694 kWh/day, while CbDO yields 1472.1725 kWh/day. This substantial reduction vs. the S0 scenario suggests that allowing BESUs to operate with a variable power factor greatly enhances network efficiency. The close difference between the analyzed methods confirms our proposal’s comparable performance.
-
Variable power factor for the PVs (S2). Scenario S2 explores the impact of operating PVs with a variable power factor while the BESUs maintain a unitary power factor. In this scenario, the SDP approach yields energy losses of 1297.2639 kWh/day, while the CbDO reports a slightly higher value (1298.9856 kWh/day). These results highlight the fact that incorporating a variable power factor operation for PVs contributes to further reducing energy losses, suggesting that flexibility in DERoperation is crucial for improving distribution system performance.
-
Variable power factor operation (S3). Scenario S3, where all DERs are dispatched with a variable power factor, reports the most significant improvement in energy losses minimization. The SDP approach achieves the lowest energy losses (1266.7221 kWh/day), followed closely by CbDO (1267.8945 kWh/day). This scenario confirms that a variable power factor operation for all DERs provides the best overall performance. The minimal difference between the results for the SDP and CbDO methods further underscores the efficacy of our proposal as a reliable optimization tool that closely approaches the more complex SDP method.
In summary, the analysis in Table IV reveals that the proposed CbDO provides competitive results across all scenarios, closely matching the performance of the SDP solution. The most significant energy losses reductions occur when operating both the PVs and the BESUs with a variable power factor(S3). While the SDP approach slightly outperforms CbDO in each scenario, the differences are small enough to validate our proposal as a practical and efficient alternative for energy losses minimization in medium-voltage distribution networks with DERs. This validation emphasizes the importance of employing a flexible power factor in DER operation to optimize network efficiency
Conclusions and future Works
The findings and numerical validations outlined in Section 5 provide important insights into the effectiveness of the proposed CbDO in solving the energy dispatch problem for medium-voltage distribution networks with DERs. In this vein, the following conclusions can be drawn:
-
Performance comparison against metaheuristic methods. The CbDO consistently outperforms traditional metaheuristic algorithms such as the CGA, PPSO, and PVSA; Table III demonstrates that our proposal achieves the lowest expected daily energy losses and CO2 emissions. Although modest, the reductions indicate that CbDO’s design effectively navigates the solution space, mitigates the risk of local optimum traps, and delivers superior optimization outcomes.
-
Benefits of BESU integration. When comparing the benchmark case against scenarios involving BESU integration, CbDO’s results reveal substantial improvements in terms of both energy losses and CO2 emissions. The inclusion of BESUs facilitates enhanced energy management and system efficiency, with approximately 4.4261% less energy losses and a 0.1840% reduction in emissions. This underscores the importance of optimal BESU coordination to achieve technical and environmental gains.
-
Impact of variable power factor operation. The comparative analysis shown in Table IV highlights the value of implementing variable power factor operation for all DERs. While the SDP approach delivers slightly better results, CbDO’s performance is closely aligned, especially in S3, where all DERs operate with a variable power factor. This scenario yields the most significant decrease in energy losses, demonstrating that flexibility regarding the power factor maximizes network performance. The small margin between CbDO and the SDP approach confirms that our proposal is a viable, efficient, and practical solution for complex, non-linear optimization problems in power systems.
Three future research directions could further advance the findings of this study. Firstly, the proposed CbDO could be enhanced to incorporate adaptive mechanisms that dynamically adjust the balance between exploration and exploitation during optimization, potentially improving convergence rates and solution accuracy. Secondly, applying the CbDO to more extensive and more complex distribution networks, including real-time simulation and control integration, could validate its scalability and practical applicability in diverse grid environments. Lastly, exploring the hybridization of our proposal with other optimization methods, e.g., combining it with machine learning techniques for improved predictive capabilities, could enhance its robustness and adaptability to changing grid conditions and uncertain renewable energy generation profiles.
Referencias

License
Copyright (c) 2025 Maria Camila Vega Peña, Oscar Danilo Montoya Giraldo, Walter Gil-González

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)