DOI:
https://doi.org/10.14483/23448393.24009Published:
2025-08-01Issue:
Vol. 30 No. 2 (2025): May-AugustSection:
EditorialGeneralized Power Flow Algorithms for Monopolar DC Networks Using Broyden’s Method
Keywords:
Power flow, Transmission network, System stability (en).Downloads
References
S. Sarhan, A. M. Shaheen, R. A. El-Sehiemy, and M. Gafar, “Enhanced Teaching Learning-Based Algorithm for Fuel Costs and Losses Minimization in AC-DC Systems,” Mathematics, vol. 10, no. 13, p. 2337, Jul. 2022. https://doi.org/10.3390/math10132337
Z. Liu and M. Li, “Research on Energy Efficiency of DC Distribution System,” AASRI Proc., vol. 7, pp. 68–74, 2014. https://doi.org/10.1016/j.aasri.2014.05.031
J. Li, F. Liu, Z. Wang, S. H. Low, and S. Mei, “Optimal Power Flow in Stand-Alone DC Microgrids,” IEEE Trans. Power Syst., vol. 33, no. 5, pp. 5496–5506, sep 2018. https://doi.org/10.1109/tpwrs.2018.2801280
J. W. Simpson-Porco, F. Dorfler, and F. Bullo, “On resistive networks of constant-power devices,” IEEE Trans. Circ. Syst. II Exp. Briefs, vol. 62, no. 8, pp. 811–815, aug 2015. https://doi.org/10.1109/tcsii.2015.2433537
A. Garces, “Uniqueness of the power flow solutions in low voltage direct current grids,” Elec. Power Syst. Res., vol. 151, pp. 149–153, oct 2017. https://doi.org/10.1016/j.epsr.2017.05.031
A. Garces, “On the Convergence of Newton's Method in Power Flow Studies for DC Microgrids,” IEEE Trans. Power Syst., vol. 33, no. 5, pp. 5770–5777, sep 2018. https://doi.org/10.1109/tpwrs.2018.2820430
J. Beerten, S. Cole, and R. Belmans, “A sequential AC/DC power flow algorithm for networks containing multi-terminal VSC HVDC systems,” in IEEE PES Gen. Meet. IEEE, jul 2010. https://doi.org/10.1109/pes.2010.5589968
O. D. Montoya, W. Gil-González, and A. Garcés, “Numerical methods for power flow analysis in DC networks: State of the art, methods and challenges,” Int. J. Elec. Power Energy Syst., vol. 123, p. 106299, dec 2020. https://doi.org/10.1016/j.ijepes.2020.106299
A. Marini, S. Mortazavi, L. Piegari, and M.-S. Ghazizadeh, “An efficient graph-based power flow algorithm for electrical distribution systems with a comprehensive modeling of distributed generations,” Elec. Power Syst. Res., vol. 170, pp. 229–243, may 2019. https://doi.org/10.1016/j.epsr.2018.12.026
T. Shen, Y. Li, and J. Xiang, “A Graph-Based Power Flow Method for Balanced Distribution Systems,” Energies, vol. 11, no. 3, p. 511, feb 2018. https://doi.org/10.3390/en11030511
A. Garcés and O.-D. Montoya, “A Potential Function for the Power Flow in DC Microgrids: An Analysis of the Uniqueness and Existence of the Solution and Convergence of the Algorithms,” J. Control Autom. Elec. Syst., vol. 30, no. 5, pp. 794–801, jun 2019. https://doi.org/10.1007/s40313-019-00489-4
A. Ramli, M. L. Abdullah, and M. Mamat, “Broyden's method for solving fuzzy nonlinear equations,” Adv. Fuzzy Syst., vol. 2010, pp. 1–6, 2010. https://doi.org/10.1155/2010/763270
H. Yang, F. Wen, and L. Wang, “Newton-Raphson on power flow algorithm and Broyden Method in the distribution system,” in 2008 IEEE 2nd Int. Power Energy Conf. IEEE, dec 2008. https://doi.org/10.1109/pecon.2008.4762737
F. Tolner, B. Barta, and G. Eigner, “Comparison of Newton’s and Broyden’s Method as Nonlinear Solver in the Implementation of MFV-robustified Linear Regression,” in 2022 IEEE Int. Conf. Syst. Man Cybernetics (SMC). IEEE, oct 2022. https://doi.org/10.1109/smc53654.2022.9945222
L. M. Riaño-Enciso, O. Danilo Montoya, and W. Gil-González, “Implementation of Broyden’s Method to Compute the Three-Phase Power Flow in Electrical Distribution Networks with Asymmetric Loading,” in 2023 IEEE Colombian Caribbean Conf. (C3). IEEE, Nov. 2023, pp. 1–6. https://doi.org/10.1109/c358072.2023.10436180
M. Mirzaee, A. Zolfaghari, and A. Minuchehr, “The Broyden method applied for the analysis of two-phase flow in a BWR fuel bundle based on the drift-flux model,” Prog. Nuclear Energy, vol. 112, pp. 80–95, apr 2019. https://doi.org/10.1016/j.pnucene.2018.12.004
W. Yi, Z. Lin, Y. Lin, S. Xiong, Z. Yu, and Y. Chen, “Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution,” Mathematics, vol. 11, no. 5, p. 1250, Mar. 2023. https://doi.org/10.3390/math11051250
O. B. Adewuyi and S. Krishnamurthy, “Performance Analysis for Predictive Voltage Stability Monitoring Using Enhanced Adaptive Neuro-Fuzzy Expert System,” Mathematics, vol. 12, no. 19, p. 3008, Sep. 2024. https://doi.org/10.3390/math12193008
U. Hussan, H. Wang, M. A. Ayub, H. Rasheed, M. A. Majeed, J. Peng, and H. Jiang, “Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems,” Mathematics, vol. 12, no. 19, p. 3064, Sep. 2024. https://doi.org/10.3390/math12193064
L. F. Grisales-Noreña, O. D. Montoya, W. J. Gil-González, A.-J. Perea-Moreno, and M.-A. Perea-Moreno, “A Comparative Study on Power Flow Methods for Direct-Current Networks Considering Processing Time and Numerical Convergence Errors,” Electronics, vol. 9, no. 12, p. 2062, dec 2020. https://doi.org/10.3390/electronics9122062
O. D. Montoya, V. M. Garrido, W. Gil-González, and L. F. Grisales-Noreña, “Power Flow Analysis in DC Grids: Two Alternative Numerical Methods,” IEEE Trans. Circ. Syst. II Exp. Briefs, vol. 66, no. 11, pp. 1865–1869, nov 2019. https://doi.org/10.1109/tcsii.2019.2891640
O. D. Montoya, “On the Existence of the Power Flow Solution in DC Grids With CPLs Through a Graph-Based Method,” IEEE Trans. Circ. Syst. II Exp. Briefs, vol. 67, no. 8, pp. 1434–1438, aug 2020. https://doi.org/10.1109/tcsii.2019.2937564
O. D. Montoya, L. F. Grisales-Noreña, and W. Gil-González, “Triangular Matrix Formulation for Power Flow Analysis in Radial DC Resistive Grids With CPLs,” IEEE Trans. Circ. Syst. II Exp. Briefs, vol. 67, no. 6, pp. 1094–1098, jun 2020. https://doi.org/10.1109/tcsii.2019.2927290
A. Garcés, “A Linear Three-Phase Load Flow for Power Distribution Systems,” IEEE Trans. Power Syst., vol. 31, no. 1, pp. 827–828, jan 2016. https://doi.org/10.1109/tpwrs.2015.2394296
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Solving the power flow problem in transmission networks is crucial for ensuring the reliable and efficient operation of electrical power systems. Power flow analysis allows engineers to determine the voltage, current, and power flows of a network, which is essential for maintaining system stability and avoiding overloads. Accurate power flow solutions aid in identifying potential issues such as voltage drops, line losses, and system inefficiencies, enabling the proactive maintenance and optimization of the grid. This analysis is vital for integrating renewable energy sources, as it ensures an effective power distribution, even when dealing with variable generation. Ultimately, solving the power flow problem enhances the overall resilience, reliability, and economic performance of the transmission network, supporting a stable supply of electricity to consumers.
Introduction
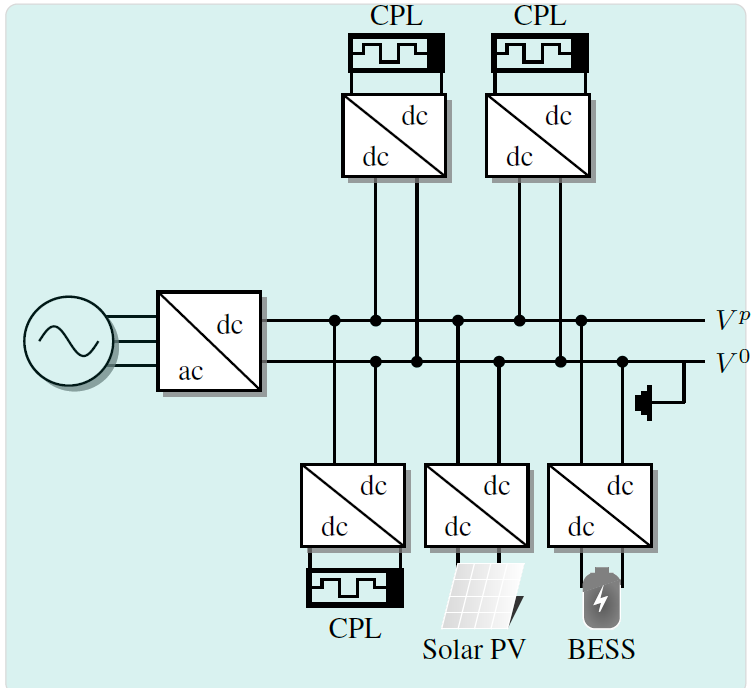
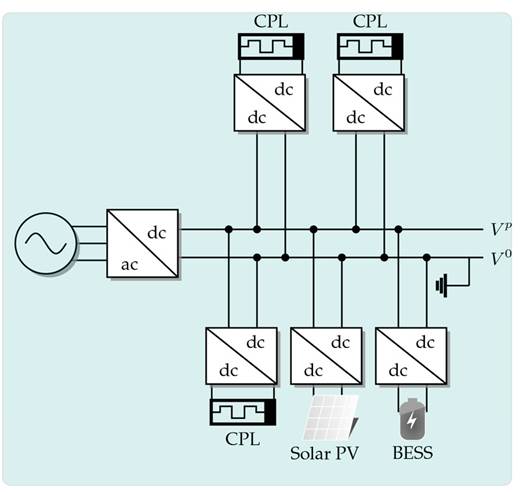
Direct-current (DC) networks have garnered increasing attention in applications employing all voltage levels, given their reduced power losses and improved voltage profiles when compared to traditional alternating-current (AC) grids 1, 2. An illustrative representation of a monopolar DC network is shown in Fig. 1.
Figure 1: Schematic representation of a monopolar DC network with multiple distributed energy resources
To accurately analyze these emerging systems in the presence of multiple constant power terminals, including loads, generators, and energy storage devices, using advanced numerical methods, optimization algorithms, and control strategies is essential3. This editorial note focuses on evaluating the numerical techniques commonly employed to solve the steady-state power flow equations of monopolar DC grids. Addressing this challenge is particularly complex duetothenonlinearities introducedbyconstantpower loads (CPLs) 4. Over the years, classical numerical approaches such as the Gauss-Seidel andNewton-Raphsonmethods 5, 6havebeenwidelyutilized to compute the voltage vector that satisfies the power equilibrium equations. This voltage vector serves as a fundamental indicator of the overall state of the electrical network, enabling the assessment of key performance metrics such as power losses, voltage regulation, and line loading conditions7.
Monopolar DC networks have become increasingly attractive over the past decade, particularly due to their straightforward implementation at medium- and low-voltage levels. Their operational advantages include the absence of reactive power management and frequency control requirements, making them an attractive alternative for modern power distribution systems 3. To facilitate the analysis of these systems, various power flow algorithms have been proposed in the scientific literature. These algorithms are broadly categorized into derivative-free and derivative-based approaches 8. In the case of the former, graph theory serves as the foundation for their development, with notable examples including the triangle-based power flow and the matricial backward/forward algorithms 9, (10). Conversely, derivative-based approaches encompass classical numerical techniques such as the Newton-Raphson method 6 and the product and hyperbolic power flow algorithms8.
The power flow algorithms referenced in the literature share a fundamental similarity: their recursive formulations generally define a fixed-point iteration, expressed as vt+1 d = g(vt d), where vt d represents the voltage vector and g(vt d) is a nonlinear function of the voltages. The function g(vt d) can be derived through algebraic manipulations, as seen in derivative-free power flow methods, or via linear transformations, e.g., Taylor series expansions, as employed in derivative-based power flow approaches5, (6
Considering the general structure of the power flow problem in monopolar DC networks, this editorial note proposes a unifying generalization of power flow algorithms using Broyden’s numerical method. This generalization demonstrates that all power flow formulations can be obtained by appropriately selecting the structure of the ∇f (vt d) matrix and Broyden’s matrix At. A key feature of this approach is that the gradient vector ∇f (vt d) is derived from a general function f (vt d), which allows formulating the the power flow problem as an unconstrained optimization model 11
The remainder of this express brief is structured as follows. Section 2 outlines the general theory of Broyden’s numerical method and its recursive formula, including the general procedure for updating the At matrix. Section 3 describes the most common derivative-free and derivative-based power flow formulas, whichincludethematricialbackward/forwardandthetriangle-basedpowerflowalgorithms, as well as the Newton-Raphson, hyperbolic, and product power flow methods. Section 4 presents the generalization of the power flow formulas, which leverages Broyden’s numerical method by adequately selecting the ∇f (vt d) vector and the At matrix. Finally, Section 5 presents the Gauss-Seidel case, and Section 6 states the main conclusions of this work.
2. Broyden’s numerical method
Broyden’s approach (also known as the secant method) is a numerical method originally proposed by C. G. Broyden in 1965, in an attempt to find the numerical solution to a set of nonlinear equations with the form ∇f (x) = 0, as an alternative version of the Newton-based approaches 12. Broyden’s general iterative formula is presented in Eq. (1) 13
with t being the iterative counter and At a variable matrix that may be equivalent to the Jacobian matrix in Newton-based methods. Nevertheless, the main contribution of Broyden’s approach is its updating process, which uses secant hyperplanes 14. Note that xt represents the current solution of the vector decision variables at iteration t15.
To obtain a general rule for approximating At, consider the following linear relation between the solution vectors in iteration t and the gradient functions evaluated in them
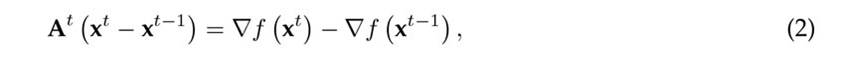
Which can be simplified as presented in(3) by considering the following definitions: st =(xt − xt−1)and yt = ∇f(xt)−∇f (xt−1)
To obtain a general formula for updating the At matrix, the following two hyperplanes are defined
The main idea of Broyden’s method is that, at the solution point, the Hyperplanes (4) and (5) must be equal, i.e.,
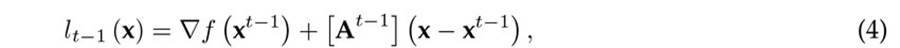
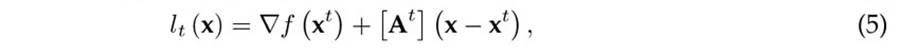
In Eq. (6), if x = xt is defined while considering the definition in (3) and making some algebraic manipulations, the following result is reached
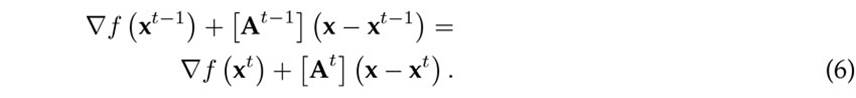
By simplifying Eq. (7), the general updating formula for At can be determined as presented in (8).
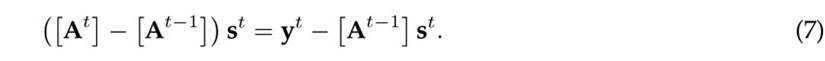
For the general iteration t + 1, the way to update At+1 is obtained from (8), as defined in (10).
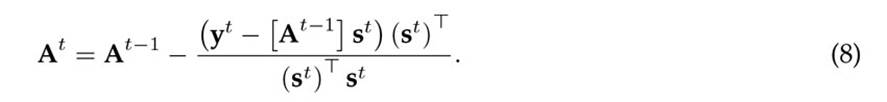
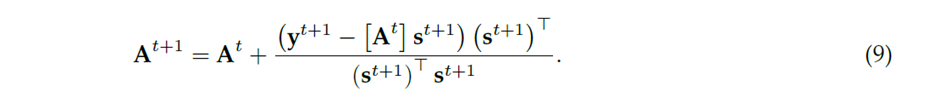
The general algorithm for solving the set of equations ∇f (x) = 0 is presented in Algorithm 1 16.
Algorithm 1: General implementation of Broyden’s method for solving sets of nonlinear equations
Note that, for the numerical demonstrations associated with the power flow algorithms considered in this research, a constant factor α is added in order to update the Matrix Formula (10).
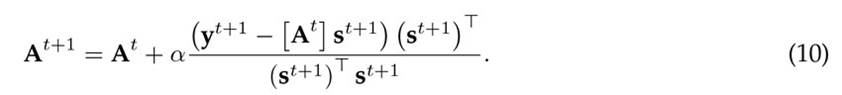
where α can be set as 0 or 1. However, for demonstration purposes, it will take a value of 0 in this research
3. Power Flow problema and iterative formulas
The power flow problem is fundamental in the analysis of power systems, as it determines their steady-state operating conditions 17. Its solution provides crucial insights into voltage magnitudes, power losses, and branch flows, allowing grid operators to guarantee reliability, efficiency, and stability18. However, solving the power flow problem poses several challenges due to the nonlinear nature of the power balance equations, the complexity introduced by large-scale networks, and the presence of various types of loads and generation units19. Advanced numerical methods are essential for achieving accurate and computationally efficient solutions, particularly in modern power grids with increasing penetration of renewable energy sources. In other words,
-
The power flow analysis helps to maintain voltage stability, preventing voltage collapse and ensuring that the power system operates within safe limits.
-
Solving the power flow problem is critical for optimizing generation dispatch, minimizing power losses, and improving overall system efficiency.
-
The power flow equations are inherently nonlinear, which makes their solution computationally intensive, especially for large-scale transmission and distribution networks.
-
Modern power grids incorporate renewable energy sources with variable generation, adding further complexity to power flow solutions due to fluctuations and uncertainties in power generation.
Given the importance of the power flow problem in ensuring the proper operation of DC networks while complying with regulatory policies and technical requirements, the next section presents the most commonly used numerical methods for its solution
3.1. General power flow problema
The power flow problem for monopolar DC networks is generally formulated as a set of nonlinear equations that must be solved in order to obtain the set of voltage values that fulfill them, i.e., the circuit solution to satisfy the power equilibrium at each node 4. However, as demonstrated by 11, this problem can be defined as an optimization model, i.e.,
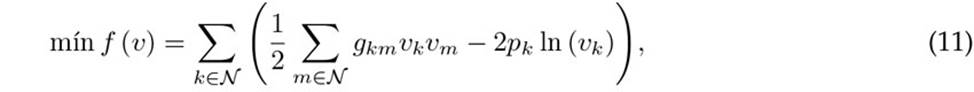
where pk represents the net power injection at node k; gkm is the component of the conductance matrix that relates nodes k and k; and vk and vk are the voltage variables for nodes k and m, so that v > 0, given the domain of the natural logarithmic function.
Since this is an unconstrained problemwithcontinuousvariables, solving the minimization problem in 11 is equivalent to solving the set of simultaneous equations regarding its gradient, in order to determine the critical point associated with the voltage values, i.e.,
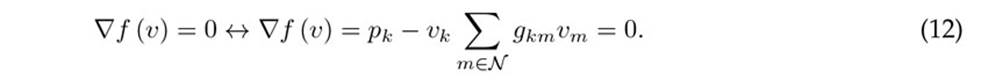
3.2. Iterative power flow formulas
The current literature has reported multiple power flow algorithms to solve the studied problem, which can be classified as derivative-free and derivative-based approaches8. The former are typically developedusinggraphtheoryinordertoobtainarecursiveformulathatconvergeslinearlytothepower f low solution5. In contrast, derivative-based power flow methods apply Taylor’s series truncated to the first order approximation, with quadratic convergence to the power flow solution6.
3.2.1. Derivative-free power flow formulas
In the current literature, derivative-free methods are typically developed using graph-based theory. This brief considers two iterative formulas. The first approach is known as the matricial backward/forward power flow method (MBFPFM), which is equivalent to the successive approximations power flow method20, (21). The second method is based on the well-known upper-triangular matrix, which provides a recursive power flow formula for radial distribution networks that can be adapted for meshed distribution systems, as demonstrated in 9 for AC grids. The MBFPF formula is presented in (13).
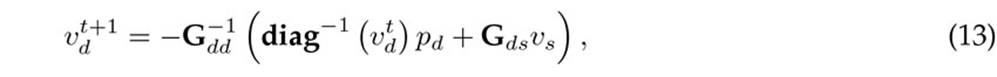
where Gdd is a square matrix with dimensions d×d that represents the nodal conductance relations between demand nodes; Gds is a rectangular matrix that contains the conductances that associate the demanded nodes with the substation bus; diag−1(vt d) is a matricial operation that turns the column vector vt d with dimension d into a diagonal matrix with dimensions d × d; pd corresponds to a column vector containing all the CPLs in the demand vectors; vs is the substation output voltage; and vd t+1 is the voltage vector at iteration t+1. For more details regarding the MBPFM, please refer to 10 and22.
The formula for the upper-triangular power flow method (UTPFM) formula is defined in (14).
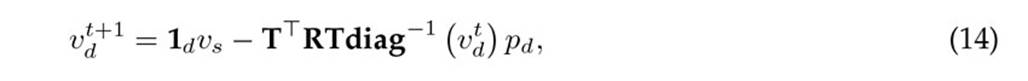
Where T represents the upper-triangular matrix; R is a square matrix whose diagonal contains all the resistive values of the branches; and 1d is a column vector with dimension d. For more details regarding the UTPFM, please refer to 23. Note that, for the sake of simplicity, the matricial operation T⊤ZT can be defined as Rdd, which can be interpreted as the nodal resistance matrix
3.2.2. Derivative-based power flow formulas
The most common derivative-based power flow method involves applying the Newton-Raphson iterative formula to determine the simultaneous roots of nonlinear equations 6. In general, the Newton-Raphson power flow method (NRPFM) defines the Recursive Power Flow Formula (15) 11
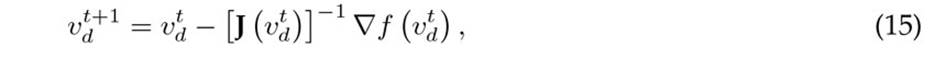
where J(vd
t) corresponds to the Jacobian matrix, which is filled with the partial derivatives of the demanded power pk with respect the voltages at nodes k and m in (12), i.e.,
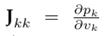and 
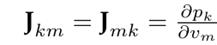, respectively. Note that ∇f(vd
t) was defined in (12) by changing v to vd
t.
Derivative-based power flow methods are well-known in the current literature, as is the case of the hyperbolic and product algorithms8. The iterative power flow formulas for the hyperbolic (HPFM) and the product (PPFM) power flow methods are defined in (16) and (17).
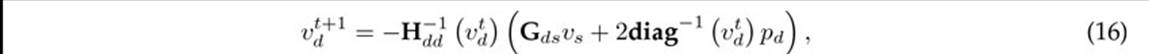
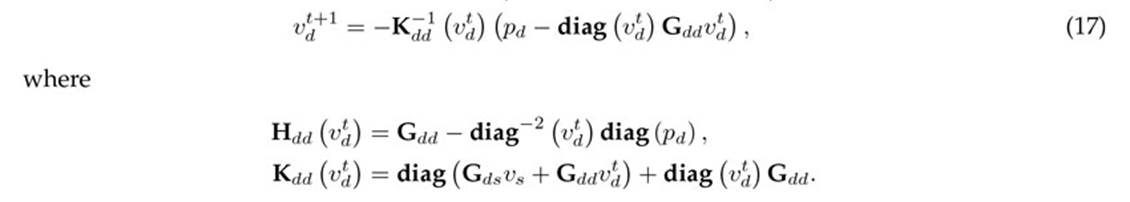
4. Broyden’s generalization
To demonstrate that all the recursive power flow formulas defined in the previous section can be obtained via Broyden’s iterative formula, some manipulations to the General Power Flow Problem (12) must be made. To this effect, the set of nonlinear equations in (12) is compacted as presented in (18).
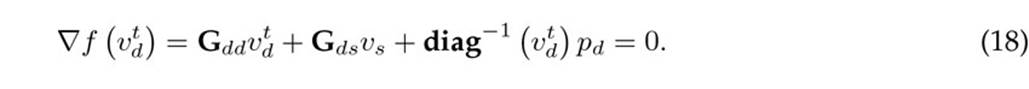
4.1. Derivative-free approaches and Broyden’s numerical method
To demonstrate that Broyden’s formula allows reaching the MBFPF Recursive Formula (13), the At+1 = At matrixis assumed to be constant. This, it is selected as Gdd. Note that, with this selection, the following recursive formula is reached in Eq. (1) by replacing x with vector vd
Now, if Eq. (19) is substituted into Eq. (18), the following set of equalities is obtained:
Here, Eq. (20) corresponds to the iterative power flow formula for the MBFPFM defined in (13). This demonstrates that, via Broyden’s numerical method, it is possible to obtain the well-known MBFPFM for monopolar DC networks, thus completing the proof.
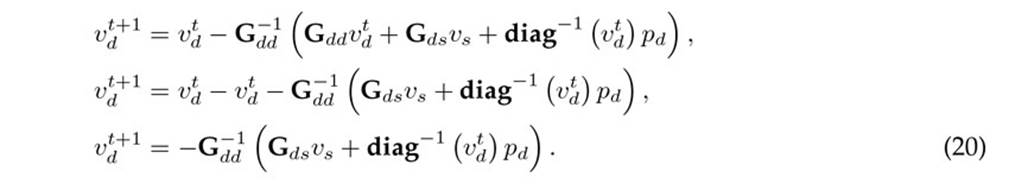
In the case of the UTPFM, prior to the application of Broyden’s iterative formula, Eq. 18 must be algebraically manipulated.
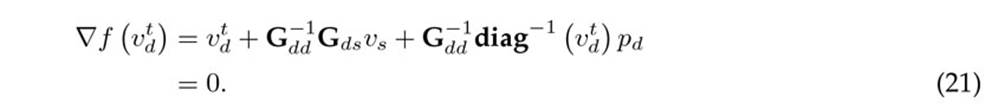
Here, it can be clearly demonstrated that
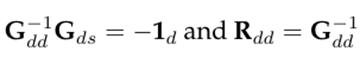which implies that Eq. (21) can be rewritten as Eq. (22)
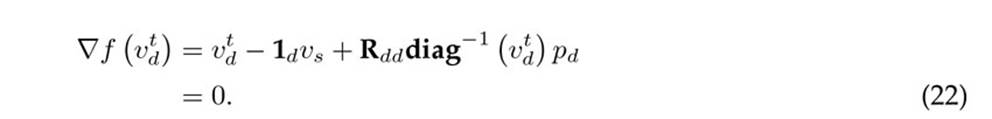
Now, if At+1 = At = Idd is selected (i.e., an identity matrix with d × d dimensions), then the application of Broyden’s recursive formula in (1) yields the following set of equalities:
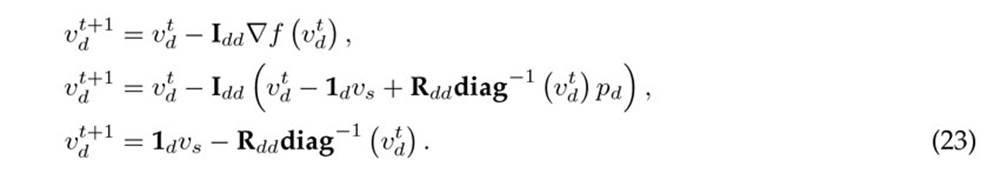
This confirms that, with an adequate selection of At in Broyden’s method, it is possible to obtain the UTPFrecursive formula defined in (14) for monopolar DC networks, which completes the proof
4.2. Derivative-based methods and Broyden’s numerical method
By mathematical induction, when comparing the NRPF Formula (15) against Broyden’s Formula (1), it can be concluded that At is selected as the Jacobian matrix, i.e., At = J(vt d). Therefore, both iterative methods are entirely equivalent.
In the case of the HPFM, prior to the application of Broyden’s recursive formula, a first-order Taylor series expansion is applied to the nonlinear component of (18), i.e., to the inverse matrix diag−1 (vt d). This nonlinear function can be linearized using a hyperplane (24):
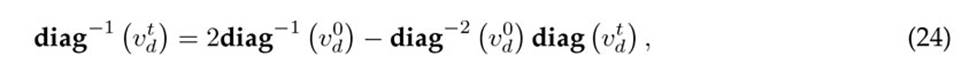
where v0 d corresponds to the linearizing point.
Note that, if 24 is substituted into (18), then ∇f (vt d) takes the form presented in Eq. (25).
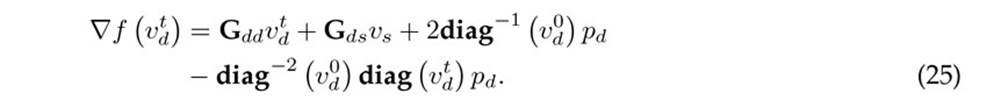
Eq. (25) can be simplified as (26) if the properties of the diagonal matrices and vectors are applied, i.e., diag (x)y = diag(y)x.
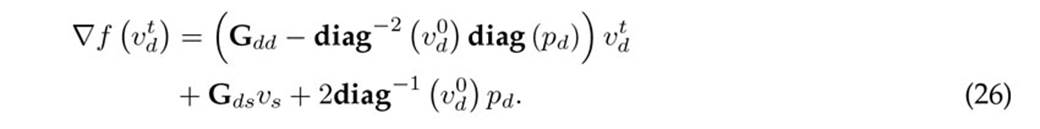
Here, it is clearly shown that Hdd (v0 d) = Gdd −diag−2 (v0 d) diag(pd) , which implies that, in the next iteration (i.e., vt+1), the value of v0 is generally vt
Now, if Broyden’s formula is applied to the gradient vector in (26), in the case of the HPF, the At matrix is selected as Hdd(vt d), which implies the following condition:
This is equivalent to the HPF formula defined in (16), which completes the proof. (27) In the case of the PPF formula, prior to the application of Broyden’s formula, the general nonlinear structure of ∇f (vt d) in (18) should be rewritten as follows:
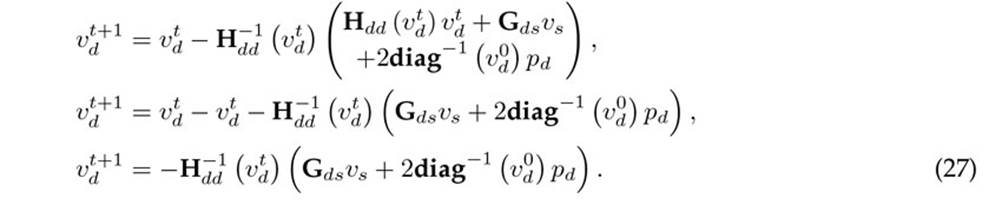
Now, in order to approximate the nonlinearities in (28) as a linear component, the product diag(vt d)Gddvt d can be relaxed as defined in Eq. (29).
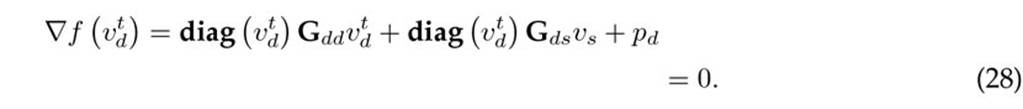
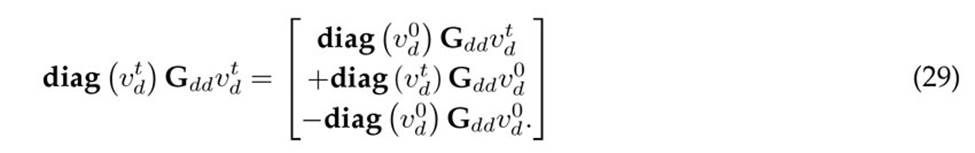
By considering the properties of the product between the diagonal matrices and vectors when substituted into (28), the following expression for ∇f (vt d) is reached.
Here, Hdd (v0 d)= (diag (v0 d) Gdd +diag(Gddv0 d +Gdsvs , which implies that, in the next iteration (i.e., vt+1), the value of v0 is generally vt
Now, if Broyden’s formula is applied to the gradient vector in (30), in the case of the PPF, the At matrix is selected as Kdd (vt d), which implies the following condition
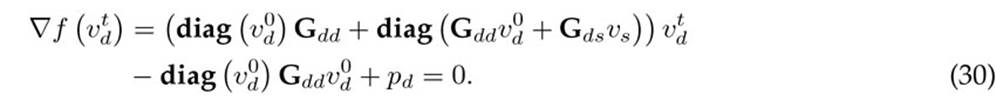
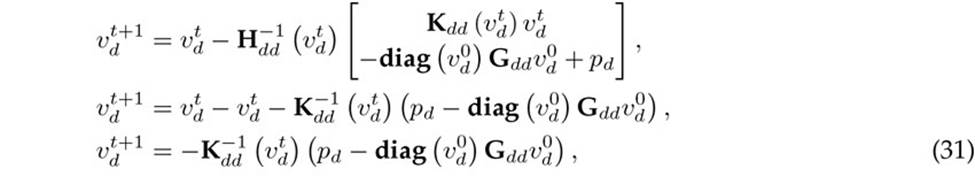
which is equivalent to the PPF formula defined in (17), which completes the proof.
5. The Gauss-Seidel case
One of the most classical and well-known numerical methods for dealing with the power flow problem in electrical networks is the Gauss-Seidel approach5. This method improves upon the Gauss-Jacobi approach for solving sets of linear equations, and it can be easily adapted to solve the power flow equations by analogy with a linear set of equations with the form Ax = b. Here, for the power flow problem, b is a function of the decision variables x, i.e., Ax = b(x) 6. The general iterative formula for the Gauss-Seidel method applied to monopolar DC networks is defined below
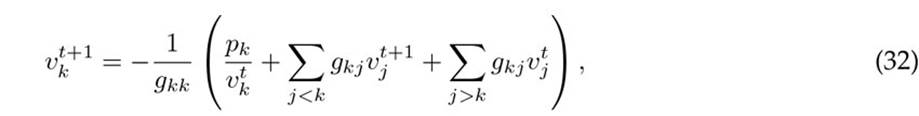
where gkk represents the diagonal component of the conductance matrix at node k, and gkj is the position of the conductance matrix that relates nodes k and j. Note that, if the conductance matrix Gdd is separated in the lower, diagonal, and upper matrices (i.e., the LDU representation Gdd = Ldd +Ddd + Udd), then the general Gauss-Seidel formula can be expressed as follows
The main characteristic of the Gauss-Seidel formula in (33) is that it can be directly obtained by manipulating the gradient vector ∇f (vt d).
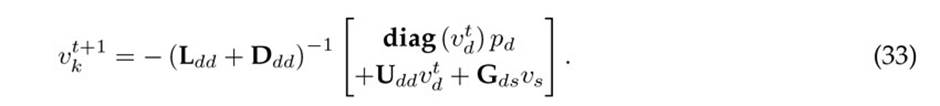
Note that, given the structure of the gradient vector in (34), if At+1 = At is selected as a constant matrix (i.e., Ldd + Ddd), then Broyden’s formula in (1) takes the following structure:
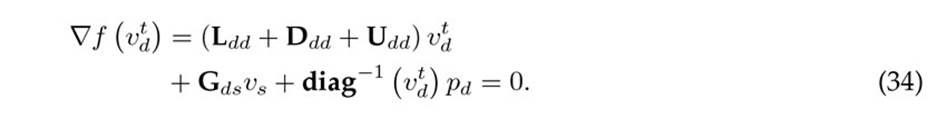
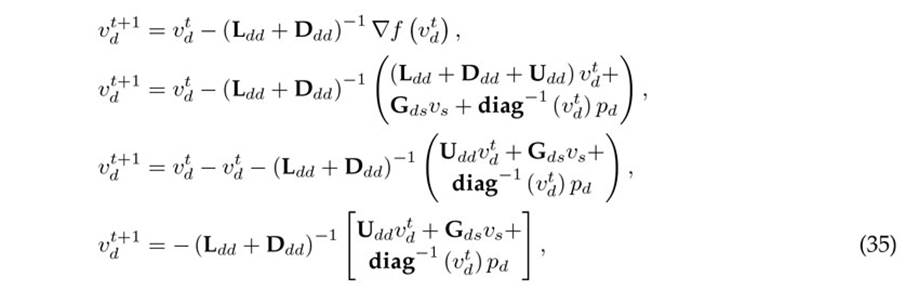
which, as expected, is equivalent to the general Gauss-Seidel power flow formula defined in (33), confirming that, with Broyden’s formula, the Gauss-Seidel formulation can be obtained for power flow analysis in monopolar DC networks
One of the main findings regarding the Gauss-Seidel method is that the MBFPFM is indeed an improvement of the Gauss-Seidel formula, where all the information in Gdd is used. In contrast, the Gauss-Seidel approach divides it into sub-components, directly affecting the total number of iterations, as demonstrated in 8
6. Conclusions
This editorial note provided a comprehensive derivation of the most widely used derivative-free and derivative-based power flow methods for monopolar DC networks with constant power loads, utilizing Broyden’s numerical approach. It was demonstrated that, by appropriately selecting the matrix At and structuring ∇f (vt d), all power flow formulations reported in the literature can be systematically derived within a unified successive approximations framework
As a future work direction, a rigorous convergence analysis of the Broyden family of power flow methods could be conducted using fixed-point theorems. Given that all the power flow formulations examined inherently exhibit a fixed-point structure, i.e., vd t+1 = g(vt d), such an analysis will provide deeper insights into the stability and reliability of these numerical approaches.
Acknowledgements
7. Acknowledgments
This research received support from the Ibero-American Program of Science and Technology for Development (CYTED), through thematic network 723RT0150, i.e., Red para la integración a gran escala de energías renovables en sistemas eléctricos (RIBIERSE-CYTED).
References
License
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
2.jpg)
