DOI:
https://doi.org/10.14483/23448393.2691Published:
2002-11-30Issue:
Vol. 8 No. 2 (2003): July - DecemberSection:
Science, research, academia and developmentIdentificación con Modelos Discretos para Sistemas Lineales. Modelo Matemático y Aplicaciones
Keywords:
Identificación, modelo discretos, lineal, recursivo, mínimos cuadrados, control, simulación (es).Downloads
References
NELLES, O. Nonlinear system identification. Alemania. Spriger, 2001. 785 p.
ASTROM, K WITTENMARK, B. Adaptive Control. Segunda edición. California. Addison Wesley. 1995. 574 pag
LJUNG, L. System identification: Theory for the user. United States of America. Prentice Hall, 1995. 519 p.
LJUNG, L. Theory and practice of recursive Identification. Primera Edición. United States of America. The MIT press., 1987. 529p.
LJUNG, L. System identification Toolbox. United States of America. MathWorks,Inc. 2001.
RUBIO, Francisco y LOPEZ, Manuel. Control adaptativo y robusto. España. Universidad de Sevilla. 1996. 365 p.
RICO, Jairo. Control identificación y estimación. Colombia. Universidad Distrital "Francisco José de Caldas ". 1997. 138p.
OGATA, Katsuhiko. Sistemas de control en tiempo discreto. Segunda edicion. México. Prentice Hall, 1996. 745p.
OPPENHEIM, A. Willsky, A. y Nawab, H. Señales y Sistemas, 2ª Ed.. Prentice Hall Hispanoamericana, Mexico, 1998. 532p.
PROAKIS, J y Manolakis, D. Tratamiento Digital de señales, 3ª Ed. Prentice Hall INC. España, 1998. 22 p.
MONTGOMERY, D y Runger, G. Probabilidad y Estadística, aplicadas a la ingeniería. Mc Graw Hill. Mexico, 1996. 506p.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:2 pág:47-55
Identificación con modelos discretos para sistemas lineales. Modelo matemático y aplicaciones
Identification with discrete models for lineal systems. Mathematical model and applications.
José Jairo Soriano
Profesor Universidad Distrital Francisco José de Calda. Área de Control.
Andrés Escobar Díaz
Miembro de IEEE y particularmente de la sociedad de sistemas de control, Universidad Distrital Francisco José de Calda. Área de Control.
Rodrigo Peña Ospina
Miembro de IEEE, Universidad Distrital Francisco José de Calda. Área de Control.
Resumen
Este documento desarrolla una técnica de identificación de sistemas basada en modelos lineales. Esta es una alternativa muy poderosa para identificar cualquier tipo de proceso real. Se trabaja sobre el análisis de procesamiento discreto y en el área de identificación de sistemas. El artículo empieza con el estudio de los Sistemas discretos lineales, que sirven para representar procesos reales. Se utiliza un algoritmo de identificación de parámetros para estos modelos basado en el método de mínimos cuadrados. Después se define como se prueba el algoritmo de identificación, se hace análisis de datos e implementación con Matlab® y LabView®, se precisa los procesos que se manipulan para identificación etc. Por último se da una base matemática para evaluar el sistema de identificación, mostrando resultados de los experimentos hechos y aplicaciones para el sistema de identificación en control.
Palabras Clave: Identificación, modelos discretos, lineal, recursivo, mínimos cuadrados, control, simulación.
Abstract
This document develops a technical of identification of systems based on lineal models. This is a very powerful alternative to identify any type of real process. Here works on the analysis of discrete processing and in the area of system identification. The article begins with the study of the lineal discrete models that they are used to represent real processes. An algorithm of identification of parameters is used for these models based on the method of least squares. After a methodology is defined to prove test the identification algorithm, which makes analysis of data and implementation with Matlab® and LabView®, also precise the processes that are manipulated for identification etc. Lastly a mathematical base is given to evaluate the identification system, showing results of the made experiments and applications for the identification system in control.
Key words. System identification, discrete models, lineal, recursive, least square, control, simulation.
INTRODUCCIÓN
Modelos matemáticos de procesos reales son necesarios y tienen mucha importancia en todas las disciplinas; son muy utilizados para el análisis de sistemas y permiten tener un mejor entendimiento del comportamiento de los procesos que se están estudiando. Igualmente permiten el diseño de nuevos procesos y la implementación de técnicas avanzadas como en el diseño de controladores, supervisión, optimización, detección de fallas, diagnostico etc. Incluso en aplicaciones para representar modelos no lineales, se piensa primero en un modelo lineal y si este no tiene un comportamiento satisfactorio entonces si y solo si se busca un modelo no lineal. Esto entonces implica que la calidad del modelo determina la calidad de la solución que se esta buscando para un determinado problema, de esta forma el modelaje de todo un sistema es parte crucial para analizar un proceso. Por todo esto en necesario tener a la mano herramientas de identificación de sistemas, y tener muy en claro las herramientas mas sencillas y practicas como son la identificación de sistemas lineales sobre plataformas discretas, que permiten ser mas flexibles y versátiles.
En el capitulo uno se describen los modelos matemáticos que pueden representar los procesos reales; en el capitulo dos se habla sobre el método de identificación de parámetros (mínimos cuadrados), a partir de datos entrada y salida de un proceso real. Cálculos recursivos, cálculos sobre modelos estáticos, las ecuaciones que se deben utilizar dependiendo el modelo utilizado son definidos también. El capitulo tres define como se prueba el algoritmo de identificación, se hace implementación con Matlab® y LabView®, se precisa los procesos que se manipulan para identificación etc. Por ultimo en los capítulos tres, cuatro y cinco se da una base matemática para evaluar el sistema de identificación, se muestra resultados de los experimentos hechos y aplicaciones para el sistema de identificación respectivamente. Al final se da conclusiones todo el trabajo hecho.
I. MODELOS DISCRETOS LINEALES.
En el momento que se quiere representar el comportamiento de un proceso, es necesario tener modelos matemáticos predefinidos. Al conocer estos modelos, se analizan y se comparan, con el objetivo de decidir cual puede representar el proceso que se esta estudiando.
Los modelos que se estudian son paramétricos [2] esto quiere decir que se asume que son capaces de describir el verdadero comportamiento de un proceso con un número finito de parámetros. Las ecuaciones diferenciales o en diferencias son ejemplos de este tipo de modelos. En ocasiones los parámetros tienen una relación directa con cantidades físicas del proceso, Ej., masa, volumen, longitud, etc.
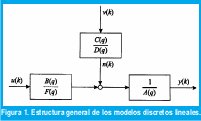
Estructura general de los modelos lineales discretos.Se introduce una estructura general de un modelo lineal y sobre esta se puede derivar los demás modelos específicos por simplificación. La salida y(k) de un sistema linear determinístico en el tiempo k puede ser calculada filtrando las entradas u(k) a través de un filtro lineal G(q), donde es el operador de desplazamiento[1].
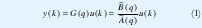
B˜ (q) y à (q) son el numerador y el denominador de la función de transferencia lineal G(q) respectivamente. En adición a la parte determinística, un parte estocástica puede ser introducida. Filtrando un ruido blanco v(k) a través de un filtro lineal H(q), cualquier característica de frecuencia de ruido puede ser modelada. Así una señal arbitraria n(k) de ruido puede ser modelada.
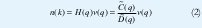
Un modelo lineal general describiendo influencias determinísticas y estocásticas es obtenido combinando las dos partes, Fig. 1.
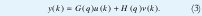
El filtro G(g) es llamado la función de transferencia de entrada, desde que esta relacione la entrada u(k) con la salida y(k), y el filtro H(q) es llamado función de transferencia del ruido, desde que esta relacione el ruido con la salida. Las funciones de transferencia G(q) y H(q) pueden ser divididas en polinomios que representan sus numeradores y sus denominadores, Fig. 1. Es de ayuda separar una posible existencia de dinámicas con denominador común, A(q) de G(q) y H(q). Así F(q) A(q) = à y D (q) A(q) = D˜. Si à (q) y D˜(q) no comparten factores comunes entonces A(q) = 1. Entonces el modelo general lineal puede ser escrito.
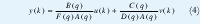
Asumiendo ciertas casos especiales sobre los polinomios A, B, C, D, F ; los modelos lineales ampliamente aplicados son obtenidos de la forma general de los modelos lineales.
Clasificación y terminología de los modelos. Se empieza analizando las series de tiempo, es decir no se toman en cuenta la entrada del modelo, entonces u(k) = 0, así los modelos analizados serán totalmente estocásticos. Una serie de tiempo con solo polinomio del denominador D(q) es llamado un modelo Autoregressive (Autoregresivo) AR. Un modelo de serie de tiempo solo con el polinomio del numerador C(q), es llamado un modelo Moving average (promedio móvil) MA. Un modelo de serie de tiempo con polinomio numerador C(q) y D(q) denominador es un modelo llamado autoregressive moving average (promedio móvil y auto regresivo) ARMA. Es obvio que un modelo basado en una serie de tiempo, sin tener en cuenta las variables de entrada, no puede ser preciso. Por esto modelos más precisos pueden ser construidos incorporando las variables de entrada dentro del modelo. Esta entrada u(k) es llamada una entrada exogenous (exógena). Teniendo en cuenta lo anterior, los modelos de series de tiempo pueden ser extendidos, incorporando una "X" por la entrada exógena.
Cuando se tiene en cuenta las entradas a los modelos, estos se convierten en modelos entrada/salida. Los modelos denominados AR, pertenecen a la clase de modelos equation error (error de ecuación). Su característica es que el filtro 1/A(q) es común a ambos, al modelo del proceso determinístico y al modelo de ruido estocástico. Los modelos los cuales son caracterizados por un modelo de ruido que es independiente del modelo del proceso determinístico, pertenecen a la clase de modelos output error (error de la salida).
El modelo ARX, autoregressive with exogenous input, (auto regresivo con variable exógena) es una extensión del modelo AR. Fig. 1.
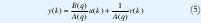
El termino "auto regresivo" se relaciona a que la función de transferencia esta afectada desde la entrada u(k) a la salida y(k) tambien como la función de transferencia del ruido desde v(k) a y(k). Así, la parte estocástica y la parte determinística del modelo ARX tienen dinámicas con idéntico denominador.
El modelo autoregressive moving average with exogenous input (auto regresivo y promedio móvil con variable exógena) ARMAX es un extensión del modelo ARMA. Fig.1.

Como para el modelo ARX, el modelo ARMAX asume igual dinámica con idéntico denominador para la entrada y la función de transferencia del ruido. Sin embargo la función de transferencia del ruido es más flexible debido al polinomio de promedio móvil C(q). [2][3][4].
Todos los modelos AR comparten el polinomio A(q) como dinámica en el denominador en la función de transferencia de entrada y la función de transferencia del ruido. Esto corresponde a que el ruido no influye directamente a la salida y(k) del modelo pero en cambio se introduce al modelo antes del filtro 1/A(q). Estos modelos adoptados son razonables si verdaderamente el ruido se introduce al proceso primero, entonces sus características de frecuencia son determinadas por la dinámica del proceso. Si el ruido es principalmente medidas de ruido que típicamente y directamente perturba la salida, los llamados modelos output error (error de salida) son mas realistas.
Los modelos output error son caracterizados por modelos de ruido que no contienen la dinámica del proceso. Así, el ruido se asume que afecta la salida del proceso directamente. El mas evidente de los modelos output error es el output error (error de salida) OE. Fig.1.
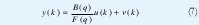
Este modelo OE es un modelo especial en la clase de los modelos output error. Note que por simplicidad los procesos y los modelos se asumen que no tienen tiempo muerto. Sin embargo, en cualquier ecuación el tiempo muerto puede ser fácilmente introducido reemplazando la entrada u(k) con la entrada retrasada d pasos u(k-d). A demás, esto supone que los procesos y los modelos no tienen camino directo desde la entrada a la salida, entonces u(k) no afecta inmediatamente la salida. Entonces, los términos como bou (k) no aparecen en las ecuaciones de diferencia. Estas suposiciones son cumplidas por casi cualquier proceso del mundo real. [2][3][4].
II. IDENTIFICACIÓN DE PARÁMETROS.
En este capitulo se desarrolla un método de estimación de parámetros, llamado míninos cuadrados, LS. El método LS es ampliamente utilizado por su eficacia, sencillez y eficiencia computacional. Se trabaja con sistemas SISO (Single input, Single Output). El método de mínimos (LS) cuadrados es la técnica básica de identificación paramétrica, es simple si el modelo tiene la propiedad de ser lineal en sus parámetros, así las estimación de los parámetros por este método puede ser calculado analíticamente.
Mínimos cuadrados (LS) y modelos de regresión. El modelo matemático es particularmente simple y puede ser escrito de la siguiente manera [1][2][3][4].
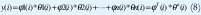
Donde y es la variable observada, que en términos de control es el valor de salida de un proceso en un instante i; θ1, θ2,..., θn son los parámetros del modelo para ser determinados, y φ1, φ2,..., n son funciones conocidas que quizás dependan de otras funciones conocidas. En términos de control estas funciones son datos de entrada y salida pasados.
Definiendo los siguientes vectores como:
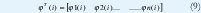
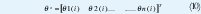
El modelo es indexado por la variable i, la cual generalmente denota la variable tiempo. Se asume que el conjunto indexado es un conjunto discreto. Las variables φ.i son llamadas variables de regresión o regresores, y el modelo de la EC. (1) es llamado modelo de regresión. La pareja de observaciones y regresores {(y(i), φ(i)), i = 1,2,...t } son obtenidos en un experimento.
El problema es entonces deter minar los parámetros de tal forma que las salidas calculadas del modelo de la EC. (8) concuerde tan cerca como se posible con la medida de las variables y(i) en el sentido de mínimos cuadrados. Esto es, los parámetros θ° deben ser escogidos para minimizar la función de perdida mínimos cuadrados.
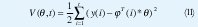
Desde que la variable medida y(i) es lineal en parámetros θ° y el criterio de mínimos cuadrados es cuadrático, el problema admite una solución analítica. Introduciendo la notación.
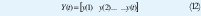

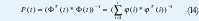
Donde los residuos ee(i) son definidos por.
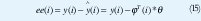
La solución para el problema de mínimos cuadrados es dada por lo siguiente, la función de la Ecuación (EC) 11 es mínimo para parámetros θˆ tal que.
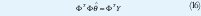
Si la matriz ΦT Φ es no singular, el mínimo es único y es dada por [1].
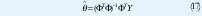
Cálculos Recursivos. En muchas aplicaciones las observaciones son obtenidas secuencial mente en tiempo real. Por esto es necesario hacer cálculos recursivos para ahorrar tiempo de cálculo. El cálculo de la estimación de mínimos cuadrados puede ser reconfigurada de tal forma que los resultados obtenidos en el tiempo t-1, puedan se usados para la estimación en el tiempo t.[1][2]. Las Ecuaciones en forma recursiva son.
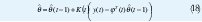
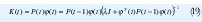
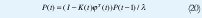
Parámetros variantes en el tiempo. En el modelo de mínimo cuadrados EC 1 los parámetros θ°i se asumen que son constantes. En muchos problemas de control y filtros adaptativos es importante considerar la situación en la cual los parámetros son variantes en el tiempo. Dos casos son cubiertos con una simple extensión del método de los mínimos cuadrados. Uno es el caso en que los parámetros cambian abruptamente pero no con mucha frecuencia. El otro caso es que los parámetros cambien continuamente pero lentamente. El caso en que los parámetros cambian abruptamente la solución es reestablecimiento. La matriz P en el algoritmo de mínimos cuadrados es periódicamente reestablecida a αI, donde α es un numero grade. Esto implica que la ganancia K(t) en el estimador llega a ser grande y la estimación puede ser actualizada con un paso más grande. El caso en el cual los parámetros varían en el tiempo pero lentamente puede ser trabajando con un simple modelo matemático. Una aproximación simple es cambiar el criterio de mínimos cuadrados de la EC 11 con.
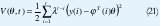
Donde λ es un parámetro tal que 0 < λ ≤ 1. El parámetro λ es llamado factor de olvido. La función de perdida de la EC 21 implica que una ponderación variante en el tiempo es introducida. El más reciente dato se la da una ponderación de uno, pero el dato que esta n antiguas unidades de tiempo es ponderado por λn . El método es llamado olvido exponencial.
Se asume que la matriz φ(t) tiene rango completo para t ≥ to. Los parámetros θ, los cuales minimizan la EC 21 son dados recursivamente en las EC 18, 19, 20. Queda entonces definido el método de mínimos cuadrados recursivos (RLS) con olvido exponencial.
Condiciones iniciales para P(t) y para θ(t). Para que el algoritmo de identificación converja rápidamente se inicializa las variables θˆ(0) = 0 , P(0) = kI, donde k es un número grande[1][3].
Estimación de parámetros en sistemas dinámicos. El método de mínimos cuadrados puede ser usado para estimar los parámetros en modelos de sistemas dinámicos. Esto depende de las características del modelo y de su parametrización. Esto quiere decir que todas las ecuaciones antes formuladas pueden ser utilizadas con estos modelos haciendo unos pequeños ajustes.
Modelos de funciones de transferencia. Dado el sistema descrito por el modelo EC 5 Y A(q) y B(q) son los polinomios.

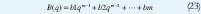
Los parámetros del polinomio A(q) define la cantidad de polos de sistema, y B(q) define la cantidad de ceros del sistema , esto desde el punto de vista de control. La EC 5 como ecuación en diferencias sin tener en cuenta la entrada de ruido es.

Se asume que la secuencia de entrada {u(1), u(2),... u(t)} ha sido aplicada a el sistema y la correspondiente secuencia de salida {y (1), y (2),...,y(t)} ha sido observada. El vector de parámetros es.

y el vector de regresión.
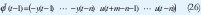
El modelo puede ser escrito formalmente como el modelo de regresión.
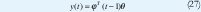
La estimación de parámetros puede ser hecha aplicando la estimación de míninos cuadrados, LS o RLS. La matriz Φ es.
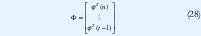
Si se usa interpretación estadística de la estimación de mínimos cuadrados, el método descrito trabajara bien cuando las perturbaciones puedan ser caracterizadas con ruido blanco como en la EC 5, lo que quiere decir que se tiene ya un estimador de parámetros para un modelo ARX.[1][3].
Una pequeña variación del método es mejor si las perturbaciones son descritas como ruido blanco sumado a la salida del sistema, EC 7. El método es el siguiente, sea u la entrada y yˆ la salida de un sistema con la relación entrada salida.

Entonces

Determina los parámetros que minimice el criterio
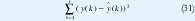
Donde y(t) = yˆ(t) + e(t). Así el problema puede ser interpretado como problema de mínimos cuadrados el la cual la solución esta dada por
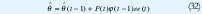
Donde

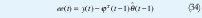
Con las ecuaciones anteriormente descritas ya se puede estimar los parámetros de un modelo OE.
Modelos Estocásticos. La estimación de mínimos cuadrados es parcial cuando el error e(i) es correlacionado. Una posibilidad de solucionar este problema con el método de estimación de mínimos cuadrados es modelar la correlación de las perturbaciones y estimar los parámetros describiendo la correlación. Considere el modelo de la EC 6.
Donde A(q), B(q), C(q) son polinomios y e(t) = v(t) es ruido blanco. Los parámetros del polinomio C describe la correlación de las perturbaciones. El modelo de la EC 6 no puede ser convertido directamente a un modelo de regresión, puesto que las variables relacionadas con el ruido no se conocen. Un modelo de regresión puede ser definido con apropiadas aproximaciones de todas formas. Para describir esto se define.
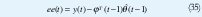
Donde
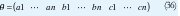

Las variables e(t) son aproximadas por la predicción del error ee (t) . El modelo puede ser aproximado a.
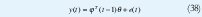
y entonces se puede aplicar la estimación recursiva de mínimos cuadrados. El método obtenido es llamado mínimos cuadrados extendidos (ELS). Las ecuaciones para la actualización de la estimación queda definida por:
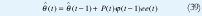
III. EVALUACIÓN PRÁCTICA
Después del planteamiento del algoritmo, el paso siguiente es evaluar su desempeño dentro de un ambiente controlado. Para tal caso el experimento destinado a la evaluación debe cumplir con ciertos requerimientos, tales que lo sitúen dentro de condiciones conocidas, pero que no lo distancien demasiado del ambiente que deberá enfrentar ante las condiciones de operación reales para las que esta destinado. Teniendo esto en mente se ejecutó el algoritmo de estimación en sistemas lineales de primer y segundo orden sin tiempo muerto, representados mediante circuitos eléctricos de estos ordenes Fig. 2. La elección de este tipo de sistemas obedece a que son lo suficientemente conocidos y a que los modelos físicos que los representan son tan confiables que cualquier particularidad en los datos de evaluación no podrá ser confundido con comportamientos "desconocidos" del sistema.
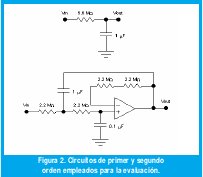
De otro lado, dado que el sistema esta destinado a la identificación de sistemas lineales mediante un modelo ARX, y que la cantidad de parámetros limite definida es de dos polos y un cero para el modelo de la planta, la evaluación debe estar sobre estos márgenes, para obtener un panorama claro del comportamiento del algoritmo. Ahora bien, en lo referente a la selección de los valores de los elementos del circuito, ambos sistemas deben encajar dentro de ciertos límites. En primera instancia, la respuesta en frecuencia de estos sistemas (especialmente el de segundo orden, debido a la naturaleza oscilatoria de su repuesta) debe estar de acuerdo al teorema de Nyquist [9] para el periodo de muestreo escogido, dado que el algoritmo esta destinado a correr en tiempo real. Más aun, si una posible aplicación del procedimiento es la ejecución de un control discreto de autosintonía, los requerimientos son mas críticos en torno al muestreo y es deseable que se ejecute un muestreo de ocho a diez veces durante un ciclo de oscilaciones sub-amortiguadas o en caso tal, ocho a diez veces el tiempo de levantamiento de la respuesta sobre-amortiguada [8]. Asociado a este conjunto de parámetros están los requerimientos técnicos del proceso, los cuales son básicamente el tiempo de muestreo mínimo logrado por la máquina, ante una aplicación montada en plataformas de alto nivel tal como lo son Matlab® Y LabView®.
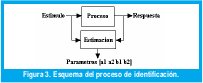
Refiriéndose ya a las pruebas en sí, el procedimiento es el de recopilar información del proceso Fig. 3, de la cual se obtenga la información suficiente para su evaluación; como tal los datos necesarios por cada periodo de muestreo, son el estímulo, la respuesta y los parámetros calculados cada vez por el algoritmo de estimación. Este conjunto de datos se recoge para tres diferentes tipos de señal de entrada, cuadrada, triangular y senoidal [4]. Así como para diferentes condiciones del algoritmo en términos del retardo, aplicándose el procedimiento a ambos sistemas de primer y segundo orden. La información obtenida del sistema, se emplea para el calculo de la señal de salida de acuerdo a los valores de parámetros y la señal de excitación para ese instante de muestreo, teniendo en cuenta además el valor del retardo d, con el que fue efectuada la estimación (41).
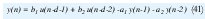
IV. MÉTODO DE ANÁLISIS
Definida ya la estructura de la evaluación, es preciso introducir ahora los criterios matemáticos y estadísticos que permiten evaluar cuantitativamente el comportamiento del algoritmo. A grandes rasgos un algoritmo de estimación es eficiente si es capaz de calcular el comportamiento de un sistema para una señal de excitación conocida y los resultados coinciden con el comportamiento real del sistema. Esto a la larga puede ser evaluado a simple vista observando las respuestas real y calculada sobre una misma gráfica, sin embargo esto aparte de ser práctico no es muy objetivo y suele ser necesario acudir a algo mas formal para emitir un juicio confiable. Para tal caso lo mas adecuado es recurrir a la evaluación de los residuos de estimación, EC 15, de modo que estos tengan una distribución aproximadamente normal con media cero y varianza constante, esto es verificable a través de diversos métodos, algunos acuden al análisis gráfico y otros al análisis analítico, para este caso se restringen las opciones al estudio de la media, la desviación estándar y el porcentaje de los residuos estandarizados dentro del rango [-2, 2] EC 42 [11]. Este último indica que la distribución probabilística de los residuos se aproxima a la Gaussiana si este porcentaje es cercano al 95%, siendo óptimo un 100%.
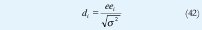
En lo que respecta a la interpretación de estas mediciones, ninguna de estas es útil por separado y solo es posible obtener una visón clara del comportamiento de la estimación al analizarlas paralelamente. Como ya se dijo, una distribución normal de los residuos debe poseer una media igual o muy cercana a cero con el fin de que los residuos sean lo más parecidos a un ruido blanco no correlacionado con la entrada. Para la desviación estándar se desean valores pequeños, que muestren baja dispersión de los residuos, o en otras palabras, pocos errores que sean significativos con respecto al resto de la muestra (esto es muy válido para descartar muestras con residuos grandes durante los primeros instantes de muestreo). Finalmente, la evaluación del porcentaje de residuos estandarizados dentro del rango [-2, 2] es especialmente engañosa, ya que esta operación puede dar una calificación excelente aunque la identificación en sí haya sido un desastre, esto se debe a que el residuo estandarizado es inversamente proporcional a la desviación estándar de la muestra. En contraste el que el porcentaje dentro de la región [-2, 2] esté por debajo de un 90% aproximadamente, definitivamente deja ver un proceso de identificación deficiente, por ello, este tipo de medición solo es útil como un primer acercamiento.
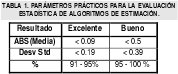
A partir de los resultados de múltiples experiencias en este trabajo, es posible enunciar un conjunto de parámetros prácticos útiles para evaluar la estimación a partir de las estadísticas mencionadas Tabla 1. Por debajo de estos valores el resultado es bastante pobre y realmente los modelos obtenidos no serán fiables posiblemente durante un gran intervalo de tiempo o en ningún momento.
V. RESULTADOS OBTENIDOS
Dadas las condiciones, lo primero que se debió verificar fue la opción práctica de lograr un periodo de muestreo (Ts) ajustable y dinámico, es decir que tendiese hacia el menor valor posible de acuerdo a la capacidad de procesamiento de la máquina. Aunque esto es posible sin mayor dificultad técnica, las implicaciones en el desempeño no son muy atractivas, ya que las desviaciones en Ts son claramente significativas Fig. 4, y dependen de las interrupciones a la secuencia causadas por software y hardware (Ej. mouse, teclado, etc.). Por otra parte la teoría convencional del procesamiento digital de señales suele estar soportada por un periodo de muestreo periódico o uniforme[10]; Entonces el caso contrario podría llevar a inconsistencias matemáticas en los algoritmos. Por último y no por ello menos importante, ya que la información del valor del periodo de muestreo es útil en la implementación de controladores adaptativos, y este valor es calculado a partir de los contadores del procesador (los cuales son finitos y se desbordan, ocasionando errores en la medida), cualquier error en este valor puede llevar a desviaciones en el control, que pueden llegar a ser inaceptables en muchos casos.
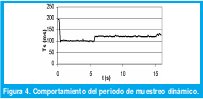
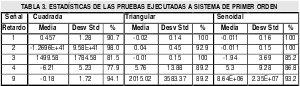
Luego de haber precisado la necesidad de un periodo de muestreo fijo, el evaluar el comportamiento del algoritmo empleando una frecuencia de muestreo insuficiente, ilustra los requerimientos mínimos para lograr resultados aceptables en cuestión de identificación, Tabla 2. Dichas pruebas fueron ejecutadas a un circuito RC de primer orden con τ=1.1 s y Ts=0.5s, lo que ocasiona aproximadamente cinco muestras durante el tiempo de levantamiento; Para el caso del circuito de segundo orden el periodo de la oscilación amortiguada es de 4.6 s con Ts=0.8 s para aproximadamente seis muestras por ciclo de oscilación, Fig 5. En las gráficas el eje horizontal denota número de muestras.

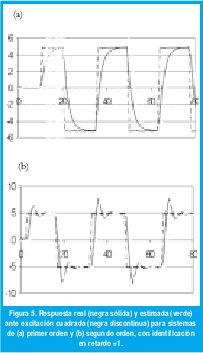
Del análisis de las gráficas y de las estadísticas se aprecia que periodos de muestreo insuficientes ocasionan desviaciones importantes en la estimación aun cuando esta tienda a converger en algún momento, por ello se encuentra que la relación entre los tiempos de respuesta del sistema con el periodo de muestreo deben por encima de 8 muestras.
Consecuentemente con estas pruebas y para los sistemas tomados para la experimentación Fig 2. Se determinó un periodo de muestreo que cumpliese con los requerimientos de la teoría de control discreto [1][8] (estabilidad y contralabilidad) y que adicionalmente contenga un margen de error suficiente para cumplir con operaciones adicionales, dentro reprocesamiento en tiempo real [1][10]. En la práctica este periodo fue de 0.5 s y con el se desarrollo todo el conjunto de pruebas que se describen a continuación.
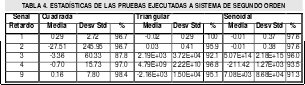
Para cualquier sistema discreto la respuesta ocurre en el segundo instante de muestreo, por esto se requiere un retardo de uno como mínimo en el modelo[1][4] y esto es aun mas evidente para los sistemas empleados para la experimentación, los cuales por su dinámica no poseen tiempo de retardo y el retardo d, necesario para la ejecución del algoritmo identificación es de uno. Sin embargo el comportamiento de los residuos a medida que cambia el retardo es de suma importancia ya que permite ver que tan crítica es la elección de su valor para sistemas de cuyo conocimiento no se tenga tanta certeza. De esta forma se aplico el algoritmo con diversos valores de retardo a ambos sistemas; Observándose en las estadísticas Tabla 3 y Tabla 4, que la respuesta de la estimación no solo varia de acuerdo al retardo sino también de acuerdo a el tipo de excitación aplicada y si bien es necesario que la señal excite todos los modos del sistema [4], del mismo modo es cierto que señales como la onda cuadrada ejercen un cambio abrupto cuyo espectro no es del todo contemplado por el muestreo y consecuentemente por el algoritmo. Esto se evidenció por primera vez en las estadísticas con bajas frecuencias de muestreo y aparece de nuevo, especialmente en la respuesta del sistema de segundo orden, aun para estos casos en donde se supone un periodo de muestreo adecuado de acuerdo a lo enunciado párrafos mas arriba; Aun así el elevar la tasa de muestreo con respecto a las pruebas de la tabla 2, muestra ligeras mejoras en las estadísticas.
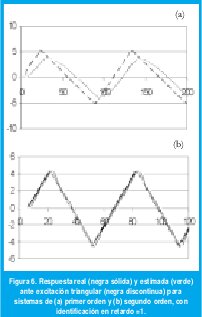
Por otra parte los resultados en cuanto a las excitaciones senoidal y triangular son bastante alentadores y muestran una ligera inclinación de los indicadores a favor de la onda triangular, lo cual se debe a que esta es un punto intermedio en riqueza espectral entre las señales senoidal y cuadrada Fig 6.
VI. PERSPECTIVAS DE APLICACIÓN
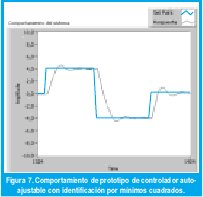
El abanico de aplicaciones posibles para la identificación de sistemas es muy amplio y si bien no es el objeto de este documento, es interesante mostrar un prototipo de aplicación hacia el control adaptativo; Más específicamente hacia la realización de un controlador auto-ajustable, implementado mediante el método de diseño por ubicación de polos y ceros propuesto por Astrom y Wittenmark [1][6]. En la figura 7 se aprecia un detalle del panel de control del instrumento virtual, en el que se observa la respuesta del sistema de primer orden de la figura 2, en el que se especifica la respuesta transitoria deseada, en este caso para una constante de amortiguamiento de 0.59 y una frecuencia natural de 1.56 rad/s.
VII. CONCLUSIONES
En un proceso de estimación de parámetros es muy importante escoger el modelo con se quiere representar el comportamiento de un proceso o unos datos de entrada-salida sistema. Si se escoge un modelo con pocos parámetros para estimar, este no representa tan precisamente el comportamiento del proceso; pero también si se escoge modelo con demasiados parámetros, se pueden tener los mismos resultados representando el proceso con un modelo con menos parámetros. A esto último se le conoce como sobre ajuste del modelo.
La estimación de mínimos cuadrados se puede utilizar en una infinidad de aplicaciones; ecuaciones algebraicas, ecuaciones que representen modelos de sistemas, ecuaciones no lineales, ecuaciones discretas, ecuaciones continuas etc., pero lo importante es que las ecuaciones utilizadas sean lineales en sus parámetros.
El algoritmo de estimación de mínimo cuadrados puede utilizarse para identificar los parámetros de cualquier modelo paramétrico, lo importante es identificar la estructura de los vectores; parámetros de estimación y regresión, para cada tipo de modelo. Así se puede estar seguro de los datos necesarios para el calculo de la estimación como el conocimiento y ubicación exacto de los parámetros que se están calculando.
La estimación recursiva es vital en la síntesis de controladores adaptativos, puesto que los datos de entrada salida de un sistema son obtenidas se sequencialmente en tiempo real. Esta estimación debe estar comprometida con el tiempo de muestreo del sistema, ya que compromete la estabilidad del sistema; no obstante es posible también efectuar la identificación no recursiva a partir de datos estadísticos de un proceso tomados previamente y obtener un modelo para el. Así cuando se tiene un modelo de un proceso se puede; predecir su salida, simular su comportamiento, hacer un estudio más amplio del proceso, intentar diferentes estrategias de control para cumplir un objetivo de comportamiento etc. Definitivamente es una gran ventaja tener el modelo de un proceso con lo cual se esta acotando la ventana de incertidumbre que se tiene sobre un determinado sistema.
La ejecución del algoritmo de identificación sobre un sistema en particular si bien esta destinada al modelaje del mismo, no puede ser llevada a cabo sin tener un conocimiento previo de la dinámica de este, como se vio en los experimentos llevados a cabo, para lograr un éxito relativo con la estimación, como mínimo es necesario conocer el orden del sistema, sus tiempos de respuesta, el retardo y las señales por las que va a ser influenciado. A la larga los requerimientos nombrados hacen parte de unas nociones poco menos que intensivas del sistema. De esta forma la identificación de sistemas se convierta en una herramienta del analista o diseñador mas que en su sustituto.
Fue posible evidenciar que la evaluación del desempeño del algoritmo bien pudo ser ejecutada en términos analíticos, lo cual deja espacio para realizar este tipo de tarea secuencialmente por una máquina, o de manera inteligente aprovechando los calificativos de las estadísticas hechas, para utilizar sistemas de inferencia difuso (FIS).
VII. REFERENCIAS BIBLIOGRÁFICAS.
[1] NELLES, O. Nonlinear system identification. Alemania. Spriger, 2001. 785 p.
[2] ASTROM, K WITTENMARK, B. Adaptive Control. Segunda edición. California. Addison Wesley. 1995. 574 pag
[3] LJUNG, L. System identification: Theory for the user. United States of America. Prentice Hall, 1995. 519 p.
[4] LJUNG, L. Theory and practice of recursive Identification. Primera Edición. United States of America. The MIT press., 1987. 529p.
[5] LJUNG, L. System identification Toolbox. United States of America. MathWorks,Inc. 2001.
[6] RUBIO, Francisco y LOPEZ, Manuel. Control adaptativo y robusto. España. Universidad de Sevilla. 1996. 365 p.
[7] RICO, Jairo. Control identificación y estimación. Colombia. Universidad Distrital "Francisco José de Caldas ". 1997. 138p.
[8] OGATA, Katsuhiko. Sistemas de control en tiempo discreto. Segunda edicion. México. Prentice Hall, 1996. 745p.
[9] OPPENHEIM, A. Willsky, A. y Nawab, H. Señales y Sistemas, 2ª Ed.. Prentice Hall Hispanoamericana, Mexico, 1998. 532p.
[10] PROAKIS, J y Manolakis, D. Tratamiento Digital de señales, 3ª Ed. Prentice Hall INC. España, 1998. 22 p.
[11] MONTGOMERY, D y Runger, G. Probabilidad y Estadística, aplicadas a la ingeniería. Mc Graw Hill. Mexico, 1996. 506p.
José Jairo Soriano
Profesor Universidad Distrital Francisco José de Calda. Área de Control.
Andrés Escobar Díaz
Estudiante de ingeniería electrónica, decimo semestre, Universidad Distrital Francisco José de Caldas. Sigue las líneas de profundización control y Procesamiento Digital de Señales. Miembro de IEEE y particularmente de la sociedad de sistemas de control. escobarand1@hotmail.com
Rodrigo Peña Ospina
Estudiante de ingeniería electrónica, decimo semestre, Universidad Distrital Francisco José de Caldas. Sigue las líneas de profundización de control y Procesamiento Digital de Señales. Miembro de IEEE. rodrigo_p@rocketmail.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










