DOI:
https://doi.org/10.14483/23448393.2094Published:
2006-11-30Issue:
Vol. 12 No. 1 (2007): January - JuneSection:
Science, research, academia and developmentDiseño de un modelo de tráfico a través de series de tiempo para pronosticar trafico Wimax
Design Of A Traffic Model Through Time Series To Forecast Wimax Traffic
Keywords:
ARIMA, autocorrelación, correlación, estocástico, modelo de tráfico, serie de tiempo, red de comunicaciones (es).Downloads
References
AKAIKE, H. Fitting autoregressive models for prediction. Annals of the institute of statistical mathematics. 1969. p. 243-247.
AKAIKE, H. Information theory and an extension of the maximum likelihood principle. Second international symposium on information theory. Budapest. 1973. p. 267-281.
ALZATE, Marco Aurelio. Modelos de tráfico en análisis y control de redes de comunicaciones. En: Revista de ingeniería de la Universidad Distrital Francisco José de Caldas. Bogotá. Vol. 9, No. 1 (Junio 2004); p. 63-87.
ANDERSON, T. W. Maximum likelihood estimation for vector autoregressive moving-average models, directions in time series. Institute of mathematical statistics. 1980. p. 80-111.
ANSLEY, C. F. y KOHN, R. On the estimation of ARIMA models with missing values, Time series analysis of irregularly observed data. Editorial Parzen, 1985. p. 9-37.
ARMSTRONG, J.S. Principles of forecasting. Editorial Springer. 2001.
ARVIDSSON, Å. y KARLSSON, P. "On traffic models for TCP/IP". Proc. of 16th international teletraffic congress (ITC). Edinburgh. Junio, 1999; p. 457-466.
BERAN, J. Statistics for long-memory processes. Chapman & Hall. 1994.
BERTSEKAS, Dimitri y GALLAGER, Robert. DataNetworks. Segunda edición. New Jersey: Prentice Hall, 1987.
BOX, G. E. P. y COX, D. R. An analysis of transformations. Stat. soc. 1964. p. 211-252.
BOX, G. E. P. y JENKINS, Gwilym M. Time series analysis: Forecasting and control. Revised Edition. Oakland, California: Editorial HoldenDay, 1976.
BOX, G. E. P. y PIERCE, D. A. Distribution of residual autocorrelations in autoregressive-integrated moving-average time series models. Stat. assoc. p. 1509-1526.
BRILLINGER, D.R. Time series: data analysis and theory. Universidad de California. Holden-Day. SIAM. 2001.
BROCKWELL, P.J. On continuous-time ARMA processes. En: Handbook of statistics. Elsevier, Amsterdam: Vol. 19, 2001. p. 249276.
BROCKWELL, P.J. y DAVIS, R.A. Introduction to time series and forecasting. Second edition. New York: Editorial Springer, 2002.
BROCKWELL, P.J. y DAVIS, R.A. Time series: theory and methods. Springer Verlag, New York. 1991.
CAMERANO FUENTES, Rafael. Teoría de colas. Bogota: Fondo de publicaciones Universidad Distrital Francisco José de Caldas, 1997.
CAMPOS, Manuel. Estadística actuaría III. Campus de colmenarejo. Departamento de estadística. Universidad Carlos III de Madrid. Madrid. 2006.
CASILARI, E.; REYES, A.; LECUONA, A.; DIAZ ESTRELLA, A. y SANDOVAL, F. Caracterización de tráfico de video y tráfico Internet. Universidad de Malaga, Campus de Teatinos. Málaga. 2002.
CASILARI, E.; REYES, A.; LECUONA, A.; DIAZ ESTRELLA, A. y SANDOVAL F. Modelado de tráfico telemático. Departamento de Tecnología electrónica, E.T.S.I. telecomunicación. Universidad de Málaga, Campus de Teatinos. Malaga. 2003.
CORREA MORENO, Emilia. Series de tiempo: conceptos básicos. Medellín:Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de matemáticas, 2004.
COUCH, L. Digital and analog communication system. New Jersey: Prentice Hall, 2001.
DAVIS, R. A. Maximum likelihood estimation for MA(1) processes with a root on or near the unit circle. In: Econometric theory. Vol. 12, 1996. p. 1-29
DETHE, Chandrashekhar y WAKDE D.G. On the prediction of packet process in network traffic using FARIMA time series model. Department of Electronics, College of Engineering, India. 2003.
DEVORE, Jay L. Probabilidad y estadística para ingeniería y ciencias. Quinta edición. México: Editorial Thomson, 2001.
DICKEY, D. A. and FULLER, W. A. Distribution of the estimators for autoregressive time series with a unit root. J. Amer. stat. assoc. Vol. 74, 1979. p. 427-431.
FILLATRE, Lionel; MARAKOV, Dimitry y VATON, Sandrine. Forecasting seasonal traffic flows. Computer Science Department, ENST Bretagne, Brest, Paris. 2003.
FULLER, W. A. Introduction to statistical time series. A survey, int. stat. Review, Vol. 53, 1976. p. 301-329.
GHADERI, M. On the relevance of self-similarity in network traffic prediction. Tech. Rep. School of computer science. University of Waterloo. Waterloo. 2003.
GRANGER C., W. J. Some properties of time series data and their use in econometric model specification. J. econometrics. Vol. 16, 1981. p. 121-130.
GRANGER C., W. J. The typical spectral shape of an economic variable. En: Econometrica. Vol. 34, 1996; p. 150-161.
GROSCHWITZ, Nancy K. y POLYZOS, George C. A time series model of long-term NSFNET backbone traffic. Computer Systems Laboratory, Department of Computer Science and Engineering, University of California. San Diego. 2005.
GROSSGLAUSSER, M. y BOLOT, J. C. On the relevance of longrange dependence in network traffic source. En: IEEE/ACM Trans. Networking 7. 1999.
GUERRERO GUZMAN, Víctor Manuel. Análisis estadístico de series de tiempo económicas. Segunda edición. México: Editorial Thomson, 2003.
HALANG, Z. Li and CHEN, G. Integration of fuzzy logic and chaos theory. Springer, 2006.
HAMILTON, James D. Time series analysis. New Jersey: Princeton university press, 1994. p. 25-152.
HARMANTZIS, F. C. y HATZINAKOS, D. Heavy network traffic modeling and simulation using stable FARIMA processes. Stevens institute of technology, Castle point on the Hudson. Hoboken. 2005.
HARVEY, A.C. Time series models. Harvester Wheatsheaf. 1993. 84 p.
JANG, J.-S. ANFIS: Adaptive-network-based fuzzy inference systems. En: IEEE Transactions on systems, man, and cybernetics. Vol. 23, 1993.
JANG, J.-S. and MIZUTANI, Sun E. Neuro-fuzzy and soft computing-A computational approach to learning and machine intelligence. Prentice Hall, 1997.
JONES, R. H. Fitting autoregressions. J. amer. Stat. assoc. Vol. 70, 1975. p. 590-592.
JONES, R. H. Multivariate autoregression estimation using residuals, applied time series analysis. New York: Academic Press, 1978. p. 139-162.
KAMARIANAKIS, Yiannis y PRASTACOS, Poulicos. Forecasting traffic flow conditions in an urban network: comparison of multivariate and univariate approaches. 82nd transportation research board annual convention. Paper number 03-4318. 2003.
LELAND W. E.; TAQQU, M. S.; WILLINGER, W. y D. V., Wilson. On the self-similar nature of ethernet traffic. En: IEEE/ACM Trans. Networking 2. 1994.
LOPEZ ARDAO, José Carlos. Contribución al análisis del impacto de la correlación en las prestaciones de las redes de alta velocidad. Departamento de tecnologías de las comunicaciones. Universidad de Vigo. 2004.
MAKRIDAKIS, Spyros G.; WHEELWRIGHT, Steven C. y HYNDMAN, Rob J. Forecasting: methods and applications. Tercera edición. USA: Editorial Wiley, 1997.
MONTGOMERY DOUGLAS, C.; PECK, Elizabeth A. y VINING, G. Geoffrey. Introducción al análisis de regresión lineal. Tercera edición. Editorial Continental, 2002.
OLEXA, Ron. Implementing 802.11, 802.16, and 802.20 Wireless Networks: Planning, Troubleshooting, and Operations. Editorial Newnes. 2004.
PAJOUH, Danech. Methodology for traffic forescating. The French National Institute for Transport and Safety Research (INRETS). Arcuel. 2002.
PAPADOPOULI, María; SHENG, Haipeng; RAFTOPUULOS, Elias; PLOUMIDIS, Manolis y HERNANDEZ, Felix. Short-term traffic forecasting in a campus-wide wíreles network. 2004.
PITKOW, J. E. "Summary of WWW Traffic Characterizations", Computer Networks and ISDN Systems, Vol. 30; p. 551-558. 1998.
REYES, A.; LECUONA, A.; GONZALEZ PARADA, E.; CASILARI, E.; CASASOLA, J. C. y DIAZ ESTRELLA, A. "A page-oriented WWW traffic model for wireless system simulations". Proc. of 16th international teletraffic congress (ITC). Edinburgh. Junio, 1999; p. 1271-1280.
SCHWARTZ, Misha. Redes de telecomunicaciones, protocolos, modelado y análisis. Editorial Addison Wesley Iberoamericana. 1994.
STALLINGS, William. Comunicaciones y redes de computadores. Séptima edición. Madrid: Prentice Hall, 2004.
SWEENEY, Daniel. WiMax Operator's Manual: Building 802.16 Wireless Networks. Editorial Apress. 2004.
TAKAGI, M. Sugeno. Fuzzy identification of system and its applications to modeling and control. En: IEEE Transactions on systems, man, and cybernetics. Vol. 15, 1985.
TANENBAUM, Andrew S. Redes de Computadoras. Cuarta Edicion. México: Prentice Hall, 2003.
WILLINGER W.; PAXON V. y TAQQU M. S. Self-similarity and heavy tails: structural modeling of network traffic. En: A practical guide to heavy tails: statistical techniques and applications. Birkhauser, Boston. 1998; p. 27-53.
XIAOQIAO, Meng; STARSKY, Wong; YUAN, Yuan, y SONGWU, Lu. Characterizing flows in large wireless data networks. En: ACM/ IEEE international conference on mobile computing and networking. Philadelpia. 2004.
YU, Guoqiang y ZHANG, Changshui. Switching ARIMA model based forecasting for traffic flow. State key laboratory of intelligent technology and system, Departament of automation, Tsinghua University. 2003.
ZAK, S. Systems and control. Oxford: oxford university Press, 2003.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2007-00-00 vol:12 nro:1 pág:4-13
Diseño de un modelo de tráfico a través de series de tiempo para pronosticar trafico Wimax
Design of a traffic model through time series to forecast Wimax traffic
Octavio Salcedo
Director Grupo de investigación Internet Inteligente,
Universidad Distrital.
César Augusto Hernández Suárez
Investigador del Grupo de investigación Internet Inteligente y ARMOS, Universidad Distrital.
Andrés Escobar Díaz
Investigador del Grupo de investigación LAMIC, Universidad Distrital.
Resumen
Este artículo pretende iniciar al lector en modelos estadísticos con series de tiempo, que permitan estimar pronósticos futuros de tráfico en las redes de comunicaciones modernas, haciendo uso de la predecibilidad del tráfico con dependencia de rango corto (SDR), para poder realizar un control más oportuno y eficiente en forma integrada a diferentes niveles de la jerarquía funcional de la red. Este modelamiento en series de tiempo, esta basado en medidas tomadas de los eventos con una base periódica.
El objetivo de esta investigación es demostrar que las series de tiempo son una excelente herramienta para el modelamiento de tráfico de datos en redes Wimax. Lo anterior es posible a través de la metodología de Box-Jenkins que se presenta en este artículo.
Al final de esta investigación se logro modelar una serie de tráfico Wimax de 10 días a través de una serie de tiempo ARIMA con un error pequeño.
Palabras clave:
ARIMA, autocorrelación, correlación, estocástico, modelo de tráfico, serie de tiempo, red de comunicaciones.
Abstract
This paper tries to initiate to the reader in statistical models with time series, that allow to consider future forecasting of traffic in the modern Communication networks, making use of the forecasting of the traffic with dependency of long rank (LDR) and dependency of short rank (SDR), to be able to make a more opportune and efficient control in form integrated at different levels from the functional hierarchy of the network. This time series modeling is based on measures taken from events with a periodic base.
The objective of this research is to demonstrate that the time series are an excellent tool for modeling of data traffic on Wimax networks. This is possible through the Box-Jenkins methodology that is presented in this article.
At the end of this investigation there is a traffic model through a series of time ARIMA with surprisingly small error.
Key words:
ARIMA, autocorrelation, correlation, networks of communications, stochastic, time series, traffic models.
1. Introducción
A lo largo del desarrollo de las redes de comunicaciones en los últimos cien años, se han propuesto diferentes modelos de tráfico, cada uno de los cuales ha resultado útil dentro del contexto particular para el que se propuso. Sin embargo hoy en día se ha demostrado que el tráfico de datos es altamente correlacionado. El fenómeno de correlación hace que la variabilidad se extienda a muchas escalas de tiempo, comprometiendo la validez de las técnicas de control diseñadas para los modelos tradicionales de tráfico. Por esta razón, ha sido necesario desarrollar modelos adicionales de tráfico más complejos, capaces de representar estas correlaciones y que tengan en cuenta las características del tráfico real, en especial las correlaciones que existen entre los tiempos entre llegadas, completamente ausentes en los modelos no correlacionados. [3]
Actualmente las redes de comunicaciones modernas no tienen una herramienta confiable que permita pronosticar tráfico 24 o 48 horas hacia el futuro, por lo que se plantea el siguiente interrogante: [33] [49]
¿Es posible desarrollar un modelo estadístico que permita estimar pronósticos futuros de tráfico Wimax?
Las series de tiempo tienen como objetivo central desarrollar modelos estadísticos que expliquen el comportamiento de una variable aleatoria que varía con el tiempo permitiendo estimar pronósticos futuros de dicha variable aleatoria. [21]
Por tanto los modelos de tráfico a través de series de tiempo son beneficiosos para: la planeación de cobertura, reservación de recursos, monitoreo de la red, detección de anomalías, y producción de modelos de simulación más exactos, en la medida en que pueden pronosticar el tráfico en un tiempo de escala determinado. [50]
En la planeación, para futuras necesidades de cualquier sistema, la exactitud en el pronóstico de tráfico, es realmente importante para definir capacidad futura requerida y planear los cambios. Un modelo de series de tiempo bastante exacto podría predecir varios años hacia el futuro, cuya habilidad es una ventaja para la planeación de futuros requerimientos. [27]
En el presente documento busca:
- Desarrollar un modelo estadístico que permita estimar pronósticos futuros de tráfico en redes Wimax a través del modelamiento en series de tiempo.
- Evaluar los diferentes modelos actuales para el pronóstico de tráfico, relacionados con series de tiempo.
A continuación se describen los pasos realizados durante la investigación, a fin de construir el modelo de tráfico para una red de datos Wimax.
2. Desarrollo del modelo de tráfico
El desarrollo de este trabajo fundamenta su metodología en la de Box-Jenkins, entonces, una vez capturados los datos se analiza la estructura de correlación que presenta la muestra, de aquí se propone y se estima un modelo basado en ecuaciones en diferencias, el cual busca capturar la dinámica de la serie, de ser correcta la formulación del modelo, este se valida y después se pronostican las futuras observaciones. Con el fin de realizar un estudio profundo del modelamiento de tráfico de datos a través de series de tiempo, se desarrollaran varios tipos de modelamiento de la serie.
2.1. Extracción de la serie
El primer paso en el desarrollo de cualquier modelo de tráfico es tomar una muestra de datos, con los se pueda caracterizar el tráfico de un tipo de red predeterminada. En el presente estudio se decidió desarrollar un modelo de tráfico para una red con tecnología Wimax, en razón a que esta tecnología es la que actualmente tiene mayor auge en el ámbito de las redes de datos debido a todas sus características, igualmente debido a que esta tecnología es relativamente nueva, no existen muchos estudios acerca del comportamiento de su tráfico, sin embargo como lo han confirmado varios estudios de tráfico en redes alámbricas e inalámbricas (como WiFi) el tráfico actual como el de Internet e incluso el de video, presenta características fuertes de correlación. [19] [20] [48] [50]. Los datos de tráfico fueron extraídos a través de la herramienta Netflow Analyzer, estos datos se capturaron como una variable de paquetes por segundo y se tomaron 889 muestras.
Netflow Analyzer es una herramienta de software basada en Web que permite el monitoreo del ancho de banda de cualquier red. Los datos son exportados de los dispositivos de Routing hacia el Analizer Network Traffic el cual reporta el ancho de banda utilizado en tiempo real a través de la red monitoreada. Debido a su carácter de herramienta de software basada en Web, permite la monitorización remota de cualquier red a través de los dispositivos de red (como Routers) que se encuentren configurados en este software.
Durante el mes de enero y febrero del año 2007, se tuvo acceso a la monitorización de un router con tecnología Wimax y con el cual se realizó la extracción de los datos de tráfico, vale la pena resaltar que debido a su carácter de demo esta herramienta de software tiene bastantes limitantes funcionales, sin embargo los datos de tráfico que presenta no son simulados sino que por el contrario, son en tiempo real.
A pesar de haberse extraído 889 datos de tráfico los modelos se desarrollaran únicamente con los 672 primeros (correspondientes a 7 días), los datos restantes se utilizaran para comparar y evaluar los pronósticos de cada una de las series. [27].
2.2. Preprocesamiento de la serie
Es frecunte que se presenten algunos valores perdidos dentro de la serie de tráfico. Estos generalmente se deben a varias razones entre las cuales se destacan las siguientes cuatro: (1) el router puede estar caído debido a mantenimiento del mismo, o por un reinicio accidental de este; (2) el router puede estar ocupado resolviendo solicitudes SNMP; (3) la conexión inalámbrica entre el router y la estación de monitorización de tráfico puede estar temporalmente perdida o caída; y (4) la solicitud y respuesta de los paquetes SNMP (Simple Network Management Protocol) puede haberse perdido ya que ellos son transportados usando el protocolo UDP (User Datagram Protocol es un protocolo no confiable). [5] [50]
Para el tratamiento de los valores perdidos existen dos opciones: (1) ignorar los datos perdidos, o (2) estimarlos los valores perdidos. Para la presente investigación se decidió estimar los valores perdidos con el fin de obtener un modelo más completo, en el cual se puedan observar factores de estacionalidad, tendencia o ciclo, para una muestra de tráfico de una semana.
El procedimiento adoptado para la estimación de valores perdidos se realizo a través de un software especializado para esta tarea, dicho software es el: SEATS TRAMO WINDOWS (TSW). El procedimiento está fundamentado en la interpolación de promedios de datos de tráfico previos, estas interpolaciones se realizan examinando el patrón de tráfico y tratando en lo posible de mantener dicho patrón dentro del subconjunto de valores tráfico actuales. En algunas ocasiones se decide remplazar el valor perdido (o valores perdidos) por uno del mismo día, hora y minuto, pero de una semana anterior o una semana posterior, esto se justifica en el fuerte patrón semanal que muestra la serie de tiempo de los datos de tráfico, en esta ocasión esto no es posible en razón a que la muestra de datos de tráfico en este estudio es para una sola semana y dos días. [5].
2.3. Identificación del modelo
Debido que uno de los objetivos es comparar diferentes modelos correlacionados, es decir construir varios modelos de tráfico basados en diferentes tipos de series de tiempo y analizar cuál de ellos es el mejor estimador del tráfico Wimax capturado. Esta etapa de identificación carece de sentido para esta investigación, ya que sin importar las conclusiones de la identificación del modelo, se desarrollaran cuatro modelos de tráfico correlacionados: (1) Modelo AR (Autoregresivo), (2) Modelo MA (Promedios Móviles), (3) Modelo ARMA (AutoRegresivo y Promedio Móviles), y (4) Modelo ARIMA (AutoRegresivo e Integrado de Promedio Móvil). Vale la pena recordar que los tres primeros modelos correlacionados implican la necesidad de que la serie sea estacionaria, mientras que para el cuarto modelo no es necesario que exista estacionariedad en la serie de tiempo. [11].
El concepto de estacionariedad es importante para el análisis de series de tiempo. En general, para caracterizar completamente un proceso estocástico es necesario conocer la función de densidad conjunta de sus variables aleatorias; sin embargo en la práctica no es realista pensar que esto pueda lograrse con una serie de tiempo. Como se menciono anteriormente en lo que respecta a la covarianza, no existe dependencia del tiempo pero si de la separación (k) que hay entre las variables. Lo anterior conduce a pensar que la serie, mostrará el mismo comportamiento en términos generales sin importar el momento en el que se observe. Esto es, si se graficara un cierto numero de observaciones contiguas de una serie, la grafica que se obtendría seria bastante similar a la que se lograría al graficar el mismo numero de observaciones contiguas pero k periodos hacia delante o hacia atrás de los considerados inicialmente. [13] [36]
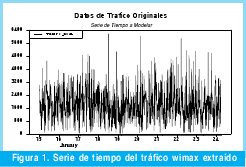
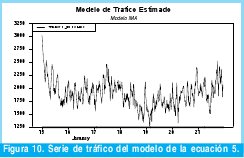
De la observación de la serie de tiempo que nos atañe, se puede concluir fácilmente que esta no es estacionaria, debido a que su media no es cero (Figura 1), aunque su varianza parece constante, dos condiciones imperiosas para que una serie de tiempo sea estacionaria (estos cálculos se desarrollaran más adelante).
De acuerdo a lo anterior los tres primeros modelos cuya condición es la estacionariedad de la serie, no tendrían mucho sentido. Por esto el único modelo que se ajusta a la serie de tiempo es el ARIMA, con esto la etapa de identificación esta terminada. Sin embargo debido a que el objetivo es comparar los cuatro modelos se desarrollara primero el modelo ARIMA, el cual cuenta con la ventaja de ser integrado "I" permitiendo volver estacionaria una serie no estacionaria (por tendencia); una vez realizado el modelo ARIMA, se tomó la serie estacionaria y con ella se estimaran los modelos AR y MA, que para este caso se convierten en los modelos ARI e IMA en un sentido estricto de la palabra, el modelo ARMA ya carecería de sentido porque al calcularlo se llegaría al mismo modelo ARIMA. [10].
2.4. Estimación de parámetros y validación
2.4.1. Modelo ARIMA
Para verificar la no estacionariedad de la serie de tiempo se realizará la prueba de Raíz Unitaria de Dickey Fuller a través del software RATS, estos son los resultados obtenidos: [23] [26] [28]
Dickey-Fuller Unit Root Test, Series
TRÁFICO_REAL Regression Run From 2007:01:15//62 to
2007:01:21//95
Observations 828
With intercept with 60 lags
T-test statistic -1.49785
Critical values: 1%= -3.443 5%=
-2.867 10%= -2.569
Según el criterio de Dickey - Fuller, la serie no es estacionaria, ya que el valor absoluto del test es menor al valor absoluto del valor crítico del 5%. Lo anterior era consecuencia de que la media de los datos no es cero como se mostro en la figura 3, aunque la varianza parece constante. Para volver esta serie estacionaria se diferenciará la serie y se vuelve a realizar la prueba de raíz unitaria.
Entonces se tomará la serie de tiempo original con sus primeros 672 datos de tráfico y se diferenciará inicialmente una sola vez, luego se diferenciará dos veces y por ultimo se diferenciará una vez el logaritmo de la serie de tiempo original de 672 valores, para cada una de las series resultantes anteriormente luego de la diferenciación, se realizará la prueba de Dickey -Fuller para verificar su respectiva estacionariedad.
Del proceso anterior se concluye que la mejor transformación es diferenciar la serie una sola vez con esto se obtiene una serie como la que muestra la Figura 2 (observe que esta vez la media de los datos si es cero).
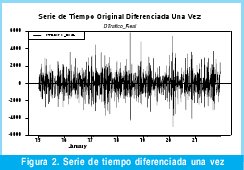
Si solo se han aplicado primeras diferencias será un ARIMA(p,1,q), si requiere segundas diferencias es un ARIMA(p,2,q), en general si se aplica (1-B)d se llega a un ARIMA(p, d, q). Para el desarrollo de esta investigación se tiene d=1. [13]
Se debe evitar el sobre-diferenciar la serie original y eliminar información valiosa que se manifestaría en la función de autocorrelación, ya que en un caso de sobre-diferenciación las autocorrelaciones se hacen aún más complicadas, y el modelo pierde parsimonia, se incrementa la varianza y se pierden d-observaciones. [15]
Ahora que ya se tiene una serie estacionaria se deben determinar el orden de "p" (autoregresivo) y de "q" (promedio móvil); para esto se utiliza la función de autocorrelación y la función de autocorrelación parcial. [2] [4] [23]
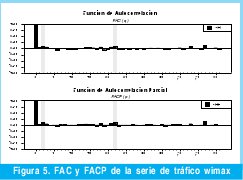
Para obtener estas gráficas de autocorrelación y autocorrelación parcial se utilizó el software RATS con el cual se generaron las gráficas que se muestran en la Figura 3. Estas dos gráficas (FAC y FACP) permiten estimar el valor de "p" y "q" para construir el modelo ARIMA(p,d,q) que nos interesa. Entonces de la FAC se obtiene, q=22, y de la FACP se obtiene, p=22, como la serie se diferenció finalmente solo una vez, entonces d=1. &Oacuxte;sea que finalmente se tiene un modelo inicial ARIMA (22,1,22).
Según los resultados de la FAC y la FACP se tiene el modelo presentado en la ecuación 1, para el cual aun no se conocen sus coeficientes.
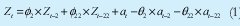
Ahora que se tiene un fuerte candidato y hay que estimar sus parámetros. En la práctica esta es una labor de cómputo, aquí se debe escoger el paquete a usar, por la flexibilidad que ofrece para este estudio se eligió el software RATS (Por encima inclusive del Software Eviews) por su gran potencialidad y estimación de máxima verosimilitud.
Lo usual es pasar de la estimación inicial, al análisis de los residuos aquí se vuelve a buscar picos pero ahora en los residuos. Estos picos revelan términos que uno debe incluir en la nueva formulación ARIMA que se volverá a estimar. Este ciclo de re-especificación dinámica termina cuando los residuos ya no presentan correlaciones (picos) y se puede decir que son residuos de ruido blanco. [12] [42] [46].
Realizando lo anterior en el software RATS se obtuvo la primera estimación de parámetros del modelo, es decir los coeficientes del modelo ARIMA que se presentan en la ecuación 1, y cuyos valores se listan en la ecuación 2.
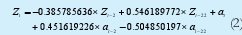
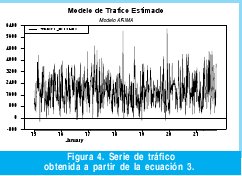
En la Figura 4 se grafica el modelo estimado en la ecuación 2 en función del tiempo para el cual se extrajeron los datos de tráfico correspondientes a una semana completa. Sin embargo, de la simple inspección de dicho modelo no es posible validarlo. La validación de los modelos de series de tiempo se realiza a través de la verificación de correlación entre los residuales de dicho modelo, para lo cual es necesario aplicar la función de autocorrelación (FAC) y la función de autocorrelación parcial (FACP) a dichos residuos.
Las FAC y FACP de los residuales del modelo estimado en la ecuación 3, se pueden observar en la Figura 7. De esta figura se puede observar que existe correlación entre los residuales del modelo de la ecuación 3, por lo tanto este modelo no incluye toda la dinámica de la serie de tiempo. En este punto es necesario volver a iterar y estimar nuevamente los coeficientes del modelo incluyendo ahora los nuevos valores de "p" y "q" que sugiere las funciones de autocorrelación y autocorrelación parcial, ósea para "p" los valores: 1, 2, 3, 4, 6, 7, 11, 12, 13, 17, 20, y para "q" los valores: 1, 18. De acuerdo con lo anterior se realiza una nueva estimación de los coeficientes incluyendo los nuevos parámetros de "p" y "q".
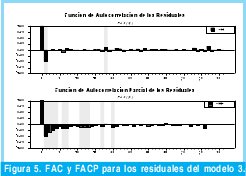
El procedimiento anterior se lleva a cabo hasta que la FAC y FACP de los residuales demuestren que no existe correlación alguna entre los residuales del modelo estimado, lo cual se logro luego de 3 iteraciones adicionales, sin embargo el número de parámetros obtenidos para el modelo correspondiente fue 18. Un modelo con un número grande de parámetros es un modelo que no presenta una buena parsimonia, por lo que se analizó el nivel de significancia de cada parámetro eliminando aquellos que presentan un valor mayor al cinco por ciento, ya que estos no resultan significativos para el modelo. Una vez realizado lo anterior es necesario validar nuevamente el modelo y dependiendo del resultado iterar una vez mas. Finalmente se llega a un modelo definitivo descrito por la ecuación 3 y cuyo comportamiento se muestra en la Figura 6.
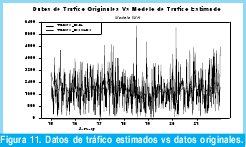
Con el fin de realizar una comparación subjetiva entre los datos estimado por el modelo desarrollado en la ecuación 3 y los datos de tráfico reales se muestra la Figura 7, donde las trazas azules indican los datos de tráfico estimados y la negra los reales.
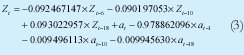
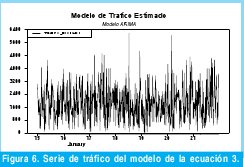
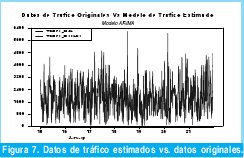
Como conclusión final se obtiene un modelo ARIMA(18,1,18) de seis parámetros el cual esta definido por la ecuación 3 y que por inspección visual de la Figura 7, modela bastante bien los 672 datos de tráfico Wimax. En la sección 2.5 se realiza una evaluación cuantitativa del presente modelo.
2.4.2. Modelo ARI
La metodología para la estimación del modelo ARI es idéntica a la utilizada en el modelo ARIMA por lo que se presentara directamente los resultados obtenidos. La ecuación 4 describe el modelo ARI definitivo y las figuras 8 y 9 muestran respectivamente, el comportamiento del modelo ARI y la comparación de dichos estimativos de tráfico con los datos originales.

En conclusión con los resultados obtenidos a partir de la metodología adoptada se construyó un modelo ARI(22) (autorregresivo e integrado una vez) definido por la ecuación 5, el cual presenta un orden de 22 y 18 parámetros, que lograr modelar el tráfico Wimax capturado de forma satisfactoria como lo demuestran las Figuras 8 y 9.
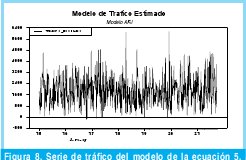
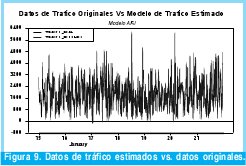
2.4.3. Modelo IMA
La metodología para la estimación del modelo IMA es idéntica a la utilizada en el modelo ARIMA y ARI por lo que se presentara directamente los resultados obtenidos. La ecuación 5 describe el modelo IMA definitivo y las figuras 10 y 11 muestran respectivamente, el comportamiento del modelo IMA y la comparación de dichos estimativos de tráfico con los datos originales.
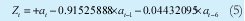
2.5. Evaluación del Modelo
Es usual encontrarse con varios modelos alternativos y se debe decidir cual escoger. En primera instancia se tiene la función de autocorrelación y la función de autocorrelación parcial, las cuales se aplican a los residuos del modelo final para determinar si existe correlación entre estos, de no tener correlación se puede decir que el modelo ha sido validado con éxito. Sin embargo en este estudio no se obtuvo correlación entre los residuales para ninguno de los tres modelos desarrollados por lo que entonces la pregunta seria ¿cual escoger? [13]
Debido a lo anterior se analizaran otros criterios a parte del análisis residual para seleccionar adecuadamente un modelo:
- Criterio de calidad de ajuste.
- Criterio de parsimonia.
- Criterios estadísticos.
2.5.1. Calidad de ajuste
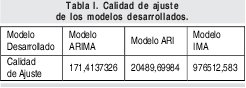
La calidad de ajuste de un modelo esta definida como la suma de los cuadrados de los residuos dividida por el tamaño de la muestra, y su objetivo es medir la habilidad del modelo para reproducir los datos de la muestra, es decir verifica que tan parecida es la serie modelada con la real. [34]. En la Tabla I se muestran los valores de la calidad de ajuste para cada modelo desarrollado.
2.5.2. Parsimonia
La idea de parsimonia es que un buen modelo tiene pocos parámetros ya que ha capturado las propiedades intrínsecas de la serie que se analiza, un modelo complicado con demasiados parámetros es un modelo sin parsimonia. Desde este punto de vista, el modelo ARI que se obtuvo anteriormente es un modelo sin parsimonia, debido a la gran cantidad de parámetros que presenta (en total 18 parámetros) en contraste con el modelo ARIMA (en total 6 parámetros) y el modelo IMA (en total 2 parámetros).
Se podría concluir que el modelo IMA es el que presenta mayor parsimonia, inclusive mayor a la del modelo ARIMA. Sin embargo este criterio siempre deberá ser el último que utilice para seleccionar un modelo, debido a su carácter cualitativo y no cuantitativo como si lo es el criterio de calidad de ajuste y los que se describen a continuación.
2.5.3. Criterios estadísticos
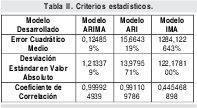
A pesar de poder seleccionar un modelo adecuado a partir de los criterios de análisis de residuos, calidad de ajuste y parsimonia, se calculo también varios criterios estadísticos que permitieran realizar objetivamente un análisis comparativo entre los modelos de serie de tiempo desarrollados. Los estadísticos calculados son:
- Error cuadrático medio
- Valor absoluto de la desviación estándar
- Coeficiente de correlación
Entre estos estadísticos el más significativo es la desviación estándar en valor absoluto, para esta investigación se decidió calcular el error cuadrático medio como el promedio de las desviaciones estándares al cuadrado de los valores estimados con respecto a los originales, con el fin de obtener un valor cuantitativo de la exactitud del modelo, ya que por definición el error cuadrático medio tendría el mismo valor del criterio calidad de ajuste, el cual no nos dice que tan eficaz es el modelo, solo nos permite compararlo con otros.
Debido a que el promedio de las desviaciones estándares de cada dato estimado no es significativamente objetivo en razón a que puede tomar valores positivos como negativos que afectan el resultado final, se decidió tomar el promedio del valor absoluto de las desviaciones estándares de cada dato.
Y por ultimo se calculo el factor de correlación entre los datos estimados y los originales, debido a que como se explico anteriormente este estadístico da un indicativo del nivel de relación entre dos variables, lo cual no puede lograr la función de covarianza Los resultados de los criterios estadísticos mencionados se muestran en la Tabla II.
2.5.4. Evaluación de los pronósticos
En la realidad se puede sosener la tesis de que un modelo es realmente útil solo en la medida que anticipa la evolución de la variable. En este sentido se está aceptando que se espere a que vengan las futuras observaciones para después analizar la calidad del modelo. Esto se denomina una evaluación ex-post, y es una validación más fuerte en el sentido común, que el análisis de residuos. [24].
Para cada modelo se pronosticaron 217 (217=889-672) datos de tráfico que fueron respectivamente comparados con los datos de tráfico originales, para generar la Tabla 3, donde se muestran la exactitud de los pronósticos en función de estadísticos como el error cuadrático medio, el promedio de la desviación estándar en valor absoluto, el coeficiente de correlación y la calidad de ajuste, lo cual permite observar detalladamente la eficacia de cada modelo desarrollado para pronosticar los respectivos datos de tráfico.
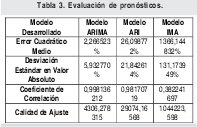
Es realmente interesante analizar la capacidad de predicción que posee el modelo ARIMA ya que tan solo tiene un 6% de error en promedio de los pronósticos de los datos de tráfico para los dos días siguientes, según la desviación estándar en valor absoluto. Pero ¿Qué tanto tiempo a futuro podría mantener tan fantásticos pronósticos?
3. Conclusiones
Las series de tiempo y en especial los modelos autorregresivos e integrados con Promedios móviles (ARIMA), resultan realmente apropiados para modelar el tráfico moderno en redes de datos Wimax con características de correlación fuertes. La evaluación de este estudio del modelo ARIMA desarrollado y seleccionado finalmente como el más apropiado, exhibe un desempeño bastante alto con relación a la magnitud de sus residuales, los cuales no experimentaron correlación alguna.
En la modelación del tráfico Wimax, de este estudio, las series de tráfico en función del tiempo en su gran mayoría, no experimentan estacionariedad debido a que los patrones de demanda que influyen sobre la serie no son relativamente estables, requiriendo la transformación de la serie, generalmente a través de la diferenciación como se realizo en el desarrollo del modelo ARIMA, destacando nuevamente la importancia de este tipo de modelado.
No todos los modelos de series de tiempo caracterizan apropiadamente el tráfico Wimax, en especial para la serie de tráfico wimax de este estudio, las series de tiempo como la de Promedios Móviles (MA) no logra capturar toda la dinámica de la serie; otros modelos como el AutoRregresivo (AR) proporcionan realizaciones bastante parecidas en magnitud a las originales, pero con un numero grande de parámetros que reduce significativamente su parsimonia y ende aumenta el costo computacional; generalmente las series de tráfico correlacionadas como la que nos ocupa, exhibe uno o mas parámetros de una componente autorregresiva y al mismo tiempo uno o mas parámetros de una componente de promedio móviles, sugeridos por las funciones de autocorrelación y autocorrelación parcial, proponiendo como fuerte candidato un modelo ARIMA, la inclusión de ambas componentes tiene por objetivo reducir significativamente el numero de parámetros necesarios para modelar la serie original, tal y como se demostró en el desarrollo de dicho modelo. Las evaluaciones realizadas a estos modelos basados en series de tiempo implicaron en su totalidad algún tipo de estadístico alrededor de los residuales (diferencia entre el valor real y el estimado por el modelo), para los cuales el modelo ARIMA obtuvo no solo los mejores resultados en comparación con los demás modelos de series de tiempo, sino además un alto grado de desempeño, confiabilidad y exactitud en sus pronósticos.
Los modelos correlacionados desarrollados a partir de las series de tiempo no experimental una relación tan compacta como la del modelo de poisson y su tratabilidad matemática se ve comprometida, sin embargo permiten modelar el tráfico wimax con una precisión y exactitud realmente significativa, debido a que son capaces de capturar los efectos de la correlación a costos computacionales razonables. Lo anterior permite a los modelos de series de tiempo ofrecer un alto desempeño en la caracterización del tráfico Wimax a diferencia del modelo Poisson, con un costo computacional que no tiene mucho que envidiarle a la tratabilidad matemática de los modelos Poissonianos.
4. Recomendaciones
Como recomendaciones de esta investigación se plantean tres propuestas, cada una de ellas enfocada a lograr un modelamiento de tráfico Wimax más exacto pero a la vez flexible, tratando de reducir al máximo el costo computacional que trae consigo los modelos correlacionados como las series de tiempo.
La primera propuesta es el desarrollo de un modelo de tráfico a través de una serie de tiempo ARIMA (p,d,q) con datos de tráfico correspondientes a por lo menos un año, con tiempos de muestreo alrededor de una hora. Lo anterior con el fin de identificar con mayor precisión los componentes de dicha serie de tiempo; de esta forma se busca poder determinar si existe o no estacionalidad en el tráfico wimax, y de existir, modelar el tráfico a través de una serie de tiempo SARIMA(p,d,q)x(P,D,Q) evaluando su desempeño y comparándolo con el modelo ARIMA(p,d,q). [52].
La segunda propuesta es el desarrollo de un modelo de tráfico wimax a través de una serie de tiempo FARIMA(p,d,q) que permita modelar el respectivo tráfico fractal, evaluar el desempeño de dicho modelo y realizar la comparación con los modelos ARIMA y SARIMA. Los procesos FARIMA han sido poco usados en los modelos de tráfico, debido fundamentalmente a que los métodos de generación sintética propuestos en la literatura son muy costosos computacionalmente. [37] [55] [57].
La tercera y última propuesta es el desarrollo de un modelo de tráfico a través de una serie de tiempo VARMA (Vector Autoregressive Moving Average) [42] [43], donde la variable dependiente (tráfico wimax) sea explicada por medio de dos o mas variables independientes como el tiempo y el numero de usuarios de la red, es decir que el modelo permita estimar el tráfico no solo a partir del tiempo sino también de variables directamente relacionadas con el tráfico como el numero de usuarios conectados a la red y/o las aplicaciones que utiliza generalmente, etc. Igualmente evaluar el desempeño de dicho modelo y realizar la comparación con los modelos ARIMA, SARIMA y FARIMA.
Referencias bibliográficas
[1] AKAIKE, H. Fitting autoregressive models for prediction. Annals of the institute of statistical mathematics. 1969. p. 243-247.
[2] AKAIKE, H. Information theory and an extension of the maximum likelihood principle. Second international symposium on information theory. Budapest. 1973. p. 267-281.
[3] ALZATE, Marco Aurelio. Modelos de tráfico en análisis y control de redes de comunicaciones. En: Revista de ingeniería de la Universidad Distrital Francisco José de Caldas. Bogotá. Vol. 9, No. 1 (Junio 2004); p. 63-87.
[4] ANDERSON, T. W. Maximum likelihood estimation for vector autoregressive moving-average models, directions in time series. Institute of mathematical statistics. 1980. p. 80-111.
[5] ANSLEY, C. F. y KOHN, R. On the estimation of ARIMA models with missing values, Time series analysis of irregularly observed data. Editorial Parzen, 1985. p. 9-37.
[6] ARMSTRONG, J.S. Principles of forecasting. Editorial Springer. 2001.
[7] ARVIDSSON, Å. y KARLSSON, P. "On traffic models for TCP/IP". Proc. of 16th international teletraffic congress (ITC). Edinburgh. Junio, 1999; p. 457-466.
[8] BERAN, J. Statistics for long-memory processes. Chapman & Hall. 1994.
[9] BERTSEKAS, Dimitri y GALLAGER, Robert. DataNetworks. Segunda edición. New Jersey: Prentice Hall, 1987.
[10] BOX, G. E. P. y COX, D. R. An analysis of transformations. Stat. soc. 1964. p. 211-252.
[11] BOX, G. E. P. y JENKINS, Gwilym M. Time series analysis: Forecasting and control. Revised Edition. Oakland, California: Editorial Holden-Day, 1976.
[12] BOX, G. E. P. y PIERCE, D. A. Distribution of residual autocorrelations in autoregressive-integrated moving-average time series models. Stat. assoc. p. 1509-1526.
[13] BRILLINGER, D.R. Time series: data analysis and theory. Universidad de California. Holden-Day. SIAM. 2001.
[14] BROCKWELL, P.J. On continuous-time ARMA processes. En: Handbook of statistics. Elsevier, Amsterdam: Vol. 19, 2001. p. 249- 276.
[15] BROCKWELL, P.J. y DAVIS, R.A. Introduction to time series and forecasting. Second edition. New York: Editorial Springer, 2002.
[16] BROCKWELL, P.J. y DAVIS, R.A. Time series: theory and methods. Springer Verlag, New York. 1991.
[17] CAMERANO FUENTES, Rafael. Teoría de colas. Bogota: Fondo de publicaciones Universidad Distrital Francisco José de Caldas, 1997.
[18] CAMPOS, Manuel. Estadística actuaría III. Campus de colmenarejo. Departamento de estadística. Universidad Carlos III de Madrid. Madrid. 2006.
[19] CASILARI, E.; REYES, A.; LECUONA, A.; DIAZ ESTRELLA, A. y SANDOVAL, F. Caracterización de tráfico de video y tráfico Internet. Universidad de Malaga, Campus de Teatinos. Málaga. 2002.
[20] CASILARI, E.; REYES, A.; LECUONA, A.; DIAZ ESTRELLA, A. y SANDOVAL F. Modelado de tráfico telemático. Departamento de Tecnología electrónica, E.T.S.I. telecomunicación. Universidad de Málaga, Campus de Teatinos. Malaga. 2003.
[21] CORREA MORENO, Emilia. Series de tiempo: conceptos básicos. Medellín:Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de matemáticas, 2004.
[22] COUCH, L. Digital and analog communication system. New Jersey: Prentice Hall, 2001.
[23] DAVIS, R. A. Maximum likelihood estimation for MA(1) processes with a root on or near the unit circle. In: Econometric theory. Vol. 12, 1996. p. 1-29
[24] DETHE, Chandrashekhar y WAKDE D.G. On the prediction of packet process in network traffic using FARIMA time series model. Department of Electronics, College of Engineering, India. 2003.
[25] DEVORE, Jay L. Probabilidad y estadística para ingeniería y ciencias. Quinta edición. México: Editorial Thomson, 2001.
[26] DICKEY, D. A. and FULLER, W. A. Distribution of the estimators for autoregressive time series with a unit root. J. Amer. stat. assoc. Vol. 74, 1979. p. 427-431.
[27] FILLATRE, Lionel; MARAKOV, Dimitry y VATON, Sandrine. Forecasting seasonal traffic flows. Computer Science Department, ENST Bretagne, Brest, Paris. 2003.
[28] FULLER, W. A. Introduction to statistical time series. A survey, int. stat. Review, Vol. 53, 1976. p. 301-329.
[29] GHADERI, M. On the relevance of self-similarity in network traffic prediction. Tech. Rep. School of computer science. University of Waterloo. Waterloo. 2003.
[30] GRANGER C., W. J. Some properties of time series data and their use in econometric model specification. J. econometrics. Vol. 16, 1981. p. 121-130.
[31] GRANGER C., W. J. The typical spectral shape of an economic variable. En: Econometrica. Vol. 34, 1996; p. 150-161.
[32] GROSCHWITZ, Nancy K. y POLYZOS, George C. A time series model of long-term NSFNET backbone traffic. Computer Systems Laboratory, Department of Computer Science and Engineering, University of California. San Diego. 2005.
[33] GROSSGLAUSSER, M. y BOLOT, J. C. On the relevance of longrange dependence in network traffic source. En: IEEE/ACM Trans. Networking 7. 1999.
[34] GUERRERO GUZMAN, Víctor Manuel. Análisis estadístico de series de tiempo económicas. Segunda edición. México: Editorial Thomson, 2003.
[35] HALANG, Z. Li and CHEN, G. Integration of fuzzy logic and chaos theory. Springer, 2006.
[36] HAMILTON, James D. Time series analysis. New Jersey: Princeton university press, 1994. p. 25-152.
[37] HARMANTZIS, F. C. y HATZINAKOS, D. Heavy network traffic modeling and simulation using stable FARIMA processes. Stevens institute of technology, Castle point on the Hudson. Hoboken. 2005.
[38] HARVEY, A.C. Time series models. Harvester Wheatsheaf. 1993. 84 p.
[39] JANG, J.-S. ANFIS: Adaptive-network-based fuzzy inference systems. En: IEEE Transactions on systems, man, and cybernetics. Vol. 23, 1993.
[40] JANG, J.-S. and MIZUTANI, Sun E. Neuro-fuzzy and soft computing- A computational approach to learning and machine intelligence. Prentice Hall, 1997.
[41] JONES, R. H. Fitting autoregressions. J. amer. Stat. assoc. Vol. 70, 1975. p. 590-592.
[42] JONES, R. H. Multivariate autoregression estimation using residuals, applied time series analysis. New York: Academic Press, 1978. p. 139-162.
[43] KAMARIANAKIS, Yiannis y PRASTACOS, Poulicos. Forecasting traffic flow conditions in an urban network: comparison of multivariate and univariate approaches. 82nd transportation research board annual convention. Paper number 03-4318. 2003.
[44] LELAND W. E.; TAQQU, M. S.; WILLINGER, W. y D. V., Wilson. On the self-similar nature of ethernet traffic. En: IEEE/ACM Trans. Networking 2. 1994.
[45] LOPEZ ARDAO, José Carlos. Contribución al análisis del impacto de la correlación en las prestaciones de las redes de alta velocidad. Departamento de tecnologías de las comunicaciones. Universidad de Vigo. 2004.
[46] MAKRIDAKIS, Spyros G.; WHEELWRIGHT, Steven C. y HYNDMAN, Rob J. Forecasting: methods and applications. Tercera edición. USA: Editorial Wiley, 1997.
[47] MONTGOMERY DOUGLAS, C.; PECK, Elizabeth A. y VINING, G. Geoffrey. Introducción al análisis de regresión lineal. Tercera edición. Editorial Continental, 2002.
[48] OLEXA, Ron. Implementing 802.11, 802.16, and 802.20 Wireless Networks: Planning, Troubleshooting, and Operations. Editorial Newnes. 2004.
[49] PAJOUH, Danech. Methodology for traffic forescating. The French National Institute for Transport and Safety Research (INRETS). Arcuel. 2002.
[50] PAPADOPOULI, María; SHENG, Haipeng; RAFTOPUULOS, Elias; PLOUMIDIS, Manolis y HERNANDEZ, Felix. Short-term traffic forecasting in a campus-wide wíreles network. 2004.
[51] PITKOW, J. E. "Summary of WWW Traffic Characterizations", Computer Networks and ISDN Systems, Vol. 30; p. 551-558. 1998.
[52] REYES, A.; LECUONA, A.; GONZALEZ PARADA, E.; CASILARI, E.; CASASOLA, J. C. y DIAZ ESTRELLA, A. "A page-oriented WWW traffic model for wireless system simulations". Proc. of 16th international teletraffic congress (ITC). Edinburgh. Junio, 1999; p. 1271-1280.
[53] SCHWARTZ, Misha. Redes de telecomunicaciones, protocolos, modelado y análisis. Editorial Addison Wesley Iberoamericana. 1994.
[54] STALLINGS, William. Comunicaciones y redes de computadores. Séptima edición. Madrid: Prentice Hall, 2004.
[55] SWEENEY, Daniel. WiMax Operator's Manual: Building 802.16 Wireless Networks. Editorial Apress. 2004.
[56] TAKAGI, M. Sugeno. Fuzzy identification of system and its applications to modeling and control. En: IEEE Transactions on systems, man, and cybernetics. Vol. 15, 1985.
[57] TANENBAUM, Andrew S. Redes de Computadoras. Cuarta Edicion. México: Prentice Hall, 2003.
[58] WILLINGER W.; PAXON V. y TAQQU M. S. "Self-similarity and heavy tails: structural modeling of network traffic". En: A practical guide to heavy tails: statistical techniques and applications. Birkhauser, Boston. 1998; p. 27-53.
[59] XIAOQIAO, Meng; STARSKY, Wong; YUAN, Yuan, y SONGWU, Lu. Characterizing flows in large wireless data networks. En: ACM/ IEEE international conference on mobile computing and networking. Philadelpia. 2004.
[60] YU, Guoqiang y ZHANG, Changshui. Switching ARIMA model based forecasting for traffic flow. State key laboratory of intelligent technology and system, Departament of automation, Tsinghua University. 2003.
[61] ZAK, S. Systems and control. Oxford: oxford university Press, 2003.
Octavio Salcedo Parra
Ingeniero de sistemas de la Universidad Autónoma de Colombia. Magíster en teleinformática de la Universidad Distrital. Magíster en economía (PEG) de la Universidad de los Andes de Bogotá. Estudiante del doctorado en ingeniería informática de la Universidad Pontificia de Salamanca, España. Se desempeña como docente de la facultad de ingeniería de la Universidad Distrital y en la Universidad Nacional de Colombia. Es director del grupo de investigación Internet Inteligente de la Universidad Distrital. ojsalcedop@unal.edu.co
César Augusto Hernández Suárez
Ingeniero Electrónico, Universidad Distrital. Especialista en Interconexión de Redes y Servicios Telemáticos, Universidad Manuela Beltrán. Magíster en Ciencias de la Información y las Comunicaciones, Universidad Distrital. Se desempeñó como docente Investigador en la U. Manuela Beltrán donde desarrolló varios proyectos, dentro de los cuales esta el proyecto Sistema Electrónico Mecánico para la enseñanza de la Lectoescritura del Braille para el cual se encuentra en curso la patente de invención. Actualmente se desempeña como Docente en la Universidad Distrital. lctsubasa@gmail.com
Andrés Escobar Díaz
Ingeniero electrónico de la Universidad Distrital. Magíster en ingeniería electrónica de la Universidad de los Andes, y actualmente adelanta estudios de Maestría en administración y negocios. Docente de planta en la Universidad Distrital. andresed@gmail.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










