Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2001-00-00 vol:6 nro:2 pág:42-50

Propuesta de Concresor basado en Relaciones Booleanas

José Jairo Soriano

Omar Lorenzo González Melo

Franck Vladimir Munar Fontecha

Andrés Augusto Ramos Acosta

Resumen

El artículo introduce un nuevo método en el diseño de controladores difusos, buscando como principal objetivo simplificar o reducir la complejidad de los concresores tradicionales sin cambios en su efectividad, el camino empleado para tal fin es partir de la lógica de Boole para llegar a una superficie de control difusa.

Palabras Clave: Lógica de Boole, control difuso, superficie de control.

Abstract

This paper introduces to a new method in the design of fuzzy controllers, looking for as main objective to simplify or to reduce the complexity of the traditional deffuzzifiers without changes on theirs effectiveness, the used way for such an end is to begin of the Boole's logic to arrive to a fuzzy control surface.

Key words: Boole's Logic, defuzzifier, Fuzzy Control, Control Surface.

INTRODUCCIÓN

A medida que la industria avanza necesita de mejores y más económicos controles para procesos. El control de procesos altamente no lineales apunta hacia la utilización de controladores difusos, aunque se incrementan los costos en proporción a los controladores tradicionales (PID). Bajar estos costos sin alterar el rendimiento del controlador, abre un nuevo camino en la construcción de controladores difusos aplicando un método alternativo de croncresión.

I. LÓGICA DE BOOLE

El álgebra de Boole difiere del álgebra común en que las variaciones involucradas solo pueden tomar uno de dos posibles estados o valores: si ó no; conectado o desconectado, etc. Es por consiguiente, un álgebra binaria. Por conveniencia, se emplean los términos 1 y 0. Estos se deben entender en el sentido de: 1 es a "encendido" como "0" es a apagado.

1.1 Función de pertenencia

En la lógica Booleana tradicional, los conjuntos son considerados como sistemas bivalentes con sus estados alternando entre inclusión y exclusión. Esto indica que la función de pertenencia para el conjunto A es cero si X no es un elemento en A y la función de pertenencia es uno si X es un elemento en A. Dado que existen solamente dos estados, la transición entre estos dos estados es siempre inmediata. La pertenencia de estos conjuntos está siempre totalmente categorizada y no existe ambigüedad o dicotomía acerca de la pertenencia.

1.2 Postulados y Teoremas

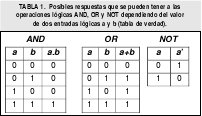
Siempre que se manipulan variables binarias, el resultado son ecuaciones. Se necesitan reglas para trabajar con estas ecuaciones. En álgebra de Boole, los estados están relacionados por dos operaciones binarias básicas unión ('+' [OR]) e intersección ('.' [AND]) que cumplen los siguientes postulados:

a) Ambas operaciones son conmutativas, es decir si a y b son elementos del álgebra, se verifica:

b)Dentro del álgebra existen dos elementos neutros, el 0 y el 1, que cumplen la propiedad de identidad con respecto a cada una de dichas operaciones:

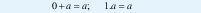
c) Cada operación es distributiva con respecto a la otra:

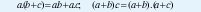
d) Para cada elemento, a, del álgebra existe un elemento denominado, a', tal que:

Este postulado define realmente una nueva operación fundamental que es la inversión o complementación de una variable ([NOT]). La variable a' se encuentra siempre en un estado binario contrario al de a.

Basados en los postulados anteriores se deducen los siguientes teoremas:

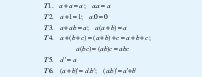
II. CONTROL BOOLEANO

La lógica booleana es básicamente una lógica bivalente que permite manejar valores extremos para definir evaluaciones convencionales como si/no, negro/blanco, verdadero/falso, etc.

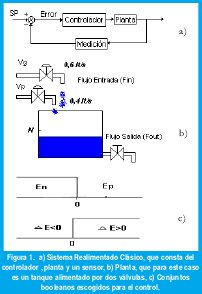
Así en un sistema de control convencional realimentado (Fig. 1. a) ), el controlador 'todo o nada' (on- off) será un elemento de actuación de solo dos estados formado por dispositivos lógicos que realizan una función determinada, de tal manera que la salida del control permanece en un valor máximo o mínimo, dependiendo de si la señal de error es positiva o negativa.

El empleo de controladores Booleanos no deriva, en general de la aplicación de una teoría científica, sino que constituye la consecuencia de una investigación empírica, basada esencialmente en la rutina adquirida por el realizador después de largas experiencias y numerosas pruebas.

Con la aparición de la teoría lógica booleana ya no se hizo necesario que estos procesos de solución de problemas fueran netamente empíricos, sino basados en un razonamiento científico. Además aplicando la lógica de Boole se obtiene la ventaja de hacer una mejor planeación y/o simplificación del sistema de control a realizar.

De la fig. 1. b), supóngase que se desea mantener en el tanque cierta cantidad de líquido, teniendo en cuenta que la salida de flujo varía debido a la presencia de tres válvulas, Vg (flujo grande) y Vp ( flujo pequeño) son las válvulas On-off de entrada de flujo y la otra válvula manual permite la salida de flujo del tanque. El controlador de acuerdo a la señal de error activará o desactivará las válvulas dependiendo de que tan rápido se esté vaciando el tanque.

Se definen dos conjuntos Booleanos (Fig 1. c), un conjunto indicará si el error es positivo (Ep) o negativo (En) y un último conjunto permitirá indicar si la variación del error es positiva (E(k+1)-E(k)>0).

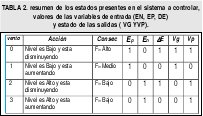
Una tabla de comportamiento del proceso definida por la experiencia [1] podría ser la mostrada en la Tabla 2.

Por consiguiente nuestras variables de salida:

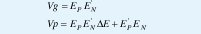
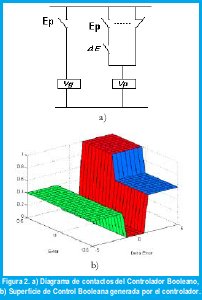
Como Ep = En' se pueden simplificar estas relaciones y entonces el controlador Booleano en lógica de contactos es mostrado en la fig. 2. a).

La superficie de control obtenida para este sistema es una superficie rústica, caracterizada por cambios fuertes debido a que en los conjuntos la transferencia de un estado a otro es instantánea.

III. LÓGICA DIFUSA

La lógica difusa es una rama de la inteligencia artificial que se funda en el concepto Todo es cuestión de grado , lo cual permite manejar información vaga o de difícil especificación si se quisiera hacer cambiar con esta información el funcionamiento o el estado de un sistema especifico.

Las reglas involucradas en un sistema difuso, pueden ser aprendidas con sistemas adaptativos que aprenden al 'observar' como operan las personas con los dispositivos reales, o estas reglas pueden también ser formuladas por un experto humano. Es entonces posible con la lógica difusa gobernar un sistema por medio de reglas de 'sentido común' , y por esto se denomina un sistema basado en el conocimiento (Knowledge Based System - [KBS]) [2].

En general la lógica difusa se aplica tanto a sistemas de control como para modelar cualquier sistema. La lógica difusa es entonces definida como un sistema matemático que modela funciones no lineales, que convierte unas entradas en salidas acordes con los planteamientos lógicos que usan el razonamiento aproximado.

3.1 Conjuntos difusos y función de pertenencia

Un conjunto difuso puede ser visto como una generalización del conjunto binario que toma sólo los valores 0 ó 1. En la lógica booleana la transferencia de un estado a otro es instantánea. En cambio en la lógica difusa la transición puede ser gradual (es decir, un elemento puede tener parcial relación en múltiples estados).

En un sistema difuso, un pequeño cambio en la variable de entrada, da como resultado un cambio más natural en el funcionamiento del sistema.

Según la teoría difusa, el grado de pertenencia de un elemento a un conjunto va a venir determinado por una función de pertenencia µ (x), que puede tomar todos los valores reales comprendidos en el intervalo [0,1]. La representación de la función de pertenencia de un elemento a un Conjunto Difuso se representa en la figura 3 a).

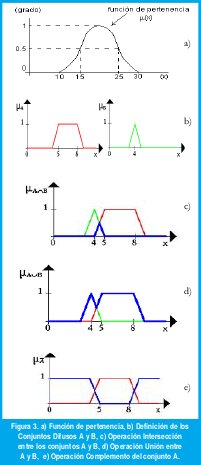
3.2 Operaciones con conjuntos difusos

Los Conjuntos Difusos se pueden operar entre sí del mismo modo que los conjuntos clásicos. Puesto que los primeros son una generalización de los segundos, es posible definir las operaciones de intersección, unión y complemento (fig. 3) haciendo uso de las mismas funciones de pertenencia:

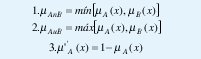
En realidad, estas expresiones son bastante arbitrarias y podrían haberse definido de muchas otras maneras. Esto obliga a considerar otras definiciones más generales para las operaciones entre los Conjuntos Difusos. En la actualidad se considera correcto definir el operador intersección mediante cualquier aplicación t-norma y el operador unión mediante cualquier aplicación s-norma.

3.3 Reglas de lógica difusa

Los sistemas de control difuso permiten describir el conjunto de reglas que utilizaría un ser humano que controlase el proceso, con toda la imprecisión que poseen los lenguajes naturales y, solo a partir de estas reglas, generan las acciones que realizan el control. Por esta razón, también se les denominan controladores lingüísticos.

El control difuso establece el algoritmo de control del proceso como un conjunto de relaciones difusas entre las variables a, b,.., que condicionan el proceso que va a ser controlado, y la entrada "r" al propio proceso. El algoritmo de control se da como un conjunto de expresiones:

IF a condición 1 AND b condición 2 THEN r condición 3

Estas expresiones son las reglas de control difuso. La parte izquierda de la regla es el antecedente y la parte derecha es el consecuente. En general las variables de condición a,b,..., son las entradas del sistema de control y la variable "r" es la salida del mismo. Las palabras pequeño, grande y medio son valores difusos que toman las variables difusas a, b y r que se definen mediante conjuntos difusos.

Se ha definido algunas relaciones que pueden ser usadas para representar la significación de las reglas del control difuso, denominadas Implicaciones [3], enunciadas a continuación

IV. CONTROL DIFUSO

Los controladores difusos son una de las tantas aplicaciones de la teoría difusa. Estos trabajan de una forma bastante diferente a los controladores convencionales; el conocimiento experto se usa en vez de ecuaciones diferenciales para describir un sistema. Este conocimiento puede expresarse de una manera muy natural, empleando las variables lingüísticas que son descritas mediante conjuntos difusos[4],[5].

Diseñar un controlador significa esencialmente escribir las reglas de control, determinando los antecedentes y los consecuentes. Para determinar los antecedentes hay que:

1. Seleccionar la información de entrada que se va a incluir en los antecedentes.
2. Fijar las particiones de los conjuntos
3. Fijar los parámetros de las funciones de pertenencia.

En lo que concierne a los consecuentes, como salida de control (entrada del proceso a controlar) está determinada por el propio proceso, lo único que hay que hacer es fijar los parámetros de las funciones de pertenencias. Así pues, el verdadero problema en el diseño de controladores difusos, es determinar los antecedentes (Esto es válido para algunos tipos de controladores como el Mandani).

Para entender lo anterior, se utilizará el mismo problema analizado con control Booleano. Ante todo, se debe definir (subjetivamente) cual es el flujo de entrada: alto, bajo, medio, los cuales aparecen en la figura 4 a). Esto se hace para especificar las funciones pertenecientes al conjunto difuso.

También se deben definir las funciones de pertenencia para el Error y la Diferencia de Error (figura 4 b) y c) ).

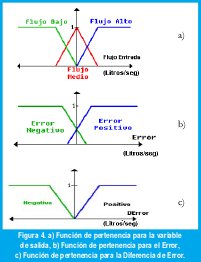
Ahora se procede a encontrar el conjunto de inferencias para este sistema

1. Si Error es Positivo y ΔError es Positivo Entonces Flujo es Alto.
2. Si Error es Positivo y ΔError es Negativo Entonces Flujo es Medio.
3. Si Error es Negativo y ΔError es Positivo Entonces Flujo es Bajo.
4. Si Error es Negativo y ΔError es Negativo Entonces Flujo es Bajo.

Estas inferencias fueron determinadas usando la experiencia obtenida a través de la interacción con la planta y la observación de su comportamiento al excitarla con patrones de prueba para diferentes casos.

El resumen de todas las inferencias aplicables se encuentra en la Tabla 3.

A continuación se mostrará como las inferencias pueden aplicarse con valores concretos para el error y diferencia de error. Para ello se define dos valores explícitos para cada uno.

Un valor actual para el error (fig. 5 a)) y un valor actual para la diferencia de Error (fig. 5 b)). Ahora se muestra como aplicar las reglas a esta situación real, es decir a los valores que se han definido.

Si Error es Positivo y ΔError es Negativo Entonces Flujo es Medio.

Para la variable lingüística Error donde se debe centrar en el conjunto difuso "Positivo", donde el valor real del Error Actual pertenece en un grado de 0.6 (figura 5 a)).

Para la variable lingüística Diferencia de Error donde se debe centrar en el conjunto difuso Negativo, donde el valor real de la Diferencia de Error Actual pertenece en un grado de 0.5 (figura 5 b)).

Como las dos partes de la condición de la inferencia están unidas por una Y se calcula el Mín(0.6,0.5) y luego se aplica la implicación de Mandani en el conjunto difuso Flujo Medio de la variable de Salida (Flujo de Entrada figura 5 c)).

Por su parte, el resultado de la inferencia

Si Error es Positivo y DError es Positivo Entonces Flujo es Alto.

Se muestra en la figura 5 d)

El resultado de la inferencia

Si Error es Negativo y DError es Positivo Entonces Flujo es Bajo.

Se muestra en la figura 5 e)

El resultado de la inferencia

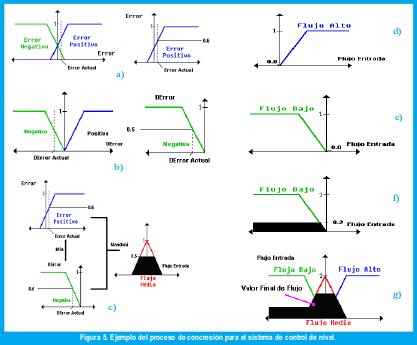
Si Error es Negativo y ΔError es Negativo Entonces Flujo es Bajo.

Se muestra en la figura 5 f)

Estas cuatro inferencias solapadas desembocan en un resultado único (figura 5 g)).

El resultado del controlador difuso es un conjunto difuso (de Flujo de Entrada), así que se tiene que escoger un valor representativo como salida final.

Para determinar este valor final (figura 5 g)) se pueden utilizar varios criterios de defusificación, entre ellos:

• Centro de Gravedad del Conjunto Difuso


• El promedio de Máximos o Mínimos de Conjunto Difuso


• El Valo r del primer Máximo o Mínimo del Conjunto Difuso

La aplicación de cualquier de estos métodos está delimitada por el conocimiento del sistema experto y de acuerdo a la respuesta deseada.

La superficie de control se obtiene a partir de mantener un valor actual de una de las variables lingüísticas mientras se realiza un barrido de todos los posibles valores actuales que puede tomar la otra variable dentro del rango establecido desarrollando la fusificación y defusificación de acuerdo a nuestro conjunto de inferencias; luego se debe ejecutar el mismo procedimiento pero manteniendo constante la variable antes barrida y variando la otra.

La herramienta permite definir los conjuntos de entrada, las inferencias requeridas y los niveles o conjuntos de salida del sistema, en este caso se tienen dos entradas (Error y Delta de error) y una salida (Flujo), proporcionándonos la superficie de control (figura6 b)) que alimentara nuestra planta.

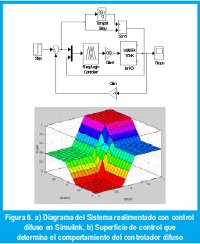
V. CONTROLADOR DIFUSO BASADO EN RELACIONES BOOLEANAS

Un controlador difuso tiene un buen comportamiento al trabajar con sistemas físicos, y aunque su diseño no es muy complicado, el problema se presenta al implementar el concresor, debido a que tiene que realizar algunos cálculos complejos para lograr encontrar el valor de la salida, demorándose un tiempo considerable y haciendo que el diseño del algoritmo no sea tan sencillo, teniendo que utilizar plataformas y/o dispositivos más robustos según el desempeño que se desee, lo cual hace que sea más costoso y menos práctico. Por esto se busca un método que sea tan sencillo de diseñar e implementar como con los sistemas expertos y que tenga el buen desempeño y las ventajas del controlador difuso.

Aunque el concepto de conjunto difuso ya ha sido introducido cabe resaltar el origen de los conjuntos difusos en los conjuntos bivalentes, es decir que se puede tener primero grupos con funciones características binarias y luego desvanecer los límites, convirtiendo la zona de corte en una zona difusa, para aprovechar así las relaciones Booleanas que se tenían originalmente, haciendo las modificaciones correspondientes, de tal forma que se puedan aplicar a los nuevos conjuntos difusos.

5.1 Diseño

Para el mismo ejemplo del control de nivel que se ha venido usando, se definen los conjuntos difusos de entrada (figura 7 a) y b)) Error y Delta de Error.

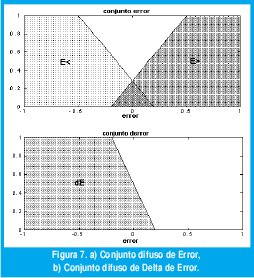
Se toman los límites y se transforman en difusos, pueden ser lineales como en este caso o usando aproximaciones no lineales como la campana de Gauss o el que se necesite. Para volverlos difusos se deben elaborar criterios según experiencia ( para saber qué forma tomar y desde donde hacer las particiones). Los conjuntos pueden tener o no zonas comunes, esto va a incidir luego en las relaciones Booleanas.

Una vez definidos los conjuntos difusos se hacen las inferencias, que son las mismas del sistema experto:

Si E<0 y dE- entonces Flujo Nulo

Si E<0 y dE+ entonces Flujo Bajo

Si E>0 y dE- entonces Flujo Medio

Si E>0 y dE+ entonces Flujo Alto

En este caso se evita definir otro conjunto dE- , utilizando simplemente el inverso de dE+, pero si se quiere se puede definir otro conjunto difuso, la ventaja es que las relaciones quedan más pequeñas, debido a que hay menos variables. Se definen dos salidas (V1yV2, equivalentes a Vg y Vp en el controlador Booleano), que combinadas generan las cuatro salidas que se desean, donde Flujo de V2 > Flujo de V1. Las variables, las relaciones y las salidas se pueden plantear en una tabla de verdad como la mostrada en la Tabla 4.

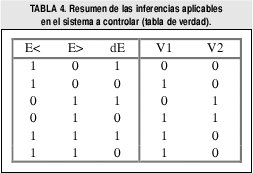
A diferencia de la tabla del sistema experto se tiene en cuenta la zona donde se cruzan las dos curvas y son las dos últimas filas de la tabla, si no se cruzaran quedarían iguales.

Solucionando para V1 y V2 nos queda:

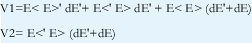
Hasta el momento no hay una gran diferencia entre el diseño Booleano y el difuso, pero en este caso no se ha hecho simplificación debido a que ya no se trabajan conjuntos Booleanos, sino difusos.

Se tienen entonces las ecuaciones Booleanas, pero con estas no se puede trabajar conjuntos difusos debido a que funciones tales como la AND, OR y demás están definidas para variables bivalentes y no multivalentes como lo es una variable difusa, entonces se reemplazan por funciones equivalentes o similares pero que operen con conjuntos difusos. Para esto se definen las operaciones lógicas a usar, en este caso se reemplazan la AND por la función Mínimo y la OR por la función Máximo, pero también se pueden usar el producto, la suma o las que se ajusten mejor al sistema.

Según lo anterior no se pueden usar simplificaciones típicas en la lógica de Boole, i.e.:

en bivalente dE'+dE=1

en multivalente Max [1-U(dE),U(dE)]<=1

lo mismo sucede con el mínimo y por tanto con todas las simplificaciones Booleanas. En algunos casos cuando el conjunto difuso tiene una pendiente muy alta, es decir que es muy similar a un conjunto binario, se pueden utilizar estas simplificaciones sin afectar el funcionamiento del controlador.

Finalmente, las relaciones en difuso quedan:

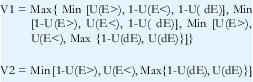
Estas relaciones son sencillas y basadas simplemente en operaciones de comparación básicas así que cualquier lenguaje de programación lo puede realizar.

Al igual que en el controlador Booleano se obtuvieron dos salidas (V1 y V2), donde estas salidas controlaban las válvulas de entrada de flujo (Vg y Vp que tenían diferentes flujos de entrada), se debe buscar una respuesta única o salida total (Vt) , debido a que se va a usar una sola válvula proporcional (como en el controlador difuso clásico), la cual va a manejar el flujo total de entrada.

La salida total (Vt) va a equivaler a la suma de las salidas, pero cada una va a tener un peso diferente:

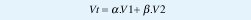
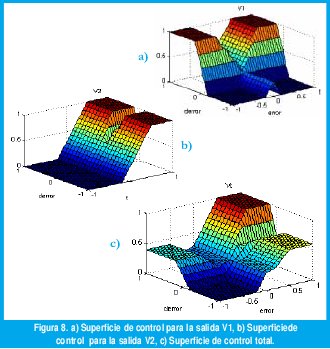
Como se ve en la figura 8 a) y b) ,V1 y V2 tienen valores entre 0 y 1, Vt debe tener también valores entre 0 y 1, por lo tanto:

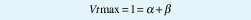
Según esto se podrían dar pesos de 0.6 y 0.4 ó, 0.3333 y 0.6666, en fin según criterio del diseñador, donde β>α para que se cumpla la condición que se había dado de Flujo de V2 > Flujo de V1. Para el ejemplo se tiene β=0.6 y α=0.4. La suma de las dos superficies es nuestra superficie de control (figura 8. c) que manejara la válvula proporcional que alimenta el tanque.

Para obtener la superficie de control simplemente se van dando v es, en donde la velocidad máxima o alta está representada por 1, la media por 0.6, la baja 0.4 y nula es cero.

VI. IMPLEMENTACIÓN DEL CONTROLADOR

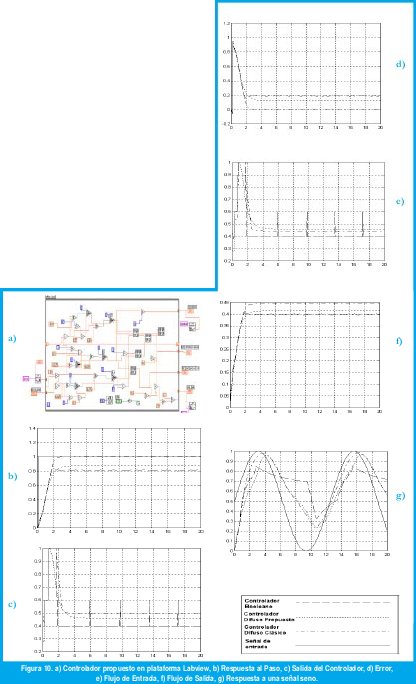
El controlador difuso basado en relaciones Booleanas, por sus procesos tan sencillos, puede ser implementado en cualquier lenguaje de programación, y una interfaz apropiada entre este y el sistema físico.

Si se aprovechan algunos programas para adquisición y manejo de datos como Labview, se obtiene un controlador muy flexible, debido a que se pueden hacer ajustes rápidos, como al tiempo de muestreo, a los pesos de la salida, el lugar y la forma de los conjuntos, difusos. También pueden ser programados en hardware como PICs, FPGA s, entre otros, resultando muy económico y con mejores resultados que un controlador análogo con sus problemas de sintonización y un digital que es muy dependiente del muestreo. En cambio el controlador difuso se independiza de la función característica del sistema, de tal forma que tiene unos buenos resultados en sistemas físicos similares.

VII. ANÁLISIS DE RESULTADOS

Tomando un tanque con las dimensiones altura (2m), área de la base (1m2), área de la válvula de salida (0.1m2). Los resultados de las simulaciones para los tres controladores se muestran en la figura 9.

Las respuestas del controlador difuso propuesto son un estado intermedio entre el controlador binario y el tradicional difuso, combinando la simplicidad del uno con el comportamiento del otro. Además estas respuestas estarán determinadas principalmente por la forma de los conjuntos difusos. Una ventaja importante que ofrece el controlador difuso propuesto es que, sin cambiar los conjuntos difusos y solo los pesos se puede obtener mejores respuestas, además, la simplicidad del cambio de un peso significa en una planta tan solo una ganancia sin que se altere la velocidad de procesamiento.

La optimización para un controlador difuso de este tipo se puede hacer por medio de algoritmos genéticos, en los cuales se ponen variables como los pesos de las salidas, los lugares de los conjuntos difusos, la cantidad de éstos, las formas de los conjuntos, etc. Con ello se puede buscar las mejores combinaciones para un sistema dado.

En cuanto a la implementación y velocidad del controlador, existe una técnica llamada Look-Up Table, en la cual se toma el controlador difuso y se registra la respuesta a un barrido de valores del error y de derror, de tal forma que, se genera una matriz que corresponde a un tipo de discretización del controlador, con lo cual simplemente se guarda en una memoria esta matriz. Lo que se hace es ingresar a la memoria el error y derror actual, se busca el valor discreto más cercano y se toma el dato almacenado en esa posición, luego se envía a un conversor digital a análogo (D/A), siendo ésta la salida del controlador.

VIII. CONCLUSIONES

1. Entre más conjuntos difusos de salida tenga el sistema la respuesta se ajustará a un mínimo es decir buscará la respuesta que mejor se ajuste a la situación del sistema en un momento dado.


2. El error del sistema en estado estable dependerá de la forma de los conjuntos difusos y la forma de estos será dada por el proceso.


3. El controlador propuesto, en términos de implementación, por ser más sencillo y necesitar de operadores no complejos, ofrece una solución rápida y versátil a problemas comunes de la industria.


4. La respuesta del sistema utilizando el controlador propuesto se puede variar no solamente cambiando los conjuntos difusos sino que alterando los pesos de las salidas.


5. La cantidad de iteraciones que debe hacer el controlador propuesto en una plataforma de interfaz es mucho menor que el tradicional, por tener menos componentes y procesos poco complejos.


6. Para la optimización de un sistema de control como el propuesto, se pueden presentar hacia el futuro sistemas en los que se integren algoritmos genéticos, redes neuronales y dispositivos lógicos programables.

REFERENCIAS

[1] SORIANO J., "Un Enfoque Moderno para el Diseño de Automatismos". Reporte Interno, Empresa Sorytel, 2001 Bogotá D.C.

[2] DOUGHERTY E., GYARDINA C., "Mathematical Method for Artificial Intelligent in Autonomous Systems". Prentice Hall International, Miami, 1988.

[3] DRIANKOV D., HELLENDONDOORN H., REINFRANK M., "An Introduction to Fuzzy Control". Springer, New York, 1996.

[4] KUSIAK A., "Intelligent Manufacturing Systems". Prentice Hall International. New York, 1990.

[5] WANG LI XING, "A Course in Fuzzy Systems to Control". Prentice Hall International, New York, 1997.

José Jairo Soriano
Ingeniero Electrónico Universidad Distrital, Ingeniero Químico Universidad Nacional, estudios de Maestría en Ingeniería Eléctrica Universidad de los Andes. Profesor Cátedra Universidad Distrital. e-mail: jjsorytel@latinmeil.com

Omar Lorenzo González Melo
Estudiante Ingeniería Electrónica, X Semestre, Universidad Distrital. e-mail: omarlgonz@ieee.org

Franck Vladimir Munar Fontecha
Estudiante Ingeniería Electrónica, X Semestre, Universidad Distrital. e-mail: franck_munar@usa.net

Andrés Augusto Ramos Acosta
Estudiante Ingeniería Electrónica, X Semestre, Universidad Distrital. e-mail: Andres_Ramos@ieee.org / Andres_Ramos@oxy.com