Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2003-00-00 vol:8 nro:1 pág:46-49

De la síntesis con Agrupaciones Lineales a la síntesis con Agrupaciones Circulares

FROM TO LINEAR ARRAYS SYNTHESIS TO CIRCULAR ARRAYS SYNTHESIS

Carlos A. Suárez F.

Miembro grupo de investigación en Comunicaciones, Universidad Distrital Francisco GITUD.

Elvis E. Gaona

Miembro grupo de investigación en Comunicaciones, Universidad Distrital Francisco GITUD.

Diego Yecid Rincon

Estudiante Maestría U. Andes

Miguel Ferrando Bataller

Profesor Universidad Politécnica de Valencia.

Alejandro Valero Nogueira

Profesor Universidad Politécnica de Valencia.

Resumen

Este articulo muestra una extensión de algunos métodos analíticos de síntesis comúnmente usados en arreglos lineales para el caso de arreglos circulares con elementos isotrópicos y directivos. El estudio se realizará con elementos idealmente directivos como cardioides, de varios ordenes.

Palabras Clave: Arreglos, Agrupaciones circulares, Síntesis de antenas

Abstract

This article seeks to make an extension of some of the analytic methods of synthesis commonly used in the lineal arrays to the case of the circular arrays with isotropic and directive elements. The study will be made with ideal directive elements like cardioids, with several orders.

Key words: Arrays, Circular Arrays, Antenna Synthesis.

I. INTRODUCCIÓN

La capacidad de las agrupaciones para modificar el diagrama de radiación de la antena básica puede aprovecharse para sintetizar un diagrama de radiación que cumpla con determinadas especificaciones mediante la selección apropiada de la amplitud y fase de las corrientes.

En agrupaciones lineales existen diversos métodos de síntesis que permiten obtener determinadas características de radiación (anchos de haz, relación lóbulo principal a secundario, posición de los ceros...), los cuales han sido desarrolladas por varias décadas y pueden clasificarse en varias categorías como se describe en: Lars [1], Cardama2002 [2], Rudge [3], Hansen98 [4], algunos de los mas conocidos son: Método de Schelkunoff, que parte de la especificación de los ceros en el plano Z. Métodos de modelado del haz en el que es común utilizar los métodos de series de Fourier y método de muestreo de Woodward - Lawson. Para diagramas de haz principal estrecho y bajos lóbulos secundarios se encuentran entre otros: Método de Dolph - Chebychev y Método de Taylor.

En el caso particular de una agrupación lineal el factor de la agrupación es la transformada de Fourier de la secuencia discreta de los coeficientes de la alimentación an, esta propiedad permite sintetizar diagramas de radiación de agrupaciones, puesto que basta escoger unos coeficientes de alimentación iguales a los coeficientes del desarrollo en serie de Fourier del diagrama deseado, lo cual es coherente con el hecho de que el diagrama de radiación de una antena es la transformada de Fourier de su distribución de corriente.

Dentro de las distribuciones de corrientes típicas para agrupaciones lineales se encuentran: la uniforme, triangular y binómico. Si bien estas no son las únicas distribuciones utilizadas en la práctica, la uniforme y la binómica son casos extremos con características opuestas.

Este artículo pretende hacer una extensión de los métodos anteriormente expuestos aplicados a las agrupaciones lineales al caso de las agrupaciones circulares utilizando elementos isotrópicos y directivos ideales tipo cardioide de diferente orden.

II. SINTESIS CON AGRUPACIONES CIRCULARES UTILIZANDO ELEMENTOS ISOTROPICOS

En agrupaciones lineales existe entre los coeficientes de la serie de Fourier y las corrientes que deberán aplicarse a las antenas; En el caso de agrupaciones circulares (Figura 1) se determinará esta misma relación mediante el método de síntesis, el cual consiste en desarrollar en serie de Fourier el diagrama de radiación que se desea sintetizar al igual que el factor de la agrupación circular, lo cual permite realizar numerosas síntesis y además va a servir de base para la extensión de los demás métodos de síntesis a las agrupaciones circulares de antenas.

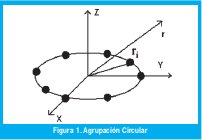
Existen diversos artículos sobre síntesis de diagramas sectoriales con agrupaciones circulares de elementos isotrópicos, utilizando métodos analíticos de Fourier Rudge [3], Vescovo [5], [6], en este caso se pretende utilizar otras técnicas de síntesis aplicadas en agrupaciones lineales, para lo cual se desarrollará la expresión analítica.

El factor de agrupación circular puede ser expresado como en [3]:

Donde se tiene que los coeficientes de alimentación y la ubicación de las antenas se determinan como:

El término de fase completo para el factor de agrupación en el plano de la agrupación e incluyendo el desfasamiento se puede expresar como una serie truncada de Fourier (con el mínimo error cuadrático medio).

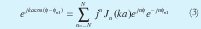
El diagrama deseado expandido en serie truncada de Fourier se puede expresar como:

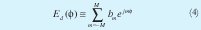
Donde los coeficientes bm se determinan de la manera convencional:

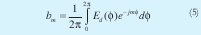
Ahora igualando las series tanto del diagrama deseado como del factor de agrupación, y garantizando que 2M + 1 = N + 1, como en Suárez [7], se tiene que:

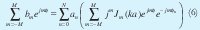
Igualando coeficientes de las series y multiplicando ambos lados de (6) por el mismo término diferente de cero y despejando términos independientes de m se tiene:

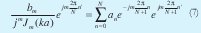
Sumamos todas las ecuaciones:

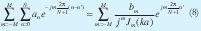
El término del lado izquierdo de (8)se puede reescribir:

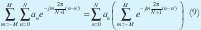
El lado izquierdo de (9) se puede escribir como:

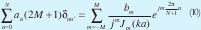
Donde δ_nn' es la delta de Kronecker: 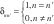Finalmente se llega a que las corrientes necesarias para la síntesis están dadas por:

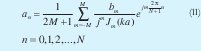
III. SINTESIS CON AGRUPACIONES CIRCULARES UTILIZANDO ELEMENTOS DIRECTIVOS.

Agrupaciones circulares que utilizan elementos directivos ideales tipo cardioide han sido estudiadas analíticamente entre otros por: Rahim [8], vescovo [9], con diagramas tipo. Una expresión general del campo radiado por una agrupación circular con elementos uniformemente distribuidos sobre el plano XY se puede expresar en el mismo plano de la agrupación como en [3]:

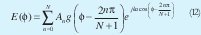
Donde la función "g" determina el diagrama del elemento en la agrupación y An determina los modos de fase y amplitud. El caso en que "g = 1" fue estudiado y constituye una agrupación con elementos isotrópicos. Como función aproximada que modela un elemento con diagrama directivo, se puede tomar la función que caracteriza los diagramas tipo cardioide dada por:

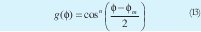
El cual ocupa una posición angular definida por m desplazando el diagrama y por otra parte el orden (n) de la función, determina su ángulo útil de (-3DB). El procedimiento de síntesis con agrupaciones circulares utilizando elementos directivos sigue las mismas pautas desarrolladas para el caso de elementos isotrópicos, de tal manera que se resumirá su estudio:

Igualando el campo radiado por una agrupación con elementos directivos (12) a la expansión en serie de Fourier del diagrama deseado (4), una vez se ha truncado la serie infinita y garantizando que 2M + 1 = N + 1se tiene:

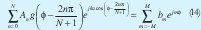
Aplicando (5) a (14) se puede despejar bm y se tiene:

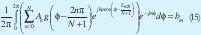
Aplicando propiedad de desplazamiento de las series de Fourier (15) se puede rescribir como:

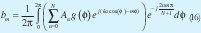
Despejando términos que no dependen de n en (16) se tiene:

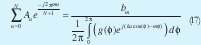
Siguiendo los mismos pasos dados para el caso de fuentes isotrópicas se llega a que:

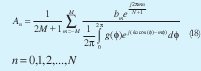
Donde el diagrama del elemento se expande en serie de Fourier como:

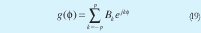
IV. RESULTADOS NUMERICOS DE SINTESIS CON ELEMENTOS DIRECTIVOS IDEALES

Diferentes autores han estudiado el problema de agrupaciones circulares utilizando elementos directivos reales, encontrándose varias soluciones con diversas antenas, Loffler [10]. Ranuras, Sureau [11]. Dipolos frente a cilindro, Suárez [7], Harper [12].

En este estudio se realiza la síntesis con una agrupación que utiliza elementos con diagramas directivos ideales tipo cardioide.

Utilizando las ecuaciones deducidas para síntesis con agrupaciones circulares de elementos isotrópicos (11) y directivos (18) se sintetiza un diagrama sectorial, con los resultados de las figuras 2 y 3 se encuentra una importante diferencia en la magnitud de las corrientes necesarias para la síntesis en cada caso y resultados muy similares en los diagramas sintetizados con las dos agrupaciones.

La figura 2 muestra el resultado de la síntesis de Fourier de un sector circular con sc = λ/12 donde la dirección de máximo es λ/4, utilizando una agrupación circular con elementos directivos tipo cardioide orden n = 2 según ecuación (13) e isotropicos con el número de elementos, radio y separación entre elementos dados por: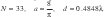

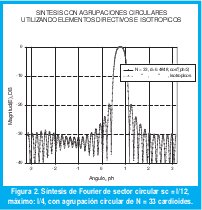
La figura 3 muestra la magnitud de las corrientes necesarias para la síntesis propuesta con los dos tipos de agrupaciones: con elementos directivos figura 3 (b) y con isotrópicos 3. (a), notándose una importante diferencia en la magnitud de las corrientes, siendo más grandes para el caso de la agrupación con elementos isotrópicos y con una distribución no uniforme a diferencia de la agrupación con elementos directivos.

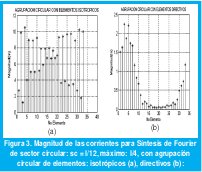
La figura 4 muestra el efecto en el diagrama sectorial sintetizado debido a la separación y directividad de los elementos en una agrupación con 13 antenas con diagrama tipo cardioide de orden n = 2, 4, 6 y 10 (según ecuación 13), para las cuales al aumentar el orden implica un aumento de su directividad, ocasionando una reducción en el nivel de los lóbulos secundarios a partir del segundo lóbulo, sin embargo la magnitud de las corrientes necesarias para la síntesis tienden a aumentar al incrementar el orden. De igual manera se nota una reducción comparable a la de aumentar de un orden n =2 a n = 4 al reducir la separación de 0.4515λ a 0.25λ como se nota en esta figura 4.

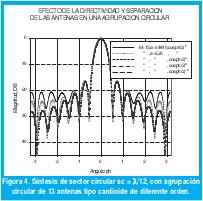
La figura 5 muestra los resultados de las síntesis realizadas con una agrupación circular de 25 elementos directivos ideales tipo cardioide de orden n = 2 según ecuación (13), separados una distancia angular d = 0.33.λ

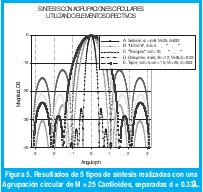
Las síntesis efectuadas mostradas en la figura 5 se enumeran a continuación:

A. Sectorial con sector circular de sc =λ/6.

B. "Uniforme": se sintetiza polinomio en "Z" de orden 5 con distribución uniforme de las corrientes (coeficientes iguales a uno) reproduciendo los mismos resultados obtenidos con una agrupación lineal alimentada con una distribución uniforme de las corrientes para un polinomio en "Z" de orden 5.

C. "Triangular": se reproducen los mismos resultados obtenidos con una agrupación lineal alimentada con una distribución triangular de las corrientes para un polinomio en "Z" de orden 10.

D. Chebychev: se sintetiza utilizando el polinomio de Chebychev de orden 5, con un factor Xo = 1.2.

E. Taylor: con base en un polinomio de Taylor en "Z" de orden 5 con distribución uniforme de las corrientes (coeficientes iguales a uno), se desplaza primer cero a 1.5 radianes.

V. CONCLUSIONES

Se presenta una solución al problema de síntesis con agrupaciones circulares utilizando elementos isotrópicos y directivos, esta solución permite en principio la síntesis de cualquier diagrama que pueda ser expandido en serie de Fourier. De igual manera el procedimiento desarrollado permite extender los resultados de síntesis conocidos con agrupaciones lineales a las agrupaciones circulares.

La magnitud y fase de las corrientes necesarias para la síntesis y el diagrama final sintetizado en cada caso, muestran una diferencia importante que tiende a ser más crítica en la medida que el diagrama deseado es más exigente en parámetros como: nivel de lóbulo principal a secundario (NLPS), directividad deseada, y en cuanto a la agrupación utilizada en aspectos como: directividad del elemento básico utilizado, separación entre los elementos.

REFERENCIAS BIBLIOGRÁFICAS

[1] Lars. Josefsson, H. Steyskal. Methods and Software Tools for the Design of Antennas and Arrays, Advanced Short Curse, Universidad de Santiago de Compostela, España, sep. 4, 2002.

[2] A. C. Cardama et al, Antenas, España, Ediciones UPC, 2000.

[3] A. W. Rudge, et al. The Handbook of Antenna Design. London: IEE pres. 1986.

[4] R. C. Hansen. Phased Array Antennas. New York, John Wiley and Sons, 1998.

[5] R. Vescovo, "Constrained and Unsconstrained Synthesis of Array Factor For Circular Arrays". IEEE Trans. Antennas Propagat. vol 43. No. 12, pp .1405-1410, December 1995

[6] R. Vescovo, "Pattern Synthesis with Assigned Field Reduction in NearField for Circular Arrays," IEEE, Int. Symp AP-S/URSI, San Antonio, TX, 541-543, June 2002.

[7] C. Suárez, M. Ferrando y A. Valero, "Síntesis con Agrupaciones Circulares" URSI Septiembre 10-12, 2003, Universidad de la Coruña España.

[8] T. Rahim, "Directional pattern synthesis in circular arrays of directional antennas", Ph. D. dissertation, London Univ, 1980.

[9] R. Vescovo, "Use of directional elements in the null synthesis for arc arrays. ". IEEE Trans. Antennas Propagat. Int sympo vol 2. pp .736- 739, Jun. 1998

[10] D. Loffler, W. Wiesbeck, B. Johannisson, "Conformal Aperture coupled microstrip phased arrays on a Cylindrical Surface," IEEE, Int. Symp APS, Orlando Florida, 11-16, July 1999.

[11] Sureau, J. C, Hessel, A, "Element Pattern for Circular Arrays of Waveguide-fed Axial Slit on large Conducting Cylinders," Trans. IEEE, Vol AP-19, Jan 1971, pp. 64-74.

[12] John C. Herper, et al. "Element pattern of an Axial Dipole in a Cylindrical Phased Array". IEEE Trans AP- 33, No. 3, March 1985, p. 259-272.

[13] C. Suárez, M. Ferrando y A. Valero, "Radiación de Dipolos Frenta a Cilindro Metálico Infinito" URSI Septiembre 10-12, 2003, Universidad de la Coruña.

Carlos Arturo Suarez F.
Profesor Asistente Universidad Distrital y Estudiante de Doctorado, Universidad Politécnica de Valencia. csuarez33@udistrital.edu.co

Miguel Ferrando Bataller , Alejandro Valero Nogueira
Profesores Titulares, Universidad Politécnica de Valencia. mferrand@dcom.upv.es

Elvis Eduardo Gaona
Profesor Asistente, Universidad Distrital egaona@udistrital.edu.co

Diego Yecid Rincón
Ingeniero Electrónico Universidad Distrital. Estudiante Magíster en Ingeniería Electrónica Universidad de los Andes dyrincon@ieee.org