DOI:
https://doi.org/10.14483/23448393.1471Published:
2000-11-30Issue:
Vol. 6 No. 1 (2001): January - JuneSection:
Science, research, academia and developmentAntenas fractales
Fractal Antennas
Keywords:
Antenas, Fractales, Antenas multifrecuencia (es).Downloads
References
Mandelbrot, B.B., "The fractal geometry of nature", San Francisco, H. W. Freeman and Company, 1983.
Peitgen, H.O., Jürgens, H. y Saupe, D. "Chaos and fractals", Springer-
Verlag, New York, 1992.
Jaggard, D.L.,"On fractal electrodynamics" en "Recent advances in electromagnetic theory", Springer-Verlag, New York, H. N. Kritikos and Jaggard, D.L. (Eds.), 1990.
Rumsey, V. H., "Frequency independent antennas". New York: Academic, 1966
Puente, C., y Pous, R. "Fractal design of multibandand low sidelobe arrays," IEEE Transaction Antennas Propagation, vol 44, May 1996, pp. 1-10.
Kim, Y. and Jaggard, D.L.,"The fractal random array", vol.74. No.9, Proceeding IEEE, 1986, pp. 1278-1280.
Puente, C., Romeu, J., Pous, R. y Cardama, A. "On the behavior of the multiband fractal antenna," IEEE Transaction Antennas and Propagation, vol 46, April 1998, pp. 517-524.
Puente, C., Romeu, J., Bartolomé, R. y Pous, R. "Perturbation of the Sierpinski antenna to allocate operating bands," Electronics Letters, vol 32, Nov. 1996, pp. 2186-2188.
Puente, C., Claret, J., Sagués, F., Romeu, J., López-Salvans, M. Q. y Pous, R. "Multiband properties of fractal tree antenna generated by electrochemical deposition," Electronics Letters, vol 32, Dec. 1996, pp. 2298-2299.
Cohen, N. "Fractal antennas Part 2" Comunications Quartterly, Summer 1996, pp 53-66.
Werner, D.H. y Werner, P.L. "Frequency independent features of self-similar fractal antennas," Radio Science, vol. 31, no. 6, Nov./Dec. 1996, pp. 1331-1343.
Song, C.T., Hall, P.S., Ghafouri, H. y Wake, D. "Fractal stacked monopole with very wide bandwidth," Electronics Letters, vol 35, Jun. 1999, pp. 945-946.
Siah, E., Ooi, B., Kooi, P. y Xhou, X. "Experimental investigation of several novel fractal antennas- variants of the Sierpinski gasket and introducing fractal FSS screens," IEEE Proceedings, 1999, pp. 170-173.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación y Desarrollo
Ingeniería, 2001-00-00 vol:6 nro:1 pág:34-38
Antenas fractales
FRACTAL ANTENNAS
Carlos Suarez
Diego Rincón
Elvis Gaona
Resumen
En este artículo se describe el comportamiento multibanda de la antena fractal Sierpinski y el mejoramiento realizado por la antena Koch. Estas son comparadas con la antena de banda estrecha bowtie y el monopolo lambda cuartos, debido a su similitud triangular y línea recta respectivamente. Los resultados numéricos y experimentales muestran que las propiedades de autosimilitud de las formas fractales se trasladan al comportamiento electromagnético. Además las propiedades de llenar espacios de muchas de las formas fractales pueden usarse también para el diseño de antenas pequeñas. Las curvas obtenidas muestran como el monopolo fractal puede mejorar las características de un monopolo común lineal. (frecuencia de resonancia, resistencia de radiación, ancho de banda).
Abstract
The multiband behavior of the fractal Sierpinski antenna and the improves of Koch antenna is described in this paper. Due to its similarity triangular shape and straight line, is compared to well-know single band bow-tie and monopole respectively. Both experimental and numerical results shows that the selfsimilarity properties of the fractal shapes are translated into its electromagnetic behavior. Moreover the space filling properties of many forms can be used to design small antennas as well. The curves obtains are show how fractal monopole can improve the radiation features of a common linear monopole (resonance frequency, radiation resistance, bandwidth).
Key words: Antenas, Fractales, Antenas multifrecuencia
I. INTRODUCCIÓN
Muchos diseños de antenas son altamente dependientes de la frecuencia, el tamaño de la antena relativo a la longitud de onda de operación es el principal factor de limitación en el ancho de banda. En los principios de los años sesenta algunas estructuras autoescalables tales como espirales, conos y arreglos logoperiódicos fueron desarrollados para el diseño de antenas independientes de la frecuencia por Rumsey en [4]. El Factor común es que la forma de estas estructuras permanece invariable bajo transformaciones de escala.
Los fractales son estructuras autoescalables. Esto significa que su forma permanece igual bajo los cambios de escala, se dice que no poseen características de tamaño [1-2]. Cuando se observa algunas de las partes que componen la estructura, se encuentra una menor forma del objeto global. Un fractal ideal es aquel que no posee características de tamaño, como se mencionó anteriormente, tiene un número infinito de escalas y tamaños que son contenidos dentro del mismo objeto. Por lo tanto podrían usarse para el diseño de sistemas radiantes, y se podría esperar comportamientos de operación multibanda. Este artículo analiza dos antenas, la antena multibanda fractal Sierpinski y el monopolo fractal de Koch.
La interacción de algunas estructuras fractales con ondas electromagnéticas ha sido estudiada recientemente por Jaggard et al. [3-6]. El primer intento por explorar las propiedades multifrecuenciales de los fractales como estructuras radiantes fue hecho por C. Puente en [5]. Algunas formas convolucionales fueron investigadas para tratar de eludir el principio de la dependencia de los parámetros de radiación con su tamaño físico relativo a la longitud de onda. Los fractales se unieron a los diseños multibanda debido a sus propiedades autoescalables. Concerniente a éste, C. Puente describió en [7] el comportamiento de la primera antena fractal multibanda, el monopolo de Sierpinski. Posteriormente se dieron otros pasos significativos en el campo de las antenas multibanda hechas también por C. Puente et. al. en [8]-[9]. Además, otras importantes contribuciones a las antenas pequeñas [10] y las antenas fractales independientes de la frecuencia [11] fueron introducidas por Cohen, et al. respectivamente. Posteriormente a estos hechos C. Song en [12] realizó variaciones a la antena fractal multibanda Sierpinski para obtener las mismas características multibanda, esto para sistemas GSM, DECT y WLAN. Luego E. Siah et al. utilizó screens fractales para mejorar el desempeño de las bandas de frecuencia de esta antena, logrando anchos de banda entre el 18 y 80% [13].
Algunos problemas teóricos emergen cuando se analiza el comportamiento electromagnético de un alambre fractal. Por lo tanto, la evaluación del vector de radiación a través de la integral de línea a lo largo de la antena no provee una convergencia para una forma fractal ideal. En el caso de no-convergencia, se tendría una conclusión apresurada, la cual una resistencia de radiación muy grande podría obtenerse siempre para un monopolo muy pequeño (pero grande en longitud) que tiene una longitud de onda particular.
Para la especificación de estos campos se asume que una antena fractal puede formarse por un arreglo de pequeños elementos lineales teniendo una distribución fractal en el espacio. En la siguiente sección se procede a realizar una breve introducción a los campos producidos por una estructura fractal.
II. CAMPOS DE UNA ESTRUCTURA FRACTAL
Los campos de un elemento lineal pueden resolverse con la ayuda del vector de Hertz [Marian y Heald, 1980]. Para resolver las ecuaciones de Maxwell definimos, en el vacío, el vector función Q que está relacionado con la densidad de corriente J y la densidad de carga ρ de la siguiente manera:
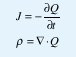
Nótese que Q resuelve la ecuación de continuidad, y además, puede usarse para definir otra función vectorial, llamada el vector de Hertz π(x,t),
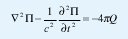
Donde entonces los campos son definidos:
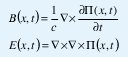
Las ecuaciones de la transformada de Fourier en el tiempo, con Q(x,ω)=j/ω(J(ω,w)) y J(x,ω)=Ll(l,ω) pueden resolverse con la ayuda del vector de Hertz π
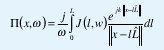
Donde el elemento tiene una orientación L y longitud l, y es parametrizada por l ⊂ [0,L]. Los valores con el superíndice "^" indican vectores unitarios, las variables en negrilla indican vectores; ω es la frecuencia, k=ω/c. La dependencia con el tiempo puede hallarse con la inversión de la ecuación anterior.
A. Campos de una antena fractal
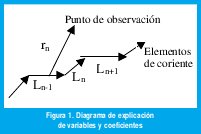
Un pulso de corriente se propaga con velocidad β=v/c a lo largo de una estructura fractal. En el elemento enésimo con orientación Ln y longitud ln, el cual se parametriza por I ⊂ [0,Ln]. teniendo una corriente dada por I(l,εn,t)=Io (t-(εn-l)/v) donde εn es el camino medido a lo largo del fractal. El campo radiado es la superposición (con las respectivas fases) de todos los pequeños elementos de corriente lineal que provee el fractal. Para un conjunto de elementos lineales tales como en la Fig. 1, el vector de Hertz está dado por:
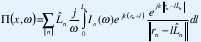
Donde rn es el vector del comienzo del enésimo elemento lineal del campo de posición x,ω es la frecuencia y k=ω/c,
En general la ecuación anterior para π(x,t) resulta muy complicada, y realmente el interés está en el campo lejano de pequeños elementos lineales (rn>>L), por lo tanto, se aproxima el campo lejano de pequeños elementos lineales para así obtener una solución en forma cerrada para la transformada de Fourier del campo, de la siguiente forma:

Donde el factor geométrico está dado por
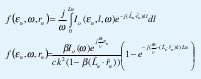
De las ecuaciones se observa que las correlaciones de fase sobre el fractal pueden ser extremadamente relevantes, y producen campos radiados espaciados no uniformente. Después de invertir la transformada de Fourier del campo para tiempo real se obtiene el patrón de radiación espacio temporal debido a la descarga de la estructura fractal.
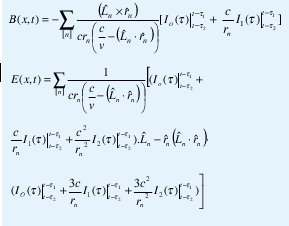
donde
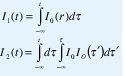
Puede calcularse exactamente para las corrientes descritas anteriormente, donde
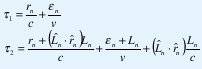
El valor de τ1 y τ2 corresponden a los retardos de tiempo causales de dos puntos terminales del elemento lineal.
Antes de terminar esta sección, es de importancia observar que existe una interesante simetría en los campos radiados. En general se podría asumir que la corriente está dada por I(t) = I0e-ατ(1- cos(2παt))θ(t), donde &theta:(t) es la función paso, y n≥ 1. Note que la carga total de esta corriente es Q=Io/α donde 1/α es el tiempo de decaimiento de la corriente, desde que la corriente se propague a lo largo del fractal, los campos radiados en una posición dada del espacio estarán en función de τ= s/v +α donde s es la longitud mayor medida a lo largo del fractal. Los campos son invariantes así como αt. Tal escalización es de importancia en el estudio de las propiedades de los campos radiados provenientes de una antena fractal.
B. El campo lejano
El campo lejano está aproximadamente dado por:
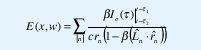
En general se usará un pulso de corriente definido como I(t)=Io(e-α-e-γt)(1+cos(ωt))θ(t), con ω=2παnf y θ(t) como la función paso. Aquí nf representa el número de oscilaciones durante el tiempo de decaimiento 1/α.
III. MONOPOLO DE SIERPINSKI
A. Descripción de la antena
El cuerpo principal de la antena es un triángulo conductor Sierpinski, el cual está impreso sobre un delgado substrato de dieléctrico (εr=2.17, h=0.127 mm) y montado sobre un plano conductor cuadrado aterrizado Figura 2. La configuración de monopolo se escoge debido a que se simplifica enormemente el esquema de alimentación, el cual puede implementarse fácilmente colocando el coaxial a través del plano de tierra.
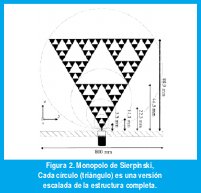
La for ma fractal es construida bajo cinco iteraciones, el triángulo de Sierpinski aparece en cinco escalas diferentes dentro de la estructura principal. La antena presenta un factor de dos entre cada escala. Esta figura en particular ha sido escogida debido a su similitud con la antena bow-tie, puesto que la forma triangular aparece en cinco diferentes escalas, se puede esperar que la antena Sierpinski se comporte similarmente a una antena triangular pero en cinco bandas.
B. Resultados experimentales y computacionales
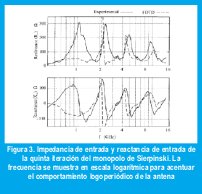
El coeficiente de reflexión de entrada (ρin) relativo a 50Ω fue medido desde 500 MHz hasta 14 GHz usando un Analizador vectorial de redes (HP8510B). También el comportamiento fue simulado usando la técnica FDTD. Las partes reales e imaginarias de la impedancia de entrada (Zin) se muestran en la figura 3. Los parámetros medidos se visualizan por las líneas sólidas, mientras que las calculadas se muestran en línea punteada.
1) Patrones de radiación
Las tres gráficas muestran un comportamiento logoperiódico (δ) el cual es aproximadamente dos. En particular la antena está acoplada en cinco bandas: 12.6, 6.4, 3.3, 1.62 y 0.64 GHz. Mientras ρin es menor a -15 dB en las cuatro bandas superiores. También esta banda aparece cambiada significativamente desde la frecuencia esperada (0.64 GHz en lugar de 1.62/δ=0.81GHz). Ambos fenómenos son predichos por el análisis y son causados por el truncamiento de la forma fractal, que no podría implementarse con un número arbitrario de escalas e iteraciones. El efecto de truncamiento puede verse relacionado con un ligero cambio y un mal acople en las bandas superiores.
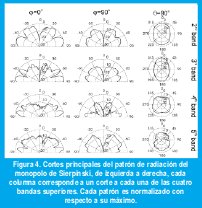
Los patrones de radiación fueron medidos en una cámara anecoica en los puntos de menor VSWR de las tres bandas superiores ( 12.6, 6.4, y 3.3 GHz). Los principales cortes phi=0, 90, tetha=90 se muestran en la Fig. 4 para las componentes del campo eléctrico Eth y Ephi respectivamente. Todos los patrones son normalizados con respecto al máximo y son representados en forma polar con un rango dinámico de 25 dB. Cada corte representa un notable grado de similitud a través de las tres bandas, especialmente para la componente Eth la cual es la principal componente con un promedio de 30 dB encima de Ephi.
IV. MONOPOLO DE KOCH
Algunas nociones geométricas tales como longitud, tamaño y dimensión han de ser aplicadas con mucho cuidado cuando se trata con geometrías fractales, por lo tanto, muchos fractales continuos, pero no diferenciables tienen una longitud infinita en un área finita. La clásica curva de Koch mostrada en la Fig. 5 es una figura de comportamiento semejante construida después de un proceso iterativo, la longitud de la curva crece con un factor de 4/3 en cada etapa, mientras que mantiene exactamente el mismo tamaño. La figura obtenida después de un número infinito de iteraciones es un fractal ideal, el cual no tiene derivada en ningún punto.

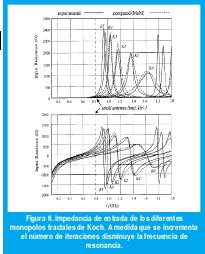
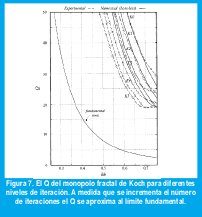
Se implementaron cinco antenas (K1-K5) correspondientes a las primeras cinco iteraciones de la curva de Koch. Para la comparación se construyó un monopolo estándar (K0) del mismo tamaño, pero obviamente no de la misma longitud, simulando las tres primeras iteraciones usando el método del momento. La Fig. 6 muestra las resistencias de entrada y las reactancias de las seis antenas, mientras que el factor Q normalizado en frecuencia se muestra en la Fig. 7.
Algunas conclusiones pueden derivarse de estas gráficas. La resistencia de entrada aumenta cada vez que la longitud (no el tamaño) aumenta. De igual forma la resistencia óhmica y de radiación crecen, sobre un amplio rango de frecuencias menores al límite de la frecuencia de la antena pequeña. También la frecuencia de resonancia cambia hacia mayores longitudes de onda, entregando antenas resonantes siempre en la región de antenas pequeñas. Análogamente el factor Q se reduce en cada iteración, tendiendo al límite fundamental. Una explicación física de tal comportamiento puede darse en el número creciente de esquinas y dobleces del monopolo de Koch, el cual colima la radiación. Estos mejoramientos no son sorprendentes si se tiene en cuenta las propiedades de llenar los espacios que tienen las figuras fractales; mientras que la unidimensionalidad del monopolo empobrece el uso del espacio disponible, el monopolo de Koch llena una dimensión mayor D>1 (D=1.26) mejorando su uso para radiar eficientemente.
V. CONCLUSIONES
Las estructuras fractales han sido usadas en los sistemas radiantes debido a sus propiedades de autosimilitud. Las principales aproximaciones han sido expuestas en las secciones III y IV, respectivamente: La antena fractal Sierpinski ha mostrado un notable grado de similitud en cinco bandas, que es el mismo número de escalas sobre el cual el fractal fue iterado. Las bandas son espaciadas por un factor de dos, el mismo espaciamiento relativo de las escalas en la forma fractal. Entonces, se concluye que las propiedades geométricas autosimilares de la estructura fractal se trasladan a su comportamiento electromagnético, y por esta razón, parece que otras formas fractales podrían ayudar al diseño de antenas multibanda e independientes de la frecuencia. Este trabajo está soportador por Grant TIC-96-0724-C0604 del Gobierno de España y por la compañía FRACTUS S.A. Los resultados experimentales y numéricos muestran que el monopolo de Koch mejora el comportamiento de monopolos pequeños. La resistencia de radiación aumenta y la reactancia está siempre en la región de antena pequeña. El factor Q se reduce en cada iteración, tendiendo al límite establecido para las antenas omnidireccionales.
En la actualidad se están simulando, implementando y probando estas antenas en la Universidad Distrital, llegando a unos resultados sorprendentes.
REFERENCIAS
- Mandelbrot, B.B., "The fractal geometry of nature", San Francisco, H. W. Freeman and Company, 1983.
- Peitgen, H.O., Jürgens, H. y Saupe, D. "Chaos and fractals", Springer-Verlag, New York, 1992.
- Jaggard, D.L.,"On fractal electrodynamics" en "Recent advances in electromagnetic theory", Springer-Verlag, New York, H. N. Kritikos and Jaggard, D.L. (Eds.), 1990.
- Rumsey, V. H., "Frequency independent antennas". New York: Academic, 1966
- Puente, C., y Pous, R. "Fractal design of multibandand low sidelobe arrays," IEEE Transaction Antennas Propagation, vol 44, May 1996, pp. 1-10.
- Kim, Y. and Jaggard, D.L.,"The fractal random array", vol.74. No.9, Proceeding IEEE, 1986, pp. 1278-1280.
- Puente, C., Romeu, J., Pous, R. y Cardama, A. "On the behavior of the multiband fractal antenna," IEEE Transaction Antennas and Propagation, vol 46, April 1998, pp. 517-524.
- Puente, C., Romeu, J., Bartolomé, R. y Pous, R. "Perturbation of the Sierpinski antenna to allocate operating bands," Electronics Letters, vol 32, Nov. 1996, pp. 2186-2188.
- Puente, C., Claret, J., Sagués, F., Romeu, J., López-Salvans, M. Q. y Pous, R. "Multiband properties of fractal tree antenna generated by electrochemical deposition," Electronics Letters, vol 32, Dec. 1996, pp. 2298-2299.
- Cohen, N. "Fractal antennas Part 2" Comunications Quartterly, Summer 1996, pp 53-66.
- Werner, D.H. y Werner, P.L. "Frequency independent features of self-similar fractal antennas," Radio Science, vol. 31, no. 6, Nov./ Dec. 1996, pp. 1331-1343.
- Song, C.T., Hall, P.S., Ghafouri, H. y Wake, D. "Fractal stacked monopole with very wide bandwidth," Electronics Letters, vol 35, Jun. 1999, pp. 945-946.
- Siah, E., Ooi, B., Kooi, P. y Xhou, X. "Experimental investigation of several novel fractal antennas- variants of the Sierpinski gasket and introducing fractal FSS screens," IEEE Proceedings, 1999, pp. 170-173.
Carlos Arturo Suárez
Profesor facultad Ingeniería, Universidad Distrital Fco. José de Caldas. Especialista en instrumentación y comunicaciones. Candidato a Dr. en Ingeniería de Telecomunicaciones en la Universidad Politécnica de Valencia (España), csuarez@atlas.udistrital.edu.co
Elvis Eduardo Gaona Garcia
Estudiante Ingeniería Electrónica. Universidad Distrital Fco. José de Caldas, elvisg@ieee.org
Diego Yecid Rincón Reyes
Estudiante Ingeniería Electrónica. Universidad Distrital Fco. José de Caldas, dyrincon@hotmail.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










