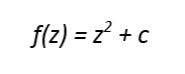
DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.3.a010Published:
2016-10-09Issue:
Vol. 21 No. 3 (2016): September - DecemberSection:
Dossier "Complexity and Engineering"Transformación de la no-Complejidad a la Complejidad
Transformation of non-complexity to complexity
Keywords:
Complexity, fractal geometry, analytical methods, change, scientific revolution (en).Keywords:
Complejidad, geometría de fractales, métodos analíticos, cambio, revolución científica (es).Downloads
Abstract (es)
Contexto: Este artículo aborda un problema nuevo y difícil: la manera como un fenómeno o sistema simple o lineal puede ser transformado gracias a la geometría de fractales en un sistema o fenómeno complejo. En este sentido, el contexto es el de las ciencias de la complejidad. El problema es altamente significativo, pues de manera general siempre se ha dicho que la complejidad trata, entre otros, con comportamientos no-lineales.
Método: El método es eminentemente teórico. En la bibliografía especializada el problema nunca se ha trabajado, y si sí, como un sistema simple o complicado puede ser cambiado en uno complejo o no-lineal.
Resultados: Los resultados indican que es posible abordar el problema y resolverlo satisfactoriamente, atendiendo a los más destacados antecedentes en la materia. Se presentan varios argumentos que remiten entre otros a G. Julia y Mandelbrot.
Conclusiones: La conclusión es que la geometría de fractales suministra bases suficientes para estudiar la transformación estudiada. Así, la importancia teórica y práctica del problema considerado puede extenderse a numerosos campos; aquí se explora y se muestra, por primera vez, como dicha transformación es posible.
Abstract (en)
Context: This paper deals with a new and most difficult problem, namely the way in which a simple or linear system or phenomenon can be transformed into a complex or non-linear phenomenon or system thanks to the fractals geometry. In this sense, the framework is set out by the sciences of complexity. Such a problem is extremely important, for in general it has been said that complex science deals, among others, with non-linear behaviors. As a conclusion, the geometry of fractals provides bases solid enough to study the transformation herewith considered. The theoretical and practical meaning of the problem raised here can be extended to numerous fields. Here such a transformation is explored and shown for the first time.
Method: The method here is theoretical. However, in the specialized bibliography the problem considered here has never been worked out, namely: whether, and if so how a simple or complicated system can be changed into a complex or non-linear one.
Results: Working on the basis of fractal geometry the transformation from linear systems into non-linear is possible. Various arguments are shown that support an idea that sends back to G. Julia and Mandelbrot.
Conclusions: As a conclusion, the geometry of fractals provides bases solid enough to study the transformation herewith considered. The theoretical and practical meaning of the problem raised here can be extended to numerous fields. Here such a transformation is explored and shown for the first time.
References
S. Kauffman, Investigations. Oxford, Oxford University Press, 2000.
C. E. Maldonado, Termodinámica y complejidad. Una introducción para las ciencias sociales. Bogotá, D.C. Desde Abajo [primera edición 2005], Ed. Universidad Externado de Colombia, 2011.
C. E. Maldonado, “Ciencias de la complejidad: Ciencias de los cambios súbitos”, Odeón. Observatorio de Economía y Operaciones Numéricas, Universidad Externado de Colombia, 2005, pp. 85-125.
D. Campos, “Caos y complejidad en el marco de cuatro revoluciones científicas”, Maldonado, C. E. (Ed.), Complejidad: revolución científica y teoría, Bogotá, D.C., Ed. Universidad del Rosario, 2009, págs. 21-33.
A. C. Scott, The Nonlinear Universe. Chaos, Emergence, Life. Springer Verlag, 2007.
E.Tiezzi, La belleza y la ciencia. Hacia una visión integradora de la naturaleza. Barcelona, Icaria, 2006.
D. Zahavi, “Beyond Empathy: Phenomenological Approaches to Intersubjectivity”. Journal of Consciousness Studies, 8, 2001, pp. 151-167.
L. Mlodinow, Euclid’s Window. The Story of Geometry from Parallel Lines to Hyperspace. New York, The Free Press, 2001.
P. Bak, How Nature Works. The New Science of Self-Organized Criticality. Copernicus, 1996.
B. Mandelbrot, La geometría fractal de la naturaleza. Barcelona, Tusquets, 1997.
G. Bateson, Espíritu y naturaleza. Buenos Aires: Amorrortu, 2004.
C. A. Pickover, La banda de Möbius. Todo sobre la maravillosa banda del Dr. Möbius: matemáticas, juegos, literatura, arte, tecnología y cosmología. Almuzara, 2009.
F. López Aguilar y F. Brambila Paz, (Eds.). Antropología fractal. México, Sociedad Matemática Mexicana, 2007.
B. Mandelbrot, Fractals and Chaos. The Mandelbrot Set and Beyond. Springer Verlag (with a Foreword by P. W. Jones and texts co-authored by C. J. G. Evertz and M. C. Gutzwiller), 2004.
H. Pagels, Los sueños de la razón. El ordenador y los nuevos horizontes de las ciencias de la complejidad. Bacelona, Gedisa, 1991.
R. Axelrod, The Complexity of Cooperation. Agent-Based Models of Competition and Collaboration. Princeton, NJ, Princeton University Press, 1997.
T. Todorov, La conquête de l’ Amérique. La question de l’ autre, Paris, Seuil, 1982.
B. Greene, El universo elegante: Supercuerdas, dimensiones ocultas y la búsqueda de una teoría final, Barcelona, Crítica, 2001.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










