Ingeniería, 2004-00-00 vol:9 nro:1 pág:4-7

Perceptrón basado en kernel para reconocimiento de dígitos manuscritos

A kernel-based perceptron implementation for hand-written digit recognition

Sergio A. Rojas
Director del Grupo de Interés en Adptación, Computación & MEnte (ACME-UD). Miembro del Grupo de Investigación LAMIC.

Resumen

Las técnicas de aprendizaje basadas en transformaciones con núcleos o matrices (kernel-based learning machines) han dado un nuevo horizonte a las redes neuronales artificiales para la solución de problemas de reconocimiento y clasificación en dominios no-lineales. En este artículo se describe el funcionamiento e implementación de un perceptrón para reconocimiento de los diez dígitos arábigos en patrones de escritura real, utilizando una transformación con núcleo polinomial. El clasificador alcanza niveles de reconocimiento con una tasa de éxito cercana al 93% en patrones no vistos durante el entrenamiento.

Palabras clave:
aprendizaje basado en kernel, redes neuronales artificiales, reconocimiento de patrones.

Abstract

Kernel-based learning machines have been proposed as a new approach to use neural networks architectures applied to non-linear classification and recognition problems with many good results reported recently. In this paper we describe the implementation of a perceptron neural network for classification of real digit number data set, based on the kernel learning method. The classifier obtains a successful recognition score near to 93% on unseen patterns.

Key words: kernel-based learning, artificial neural networks, pattern recognition.

I. INTRODUCCIÓN

Las redes neuronales artificiales (ANN, por sus siglas en inglés) aparecieron como una técnica de clasificación de patrones inspirada en el modelo biológico del cerebro: miles de procesadores simples (neuronas) interconectados entre sí pueden llegar a realizar tareas de alta complejidad como reconocimiento de imágenes, distinción de sonidos, memorización de escenas, etc. El modelo básico de ANN, conocido como perceptrón simple, es una red de dos capas de neuronas; la primera de ellas sirve para capturar las entradas, y segunda (capa de salida) permite efectuar la clasificación; es útil para clasificar datos que puedan ser separados mediante un discriminador lineal (un hiperplano en el espacio vectorial de características de entrada). Esta arquitectura se ve limitada cuando el espacio de búsqueda es no lineal. En tal caso, se pueden añadir neuronas ocultas para atenuar el efecto de las no linealidades, y convertir así a la red en un aproximador universal susceptible de entrenamiento mediante el bien conocido algoritmo de retropropagación.

Recientemente ha aparecido un nuevo enfoque que permite realizar la clasificación no lineal, manteniendo la arquitectura lineal de la red. La idea consiste en realizar primero una transformación en el espacio vectorial de los patrones de entrada mediante una función conocida como núcleo (en adelante kernel), de forma que pueden ser linealmente separables en el nuevo espacio de características definido por el kernel, y a continuación utilizar un perceptrón simple para realizar la clasificación. El resultado es un nuevo tipo de red conocido como el perceptrón basado en kernel (KP, por sus siglas en inglés). En este artículo se realiza una implementación de un KP en Mathematica y en Matlab para aplicarlo a una tarea de clasificación de dígitos arábigos escritos a mano alzada, demostrando la efectividad de este método. El artículo está organizado de la siguiente forma: En la sección 2 se presenta un repaso del perceptrón simple y el KP junto con el diseño experimental; en la sección 3 se discuten los resultados; y en la ultima sección se comentan algunas conclusiones y alternativas para trabajar con este tipo de sistemas en un futuro.

II. MÉTODOS Y MATERIALES

2.1 Perceptrón lineal

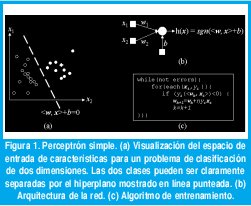
La arquitectura más sencilla para clasificación lineal en redes neuronales fue propuesta hace casi medio siglo por Rosenblatt [1]. Sea S = {(x₁,y₁),(x_m,y_m)} un conjunto de vectores etiquetados, donde xi corresponde a un patrón de entrada (medidas o características de un objeto), e y_i={-1,+1} es la clase a la que pertenece. El perceptrón se define en la fig. 1(b); la capa de neuronas de entrada se utiliza para capturar el vector de características x, y la neurona de salida produce el valor de la función dada por

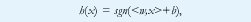
donde sgn retorna el signo de su argumento, <:,:> denota el producto punto entre vectores, y w y b son el vector de pesos y el umbral. Si los patrones de entrada son linealmente separables, esto es, si existe una línea recta (o un hiperplano en el caso de mas de dos dimensiones) que pueda trazarse para dividir las dos clases como se muestra en la fig. 1(a), el perceptrón esta en capacidad de aprender los valores adecuados para el vector de pesos (aumentado para incluir también el umbral) que definen tal hiperplano, utilizando el algoritmo mostrado en la fig. 1(c). Nótese que la red modifica el valor de los pesos siempre que la clasificación del patrón de entrada sea errónea (si <w, x_i> e y_i tienen signos distintos, o lo que es lo mismo, si (y_i <w, x_i>) < 0 ). Se puede demostrar que dadas las condiciones anteriores, el algoritmo converge en un número finito de iteraciones.

2.2 Aprendizaje basado en kernel

La principal desventaja del perceptrón simple radica en que la mayoría de problemas para su aplicación real no son linealmente separables. Por ejemplo, sería incapaz de aprender a clasificar el conjunto de vectores etiquetados S = {([0,0],0), ([0,1],1), ([1,0],1), ([1,1],0)} correspondientes a la elemental compuerta XOR. Una alternativa para superar este obstáculo puede ser la utilización de un perceptrón multicapa entrenado con el conocido algoritmo de retropropagación (backpropagation), aunque la introducción de neuronas ocultas añade un grado de mayor complejidad en la ANN.

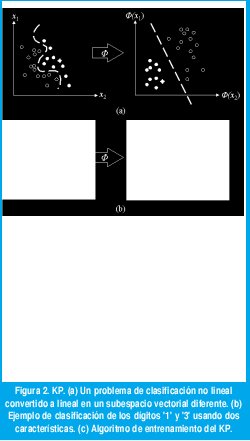
Por otra parte, recientemente se ha propuesto un nuevo modelo que conserva la característica de linealidad del perceptrón simple, y que está basado en realizar un preprocesamiento del espacio de características de entrada utilizando transformaciones conocidas como funciones de kernel [2]. La situación se muestra en la figura 2(a) para un problema imposible de separar linealmente. Al aplicar la transformación al espacio vectorial X es posible encontrar un subespacio vectorial en donde los patrones (características) puedan ser linealmente separables, utilizando un perceptrón simple (convertido por tanto en un KP) que realice la clasificación. A manera de ilustración, la figura 2(b) muestra esquemáticamente como una sencilla transformación puede separar dos clases de patrones, en este caso para los números manuscritos '1' y '3'. Las características originales pueden ser el nivel de grises de los pixeles de la imagen (las dos dimensiones mostradas en la par- te izquierda de la figura, corresponden solamente a dos pixeles), para las cuales la separación parece ser altamente no lineal. Sin embargo, cuando se transforman a dos nuevas características (por ejemplo, la proporción de blancos y la proporción de negros en la imagen completa), se obtiene un nuevo espacio en el que puede ser factible la clasificación lineal.

La inclusión del kernel es intuitiva cuando se considera la solución dual para el problema de entrenamiento del perceptrón. De la regla de aprendizaje mostrada en 1(c), se puede inferir que el vector de pesos se obtendrá a partir de una combinación lineal del producto de los vectores de entrada y la etiqueta, i.e. w=∑a_i y_i x_i,. Al reemplazar en la función de salida mostrada en 1(b), la clasificación estaría dada por h(x) = sgn(<∑w, x>) = sgn(<a_i y_i x_i, x>)= sgn(∑a_i y_i <x_i, x>), que resulta ser una función del producto interno entre vectores de características (<xi, x>). El kernel pues, es una función que transforma este, a un producto interno en un nuevo subespacio vectorial, K(x_i, x_j) = <Φ(x_i),Φ(x_j)>, donde Φ es la función de transformación vectorial. El algoritmo de entrenamiento para el KP que resulta al aplicar esta transformación, es el mismo del perceptrón simple, solo que en su representación dual, y utilizando el producto interno definido por el kernel tal como se observa en 2(c).

Algunos ejemplos de kernel son el kernel polinomial de dimensión d, K(xi, xj) = <xi, xj>d, y el kernel gaussiano, K(x_i, x_j) = exp((-||- x_j ||2 )/2). La transformación inducida por el kernel, en el caso polinomial (d=2), siendo x = (x₁, x₂) y z = (z₁, z₂), se puede apreciar de la siguiente forma,

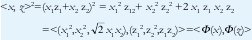
Sin embargo, otra de las características interesantes del aprendizaje con kernel, es que ni siquiera es necesario conocer de antemano la transformación Φ, ya que es suficiente con definir el valor del producto interno de cada par de vectores, y construir con esos valores una matriz de kernel (K). Esta puede ser utilizada como una tabla de búsqueda (look-up table) durante la ejecución del algoritmo, sin necesidad de ejecutar la operación de producto interno. En la práctica, la matriz K se calcula de antemano (off-line) para reducir considerablemente el tiempo de cómputo necesario para entrenar el KP.

2.3 Diseño experimental

Con el ánimo de mostrar la eficacia del KP se decidió implementar un clasificador de dígitos arábigos escritos a mano alzada. Se diseñaron dos experimentos, el primero para la clasificación de los números 1, 2 y 3, y el segundo para la clasificación del conjunto completo de los dígitos. Las instancias de datos para ambos casos, fueron obtenidas de la base de imágenes de dígitos manuscritos de la US Postal Office [7].

Para el problema de reconocimiento de los dígitos 1, 2 y 3 se implementó un clasificador con kernel polinomial. Puesto que el KP es un clasificador binario, el sistema de reconocimiento para tres dígitos se compone de tres KP diferentes, uno para identificar cada dígito (i.e. el KP que reconoce el '1', clasifica los restantes patrones '2' y '3' como si no fueran '1'). Ahora bien, cuando un nuevo patrón no presentado anteriormente al clasificador es reconocido en diferentes clases (varios KP generan +1 como resultado de de h(x)), la decisión final se toma designando ganador al KP con mayor nivel de activación (aquel con el valor más alto para <w, x>).

En este caso se utilizó un archivo con 329 registros (patrones) para el entrenamiento, y 456 registros para la prueba. La escogencia del valor más apropiado de la dimensión del kernel polinomial, se realizó buscando evitar el sobreajuste o saturación (overfitting) del KP. En este sentido, el archivo de entrenamiento se dividió en dos subconjuntos disyuntos, uno para el aprendizaje (2/3) y otro para la validación (1/3). Para cada dimensión d = 1,2,,7 se entrenó el KP con los registros de aprendizaje y se probó con los de validación, y en definitiva se escogió la dimensión para cual el error en la validación fue menor. Con este parámetro se reentrenó cada KP con los patrones incluidos en ambos subconjuntos, y el sistema resultante se comprobó finalmente con el archivo de prueba para medir su efectividad (capacidad de generalización). La implementación se realizó en el lenguaje Mathematica.

Por otra parte, el experimento para el reconocimiento de los digitos 0,...,9 se diseñó de manera análoga al anterior. El archivo de datos para entrenamiento constó de 7291 registros, mientras que el archivo de prueba contuvo 2007 registros. Sin embargo la implementación en este caso se realizó en Matlab, pues los requerimientos de cómputo fueron mayores dada la cantidad de datos a procesar, y la ejecución en Mathematica resultó ser excesivamente lenta. A pesar de que los experimentos fueron conducidos en un computador monoprocesador, se aprovecharon las características de procesamiento vectorizado ofrecidas por Matlab para agilizar el tiempo de entrenamiento y prueba. Los resultados de ambos experimentos se describen en la siguiente sección.

III. RESULTADOS Y DISCUSIÓN

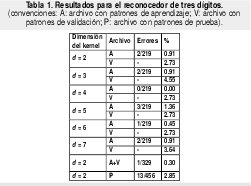
El primer experimento se realizó con el fin de probar la eficacia del KP para un problema real de mediana envergadura. Los resultados fueron bastante buenos y por tal razón se decidió implementar el sistema de reconocimiento para el problema completo. En la figura 3(a) se muestra un subconjunto de los patrones utilizados para el entrenamiento del primer clasificador. Las tasas de error durante el entrenamiento y la prueba se observan en la tabla 1. En algunos casos se alcanzó un error durante el aprendizaje de 0% (d=4), aunque con un error en los patrones de validación de 2.73% (seguramente ocurrió sobreaprendizaje). Inclusive para d=7 este error comenzó a aumentar. Dado que para d=2 el error durante la validación fue igualmente 2.73%, se escogió esta dimensión como la más adecuada pues además requiere menor esfuerzo computacional (es más rápido computar la segunda potencia que la cuarta o la sexta). Se reentrenó de nuevo el clasificador, y al ensayarlo con el archivo de prueba (cuyos patrones no habían sido presentados anteriormente) el error alcanzó tan solo un 2.85%, es decir, de los 456 nuevos ejemplos presentados, el sistema no pudo identificar trece, que se muestran en la figura 3(b). Como se puede apreciar corresponden a patrones bastante ambiguos, difícilmente reconocibles incluso a simple vista por un experto humano. Estos resultados se consideraron un buen indicio para avanzar con el segundo experimento.

Los resultados para el reconocedor de diez dígitos se muestran en la tabla 2. Dada la cantidad de patrones de entrenamiento, validación y prueba, los experimentos fueron ejecutados durante más iteraciones con el fin de darle mayor oportunidad de aprendizaje a la red. El mejor aprendizaje para d=2 se logró con 50 épocas de 4000 iteraciones cada una; para d = 3 se necesitaron 100 épocas, y para d=4,80 épocas. En este experimento el mejor puntaje fue alcanzado por el kernel de dimensión 4, con una tasa de éxito cercana al 92.6%.

IV. CONCLUSIONES Y ALTERNATIVAS DE TRABAJO FUTURO

El enfoque de aprendizaje basado en kernel le ha dado un nuevo impulso a las ANN. De manera similar a como ocurrió cuando se introdujo el algoritmo de retropropagación, el KP ha abierto un potencial inmenso de nuevas aplicaciones donde el principal atractivo es la posibilidad de resolver problemas que incluyan altos niveles de no linealidad, que resultan ser precisamente, los más comunes cuando se trata de datos reales. En el presente artículo se describió una implementación sencilla de un clasificador de dígitos manuscritos utilizando KP con una tolerancia de error inferior al 8% en un conjunto extenso de datos reales, lo cual da indicios de una eficacia exitosa. Inclusive algunos de los patrones no reconocidos por la red, tampoco fueron identificados por examinadores humanos.

En la actualidad este es uno de los temas que mayor atención genera en la comunidad académica dedicada a los algoritmos de aprendizaje (machine learning). El KP puede considerarse una versión simplificada de un enfoque conocido como máquinas de vectores de soporte (SVM, por sus siglas en inglés) el cual es reconocido como uno de los métodos más exitosos recientemente reportados para tareas de clasificación[3]. Las perspectivas de trabajo futuro son enormes, y a nuestro parecer, prometedoras. Por un lado, se puede continuar experimentando con diferentes tipos de kernel apropiados para diferentes tareas. Por otra parte, se pueden comenzar a combinar con otras técnicas como lógica difusa, para darle mayor versatilidad [4]. También se puede intentar implementaciones en hardware [5]. O aplicarlo a líneas tradicionales de reconocimiento de patrones tales como reconocimiento invariante ante transformaciones lineales [6]. Finalmente, no sobra recalcar que dado que el aprendizaje con kernel se basa principalmente en la definición de un producto interno en un espacio vectorial transformado, es posible aplicarlo en situaciones donde los datos no son típicamente numéricos como las imágenes (niveles de grises), sino por ejemplo textos (clasificación de páginas web), cadenas de moléculas (clasificación del genoma humano, descubrimiento y diseño de proteínas), o movimientos en juegos de computador (ajedrez, go, etc.).

REFERENCIAS BIBLIOGRÁFICAS

[1] F. Rosenblatt. "The perceptron: A probabilistic model for information storage and organization in the brain". Psychological Review, 65(6):386-408, 1958.

[2] Herbrich, R, Learning Kernel Classifiers, The MIT Press, 2002.

[3] Cristianini, N.; Shawe-Taylor, J. Kernel Methods for Pattern Analysis. Cambridge University Press, 2004

[4] Chen, J.H; Chen C.S. "Fuzzy Kernel Perceptron". IEEE Transactions On Neural Networks, Vol. 13, No. 6: 1364-1373, 2002.

[5] Anguita, D.; Boni, A.; Ridella, S. "The Digital Kernel Perceptron". Electronics Letters Vol. 38 No. 10 pp. 445 446, 2002.

[6] Graepel, T; Herbrich, R. "Invariant Pattern Recognition by Semidefinite Programming Machines". Proceedings of Neural Information Processing Systems Conference, NIPS 2003.

[7] Mayor información en http://www.cedar.buffalo.edu/Databases/ CDROM1/

Sergio A. Rojas
Ingeniero de Sistemas, U. Nacional de Colombia. Especialista en Ingeniería de Software, U. Distrital. Estudiante de MS.c. Intelligent Systems, University of London. Profesor/investigador de la Facultad de Ingeniería, U. Distrital. Director del Grupo de Interés en Adptación, Computación & MEnte (ACME-UD). Miembro del Grupo de Investigación LAMIC. srojas@udistrital.edu.co