DOI:
https://doi.org/10.14483/23448393.2117Publicado:
2008-11-30Número:
Vol. 14 Núm. 1 (2009): Enero - JunioSección:
Ciencia, investigación, academia y desarrolloMinimización de la tardanza ponderada total en talleres de manufactura aplicando colonia de hormigas
Palabras clave:
meta-heurística, colonia de hormigas, búsqueda tabú, programación de talleres (es).Descargas
Referencias
Lenstra Jk, Rinnoy Kan AHG, Bruckner P. Complexity of machine scheduling problems. In: Hammer PL, Johnson EL, Korte BH, nemhauser GL (eds) Studies in Integer Programming, Annals of Discrete Mathematics 1. North- Holland, Amsterdam, 1997, pp 343- 362.
Graham, R. ; Lawlwer, E :L ; Lenstra, J.K ; Rinnoy Kan A.H.G. Optimization and approximation in deterministic sequencing and scheduling ; A survey, Annals of Discrete Mathematics 5, 1979, pp 287 326.
Dorigo M. Optimization, Learning and Natural Algorithms (in Italian). PhD thesis, Dipartimento di Elettronica e Informazione, Politecnico di Milano, IT, 1992.
Gambardella L.M. and Dorigo M. Ant colonies for the traveling salesman problem. BioSystems, 43, 1997, pp. 73-81.
Deneubourg Jl, PasteelsJm and Verhaeghe JC. Probabilistic behavior in ants: a strategy of errors? J Theor Biol 105, 1983, pp. 259-271.
Bauer A., Bullnheimer B., Hartl F. and Strauss C. Minimizing total tardiness on a single machine using Ant Colony Optimization. Cejor 8, 2000, pp. 125-141.
Gagne C., Gravel M & Pric W I. Comparing an ACO algorithm whit other heuristics for the single machine scheduling problem with sequence dependent setup times. Journal of the Operational Research Society. 53, 2002, pp. 895 906
Pinedo M. & X.Chao. Operations Scheduling With Applications in Manufacturing And Service. Boston: Irwin/McGraw-Hill, 1999.
Pinedo,M. & Singer, M. A shifting bottleneck heuristic for minimizing the total weighted tardiness in a job shop., Naval Research Logistics; 46, 1999, pp.117.
Bauer A., Bullnheimer B., Hartl F. and Strauss C. Minimizing total tardiness on a single machine using Ant Colony Optimization. Cejor 8, 2000, pp. 125-141.
Gagne C., Gravel M & Pric W I. Comparing an ACO algorithm whit other heuristics for the single machine scheduling problem with sequence dependent setup times. Journal of the Operational Research Society. 53, 2002, pp. 895 906
Montgomery D. C. (1997). Design and Analisis of Experiments, United States. Jhon Wiley & Sons.
Cox G M and Cocharan W. Diseños experimentales. Jhon Wiley & Sons, 1965.
Villaveces J. La optimización de procesos con ayuda del simplex. Química e Industria 13, 1987, pp. 2-14.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ciencia, Investigación, Academia y Desarollo
Ingeniería, 2009-00-00 vol:14 nro:1 pág:25-30
Minimización de la tardanza ponderada total en talleres de manufactura aplicando colonia de hormigas
Oscar Yecid Buitrago Suescún
Profesor Universidad Central. Miembro del grupo de investigación CIPO.
Rodrigo Britto Agudelo
Estudiante del Doctorado en Logística de la Universidad de Maryland, USA.
Gonzalo Mejía Delgadillo
PhD., Profesor de la Universidad de los Andes. Miembro del grupo de investigación PYLO.
Resumen
Se estudio el job shop scheduling problem (JSSP) con el objetivo de minimizar la tardanza ponderada total. Este es un problema NPHard en el sentido fuerte y para resolverlo constructivamente se propone una implemen- tación de la meta-heurística colonia de hormigas. Las soluciones generadas se basan en el principio que la secuencia óptima se encuentra en el conjunto de los programas activos.
El valor de los diferentes parámetros de colonia de hormigas se determino por diseño de experimentos. Se comparo el desempeño del algoritmo propuesto con los resultados obtenidos a través de reglas de despacho y las meta-heurísticas búsqueda tabú y recocido simulado, en la solución de problemas de tamaño 5×5, 6×6 y 10×10 de los cuales se han reportado las soluciones óptimas.
Palabras clave: meta-heurística, colonia de hormigas, búsqueda tabú, programación de talleres
Abstract
This research studies the minimization of the total weighted tardiness in the job shop scheduling problem (JSSP). This problem is NP strongly Hard and to solve it constructively an implementation of the metaheuristic Ant Colony is proposed. The generated solution is based on the principal of optimal solution that is found in the set of active schedules. The values of different parameters were determined by experimental design.
The performance of the proposed heuristic was compared with priority rules and meta-heuristics such as Tabu Search and Simulating Annealing in the solution of instances 5×5, 6×6 y 10×10 that had their optimal solution reported in the literature.
Key words: meta-heuristics, ants colony optimization, tabu search, job hhop scheduling.
1. INTRODUCCIÓN
En un mundo globalizado como el actual, para las empresas manufactureras la forma de programar la producción es muy importante porque les permite aumentar la productividad y lograr la satisfacción de sus clientes mediante el cumplimiento en los compromisos de entrega de los pedidos sin incurrir en costos innecesarios de almacenamiento.
Por otra parte, en nuestro medio es común encontrar ambientes de trabajo tipo taller, que consisten en un conjunto de máquinas en las que se debe procesar un determinado número de trabajos siguiendo un orden predeterminado. Aunque programar la producción en talleres parece un problema sencillo, dista mucho de serlo y esta clasificado como NP-Hard según [1] y [2].
Dada la imposibilidad práctica de aplicar procedimientos matemáticos que garanticen la solución óptima en este tipo de problemas, se recurre a las meta-heurísticas ya que estas técnicas proporcionan soluciones buenas en tiempos razonables. Las más conocidas son los algoritmos genéticos, recocido simulado, búsqueda tabú y a partir de los años 90 Colonia de Hormigas (ACO).
Con respecto a Colonia de Hormigas, fue propuesta por Marco Dorigo [3] para la solución de problemas combinatorios como el del agente viajero y el de asignación cuadrática [4] y se basa en la observación de hormigas reales ya que estos insectos tienen características de comportamiento que han llamado la atención de varios investigadores. Una de estas es la capacidad de la colonia para encontrar la ruta más corta entre el hormiguero y las fuentes de alimento a través de cooperación y comunicación por estímulos.
Mientras hacen sus recorridos las hormigas dejan un rastro de una sustancia química llamada feromona la cual es percibida por toda la colonia, así cuando tienen que escoger una ruta se deciden por aquella que tenga el rastro más fuerte. Este también les permite encontrar el camino de regreso al hormiguero (ó a la fuente de alimento) y transmitir esta información a otras hormigas [5].
Colonia de Hormigas se implementa en este trabajo porque es más nueva que las otras meta-heurísticas, es prometedora, no se encuentran reportadas muchas aplicaciones a situaciones de producción [6] [7], ninguna al problema considerado y porque es de tipo constructivo (no necesita una solución inicial).
Es importante anotar que en esta investigación se pretende evaluar el efecto puro de la cooperación de los agentes (hormigas) que conforman una colonia para encontrar buenas soluciones. Es por ello que en el algoritmo ACO diseñado no se consideran pasos de mejoramiento local para las soluciones creadas, como si se hace en otras investigaciones. Los procedimientos de mejoramiento local consisten en realizar modificaciones sobre las soluciones obtenidas, por lo tanto cuando se reporta una buena solución queda la duda si fue merito de la comunicación y cooperación entre las hormigas ó del procedimiento de mejoramiento local.
Para la implementación de colonia de hormigas se adapto el algoritmo ACO general a la situación específica del problema de programación de la producción en talleres, se codificó en lenguaje de C de computador y con el programa obtenido se solucionaron problemas reportados en la literatura especializada para luego realizar las comparaciones con otros procedimientos; reglas de despacho, recocido simulado y búsqueda tabú disponibles en el software LISA.
2. EL PROBLEMA DE PROGRAMACIÓN DE PRODUCCIÓN EN TALLERES (JSSP)
Un taller es un ambiente de producción en el que los trabajos deben ser procesados mediante múltiples operaciones que se realizan en diferentes máquinas. Cada trabajo para ser procesado, debe seguir un orden (ruta) a través de las máquinas. Si la ruta de todos los trabajos es la misma entonces se tiene un ambiente Flow Shop.
Debido a que los talleres están diseñados para permitir la flexibilidad, en ellos usualmente se producen pequeñas cantidades de una gran variedad de artículos, incluyendo productos que son individualizados para cada cliente. Los bienes que son comúnmente elaborados utilizando un ambiente tipo taller incluyen partes de máquinas, muebles, químicos, semiconductores y productos farmacéuticos.
En un problema de manufactura tipo taller de tamaño m × n, hay m máquinas y n trabajos. Cada trabajo tiene una secuencia de operaciones que indica el orden en que se procesan (la operación oij es la k-ésima operación del trabajo j, y debe ser procesada en la máquina i), con un tiempo de proceso pij. Cada trabajo puede tener un tiempo de inicio rj antes del cual, ningún procesamiento del trabajo i puede llevarse a cabo y cada máquina puede tener un tiempo de alistamiento ui antes del cual no se puede realizar ninguna operación en ella. También existen un tiempo de entrega para cada trabajo, dj, y una medida de que tan importante es comparado con los otros, wj. Estos datos suelen ser de tipo entero. Además, cada máquina solo puede procesar una operación al mismo tiempo y solo una operación de cada trabajo puede ser procesada en cada máquina y sin permitir interrupciones. La solución se expresa mediante un programa que es la descripción de los tiempos en que deben ser procesadas cada una de las operaciones satisfaciendo las restricciones.
En general, si se tienen m máquinas, n trabajos y cada uno requiere una operación en cada máquina, entonces existen n! formas diferentes de ordenar los trabajos en cada una de las máquinas, por lo tanto el número de máximo de soluciones posibles (si todas son factibles) esta dado por (n!)m. Por ejemplo, si se deben procesar 10 trabajos en 10 máquinas, el número máximo de soluciones esta acotado por 3.95 × 10 65, esta cifra es mucho más grande que la edad estimada del universo medida en milisegundos ó que el número de Avogadro.
2.1 Representación gráfica del problema.
Una representación con grafos, G(N,A,B), como la mostrada en la figura 1 es útil para visualizar mejor el problema. En esté los nodos N representan las operaciones oij que se deben realizar sobre los n trabajos (una operación oij significa el proceso del trabajo j en la máquina i), los arcos continuos A representan las rutas que debe seguir cada trabajo y la longitud |(i,j)→(k,j)| = pij representa el tiempo de proceso de la operación (oij ).
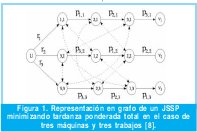
B es el conjunto de arcos disyuntivos (punteados bidirigidos), que conectan las operaciones pertenecientes a diferentes trabajos pero se realizan en la misma máquina, formando un clíque.
Del nodo U salen las primeras operaciones en la secuencia de cada uno de los n trabajos, cuyas operaciones finales concurren a los n nodos terminales Vj. La longitud de la ruta más larga desde el nodo U hasta el nodo terminal Vj representa el tiempo de terminación del trabajo j.
3. METODOLOGÍA
Teniendo en cuenta las características del JSSP y de ACO se diseño un algoritmo, factores de visibilidad y se propusieron formas de inicialización y de construcción progresiva de soluciones, basándose en el principio que la solución óptima es un programa activo. Para medir la eficiencia del algoritmo ACO propuesto, se buscaron en la literatura problemas empleados en estudios de comparación de los que se conoce la solución óptima [7]. Se seleccionaron el ABZ5, ABZ6, LA16 - LA20 y el MT10, todos disponibles en la ORLibrary (http:// mscmga.ms.ic.ac.uk/info.html). En la determinación de los tiempos de entrega, dj, se utilizó la regla de trabajo total (TWK) según la cual dj = k Pj, siendo Pj la suma de los tiempos de proceso de las operaciones del trabajo j y k un parámetro. Se asignaron tiempos de entrega con k = 1.3 y con k = 1.5.
También se generaron diez problemas de tamaño 5 × 5 y diez de 6 × 6, a los cuales por medio del programa LISA se les encontró la solución óptima aplicando procedimientos de ramificación y acotación. Tanto los problemas generados como los obtenidos de la literatura, se solucionaron por medio de reglas de las despacho; WSPT , EDD, SPT y LPT y de las meta- heurísticas búsqueda tabú y recocido simulado del software LISA, luego se corrieron en el algoritmo ACO codificado en lenguaje de computador C utilizando un computador Athlon 900 MHz con 256 megas de memoria RAM. Los resultados obtenidos se tabularon para su posterior comparación y análisis.
3.1 Descripción del algoritmo ACO propuesto
En el algoritmo ACO se crea una colonia de h hormigas que construyen secuencias activas de los n trabajos del problema en las m máquinas del mismo, obedeciendo ciertas reglas. Se indica un número máximo de iteraciones (tmáx ) y en cada iteración cada una de las h hormigas construye una solución activa factible. Finalmente se reporta la mejor secuencia de las h × tmáx construidas durante todo el proceso.
Debido a la analogía en que se basa ACO, resulta conveniente visualizar el problema mediante la representación de la figura 1 ya que el algoritmo lo que hace es construir buenas rutas que conecten el nodo inicial con los nodos terminales. Con el fin de disminuir el número de búsquedas que realiza una hormiga en cada iteración, se crea un conjunto Ω [8]en el que se incluyen las operaciones que hacen que la secuencia que se construye sea activa y se escoge entre ellas de acuerdo con el rastro de feromonas Ωi,j y un factor de visibilidad fv. El factor que se utilizo en el presente trabajo esta definido por:
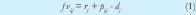
y con él se pretende ayudar en la elección del siguiente paso, dando prioridad a las operaciones que estén disponibles más rápido para ser programadas y que deben ser entregadas con mayor premura. Una hormiga escoge el nodo al que se va a ir, fijando el valor de un parámetro qo en el intervalo (0, 1), y generando en cada iteración un número aleatorio q en el mismo intervalo. Si qo≥ q, la siguiente operación de la secuencia se escoge del conjunto Ω considerando la siguiente regla:
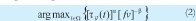
El subíndice l indica que la operación pertenece al conjunto Ω, mientras que α y β representan los exponentes del rastro de feromonas y del factor de visibilidad. Según las recomendaciones de la literatura [5] [6], estos exponentes toman valores entre 1 y 4. Si qo<q, entonces la siguiente operación en la secuencia se elige aleatoriamente del conjunto Ω. Para evitar caer en un óptimo local de forma prematura, se realiza una "evaporación" de feromonas mediante una disminución local del rastro τi,j dada por la Eq(3):
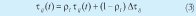
donde

ρ l es una medida del nivel de disminución ó "evaporación" del rastro de feromona, τij(t), y su valor esta entre 0 y 1.
Finalmente se evalúan las h secuencias halladas durante la iteración y si el valor de la función objetivo en alguna de ellas es mejor que el que se tiene hasta el momento, entonces se realiza la actualización del mejor valor encontrado para la tardanza ponderada total y para la respectiva secuencia. Después de evaluadas todas las soluciones, se hace una actualización global de la intensidad de τij en la que se incrementa este nivel para cada par de operaciones ó nodos pertenecientes a la mejor secuencia de las h construidas durante la iteración. El incremento depende de la calidad de la solución y se realiza de acuerdo con la ecuación (5).
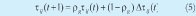
donde
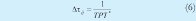
La magnitud del incremento del rastro de feromonas esta dado por ρg , este parámetro toma valores en el intervalo (0,1). TPT* es el valor de la función objetivo correspondiente a la mejor secuencia de la iteración.
4. RESULTADOS Y DISCUSIÓN
Se presentan los resultados obtenidos en cada una de las fases de la investigación.
4.1 Diseño de experimentos
Para determinar los valores de parámetros exponente del rastro de feromona (α), exponente del factor de visibilidad (β), parámetro de evaporación de feromona (ρl), parámetro de incremento de feromona (ρg) y el número aleatorio (q0), inicialmente se aplico el método del descenso más rápido [10], para ubicar la región donde se encuentra la respuesta óptima. El diseño escogido fue un factorial de dos niveles completo con dos replicas ya que es ortogonal y permite un buen ajuste de superficies de primer orden [11]. Para α y β el nivel bajo se fijo en 1 y el nivel alto en 2, mientras que para los restantes parámetros se fijaron 0.85 y 0.95 como niveles bajo y alto respectivamente. Con los datos obtenidos se realizo un análisis de regresión llegando a la siguiente superficie de respuesta lineal para la tardanza ponderada total TPT:
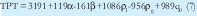
Para verificar la validez del supuesto de linealidad de la superficie de respuesta, se realizó un análisis de varianza obteniéndose un valor p de 0.89, indicador de que la superficie lineal no es adecuada y por lo tanto no es correcto aplicar el método del descenso más pronunciado.
Se procedió entonces a aplicar un diseño de experimentos simplex ya que permite acercase a la región del óptimo de manera eficiente, [12]. Cada combinación de parámetros se corrió cuatro veces.
Para la aplicación se toma como valor del paso Δq0= 0.5. El simplex de partida esta formado por los 6 primeros puntos de la tabla 1. Los puntos que salieron son el 5, 2, 9 y 4 remplazados por 7, 8, 9 y 10.
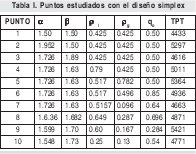
El valor de los parámetros se fijó de acuerdo al punto que obtuvo la mejor tardanza ponderada total (TPT) en promedio. En la figura 2 se ilustra la superficie de respuesta en la región de los exponentes α y β.
4.2 Resultados obtenidos con reglas de despacho
Se emplearon las reglas de despacho longest procesing time (LPT), eaeliest due date (EDD), weigthted shortest procesing time (WSPT) y shortest procesing time (SPT). Los resultados son bastante altos y no resultan competitivos frente a los obtenidos por medio de las meta-heurísticas. En el mejor de los casos el alejamiento de la solución óptima supera el 20000%.

Las mejores respuestas se obtuvieron el 65% de las veces al aplicar la regla WSPT, seguida del regla SPT con el 27 %. Esporádicamente alguna de las otras reglas reportaba mejores soluciones. Teniendo en cuenta los resultados no parece conveniente ubicar en las primeras posiciones de las secuencias las operaciones con tiempos de proceso grandes (por lo menos formar cadenas grandes siguiendo esta tendencia). Bajo esta observación se diseño el factor de visibilidad de las hormigas.
4.3 Comparación de ACO frente a búsqueda tabú y recocido simulado
Las meta-heurísticas búsqueda tabú y recocido simulado utilizadas son las disponibles en el software LISA. Para cada una de ellas se crearon 5000 soluciones y el tiempo promedio de ejecución fue diez segundos. En cuanto a colonia de hormigas, para los problemas de 10×10 las corridas se hicieron con 15 iteraciones y 10 hormigas lo que da 150 soluciones creadas, el tiempo promedio de cada procedimiento fue 130 segundos.
Para iniciar el procedimiento se empleo un tao inicial (τ0) de 0.001 y los valores de los parámetros son los que se determinaron mediante la optimización por diseño simplex (puntos 1 y 10 de la tabla 1). Para los problemas de 5 × 5 y 6 × 6 se emplearon 10 hormigas y se realizaron 50 iteraciones con lo que el tiempo de ejecución fue de dos minutos 20 segundos sin prácticamente ninguna variabilidad. La diferencia en el número de iteraciones esta claramente justificada por el consumo de tiempo computacional.
Para analizar los resultados se elaboró un indicador llamado relación de calidad para las soluciones alcanzadas, el cual se define como la división entre el valor de la solución obtenida y el óptimo reportado. De esta forma, si un procedimiento permite encontrar la solución óptima el valor reportado del factor de calidad es 1. Si el valor óptimo reportado es 0 y la solución obtenida con la meta-heurística es diferente, entonces se deja indicada la división.
4.3.1 Problemas de 5 × 5
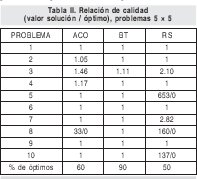
De los resultados reportados en la tabla II se puede observar que la meta-heurística que reportó los mejores resultados es la búsqueda tabú (BT), encontró el óptimo el 90 % de las veces. La colonia de hormigas (ACO) acertó un 60% y recocido simulado (RS) el 50%. También es notorio que los peores resultados son los logrados con este último procedimiento, reportando la peor solución en la mitad de los problemas considerados. En tres ocasiones se presentan empates entre los tres procedimientos.
4.3.2 Problemas de 6 × 6
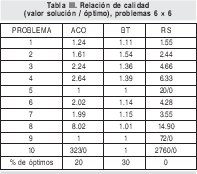
Las soluciones de más alta calidad siguen siendo las obtenidas con búsqueda tabú, aunque el porcentaje de óptimos hallados disminuyo a un 30%. Sin embargo en todas las ocasiones estuvo bastante cerca de alcanzar la solución óptima. Por otra parte, los resultados obtenidos con colonia de hormigas son claramente superiores a los del recocido simulado y competitivos con los obtenidos al aplicar la búsqueda tabú. Es notorio que con recocido simulado nunca se encontró la solución óptima. Los resultados se reportan en la tabla III.
4.3.3 Problemas de 10 × 10
Al incrementar significativamente el tamaño de los problemas con ninguno de los procedimientos se logró obtener soluciones óptimas, pero los mejores resultados siguen siendo los obtenidos con búsqueda tabú.
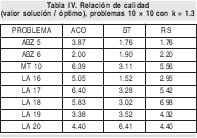
Cuando el factor k es 1.3, tabla IV, el recocido simulado (a diferencia de los problemas 5×5 y 6×6) muestra un mejor desempeño promedio que compite con el de colonia de hormigas. En el 50% de las veces, colonia de hormigas supera a recocido simulado y a su vez es superada en la restante mitad de los problemas analizados. Solamente en un problema la búsqueda tabú es superada por colonia de hormigas y recocido simulado.
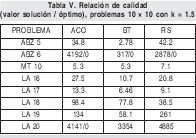
La tabla V muestra los resultados cuando el valor k se incrementa a 1.5. Con búsqueda tabú siguen reportándose los mejores valores de tardanza ponderada total. Es evidente que la calidad de las soluciones decreció y la colonia de hormigas y el recocido simulado no muestran diferencias significativas en cuanto a la proporción de veces que uno supera al otro.
5. CONCLUSIONES
Para problemas de tamaño 5×5 y 6×6 la meta- heurística colonia de hormigas reporta resultados competitivos frente a la de búsqueda tabú, la cual a su vez es la mejor de las analizadas.
Como era de esperarse con el tamaño aumenta la dificultad del problema, en los problemas de 5×5 se logra encontrar el óptimo el 60% y 90% de las veces con colonia de hormigas y búsqueda tabú respectivamente. En los problemas de tamaño 6×6 esta proporción disminuye para las mismas meta- heurísticas a 20 % y 30% y en los de 10×10 nunca se encuentra la solución óptima.
Al aumentar el valor del factor k empleado para la generación de los tiempos de entrega, se vuelve más difícil encontrar la solución óptima. Esto se evidencia observando el factor de calidad (a menor valor mejor solución) el cual es mayor para problemas generados con k = 1.5 que para los generados con k = 1.3.
Para los problemas de tamaño cinco y seis, colonia de hormigas proporciona soluciones de prácticamente la misma calidad que búsqueda tabú y es superior al recocido simulado.
Para problemas grandes el algoritmo de colonia de hormigas sin incluir pasos de mejoramiento local para las soluciones obtenidas, no resulta competitivo frente a la búsqueda tabú si se consideran a la vez el tiempo de ejecución y la calidad de las soluciones.
Los resultados obtenidos por colonia de hormigas son alentadores y estimulan nuevas investigaciones, dado que con solo 150 soluciones generadas es competitiva frente a la búsqueda tabú (en problemas pequeños) y superior a recocido simulado, considerando que en estas dos últimas se prueban de a 5000 soluciones.
El efecto cooperativo de la colonia de hormigas no es suficiente para construir buenas soluciones, por ello se espera que al incluir pasos de mejoramiento local para las soluciones, la calidad de las soluciones se incremente de forma significativa.
6. REFERENCIAS BIBLIOGRAFÍCAS
[1] Lenstra Jk, Rinnoy Kan AHG, Bruckner P. Complexity of machine scheduling problems. In: Hammer PL, Johnson EL, Korte BH, nemhauser GL (eds) Studies in Integer Programming, Annals of Discrete Mathematics 1. North- Holland, Amsterdam, 1997, pp 343- 362.
[2] Graham, R. ; Lawlwer, E :L ; Lenstra, J.K ; Rinnoy Kan A.H.G. Optimization and approximation in deterministic sequencing and scheduling ; A survey, Annals of Discrete Mathematics 5, 1979, pp 287 - 326.
[3] Dorigo M. Optimization, Learning and Natural Algorithms (in Italian). PhD thesis, Dipartimento di Elettronica e Informazione, Politecnico di Milano, IT, 1992.
[4] Gambardella L.M. and Dorigo M. Ant colonies for the traveling salesman problem. BioSystems, 43, 1997, pp. 73-81.
[5] Deneubourg Jl, PasteelsJm and Verhaeghe JC. Probabilistic behavior in ants: a strategy of errors? J Theor Biol 105, 1983, pp. 259-271.
[6] Bauer A., Bullnheimer B., Hartl F. and Strauss C. Minimizing total tardiness on a single machine using Ant Colony Optimization. Cejor 8, 2000, pp. 125-141.
[7] Gagne C., Gravel M & Pric W I. Comparing an ACO algorithm whit other heuristics for the single machine scheduling problem with sequence dependent setup times. Journal of the Operational Research Society. 53, 2002, pp. 895 - 906
[8] Pinedo M. & X.Chao. Operations Scheduling With Applications in Manufacturing And Service. Boston: Irwin/McGraw-Hill, 1999.
[9] Pinedo,M. & Singer, M. A shifting bottleneck heuristic for minimizing the total weighted tardiness in a job shop., Naval Research Logistics; 46, 1999, pp.1-17.
[8] Bauer A., Bullnheimer B., Hartl F. and Strauss C. Minimizing total tardiness on a single machine using Ant Colony Optimization. Cejor 8, 2000, pp. 125-141.
[9] Gagne C., Gravel M & Pric W I. Comparing an ACO algorithm whit other heuristics for the single machine scheduling problem with sequence dependent setup times. Journal of the Operational Research Society. 53, 2002, pp. 895 - 906
[10] Montgomery D. C. (1997). Design and Analisis of Experiments, United States. Jhon Wiley & Sons.
[11] Cox G M and Cocharan W. Diseños experimentales. Jhon Wiley & Sons, 1965.
[12] Villaveces J. La optimización de procesos con ayuda del simplex. Química e Industria 13, 1987, pp. 2-14.
Oscar Yecid Buitrago Suescún
obuitragos@ucentral.edu.co
Rodrigo Alberto Britto Agudelo
Ingeniero Químico de la Universidad Nacional de Colombia, sede Bogotá. Magíster en Ingeniería Industrial en la Universidad de los Andes. Se desempeñó como profesor de la Facultad de Administración de Empresas de la Universidad de los Andes (a la cual esta vinculado). Actualmente adelanta estudios de Doctorado en Logística en la Universidad de Maryland en los Estados Unidos. robritt@uniandes.edu.co
Gonzalo Mejia Delgadillo
Ingeniero Mecánico de la Universidad de los Andes. Magíster en Ingeniería Mecánica en la Universidad de los Andes. PhD en Ingeniera Industrial en la Universidad Lehigh de Pensilvania, Estados Unidos. Actualmente se desempeña como profesor Asistente del Departamento de Ingeniería Industrial de la Universidad de los Andes en el área de Producción y pertenece como investigador al grupo PYLO donde realiza investigaciones sobre Producción y Logística gmejia@uniandes.edu.co
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)