DOI:
https://doi.org/10.14483/23448393.2716Published:
2004-11-30Issue:
Vol. 10 No. 2 (2005): July - DecemberSection:
Science, research, academia and developmentPlaneamiento de Sistemas de Distribución de Energía Eléctrica Usando Branch and Bound
Keywords:
Sistemas de Distribución, programación lineal, Branch and Bound, optimización (es).Downloads
References
Sun et al: «Optimal Distribution Substation and Primary Feeder Via the Fixed Charge Network Formulation», IEEE Transactions on Power Apparatus and Systems, Vol. PAS-100, No. 5.
Ponnavaiko et al.: «Distribution System Planning Trough Mixed Integer Programming Approach», IEEE Transactions on Power Delivery, Vol. PWRD-2, No. 4, pp1157-1163.
Kagan, N., Adams, R.N.: «A Benders Descomposition Approach to the Multiobjetive Distribution Planning Problem», Internacional Journal of Electrical Power & Energy Systems, Vol. 15, No. 5, pp259-271.
Ramírez-Rosado, I.J., Bernal-Agustín, J.L.: «Genetic Algorithms Applied to the Design of Large Power Distribution Systems», IEEE Transactions on Power Systems, Vol. 13 No. 2, pp696-703, May 1998.
Bazán, F.A., Mantovani, J.R.S., Romero, R.A.: «Planeamiento de Expansión de Sistemas de Distribución de Energía Eléctrica Usando un Algoritmo de Búsqueda Tabú», XIV Congreso Brasileño de Automatización, Natal-Brasil, Septiembre 2002.
Almeida, M.S., Mantovani, J.R.S., Romero, R.A.: «Colocación Óptima de Subestaciones y Alimentadores en Sistemas de Distribución de Energía Eléctrica Usando un Algoritmo de Branch and Bound», XIV Congreso Brasileño de Automatización, Natal-Brasil, Septiembre 2002.
Gallego R., Ramón y Romero L., Rubén. «Optimización En Sistemas Eléctricos II», Texto Guía en Maestría en Ingeniería Eléctrica, Universidad Tecnológica de Pereira.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2005-00-00 vol:10 nro:2 pág:44-50
Planeamiento de sistemas de distribución de energía eléctrica usando Branch and Bound
Mauricio Granada Echeverri
Docente del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira.
Ramón Alfonso Gallego Rendón
Docente del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira.
Ricardo Alberto Hincapié Isaza Docente del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira.
Resumen
Este trabajo presenta un algoritmo de Branch and Bound para resolver el problema del planeamiento de Sistemas de Distribución de Energía Eléctrica considerando el dimensionamiento y localización de nuevas subestaciones, así como también las rutas de nuevos alimentadores primarios. El modelo matemático del problema es clasificado como Lineal Entero Mixto (PLEM) y presenta explosión combinatorial.
Palabras clave:
Sistemas de Distribución,programación lineal, Branch and Bound,optimización.
Abstract
This paper presents a Branch and Bound algorithm to solve the planning problem of the electrical energy Distribution Systems considering the dimension and location of new substations, as the way of new primary feeders too. The mathematical model employed is clasified as Mixed Integer Linear (PLEM), the model presents combinatorial explosion.
Key words:
Distribution Systems, linear programming, Branch and Bound, optimization.
1. INTRODUCCIÓN
El desarrollo industrial para la producción de bienes y servicios básicos como iluminación, cocción, refrigeración, recreación y calefacción en viviendas, hoteles y negocios, los servicios de comunicación y financieros de algunas empresas y el crecimiento natural de la población, entre otros, son factores que requieren cada vez mayores cantidades de energía eléctrica, con ciertos estándares de calidad, confiabilidad y costos. El suministro de esta energía debe ser oportuno y de calidad, garantizando un suministro de energía a corto, mediano y largo plazo sin incurrir en sobrecostos para los usuarios, lo cual representa un reto para las empresas de energía eléctrica. Este estudio del crecimiento de la demanda de energía eléctrica y la adecuada expansión de los sistemas de distribución es conocido como el planeamiento de sistemas de distribución.
Para mostrar la complejidad involucrada en el planeamiento de los sistemas de distribución se ilustra en la figura 1 un sistema de distribución primario que incluye la localización de nuevos alimentadores y subestaciones. En este ejemplo hay 13 posibles alimentadores (coárbol de líneas punteadas) y una nueva subestación. Las decisiones de instalación de estos elementos ascienden al orden de 214 =16384 alternativas que componen el conjunto de posibles soluciones.
El planeamiento de los sistemas de distribución puede hacerse en una o en varias etapas. En el modelo multietapa generalmente cada etapa tiene el mismo período de tiempo. Así por ejemplo, si la planeación es dividida en 5 etapas, para el sistema de la figura 1, entonces el nuevo conjunto de soluciones sería de (214)5= 1805 x 1021 alternativas.

Por lo tanto para la solución del problema anterior se han propuesto en la literatura técnicas heurísticas, optimización clásica y optimización combinatorial. En la línea de solución usando optimización clásica son propuestas técnicas de programación lineal entera mixta usando Branch and Bound con modelos de transporte [1], programación cuadrática entera mixta [2] y algoritmos basados en técnicas de descomposición [3]. En los trabajos que proponen técnicas combinatoriales se encuentran frecuentemente los Algoritmos Genéticos [4] y Búsqueda Tabú [5].
En este trabajo, el problema del Planeamiento de Sistemas de Distribución es formulado como un problema Lineal Entero Mixto (PLEM), considerando las restricciones de radialidad del sistema, capacidades máximas de subestaciones y alimentadores y balance nodal de todo el sistema. La técnica de solución adoptada es un Algoritmo de Branch and Bound aplicada a dos sistemas de la literatura [6].
2. DESCRIPCIÓN DEL PROBLEMA
Un crecimiento en la demanda implica un crecimiento en lo sistemas de distribución dado que es necesario atenderla adecuadamente. Este crecimiento se traduce esencialmente en: la instalación de nuevos alimentadores, la instalación de nuevas subestaciones, la ampliación de las subestaciones existentes, el cambio del calibre de los alimentadores existentes, la reconfiguración de la topología de la red y la redistribución de cargas entre los alimentadores o subestaciones.
Si el crecimiento de la demanda no se atiende adecuadamente se pueden presentar problemas como: sobrecargas en los alimentadores cuando su capacidad máxima de potencia es excedida, sobrecargas en los transformadores primarios cuando su capacidad máxima de potencia es excedida, desmejoramiento del perfil de tensión debido a problemas de regulación, incremento en las pérdidas que se presentan en transformadores y alimentadores y se puede perder la configuración radial del sistema. Lo anterior se constituye en un conjunto de restricciones cuyo cumplimiento es necesario para garantizar una adecuada operación de la red.
La mayoría de los estudios de planeamiento sólo tienen en cuenta los aspectos económicos y técnicos. El aspecto económico es incluido como una función objetivo a ser minimizada y los requerimientos técnicos son incluidos como restricciones en el modelo matemático.
La función objetivo involucra la suma de tres términos que deben ser minimizados. El primero corresponde a los costos fijos asociados a la instalación de todos los nuevos alimentadores involucrados en la propuesta de solución en estudio. La variable binaria δij∈{1,0} indica la instalación (δij=1) o no (δij=0) del alimentador ubicado entre el nodo i y el nodo j y CFij es el costo de adicionar el alimentador propuesto entre el nodo i y el nodo j. Para calcular el costo fijo de todos los alimentadores nuevos el primer término adopta la siguiente forma:
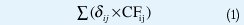
El segundo término involucra, de forma lineal, los costos variables de operación del sistema asociados a las pérdidas óhmicas. Si se considera que la corriente a través de un alimentador es proporcional al flujo de potencia, es posible definir los costos totales de operación en todo el sistema así:
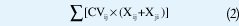
Donde Xij es el flujo de potencia que circula del nodo i al nodo j y CVij son los costos variables de operación del alimentador ubicado entre el nodo i y el nodo j. Como el flujo de potencia circula en ambos sentidos se debe considerar el flujo del nodo j al nodo i (Xji).
El tercer término recoge el costo fijo total de adicionar subestaciones nuevas. Al igual que en los alimentadores nuevos, se cuenta con una variable binaria δi ∈{1,0} que indica la instalación o no de la subestación. Para calcular el costo fijo total de todas las subestaciones nuevas adicionadas se emplea la siguiente expresión:
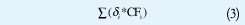
La minimización de estos tres términos conforman la función objetivo z del modelo, de la siguiente manera:
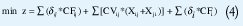
Las restricciones asociadas son:
Cumplimiento del balance de potencia: esta restricción consiste en garantizar que en cada nodo i el flujo neto de potencia que llega por las líneas conectadas al nodo i más la potencia Si suministrada por la subestación sea igual a la demanda Di (ver figura 2), es decir que cumpla con la siguiente ecuación:
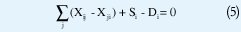
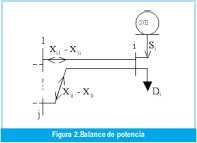
•Capacidad máxima de los alimentadores y subestaciones: una solución factible será aquella que no viole la capacidad máxima Xij de la línea y la capacidad máxima δi de la subestación:
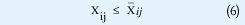
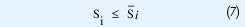
•Finalmente se establecen la restricciones de variables enteres y continuas:
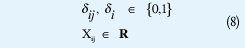
El modelo matemático formulado corresponde a un problema de Programación Lineal Entero Mixto (PLEM), debido a que incluyen variables binarias y continuas. Las binarias son variables de decisión que corresponden a la instalación de nuevos alimentadores y nuevas subestaciones y las variables continuas corresponden al flujo de potencia por los alimentadores. El problema es lineal debido a que las pérdidas del sistema (costos de operación) son linealizadas.
Para implementar el modelo matemático de deben tener en cuenta los siguientes aspectos:
- Los alimentadores y subestaciones existentes no tienen asignado un costo de inversión pero si tienen asignado un costo de operación
- Con el fin de facilitar el modelamiento matemático y la solución del problema del planeamiento, los centros de demanda son definidos y representan un grupo de alimentadores primarios y/o secundarios, los cuales para propósitos eléctricos y de cálculos son considerados como un único nodo.
- No hay pérdida de potencia por el tramo de un alimentador.
- Los costos de inversión y la localización de los alimentadores y subestaciones propuestas son conocidos de antemano.
- El factor de potencia del sistema es considerado constante.
- Las cargas son representadas por un modelo de corriente continua.
3. TÉCNICA DE SOLUCIÓN
El algoritmo de Branch and Bound (ramificar y acotar) es un método exacto para encontrar la solución a problemas lineales con soluciones enteras (PLE) y enteras mixtas (PLEM) [7].
La filosofía del Branch and Bound consiste en resolver un PLEM a través de la solución sucesiva de problemas de programación lineal (PL) que son versiones relajadas del PLEM original y que pueden ser resueltos por técnicas conocidas de solución.
Inicialmente se resuelve el problema original relajando la integralidad de sus variables enteras, es decir, permitiendo que las variables enteras tengan valores reales. Esta primera fase se denomina solución al problema P0.
Si el problema tiene solución entera en todas las variables enteras, significa que se ha encon trado la solución óptima global. De lo contrario, se elige de forma aleatoria una de las variable con solución no entera y se le aplica unproceso iterativo de ramificación que permita encontrar su valor entero. El proceso de división de la variable consiste en generar dos subproblemas de la siguiente manera:
Subproblema P1: consiste en resolver el problema P0 sumándole una restricción de la forma
Subproblema P2: consiste en resolver el problema P0 sumándole una restricción de la forma
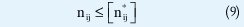
Donde [n*ij] es el mayor entero contenido en la variable nij que está siendo separada.
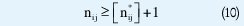
La solución de estos dos PLs permiten buscar en un espacio reducido de soluciones el valor entero de la variable. Por lo tanto estos subproblemas se deben resolver de la misma forma que el problema P0. Es decir, si no tiene solución entera se repite el proceso hasta que el espacio de solución sea agotado.
Las configuraciones resultantes son almacenadas, de forma ordenada según su función objetivo, en un arreglo. Esta metodología tiene como ventaja encontrar soluciones óptimas alternativas. Sin embargo, presenta problemas de eficiencia computacional debido a la gran cantidad de información que se debe almacenar en problemas de gran tamaño.
Existen algunos criterios para determinar cuales problemas resolver y cuales no denominados criterios de sondaje o acotamiento. Estos criterios orientan la búsqueda y disminuyen el esfuerzo computacional:
•El problema resuelto tiene solución entera,por lo tanto no se puede separar.
•El problema no tiene solución entera pero presenta una solución de peor calidad que la de una solución entera ya encontrada. E decir, el problema puede tener solución entera dentro de su región factible, pero ésta no entrega una mejor respuesta que la mejor conocida (incumbente). Por esta razón es importante encontrar una buena incumbente inicial para acelerar el proceso de convergencia.
•La solución del problema es infactible, por lo tanto cualquier problema que se desprenda de él posee mayor nivel de infactibilidad.
Con el fin de disminuir el esfuerzo computacional invertido en el proceso de optimización se utiliza la regla LIFO (acrónimo en inglés de Last In First Out), la cual consiste en resolver el ultimo PL generado a partir de la respuesta inmediatamente anterior (sin resolver todo el problema de nuevo) mediante una técnica de dual Simplex canalizado.
Una ventaja de los algoritmos enumerativos es la de obtener el óptimo global del problema abordado, ya que realizan una búsqueda de todo el espacio de soluciones. Pero a medida que el número de variables crece el tiempo necesario para la resolución de un problema puede hacer inviable su utilización práctica.
4. PRUEBAS Y RESULTADOS
El algoritmo de Branch and Bound fue implementado en el software de optimización GAMS. Fueron simulados dos sistemas eléctricos, considerando una sola etapa de planeamiento. Para ambos sistemas se consideró solamente un calibre de conductor (no se considera reconductorización de alimentadores existentes).
4.1 Sistema I
El sistema de la Figura 3 está constituido por once (11) nodos (nueve de los cuales son de carga), una subestación existente (Nodo 20), cuatro alimentadores existentes (L1_20, L1_2, L3_20, L3_7), una subestación futura o candidata (Nodo 21) y diez (10) alimentadores futuros o candidatos (líneas punteadas).
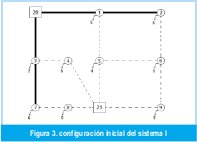
Los parámetros eléctricos del sistema son:
- La capacidad máxima de los alimentadores(existentes y candidatos) es 20 MVA.
- La capacidad máxima de las subestaciones(existentes y candidatas) es 60 MVA.
- El Costo Fijo de los alimentadores nuevos es 20 (Unid/Km).
- El Coto Fijo de la subestación nueva es 400 (Unid/Km).
- El Costo Variable de los alimentadores (nuevos y existentes) es 4 (Unid/MVA/Km).
- El Costo Variable para las subestaciones no es considerado.
Las longitudes de los alimentadores y los valores de las cargas del sistema se ilustran en las Tablas 1 y 2 respectivamente.


En la Figura 4 se observa la configuración óptima encontrada la cual tiene un valor de 820 Unidades.
En la figura 4 se observa el sentido y el valor de los flujos de potencia del sistema. Se puede observar como todas las cargas quedan abastecidas completamente.
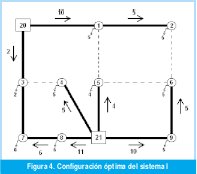
4.2 Sistema II
El sistema de la Figura 5 está conformado por doce (12) nodos (once de los cuales son de carga), una subestación existente (Nodo 20), tres alimentadores existentes (L1_20, L1_2, L3_20), dos subestaciones futuras o candidatas (Nodos 21 y 22) y trece (13) alimentadores futuros o candidatos.
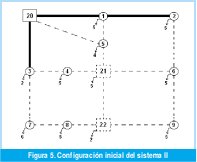
Los parámetros eléctricos del sistema son:
- La capacidad máxima de los alimentadores (existentes y candidatos) es 20 MVA.
- La capacidad máxima de las subestaciones (existentes y candidatas) es 30 MVA.
- El Costo Fijo de los alimentadores nuevos es 20 (Unid/Km).
- El Coto Fijo de las subestaciones nuevas es 400 (Unid/Km).
- El Costo Variable de los alimentadores (nuevos y existentes) es 4 (Unid/MVA/Km).
- El Costo Variable para las subestaciones no es considerado.
Las longitudes de los alimentadores y los valores de las cargas del sistema se ilustran en las Tablas 3 y 4 respectivamente.

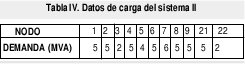
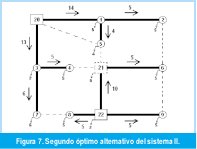
Para este sistema se encontraron dos configuraciones óptimas (óptimos alternativos). En las Figuras 6 y 7 se observan ambas configuraciones las cuales tienen un valor de 936 Unidades monetarias. De igual forma se observa que todas las cargas quedan abastecidas completamente.
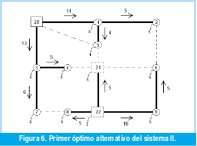
5. CONCLUSIONES
En este trabajo se propuso e implementó un algoritmo de Branch and Bound el cual es un método exacto de optimización aplicado a la solución del problema de la expansión de sistemas de distribución.
Los resultados obtenidos con las simulaciones de los dos sistemas de potencia comprueban la eficiencia de la metodología propuesta debido a que se encontró la configuración óptima para el modelo lineal entero mixto alcanzando la misma configuración óptima encontrada en la literatura especializada.
Con el fin de reducir el número de problemas a ser resuelto por el algoritmo planteado se generaron soluciones incumbentes iniciales de buena calidad incluyendo la restricción de caída de tensión en el modelo después de decidir la instalación de un nuevo alimentador. Estas particularidades permitieron obtener un buen desempeño de la metodología propuesta en la simulación de sistemas con un gran número de variables de decisión, considerando varios escenarios y la posibilidad de que durante el proceso de búsqueda se pudieran analizar diferentes tipos de recursos a ser colocados en el sistema.
Para el sistema de distribución de la ciudad de Pereira se obtuvo un plan de expansión que difiere del propuesto actualmente. Un estudio interesante, consiste en realizar un análisis comparativo entre los planes realizados con el fin de determinar comportamientos económicos.
El planeamiento de sistemas de distribución efectuado por las empresas del sector eléctrico se realiza, tradicionalmente, basándose en la experiencia del ingeniero encargado de esta área. La metodología propuesta en este trabajo realiza un plan de expansión para estos sistemas cuyo resultado final podría traducirse en grandes ahorros económicos para las empresas.
Con el fin de mejorar la solución del problema de la expansión de sistemas de distribución se recomienda tener en cuenta para futuros trabajos los siguientes aspectos:
Involucrar en el modelo matemático los costos variables de las subestaciones pues en la literatura es difícil encontrar autores que hallan tenido en cuenta este costo de operación (administración, operación, mantenimiento, etc) en la función objetivo.
Siempre que las condiciones de la red lo permitan, tener en cuenta la expansión de las subestaciones existentes pues en algunos casos podría ser más económico ampliar una subestación existente que instalar una nueva.
Trabajar con un modelo no lineal entero mixto, es decir, en lugar de involucrar las pérdidas de la red en forma linealizada se deben trabajar dichos valores (costos variables de los alimentadores) en forma no lineal con el fin de obtener un modelamiento más exacto.
Resolver el sistema de distribución teniendo en cuenta varias funciones objetivo como impactos ambientales o confiabilidad de la red. En la literatura especializada a pesar de que en la última década se han publicado diversos trabajos con un tratamiento multiobjetivo del problema, la tendencia se mantiene en considerar solamente una función objetivo que considera los costos de inversión y operación de la red.
Implementar nuevas metodologías de solución como Algoritmos Genéticos y Búsqueda Tabú , entre otros.
6. AGRADECIMIENTOS
Los autores expresan su agradecimiento a la Universidad Distrital Francisco José de Caldas por facilitar los medios para esta publicación y a la Universidad Tecnológica de Pereira (U.T.P.) por el apoyo prestado al grupo de investigación en planeamiento eléctricos y al grupo DINOP (desarrollo en investigación operativa) de la U.T.P.
7. REFERENCIAS BIBLIOGRÁFICAS
[1] Sun et al: «Optimal Distribution Substation and Primary Feeder Via the Fixed Charge Network Formulation», IEEE Transactions on Power Apparatus and Systems, Vol. PAS-100, No. 5.
[2] Ponnavaiko et al.: «Distribution System Planning Trough Mixed Integer Programming Approach», IEEE Transactions on Power Delivery, Vol. PWRD-2, No. 4, pp1157-1163.
[3] Kagan, N., Adams, R.N.: «A Benders Descomposition Approach to the Multiobjetive Distribution Planning Problem»,Internacional Journal of Electrical Power & Energy Systems, Vol. 15, No. 5, pp259-271.
[4] Ramírez-Rosado, I.J., Bernal-Agustín, J.L.: «Genetic Algorithms Applied to the Design of Large Power Distribution Systems», IEEE Transactions on Power Systems, Vol. 13 No. 2, pp696-703, May 1998.
[5] Bazán, F.A., Mantovani, J.R.S., Romero, R.A.: «Planeamiento de Expansión de Sistemas de Distribución de Energía Eléctrica Usando un Algoritmo de Búsqueda Tabú», XIV Congreso Brasileño de Automatización, Natal-Brasil, Septiembre 2002.
[6] Almeida, M.S., Mantovani, J.R.S., Romero, R.A.: «Colocación &Oacuxte;ptima de Subestaciones y Alimentadores en Sistemas de Distribución de Energía Eléctrica Usando un Algoritmo de Branch and Bound», XIV Congreso Brasileño de Automatización, Natal-Brasil, Septiembre 2002.
[7] Gallego R., Ramón y Romero L., Rubén. «Optimización En Sistemas Eléctricos II», Texto Guía en Maestría en Ingeniería Eléctrica, Universidad Tecnológica de Pereira.
Mauricio Granada Echeverri
Nació en Pereira, Colombia. Recibió su título como ingeniero electricista en 2001 en la UTP. Magíster en Ingeniería eléctrica en lamisma universidad en 2003. Docente del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira.
Ramón Alfonso Gallego Rendón
Recibió su título como ingeniero electricista en 1981 en la Universidad Tecnológica de Pereira. Magíster en sistemas de potencia 1985 (Universidad Nacional). Ph.D en Ingeniería Eléctrica 1997. (Universidad de Campinas -Brazil). Docente del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira.
Ricardo Alberto Hincapié
Isaza Recibió su título como ingeniero electricista en 2002 en la Universidad Tecnológica de Pereira. Magíster en Ingeniería eléctrica en la misma universidad en 2005.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










