DOI:
https://doi.org/10.14483/udistrital.jour.reving.2013.2.a04Publicado:
2014-12-14Número:
Vol. 18 Núm. 2 (2013): Julio - DiciembreSección:
ArtículosAnálisis del Desempeño Estudiantil en las Pruebas de Estado para Educación Media en Colombia mediante Modelos Jerárquicos Lineales
Analysis of student performance in Colombian high school government tests using hierarchical lineal models
Palabras clave:
High Schools Education in Colombia, High School Government Tests, Hierarchical Lineal Models. (en).Palabras clave:
educación media en Colombia, resultados de pruebas de estado, Modelos Jerárquicos Lineales. (es).Descargas
Referencias
A. G. &. J. Barrientos, «Determinantes de la calidad de la educación en Colombia.,» Archivos de Economía, p. 88, Noviembre 2001.
T. P. &. K. Wolpin, «The production of cognitive achievement in children: Home, school and racial test score gaps,» University of Pensilvania, p. 70, 2006.
L. Gamboa, «La teoria del valor agregado: una aproximación a la calidad de la educación en Colombia,» Revista de Economía Universidad del Rosario, pp. 95-116, 2003.
A. M. e. A. Iregui, «Evaluación y análisis de efi ciencia de la educación en Colombia,» Banco de la República, p. 105, 2006.
M. Lara, «Asociación entre la efectividad de la funcionalidad familiar en las familias de los estudiantes de la facultad de enfermería de la fundación universitaria Sanitas y el rendimiento económico,» Universidad Nacional de Colombia, p. 70, 2009.
PISA, «Data Analysis Manual,» PISA, OECD, 2009.
H. Goldstein, «Multilevel Statistical Models,» Bristol University, p. 192, 1999.
S. Raudenbush, Hierarchical Linear Models, Applications and Data Analysis Methods, Chicago US: Sage, 2002.
J. Figel, «Competencias clave para el aprendizaje permanente,» Al tablero, p. 11, 2009.
L. G. Diaz, Estadística Multivariada: inferencia y métodos, Bogotá: Universidad Nacional de Colombia, 2002.
Icfes, Metodología de construcción del índice de nivel socioeconómico de los estudiantes INSE y de la clasifi cación socioeconómica CSE de los colegios., Bogotá: Icfes, 2010.
Min. Educación, «Decreto 299 de 2009: Por el cual se reglamentan algunos aspectos relacionado con la validación del Bachillerato en un sólo examen,» Imprenta Nacional, Bogotá, 2009.
D. C. Montgomery, Introduction to linear regression analysis, Arizona State University: Jolm Wiley & Sons, Inc., 2006.
J. Albright, «Estimating Multilevel Model using SPSS, Stata, SAS and R,» University of Michigan, p. 35, 2010.
M. O’Neill, ANOVA & REML: A guide to linear mixed models in an experimental design context, STatistical Advisory & Training Service Pty Ltd, 2010.
A. Gaviria, «Determinantes de la calidad de educación en Colombia,» Archivos de Economía, p. 19, 2001.
PISA, «PISA 2009 Results: what students know and can do. Students performance in reading, mathematics and science,» OECD, 2009.
PISA, «PISA 2012 Results in focus: what 15-years-old know and what they can do with what they know,» OECD, 2012.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
ANÁLISIS DEL DESEMPEÑO ESTUDIANTIL EN LAS PRUEBAS DE ESTADO PARA EDUCACIÓN MEDIA EN COLOMBIA MEDIANTE MODELOS JERÁRQUICOS LINEALES
ANALYSIS OF STUDENT PERFORMANCE IN COLOMBIAN HIGH SCHOOL GOVERNMENT TESTS USING HIERARCHICAL LINEAL MODELS
Jaime Orjuela Viracachá
Empresa de Telecomunicaciones de Bogotá jaimeorjuela@etb.net.co
Recibido: 17/11/2013 - Aceptado: 19/12/2013
RESUMEN
En este artículo se describe la utilización de los Modelos Jerárquicos Lineales para hallar los determinantes individuales de desempeño en las pruebas de estado para educación media en Colombia, con los datos del año 2009, que son los últimos disponibles públicamente y provistos por el Instituto Colombiano para el Fomento de la Educación Superior (ICFES).
Inicialmente se hace la presentación detallada de los datos así como de las exclusiones, consideraciones y justificación del subconjunto de datos finalmente procesados. Posteriormente se expone brevemente el marco teórico de los Modelos Jerárquicos Lineales, así como su aplicación concreta en la investigación de los determinantes de desempeño en las pruebas de estado. El análisis de los resultados permite concluir que existe una relación directa entre algunas características no académicas del estudiante y las competencias evaluadas en la prueba de estado al finalizar su formación media y que dichas características (sociales y económicas) difieren notoriamente entre colegios públicos y privados, y entre jornadas diurnas ordinarias y otras jornadas.
Palabras clave: educación media en Colombia, resultados de pruebas de estado, Modelos Jerárquicos Lineales.
ABSTRACT
In this paper, Hierarchical Lineal Models are applied for analyzing individual factors of student performance in Colombian High School Government Tests, using data from 2009 , which are the latest results publicly available from the Instituto Colombiano para el Fomento de la Educación Superior (ICFES).
Initially the paper describes the data as well as assumptions for cleaning and pre-processing steps that were necessary. After that, concepts related to Hierarchical Lineal Models are introduced, and the models are applied to the data. According to the obtained results, there exists a direct relationship between non academics features and student performance, evaluated in Colombian High School Government Tests. These features (social and economic) are different between public and private schools, and also between daytime schools and other-time schools.
Key words: High Schools Education in Colombia, High School Government Tests, Hierarchical Lineal Models.
1. INTRODUCCIÓN
Uno de los principales temas de investigación en el área de educación, es la relación existente entre variables no académicas con los resultados en las evaluaciones académicas, así como el impacto que tiene el colegio frente a estos resultados. Varios métodos han sido utilizados para abordar este tema, como modelo lineales [1], [2]; análisis de componentes principales [3] y estadística gráfica descriptiva [4], [5]; sin embargo se han encontrado inconvenientes como que en su modo básico y por su naturaleza sólo buscan relaciones lineales o en el caso del análisis de componentes principales el hecho de que cada componente principal sea una combinación lineal de todos los atributos de entrada, suele complicar la interpretación de resultados; así como que estos modelos desconocen que los datos se encuentran agrupados en varios niveles: un ejemplo de estos niveles se puede ver cuando se compara al mejor estudiante del mejor colegio con el mejor estudiante del peor colegio, encontrando que existen diferentes competencias académicas entre uno y otro estudiante, evidenciando diferencias en el nivel de colegio y en el de estudiante.
Tal como lo expone [6], durante los últimos años, los estudios cuantitativos en educación han utilizado exhaustivamente los modelos multinivel [7] también llamados modelos jerárquicos lineales [8] debido a que resuelven los inconvenientes de otros modelos utilizados anteriormente y que tienen en cuenta los efectos potenciales que surgen de la forma como los estudiantes son asignados a los colegios. En efecto se encuentra que [6, pag. 200]:
“En algunos países, por ejemplo, el estatus socio-económico de un estudiante determina en gran parte el tipo del colegio al cual él o ella asistirán y existe una estrecha relación entre el estatus socio-económico de éste y los demás estudiantes dentro del colegio. En contraste, otros países o sistemas, tienen colegios en los que los estudiantes pertenecen a una amplia variedad de estatus socio-económicos, pero dentro del colegio, hay diferenciación de los cursos en que son asignados, afectando la variabilidad al interior del colegio”
En ese sentido existe entonces un impacto en los resultados en las pruebas académicas que depende del estudiante, de los colegios, de la varianza al interior de cada colegio y de la varianza entre colegios. En el presente artículo se presenta la utilización de los modelos jerárquicos lineales aplicados a la determinación de factores individuales no académicos de desempeño en las pruebas de estado para la educación media en Colombia con los datos del año 2009, que son los últimos disponibles públicamente y provistos por el Instituto Colombiano para el Fomento de la Educación Superior (ICFES).
2. MATERIALES
Los datos utilizados en el presente artículo fueron provistos por el ICFES y son los últimos disponibles públicamente que corresponden a la aplicación de la prueba de estado para educación media (SABER11) del primer semestre del año 2009 (69.740 registros), aunque existen resultados en trece áreas, se analizan dos de las que en el criterio de los expertos evalúan competencias básicas clave para el aprendizaje, que son: matemáticas y lenguaje [9].
Hay 32 variables predictoras relacionadas con 4 grupos de características: 2 relacionadas con las características del Colegio, 21 relacionadas con las características socio económicas, 3 relacionadas con las características del estudiante y 5 relacionadas con las características del grupo familiar. Teniendo en cuenta que de los 4 grupos expuestos en el ítem anterior, los atributos que están relacionados con las características socio económicas son 21, resulta una buena alternativa hacer una reducción de la dimensionalidad utilizando el Análisis de Componentes Principales (PCA). El análisis de componentes principales es un método de interdependencia y su objetivo es la estructuración de un conjunto de datos multivariado mediante la reducción del número de variables conteniendo la mayor cantidad de varianza posible en los primeros componentes [10]. Las componentes resultantes se nombraron: índice de nivel socioeconómico del estudiantes (INSE) y clasificación socioeconómica del colegio (CSE) [11].
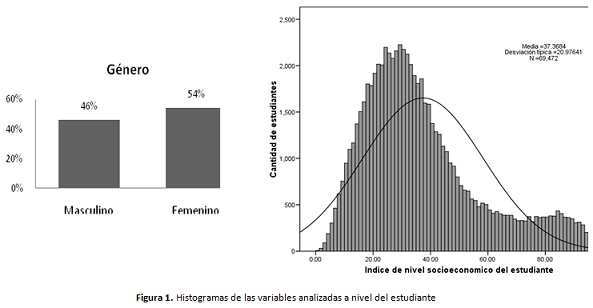
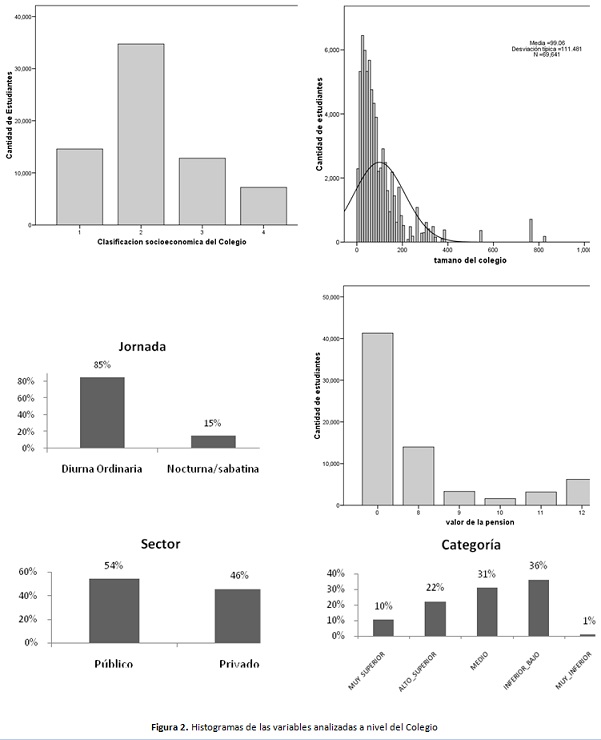
Teniendo en cuenta que la prueba de estado es de carácter obligatorio para todos las personas que terminan su ciclo de formación media, se distinguen varios grupos bien diferenciados, el primero que corresponde al tipo de jornada: por un lado quienes asisten a jornadas mañana, tarde o completa, que son jóvenes de no más de 20 años, generalmente dependientes de sus padres y por otro lado, quienes asisten a jornadas nocturnas, sabatinas y/o dominicales que hacen programas de validación del bachillerato que por ley deben ser mayores de edad al momento de presentar la prueba de validación [12] y por tanto en condiciones sociales, familiares y culturales diferentes a las de jornadas diurnas ordinarias. Como segundo criterio diferenciador se puede distinguir el sector del Colegio, es decir si es público o privado, en [4] se hace una evaluación y análisis de la eficiencia de la educación en Colombia comparando colegios públicos y privados, llegando a la conclusión que el sector del colegio es un factor diferenciador. No obstante las diferencias expuestas, se realizó el análisis tanto para el conjunto de datos completo como para los grupos identificados. En las Figuras 1 y 2, se muestran los histogramas correspondientes a las variables analizadas. En la figura 1 se muestra la distribución de género en términos porcentuales y el índice de nivel socioeconómico del estudiante en términos absolutos, es decir en cantidad de estudiantes. En la figura 2 se muestran las variables analizadas a nivel de colegio. Para la clasificación socioeconómica del colegio existen 4 valores ordinales. Para el valor mensual de la pensión hay 12 categorías, donde 0 corresponde a los estudiantes que no pagan y 12 a quienes pagan $250.000 o más por la mensualidad. Con base en los datos analizados, se puede evidenciar teniendo en cuenta la jornada que gran parte de los estudiantes de educación media (85%) asisten en la edad esperada (siendo menores de edad). También se aprecia que la oferta educativa pública a nivel nacional es comparativamente mayor que la privada, situación que se evidencia ampliamente en las zonas rurales, no obstante en la mayoría de ciudades capitales, la cifra puede ser inversa.
En general y como era de esperarse, los colegios públicos atienden a estudiantes de menores recursos. En términos de tamaño existen más colegios pequeños que grandes, En promedio los estudiantes que asisten a colegios privados en jornada diurna pagan más que quienes asisten a colegios públicos. La distribución de género es homogénea con sutiles diferencias en la jornada diurna. Por otro lado, la mayoría de estudiantes que asisten a colegios públicos se circunscriben en colegios de categoría académica media, baja e inferior.
3. MÉTODOS
El análisis de regresión es una técnica estadística para investigar y modelar la relación entre variables regresoras y de respuesta. Para un modelo de regresión general, la expresión matemática es:
Dónde: γ es el vector de n respuestas conocidas, X es una matriz de n observaciones por k variables regresoras, β es un vector de k+1 coeficientes de regresión y ε es un vector de n errores aleatorios. Se desea determinar un vector β que estime la variable de respuesta para otros valores de X minimizando el error
. Uno de los métodos más comúnmente utilizados para resolver este problema es la de estimación por mínimos cuadrados:
La matriz inversa siempre existe si los regresores son linealmente independientes, esto es, si ninguna columna de la matriz X es una combinación lineal de las demás columnas [13].
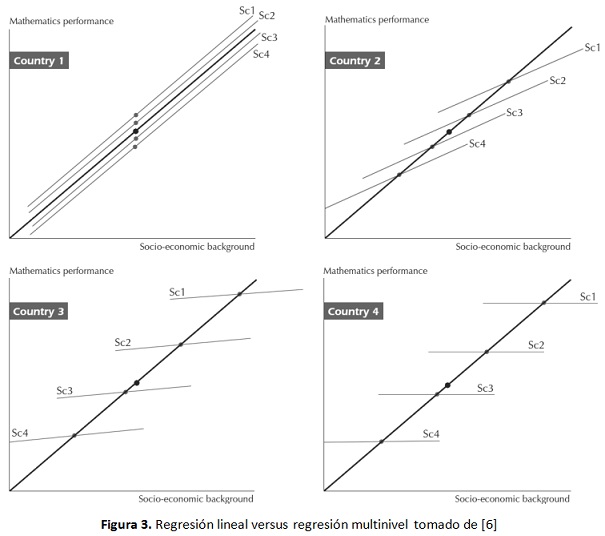
Si bien los modelos de regresión han sido los más usados en muchas áreas de las ciencias y la ingeniería, en los últimos años los modelos multinivel han sido preferidos para el análisis de datos en la educación, justificado principalmente porque los modelos clásicos de regresión no tienen en cuenta los efectos potenciales que surgen de la forma como los estudiantes están distribuidos en los colegios. En [6, pág. 201] se presenta el siguiente ejemplo que explica la diferencia entre los modelos de regresión lineal simple y los de regresión multinivel. La figura 3 (tomada de [6]) muestra la relación entre el estatus socio económico y el desempeño estimado en matemáticas para cuatro países hipotéticos. La línea negra representa el estimado obtenido de la regresión lineal simple general mientras que las líneas grises muestran ese estimado calculado para cada colegio por separado. El punto negro representa la media del estatus socio económico de todos los estudiantes intersecado con la media de desempeño de todos los colegios. Los puntos grises representan la media del estatus socio económico para cada colegio intersecado con la media de desempeño para cada colegio.
En el análisis de regresión simple general, gráficamente representado por las líneas negras, los cuatro países tienen un comportamiento idéntico, esto es que el resultado esperado para un estudiante de un alto nivel socio económico es considerablemente mayor que el esperado para un estudiante de bajo nivel socioeconómico. En contraste, si se considera un modelo de regresión independiente para cada colegio saltan a la vista diferencias sustanciales entre países, colegios y estudiantes: Para el país 1, el modelo multinivel es similar al de la regresión multinivel, lo que indica que diferentes colegios atienden a estudiantes de diversos niveles socio económicos, es decir que no hay segregación social, así mismo se ve que el desempeño de los estudiantes está distribuido uniformemente en la escala de resultados, por lo cual se puede decir que tampoco hay segregación académica, se ve también que estudiantes de niveles socioeconómicos menores tienden a obtener resultados menores. En el otro extremo se muestra la situación del país 4, en donde las líneas de regresión para cada colegio, difieren considerablemente de la línea de regresión lineal general, lo que podría ser interpretado como que los colegios no cubren todo el rango de niveles socio económicos, se nota que el colegio 1 (Sc1) atiende principalmente a estudiantes del alto estatus socio económico, mientras que el colegio 4 (Sc4) atiende principalmente a los estudiantes de los estatus menos favorecidos, evidenciando por lo mismo un alto nivel de segregación; por otro lado los estudiantes del colegio 1 tienden a obtener los mejores resultados en disparidad al colegio 4, evidenciando también una alta segregación académica. Se concluye entonces que para el país 4, dentro de cada colegio el estatus socio económico del estudiante no es un factor de desempeño escolar, sin embargo sí lo es el estatus socioeconómico de cada colegio. Los países 2 y 3 presentan situaciones intermedias entre los dos extremos mostrados para los países 1 y 4.
Para el desarrollo del análisis multinivel, se descompone el modelo en dos niveles: las variables a nivel del estudiante (primer nivel) y las variables a nivel del colegio (segundo nivel). Se utiliza el modelo de regresión presentado en [14]:
Manteniendo la estructura matricial de (2), γ es el vector de resultados en la prueba de matemáticas o lenguaje de los n estudiantes evaluados; X es una matriz de n observaciones por k variables regresoras, que en este caso son cuatro: CSE (Clasificación Socio Económica del Colegio), Sector del Colegio (público o privado), Género (Masculino y Femenino) e INSE (índice de Nivel Socio-Económico) [11]; βes un vector columna de tamaño (k+1) que contiene los coeficientes de regresión; Z es una matriz unitaria de tamaño (n ×2) ; u es un vector de (2×1) que contiene las dos varianzas de las variables aleatorias de error: a nivel de los colegios y
a nivel del estudiante; y ε es el vector de residuales del modelo.
Modelo Multinivel nulo (sin variables regresoras)
Inicialmente se realiza el análisis de regresión multinivel en los dos niveles propuestos sin incluir variables regresoras, es decir . Reemplazando en la expresión (4) quedaría de forma expandida:
Que se interpreta como sigue: el puntaje γij en la prueba de matemáticas o lenguaje para un estudiante i que asiste a un colegio j es igual al promedio del colegio en la prueba β0 (matemáticas o español) más un efecto individual. Ahora bien, teniendo en cuenta que hay un efecto común para los estudiantes de un mismo colegio, es necesario adicionar un efecto a nivel del colegio:
Donde γ00 es el promedio poblacional y υ0j es el efecto específico del colegio. Reemplazando las expresión (6) en (5), se obtiene:
Si se supone que u y r son variables aleatorias normalmente distribuidas con varianza constante, entonces sus varianzas mostrarán el impacto del efecto de esas variables en el modelo. Se denotará la varianza de υ0j, que corresponde a la varianza al interior de los colegios y la de rij como
, que corresponde a la varianza entre colegios.
Para justificar la utilización de un método multinivel, es necesario conocer el porcentaje de variación de la variable resultante atribuible al efecto del colegio (segundo nivel implicado), que se obtiene de la relación entre la varianza entre colegios y la varianza total:
En el argot del análisis multinivel, ρ se conoce como el índice de correlación intraclase. Un valor de ρ cercano a 0 indica que no hay heterogeneidad entre colegios (caso del País 1 de la Figura 3), mientras que valores superiores y hasta un máximo hipotético de 1 indican que existe heterogeneidad entre colegios (caso de los Países 2, 3 y 4 de la Figura 3) y justifica la utilización de métodos multinivel. Un referente comparativo para la interpretación de la correlación intraclase ρ es [18], que lista las correlaciones intraclase en diferentes países para las pruebas PISA del año 2012, donde Finlandia aparece con un ρ de 0.09, Estados Unidos con 0.26, México con 0.43 y Chile con 0.53, sólo por citar algunos ejemplos. Si bien los valores mostrados en [18] dan un referente práctico del índice de correlación intraclase a nivel mundial, no son directamente comparables con los valores obtenidos para el presente artículo, pues en las pruebas PISA se evalúa una muestra de jóvenes de 15 años, sin considerar su escolaridad; mientras que en SABER11 se evalúa toda la población de jóvenes que finalizan su formación media, sin considerar la edad.
Modelo Multinivel incluyendo variables a nivel del colegio
Para continuar con el análisis, se introducen las variables explicativas a nivel del Colegio, partiendo de la hipótesis que éstas inciden en el desempeño de los estudiantes:
Donde CSE corresponde a la Clasificación Socio-Económica del Colegio y Sector corresponde al tipo de actividad económica que desarrolla el colegio (público ó privado). Sector es una variable categórica donde 0 es público y 1 es privado. En [11] se presenta la metodología utilizada para reducir las 32 variables socioeconómicas relacionadas con el colegio y el estudiante a 2 variables independientes: CSE (Clasificación socioeconómica del colegio) e INSE (índice de nivel socioeconómica del estudiante).
Modelo Multinivel incluyendo variables a nivel del colegio y del estudiante
Al modelo propuesto en la expresión (9), se adicionan ahora las variables explicativas a nivel del estudiante, que son el índice de nivel socioeconómico del estudiante y el género, por lo que el modelo completo propuesto en (4) queda de forma expandida así:
Métodos de estimación
Para la estimación de componentes de varianza, el método más usado ha sido el de análisis de varianzas ANOVA; método que implica la presencia de errores aleatorios normales, independientes y con varianza constante. En la actualidad otros métodos como el de máxima verosimilitud restringida (REML, por sus siglas en inglés), permiten tener errores normales, posiblemente correlacionados y con varianzas no constantes [15] . Los resultados presentados en este trabajo utilizan el método de estimación REML.
Presentación de los resultados
Del modelo sin covariables, propuesto en (7), se obtuvieron los siguientes parámetros:
Varianza entre colegios: var(u_(0j))==57.74 para Matemáticas y 18.95 para Lenguaje
Varianza al interior de los colegios: var(rij) = = 89.32 para Matemáticas y 48.80 para Lenguaje
Coeficiente de correlación intraclase: ρ=0.39 para Matemáticas y 0.28 para Lenguaje.
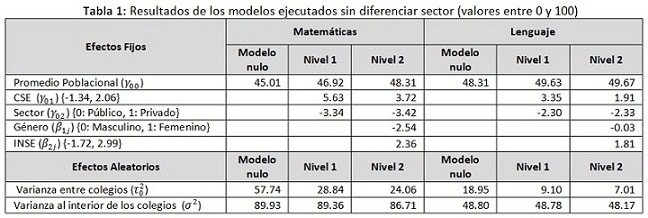
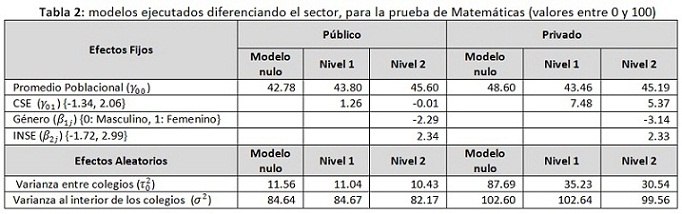
Según lo expuesto en la sección 2.1, los coeficientes de correlación intraclase de 0.39 y 0.28 justifican la utilización de métodos multinivel para el análisis de los datos. En la tabla 1 se muestra el resultado de la ejecución de los modelos propuestos, sin diferenciar el sector. En la tabla 2 se muestra el resultado de ejecutar modelos independientes para los colegios públicos y privados.
ANÁLISIS DE RESULTADOS
Teniendo en cuenta los valores promedio poblacionales, se esperan mejores resultados en las pruebas de lenguaje que en las de matemáticas. Valores negativos en el parámetro Sector, indican que se espera que haya mejores resultados en los colegios públicos que en los privados, situación justificada teniendo en cuenta la mayor disparidad académica entre colegios privados comparados con sus homólogos públicos que tienen un mayor control estatal.
De los modelos ejecutados diferenciando el sector de los colegios, se puede concluir que en los colegios públicos el factor no académico que más influye en los resultados de las pruebas de estado es el índice de nivel socio-económico del estudiante (INSE=2.34), mientras que en los colegios privados pesa más el nivel socio-económico del colegio (CSE=5.37).
Con referencia a las diferencias entre géneros, se puede observar una tendencia en los hombres a obtener mejores puntajes que las mujeres principalmente en matemáticas. Al respecto [16] expone cómo la brecha entre hombres y mujeres en las pruebas de aptitud escolástica han sido fuente de polémica en los Estados Unidos, pues aunque los hombres tienden a tener mejores puntajes en las pruebas para educación media, las mujeres presentan mejores puntajes en la universidad. En ese sentido, no se puede calificar al género como factor determinante de desempeño.
Si se compara la varianza entre colegios del Modelo nulo y el Nivel 1 mostradas en la Tabla 1, se obtiene:
Se concluye de este resultado que el nivel socioeconómico y el sector del colegio explican la varianza entre colegios en un 50% y un 52% para matemática y lenguaje respectivamente, lo que justifica aún más la utilización de un modelo multinivel. Es decir, que algunos colegios atienden principalmente a estudiantes acomodados, mientras que otros atienden principalmente a estudiantes con pocos recursos, encontrando al interior de cada colegio una relativa homogeneidad del nivel socioeconómico. Por otro lado si se considera el sector del colegio (público o privado) como determinante de desempeño en las pruebas de estado se evidencia que aunque los colegios públicos tienen una media inferior, los colegios privados tienen mayor desviación estándar indicando disparidad entre colegios privados, esto es: la mayoría de los colegios públicos tienen un desempeño promedio, mientras que en la oferta de privados hay muchos colegios con desempeño inferior bajo y unos pocos con desempeño muy superior que mejoran el promedio, pero aumentan la varianza.
CONCLUSIONES
Con base en los resultados se concluye que existe una relación directa entre algunas características no académicas del estudiante y las competencias evaluadas en la prueba SABER11. Colombia como la mayoría de países latinoamericanos exhiben segregación escolar, esto es, que hay colegios que atienden principalmente a estudiantes acomodados y otros que atienden principalmente a estudiantes con pocos recursos. El control estatal sobre las instituciones de educación media se manifiesta principalmente en los colegios públicos, donde existen estándares académicos promedio; dado que hay más colegios públicos que privados, un mayor control y más interés estatal en la calidad de la educación en este sector podría mejorar notablemente la media de educación a nivel nacional. Si bien la prueba PISA no es completamente comparable con la prueba SABER11, si da un referente de educación nacional, la primera para estudiantes de 15 años con diferentes escolaridades y la segunda para todos los estudiantes que finalizan su ciclo de educación media. Para la prueba PISA del año 2009 Colombia ocupó los puestos 48 y 54 en habilidad lectora y matemáticas respectivamente, de entre 61 países participantes [17]; este resultado es coherente con los resultados obtenidos en el presente estudio, donde se obtuvieron mejores puntajes en Lenguaje que en Matemáticas. Para el año 2012 Colombia ocupó los puestos 53 y 58 en habilidad lectora y matemáticas respectivamente [18], perdiendo 4 puestos en cada categoría comparado con los resultados de 2009, esto evidencia la necesidad apremiante de mejorar la calidad a nivel nacional.
Finalmente, considerando la clasificación de colegios establecida por el ICFES: muy superior, superior, medio, inferior y muy inferior, se evidencia que aunque la gran mayoría de colegios en el nivel muy superior corresponden a colegios privados de alto costo, la diferencia entre públicos y privados en la categoría alto superior es menor, mientras que en la categoría medio la cifra es inversa, es decir hay más colegios públicos en esta categoría que privados, lo que sugiere que en carencia de recursos económicos para costear educación privada de calidad (Niveles alto superior y muy superior) resulta una mejor opción asistir a colegios públicos de categoría media, que a planteles privados en la misma.
Referencias
- A. G. &. J. Barrientos, «Determinantes de la calidad de la educación en Colombia.,» Archivos de Economía, p. 88, Noviembre 2001.
- T. P. &. K. Wolpin, «The production of cognitive achievement in children: Home, school and racial test score gaps,» University of Pensilvania, p. 70, 2006.
- L. Gamboa, «La teoria del valor agregado: una aproximación a la calidad de la educación en Colombia,» Revista de Economía Universidad del Rosario, pp. 95-116, 2003.
- A. M. e. A. Iregui, «Evaluación y análisis de eficiencia de la educación en Colombia,» Banco de la República, p. 105, 2006.
- M. Lara, «Asociación entre la efectividad de la funcionalidad familiar en las familias de los estudiantes de la facultad de enfermería de la fundación universitaria Sanitas y el rendimiento económico,» Universidad Nacional de Colombia, p. 70, 2009.
- PISA, «Data Analysis Manual,» PISA, OECD, 2009.
- H. Goldstein, «Multilevel Statistical Models,» Bristol University, p. 192, 1999.
- S. Raudenbush, Hierarchical Linear Models, Applications and Data Analysis Methods, Chicago US: Sage, 2002.
- J. Figel, «Competencias clave para el aprendizaje permanente,» Al tablero, p. 11, 2009.
- L. G. Diaz, Estadística Multivariada: inferencia y métodos, Bogotá: Universidad Nacional de Colombia, 2002.
- ICFES, Metodología de construcción del índice de nivel socioeconómico de los estudiantes INSE y de la clasificación socioeconómica CSE de los colegios., Bogotá: ICFES, 2010.
- Min. Educación, «Decreto 299 de 2009: Por el cual se reglamentan algunos aspectos relacionados con la validación del Bachillerato en un sólo examen,» Imprenta Nacional, Bogotá, 2009.
- D. C. Montgomery, Introduction to linear regression analysis, Arizona State University: Jolm Wiley & Sons, Inc., 2006.
- J. Albright, «Estimating Multilevel Model using SPSS, Stata, SAS and R,» University of Michigan, p. 35, 2010.
- M. O’Neill, ANOVA & REML: A guide to linear mixed models in an experimental design context, STatistical Advisory & Training Service Pty Ltd, 2010.
- A. Gaviria, «Determinantes de la calidad de educación en Colombia,» Archivos de Economía, p. 19, 2001.
- PISA, «PISA 2009 Results: what students know and can do. Students performance in reading, mathematics and science,» OECD, 2009.
- PISA, «PISA 2012 Results in focus: what 15-years-old know and what they can do with what they know,» OECD, 2012.
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.



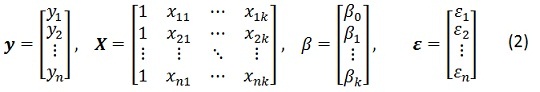






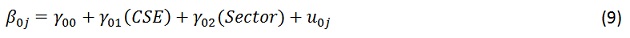
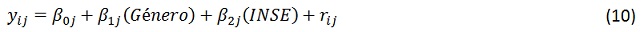
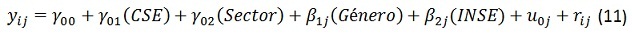
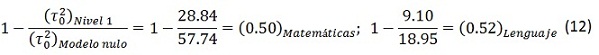




2.jpg)