DOI:
https://doi.org/10.14483/2256201X.12249Publicado:
01-07-2018Número:
Vol. 21 Núm. 2 (2018): Julio-DiciembreSección:
Artículos de investigación científica y tecnológicaModelos compatibles de ahusamiento-volumen para árboles de Gmelina arborea Roxb. en el Alto Magdalena, Colombia
Compatible volume-taper models for Gmelina arborea Roxb. trees grown in the upper Magdalena basin, Colombia
Palabras clave:
forest biometrics, taper, stem diameter, merchantable volume (en).Palabras clave:
biometría forestal, conicidad, diámetro fustal, volumen comercial (es).Descargas
Referencias
Alo, A. A., Onyekwelu, J. C. y Akindele, S. O. (2011). Taper equations for Gmelina arborea in Omo forest reserve, southwestern Nigeria. Journal of Applied Tropical Agriculture, 16(1-2), 120-127.
Avery, T. E. y Burkhart, H. E. (2001). Forest measurements (5a ed.). Nueva York: McGraw-Hill.
Barrios, A., López, A. y Nieto, V. (2014). Predicción de volúmenes comerciales de Eucalyptus grandis a través de modelos de volumen total y de razón. Colombia Forestal, 17(2), 137-149. DOI: https://doi.org/10.14483/udistrital.jour.colomb.for.2014.2.a01
Beal, D. J. (2007). Information criteria methods in SAS® for multiple linear regression models. En: Sesug: Proceedings of the 15th annual SouthEast SAS Users Group Conference. Paper SA05. (pp. 1-10). Carolina del Sur, EE. UU.: Southeast SAS Users Group.
Bi, H. y Long, Y. ( 2001). Flexible taper equation for site-specific management of Pinus radiata in New South Wales. Forest Ecology and Management, 148(1-3), 79-91. DOI: https://doi.org/10.1016/S0378-1127(00)00526-0
Bruce, D., Curtis R. O. y Vancoevering, C. (1968). Development of a system of taper and volume tables for red alder. Forest Science, 14, 339-350.
Burkhart, H. y Tomé, M. (2012). Modeling forest trees and stands. Nueva York: Springer. DOI: https://doi.org/10.1007/978-90-481-3170-9
Cruz, F., De los Santos, H. M. y Valdez, J. R. (2008). Sistema compatible de ahusamiento-volumen para Pinus cooperi blanco en Durango, Mexico. Agrociencia, 42(4), 473-485.
Demaerschalk, J. (1972). Converting volume equations to compatible taper equations. Forest Science, 18(3), 241-245.
Diéguez, U., Rojo, A., Castedo, F., Alvarez, J., Barrio, M., Crecente, F., … y Sánchez, F. (2009). Herramientas selvícolas para la gestión forestal sostenible en Galicia. Galicia, España: Dirección Xeral de Montes, Consellería do Medio Rural.
Fang, Z., Borders, B. E. y Bailey, R. L. (2000). Compatible volume taper models for loblolly and slash pine based on system with segmented-stem form factors. Forest Science, 46, 1-12.
Gaillard, C., Pece, M. G. y Ríos, N. (1997). Ajuste de funciones de forma en Eucalyptus tereticornis. Quebracho, 5, 51-62.
Heidarsson, L. y Pukkala, T. (2011). Taper functions for lodgepole pine (Pinus contorta) and siberian larch (Larix sibirica) in Iceland. Icelandic Agricultural Sciences, 24, 3-11.
Hernández, D., Santos, H., Ángeles, G., Valdez, J. R. y Volke, V. (2013). Funciones de ahusamiento y volumen comercial para Pinus patula Schltdl. et Cham. en Zacualtipán, Hidalgo. Revista Mexicana de Ciencias Forestales, 4(16), 34-44.
Hernández-Ramos, J., Hernández-Ramos, A., García-Magaña, J., García-Cuevas, X., García-Espinoza, G., Muñoz-Flores, H. y Olvera-Delgadillo, E. (2017). Sistema compatible de ahusamiento-volumen comercial para plantaciones de Pinus greggii Engelm. en Hidalgo, México. Revista Mexicana de Ciencias Forestales, 8(39), 59-70. DOI: https://doi.org/10.29298/rmcf.v8i39.43
Jiang, L., Brooks, J. R. y Clark III, A. (2010). Compatible taper and volume equations for young longleaf pine plantations in southwest Georgia. En J. A. Stanturf (ed.), Proceedings of the 14th biennial southern silvicultural research conference (pp. 375-378). Asheville, EE. UU.: Department of Agriculture, Forest Service, Southern Research Station.
Kozak, A. (1988). A variable exponent taper equation. Canadian Journal of Forest Research, 18(11), 1363-1368. DOI: https://doi.org/10.1139/x88-213
Kozak, A. (2004). My last words on taper equations. The Forestry Chronicle, 80(4), 507-515. DOI: https://doi.org/10.5558/tfc80507-4
Lappi, J. (2006). A multivariate, nonparametric stem-curve prediction method. Canadian Journal of Forest Research, 36(4), 1017-1027. DOI: https://doi.org/10.1139/x05-305
López, A. M., Barrios, A., Trincado, G. y Nieto, V. (2011). Monitoreo y modelamiento del crecimiento para el manejo de plantaciones forestales comerciales. Bogotá: Corporación Nacional de Investigación y Fomento Forestal (Conif), Ministerio de Agricultura y Desarrollo Rural.
López, A. M., Barrios, A. y Trincado, G. (2015). Modelos de perfiles fustales con una estructura de error autorregresiva para plantaciones de Eucalyptus tereticornis en Colombia. Madera y Bosques, 21(2), 73-88.
Ministerio de Agricultura y Desarrollo Rural (2012). Sector forestal en Colombia. Bogotá: Proexport Colombia.
Max, T. y Burkhart, H. (1976). Segmented polynomial regression applied to taper equations. Forest Science, 22(3), 283-289.
Obregón, C. (2006). Gmelina arborea: versatilidad, renovación y productividad sostenible para el futuro. Revista el Mueble y la Madera (M&M), 50, 14-20.
Özçelik, R. y Brooks, J. R. (2012). Compatible volume and taper models for economically important tree species of Turkey. Annals of Forest Science, 69, 105-118. DOI: https://doi.org/10.1007/s13595-011-0137-4
Özçelik, R., Yavuz H., Karatepe, Y., Gürlevik, N. y Kırış, R. (2012). Compatible stem taper and volume equations for brutian pine stands in Burdur Region. SDU Faculty of Forestry Journal, 13, 85-91.
Özçelik, R. y Göçeri, M. (2015). Compatible merchantable stem volume and taper equations for Eucalyptus plantations in the Eastern Mediterranean Region of Turkey. Turkish Journal of Agriculture and Forestry, 39, 851-863. DOI: https://doi.org/10.3906/tar-1501-27
Parresol, B. R. (1999). Assessing tree and stand biomass: A review with examples and critical comparisons. Forest Science, 45(4), 573-593.
Parresol, B. R., Hotvedt, J. E. y Cao, Q. V. (1987). A volume and taper prediction system for bald cypress. Canadian Journal of Forest Research, 17, 250-259. DOI: https://doi.org/10.1139/x87-042
Pérez, M. A. (2004). Compatibilidad de funciones de volumen y ahusamiento para renovales de Roble en la Décima Región (tesis de pregrado, Ingeniería Forestal). Universidad Austral de Chile, Valdivia, Chile.
Pompa, M., Corral, J., Díaz, M. y Martínez, M. (2009). Funciones de ahusamiento y volumen compatibles para Pinus arizonica Engelm. en el suroeste de Chihuahua. Revista Ciencia Forestal en Mexico, 34(105), 119-136.
Quiñonez, J., De los Santos, H., Álvarez, J. y Velázquez, A. (2014). Sistema compatible de ahusamiento y volumen comercial para las principales especies de Pinus en Durango, México. Agrociencia, 48(5), 553-567.
Quirós, S. (2015). Modelos de volumen comercial, perfil de fuste y crecimiento para plantaciones clonales de Gmelina arborea Roxb. ex Sm. en Costa Rica (tesis de pregrado, Ingeniería Forestal). Instituto Tecnológico de Costa Rica, Cartago, Costa Rica.
Rodríguez-Toro, A., Rubilar-Pons, R., Muñoz-Sáez, F., Cártes-Rodríguez, E., Acuña-Carmona, E. y Cancino-Cancino, J. (2016a). Modelo de ahusamiento para Eucalyptus nitens, en suelos de cenizas volcánicas de la región de La Araucanía (Chile). Revista de la Facultad de Ciencias Agrarias, 48(1), 101-114.
Rodríguez-Toro, A., Rubilar-Pons, R., Muñoz-Sáez, F., Cártes-Rodríguez, E., Acuña-Carmona, E. y Cancino-Cancino, J. (2016b). Modelo de ahusamiento por tipo de suelo para Pinus radiata en las regiones del Biobío y la Araucanía, Chile. Revista Chapingo Serie Ciencias Forestales y del Ambiente, 22(2), 203-220. DOI: https://doi.org/10.5154/r.rchscfa.2015.05.021
Rojas, F., Arias, D., Moya, R., Meza, A., Murillo, O. y Arguedas, M. (2004). Manual para productores de melina Gmelina arborea en Costa Rica. Cartago: Fonafifo.
SAS Institute Inc. (2009). SAS/STAT® 9.2 User’s Guide, Second Edition. Cary, EE. UU.: SAS® Publishing.
Tamarit, J. C., De los Santos, H. M., Aldrate, A., Valdez, L. J., Ramírez, M. H. y Guerra, V. (2014). Sistema de cubicación para árboles individuales de Tectona grandis L.F. mediante funciones compatibles de ahusamiento-volumen. Revista Mexicana de Ciencias Forestales, 5(21), 59-73.
Tang, C., Wang C. S., Pang, S. J., Zhao, Z. G., Guo, J. J., Lei, Y. C. y Zeng, J. (2017). Stem taper equations for Betula alnoides in south China. Journal of Tropical Forest Science, 29(1), 80-92. DOI: https://doi.org/10.1371/journal.pone.0147610
Tang, X., Pérez-Cruzado, C., Fehrmann, L., Álvarez-González, J.G., Lu, Y. y Kleinn, C. (2016). Development of a compatible taper function and stand-level merchantable volume model for Chinese fir plantations. PloSOne, 11(1), 1-15. DOI: https://doi.org/10.1371/journal.pone.0147610
Thomas, C. y Parresol, B. (1991). Simple, flexible, trigonometric taper equations. Canadian Journal of Forest Research, 21, 1132-1137. DOI: https://doi.org/10.1139/x91-157
Unidad de Planificación Rural Agropecuaria (Upra) (2014). Zonificación para plantaciones forestales con fines comerciales escala 1:100.000, memoria técnica. Bogotá: Upra.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 22 de junio de 2017; Aceptado: 22 de marzo de 2018
Resumen
La estimación precisa del volumen y el ahusamiento de los árboles es importante para el manejo eficiente de los recursos forestales. El objetivo principal del estudio fue generar un sistema de ecuaciones compatibles de ahusamiento-volumen para Gmelina arborea Roxb. Los datos corresponden a perfiles fustales de 97 árboles en edad de cosecha, con edades entre 13-18 años, cultivados en el Alto Magdalena, Colombia. Se evaluaron cuatro sistemas compatibles de ahusamiento-volumen en la predicción de diámetros fustales y volúmenes comerciales. Los sistemas de ecuaciones fueron ajustados simultáneamente para minimizar los errores en la estimación de parámetros y evaluados empleando medidas de bondad de ajuste y de predicción. Los modelos evaluados presentaron sesgos entre -0.07-0.92 cm y -0.0003-0.0009 m3 y errores promedio entre 1.62-2.76 cm y 0.019-0.021 m3 en la predicción de diámetros fustales y volúmenes comerciales, respectivamente. Finalmente, el sistema de ahusamiento-volumen seleccionado fue el propuesto por Fang.
Palabras clave:
biometría forestal, conicidad, diámetro fustal, volumen comercial..Abstract
The accurate estimation of tree volume and taper is important for the efficient management of forest resources. The main objective of the study was to generate a compatible volume-taper equations system for Gmelina arborea Roxb. Data used in the study correspond to 97 trees at harvest age, between 13 and 18 years-old, grown in the upper Magdalena basin, Colombia. Four compatible volume-taper systems were evaluated for stem diameter and merchantable volume prediction. The equations systems were fitted simultaneously to minimize the errors during the parameter estimation and evaluated considering measures of fit goodness and prediction. The evaluated models showed bias in the range of -0.07-0.92 cm and -0.0003-0.0009 m3 and mean errors in the range of 1.62-2.76 cm and 0.019-0.021 m3 in stem diameters and merchantable volumes prediction, respectively. Finally, the selected volume-taper system was the one proposed by Fang.
Keywords:
forest biometrics, taper, stem diameter, merchantable volume..INTRODUCCIÓN
La cuantificación precisa de las existencias de madera de una plantación es de gran relevancia en la planificación y evaluación económica de proyectos de reforestación comercial. El desarrollo de herramientas para la estimación del volumen permite a los reforestadores y silvicultores calcular de forma precisa y confiable la producción generada por las plantaciones forestales. Las estimaciones de volumen para las plantaciones forestales en países tropicales se basan principalmente en modelos de volumen y de rendimiento, los cuales no permiten clasificar el volumen entre los productos ofertados por los fustes cosechados. Es importante resaltar que las ecuaciones de volumen y ahusamiento deben ser generadas de manera específica para cada especie (Bi y Long, 2001; Özçelik y Göçeri, 2015) e incluso para cada sitio (Rodríguez-Toro et al., 2016a; 2016b). La falta de conocimiento en este tema se hace más evidente cuando las predicciones de volumen no representan con fidelidad la realidad y muchas veces se sobrestima o subestima la producción de madera, lo cual causa incertidumbre en la planificación forestal. Las funciones de ahusamiento o modelos fustales son ecuaciones matemáticas utilizadas en el modelamiento de la forma y ahusamiento fustal (Burkhart y Tomé, 2012). Estos modelos permiten predecir tres atributos: I) diámetro (d) para una altura fustal h, II) altura fustal (h) para un diámetro (d) y III) volumen entre dos alturas fustales (v (h 1, h 2)). El volumen es calculado resolviendo la integral a través de la cual se obtiene el volumen de un sólido de revolución.
Diferentes formulaciones de modelos de ahusamiento han sido presentadas en la literatura forestal de las últimas décadas, tales como funciones polinomiales simples (Bruce, Curtis y Vancoevering, 1968), segmentadas (Max y Burkhart, 1976), de exponente o forma variables (Kozak, 2004), enfoques no paramétricos (Lappi, 2006) y funciones trigonométricas (Thomas y Parresol, 1991). Una aproximación para el modelamiento de la forma de los árboles es dividir el fuste en tres secciones: la sección basal correspondiendo a la forma de un neiloide, la sección central correspondiendo a un paraboloide y la sección apical correspondiendo a un cono (Avery y Burkhart, 2001).
Los primeros estudios incluyeron el uso de polinomios con potencias altas para describir principalmente la sección basal del fuste (Bruce et al., 1968). Max y Burkhart (1976) presentaron un modelo polinomial segmentado que usaba dos puntos de unión para conectar estas tres secciones fustales a lo largo del tronco. Otros investigadores introdujeron ecuaciones de exponente y/o forma variable (Kozak, 2004), las cuales usan un exponente cambiante o una forma cambiante para continuamente describir la forma del fuste del árbol desde el nivel del suelo hasta el ápice, exhibiendo más flexibilidad.
El mayor inconveniente en el desarrollo de modelos de volumen y de ahusamiento es que a pesar de que se obtengan parámetros estimados a partir del mismo conjunto de datos, estos no presentan compatibilidad en sus predicciones (Burkhart y Tomé, 2012). Por lo tanto, para obviar este inconveniente se han empleado técnicas de ajuste que garanticen la compatibilidad del sistema de ahusamiento-volumen (Jiang, Brooks y Clark, 2010; Cruz, De los Santos y Valdez, 2008). La compatibilidad entre funciones de ahusamiento y volumen fue propuesta por Demaerschalk (1972) , con el propósito de que cuando se integren las ecuaciones de ahusamiento, también sean representaciones realistas de modelos de volumen total y comercial del fuste.
En los últimos años se han generado diferentes funciones compatibles de ahusamiento-volumen para diferentes especies. Cruz et al. (2008) desarrollaron un sistema compatible de ahusamiento-volumen para Pinus cooperi mediante la modificación de un modelo lineal polinómico, el cual hicieron más flexible con la inclusión de efectos mixtos que controlan la variabilidad y mejoran notablemente la capacidad predictiva. Quiñonez, De los Santos, Álvarez y Velázquez (2014) desarrollaron un sistema compatible de ahusamiento y volumen comercial para las principales especies de Pinus en Durango, México, en el que obtuvieron buenos resultados con el sistema desarrollado por Fang, Borders y Bailey (2000) , por lo cual dicho sistema se puede usar como modelo completo o reducido para caracterizar el ahusamiento y volumen comercial para las especies estudiadas. De manera similar, Özçelik y Göçeri (2015) desarrollaron un sistema compatible para Eucalyptus grandis y Eucalyptus camaldulensis en Turquía, empleando las funciones desarrolladas por Fang et al. (2000), pero requiriéndose el ajuste de un sistema para cada especie.
Gmelina arborea es una especie importante en los programas de reforestación comercial en zonas tropicales secas (MADR, 2012), debido a su rápido crecimiento (Rojas et al., 2004) y a las características tecnológicas de su madera, que han permitido su uso en diferentes procesos industriales (Obregón, 2006). Actualmente, existen en Colombia aproximadamente 14 000 ha de plantaciones comerciales de la especie, concentradas principalmente en los departamentos de Bolívar, Magdalena, Córdoba, Tolima, entre otros (Obregón, 2006). Sin embargo, de acuerdo a la Unidad de Planificación Rural Agropecuaria (Upra, 2014) en el interior del país existe una superficie potencial para la reforestación con la especie de 1.76 millones de ha, principalmente en los valles interandinos de los ríos Magdalena y Cauca. Solo en el departamento del Tolima se cuenta con un área aproximada de 221 463 ha aptas para el cultivo de la especie (Upra, 2014).
A pesar de su importancia económica, son pocos los estudios reportados encaminados a la generación de ecuaciones para la cuantificación de volúmenes comerciales para la especie (Alo, Onyekwelu y Akindele, 2011; López, Barrios, Trincado y Nieto, 2011; Quirós 2015). El desarrollo de ecuaciones compatibles de ahusamiento-volumen representa una oportunidad para mejorar las estimaciones de la oferta maderera en la planificación forestal y, de esta manera, maximizar el retorno económico de las plantaciones de G. arborea. El presente estudio tiene como objetivo desarrollar un sistema de ecuaciones compatibles de ahusamiento-volumen para Gmelina arborea, en la región central de Colombia, conocida como Alto Magdalena. Se busca optimizar la utilización del fuste previo a su industrialización. Los objetivos específicos fueron: I) seleccionar un sistema de ecuaciones de ahusamiento-volumen compatibles apropiado para la especie y II) evaluar el comportamiento de los sistemas de ecuaciones desarrolladas respecto a su capacidad para predecir diámetros fustales y volúmenes comerciales.
MATERIALES Y MÉTODOS
Datos
La base de datos utilizada corresponde a perfiles fustales de 97 árboles muestra de Gmelina arborea distribuidos en cinco rodales con edades entre 13 a 18 años, ubicados en el municipio de Armero-Guayabal, Tolima. El área de estudio se caracteriza por presentar temperaturas promedio anuales de 27 °C, precipitación media anual de 1738 mm y una humedad relativa promedio anual de 71%. Se seleccionaron árboles muestra sanos, rectos, sin daños y que sus diámetros estuvieran distribuidos en el amplio rango de clases diamétricas presente en los rodales.
Posteriormente, estos árboles fueron apeados y desramados; una vez en el suelo se procedió a marcar y medir posiciones en el fuste partiendo de la altura del tocón, 0.5 m, 1.3 m (DAP), 2 m y de ahí en adelante cada metro (1 m). En cada sección se midieron los diámetros con y sin corteza empleando una forcípula de brazos paralelos. Las secciones fueron cubicadas usando la fórmula de aproximación de Smalian (Avery y Burkhart, 2001), excepto la última sección en la cual se utilizó la fórmula del cono (Barrios et al., 2014).
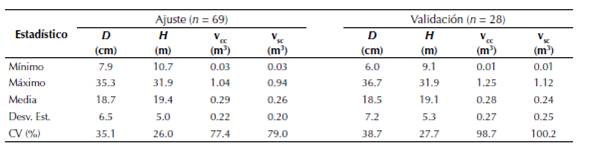
La base de datos de perfiles fustales fue dividida en una base de ajuste para la estimación de parámetros y una base para realizar la validación de los sistemas de ecuaciones (tabla 1). La base de ajuste consideró la selección de un total de 69 perfiles fustales (71% del total) y la base de validación un total de 28 perfiles fustales (29% del total). Se empleó el procedimiento propuesto por López, Barrios y Trincado (2015) en la selección de árboles para la base de validación, el cual consistió en seleccionar de manera aleatoria siete árboles dentro de cuatro clases de tamaños definidas por los percentiles de la distribución de diámetros a 1.3 m: 0-25, 25-50, 50-75 y 75-100%. Este procedimiento permitió asegurar que la base de ajuste y validación incluyera árboles de similar clase diamétrica (tabla 1).
donde D es el diámetro a 1.3 m (cm), H altura total del árbol, vcc y vsc es el volumen total con y sin corteza, respectivamente.
Tabla 1: Estadística descriptiva de los árboles muestra de G. arborea empleados en el ajuste y validación de los sistemas compatibles de ahusamiento-volumen
Modelos de ahusamiento-volumen evaluados
El perfil de los árboles se modeló a partir de cuatro modelos citados en la literatura, los cuales han sido seleccionados para otras especies (Cruz et al., 2008; Pompa, Corral, Díaz y Martínez, 2009; Özçelik, Yavuz, Karatepe, Gürlevik y Kırış, 2012; Hernández, Santos, Ángeles, Valdez y Volke, 2013; Quiñonez et al., 2014; Özçelik y Göçeri, 2015; Tang et al., 2017). Los modelos analizados corresponden al modelo polinomial simple propuesto por Demaerschalk (1972) , los modelos segmentados desarrollados por Max y Burkhart (1976) , Parresol, Hotvedt y Cao (1987) y Fang et al. (2000) . Los modelos de ahusamiento evaluados fueron integrados algebraicamente para obtener su ecuación de volumen comercial implícita. La siguiente notación fue utilizada para describir cada una de las variables incluidas en los modelos: D es el diámetro con corteza (cm) a una altura de 1.3 m sobre el suelo, H es la altura total del árbol (m), d es el diámetro sin corteza (cm) a una altura h, h es la altura fustal (m), vc es el volumen comercial (m3), k = π/40 000, y ai- 1, bi- 1, pi son parámetros a ser estimados (i = 1, 2, …, n). Los modelos se describen a continuación:
Sistema 1: Demaerschalk (1972) .
Sistema 2: Max y Burkhart (1976) .
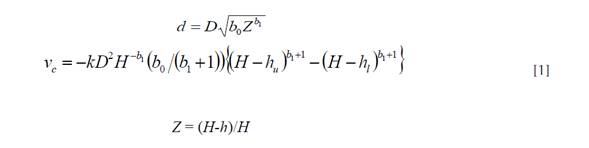
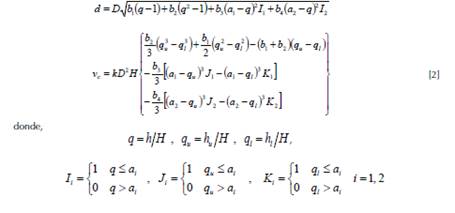
Sistema 3: Parresol et al. (1987) .
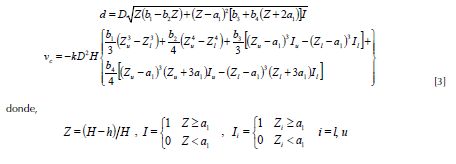
Sistema 4: Fang et al. (2000) .

Estimación de parámetros
Durante el proceso de estimación de parámetros se utilizó el procedimiento Model, contenido en Statistical Analysis System-SAS ®, empleando el algoritmo de minimización de la suma de cuadrados de Marquardt (SAS Institute Inc., 2009). Para el ajuste del sistema de ecuaciones se estimaron los parámetros de ambas ecuaciones (ahusamiento y volumen) en simultáneo, empleando el método de máxima verosimilitud con información completa (FIML) (Quiñonez et al., 2014). Esta estrategia minimiza la suma de cuadrados del error del sistema entero, optimizando el ajuste de ambas funciones (Özçelik y Brooks, 2012).
Criterios de decisión
La bondad de ajuste de los sistemas de ecuaciones fue evaluada considerando el error estándar de estimación (Syx),
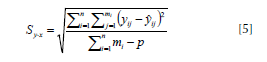
un índice de ajuste (IA) (Parresol, 1999),
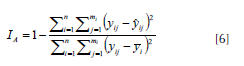
y el criterio de información de Akaike (Beal, 2007
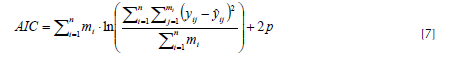
donde, n es el número de árboles; mi es el número de puntos de medición en el i-ésimo árbol; yij y ŷij es la variable dependiente observada y predicha en el j-ésimo punto de medición en el i-ésimo árbol, respectivamente; ȳi es la media de la variable dependiente en el i-ésimo árbol; y p es el número de parámetros del modelo. El criterio de Akaike fue utilizado como una medida para observar la calidad relativa de los modelos utilizados. Se realizó una evaluación de los residuales obtenidos en el ajuste de cada sistema de ecuaciones con el fin de detectar problemas de heterocedasticidad y evaluar la normalidad de los residuales.
La base de datos de validación (n = 28) se utilizó para calcular medidas de bondad de predicción (sesgo y error) ponderadas por los diámetros fustales. El sesgo se evaluó a través de la diferencia agregada ponderada,
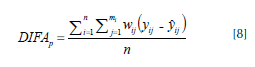
y el error se evaluó empleando la raíz del error medio cuadrático ponderado,
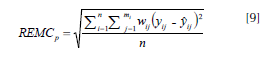
donde, el factor de ponderación
wij
es el cociente entre el diámetro en el j-ésimo punto de medición en el i-ésimo árbol y la suma total de las j-ésimas mediciones de diámetro del i-ésimo árbol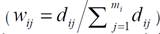 . Al utilizar esa expresión se da mayor peso a diámetros más grandes en el árbol (sección basal), donde efectivamente interesa ser más preciso en la estimación de diámetros y volúmenes.
. Al utilizar esa expresión se da mayor peso a diámetros más grandes en el árbol (sección basal), donde efectivamente interesa ser más preciso en la estimación de diámetros y volúmenes.
Adicionalmente, se realizó un análisis comparativo del comportamiento de las medidas de sesgo y error de los modelos en la predicción de diámetros fustales y volúmenes comerciales a diferentes alturas relativas (décimos de h/H). Este análisis permitió identificar los modelos con menores errores, principalmente, en la sección basal del árbol, donde habitualmente se acumula la mayor cantidad de volumen y de la cual se obtienen productos de mayor valor comercial (Pérez, 2004; Pompa et al., 2009; Özçelik et al., 2012; Özçelik y Göçeri, 2015).
RESULTADOS
Bondad de ajuste
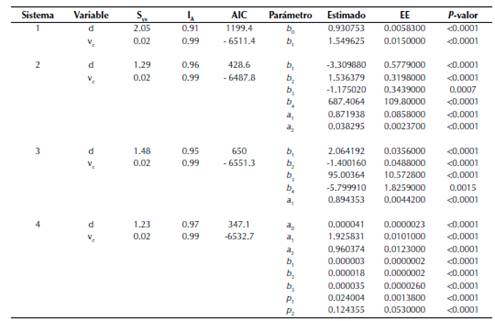
Los parámetros estimados y los estadísticos de bondad de ajuste de los sistemas de ecuaciones evaluados se presentan en la tabla 2. Todos los parámetros estimados de manera simultánea fueron altamente significativos (P < 0.01), lo cual indica que todas las variables independientes aportan significativamente a la predicción de las variables dependientes.
De acuerdo a los estadísticos de bondad de ajuste, no se aprecian diferencias notables entre los sistemas de ecuaciones evaluadas en cuanto a los modelos de volumen comercial. Sin embargo, estos presentan diferencias notorias al considerar los modelos de ahusamiento, principalmente entre el sistema 1 (con los estadísticos de bondad de ajuste más bajos) y los sistemas restantes. El sistema 3 presentó ligeramente mejores estadísticos de bondad de ajuste (menor AIC) en la predicción de volúmenes comerciales (tabla 2). Entre los sistemas evaluados, el sistema 4 presenta la mejor bondad de ajuste en el modelo de ahusamiento, con menores valores de Syx y AIC y mayor IA.
donde d es el diámetro fustal, vc es el volumen comercial y EE es el error estándar.
Tabla 2: Parámetros estimados y bondad de ajuste para los sistemas de ecuaciones de ahusamiento-volumen ajustados a perfiles fustales de G. arborea.
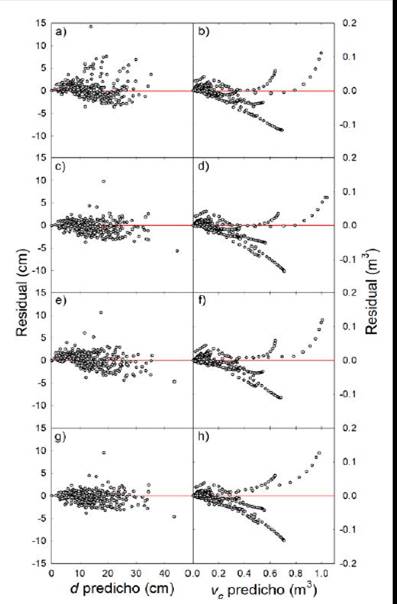
Para la predicción de diámetros fustales se encontró que los sistemas 2, 3 y 4 no presentan diferencias notables en la distribución de sus residuales, los cuales tienden a una distribución normal. El sistema 1 presenta residuales con distribución heterogénea en el rango de valores predichos (figura 1a). Para la predicción de volúmenes comerciales se observan patrones de comportamiento en los residuales similares entre los modelos evaluados (figura 1b, d, f y h). Entre los cuatro sistemas de ecuaciones evaluados sobresale el sistema 4, con residuales sin ninguna tendencia y distribuidos homogéneamente a lo largo de los valores predichos ( figura 1). Los residuales generados en la predicción de volúmenes comerciales tienden a aumentar a medida que el tamaño del árbol aumenta, este comportamiento es típico en los modelos de volumen total.
Figura 1: Residuales para los cuatro sistemas de ecuaciones evaluados en la predicción de diámetros fustales y volúmenes comerciales de árboles de G. arborea. Sistema 1 (a, b), sistema 2 (c, d), sistema 3 (e, f), y sistema 4 (g, h).
Bondad de predicción
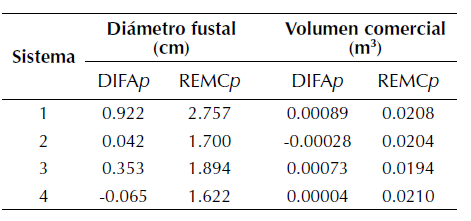
Los estadísticos usados en la validación de los sistemas de ecuaciones de volumen y ahusamiento no presentaron diferencias notorias entre los cuatro sistemas evaluados (tabla 3). El sistema 4 tiende a sobrestimar los diámetros fustales y subestimar ligeramente el volumen comercial. Los restantes sistemas tienden a subestimar las variables estudiadas; excepto el sistema 2, el cual tiende a la sobrestimación del volumen. El menor sesgo promedio lo presentaron los sistemas 2 (0.04 cm) y 4 (0.00004 m3) en la predicción de diámetros fustales y volúmenes comerciales, respectivamente. El sistema 4 presentó los menores errores promedio en la predicción de diámetros fustales (1.622 cm) y el sistema 3 los menores errores promedio en la predicción de volúmenes comerciales (0.0194 m3) (tabla 3).
Tabla 3: Bondad de predicción para la estimación de diámetros fustales y volúmenes comerciales para cuatro sistemas de ecuaciones de ahusamiento-volumen
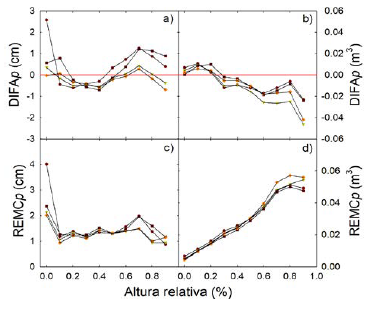
La figura 2 muestra el comportamiento del sesgo (a, b) y error (c, d) a lo largo del fuste (altura relativa h/H). Los sistemas evaluados tienden a subestimar los diámetros fustales en la base del árbol (hasta 20% de h/H), para luego sobrestimar los diámetros fustales hasta una altura relativa del 50-60%, desde ese punto el comportamiento cambia a la subestimación. Los sistemas 2 y 4 presentan un menor sesgo en la predicción de diámetros a lo largo del fuste del árbol. En cuanto a la predicción de volúmenes comerciales, los sistemas evaluados presentan un comportamiento similar hasta el 50% de la altura fustal, desde ese punto se destacan los sistemas 3 y 1. Todos los modelos evaluados subestiman el volumen comercial hasta aproximadamente 20% de h/H y desde ese punto tienden a la sobrestimación del volumen comercial. Estas variaciones en la tendencia (de subestimación a sobrestimación) podrían responder, principalmente, a cambios en la forma geométrica del árbol.
Figura 2: Sesgo (panel superior) y error promedio (panel inferior) en la predicción de diámetros (a, c) y volúmenes comerciales (b, d) para diferentes alturas relativas.
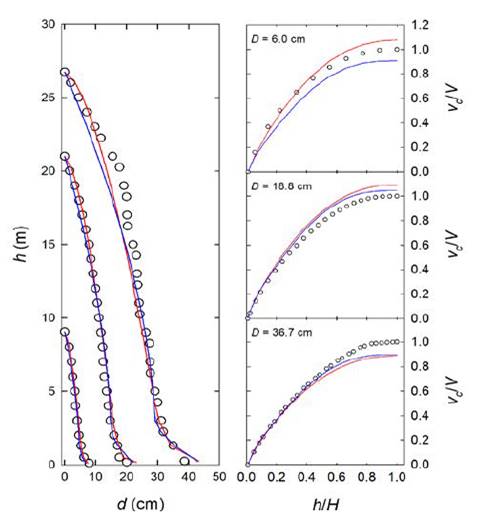
Los errores promedio en la predicción de diámetros fustales son más altos en la base y hacia el ápice del árbol, principalmente en los sistemas 1 y 3. Los sistemas 2 y 4 presentan menor REMCp en la predicción de diámetros a lo largo del fuste (figura 2c). En cuanto a la predicción de volúmenes comerciales, no se aprecian diferencias importantes entre los sistemas evaluados hasta aproximadamente 60% de la altura relativa, desde ese punto el sistema 4 presenta valores más altos de REMCp hasta el ápice del árbol (60-100% de altura relativa). El sistema 3 presenta ligeramente menores REMCp en la predicción de volúmenes comerciales a lo largo del fuste (figura 2d). De acuerdo a los estadísticos de bondad de ajuste y predicción empleados (tablas 2 y 3), los sistemas compatibles mejor evaluados fueron el 3 y 4. La figura 3 muestra una representación gráfica de los perfiles fustales predichos a partir de los sistemas 3 y 4 para tres árboles de diferente tamaño de la base de datos de validación (árbol de diámetro a 1.3 m mayor, menor y medio). Los dos sistemas son consistentes en sus estimaciones para árboles de diferente tamaño y representan de manera fiel a las formas geométricas típicas de árboles de G. arborea: neiloide en la base, paraboloide en la sección central y conoide en el ápice del árbol (figura 3). En la figura 3 se aprecian leves diferencias en los diámetros fustales predichos por los dos sistemas en la sección apical del árbol; así mismo, en los dos sistemas se aprecia una disminución en la precisión para árboles de mayor tamaño (principalmente en la base). En cuanto a la predicción de volúmenes comerciales, se observan diferencias entre los valores predichos por los dos sistemas en árboles de pequeñas dimensiones (D = 6 cm). El sistema 3 tiende a subestimar y el sistema 4 a sobrestimar el volumen comercial en árboles pequeños. Los dos sistemas predicen valores sobrestimados de volumen comercial en árboles medianos (D = 19 cm) y subestimados en árboles grandes (D = 37 cm; figura 3).
DISCUSIÓN
En el estudio se comparan cuatro sistemas compatibles de ahusamiento-volumen en cuanto a su capacidad predictiva de diámetros y volúmenes comerciales de árboles de G. arborea, en el Alto Magdalena, Colombia. Estos sistemas de ecuaciones compatibles son una herramienta importante para la planificación y el manejo de la especie creciendo en plantaciones, ya que disminuyen la incertidumbre al permitir cubicar y calcular los productos a extraer de un árbol (Diéguez et al., 2009). El ajuste simultáneo de las funciones de ahusamiento-volumen permitió obtener predicciones consistentes tanto de diámetros fustales como de volúmenes comerciales, ya que las ecuaciones comparten parámetros en sus expresiones (Tang et al., 2016; Hernández-Ramos et al., 2017).
Entre los cuatro sistemas evaluados, el sistema de ecuaciones propuesto por Demaerschalk (1972) presentó resultados inferiores en cuanto a bondad de ajuste y predicción de las variables examinadas. Otros estudios han mostrado que los modelos polinomiales simples presentan deficiencias para describir la sección basal de los árboles, especialmente en árboles que exhiben una alta conicidad (Heidarsson y Pukkala, 2011; Quirós, 2015). Similar a los resultados del presente estudio, Gaillard, Pece y Ríos (1997) encontraron que el modelo de Demaerschalk (1972) presentaba deficiencias para describir la base y el ápice de árboles de Eucalyptus tereticornis en Argentina. Igualmente, López et al. (2015) reportaron que los modelos polinomiales simples mostraron deficientes capacidades predictivas en Eucalyptus tereticornis creciendo en el norte de Colombia.
Varios estudios han demostrado que las ecuaciones segmentadas proporcionan estimaciones consistentes y precisas tanto para los diámetros a lo largo del fuste como para volúmenes comerciales (Tamarit et al., 2014; Pompa et al., 2009; Quiñonez et al., 2014; Özçelik y Göçeri, 2015; Tang et al., 2016). En el presente estudio, el sistema de ecuaciones segmentadas de Max y Burkhart (1976) tuvo un buen comportamiento en el ajuste y validación para la estimación de diámetros a diferentes alturas. El sistema 3, propuesto por Parresol et al. (1987) , presentó el menor error en la predicción de volúmenes comerciales y el sistema 4 propuesto por Fang et al. (2000) fue el más consistente en la predicción de diámetros fustales.
Escasos estudios han reportado el desarrollo de modelos de ahusamiento para G. arborea. Quirós (2015) ajustó un modelo polinómico simple a 223 perfiles fustales de G. arborea de 3 a 6 años de edad en Costa Rica. El autor reporta sesgos negativos hasta del 17.3% en la predicción de diámetros fustales, originados principalmente en la base del árbol. De manera similar, en el presente estudio la sección basal fue la que más sesgo (máximo 2.6 cm) y error (máximo 4.0 cm) promedio presentó en la predicción de diámetros fustales.
Alo et al. (2011) desarrollaron ecuaciones de ahusamiento para G. arborea en Nigeria usando un polinomio de orden dos. Los autores encontraron que el ahusamiento de G. arborea aumentaba directamente con el tamaño de los árboles (clase diamétrica), por lo que se requirió del ajuste de una ecuación de ahusamiento por clase diamétrica, obteniendo R2 adj entre 0.45-0.86. En la presente investigación, los sistemas evaluados tuvieron IA entre 0.91 a 0.97 y no se requirió del ajuste de ecuaciones por clase de tamaño, ya que los sistemas de ecuaciones seleccionados presentaron estimaciones consistentes para árboles de diferente diámetro (figura 3).
Figura 3: Perfiles fustales (panel de la izquierda) y volúmenes comerciales (panel de la derecha) observados (círculos) y predichos (líneas) a partir del ajuste del sistema 3 (azul) y 4 (rojo) para tres árboles de diferente tamaño de la base de datos de validación.
López et al. (2011) ajustaron modelos de ahusamiento a una muestra de árboles de G. arborea en Colombia. Los autores seleccionaron el modelo de exponente variable propuesto por Kozak (1988) para describir el perfil fustal de la especie. La debilidad de este modelo es que requiere utilizar métodos de integración numérica para el cálculo de volúmenes totales y comerciales (López et al., 2015). En contraste, los sistemas compatibles desarrollados en el presente estudio presentan la ventaja de no requerir métodos iterativos para la determinación del volumen total y/o comercial.
De acuerdo a los estadísticos de bondad de ajuste y predicción y al análisis gráfico, no se encontraron diferencias notorias entre el sistema 3 y 4 para la estimación de diámetros fustales y volúmenes comerciales de G. arborea. Sin embargo, debido a que el uso principal proyectado del sistema compatible de ahusamiento-volumen desarrollado será optimizar la utilización del fuste, previo a su industrialización y dada la importancia de la predicción de diámetros fustales para la clasificación de productos, se recomienda el sistema 4 por los mejores resultados obtenidos en la predicción de diámetros fustales. A pesar de ello, el sistema 3 podría servir como alternativa para la predicción principalmente de volúmenes comerciales en sistemas de procesamiento de inventarios forestales, debido a su mayor simplicidad.
El sistema de ecuaciones compatibles de Fang et al. (2000) ha sido seleccionado para otras latifoliadas (Özçelik y Göçeri, 2015) y coníferas (Quiñonez et al., 2014). El sistema seleccionado es un sistema flexible que proporciona estimaciones muy precisas de diámetros fustales y aceptables de volumen comercial, principalmente en la sección basal del árbol, lo cual es importante en términos prácticos, debido a que es la zona de mayor importancia comercial del árbol.
CONCLUSIONES
El ajuste simultáneo de las funciones de ahusamiento-volumen permitió tener predicciones consistentes tanto de diámetros fustales como de volúmenes comerciales, ya que las ecuaciones comparten parámetros en sus expresiones, asegurando su compatibilidad. En el presente estudio, los sistemas basados en ecuaciones segmentadas (sistemas 2, 3 y 4) mostraron mejores resultados en términos de bondad de ajuste y predicción comparados con el sistema de ecuaciones polinomiales simples (sistema 1).
El sistema de ecuaciones propuesto por Fang et al. (2000) presentó mejor comportamiento en la predicción de diámetros fustales y el sistema de Parresol et al. (1987) de volúmenes comerciales (acumulados a lo largo del fuste). Adicionalmente, a partir de un análisis gráfico se demostró que no existen diferencias notorias en las predicciones de diámetros fustales y volúmenes comerciales en árboles de diferente tamaño entre los dos sistemas.
De acuerdo a lo anterior, y debido a la importancia de la predicción de diámetros fustales para la clasificación de productos, se recomienda el sistema 4 debido a los mejores resultados obtenidos en la predicción de diámetros fustales. Sin embargo, considerando que el sistema 3 presenta mayor simplicidad, este podría servir como alternativa para la predicción principalmente de volúmenes comerciales de árboles de G. arborea.
El sistema compatible de ahusamiento-volumen desarrollado puede ser incorporado en sistemas de simulación de crecimiento y rendimiento para cuantificar volúmenes totales y en sistemas de simulación de trozado en los que se requiera conocer volúmenes acumulados hasta diferentes índices de utilización de productos demandados por la industria.
AGRADECIMIENTOS
Los autores agradecen a la Oficina de Investigaciones y Desarrollo Científico de la Universidad del Tolima por el apoyo financiero otorgado para desarrollar la presente investigación a través del proyecto n.° 150220516.
CONFLICTO DE INTERESES
Los autores declaran no tener conflicto de intereses.
CONTRIBUCIÓN POR AUTOR
Los autores son los únicos responsables de la obra en todos los aspectos que condujeron a la elaboración de su publicación.
REFERENCIAS BIBLIOGRÁFICAS
Licencia
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).