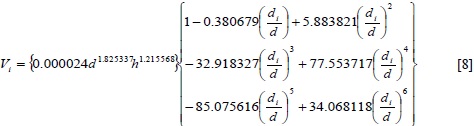DOI:
https://doi.org/10.14483/udistrital.jour.colomb.for.2014.2.a01Publicado:
01-07-2014Número:
Vol. 17 Núm. 2 (2014): Julio-DiciembreSección:
Artículos de investigación científica y tecnológicaPredicción de volúmenes comerciales de Eucalyptus grandis a través de modelos de volumen total y de razón
Predicting merchantable volumes of Eucalyptus grandis through total volume and volume-ratio models
Palabras clave:
forest biometrics, production models, forest management (en).Palabras clave:
biometría forestal, modelos de producción, manejo forestal (es).Descargas
Referencias
Akinnifesi, F. (1995). Linear equations for estimating the merchantable wood volume of Gmelina arborea in South-West Nigeria. Journal of Tropical Forest Science, 7 (3), 391-397.
Alegría, C. (2011). Modelling merchantable volumes for uneven aged maritime pine (Pinus pinaster Aiton) stands established by natural regeneration in the central Portugal. Annals of Forest Research, 54 (2), 197-214.
Álvarez, J.G., Barrio, M., Castedo-Dorado, F., Diéguez-Aranda, U., & Ruiz-González A.D. (2005). Modelos para la gestión forestal: una revisión de las metodologías de construcción de modelos de masa. 5° Congreso Forestal Nacional, Portugal. 13 p.
Barrio, M., González, J., & Díaz, J. (2004). Elaboración de una tarifa con clasificación de productos para Quercus robur L. en Galicia basada en un modelo de volumen porcentual. Investigación Agraria: Sistemas y Recursos Forestales, 13 (3), 506-517.
Barrio, M., Sixto, H., Cañellas, I., & González, F. (2007a). Sistema de cubicación con clasificación de productos para plantaciones de Populus x euramericana (Dode) Guinier cv. ‘I-214’ en la meseta norte y centro de España. Investigación Agraria: Sistemas y Recursos Forestales, 16 (1), 65-75.
Barrio, M., Diéguez-Aranda, U., Castedo-Dorado, F., álvarez, J., & Gadow, K.V. (2007b). Merchantable volume system for pedunculate oak in northwestern Spain. Annals of Forest Science, 64, 511-520.
Beal, D.J. (2007). Information Criteria Methods in SAS® for multiple linear regression models. 15th Annual SouthEast SAS Users Group (SESUG) Proceedings, South Carolina, Paper SA05. 10 p.
Burkhart, H. (1977). Cubic-foot volume of loblolly pine to any merchantable top limit. Southern Journal of Applied Forestry, 1 (2), 7-9.
Cano, N. (2002). Efecto de la distancia de siembra sobre el crecimiento en diámetro y altura a los dos años de edad en Eucalyptus grandis. CINOC. Boletín Técnico No 1, 15-19.
Cao, Q., Burkhart, H., & Max, T. (1980). Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science, 26 (1), 71-80.
Chauchard, L., & Sbrancia, R. (2005). Funciones de razón para la estimación de los volúmenes maderables de Pino radiata en el País Vasco. Investigación Agraria: Sistemas y Recursos Forestales, 14 (2), 185-194.
Da Cunha, T., & Guimarães, C. (2009). Modelo de regresión para estimar el volumen total con corteza de árboles de Pinus taeda L. en el sur de Brasil. Kurú: Revista Forestal, 6 (16), 1-15.
Davel, M, Trincado, G. (2000). Evaluación de modelos fustales para Pseudotsuga menziesii en la Patagonia Andina Argentina. Investigación Agraria: Sistemas y Recursos Forestales, 9 (1), 103-116.
Gilabert, H., & Paci, C. (2010). An assessment of volume-ratio functions for Eucalyptus globulus and E. nitens in Chile. Ciencia e Investigación Agraria, 37 (1), 5-15.
Guimarães, D., & Leite, H. (1996). Influência do número de árvores na determinação de equação volumétrica para Eucalyptus grandis. Scientia Forestalis, 50, 37-42.
Harvey, A.C. (1976). Estimating regression models with multiplicative heteroscedasticity, Econometrica, 44, 461-465.
López, A.M., Barrios, A., Trincado, G. & Nieto, V.M. (2011). Monitoreo y modelamiento del crecimiento para el manejo de plantaciones forestales comerciales. Bogotá: Corporación Nacional de Investigación y Fomento Forestal-CONIF - Ministerio de Agricultura y Desarrollo Rural-MADR. 90 p.
López, A.M. (2007). Modelos de crecimiento y rendimiento para Pinus caribaea, Eucalyptus pellita y Eucalyptus grandis y determinación de su edad óptima de rotación en plantaciones forestales en Colombia. (Tesis Magister)Valdivia: Facultad de Ciencias Forestales, Universidad Austral de Chile. 87 p.
Moret, A., Jerez, M., & Mora, A. (1998). Determinación de ecuaciones de volumen para plantaciones de teca (Tectona grandis L.) en la unidad experimental de la reserva forestal Caparo, Estado Barinas - Venezuela. Revista Forestal Venezolana, 42 (1), 41-50.
Ospina, C., Hernández, R., Rodas, C., Urrego, J., Godoy, J., Aristizabal, F., Osorio, O., &Â Riaño, N. (2006). Guías silviculturales para el manejo de especies forestales con miras a la producción de madera en la zona andina colombiana: El Eucalipto (Eucalyptus grandis W.Hill ex Maiden). Bogotá:Cenicafe. 52 p.
Parresol, B.R., Hotvedt, J.E., & Cao, Q.V. (1987). A volume and taper prediction system for bald cypress. Canadian Journal of Forest Research, 17, 250-259.
Prodan, M., Peters, R., Cox, F., & Real, P. (1997). Mensura Forestal. San José: IICA-GTZ. 561 p.
Proexport. (2009). Sector Forestal: Invierta en Colombia. Bogotá, Colombia. Proexport, 1, 1, 26 p.
Quevedo, A., Jerez, M., Moret, A., & Noguera, O. (2010). Ecuaciones de volumen y calidad de forma para Tabebuia rosea (Bertol.) en plantaciones en líneas. Barinas, Venezuela. Revista Forestal Venezolana, 54 (2), 195-205.
Riaño, H., Ospina, P., Gómez, L., López, J., Urrego, C., Osorio, L., Obando, B., & Tangarife, G. (2004). Determinación de la capacidad de captura de carbono en ocho especies forestales. Informe final del proyecto “Convenio especial para la investigación No CEN 269 del 2002 entre CONIF, FEDERACAFé y CENICAFé. Chinchiná: CENICAFé. 78 p.
Rojo, A., Perales, X., Sánchez-Rodríguez, F., Álvarez-González, J.G., & von Gadow, K. (2005). Stem taper functions for maritime pine (Pinus pinaster Ait.) in Galicia (Northwestern Spain). European Journal of Forest Research, 124, 177-186.
SAS Institute Inc. (1999). SAS User’s Guide: SAS STAT Version 8. SAS Institute Inc. Cary. NC.
Schumacher, F., & Hall, F. (1933). Logarithmic expression of timber-tree volume. Journal of Agricultural Research, 47 (9), 719-734.
Spurr, S.H. (1952). Forest inventory. New York: The Ronald Press Co. 476 p.
Trincado, G., Â Von Gadow, K., & Sandoval, V. (1997). Estimación de volumen comercial en latifoliadas. Bosque, 18 (1), 39-44.
Van Deusen, P., Sullivan, A., & Matney, T. (1981). A prediction system for cubic foot volume of loblolly pine applicable through much of its range. Southern Journal of Applied Forestry, 5 (4), 186-189.
Verbeek, M. (2004). A guide to modern econometrics, 2 ed. West Sussex: John Wiley & Sons. 429 p.
Zimmerman, D., & Núñez-Antón, V. (2001). Parametric modelling of growth curve data: An overview. Test, 10 (1), 1-73.
Zhang, J., & Chen, D. (2001). Interpolation calculation made EZ. 14th Annual Conference Proceedings, NorthEast SAS Users Group NESUG, Baltimore, MD. 4 p.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
 |
Barrios, A. López A. M. Nieto V. (2014). Predicción de volúmenes comerciales de Eucalyptus grandis a través de modelos de volumen total y de razón. Colombia Forestal, 17(2), 137-149. |
PREDICCIÓN DE VOLÚMENES COMERCIALES DE EUCALYPTUS GRANDIS A TRAVÉS DE MODELOS DE VOLUMEN TOTAL Y DE RAZÓN
Predicting merchantable volumes of Eucalyptus grandis through total volume and volume-ratio models
Alonso Barrios1, Ana M. López2, Víctor Nieto3
1 Universidad del Tolima, Ibagué, Colombia. abarriost@ut.edu.co
2 Universidad del Tolima, Ibagué, Colombia. amlopeza@ut.edu.co Autor para correspondencia.
3 Corporación Nacional de Investigación y Fomento Forestal (CONIF), Bogotá, Colombia. victornieto@conif.org.co
Recepción: 22 de abril de 2014 / Aprobación: 3 de julio de 2014
RESUMEN
Ocho ecuaciones de volumen total y cuatro modelos de volumen de razón fueron evaluados con el objetivo de seleccionar el mejor modelo de volumen total y de razón de volumen, a fin de ser utilizados en un sistema para la predicción de volúmenes comerciales en plantaciones de Eucalyptus grandis. Los datos usados en el estudio corresponden a 101 árboles colectados en rodales a la edad de cosecha, ubicados en el municipio de Salento, Quindío. Técnicas de regresión ponderada fue utilizada para evitar problemas de heterocedasticidad en el ajuste de modelos de volumen total. Una estructura autorregresiva del error se empleó para disminuir la autocorrelación, propia de los datos longitudinales utilizados en el ajuste de los modelos de volumen de razón. A partir de la evaluación de la bondad de ajuste y predicción fueron seleccionados los modelos de: Schumacher & Hall (1993), como modelo de volumen total, y Cao etal. (1980) como modelo de volumen de razón. El sesgo y el error promedio en la predicción de volúmenes comerciales hasta los índices de utilización 0, 5 y 10 cm estuvieron siempre por debajo de 4.4% y 11.5%, respectivamente. Finalmente, se demuestra la funcionalidad del sistema de cuantificación de volúmenes comerciales en la construcción de tablas de rodal y existencias.
Palabras clave: biometría forestal, modelos de producción, manejo forestal.
ABSTRACT
Eight total volume and four volume-ratio models were evaluated for use in a system for predicting marketable volumes in Eucalyptusgrandis plantations. Data were collected from 101 trees in stands at harvest age, located in Salento, Quindio. Weighted regression was used to avoid problems of heteroscedasticity in the fit of total volume models. An autoregressive error structure was used to reduce autocorrelation of longitudinal data used in the fit of the volume-ratio models. After evaluation of goodness of fit and prediction, the models of Schumacher & Hall (1993) as total volume model and Cao etal. (1980) as volume-ratio model were selected. The bias and average error in the prediction of marketable volumes to variable-top diameter limits of 0, 5 and 10 cm were always below 4.4% and 11.5%, respectively. The functionality of the system to quantify marketable volumes during the construction of stand and stocks tables was demonstrated.
Key words: forest biometrics, production models, forest management.
INTRODUCCIÓN
Con más de 17 000 hectáreas plantadas, Eucalyptus grandis (W. Hill ex Maiden) se ha convertido en una de las principales especies empleadas en los proyectos de reforestación comercial en la región central en Colombia, alcanzando rendimientos de 25 a 40 m3 ha-1 año-1, en turnos de 8 años (Proexport, 2009); dichas plantaciones constituyen la fuente de materia prima para la industria papelera del país, principalmente en la región andina del suroccidente colombiano. Sin embargo, a pesar de la importancia de la especie, son escasos los estudios reportados en la literatura. En este sentido, Marín & Uribe (1996), citados por Ospina et al. (2006), elaboraron tablas de peso fresco y volumen para árboles de E. grandis sembrados en cercos vivos. Riaño et al., (2004) generaron ecuaciones de biomasa y de carbono, así como ecuaciones de volumen total, con y sin corteza, a través de la cubicación de árboles en los departamentos de Cauca y Valle del Cauca, en el marco del proyecto “Cuantificación del efecto de sumidero de Carbono por especies forestales nativas e introducidas” realizado por CONIF y CENICAFé. López (2007) y López et al. (2011) ajustaron modelos de crecimiento y rendimiento para la especie, a partir de datos colectados en mediciones de parcelas permanentes en los departamentos de Quindío y Risaralda. Cano (2002) evaluó el efecto de la densidad de siembra sobre el crecimiento en diámetro y altura a los dos años de edad en el municipio de Pensilvania, Caldas.
A fin de responder efectivamente al manejo sostenible de este recurso forestal, se debe trabajar en la construcción de herramientas que permitan realizar estimaciones confiables de volúmenes comerciales y productos posibles de obtener, con el propósito de evaluar sus existencias en pie y flujos de materia prima. Para lograr estimaciones precisas, los planificadores forestales deben disponer de herramientas que permitan calcular de manera eficiente el volumen de las plantaciones, a partir de variables de fácil medición en terreno (Barrio et al., 2004). Uno de los procedimientos más sencillos es la estimación indirecta del volumen de árboles individuales (con o sin corteza) a partir de variables predictoras como el diámetro (d), altura total del árbol (h) y alguna expresión de la forma del fuste (ff), v = f(d, h, ff) (Schumacher & Hall, 1933; Spurr, 1952; Burkhart, 1977; Prodan et al., 1997). Sin embargo, estos modelos no brindan información de volúmenes comerciales de los diferentes productos a obtener en la cosecha.
Burkhart (1977) desarrolló un modelo denominado modelo de volumen de razón o de volumen porcentual, el cual permite estimar el volumen maderable según destinos industriales. Mediante el empleo de un factor de razón (R) que permite estimar el volumen comercial de un individuo como porcentaje del volumen total de este (R = Vi/V), donde (Vi) es el volumen en metros cúbicos hasta un índice de utilización o diámetro en punta delgada (i), mientras que (V)es el volumen total del fuste (Chauchard & Sbrancia, 2005; Barrio et al., 2007a; Gilabert & Paci, 2010). A partir de esta formulación, otros autores han orientado sus estudios a aumentar la consistencia a las estimaciones y mejorar la formulación matemática (Van Deusen, 1981; Parresol et al., 1987; Cao et al., 1980). Los sistemas de ecuaciones integradas por modelos de volumen total y de razón son una buena alternativa en lo que se refiere a la estimación de volúmenes hasta un determinado índice de utilización, ya que no requieren métodos numéricos complejos de integración para calcular el volumen comercial de productos (Trincado et al., 1997).
En el presente estudio se desarrolla una herramienta para la cuantificación de volúmenes comerciales de E. grandis conformada por un modelo de volumen total y un modelo de volumen de razón. Los objetivos específicos fueron: a) realizar una evaluación de la bondad de ajuste y predicción de modelos de volumen total y de razón, b) realizar una comparación entre tipos de modelos con base en indicadores de bondad de ajuste y predicción y c) seleccionar el mejor modelo de volumen total y de volumen de razón para ser utilizados en un sistema para la predicción de volúmenes comerciales de E. grandis en labores de inventario.
MATERIALES Y MÉTODOS
DATOS
Se utilizó una base de datos integrada por 101 árboles muestra de E. grandis cubicados en dos rodales de 8 años de edad ubicados en el suroccidente colombiano. Se seleccionaron árboles sanos, rectos, sin daños ni defectos, cubriendo la mayor cantidad de clases diamétricas y de altura posible. Los árboles seleccionados fueron apeados y desramados, posteriormente, se procedió a medir y a marcar a lo largo del fuste secciones de un metro (1 m) de longitud a partir de la base del árbol. Las longitudes de cada sección fueron medidas utilizando una cinta métrica, marcándose el punto de cada medición. Una vez completada la medición y marcación de secciones sobre el fuste se procedió a la medición de diámetros con corteza utilizando una forcípula. A continuación, se retiró la corteza del árbol en los puntos anteriormente marcados y se tomaron diámetros sin corteza. Cada sección fue cubicada usando la fórmula de Smalian, excepto la última sección en la cual se utilizó la fórmula de volumen de un cono.
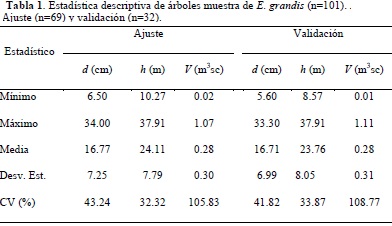
La base de datos fue dividida en dos: una base de ajuste para la estimación de los parámetros y una base para realizar la validación de los modelos. La selección de árboles consideró la formación de cuatro clases diamétricas conformadas por los percentiles 0-25%, 25-50%, 50-75% y 75-100%. Los árboles para la base de ajuste, tanto como los de validación, fueron seleccionados aleatoriamente dentro de cada uno de los grupos anteriores mencionados. Aproximadamente un 70% de los árboles fueron seleccionados aleatoriamente para el ajuste de los modelos y el restante 30% para su validación. Los estadísticos descriptivos de la muestra empleada en el ajuste y validación de los modelos se presentan en la tabla 1.
MODELOS DE VOLUMEN TOTAL
En el estudio se seleccionaron para su evaluación ocho modelos de volumen total (M1 a M8) (Tabla 2), los cuales han sido ampliamente utilizados en otros estudios (Gilabert & Paci, 2010; Quevedo et al., 2010; Alegría, 2011). La principal diferencia entre los modelos evaluados es el número de parámetros a ser estimados. La estimación de parámetros de los modelos de volumen total fue realizada utilizando métodos de regresión lineal (M1, M4, M5, M7 y M8) y no lineal (M2, M3, M6). Durante el proceso de estimación de parámetros se utilizaron los procedimientos REG y MODEL contenidos en Statistical Analysis System - SAS. El algoritmo de minimización de la suma de cuadrados de Marquardt (SAS Institute, 1999) fue empleado para la estimación de parámetros de modelos no lineales. Con el propósito de evitar problemas de heterocedasticidad en el ajuste de los modelos de volumen total se empleó regresión ponderada, asumiendo que la varianza del error puede ser modelada como una función potencial de la variable combinada ![]() . Los valores de m fueron estimados a través de regresión lineal, utilizando el método propuesto por Harvey (1976) descrito por Barrio et al. (2007b).
. Los valores de m fueron estimados a través de regresión lineal, utilizando el método propuesto por Harvey (1976) descrito por Barrio et al. (2007b).
MODELOS DE VOLUMEN DE RAZÓN
Cuatro modelos de volumen de razón (M9 a M12) fueron seleccionados para su evaluación (Tabla 3), los cuales han sido empleados en otros estudios (Barrio et al., 2007a; Barrio et al., 2007b; Gilabert & Paci, 2010; Quevedo et al., 2010; Alegría, 2011).Al considerar la estructura longitudinal presente en los datos, usada en el ajuste de los modelos de volumen de razón, no se descarta la presencia de autocorrelación, ya que se dispone de varias mediciones a lo largo del fuste de cada árbol; por lo tanto, se utilizó un modelo autorregresivo en tiempo continuo (CAR) a fin de modelar la estructura del error (Zimmerman & Núñez-Antón, 2001). Los modelos de volumen de razón fueron ajustados considerando una estructura del error de un modelo autorregresivo CAR(x) de la siguiente forma:
donde Yij es el vector de la variable dependiente, Xij es la matriz de las variables independientes, β es el vector de los parámetros a estimar, eij es el j-ésimo residuo del árbol i, Ik=1 para j > k y es 0 para j ≤ k, ρk es el parámetro autorregresivo de orden k a estimar, hij-hij-k es la distancia que separa la altura de medición j-ésima de la altura de medición j-ésima-k en cada árbol (hij > hij-k) y εij es el error aleatorio (álvarez et al., 2005). El orden x del modelo autorregresivo se determinó al evaluar el estadístico Durbin-Watson (D-W); así, valores cercanos a 2 indican ausencia de autocorrelación (Verbeek, 2004).
CRITERIOS DE EVALUACIÓN
Para la evaluación y comparación de modelos se emplearon medidas de bondad de ajuste y predicción. Como medidas de bondad de ajuste se utilizó el error estándar de estimación
el coeficiente de determinación ajustado
y el criterio de información de Akaike definido por Beal (2007) como
donde yi es la variable dependiente observada, es la variable dependiente estimada, es la media de la variable dependiente, n es el número total de observaciones, y p es el número de parámetros del modelo, y k = p + 1.
Utilizando la base de datos de validación se generaron residuales con los que se calcularon medidas de bondad de predicción (sesgo y error) (Gilabert & Paci, 2010; Davel & Trincado, 2000). Como medida de sesgo se utilizó la diferencia agregada en porcentaje
y como medida de error se empleó la raíz del error medio cuadrático en porcentaje
donde yi es el valor observado (i=1, 2,...,n), ý es el valor estimado (i=1, 2,..., n), n es el número de observaciones.
Los estadísticos de bondad de ajuste y predicción fueron calculados para los dos tipos de modelos (volumen total y de razón). Un índice fue utilizado para calificar a cada uno de los modelos (Alegría, 2011). El índice tiene un intervalo de 0 a 1, donde el modelo con el mejor valor en cada estadístico tiene un valor de índice de 1, y el modelo con el peor valor tiene un índice de 0. La formulación necesaria para calcular este índice es
donde x es el valor del estadístico de evaluación. Para el caso del el índice se computó como El índice fue calculado de manera separada para los estadísticos en la fase de ajuste y validación y posteriormente se obtuvo un índice promedio para el modelo. El modelo con el índice promedio más cercano a 1 es el mejor evaluado y por consiguiente el modelo a seleccionar. Por último, se elaboró un análisis gráfico de los residuales originados por cada modelo para detectar tendencias anómalas y asegurar la normalidad de los residuos.
DETERMINACIÓN DE VOLÚMENES COMERCIALES
Con el propósito de evaluar la bondad de predicción del sistema para la cuantificación de volúmenes comerciales integrado por el mejor modelo de volumen total y de razón, se determinaron volúmenes comerciales hasta los índices de utilización 0,5 y 10 cm, para ello se consideraron los árboles de la base de validación que contenían todos los anteriores índices de utilización. Como medidas de bondad de predicción se utilizaron los estadísticos DIFA y REMC en porcentaje. Para los casos en los que el diámetro índice de utilización se encontraba entre dos secciones, el volumen comercial, hasta ese índice de utilización, fue calculado a través de interpolación lineal (Zhang & Chen, 2001).
RESULTADOS
MODELOS DE VOLUMEN TOTAL
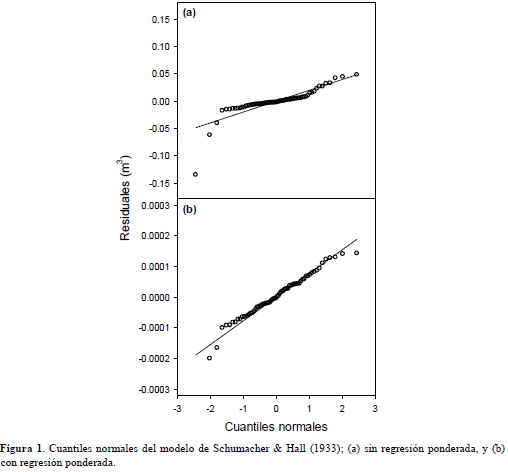
Los modelos de volumen total (M1 a M8) fueron ajustados con regresión ponderada para evitar problemas de heterogeneidad de varianzas. Los exponentes m en el factor de ponderación de las ecuaciones de volumen total variaron entre 0.73 y 1.60. El uso de regresión ponderada permitió obtener residuos más homogéneos (Figura 1), estimaciones de los parámetros de mínima varianza y unos intervalos de predicción más realistas. Los modelos M3 y M5 fueron los únicos que presentaron significancia en todos sus parámetros (p < 0.05), por lo que solo estos fueron evaluados en cuanto a su capacidad predictiva.
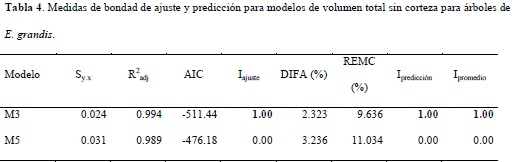
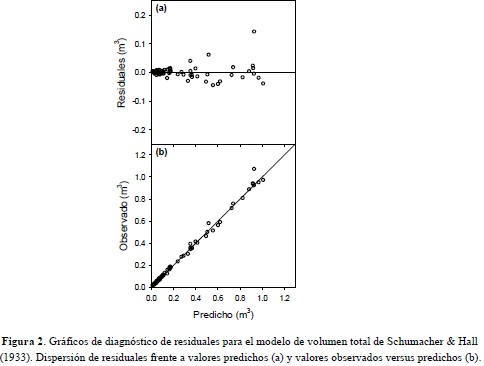
Los modelos de volumen total M3 y M5 presentaron diferencias apreciables en cuanto a los estadísticos de ajuste y validación (Tabla 4). Se aprecia que el modelo M3 presentó mejores características, con menor sesgo y error en las predicciones. El modelo M3 obtuvo la mejor posición (Ipromedio = 1) en todos los estadísticos evaluados, por lo tanto fue seleccionado como modelo de volumen total sin corteza para E. grandis. Los residuales generados por el modelo presentan una distribución aleatoria, homogénea en todo el espectro de volúmenes observados, no se aprecian tendencias que hagan suponer el incumplimiento de las hipótesis del análisis de regresión (Figura 2a). Los valores predichos, frente a los valores observados (Figura 2b), no demuestran problemas de sesgo (y=1.0027x R2=0.99).
MODELOS DE VOLUMEN DE RAZÓN
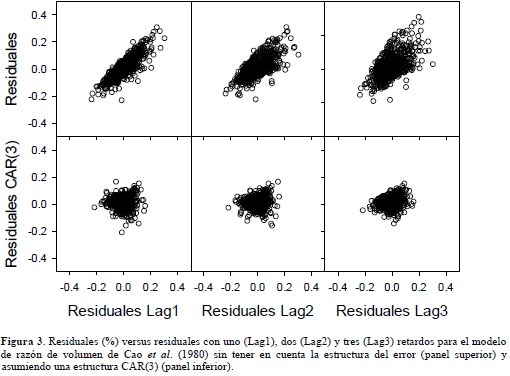
En una fase inicial los modelos de volumen de razón fueron ajustados sin expandir el término del error, con el propósito de observar tendencias de los residuos frente a sus tres primeros retardos lag1, lag2 y lag3 (Figura 3, panel superior). El valor del estadístico D-W alcanzó valores entre 0.40 y 0.42, lo cual demostró la existencia de una fuerte autocorrelación de los datos empleados en el estudio. Se decidió emplear una estructura del error autorregresiva de orden tres CAR(3), la cual eliminó la autocorrelación de los residuales de todos los modelos evaluados (Figura 3, panel inferior) y con la cual se obtuvieron valores de estadístico D-W entre 1.85 y 1.88, valores más cercanos a 2. Todos los modelos de razón de volumen (M9 a M12) presentaron parámetros significativamente diferentes de cero (p < 0.05).
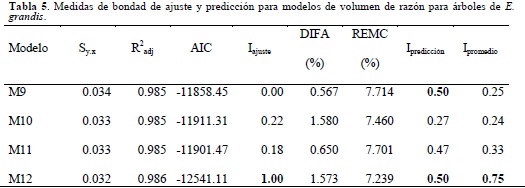
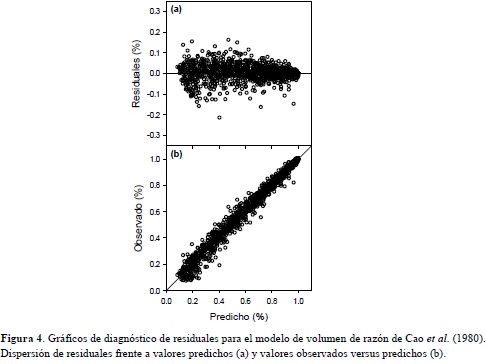
Los modelos de volumen de razón no presentaron mayores diferencias en los estadísticos de evaluación (Tabla 5). En cuanto a los estadísticos de ajuste fue el criterio Akaike el que presentó mayores diferencias, 6% entre el mejor y el peor modelo. Los estadísticos de bondad de predicción no mostraron diferencias evidentes, sin embargo, la DIFA de los modelos M9 y M11 fue considerablemente más baja. El Ipromedio indica que el modelo M12 presentó constantemente los mejores indicadores de ajuste y validación, por lo cual es seleccionado como modelo de razón de volumen para E. grandis. Los residuales generados por el modelo presentaron una estructura homogénea, sin tendencias anómalas (Figura 4a). La figura 4b presenta los valores predichos versus los valores observados, donde se confirma que el modelo no presenta sesgo en sus predicciones (y=1.003x R2=0.99).
EVALUACIÓN EN LA DETERMINACIÓN DE VOLÚMENES COMERCIALES
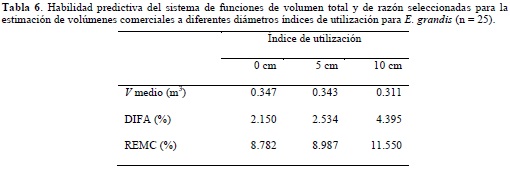
Una evaluación del sistema de ecuaciones en la cuantificación de volúmenes comerciales de los árboles de la base de validación se presenta en la tabla 6. El sistema fue usado para predecir los volúmenes acumulados hasta los índices de utilización 0.5 y 10 cm, considerando solamente aquellos árboles que contenían todos los índices de utilización (25 árboles). Los valores de sesgo y error muestran una tendencia a aumentar al tiempo que aumenta el índice de utilización. Es decir, el sistema disminuye su precisión al acercarse a la base del árbol. Sin embargo, los errores que se producen al predecirse volúmenes para un índice de utilización de 10 cm están dentro de los márgenes de error previsibles para modelos de este tipo y en todo caso no excedieron 11.55%.
APLICACIÓN EN LA CONSTRUCCIÓN DE TABLAS DE RODAL Y EXISTENCIAS
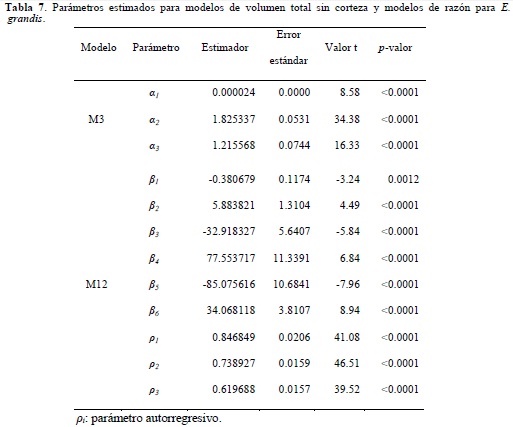
A modo ilustrativo se presenta una aplicación práctica en la construcción de tablas de rodal y existencias en labores de inventario de plantaciones de E. grandis. En una primera instancia se reestimaron los parámetros para los modelos seleccionados (M3 y M12) a partir de la unión de las bases de datos de ajuste y validación (Tabla 7). Todos los parámetros mantuvieron sus signos y fueron altamente significativos (p < 0.01), con valores de R2 ajustado de 0.993 y 0.986 y Sy.x de 0.0248 m3 y 0.0322% para el modelo de volumen total y de razón, respectivamente. Cabe resaltar que desde el punto de vista práctico, los parámetros de autocorrelación se pueden ignorar, a no ser que se esté trabajando con varias mediciones del diámetro a diferentes alturas para el mismo individuo (Barrio et al., 2007a).
Teniendo en cuenta que el modelo ajustado permite encontrar la razón de reducción entre el volumen total y el volumen correspondiente a un diámetro límite de utilización di, la expresión matemática que permite estimar el volumen a diferentes diámetros fustales es:
donde Vi es el volumen (m3) de producto a un diámetro límite de utilización definido, di, d es el diámetro a la altura del pecho (cm) y h es la altura total del árbol (m).
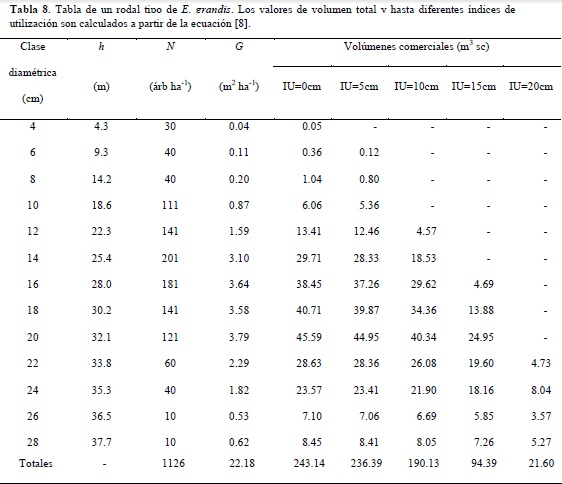
Utilizando una tabla de rodal proveniente de un rodal tipo de E. grandis se ilustra la aplicación de la ecuación [8] en la cuantificación de volúmenes comerciales (Tabla 8). La estimación del volumen total (IU = 0 cm) y a diferentes diámetros de utilización para cada marca de clase de la distribución diamétrica (d) y su respectiva altura total (h) es obtenida aplicando la ecuación [8] reemplazando di por cada uno de los límites de utilización (0, 5, 10, 15 y 20 cm) y multiplicando por el número de árboles de la clase (Tabla 8).
DISCUSIÓN
Se presenta una metodología fácilmente aplicable para el desarrollo de sistemas de cuantificación de volúmenes comerciales de plantaciones forestales. Los modelos desarrollados representan una importante herramienta que puede ser usada para la cuantificación de volúmenes de productos pulpables principalmente.
El empleo de regresión ponderada en el ajuste de modelos de volumen total presenta una mejora en la estimación de parámetros y una notable disminución de la heterogeneidad de varianzas producto del uso en el ajuste de datos de cubicación de árboles de diferentes tamaños (Barrio et al., 2004). Sin embargo, en la mayoría de los casos se obtuvieron errores estándar elevados asociados a los parámetros que acompañan los términos de las funciones evaluadas, presentándose diferencias no significativas; lo anterior puede obedecer a que la inclusión de funciones polinómicas complejas con productos cruzados entre variables no tienen aporte significativo en la estimación del volumen total.
El número de árboles para el desarrollo de ecuaciones de volumen ha sido la principal debilidad de los modelos desarrollados, no obstante mostraron ser bastante consistente en sus predicciones. Dichos resultados coinciden con los de Guimaraes & Leite (1996), quienes demostraron que un número de 150 árboles resultó ser suficiente para lograr predicciones similares a las de un modelo desarrollado con 500 árboles de E. grandis en Brasil. Las predicciones de volumen total sin corteza realizadas con el modelo ajustado representan una disminución del 20.4 % y 8.6 % en REMC frente a los modelos desarrollados por Marín & Uribe (1996) citado por Ospina et al. (2006) y Riaño et al. (2004), respectivamente.
Los modelos de razón de volumen son una buena alternativa para la cuantificación de volúmenes comerciales hasta diferentes índices de utilización (Trincado et al., 1997). Comparaciones entre volúmenes estimados con funciones de razón frente a los estimados con funciones de ahusamiento han demostrado que las primeras son bastantes consistentes y para algunas especies de Eucalyptus han mostrado ser más precisas (Gilabert & Paci, 2010). Considerar una estructura continua autorregresiva del error CAR(3) en la estimación de parámetros de los modelos de razón de volumen disminuye la autocorrelación espacial medida a través del estadístico D-W, el cual alcanzó valores en promedio de 1.86 frente a 0.40 sin emplear la estructura. Este resultado está de acuerdo con lo encontrado en otros estudios donde se han evaluado las bondades de las estructuras autorregresivas del error (Barrio et al., 2004; Rojo et al., 2005; Barrio et al., 2007a; 2007b).
La combinación de la función de volumen total y la de razón en un sistema de cuantificación de volúmenes comerciales permitirá obtener predicciones volumétricas de manera fácil y rápida. Una leve pérdida de precisión del sistema para índices de utilización mayor e iguales a 10 cm fue observada. Sin embargo, a pesar que el sistema tiende a subestimar el volumen comercial en la parte basal del fuste, las estimaciones son buenas ya que el valor del sesgo y error promedio fue menor a 4.4% y 11.5% respectivamente, para el índice de utilización de 10 cm.
CONCLUSIONES
Las técnicas de regresión ponderada y la incorporación de una estructura continua autorregresiva del error CAR(3), permitió disminuir el efecto de la heterogeneidad de varianzas, producto de la diferencia en el tamaño de los árboles empleados en el estudio y la autocorrelación espacial común en los datos provenientes de muestreo destructivo utilizados en el ajuste de las funciones de razón de volumen. Estos procedimientos permiten dar mayor consistencia estadística a los modelos ajustados.
Las medidas de bondad de ajuste y de predicción permitieron seleccionar el modelo de Schumacher & Hall (1933) como modelo de volumen para la especie, el cual tiene tres parámetros a estimar. En la selección de los modelos de volumen se deben descartar funciones demasiado complejas para esta especie, ya que la incorporación de parámetros adicionales no representó un aporte significativo en la precisión de la predicción del volumen fustal. Como modelo de razón de volumen para E. grandis se seleccionó la función propuesta por Cao et al. (1980) considerando que presentó los mejores estadísticos de ajuste y validación
El sistema integrado por la función de volumen y de razón fue evaluado para predecir volúmenes de 25 árboles de la base de validación hasta los índices de utilización 0, 5 y 10 cm. El sesgo y error promedio en la predicción de volúmenes comerciales estuvieron siempre por debajo de 4.4% y 11.5%, respectivamente. La sencillez del sistema de cuantificación de volúmenes comerciales hasta diferentes diámetros índices de utilización de árboles en pie, así como su exactitud en la predicción, constituyen las principales bondades de la herramienta desarrollada.
AGRADECIMIENTOS
El financiamiento necesario para el desarrollo de esta investigación se obtuvo de los proyectos de investigación 2008K7852-3463 y 2008K7852-3485 ejecutados por La Corporación Nacional de Investigación y Fomento Forestal-CONIF en alianza con La Universidad del Tolima, La Gobernación del Tolima, CORCUENCAS, cofinanciados por el Ministerio de Agricultura y Desarrollo Rural y con colaboración de Smurfit Kappa Cartón de Colombia S.A.
REFERENCIAS BIBLIOGRÁFICAS
Akinnifesi, F. (1995). Linear equations for estimating the merchantable wood volume of Gmelina arborea in South-West Nigeria. Journal of Tropical Forest Science, 7 (3), 391-397.
Alegría, C. (2011). Modelling merchantable volumes for uneven aged maritime pine (Pinus pinaster Aiton) stands established by natural regeneration in the central Portugal. Annals of Forest Research, 54 (2), 197-214.
Álvarez, J.G., Barrio, M., Castedo-Dorado, F., Diéguez-Aranda, U., & Ruiz-González A.D. (2005). Modelos para la gestión forestal: una revisión de las metodologías de construcción de modelos de masa. 5° Congreso Forestal Nacional, Portugal. 13 p.
Barrio, M., González, J., & Díaz, J. (2004). Elaboración de una tarifa con clasificación de productos para Quercus robur L. en Galicia basada en un modelo de volumen porcentual. Investigación Agraria: Sistemas y Recursos Forestales, 13 (3), 506-517.
Barrio, M., Sixto, H., Cañellas, I., & González, F. (2007a). Sistema de cubicación con clasificación de productos para plantaciones de Populus x euramericana (Dode) Guinier cv. ‘I-214’ en la meseta norte y centro de España. Investigación Agraria: Sistemas y Recursos Forestales, 16 (1), 65-75.
Barrio, M., Diéguez-Aranda, U., Castedo-Dorado, F., álvarez, J., & Gadow, K.V. (2007b). Merchantable volume system for pedunculate oak in northwestern Spain. Annals of Forest Science, 64, 511-520.
Beal, D.J. (2007). Information Criteria Methods in SAS® for multiple linear regression models. 15th Annual SouthEast SAS Users Group (SESUG) Proceedings, South Carolina, Paper SA05. 10 p.
Burkhart, H. (1977). Cubic-foot volume of loblolly pine to any merchantable top limit. Southern Journal of Applied Forestry, 1 (2), 7-9.
Cano, N. (2002). Efecto de la distancia de siembra sobre el crecimiento en diámetro y altura a los dos años de edad en Eucalyptus grandis. CINOC. Boletín Técnico No 1, 15-19.
Cao, Q., Burkhart, H., & Max, T. (1980). Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science, 26 (1), 71-80.
Chauchard, L., & Sbrancia, R. (2005). Funciones de razón para la estimación de los volúmenes maderables de Pino radiata en el País Vasco. Investigación Agraria: Sistemas y Recursos Forestales, 14 (2), 185-194.
Da Cunha, T., & Guimarães, C. (2009). Modelo de regresión para estimar el volumen total con corteza de árboles de Pinus taeda L. en el sur de Brasil. Kurú: Revista Forestal, 6 (16), 1-15.
Davel, M, Trincado, G. (2000). Evaluación de modelos fustales para Pseudotsuga menziesii en la Patagonia Andina Argentina. Investigación Agraria: Sistemas y Recursos Forestales, 9 (1), 103-116.
Gilabert, H., & Paci, C. (2010). An assessment of volume-ratio functions for Eucalyptus globulus and E. nitens in Chile. Ciencia e Investigación Agraria, 37 (1), 5-15.
Guimarães, D., & Leite, H. (1996). Influência do número de árvores na determinação de equação volumétrica para Eucalyptus grandis. Scientia Forestalis, 50, 37-42.
Harvey, A.C. (1976). Estimating regression models with multiplicative heteroscedasticity, Econometrica, 44, 461-465.
López, A.M., Barrios, A., Trincado, G. & Nieto, V.M. (2011). Monitoreo y modelamiento del crecimiento para el manejo de plantaciones forestales comerciales. Bogotá: Corporación Nacional de Investigación y Fomento Forestal-CONIF - Ministerio de Agricultura y Desarrollo Rural-MADR. 90 p.
López, A.M. (2007). Modelos de crecimiento y rendimiento para Pinus caribaea, Eucalyptus pellita y Eucalyptus grandis y determinación de su edad óptima de rotación en plantaciones forestales en Colombia. (Tesis Magister)Valdivia: Facultad de Ciencias Forestales, Universidad Austral de Chile. 87 p.
Moret, A., Jerez, M., & Mora, A. (1998). Determinación de ecuaciones de volumen para plantaciones de teca (Tectona grandis L.) en la unidad experimental de la reserva forestal Caparo, Estado Barinas - Venezuela. Revista Forestal Venezolana, 42 (1), 41-50.
Ospina, C., Hernández, R., Rodas, C., Urrego, J., Godoy, J., Aristizabal, F., Osorio, O., & Riaño, N. (2006). Guías silviculturales para el manejo de especies forestales con miras a la producción de madera en la zona andina colombiana: El Eucalipto (Eucalyptus grandis W.Hill ex Maiden). Bogotá:Cenicafe. 52 p.
Parresol, B.R., Hotvedt, J.E., & Cao, Q.V. (1987). A volume and taper prediction system for bald cypress. Canadian Journal of Forest Research, 17, 250-259.
Prodan, M., Peters, R., Cox, F., & Real, P. (1997). Mensura Forestal. San José: IICA-GTZ. 561 p.
Proexport. (2009). Sector Forestal: Invierta en Colombia. Bogotá, Colombia. Proexport, 1, 1, 26 p.
Quevedo, A., Jerez, M., Moret, A., & Noguera, O. (2010). Ecuaciones de volumen y calidad de forma para Tabebuia rosea (Bertol.) en plantaciones en líneas. Barinas, Venezuela. Revista Forestal Venezolana, 54 (2), 195-205.
Riaño, H., Ospina, P., Gómez, L., López, J., Urrego, C., Osorio, L., Obando, B., & Tangarife, G. (2004). Determinación de la capacidad de captura de carbono en ocho especies forestales. Informe final del proyecto “Convenio especial para la investigación No CEN 269 del 2002 entre CONIF, FEDERACAFé y CENICAFé. Chinchiná: CENICAFé. 78 p.
Rojo, A., Perales, X., Sánchez-Rodríguez, F., Álvarez-González, J.G., & von Gadow, K. (2005). Stem taper functions for maritime pine (Pinus pinaster Ait.) in Galicia (Northwestern Spain). European Journal of Forest Research, 124, 177-186.
SAS Institute Inc. (1999). SAS User’s Guide: SAS STAT Version 8. SAS Institute Inc. Cary. NC.
Schumacher, F., & Hall, F. (1933). Logarithmic expression of timber-tree volume. Journal of Agricultural Research, 47 (9), 719-734.
Spurr, S.H. (1952). Forest inventory. New York: The Ronald Press Co. 476 p.
Trincado, G., Von Gadow, K., & Sandoval, V. (1997). Estimación de volumen comercial en latifoliadas. Bosque, 18 (1), 39-44.
Van Deusen, P., Sullivan, A., & Matney, T. (1981). A prediction system for cubic foot volume of loblolly pine applicable through much of its range. Southern Journal of Applied Forestry, 5 (4), 186-189.
Verbeek, M. (2004). A guide to modern econometrics, 2 ed. West Sussex: John Wiley & Sons. 429 p.
Zimmerman, D., & Núñez-Antón, V. (2001). Parametric modelling of growth curve data: An overview. Test, 10 (1), 1-73.
Zhang, J., & Chen, D. (2001). Interpolation calculation made EZ. 14th Annual Conference Proceedings, NorthEast SAS Users Group NESUG, Baltimore, MD. 4 p.
Licencia
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).



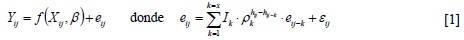


 .
.