Modelos de altura dominante para Gmelina arborea Roxb. en Colombia

Área de estudio y base de datos

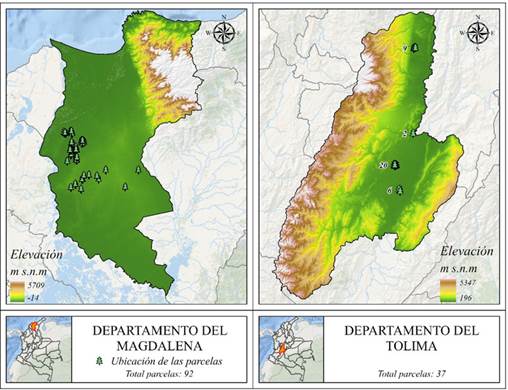
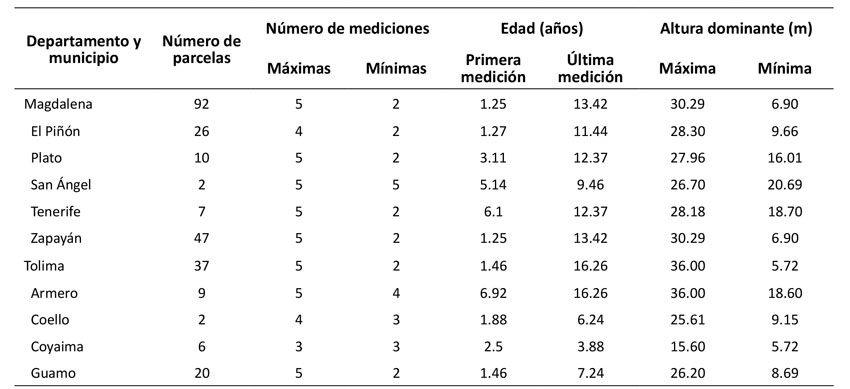
Se empleó una red de 129 parcelas permanentes de monitoreo instaladas durante el periodo 2008-2013. Las parcelas se establecieron en 5 municipios del departamento del Magdalena, ubicado en la región Caribe de Colombia, y en 4 municipios del departamento del Tolima, el cual se encuentra en la región Andina del centro-oeste del país (Figura 1). Se registraron mediciones dasométricas desde el primer año de establecimiento hasta los 16 años, con un total de 2 a 5 remediciones en cada parcela. En cada parcela y medición, se registró el diámetro a la altura del pecho (DAP), tomado a 1.30 m del suelo (DAP) con cinta diamétrica, y la altura total (HT), medida con un hipsómetro laser.

Figura 1: Distribución espacial de las unidades muestrales en los departamentos de Magdalena y Tolima

En el departamento del Magdalena, la altura dominante media fue de 23.28 m, con un rango de 6.9-30.28 m. En el departamento del Tolima, la altura dominante varió entre 5.72 y 36.0 m, con una media de 18.6 m (Tabla 1). La base de datos presenta mediciones a edades tempranas (mayores a un año del establecimiento de la plantación), intermedias (antes de la edad de corta) y mayores a la edad de aprovechamiento, lo que permite afirmar la idoneidad de los datos para el ajuste del modelo predictor.

Tabla 1: Resumen de las mediciones realizadas en parcelas permanentes de G. arborea en cada departamento y municipio

Altura dominante

Existen diferentes criterios para determinar la altura dominante de un rodal. Para este estudio, la altura dominante se considera como la altura media aritmética de los 100 árboles.ha^-1 con los diámetros de mayor tamaño, tal como lo explica Johansson (2013). Una correcta predicción de la altura dominante basada en modelos de IS no sesgados y precisos es esencial para modelar el crecimiento y la producción (Vargas et al., 2013).

La Tabla 1 resume las características temporales y los rangos de altura dominante de la base de datos a nivel de departamento y municipio.

Modelos de altura dominante evaluados

Se usó un total de 9 funciones derivadas de 2 modelos de crecimiento (Hossfeld y Bertalanffy-Richards), los cuales han sido reportados por Burkhart & Tomé (2012), Panik (2014) y Tamarit-Urias et al. (2022). Se generaron 4 ecuaciones dinámicas del modelo Hossfeld y 5 ecuaciones del modelo de Bertalanffy-Richards, usando el EDA y el EDAG. En la Tabla 2 se presenta el modelo en su forma base, los parámetros seleccionados para el despeje de cada ecuación y la respectiva forma del modelo dinámico que se utiliza para modelar el IS.

Tabla 2: Modelos de crecimiento ajustados para la predicción del desarrollo en altura dominante

El EDA solo admite una hipótesis de crecimiento respecto a los parámetros, es decir, se tiene una sola asíntota común (modelos polimórficos) o se tienen asíntotas variables (modelos anamórficos), pero no es posible incluir ambas hipótesis en un modelo (Pacheco-Aguilar et al., 2016). Esta metodología, formalizada por Bailey & Clutter (1974), involucra esencialmente la sustitución de un parámetro del modelo base para expresarlo como una función del IS o de una condición inicial de la variable de interés. Estas ecuaciones poseen una asíntota horizontal y generan curvas anamórficas o polimórficas siguiendo un patrón de crecimiento sigmoide y un punto de inflexión correspondiente a un comportamiento esperado para cada especie (Talavera García, 2013).

El enfoque por diferencias algebraicas generalizadas (EDAG), desarrollado por Cieszewski & Bailey (2000), considera dos parámetros como dependientes de la calidad de sitio, lo que permite la generación de curvas polimórficas con múltiples asíntotas. Este procedimiento se considera como un método que produce estimaciones imparciales para ecuaciones invariantes a la edad base (Nunes et al., 2011). Esta es una propiedad deseable al momento de describir el crecimiento en altura dominante y clasificar la productividad de sitio (Pacheco-Aguilar et al., 2016).

Las ecuaciones dinámicas generadas son de la forma Y = f(t, Y ₀, t ₀, β _i ), donde Y y Y ₀ indican la altura dominante futura y la altura dominante de referencia respectivamente, t y t ₀ son las edades respectivas para cada altura dominante y β _i representa los parámetros a estimar.

Aquí, a, b y c son los parámetros propios en cada ecuación; b₁, b₂ y b₃ son los parámetros de la ecuación dinámica; X ₀ y L ₀ son los parámetros dependientes de la calidad de sitio; ln es el logaritmo natural; y e es la función exponencial.

Ajuste y validación

Los parámetros de estos modelos se estimaron mediante el procedimiento Model en la interfaz del Statistical Analysis System (SAS) 9.4 (Statistical Analysis System, 2021), con el algoritmo de minimización de Marquardt y utilizando el método de máxima verosimilitud con información completa (FIML). Se empleó regresión no lineal ponderada asumiendo que la varianza de los residuales puede ser modelada como una función potencial de la altura dominante predicha w _i = ŷ _i ^m (Tamarit-Urias et al., 2022). La potencia (m) se determinó empleando la metodología descrita por Barrios et al. (2014). Adicionalmente, para evitar problemas de autocorrelación, los residuales fueron modelados a través de una estructura autorregresiva en tiempo continuo AR(1), empleando el macro %(ar) del procedimiento Model.

Se usó la técnica de validación cruzada para valorar la precisión de los modelos, la cual permite evaluar la generalización de los resultados empleando un conjunto independiente de datos (Refaeilzadeh et al., 2008). Para ello, los datos se dividieron aleatoriamente en 10 grupos de igual tamaño que contenían 13 parcelas (10 % de los datos totales). El procedimiento de validación cruzada (k-fold cross-validation) consistió en una división aleatoria en k número de grupos. Para este estudio, el total de subconjuntos fue 10; cada grupo contenía 13 parcelas (aproximadamente 10 % de los datos totales). Posteriormente, se realizaron k iteraciones (proceso de validación), de tal manera que, en cada iteración, se mantuvo un conjunto diferente de los datos, mientras que el resto (k-1) se utilizó para ajuste (Krkač et al., 2020). La bondad de ajuste se evaluó considerando el coeficiente de determinación ajustado (Burkhart & Tomé, 2012):

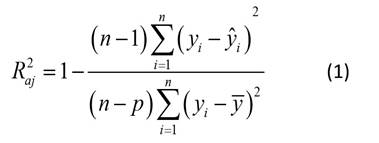
Como medidas de bondad de predicción, se utilizaron el sesgo promedio (Sesgo), el error absoluto medio (EAM) y la raíz del error medio cuadrático (REMC) (Barrios-Trilleras et al., 2021):

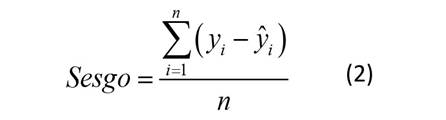
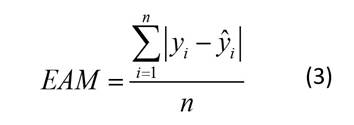
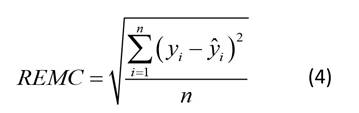
donde y _i es la altura dominante observada, ŷ _i es la altura dominante predicha, ȳ es la altura dominante media, n es el número de observaciones y p es el número de parámetros del modelo.

La evaluación de la autocorrelación se realizó con el análisis estadístico de Durbin-Watson (DW) (Panik, 2014), y los residuos de cada modelo se graficaron frente a los valores predichos para evaluar su distribución y heterocedasticidad (Barrios-Trilleras et al., 2021).

A partir de los análisis estadísticos de bondad de ajuste y la validación, se construyó un sistema de clasificación donde se establece un orden jerárquico de calidad y desempeño estadístico, en el cual se selecciona el modelo que obtenga la calificación más baja (Tewari & Singh, 2018), que finalmente se utiliza para predecir el IS de cada parcela, considerando una edad base igual a 10 años, usualmente empleada para determinar el IS de G. arborea (López et al., 2011; Martínez-Zurimendi et al., 2015).

Modelos ajustados de crecimiento de altura dominante

La Tabla 3 presenta el valor de los parámetros estimados, la bondad de ajuste y la bondad de predicción para los modelos evaluados, así como la calificación total de cada uno. En términos generales, los modelos restantes evaluados presentaron buenos ajustes. Todos los modelos presentaron R² _aj ≥ 0.914, a excepción de los modelos 3 y 4, los cuales presentaron R² _aj = 0.88.

Tabla 3: Parámetros estimados y bondad de ajuste y predicción para los modelos de crecimiento de altura dominante evaluados

En paréntesis: el intervalo de confianza para cada parámetro estimado.

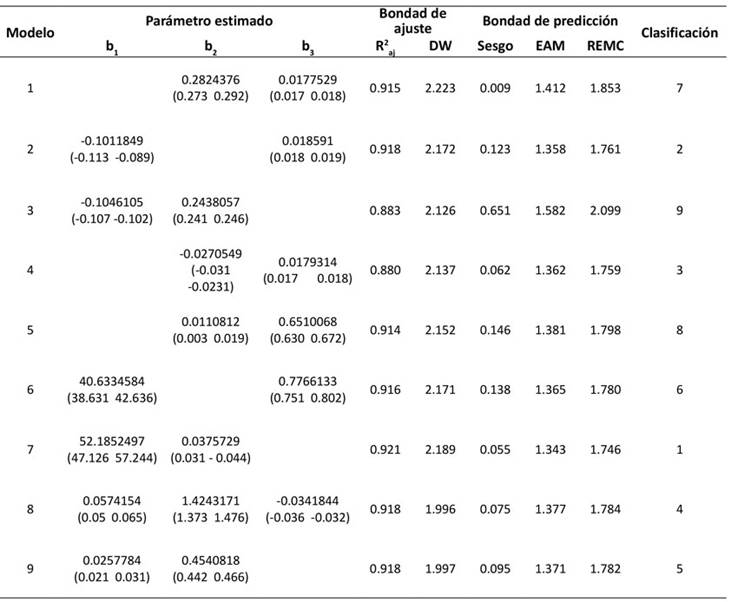
Los datos estadísticos de bondad de predicción se consideran aceptables. Los valores de sesgo indican que los modelos tendieron a subestimar los valores de altura dominante con sesgos entre 0.009 y 0.651 m. Los modelos presentaron EAM entre 1.343 y 1.582 m, y el REMC presentó valores entre 1.746 y 2.099 m.

De acuerdo con los resultados del sistema de clasificación implementado, el modelo 7 (Bertalanffy-Richards), el modelo 2 y el modelo 4 sobresalieron con los mejores datos estadísticos. En relación con el análisis estadístico DW, los valores oscilaron entre 1.996 y 2.223, en general fueron próximos a 2 y, de acuerdo con Trim et al. (2020), se evidencia la inexistencia de autocorrelación.

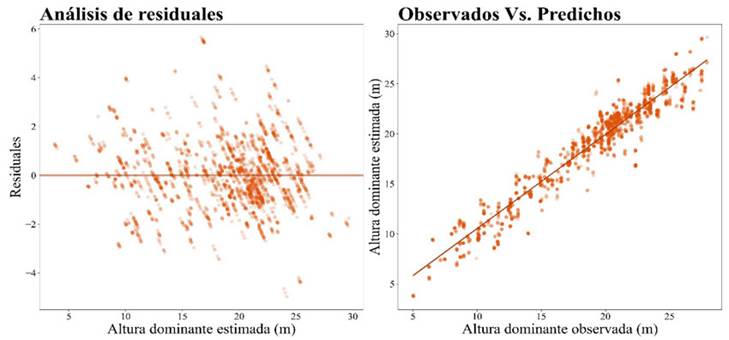
La Figura 2 muestra el comportamiento de los residuales del modelo 7. Como se aprecia, no hay tendencias anómalas, indicando la ausencia de heterocedasticidad. Al graficar los valores observados frente a los predichos, se observa que el modelo 7 no presenta tendencias significativas de sobrestimación o subestimación, lo que lo vuelve una ecuación idónea para la proyección del IS, facilitando la construcción de planes precisos para la planificación de la especie.

Figura 2: Dispersión de residuales y valores observados frente a valores predichos para el modelo 7 (modelo de Richards, parámetro c).

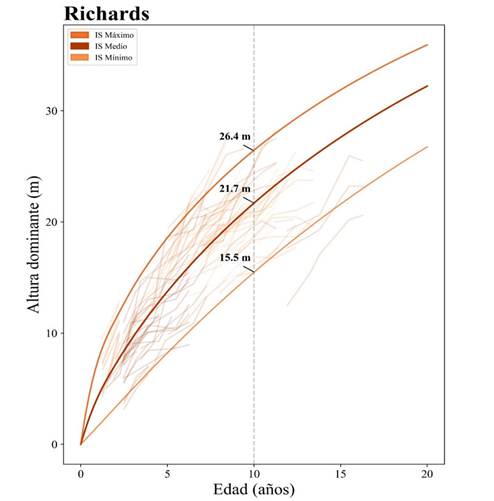
Finalmente, se analiza la familia de curvas generadas por la ecuación de Richards. Se presentan curvas ajustadas a IS con edad de referencia de 10 años superpuestas a las trayectorias de las parcelas observadas a través de la edad. De esta manera, se buscó evaluar el comportamiento biológico de los modelos, representado en una familia de tres curvas generadas para clasificar la productividad de los sitios como alto, medio y bajo, que corresponden al percentil 95, la mediana y el percentil 5 de los datos observados respectivamente.

Las curvas de IS generadas por los modelos presentan diferentes tasas de crecimiento a edades tempranas (de 0 a 5 años). En edades medias o mayores de 5 años, se ve un crecimiento continuo hacia la formación de una asíntota horizontal, lo cual indica un punto de inflexión en los niveles de desarrollo de la especie. Esta información generalmente se utiliza para la planificación de prácticas silvícolas y la proyección de la productividad.

Para el modelo de Richards, parámetro c (modelo 7), se observa en la Figura 3 un ajuste claro para las tres curvas evaluadas, donde, a edades tempranas, se presenta un crecimiento acelerado, marcado por una deflexión donde la tasa de crecimiento se reduce en el tiempo. Esto es bastante acertado para un comportamiento biológico promedio. Este modelo mostró un rango de IS entre los 15.5 y los 26.4 m a una edad base de 10 años. Para clasificar la productividad de plantaciones de Gmelina arborea, se generaron tres rangos basados en las curvas de la Figura 3: sitios con bajas productividades, o aquellos con IS ≤ 18.6 m; sitios con productividades medias entre 18.6 m < IS ≤ 24.1 m; y sitios con productividad alta, con IS > 24.1 m.

Figura 3: Familia de curvas de índice de sitio para G. arborea obtenidas a partir del modelo de Richards, parámetro c (modelo 7)

Finalmente, se contrastan los valores de IS para el modelo 7 para cada uno de los municipios muestreados en ambos departamentos (Tabla 4).

Tabla 4: Índice de sitio promedio para plantaciones de G. arborea por municipio y departamento

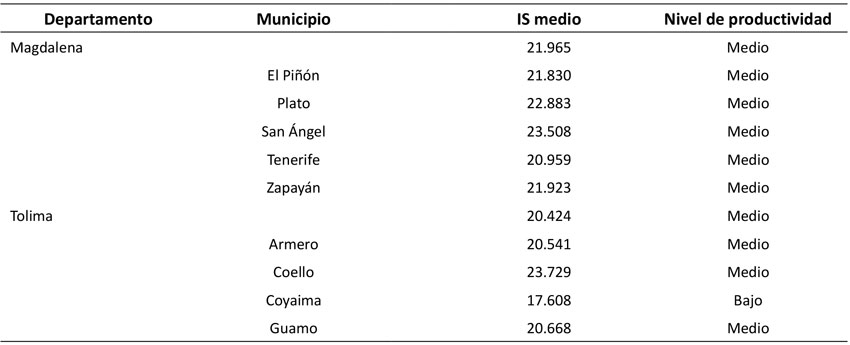
Como se evidencia en la Tabla 4, los departamentos presentan el mismo nivel de productividad. Todos los municipios fueron categorizados como de productividad media, excepto el municipio de Coyaima en el departamento del Tolima, que presenta un valor más bajo de productividad. La Ecuación (5) de IS para G. arborea según el modelo 7 se muestra a continuación:

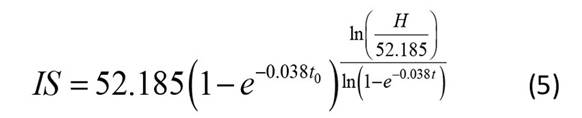
donde t₀ hace referencia a la edad base o edad clave (10 años) y H y t son la altura dominante y edad del rodal.