DOI:
https://doi.org/10.14483/2256201X.15345Publicado:
01-01-2021Número:
Vol. 24 Núm. 1 (2021): Enero-JunioSección:
Artículos de investigación científica y tecnológicaModelamiento de la productividad de Gmelina arborea Roxb. con base en variables biofísicas y de rodal
Productivity modeling of Gmelina arborea Roxb. using biophysical and stand variables
Palabras clave:
Manejo forestal, Altura dominante, Productividad forestal, Índice de sitio (es).Palabras clave:
Forest management, Dominant height, Forest productivity, Site index (en).Descargas
Referencias
Antón-Fernández, C., Burkhart, H., Strub, M. y Amateis, R. (2011). Effects of initial spacing on height development of loblolly pine. Forest Science, 57(3), 201–211. https://doi.org/10.1093/forestscience/57.3.201
Battie-Laclau, P., Delgado-Rojas, J. S., Christina, M., Nouvellon, Y., Bouillet, J. P., Piccolo, M., Moreira, M. Z., Gonçalves, J. L., Roupsard, O. y Laclau, J. P. (2016). Potassium fertilization increases water-use efficiency for stem biomass production without affecting intrinsic water-use efficiency in Eucalyptus grandis plantations. Forest Ecology and Management, 364, 77-89. https://doi.org/10.1016/j.foreco.2016.01.004
Bjelanovic, I., Comeau, P. y White, B. (2018). High resolution site index prediction in boreal forests using topographic and wet areas mapping attributes. Forests, 9(3), 113. https://doi.org/10.3390/f9030113
Bravo-Oviedo, A., Gallardo-Andrés, C., del Río, M. y Montero, G. (2010). Regional changes of Pinus pinaster site index in Spain using a climate-based dominant height model. Canadian Journal of Forest Research, 40(10), 2036-2048.
Bravo-Oviedo, A., Tomé, M., Bravo, F., Montero, G. y Río, M. (2008). Dominant height growth equations including site attributes in the generalized algebraic difference approach. Canadian Journal of Forest Research, 38(9), 2348-2358.
Burkhart, H. y Tomé, M. (2012). Modeling forest trees and stands. Nuewva York: Springer.
Castillo, A., Santiago, W., Vargas, B., Quiñonez, G., Solís, R. y Corral, J. (2018). Modelos dinámicos de índice de sitio para cuatro especies de pino en Oaxaca. Revista Mexicana de Ciencias Forestales, 9(49), 4-27.
Diéguez, U., Rojo, A., Castedo, F., Álvarez, J., Barrio, M., Crecente, F., González, J. M., Pérez-Cruzado, C., Rodríguez, R., López-Sánchez, C. A., Balboa-Murias, M. Á., Gorgoso, J. J. y Sánchez, F. (2009). Herramientas selvícolas para la gestión forestal sostenible en Galicia. Lugo: Dirección Xeral de Montes, Consellería do Medio Rural, Xunta de Galicia.
Dilts, T. (2015). Topography Tools for ArcGIS 10.1. Reno: University of Nevada.
Dvorak, W.S. (2004). World view of Gmelina arborea: opportunities and challenges. New Forest, 28, 111-126.
Elli, E., Caron, B., Behling, A., Eloy, E., Queiróz, V., Schwerz, F. y Stolzle, J. (2017). Climatic factors defining the height growth curve of forest species. iForest, 10(3), 547-553. https://doi.org/10.3832/ifor2189-010
Erkan, N. y Aydin, A. (2016). Effects of spacing on early growth rate and carbon sequestration in Pinus brutia Ten. Plantations. Forest Systems, 25(2), e064.
Ferraz, A., Scolforo, J., Ferreira, M., Maestri, R., Assis, A., Oliveira, A. y Mello, J. (2011). Dominant height projection model with the addition of environmental variables. Cerne, 17(3), 427-433. https://doi.org/10.1590/s0104-77602011000300018
Florez, J. y Florez, O. (2013). Estudio del crecimiento de “Gmelina arborea” en los consejos comunitarios de Quiparadó y Domingodó (Chocó – Colombia) (Ttesis de Mmaestría). Universidad de Manizales, Manizales, Colombia.
Franklin, K. y Wigge, P. (2013). Temperature and plant development. Hoboken (New, Nueva Jersey):, EE. UU.: John Wiley & Sons, Inc.
Guzmán, R. (1988). Site productivity evaluation of some yemane (Gmelina arborea Roxb.) plantations in the Philippines. Laguna, Philippines: University of the Philippines.
Hengl, T., Mendes, J., Heuvelink, G., Ruiperez, M., Kilibarda, M., Blagotić, A., Shangguan, W., Wright, M., Geng, X., Bauer-Marschallinger, B., Guevara, M., Vargas, R., MacMillan, R., Batjes, N., Leenaars, J., Ribeiro, E., Wheeler, I., Mantel, S. y Kempen, B. (2017). SoilGrids250m: Global gridded soil information based on machine learning. PLoOS ONE, 12(2), e0169748. https://doi.org/10.1371/journal.pone.0169748
Henri, C. (2001). Soil-site productivity of Gmelina arborea, Eucalyptus urophylla and Eucalyptus grandis forest plantations in western Venezuela. Forest Ecology and Management, 144, 255-264. https://doi.org/10.1016/S0378-1127(00)00390-X
Kees, S., López, A., Rojas, J., Roldán, M., Zurita, J. y Brest, E. (2017). Características edáficas y su relación con la altura dominante en plantaciones de Prosopis alba en la provincia del Chaco. Revista Forestal Yvyrareta, 24, 13-19.
Kiviste, A., Álvarez, J., Rojo, A. y Ruíz, A. (2002). Funciones de crecimiento de aplicación en el ámbito forestal. Madrid: Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria.
Lamprecht, H. (1990). Silvicultura en los trópicos: los ecosistemas forestales en los bosques tropicales y sus especies arbóreas-posibilidades y métodos para un aprovechamiento sostenido. Eschborn: TZ-Verlag-Ges.
López, A., Barrios, A., Trincado, G. y Nieto, V. (2011). Monitoreo y modelamiento del crecimiento para el manejo de plantaciones forestales comerciales. Bogotá: Corporación Nacional de Investigación
Louw, J. y Scholes, M. (2006). Site index functions using site descriptors for Pinus patula plantations in South Africa. Forest Ecology and Management, 225, 94-103. https://doi.org/10.1016/j.foreco.2005.12.048
MacFarlane, D., Green, E. y Burkhart, H. (2000). Population density influences assessment and application of site index. Canadian Journal of Forest Research, 30(9), 1472-1475. https://doi.org/10.1139/cjfr-30-9-1472
Martínez-Zurimendi, P., Domínguez-Domínguez, M., Juárez-García, A., López-López, L.M., Cruz-Arias, V. y Álvarez-Martínez, J. (2015). Índice de sitio y producción maderable en plantaciones forestales de Gmelina arborea en Tabasco, México. Revista fitotecnia mexicanaFitotecnia Mexicana, 38(4), 415-425.
Mayorga, R., Hurtado, G. y Benavides, H. (2011). Evidencias de cambio climático en Colombia con base en información estadística. Bogotá: Instituto de Hidrología, Meteorología y Estudios Ambientales.
Meredieu, C., Perret, S. y Dreyfus, P. (2003). Modelling dominant height growth: effect of stand density. En: A. Amaro, D. Reed, & y P. Soares (eds.), Modelling forest systems (pp. 111-121). Cambridge: CABICabi Publishing.
Miyamoto, A., Terazono, R., Sano, M. y Shimizu, A. (2018). Prediction of the site index for a subtropical broad-leaved forest on Okinawa island using topographic factor. Open Journal of Forestry, 8(3), 267–282.
Mokarram, M., Roshan, G. y Negahban, S. (2015). Landform classification using topography position index (case study: salt dome of Korsia-Darab plain, Iran). Modeling Earth Systems and Environment, 1, 40.
Newton, P. (2015a). Occurrence of density-dependent height repression within jack pine and black spruce populations. Forests, 6(7), 2450-2468.
Newton, P. (2015b). Evaluating the ecological integrity of structural stand density management models developed for Boreal conifers. Forests, 6(4), 992-1030.
Obregón, C. (2006). Gmelina arborea: versatilidad, renovación y productividad sostenible para el futuro. Revista el Mueble y la Madera (M&M), 50, 14-20.
Pardé, J. y Bouchon, J. (1988). Dendrométrie. Nancy, Francia: ENGREFEngref.
Paulo, J., Palma, J., Gomes, A., Faias, S., Tomé, J. y Tomé, M. (2015). Predicting site index from climate and soil variables for cork oak (Quercus suber L.) stands in Portugal. New Forests, 46(2), 293-307.
Pinjuv, G., Mason, E. y Watt, M. (2006). Quantitative validation and comparison of a range of forest growth model types. Forest Ecology and Management, 236(1), 37-46. https://doi.org/10.1016/j.foreco.2006.06.025
Quinn, G. y Keough, M. (2002). Experimental design and data analysis for biologists. Cambridge: Cambridge University Press.
Refaeilzadeh, P., Tang, L. y Liu, H. (2009). Cross Validation. En L. Liu &y M. Özsu (eds.), Encyclopedia of database systems (pp. 532–538). Nuewva York: Springer.
Reineke, L. (1933). Perfecting a stand-density index for even-aged forests. Journal of Agricultural Research, 46(7), 627-638.
Rodríguez, R., Sánchez, F., Gorgoso, J., Castedo, F., López, C. y Gadow, K. (2002). Evaluating standard treatment options for Pinus radiata plantations in Galicia (north-western Spain). Forestry, 75(3), 273-284.
Rojas, A., Moreno, L., Melgarejo, L. y Rodríguez, M. (2012). Physiological response of gmelina (Gmelina arborea Roxb.) to hydric conditions of the colombian Caribbean. Agronomía Colombiana, 30(1), 52-58.
Rojas, F., Arias, D., Moya, R., Meza, A., Murillo, O. y Arguedas, M. (2004). Manual para productores de Melina Gmelina arborea en Costa Rica. Cartago, Costa Rica: FONAFIFOFonafifo.
Scolforo, J., Maestri, R., Ferraz, A., Mello, J., Oliveira, A. y Assis, A. (2013). Dominant height model for site classification of Eucalyptus grandis incorporating climatic variables. International Journal of Forestry Research, 2013, 1-7.
Sharma, M., Subedi, N., Ter-Mikaelian, M. y Parton, J. (2015). Modeling climatic effects on stand height/site index of plantation-grown jack pine and black spruce trees. Forest Science, 61(1), 25–34. https://doi.org/10.5849/forsci.13-190
Sharma, M., y Parton, J. (2018). Analyzing and modelling effects of climate on site productivity of white spruce plantations. The Forestry Chronicle, 94(2), 173-182.
Sharma, M., y Parton, J. (2019). Modelling the effects of climate on site productivity of white pine plantations. Canadian Journal of Forest Research, 49(10),1289-1297.
Socha, J. (2008). Effect of topography and geology on the site index of Picea abies in the West Carpathian, Poland. Scandinavian Journal of Forest Research, 23(3), 203-213. https://doi.org/10.1080/02827580802037901
Spittlehouse, D. (2003). Water availability, climate change and the growth of Douglas-fir in the Georgia basin. Canadian Water Resources Journal, 28(4), 673-688.
Statistical Analysis System Institute Inc. (SAS). (2009). User’s guide 2a ed. Version 9.2 for Windows. Cary, NC, EUA.
Urrego, J. (2004). Growth potential of Gmelina arborea at 3 years of age in Colombia. New Forests, 28, 269-276.
Vallejos, O. (1996). Productividad y relaciones de índice de sitio con variables fisiográficas, edafoclimáticas y foliares para Tectona grandis L., Bombacopsis quinatum (Jacq) Dugand y Gmelina arborea Roxb en Costa Rica (Ttesis de Maestría). CATIEmaestría). Catie, Turrialba, Costa Rica.
Vanclay, J., Baynes, J. y Cedamon, E. (2008). Site index equation for smallholder plantations of Gmelina arborea in Leyte Province, the Philippines. Small-scale Forestry, 7(1), 87-93. https://doi.org/10.1007/s11842-008-9042-6
y Fomento Forestal, Ministerio de Agricultura y Desarrollo Rural.
Yepes, A. y Buckeridge, M. (2011). Respuestas de las plantas ante los factores ambientales del cambio climático global -. Revisión. Colombia Forestal, 14(2), 213-232. https://doi.org/10.14483/udistrital.jour.colomb.for.2011.2.a06
Zhao, D., Kane, M., Teskey, R., Fox, T., Albaugh, T., Allen, H. y Rubilar, R. (2016). Maximum response of loblolly pine plantations to silvicultural management in the southern United States. Forest Ecology and Management, 375(1), 105-111.
Zhou, Y., Lei, Z., Zhou, F., Han, Y., Yu, D.,. y Zhang, Y. (2019). Impact of climate factors on height growth of Pinus sylvestris var. mongolica. PLoOS ONE, 14(3), e0213509. https://doi.org/10.1371/journal.pone.0213509
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 21 de septiembre de 2019; Aceptado: 20 de agosto de 2020
Resumen
El estudio desarrolló un modelo empírico para predecir la altura dominante (H) y el índice de sitio (IS) de plantaciones de Gmelina arborea Roxb., considerando para ello variables biofísicas y de rodal. Se utilizaron datos de 160 rodales localizados en las regiones Andina, Caribe y Pacífica de Colombia. El modelo de Chapman-Richards fue seleccionado para predecir la H e IS de cada rodal. Un análisis de correlación identificó al espaciamiento relativo, la altitud y la precipitación como variables relacionadas al IS. Un modelo de regresión lineal múltiple con estas variables explicó el 70 % de la variación total observada en el IS. Estas variables incorporadas al modelo de H permitieron aumentar en 30 % y reducir en 40 y 41 % el índice de ajuste, error absoluto y error medio cuadrático, respectivamente. Los modelos desarrollados son adecuados para estimar la productividad en áreas sin historia de plantaciones forestales, adicionando flexibilidad y capacidad predictiva en un entorno cambiante.
Palabras clave:
manejo forestal, altura dominante, productividad forestal, índice de sitio..Abstract
The study developed an empirical model for predicting the dominant height (H) and site index (SI) of Gmelina arborea Roxb. plantations considering biophysical and stand variables. Data from 160 stands located in the Andean, Caribbean and Pacific regions of Colombia were used. The Chapman-Richards model was selected for predicting H and SI of each stand. A correlation analysis identified the relative spacing, elevation and precipitation as variables related to SI. A multiple linear regression model with these variables explained 70 % of the total variation observed in SI. These variables included in the H model allowed to increase the fit index by 30 % and reduce the absolute error and mean square error by 40 and 41 %, respectively. The developed models are suitable for estimating productivity in areas with-out a history of forest plantations, adding flexibility and predictive capacity in a changing environment.
Keywords:
forest management, dominant height, forest productivity, site index..INTRODUCCIÓN
Gmelina arborea Roxb. es una especie de rápido crecimiento originaria del sudeste asiático (Dvorak, 2004). En Colombia, las plantaciones forestales con esta especie cubren más de 20 000 hectáreas plantadas en la costa Atlántica y en los valles interandinos por debajo de 1000 m de altitud. Estas plantaciones constituyen una fuente importante de materia prima para la industria de aserrío y tableros en la región y su productividad muestra una gran variabilidad estrechamente relacionada con la altitud y variables asociadas como la temperatura, la precipitación y la radiación solar (Obregón, 2006). G. arborea se desarrolla mejor con una precipitación anual de entre 1750 y 2300 mm, una estación seca definida de tres a cinco meses y una temperatura media de entre 18 y 35°C (Lamprecht, 1990).
La evaluación de la productividad del sitio es esencial para identificar el potencial productivo, proporcionar un marco de referencia para el diagnóstico correcto y la prescripción silvícola durante el proceso de planificación forestal y, finalmente, para predecir el crecimiento y el rendimiento de los recursos forestales (Burkhart y Tomé, 2012). La productividad forestal es el resultado de la interacción entre la genética de la especie, el suelo y el clima (Diéguez et al., 2009). El método más utilizado para evaluar la productividad del sitio se basa en la relación entre la altura dominante (H) y la edad de los árboles (Antón-Fernández et al., 2011).
La altura de los árboles dominantes y codominantes se prefiere como medida de la productividad forestal porque es poco afectada por las densidades de los rodales o los tratamientos de raleo (Bravo-Oviedo et al., 2008). Sin embargo, para algunas especies se ha reportado un efecto significativo del espaciamiento del rodal sobre el índice del sitio (IS) (Meredieu et al., 2003; Antón-Fernández et al., 2011). Antón-Fernández et al. (2011) encontraron un efecto significativo negativo del espaciamiento en la H para Pinus taeda L.; las diferencias entre las densidades de los rodales fueron evidentes a partir de los seis años y se mantuvieron consistentes hasta el final del período de estudio de 25 años. Estudios de raleo para Pinus nigra Arn. demostraron que la zona óptima de densidad de rodal para el aumento de la H (definida en términos de espaciamiento relativo) fue del 17 al 62 %; fuera de ese rango no se alcanza el aumento de la H relativa máxima (Meredieu et al., 2003).
Modelos de H para G. arborea han sido desarrollados previamente. López et al. (2011) modelaron la H para rodales de G. arborea en la costa Atlántica y la región Andina de Colombia, utilizaron el enfoque de diferencia algebraica (ADA) y seleccionaron los modelos de Chapman-Richards y de Korf para generar curvas polimórficas. Martínez-Zurimendi et al. (2015) seleccionaron el modelo de Hossfeld para generar curvas de índices de sitio anamórficas usando el método de la curva guía en plantaciones de G. arborea de Tabasco, México. Sin embargo, esos modelos se consideran débiles debido a la falta de flexibilidad para adaptarse a los cambios en la productividad causados por la estructura del rodal y la variabilidad climática (Mayorga et al., 2011). Así mismo, estos modelos no son aplicables en zonas carentes de plantaciones forestales pues se requiere conocer la H a una determinada edad del rodal.
Estudios previos han mostrado que el IS puede ser predicho a partir de variables biofísicas. Vanclay et al. (2008) modelaron el IS de G. arborea en Filipinas empleando un modelo de regresión lineal con la pendiente y la profundidad del suelo como predictores. Guzmán (1988) correlacionó el IS de G. arborea con variables fisiográficas, suelo y clima en Filipinas y encontró correlaciones significativas con los factores climáticos; sin embargo, solo la precipitación mostró correlaciones positivas, en tanto que la temperatura y la humedad relativa se correlacionaron de forma negativa. Vallejos (1996) ajustó modelos de crecimiento de H y determinó que el IS de G. arborea en Costa Rica se relacionaba con la posición topográfica, el viento y el contenido de calcio a una profundidad de 0-20 cm.
Los factores climáticos y la variación espacial del suelo se han incorporado en los modelos de H para especies como Pinus patula Schiede ex Schtldl. & Cham., Pinus radiata D. Don, Eucalyptus globulus Labill. y Eucalyptus grandis Hill ex Maiden (Louw y Scholes, 2006; Pinjuv et al., 2006; Ferraz et al., 2011; Scolforo et al., 2013). Los modelos de crecimiento de H que incluyen variables climáticas permiten evaluar la incidencia del clima en la productividad del sitio y son una herramienta útil para estimar los efectos debido al cambio climático (Sharma et al., 2015). Incluir tales variables en los modelos de H ha permitido un aumento significativo en la precisión. Además, para sitios sin información previa sobre plantaciones este tipo de modelos permite evaluar la productividad del rodal antes de plantar para así elegir los mejores en donde se maximizarán los retornos (Kees et al., 2017). Los modelos de este tipo son de utilidad pues proporcionan información sobre las áreas potenciales para la inversión en plantaciones forestales comerciales.
El objetivo principal del estudio fue estimar la productividad de sitios forestales a través de un modelo de crecimiento empírico para predecir la H y el IS de G. arborea mediante la incorporación de variables biofísicas y de rodal, lo que posibilitó las estimaciones de productividad en áreas sin historia de plantaciones forestales y al tiempo que agrega flexibilidad y capacidad predictiva en un entorno climático cambiante.
Los objetivos específicos del estudio fueron: I) seleccionar un modelo de crecimiento base de H; II) obtener un modelo predictivo de IS para G. arborea a partir de variables biofísicas y de rodal con el potencial de representar espacialmente su variación; y III) evaluar la ganancia de precisión al incluir variables biofísicas y de rodal en el modelo de crecimiento de H.
MATERIALES Y MÉTODOS
Datos
Se utilizaron datos de parcelas de muestreo temporales y permanentes cuya área varió entre 500 a 800 m2 provenientes de 160 rodales de plantaciones forestales de G. arborea. Los rodales se ubicaron en los departamentos de Tolima, Magdalena, Atlántico, Cesar, Bolívar, Sucre y Chocó, en Colombia (López et al., 2011; Florez y Florez, 2013). En cada rodal se estableció un mínimo de uno y un máximo de 38 parcelas. Las edades de los rodales oscilaron entre uno y 16 años, con densidades actuales entre 125 y 1327 árboles por hectárea (tabla 1).
Tabla 1: Estadísticas descriptivas de las variables utilizadas para modelar la H
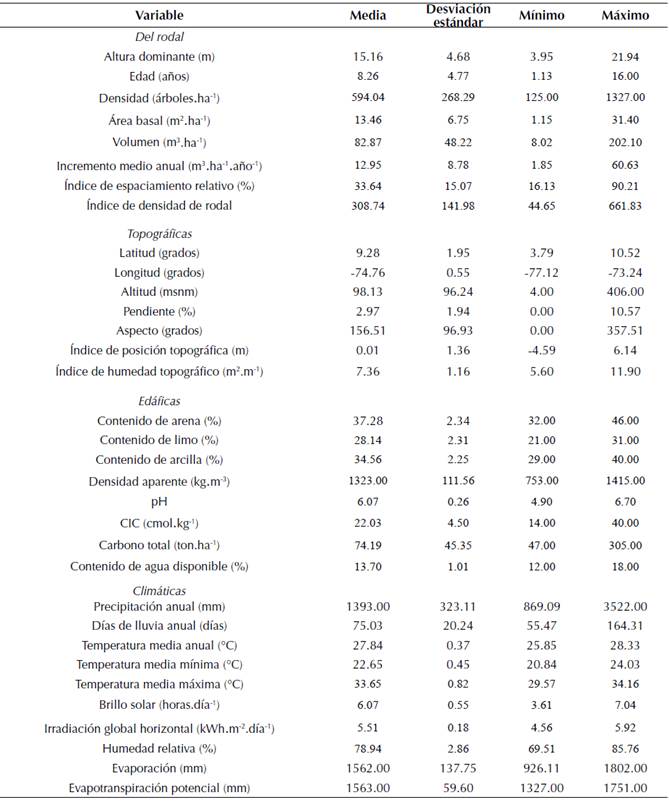
Variables de rodal
La H de cada parcela se estimó como la altura media de los 100 árboles de mayor diámetro por hectárea. Los atributos de rodal evaluados fueron: I) número de árboles por hectárea (N); II) área basal (G); III) índice de espaciamiento relativo (índice de Hart-Becking, IHB) (Pardé y Bouchon, 1988); y IV) índice de densidad del rodal (IDR) (Reineke, 1933). El índice de espaciamiento relativo se calculó como se muestra en la ecuación 1:
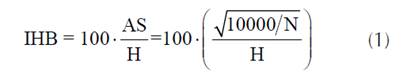
donde H es la altura dominante del rodal (m) y AS es el espacio promedio entre los árboles (m). El AS se calculó a partir de N, asumiendo que los árboles estaban posicionados en una cuadrícula.
El índice de densidad de rodal se calculó como se muestra en la ecuación 2:
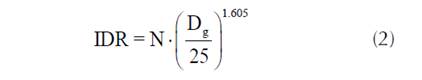
donde N es la densidad del rodal y Dg es el diámetro cuadrático medio.
Variables biofísicas
Se empleó un modelo digital de elevación (MDE) obtenido de la Nasa, denominado shuttle radar topographic mission (SRTM), con una resolución de 30 m. El MDE fue utilizado para determinar la altitud, la pendiente y el aspecto de cada parcela, así como para estimar el índice de posición topográfica (IPT) e índice de humedad topográfico (IHT) (Mokarram et al., 2015; Miyamoto et al., 2018) utilizando la herramienta topography tools del software ArcGIS 10.2 (Dilts, 2015).
El IPT compara la elevación de cada celda en el MDE con la elevación media de un vecino específico alrededor de esa celda (Mokarram et al., 2015). Un valor positivo (negativo) de IPT significa que la celda es más alta (más baja) que las celdas circundantes; los valores cercanos a cero son áreas planas. El IPT se calculó utilizando un cuadrado de 33 × 33 celdas al aplicar la ecuación 3.
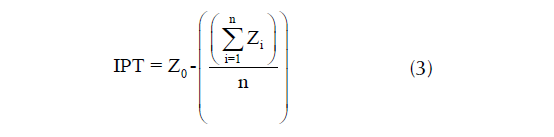
donde Z0 es la elevación de una celda específica, Zi la elevación y n el número total de celdas circundantes.
El IHT (ecuación 4) se calcula utilizando el área de captación específica (α) y el gradiente de pendiente (β). Este caracteriza la cantidad de acumulación de agua en función de la posición de la pendiente (Miyamoto et al., 2018).
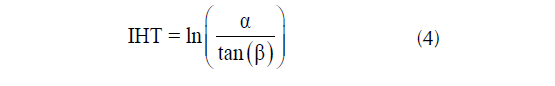
La información edáfica usada se obtuvo de Soil Grids v0.5.3 a una resolución espacial de 250 m (Hengl et al., 2017). Los parámetros de suelo empleados fueron el contenido de arena, limo y arcilla de la capa superior de suelo (30 cm), densidad aparente, pH, capacidad de intercambio catiónico (CIC), carbono total y contenido de agua disponible. Los datos climáticos se obtuvieron del Instituto de Hidrología, Meteorología y Estudios Ambientales (Ideam) de Colombia, los cuales son correspondientes a los promedios anuales del periodo 1981-2010 y se interpolaron utilizando el método de valores ponderados por el inverso de la distancia (IDW) con una resolución espacial de 250 m utilizando el software ArcGIS 10.2. Las variables climáticas fueron la temperatura mínima, máxima y media anual, la precipitación y el número de días de lluvia anual, el brillo solar anual, la humedad relativa anual, la evaporación y la evapotranspiración potencial anual. Las estadísticas descriptivas de las variables biofísicas y de rodal se muestran en la tabla 1.
Selección de un modelo base de H
La primera etapa de este estudio consistió en la selección de un modelo base de crecimiento de H para describir la variación observada en el conjunto de datos. Se evaluaron cuatro modelos de crecimiento utilizados en biometría y modelamiento forestal considerando medidas de bondad de ajuste y predicción. Los modelos evaluados corresponden a las ecuaciones de Chapman-Richards, Korf, Schumacher y Weibull (Kiviste et al., 2002; tabla 2).
donde H es la altura dominante; A es la edad; IS es el índice del sitio; A0 es la edad base definida en 10 años; β0, β1 y β2 son parámetros a estimar; y e es la base de los logaritmos naturales.
Tabla 2: Modelos de crecimiento evaluados para la H e IS

Los parámetros de estos modelos se estimaron mediante el procedimiento Model de Statistical Analysis System-SAS (SAS Institute Inc., 2009) con el algoritmo de minimización de Marquardt y utilizando el método de máxima verosimilitud con información completa (FIML). Se usó la técnica de validación cruzada para valorar la precisión de los modelos; esta permite evaluar la generalización de los resultados empleando un conjunto independiente de datos (Refaeilzadeh et al., 2009). Para ello, los datos se dividieron aleatoriamente en 10 grupos de igual tamaño que contenían 16 rodales (10 % de los datos totales). Posteriormente, se realizaron 10 iteraciones de estimación y validación, donde se usaron nueve grupos para estimar los parámetros del modelo y el grupo restante se usó para la validación del modelo.
La bondad de ajuste se evaluó considerando un índice de ajuste (IA); como se muestra en la ecuación 5:
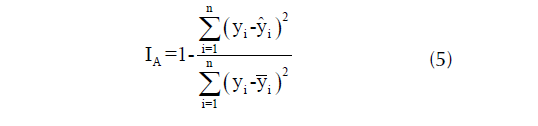
y como medidas de bondad de predicción se utilizó el error absoluto medio (EAM):
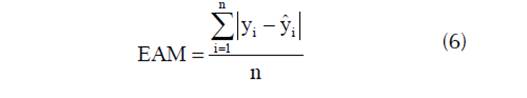
y la raíz del error medio cuadrático (REMC)
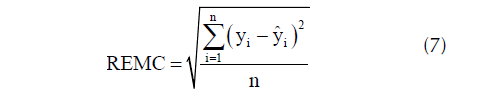
donde yi es la altura dominante observada; ŷi es la altura dominante predicha, ȳi es la altura dominante media; y n es el número de observaciones.
Los residuos de cada modelo se graficaron frente a los valores predichos para evaluar su distribución y probar la normalidad y heterocedasticidad. Debido a que se usó un único valor de H por cada rodal se espera que no exista autocorrelación en los datos usados para el ajuste de los modelos. La curva promedio de H predicha de cada modelo se trazó sobre los valores observados de H para evaluar su forma y sentido biológico. Finalmente, el modelo seleccionado se usó para predecir el IS de cada rodal, considerando una edad base igual a 10 años, la cual es usualmente empleada para determinar el IS de G. arborea (López et al., 2011; Martínez-Zurimendi et al., 2015).
Predicción y representación espacial del IS
Se utilizó un análisis de correlación de Pearson para evaluar y seleccionar las variables biofísicas y de rodal que se relacionan significativamente con el IS. Este análisis se efectuó mediante el procedimiento Corr (SAS Institute Inc., 2009). Posterior a esto, se desarrolló un modelo de regresión lineal múltiple con las variables que se correlacionaron significativamente con el IS utilizando el procedimiento REG (SAS Institute Inc., 2009).
El ingreso de las variables en el modelo de regresión lineal múltiple se llevó a cabo de forma secuencial con la variable que mostró la correlación más fuerte con el IS, hasta que las variables adicionadas no fueron significativas al nivel de 0.05. En el análisis de correlación y regresión lineal, el IS se transformó aplicando logaritmo natural para corregir la distribución no normal de esta variable, el modelo de regresión lineal múltiple presentó la siguiente estructura (ecuación 8):
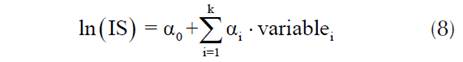
donde IS es el índice de sitio; variablei es la i-ésima variable ingresada en el modelo; α0, αi son los parámetros del modelo; y ln es el logaritmo natural.
El grado de multicolinealidad entre las variables independientes se evaluó con el factor de inflación de varianza (VIF), con el cual los valores menores de cinco indican que la multicolinealidad está dentro de límites aceptables (Quinn y Keough, 2002). La significancia de los parámetros del modelo se evaluó a través de una prueba F y la bondad de ajuste mediante el coeficiente de determinación. Para mostrar la aplicación práctica del modelo de IS ajustado (ecuación 8), se utilizó para representar espacialmente el IS en el departamento del Tolima, Colombia.
Modelo de H con variables biofísicas y de rodal
Para garantizar la compatibilidad de las predicciones del modelo de H y de IS se ajustó el modelo base de H junto con el modelo de IS generado con regresión lineal múltiple de manera simultánea empleando el procedimiento Model (SAS Institute Inc. 2009). El modelo final de H con variables biofísicas y de rodal fue evaluado utilizando el mismo proceso usado para la selección del modelo base. Este procedimiento permitió comparar el modelo base con el modelo con covariables en términos de ganancia de precisión.
RESULTADOS
Modelo base de H
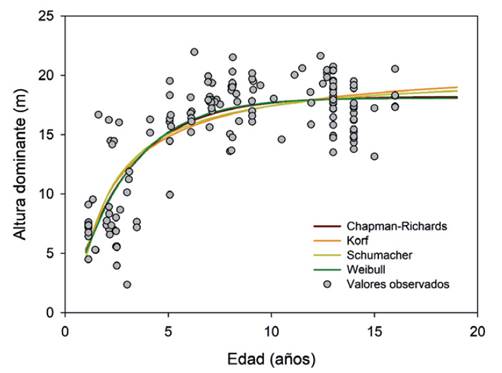
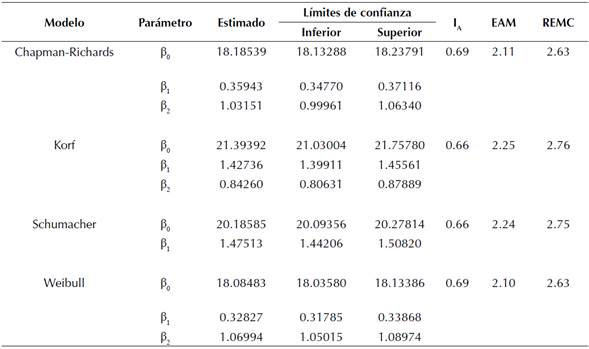
Los parámetros estimados y los estadísticos de bondad de ajuste y validación para los modelos evaluados se presentan en la tabla 3. En general, no se encontraron diferencias notorias entre los modelos con respecto a los estadísticos evaluados. Los mejores indicadores se obtuvieron con los modelos de Chapman-Richards y Weibull, los cuales explicaron el 69 % de la varianza total de los datos observados. Las diferencias en los estadísticos de bondad de validación de los modelos fueron mínimas. De manera gráfica se observó que el modelo de Chapman-Richards presentaba un mejor comportamiento, con una asíntota levemente mayor que el modelo Weibull (figura 1). Por ello, se eligió la ecuación de Chapman-Richards como base para modelar el crecimiento en H y se empleó para predecir el IS de cada rodal.
Figura 1: Tendencia de crecimiento promedio en H que describe cada modelo base de H evaluado.
Tabla 3: Coeficientes estimados y bondad de ajuste para los modelos base de crecimiento evaluados para la H
Variables biofísicas y de rodal relacionadas con el IS
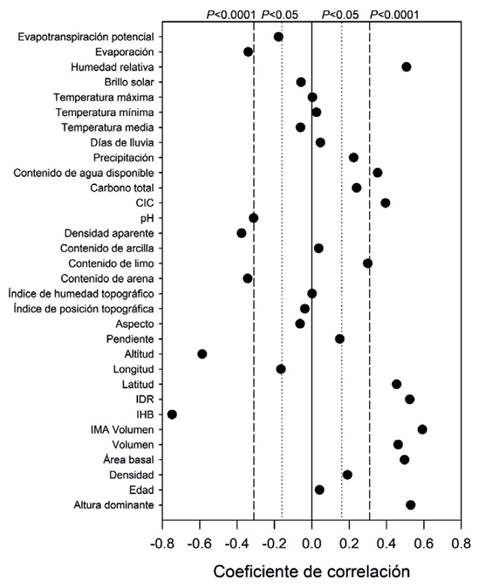
El análisis de correlación mostró que el espaciamiento relativo y la altitud fueron las variables que mayor asociación tuvieron con el IS con una relación inversa. Por otra parte, el IS se correlacionó positiva y significativamente con la humedad relativa, el contenido de agua disponible, la CIC, el contenido de limo y la latitud; mientras que, con la evaporación, la densidad aparente, el contenido de arena y el pH se relacionó negativamente. La temperatura, el brillo solar, los índices y variables topográficas y el contenido de arcilla no se correlacionaron con el IS (figura 2).
Figura 2: Coeficientes de correlación para las variables biofísicas y de rodal empleando el logaritmo natural del IS como variable dependiente.
Predicción del IS
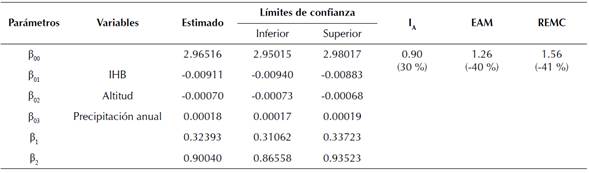
Los coeficientes estimados y estadísticos de ajuste se presentan en la tabla 4. El espaciamiento relativo dado por el IHB fue la variable que presentó el mayor aporte al modelo con el 56 % de la variación total del IS; mientras que la altitud y la precipitación anual tan solo explican el 9 y 4 %, respectivamente. Las tres variables en conjunto explican hasta un 70 % la variación del IS. De acuerdo con los valores del factor de inflación de varianza (VIF), la multicolinealidad se encuentra dentro de límites aceptables. Así mismo, una prueba F mostró que los coeficientes del modelo fueron altamente significativos (p < 0.0010). La estructura matemática final del modelo de IS se muestra a continuación (ecuación 9):

donde IS es el índice de sitio; IHB es el índice de espaciamiento relativo del rodal; Alt es la altitud; y Ppt es la precipitación media anual para el sitio donde está localizado el rodal.
Valores entre paréntesis corresponden al R2 parcial. *** nivel de significancia con P <0.0010. VIF: valor de inflación de varianza.
Tabla 4: Coeficientes estimados y estadísticos de bondad de ajuste para el modelo de IS

Representación espacial del IS
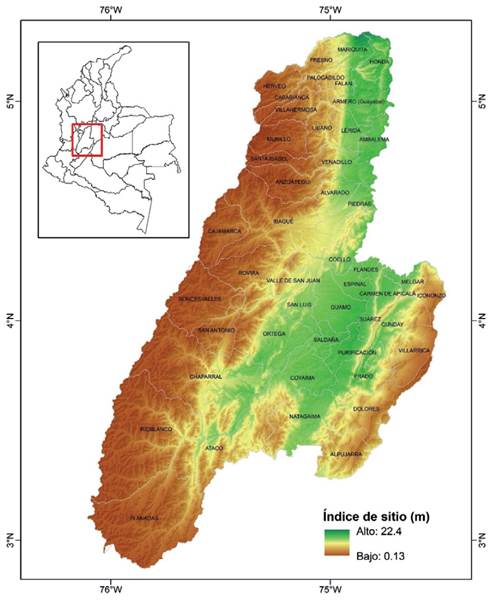
La ecuación 9 fue empleada para obtener un mapa ráster de IS para el departamento del Tolima (Colombia) utilizando un valor de IHB de 20 %, así como el modelo digital de elevación y el mapa ráster de precipitación media anual. La figura 3 muestra la variabilidad espacial del IS de G. arborea para el departamento del Tolima. Las zonas del departamento con índices de sitio mayores se presentan en el valle del río Magdalena. Considerando un IS mayor o igual a 16 m para asegurar un adecuado desempeño de las plantaciones forestales, el área disponible en el departamento para el establecimiento de plantaciones de G. arborea es de 253 549.4 ha. La aplicación del modelo desarrollado permitió identificar las áreas geográficas más adecuadas para establecer plantaciones de G. arborea.
Figura 3: Variabilidad espacial del IS predicha para G. arborea en el departamento del Tolima empleando la ecuación 9.
Modelo de H con variables biofísicas y de rodal
La inclusión de variables biofísicas y de rodal en el modelo base de H seleccionado permitió obtener estimaciones más precisas, con un IA de 0.90 (30 % ganancia), un EAM de 1.26 m (-40 % reducción) y un REMC de 1.56 m (-41 % de reducción) (tabla 5). A su vez, el respectivo modelo de IS presentó un IA de 0.69, un EAM de 1.79 m y un REMC de 2.49 m. El modelo final (ecuación 10) de H incluyendo variables biofísicas y de rodal fue:

donde H es la altura dominante; IS es el índice de sitio; A es la edad y A0 es la edad base (A0 = 10 años); IHB es el índice de espaciamiento relativo del rodal; Alt es la altitud; y Ppt es la precipitación media anual para el sitio donde está localizado el rodal.
El valor entre paréntesis corresponde al porcentaje de ganancia en la precisión en comparación con el modelo base sin covariables.
Tabla 5: Coeficientes estimados y bondad de predicción para el modelo de altura dominante de Chapman-Richards ajustado con variables biofísicas y de rodal
DISCUSIÓN
El modelo de Chapman-Richards presentó estadísticos de ajuste y validación satisfactorios para predecir el crecimiento en H e índices de sitio para plantaciones de G. arborea. Esta ecuación ha sido empleada previamente en otros estudios dada su flexibilidad y alta capacidad para describir adecuadamente los procesos biológicos que subyacen al crecimiento del árbol (Elli et al., 2017; Castillo et al., 2018). El modelo de Chapman-Richards posee las características típicas de un modelo de crecimiento biológico ya que: comienza en el punto cero; presenta crecimiento acelerado a edades juveniles; presenta un punto de inflexión donde el crecimiento se desacelera; e incluye una asíntota que refleja el valor máximo que puede alcanzar el organismo (Scolforo et al., 2013).
La relación significativa encontrada mediante correlación entre el IS y la densidad del rodal (representada por el índice de espaciamiento relativo), contradice el supuesto de que la H es independiente de la competencia y poco influenciada por la densidad (Bravo-Oviedo et al., 2008). Estudios previos expresan la posibilidad de obtener distintos valores de IS, al evaluarse parcelas con igual potencial productivo, utilizando una misma especie y durante el mismo período de tiempo, pero con diferentes densidades de plantación inicial (MacFarlane et al., 2000). La influencia de la densidad en la H de los rodales aumenta en magnitud para edades jóvenes e intermedias (Meredieu et al., 2003). El efecto de la densidad del rodal en el crecimiento en H durante las primeras etapas de desarrollo ha sido asociado a respuestas fisiológicas que se dan ya sea por subutilización del sitio o por intensa competencia (Newton, 2015a). Los datos utilizados en este estudio abarcan un amplio rango de espaciamientos, edades y sitios, por lo cual se considera que la relación entre el IS y la densidad se expresa de manera natural y podría ser inherente a la especie, relacionada con aspectos ecológicos ligados a la competencia intraespecífica.
Los efectos del espaciamiento también se han evidenciado en la optimización de los recursos. Erkan y Aydin (2016) encontraron una disminución del crecimiento en espaciamientos más amplios en los primeros años, la cual relacionaron con la pérdida de agua debido a la evaporación en los días en que aumentó la temperatura. El crecimiento de G. arborea suele ser bastante rápido en sus primeros años y, puesto que su edad de rotación es corta (12 a 14 años) (Rojas et al., 2004), los efectos de la densidad en la H pueden llegar a ser más notorios. Zhao et al. (2016) resaltan la posibilidad de optimizar las prescripciones silvícolas para sitios específicos si se cambia la intensidad de la silvicultura en función de la calidad del sitio. Los rodales en sitios más productivos pueden alcanzar niveles asintóticos más altos de ocupación relativa del sitio que los rodales en otros menos productivos (Newton, 2015b). Para plantaciones de P. radiata en Galicia un IHB de 16 % resultó ser un límite superior favorable para mantener un adecuado entrecruzamiento de copas, pues evita la mortalidad dependiente de la densidad (Rodríguez et al., 2002).
La altitud presentó una correlación negativa significativa con el IS. Socha (2008) obtuvo el mismo comportamiento para esta variable, siendo el factor de mayor influencia en la variación del IS para Picea abies L. (R2 de 0.61). Obregón (2006) reporta que la productividad de G. arborea está estrechamente relacionada con la altitud, la cual afecta variables climáticas como la temperatura, precipitación, humedad relativa y radiación solar.
En el bosque seco tropical la productividad depende de la cantidad disponible de agua y de qué tan eficiente es el organismo en el uso de esta (Yepes y Buckeridge, 2011). Los resultados señalan que la precipitación anual (cantidad disponible de agua) tiene un impacto positivo en el crecimiento de G. arborea. En plantaciones de tres años de edad, establecidas en el norte y suroccidente de Colombia, las parcelas más productivas fueron aquellas ubicadas en sitios bien drenados que recibieron entre 1000 y 1300 mm de precipitación por año (Urrego, 2004).
Debido a que la evaporación y evapotranspiración potencial están asociadas a la pérdida de agua, es lógico esperar la relación negativa con IS determinada en el presente estudio. Para rodales de Quercus suber L., empleando la evaporación media mensual y variables edáficas en la predicción del IS, se evidenció que cuando la evaporación aumenta la limitación del agua disponible para los árboles causa una disminución en la productividad del sitio (Paulo et al., 2015). El cambio en la disponibilidad de agua por descenso del 10 % en la precipitación o por un incremento del 6 % en la evapotranspiración potencial durante la vida útil de rodales de Pseudotsuga menziesii Mirb. resultó en una reducción en el volumen del rodal de hasta 80 m3.ha-1; lo que representa del 10 al 30 % de volumen comercializable (Spittlehouse, 2003).
La alta productividad de plantaciones con árboles de rápido crecimiento acarrea elevados niveles de uso del agua, por lo que las estrategias fisiológicas de la planta deberán condicionarse a los cambios ambientales. Ello con el fin de reducir la pérdida de agua por transpiración, sobre todo en temporadas secas en las cuales la disponibilidad hídrica constituye la principal limitante para la producción, sobre todo en el bosque seco tropical (Rojas et al., 2012; Battie-Laclau et al., 2016). Aunque la temperatura (media, mínima y máxima) resultó no ser significativa en el crecimiento de G. arborea, se reconoce que esta variable afecta la productividad pues regula e influye en varios procesos fisiológicos que se dan en la planta (Franklin y Wigge, 2013).
Estudios realizados por Vallejos (1996) reportan que G. arborea se desarrolla adecuadamente en sitios con pendientes menores al 20 %. De manera similar, Vanclay et al. (2008) ajustaron un modelo para predecir el IS de G. arborea en Filipinas a partir de la pendiente y la profundidad del suelo como variables predictoras de la productividad potencial del sitio. No obstante, en el presente estudio el IS no se correlacionó significativamente con la exposición ni con la pendiente. Tampoco las variables topográficas IPT y IHT se relacionaron significativamente con el IS. En este sentido, Bjelanovic et al. (2018) y Miyamoto et al. (2018) reportan que estos factores topográficos presentan una asociación significativa con el IS de Populus tremuloides Michx., Pinus contorta Douglas ex Loudon, Picea glauca Moench y Castanopsis sieboldii (Makino) Hatus. En el presente estudio se encontró una correlación positiva entre el IS y la latitud. Lo que demuestra que los sitios ubicados a mayor latitud, los cuales corresponden a la región del Caribe colombiano, presentan una mayor productividad.
La baja correlación presentada con el contenido de arcilla concuerda con lo referido por Rojas et al. (2004), en el sentido de que suelos con altos contenidos de arcilla resultan ser limitantes para el desarrollo de G. arborea. De acuerdo con Henri (2001) y Urrego (2004), esta especie se desarrolla mejor en suelos con texturas francas o franco arcillosas.
Recientemente se han desarrollado diversas ecuaciones dinámicas de IS capaces de predecir variaciones en la productividad forestal en diferentes escenarios de cambio climático. La inclusión de variables biofísicas en los modelos permite comparar las variaciones en el patrón de crecimiento entre diferentes sitios con diferentes condiciones climáticas o comparar el patrón de crecimiento del mismo en diferentes condiciones climáticas futuras (Bravo-Oviedo et al., 2010; Scolforo et al., 2013; Sharma y Parton, 2018; 2019; Zhou et al., 2019). En este estudio la inclusión de variables biofísicas y de rodal permitió mejorar las predicciones de la H, con aumentos de 30 % en índice de ajuste y disminuciones de 40 y 41 % en error absoluto promedio y error medio cuadrático, respectivamente. Así mismo, el ajuste de un modelo de IS a partir de variables biofísicas y de rodal permite la estimación de la productividad en áreas sin historia previa de plantaciones. El modelo desarrollado explicó hasta un 70 % la varianza total observada en el IS en 160 rodales de G. arborea distribuidos en el país.
El modelo de IS desarrollado es útil para modelar y describir el potencial productivo de la especie y permite la identificación de las áreas geográficas más adecuadas para establecer plantaciones de G. arborea (figura 3). Se identificó en una aplicación práctica del modelo zonas óptimas para el establecimiento de nuevas plantaciones en el departamento del Tolima, localizadas principalmente en los valles interandinos del río Magdalena. En la aplicación del modelo ajustado de IS el valor utilizado del IHB fue 20 %, el cual fue seleccionado por ser un valor en el que los árboles están en competencia sin que se vea comprometida la estabilidad del rodal. Los resultados obtenidos permitirán evaluar con mayor certeza proyectos de reforestación comercial, por lo que se podrá obtener mayor precisión en las estimaciones de H de los rodales. Una ventaja de los modelos desarrollados es su sencillez ya que la estimación de la productividad de un sitio requiere de información que puede conseguirse fácilmente mediante mapas topográficos o series climáticas.
CONCLUSIONES
El modelo de Chapman-Richards, en su modalidad de curvas anamórficas, representa de forma adecuada el crecimiento en H e IS para plantaciones de G. arborea establecidas en las regiones Andina, Caribe y Pacífica de Colombia. El IS se pudo predecir en función del nivel de ocupación en el rodal vía el espaciamiento relativo, la altitud y la precipitación anual. Se determinó la sensibilidad que tiene la productividad de esta especie al manejo silvicultural y las variables biofísicas particulares de cada sitio. El modelo desarrollado, el cual emplea correlación y regresión lineal múltiple, permite estimar el IS en áreas sin historia previa de plantaciones forestales. Lo anterior proporciona información útil para lograr una gestión forestal adecuada. La incorporación del índice de espaciamiento relativo, altitud y precipitación anual dentro del modelo de H permitió reducir el sesgo y error asociado a la estimación de H.
Acknowledgements
AGRADECIMIENTOS
Los autores agradecen a la Oficina de Investigación y Desarrollo Científico de la Universidad del Tolima el apoyo financiero concedido para desarrollar la investigación a través del proyecto n.° 340130516 y la convocatoria n.° 001 del 2019 para jóvenes investigadores. Los autores también agradecen el apoyo ofrecido por el grupo de investigación Madera & Bosques de la Universidad del Tolima.
REFERENCIAS
Licencia
Derechos de autor 2021 Colombia forestal

Esta obra está bajo una licencia internacional Creative Commons Atribución-CompartirIgual 4.0.
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).